继续卷积的讨论

浑浊度(Turbidity)研究是关于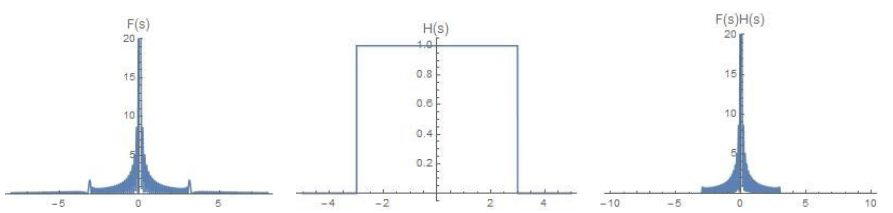测量水的清澈度的研究。大致方法是把光传感器放置到深水区域，然后测量光线的昏暗程度，测量出来的值将随时间变化。 (由于没有真实数据，下面用mathematica比较粗糙地模拟水域的浑浊度数据)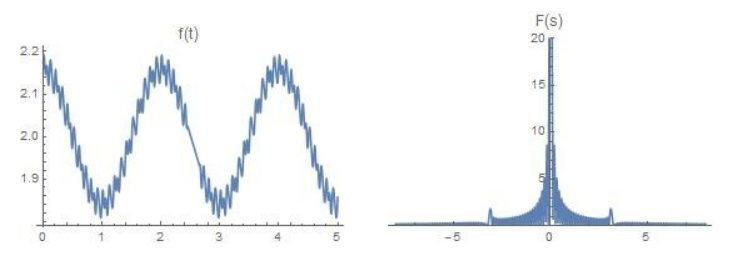

能看到信号主要集中在低频，我们需要把毛刺去除，也就是把高频去除，在频域进行低通滤波(Low Pass Filtering)。高频项是导致毛刺的原因，这和傅里叶级数的情况一样，高次谐波导致信号的快速振荡。

滤波后的波形如下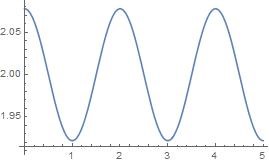

频域运算：\(\pi_{2 \nu_{c}}(s) F(s)  \)；时域运算为卷积\( 2 \nu_{c} \operatorname{sinc}\left(2 \nu_{c} t\right) * f(t) \)。根据时域卷积公式\( \mathcal{F}(g * f)=(\mathcal{F} g)(\mathcal{F} f) \)，所以\( 2 \nu_{c} \operatorname{sinc}\left(2 \nu_{c} t\right) * f(t) \)的傅里叶变换为\(\pi_{2 \nu_{c}}(s) F(s)  \)。注意\(  \pi_{2 \nu_{c}}(s)\)表示长方形的波，\( \nu_{c} \)表示截止频率。

注：
1.  前面我们已经知道\(\mathcal{F} \operatorname{sinc}=\mathcal{F} \mathcal{F} \pi=\pi^{-}=\pi  \)，即\(\pi\)函数的傅里叶变换是\(  \operatorname{sinc}\)函数，而\(  \operatorname{sinc}\)函数的傅里叶变换又回到\(\pi\)函数，即\(\pi\)函数和\(  \operatorname{sinc}\)函数同时是对方的傅里叶变换和傅里叶逆变换。
2. 因为\( \pi_{2 \nu_{c}} (s)\)的傅里叶变换是\( 2 \nu_{c} \operatorname{sinc}\left(2 \nu_{c} t\right) \)，所以\( \pi_{2 \nu_{c}} (s)\)的傅里叶逆变换是\( 2 \nu_{c} \operatorname{sinc}\left(2 \nu_{c} t\right) \)，即\( 2 \nu_{c} \operatorname{sinc}\left(2 \nu_{c} t\right) \)傅里叶变换得到\( \pi_{2 \nu_{c}} (s)\)。
3. 因为\(  \pi\)的傅里叶变换是\(  \operatorname{sinc}\)，根据尺度变化对应关系\(  f(a t) \leftrightarrow \displaystyle\frac{1}{|a|} F\left(\frac{s}{a}\right)\)，所以\(  \pi_{2 \nu_{c}} (s)\)的傅里叶变换是\( 2 \nu_{c} \operatorname{sinc}\left(2 \nu_{c} t\right) \)。这里\( f(a t) \leftrightarrow \displaystyle\frac{1}{|a|} F\left(\frac{s}{a}\right) \)中的\(  t\)和\(  s\)交换了，\( a = \displaystyle\frac { 1 }{  2 \nu_{c}}  \)

注：滤波的时候，选择留下什么频率范围的波有讲究，一方面如果选择的范围太窄(非常低频的波)，可能丢失一部分有价值的信号，另一方面，如果选择的范围太宽(保留太多的噪音相)，处理后的信号就不够平滑，噪音多。另外提一句，matlab中去几个连续数据的平均值也是一种去掉噪音的手段。

滤波概念

滤波(Filtering)通常等同于卷积，滤波是由滤波器实现的。 滤波器(Filter)是一个输入可变的函数(信号)与一个固定的函数(信号)进行卷积运算的系统。这个固定的信号叫做脉冲响应(impulse response)。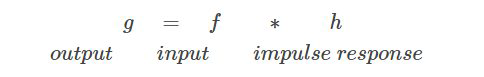卷积是在时域的表示方法，一般来说，频域的运算会比时域简单许多，因为频域只需执行相乘运算。$$G(s)=F(s) H(s)$$ \(  H(s)\)被称为传递函数(transfer function)，在设计滤波器时通常是设计合适的传递函数\(  H(s)\)。

下面是比较常用的滤波器。

低通滤波器(low pass filter)，常用于图像压缩。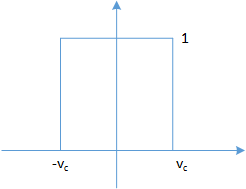

高通滤波器(high pass filter)，常用于边缘检测(edge detection)，边缘处变化非常快。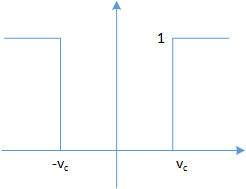

带通滤波器(band pass filter)

低通滤波器用于滤波，但是高通滤波器就不是用于滤波(存疑)。两者之间在数学上的区别是，低通滤波器是与一个函数进行卷积， 高通滤波器与分布函数或者说脉冲函数进行卷积(这不是一种滤波运算)。

卷积的含义

教授认为只需要从频域理解为函数的相乘即可，而在时域上不需要去具象化卷积。(I think it is equally idiotic to try to visualize convolution. I think the way to visualize convolution, if there is a way, is to think in terms of multiplying in the frequency domain.)不要去想像你想象不出来的东西，浪费时间。

卷积在很多方面都有应用，并不局限于单一解释，找单一解释就是自讨苦吃。在很多情况中，卷积应用于滤波或者求平均值。卷积可以继承两个函数优良的基因。

要求两个函数的卷积，其实就是先将二者分别进行傅里叶变换(转换到频域空间)，然后两个频域函数直接相乘，将相乘的结果进行逆变换即可得到卷积的结果。

卷积的性质

一般来说\( f * g \)通常比单独的\(  f\)和\(g \)更加平滑。比如：矩形函数是不连续的，但是两个矩形函数的卷积是三角函数，是连续的$$\mathcal{F}(\Pi * \Pi)=(\mathcal{F} \Pi)(\mathcal{F} \Pi)=\operatorname{sinc}^{2}=\mathcal{F} \Lambda$$矩形函数是不连续的，而三角波函数是连续的，在矩形的跳变处取平均。

如果\(  f\)可微，\(  g\)不可微，那么二者的卷积可微(继承了父母基因中的优秀的地方)，这一点可以从存钱模型想象出来$$(f *g)^{\prime}=f^{\prime}* g$$

傅里叶导数定理

微分运算变为乘法运算，对原函数进行微分后，它的傅里叶变换等于其原函数的傅里叶变换乘以\(  2 \pi i s\)(感觉好像就是对基底进行求导，反而投影大小没有变化，变化的来源来自基底的求导)$$\mathcal{F}\left(f^{\prime}\right)(s)=2 \pi i s(\mathcal{F} f)(s)$$证明如下：$$f(t)=\int_{-\infty}^{\infty} F(s) e^{2 \pi i s t} d s$$求微分$$\begin{aligned}
\frac{\partial f}{\partial t} &=\int_{-\infty}^{\infty} F(s)\left(2 \pi i s e^{2 \pi i s t}\right) d s \\
&=\int_{-\infty}^{\infty}(2 \pi i s F(s)) e^{2 \pi i s t} d s
\end{aligned}$$于是$$f^{\prime} \leftrightarrow 2 \pi i s F(s)$$推广开来有$$\mathcal{F}\left(f^{n}\right)(s)=(2 \pi i s)^{n}(\mathcal{F} f)(s)$$

无限长柱上的热方程(不无穷长就没法傅里叶变换)

\(U(x, t)  \)表示时间\( t \)位置\(x  \)的温度

初始条件\(  U(x, 0)=f(x)\)，热方程\(  U_{t}=\displaystyle\frac{1}{2} U_{x x}\)。

对热方程左边进行傅里叶变换$$\begin{aligned} \mathcal{F}\left(U_{t}\right) &=\int_{-\infty}^{\infty} e^{-2 \pi i s x} \frac{\partial}{\partial t} U(x, t) d x \\ &=\frac{\partial}{\partial t} \int_{-\infty}^{\infty} e^{-2 \pi i s x} U(x, t) d x \\ &=\frac{\partial}{\partial t} U(s, t) \end{aligned}$$右边进行傅里叶变换$$\mathcal{F}\left(\frac{1}{2} U_{x x}\right)=\frac{1}{2}(2 \pi i s)^{2} U(s, t)=-2 \pi^{2} s^{2} U(s, t)$$两边再次相等$$\frac{\partial}{\partial t} U(s, t)=-2 \pi^{2} s^{2} U(s, t)$$求偏微分方程$$U(s, t)=U(s, 0) e^{-2 \pi^{2} s^{2} t}$$而$$U(s, 0)=\int_{-\infty}^{\infty} U(x, 0) e^{-2 \pi i s x} d x=\int_{-\infty}^{\infty} f(x) e^{-2 \pi i s x} d x=F(s)$$因此$$U(s, t)=F(s) e^{-2 \pi^{2} s^{2} t}$$转换为卷积的形式$$\begin{array}{c} e^{-2 p i^{2} s^{2} t}=\mathcal{F}\left(\frac{1}{\sqrt{2 \pi t}} e^{\frac{x^{2}}{2 t}}\right) \\ U(s, t)=F(s) e^{-2 \pi^{2} s^{2} t} \\ =(\mathcal{F} f)\left(\mathcal{F}\left(\frac{1}{\sqrt{2 \pi t}} e^{\frac{x^{2}}{2 t}}\right)\right) \\ =\mathcal{F}\left(f * \frac{1}{\sqrt{2 \pi t}} e^{\frac{x^{2}}{2 t}}\right) \\ U(x, t)=f(x) * \displaystyle\frac{1}{\sqrt{2 \pi t}} e^{-\frac{x^{2}}{2 t}} \end{array}$$注意：当时间无穷大的时候，温度也都是全为零(存疑)。