[mathjax]
平面中的二重积分和线积分
二重积分
定义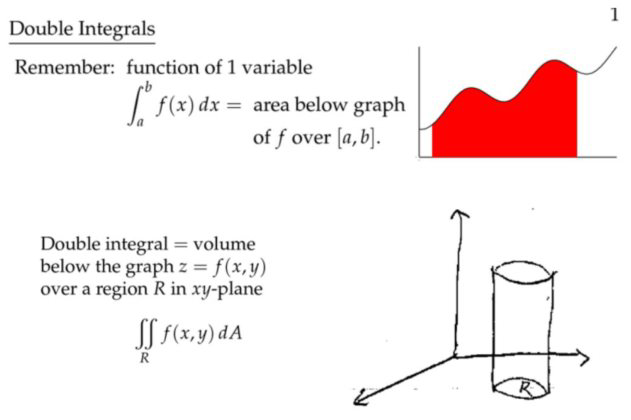

例子



交换积分顺序

注:\( \displaystyle\int_{0}^{1} \displaystyle\int_{x}^{\sqrt{x}} \frac{e^{y}}{y} d y d x \),图中\( dy d x\)写反了。先对\(y \)积分不好积,因为很难找到\(\displaystyle \frac{e^{y}}{y} \)的原函数。变换积分次序之后,立马变得简单了。(好像下面的计算有点问题)$$\begin{array}{l} \text { Inner: }\left[\frac{e^{y}}{y} x\right]_{x=y^{2}}^{y}=e^{y}-y e^{y} \quad\left(-y e^{y}\right)^{\prime}=-e^{y}-y e^{y} \\ \text { Outer: } \int_{0}^{1} e^{y}-y d y=\left[-y e^{y}+2 e^{y}\right]_{0}^{1}=e-2 \end{array}$$
极坐标二重积分

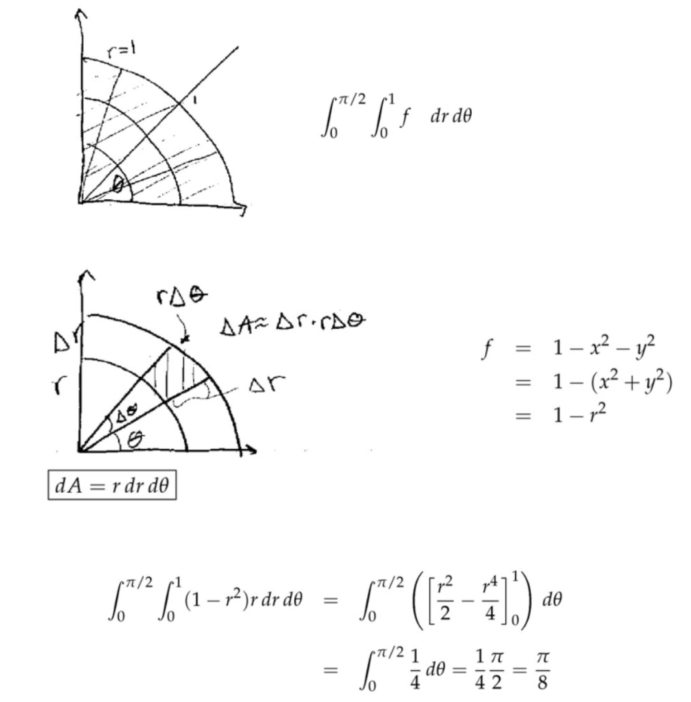 应用:质量和平均值
应用:质量和平均值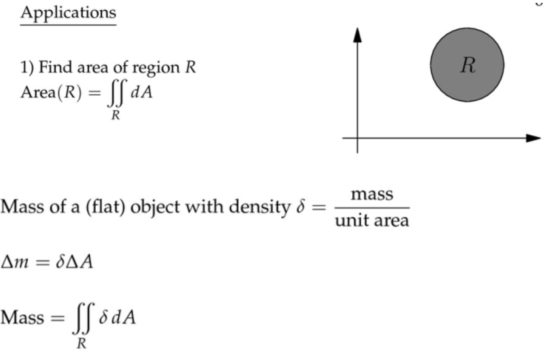
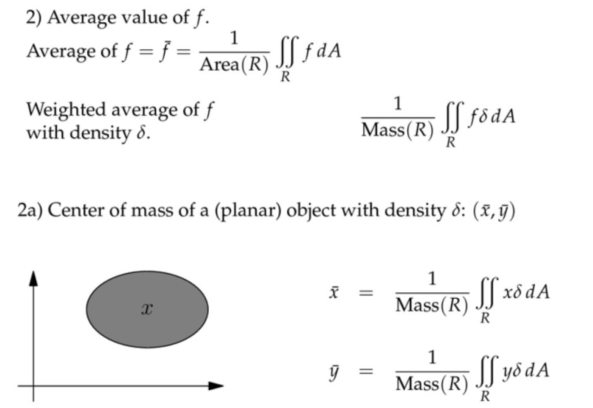
应用:转动惯量
注:translation motion平动。动能也分为平动动能和转动动能,前者为\(\displaystyle\frac{1}{2} m v^{2} \),后者为\(\displaystyle\frac{1}{2} I \omega^{2} \),其中转动惯量\( I= m r^{2} \)。
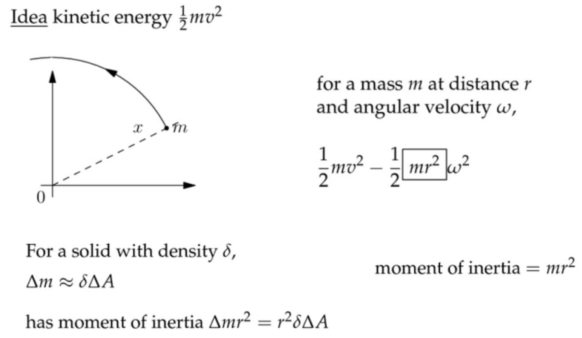

 注:在边缘转动的转动惯量是在围绕中心旋转的转动惯量的三倍。
注:在边缘转动的转动惯量是在围绕中心旋转的转动惯量的三倍。
变量替换/雅各比矩阵(Change of Variables)

注:这里相当于进行简单的线性变换(伸缩变换),两个坐标轴变换之后仍然是正交的,线性变换矩阵是对角阵,不存在耦合。 注:这里的变换矩阵不是对角阵,变换后存在两个坐标轴存在耦合关系,变换后,坐标轴的垂直关系没了。
注:这里的变换矩阵不是对角阵,变换后存在两个坐标轴存在耦合关系,变换后,坐标轴的垂直关系没了。

 $$\begin{aligned} &\text { Jacobian } J=\frac{\partial(u, v)}{\partial(x, y)}=\left|\begin{array}{cc} u_{x} & u_{y} \\ v_{x} & v_{y} \end{array}\right|\\ &\text { Then } d u d v=|J| d x d y=\left|\frac{\partial(u, v)}{\partial(x, y)}\right| d x d y \end{aligned}$$注:
$$\begin{aligned} &\text { Jacobian } J=\frac{\partial(u, v)}{\partial(x, y)}=\left|\begin{array}{cc} u_{x} & u_{y} \\ v_{x} & v_{y} \end{array}\right|\\ &\text { Then } d u d v=|J| d x d y=\left|\frac{\partial(u, v)}{\partial(x, y)}\right| d x d y \end{aligned}$$注:
(1) 第二个转化写错了,正确的是\( \langle 0, \Delta y\rangle \leadsto\langle\Delta u, \Delta v\rangle \approx\left\langle u_{y} \Delta y, v_{y} \Delta y\right\rangle \);
(2) 平行四边形的面积为两条边向量的叉乘结果大小的绝对值。那么对原来的图形,就是去叉乘\( \langle\Delta x, 0\rangle \)和\( \langle 0, \Delta y\rangle \),我们先计算叉乘的方法都是放在三维空间中的,其实这里可以给向量多加一维,只是它们对应的值都为零,于是可以写成(最后一列代数余子式展开)$$\left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \Delta x & 0 & 0 \\ 0 & \Delta y & 0 \end{array}\right|=\mathbf{k}\left|\begin{array}{ccc} \Delta x & 0 \\ 0 & \Delta y \end{array}\right|$$而转化后,求面积就是叉乘向量\( \left\langle u_{x} \Delta x, v_{x} \Delta x\right\rangle \)和\(\left\langle u_{y} \Delta y, v_{y} \Delta y\right\rangle \),即$$\left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ u_{x} \Delta x & v_{x} \Delta x & 0 \\ u_{y} \Delta y & v_{y} \Delta y & 0 \end{array}\right|=\mathbf{k}\Delta x\Delta y\left|\begin{array}{ll} u_{x} & v_{x} \\ u_{y} & v_{y} \end{array}\right|$$注意这里的行列式\( \left|\begin{array}{ll} u_{x} & v_{x} \\ u_{y} & v_{y} \end{array}\right|\)写法和雅各比矩阵行列式\( \left|\begin{array}{ll} u_{x} & u_{y} \\ v_{x} & v_{y} \end{array}\right|\)的写法有点不同,但最后的值一样。
(3) 线性变换的矩阵,就是这里的而雅各比矩阵。注意最简单的情况是这个雅各比矩阵不随\( (x,y)\)而变化,那么其实就是将原来的微元矩形进行等长和宽的固定缩放,雅各比矩阵的行列式就是最终微元面积变化的比例系数。但是更一般的情况是,这个雅各比矩阵对不同\( (x,y)\)是不同的,即每个微元矩形长和宽缩放的情况是不同的;换句话说原图像中的向量,不是乘以一个固定的线性变换矩阵,而是一个随着向量终点位置变化的矩阵(随着原图像中坐标位置而变化)。
例子1:极坐标(Polar coordinates)
\(x=r\cos \theta\)和\(y=r\sin \theta\),其实和我们上面的例子是反过来的,这里是将\( r\)和\( \theta \)看作是原始变量,\(x\)和\(y\)是两个原始变量的函数。$$\frac{\partial(x, y)}{\partial(r, \theta)}=\left|\begin{array}{ll} x_{r} & x_{\theta} \\ y_{r} & y_{\theta} \end{array}\right|=\left|\begin{array}{rr} \cos \theta & -r \sin \theta \\ \sin \theta & r \cos \theta \end{array}\right|=r \cos ^{2} \theta+r \sin ^{2} \theta = r$$于是\(d x d y=|r| d r d \theta=rdrd \theta\),同样的一块区域,在\( (x, y)\)坐标系中的面积是在\( (u, v)\)坐标系的\(r \)倍,所以极坐标计算公式\(\displaystyle\iint_{D} f(x, y) d \sigma=\displaystyle\iint_{D^{\prime}} f(r \cos \theta, r \sin \theta) r d r d \theta\)右侧多了一个\( r\)。
Remark: \(\displaystyle\frac{\partial(u, v)}{\partial(x, y)} \cdot \displaystyle\frac{\partial(x, y)}{\partial(u, v)}=1\)
注:将函数从\((x,\, y) \)坐标系转化到\((u,\,v) \)坐标系是乘以\(\displaystyle\frac{\partial(u, v)}{\partial(x, y)} \)这个雅各比矩阵;而将\((u,\,v) \)变回\((x,\, y) \)是乘以原来的雅各比矩阵的逆矩阵,或者说\( \displaystyle\frac{\partial(x, y)}{\partial(u, v)} \)。上面的等式其实也描述了这种雅各比矩阵的互逆关系。
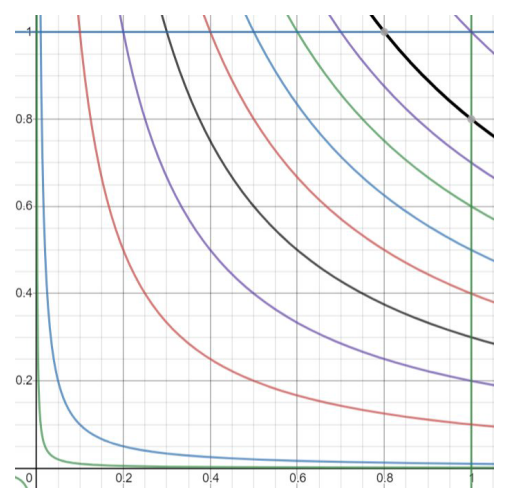 \(\displaystyle\frac { u }{ v} \)取值从非常接近\(0 \)到\( 1 \)的图像。原来我们进行二重积分求解,是沿着\( x\)轴方向或者\(y \)轴方向切一刀,求出面积,然后移动刀。那么切的时候,得到的肯定是一个底为直线的二维图形;不过在上图中,转化坐标后,切的每一刀就是图中的双曲线与正方形上边界和右侧边界的交线区域(\( v \)固定),然后沿着\(y=x \)对角线移动刀。这就解释了\(\displaystyle\int_{0}^{1} \displaystyle\int_{v}^{1} v d u d v \)(上图写错了,内积分上限应该是\( 1 \))中的积分区间。对于\( y=1\)的上边界,\( 1=\displaystyle\frac { u }{ v } \),上边界\( u=v\),下边界就是正方形右侧边界交点\( u=x=1 \),因此下边界就是\( u=1\)。
\(\displaystyle\frac { u }{ v} \)取值从非常接近\(0 \)到\( 1 \)的图像。原来我们进行二重积分求解,是沿着\( x\)轴方向或者\(y \)轴方向切一刀,求出面积,然后移动刀。那么切的时候,得到的肯定是一个底为直线的二维图形;不过在上图中,转化坐标后,切的每一刀就是图中的双曲线与正方形上边界和右侧边界的交线区域(\( v \)固定),然后沿着\(y=x \)对角线移动刀。这就解释了\(\displaystyle\int_{0}^{1} \displaystyle\int_{v}^{1} v d u d v \)(上图写错了,内积分上限应该是\( 1 \))中的积分区间。对于\( y=1\)的上边界,\( 1=\displaystyle\frac { u }{ v } \),上边界\( u=v\),下边界就是正方形右侧边界交点\( u=x=1 \),因此下边界就是\( u=1\)。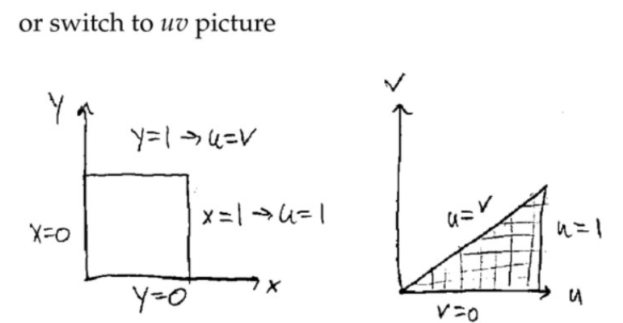 注:
注:
(1) \( d x d y=|r| d r d \theta \)中\( |r|\)表示的是雅各比矩阵的绝对值,即缩放比例系数,由于我们的积分区间中\( r\)非负数,所以可以把绝对值符号去掉。注意不要把行列式的符号和这里的绝对值符号搞混了;
(2) 极坐标变换中,缩放系数scaling factor不再是一个常数,而是一个变量。注意我们进行的\( u=3 x-2 y;\quad v=x+y\)变换,是一个纯线性变换,也就是用一个固定的矩阵对原坐标向量进行线性变换,那么得到的缩放系数就是一个确定的常数\(d u d v=5 d x d y \),这个常数就是矩阵的行列式大小的绝对值。
(3) 固定矩阵的线性变换,那么变换前是直线,变换后依然是直线,只是图形的长度和角度会发生变化。
向量场和线积分
向量场
重力场、引力场、电磁场、水流场都是向量场。

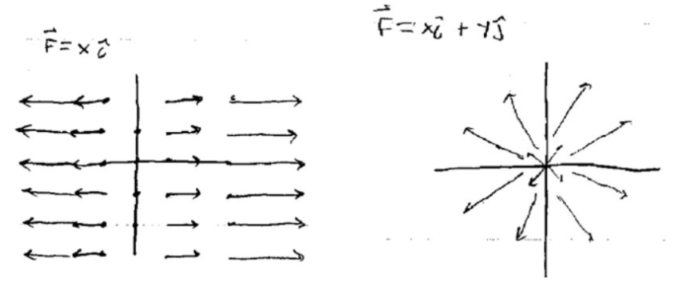 上面右侧的图视觉上可以很直观地看到流体的动态,很可能流体源就是原点,并且不断地喷出流体,然后以这样的形式流走。下面左侧的图,描述的是流体围绕着原点,匀速转动所形成的速度场。以单位角速度旋转,那么走完一圈需要的时间为\(2\pi \)。
上面右侧的图视觉上可以很直观地看到流体的动态,很可能流体源就是原点,并且不断地喷出流体,然后以这样的形式流走。下面左侧的图,描述的是流体围绕着原点,匀速转动所形成的速度场。以单位角速度旋转,那么走完一圈需要的时间为\(2\pi \)。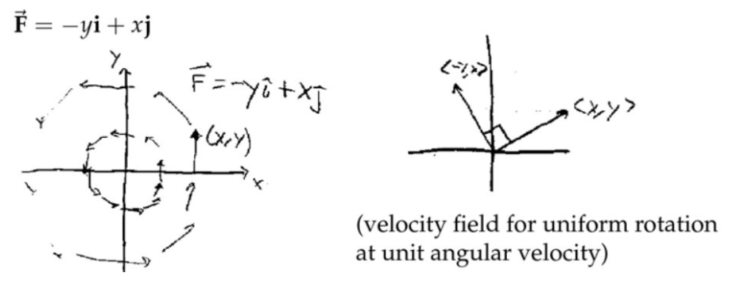 注:\( \overrightarrow{\mathbf{F}}=-y \mathbf{i}+x \mathbf{j} \)就是将\( \overrightarrow{\mathbf{F}}=x\mathbf{i}+y\mathbf{j} \)向量场每一点的向量都逆时针旋转\( 90\)度,整个向量场由纯发散的场变为旋转状的场。注意这种旋转操作就是将旋转矩阵\( \left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] \)(\( \theta=90 \))作用于原向量场\( \overrightarrow{\mathbf{F}}=x\mathbf{i}+y\mathbf{j} \)
注:\( \overrightarrow{\mathbf{F}}=-y \mathbf{i}+x \mathbf{j} \)就是将\( \overrightarrow{\mathbf{F}}=x\mathbf{i}+y\mathbf{j} \)向量场每一点的向量都逆时针旋转\( 90\)度,整个向量场由纯发散的场变为旋转状的场。注意这种旋转操作就是将旋转矩阵\( \left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] \)(\( \theta=90 \))作用于原向量场\( \overrightarrow{\mathbf{F}}=x\mathbf{i}+y\mathbf{j} \)
功和线积分
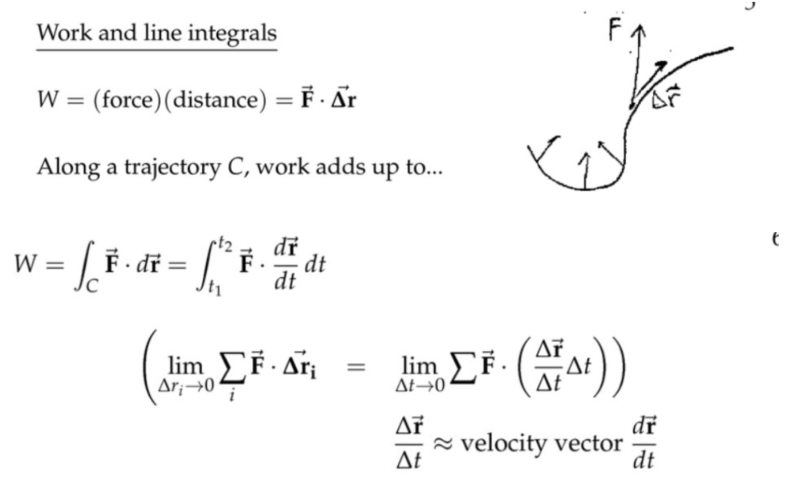

 注:
注:
(1) \( d \displaystyle\overrightarrow{\mathbf{r}}=\langle d x, d y\rangle \)这是不是严格意义上的向量,更准确地说是一种“记号”;
(2) 用最合理的方式引入参数;如果可以,直接以\( x\)作为参数,将含\( y\)的项目改写成\( x \)的;
(3) 外力做功与路径有关;
(4) 对于\(\displaystyle\int_{\mathrm{C}} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=\displaystyle\int_{\mathrm{C}} M d x+N d y\),里面的\(x \)和\( y \)是互相关联的(\( dx\)前面的系数\(M \)中可能也是\(y \)的函数,\( dy \)前面的系数\( N \)可能也是\(x \))的函数,类似“耦合”的概念,所以不能直接求出来,必须把\(x \)和\( y\)都变成同一个参数的表达式(即用参数方程表示曲线,这个唯一的参数可能是\( x \)也可能是\(y \)或者\( t \)),然后进行单变量求积分;
(5) 第一种方法是向量场的方法,第二种方法\( \displaystyle\int_{\mathrm{C}} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=\displaystyle\int_{\mathrm{C}} M d x+N d y\)实质上是微分运算;但是两个方法最终得到的表达式是一致的,结果也一样,殊途同归。这就跟求梯度和求导一样,二者标记方法不一样,但是内容是一样的。
几何方法
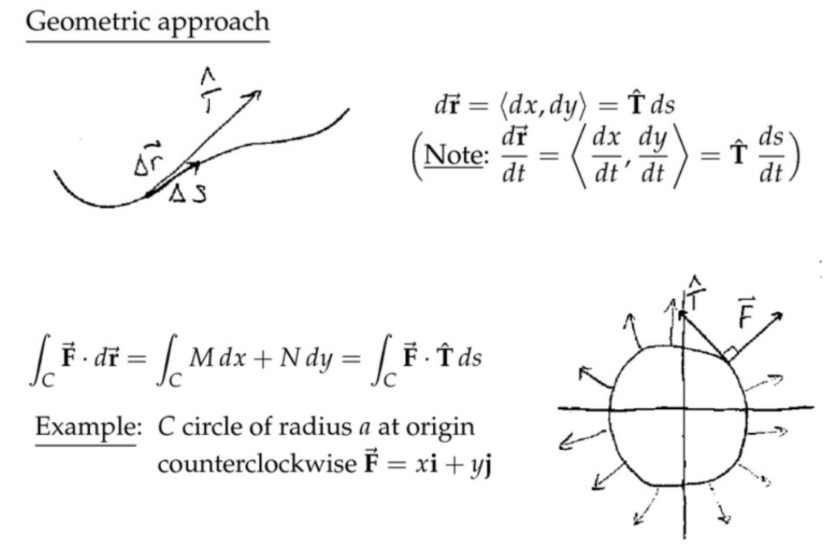
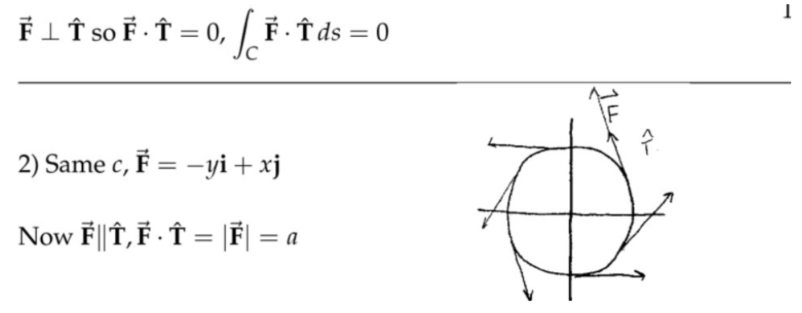
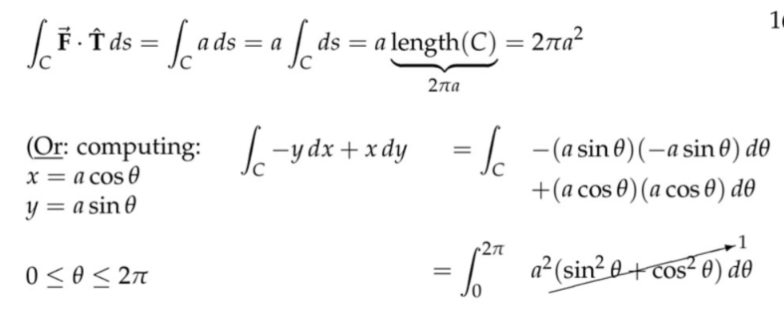 注:这里的集合方法是针对两种特殊的情况,第一种情况中质点的运动方向始终和向量场的方向垂直,所以质点和向量场之间不存在能量交换,在第二种情况中,质点的运动轨迹虽然是圆,但是向量场的方向始终和速度方法一致,其实就是等效在一维方向上用一个恒定而且和速度方向一致的力去推一个木块,或者说将这个圆周剪开铺在地上。
注:这里的集合方法是针对两种特殊的情况,第一种情况中质点的运动方向始终和向量场的方向垂直,所以质点和向量场之间不存在能量交换,在第二种情况中,质点的运动轨迹虽然是圆,但是向量场的方向始终和速度方法一致,其实就是等效在一维方向上用一个恒定而且和速度方向一致的力去推一个木块,或者说将这个圆周剪开铺在地上。
例子

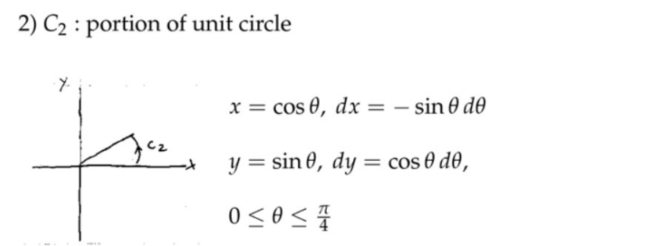
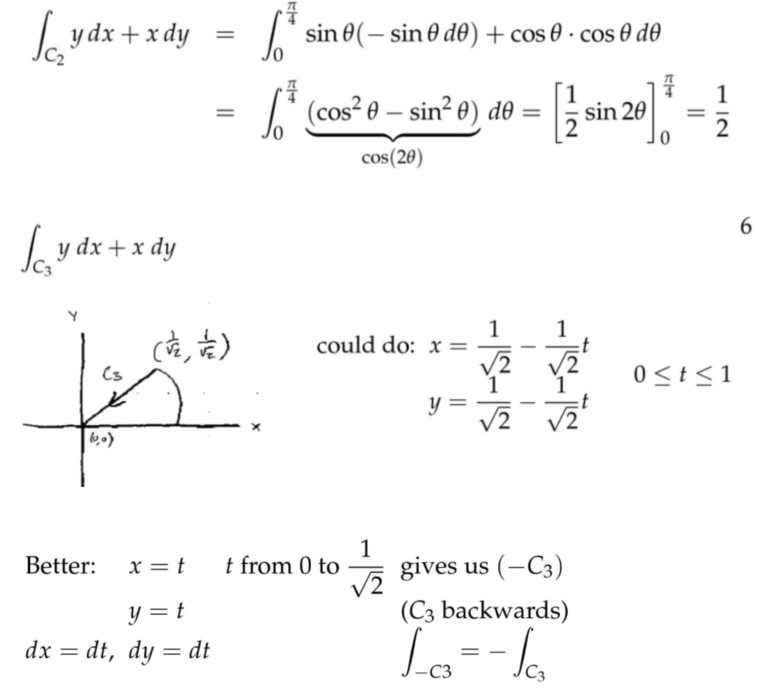
 注:将一个封闭的轨迹分成三段,分别对它们做功情况进行分析。在求解第三段的时候,可以采用小技巧简化参数方程,也就是想象成反向运动的过程,那么向量场对质点做的功就等于反向过程取负号。
注:将一个封闭的轨迹分成三段,分别对它们做功情况进行分析。在求解第三段的时候,可以采用小技巧简化参数方程,也就是想象成反向运动的过程,那么向量场对质点做的功就等于反向过程取负号。
线积分的基本定理(Fundamental Theorem for Line Integrals)
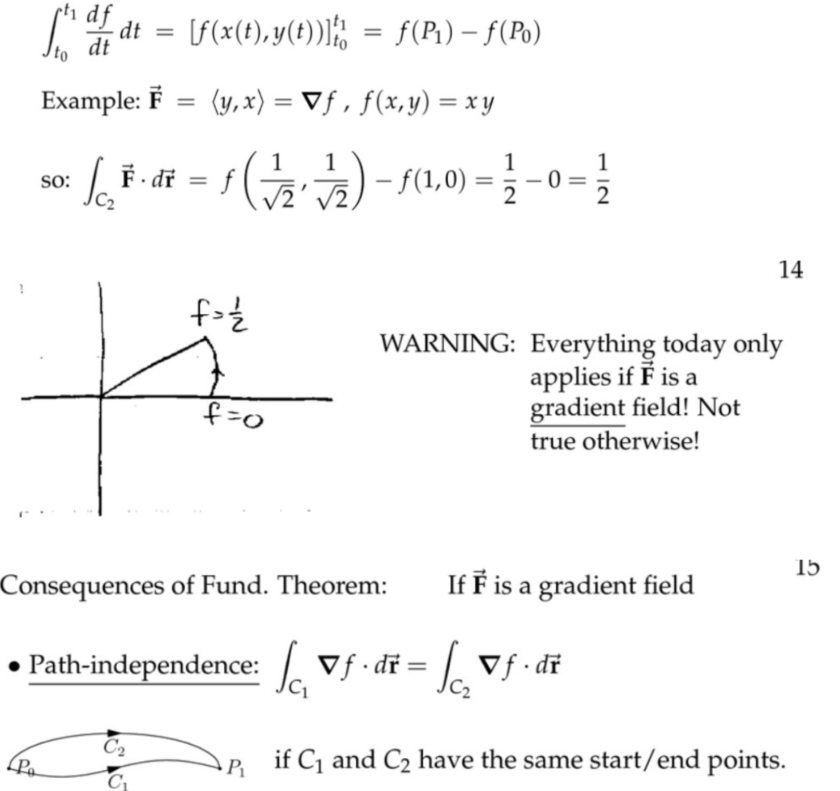
 注:如果对一个函数的梯度做线积分,就能得到原函数,但不是所有的向量场都是梯度,比如磁场就不是梯度。
注:如果对一个函数的梯度做线积分,就能得到原函数,但不是所有的向量场都是梯度,比如磁场就不是梯度。
 保守场,路径不依赖,精确微分(Conservative Fields, Path Independence, Exact Differentials)
保守场,路径不依赖,精确微分(Conservative Fields, Path Independence, Exact Differentials)
 注:力其实对应势场负的梯度,也就是物理学家的势能和数学家的势能相差一个负号(感觉这里翻译有点问题)。个人认为,差别在于数学家中势场的梯度方向是指向势场更大的地方,比如“从山底指向山顶”,但是物理学家眼中势场的梯度方向正好相反。
注:力其实对应势场负的梯度,也就是物理学家的势能和数学家的势能相差一个负号(感觉这里翻译有点问题)。个人认为,差别在于数学家中势场的梯度方向是指向势场更大的地方,比如“从山底指向山顶”,但是物理学家眼中势场的梯度方向正好相反。
 注:守恒(保守)这个词来源于物理学,如果说能量守恒,就意味你不可能从力场里面无偿地得到能量。某个地方沿着闭合曲线所做的功不是零,就不可能建立起永恒的运动(第一类永动机),因为这些力没有提供任何能量。变压器、电源适配器等类似装置,它们都是从磁场里面得到能量,当然你必须有电源供应用以维持磁场,近乎无偿地得到能量。在重力场或者电场中就做不到了,不可能无偿地从场里面提取能量,我想这就是我们称之为保守(conservative)的原因。
注:守恒(保守)这个词来源于物理学,如果说能量守恒,就意味你不可能从力场里面无偿地得到能量。某个地方沿着闭合曲线所做的功不是零,就不可能建立起永恒的运动(第一类永动机),因为这些力没有提供任何能量。变压器、电源适配器等类似装置,它们都是从磁场里面得到能量,当然你必须有电源供应用以维持磁场,近乎无偿地得到能量。在重力场或者电场中就做不到了,不可能无偿地从场里面提取能量,我想这就是我们称之为保守(conservative)的原因。
注:“磁场的高斯定理:若在磁场中作任意闭合曲面,则穿过该闭合曲面的磁通量为零. 由磁场的高斯定理可知:磁场是无源场,磁感线是封闭的曲线,因此磁场力是非保守力. 由此可以联想到均匀增大的磁场产生的环形电场也为非保守场,静电场才是保守场. 因此,存在电势但不存在“磁势”.”
就是因为做功是“位移点乘力积分”,磁场力才不好使的,因为磁场力垂直于速度方向,这个点乘永远是零。
对于一个力矢量场,有积分与路径无关,这一点可以表述为场中任意环路积分为零,然而反之不亦然。比如磁场力,符合这一判据(积分虽然路径无关但是恒为零。。。),但是磁场力与速度相关,并不是一个常量的力矢量场,而是一个关于速度的函数,所以可以不算保守场。。。
对于保守场,我们还有力场可以写作位势的梯度,这一条磁场就实锤不满足了。
梯度场(Gradient Fields)
 注:对势函数的梯度场做路径积分,只需要知道终点和起点的势函数。
注:对势函数的梯度场做路径积分,只需要知道终点和起点的势函数。

注:对于势函数的梯度场,这里巧妙的利用了\( f_{x y}=f_{y x} \)关系,从而确定了向量场两个系数\( M \)和\(N \)应该满足的关系。 注:前面说的是势函数的向量场应该具有什么样的特点,这里说的是什么样的向量场是由势函数产生的。特别注意如果向量场有定义并且可微的区域不是整个平面的话(并且满足\( M_{y}=N_{x}\)的话),那么如果是一个封闭而且没有洞的区域,,那么是势函数产生的场,如果有洞,那么不是势函数产生的,即使满足\( M_{y}=N_{x} \),这一部分会在后面讨论。
注:前面说的是势函数的向量场应该具有什么样的特点,这里说的是什么样的向量场是由势函数产生的。特别注意如果向量场有定义并且可微的区域不是整个平面的话(并且满足\( M_{y}=N_{x}\)的话),那么如果是一个封闭而且没有洞的区域,,那么是势函数产生的场,如果有洞,那么不是势函数产生的,即使满足\( M_{y}=N_{x} \),这一部分会在后面讨论。
势函数(Potential Functions)
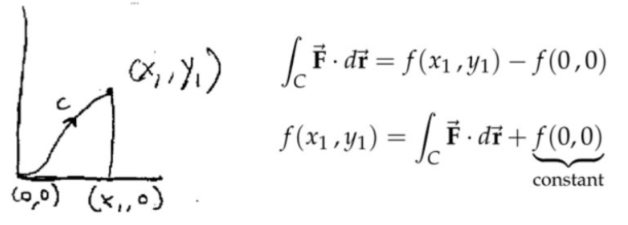 注:下面用两种方法求解梯度场对应的势函数(第二种方法更好)。注意千万不要先对\( f(x)\)积分,然后对\( f(y) \)积分,然后然两个积分值相等,从而确定势函数。
注:下面用两种方法求解梯度场对应的势函数(第二种方法更好)。注意千万不要先对\( f(x)\)积分,然后对\( f(y) \)积分,然后然两个积分值相等,从而确定势函数。
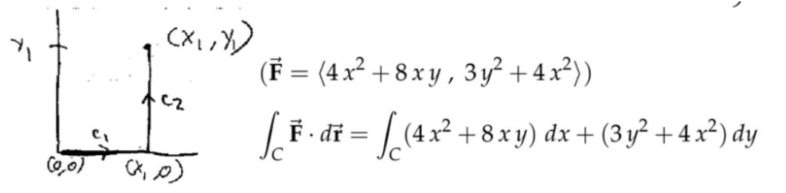

 注:记住上面的等价条件,如果向量场在平面内处处有定义,那么如下的内容等价:
注:记住上面的等价条件,如果向量场在平面内处处有定义,那么如下的内容等价:
(1) \(\overrightarrow{\mathbf{F}}=\langle M, N\rangle \)是一个梯度场;
(2) 处处都有\(N_{x}=M_{y} \)(整个平面有定义,或者单连通(无洞)区域有定义);
(3) \(\displaystyle\oint_{C} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=0\)闭合曲线的路径积分为零;
(4) 处处的旋度都为零;
(5) 向量场\( \overrightarrow{\mathbf{F}} \)是保守场。
旋度(Curl)
 注:旋度处处为零,等价于向量场为保守场(守恒场)。
注:旋度处处为零,等价于向量场为保守场(守恒场)。 注:上面第一个图这里没有旋涡(vortex)。旋度衡量的实际上是任意给定点处向量场的扭转程度有多大。第二个图旋度处处都为\( 2 \),说明的是每个点旋度是其角速度的两倍(对速度场而言),注意这里对于\( \overrightarrow{\mathbf{F}}=\langle-y, x\rangle\)向量场,每个点的矢量场(速度)的大小都是\( R \)即到原点的距离,圆周长为\( 2\pi R\),速度方向适中和矢量场方向一致,因此每旋转一整周所需要的时间为\( 2\pi\),所以角速度\( \omega =1 rad/s \),后面我们有详细证明角速度为\( \omega \)时,对应的旋度为\( 2\omega \);很多情况下,旋度是依赖位置变化的。天气预报的风速图中,高旋度的地方可能就是飓风或者龙卷风。对力场而言,旋度衡量的是每一点收到的扭矩(torque)大小。旋度的正负号对应的是旋转是“逆时针”还是“顺时针”。扭矩是力转动的对应量,类似于速度对应角速度,质量对应转动惯量。根据这个类比关系,力除以质量,会引起加速度,加速度是速度的导数;扭矩除以转动惯量,就是角速度的导数,就引出了角加速度。$$\begin{array}{l} F\Rightarrow \mathbf{M}=\mathbf{r} \times \mathbf{F}\\ m \Rightarrow I=m r^{2} \\ v\Rightarrow \omega \\ E_{\text {translational}}=\frac{1}{2} m v^{2} \Rightarrow E_{\text {rotation}}=\frac{1}{2} I \omega^{2}\\ a_{v}=\frac { F }{ m } \Rightarrow a_{w}=\frac {\mathbf{M} }{I } \\ p=mv \Rightarrow \mathbf{L}=\mathbf{r} \times \mathbf{p}=\mathbf{r} \times(m \mathbf{v})=\mathbf{r} \times(\boldsymbol{\omega} \times(m \mathbf{r}))=m r^{2} \boldsymbol{\omega}=I \boldsymbol{\omega}\\ E_{\text {translational}}=\frac {p^2 }{ 2m } \Rightarrow E_{\text {rotation}}=\frac { \mathbf{L}^2 }{ 2I } \end{array}$$
注:上面第一个图这里没有旋涡(vortex)。旋度衡量的实际上是任意给定点处向量场的扭转程度有多大。第二个图旋度处处都为\( 2 \),说明的是每个点旋度是其角速度的两倍(对速度场而言),注意这里对于\( \overrightarrow{\mathbf{F}}=\langle-y, x\rangle\)向量场,每个点的矢量场(速度)的大小都是\( R \)即到原点的距离,圆周长为\( 2\pi R\),速度方向适中和矢量场方向一致,因此每旋转一整周所需要的时间为\( 2\pi\),所以角速度\( \omega =1 rad/s \),后面我们有详细证明角速度为\( \omega \)时,对应的旋度为\( 2\omega \);很多情况下,旋度是依赖位置变化的。天气预报的风速图中,高旋度的地方可能就是飓风或者龙卷风。对力场而言,旋度衡量的是每一点收到的扭矩(torque)大小。旋度的正负号对应的是旋转是“逆时针”还是“顺时针”。扭矩是力转动的对应量,类似于速度对应角速度,质量对应转动惯量。根据这个类比关系,力除以质量,会引起加速度,加速度是速度的导数;扭矩除以转动惯量,就是角速度的导数,就引出了角加速度。$$\begin{array}{l} F\Rightarrow \mathbf{M}=\mathbf{r} \times \mathbf{F}\\ m \Rightarrow I=m r^{2} \\ v\Rightarrow \omega \\ E_{\text {translational}}=\frac{1}{2} m v^{2} \Rightarrow E_{\text {rotation}}=\frac{1}{2} I \omega^{2}\\ a_{v}=\frac { F }{ m } \Rightarrow a_{w}=\frac {\mathbf{M} }{I } \\ p=mv \Rightarrow \mathbf{L}=\mathbf{r} \times \mathbf{p}=\mathbf{r} \times(m \mathbf{v})=\mathbf{r} \times(\boldsymbol{\omega} \times(m \mathbf{r}))=m r^{2} \boldsymbol{\omega}=I \boldsymbol{\omega}\\ E_{\text {translational}}=\frac {p^2 }{ 2m } \Rightarrow E_{\text {rotation}}=\frac { \mathbf{L}^2 }{ 2I } \end{array}$$
格林公式
格林公式简介
 注:旋度是\(N_{x}-M_{y} \),而不是反过来的,因为这正好和我们做闭合曲线积分按“逆时针”路径对应,两种规定相互对应。如果旋度计算反过来,那么闭合曲线积分按照“顺时针”就行。
注:旋度是\(N_{x}-M_{y} \),而不是反过来的,因为这正好和我们做闭合曲线积分按“逆时针”路径对应,两种规定相互对应。如果旋度计算反过来,那么闭合曲线积分按照“顺时针”就行。

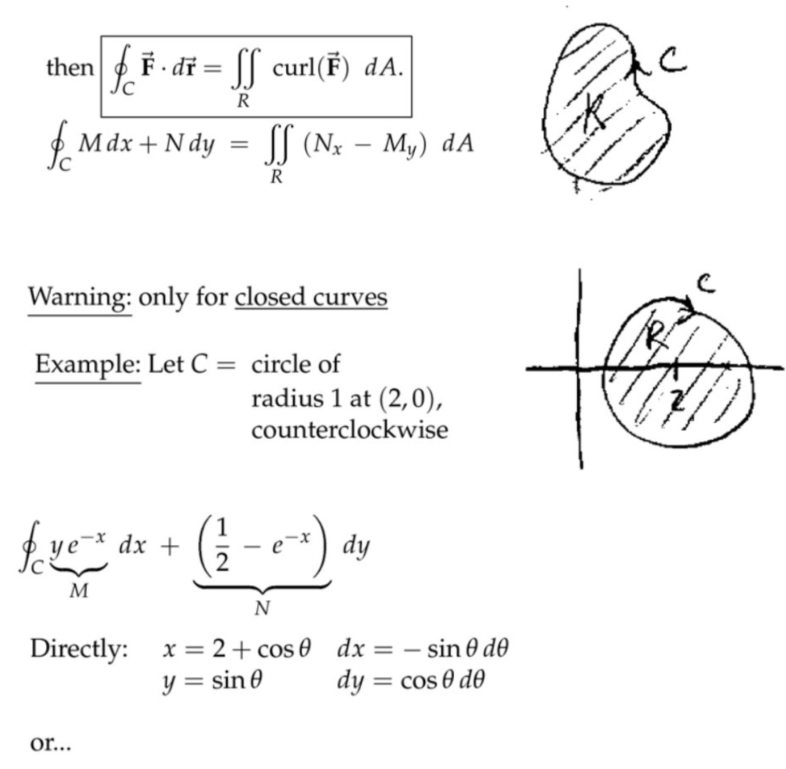 注:这里的\( N=\displaystyle\frac{1}{2}x^2-e^{-x}\),上面写错了。
注:这里的\( N=\displaystyle\frac{1}{2}x^2-e^{-x}\),上面写错了。

旋度等于零意味着保守场(Curl(F) = 0 Implies Conservative)
 注:静电场环路积分为零,因为静电场是保守力场/势函数场/旋度为零。变化的电场环路积分不为零。回忆法拉第电磁感应定律\( \nabla \times \mathbf{E}=-\displaystyle\frac{\partial \mathbf{B}}{\partial t}\)和\( \displaystyle\oint_{\mathrm{L}} \mathbf{E} \cdot \mathrm{d} \ell=-\displaystyle\frac{\mathrm{d} \Phi_{\mathrm{B}}}{\mathrm{d} t} \)。一方面我们可以理解为,变化的磁场产生感应电动势,但是另一方面,对于静电场,环路积分或者求旋度都为零,不会有磁通量变化。
注:静电场环路积分为零,因为静电场是保守力场/势函数场/旋度为零。变化的电场环路积分不为零。回忆法拉第电磁感应定律\( \nabla \times \mathbf{E}=-\displaystyle\frac{\partial \mathbf{B}}{\partial t}\)和\( \displaystyle\oint_{\mathrm{L}} \mathbf{E} \cdot \mathrm{d} \ell=-\displaystyle\frac{\mathrm{d} \Phi_{\mathrm{B}}}{\mathrm{d} t} \)。一方面我们可以理解为,变化的磁场产生感应电动势,但是另一方面,对于静电场,环路积分或者求旋度都为零,不会有磁通量变化。 注:上图的中心点处,向量场没有定义(类似有个洞),所以不可微分,旋度也就不存在,因此就不能对这个区域用格林公式。
注:上图的中心点处,向量场没有定义(类似有个洞),所以不可微分,旋度也就不存在,因此就不能对这个区域用格林公式。
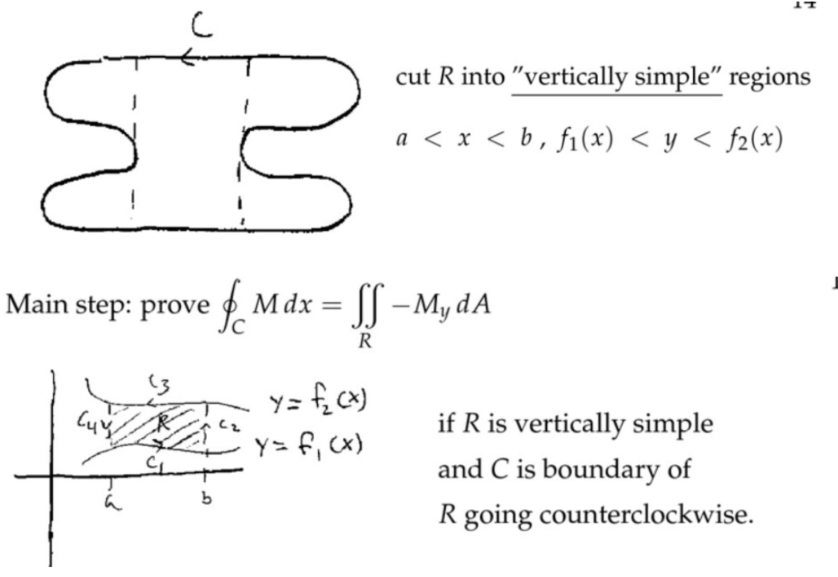
格林公式证明


Planimeter: Green's Theorem and Area

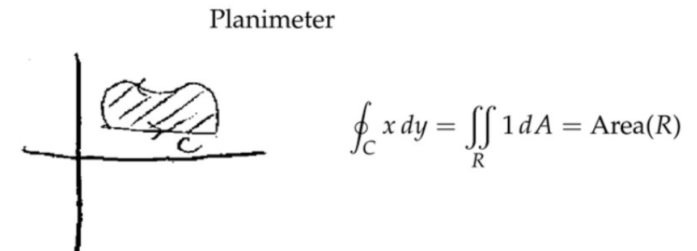 注:测面仪,能够测量出曲面的面积,以前没有计算机,只能通过这种机械的东西测量。通过格林公式,将面积分变为封闭的线积分。
注:测面仪,能够测量出曲面的面积,以前没有计算机,只能通过这种机械的东西测量。通过格林公式,将面积分变为封闭的线积分。
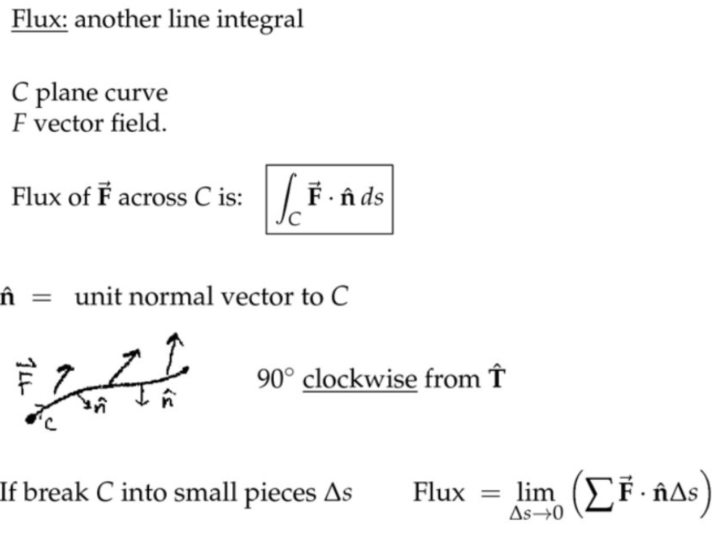
2D平面的流量(Flux in 2D)
 注:
注:
(1) 做功-力向量场往切向量方向投影
\( \overrightarrow{\mathbf{F}} \)力场做功就是将路径上每一点的向量场投影到运动方向\(\hat{\mathbf{T}} \)然后进行路径积分。垂直分量不做功。
(2) 通量-速度向量场往法向量方向投影
单位时间穿过一段路径的流量,等于路径上每一点速度向量在法向量方向投影的路径积分。(路径从左到右的话,默认法向量方向向下,其实上面已经说了,按照路径方向顺时针旋转90度,那么不就是向下吗)上图中\(\overrightarrow{\mathbf{F}} \)和\( \hat{\mathbf{n}}\)的夹角是钝角,那么点乘最后积分的结果显然是负数,这里的负号表示流量的流出而已。
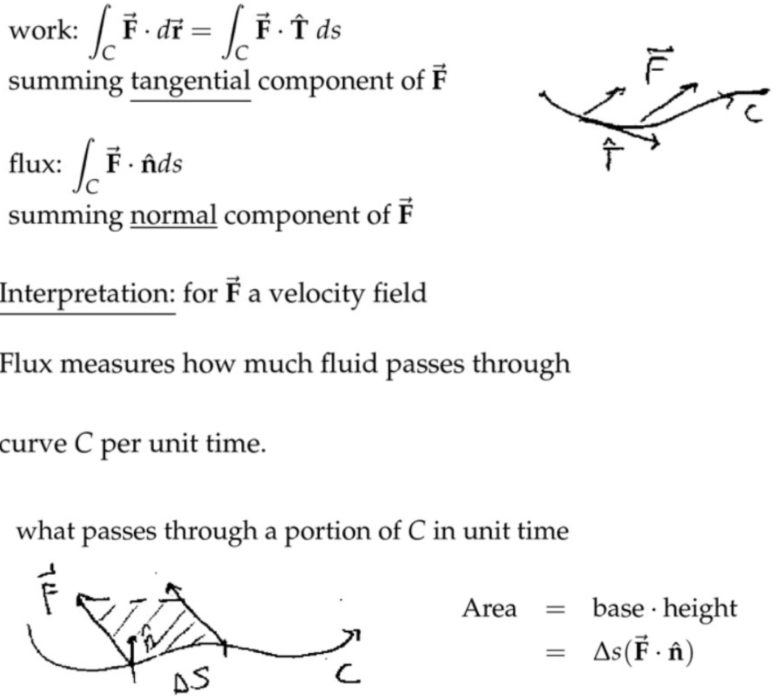

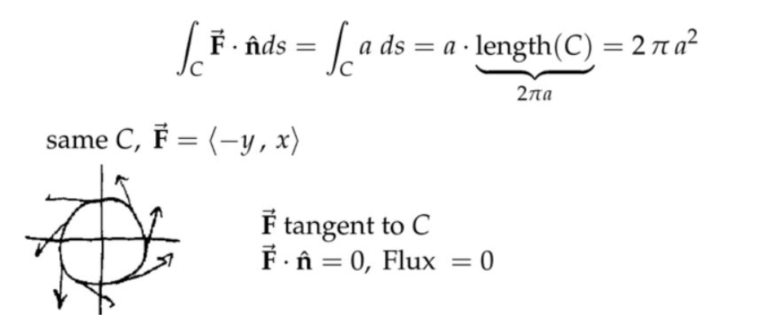 注:上面讲的是两种特殊的情况,所以可以直接用几何方法求解。第一种其实是“纯平移”,第二种其实是“纯旋转”。
注:上面讲的是两种特殊的情况,所以可以直接用几何方法求解。第一种其实是“纯平移”,第二种其实是“纯旋转”。
 注:小小思考一下从\( \langle d x, d y\rangle\)到\( \langle d y,-d x\rangle\)线性变换的矩阵。
注:小小思考一下从\( \langle d x, d y\rangle\)到\( \langle d y,-d x\rangle\)线性变换的矩阵。
格林公式的正交形(Normal Form of Green's Theorem)
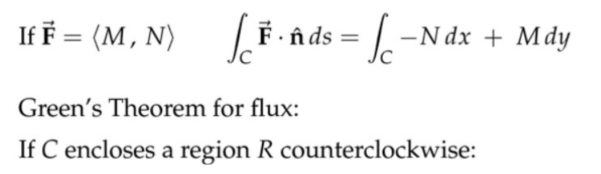 注:前面讨论的是一段曲线,这里现在讨论的是封闭曲线。上面的正交应该体现在曲线积分的时候,\( dx \)和\( dy\)前面的系数,对做功和求通量的两种情况,它们的点积结果为零。
注:前面讨论的是一段曲线,这里现在讨论的是封闭曲线。上面的正交应该体现在曲线积分的时候,\( dx \)和\( dy\)前面的系数,对做功和求通量的两种情况,它们的点积结果为零。
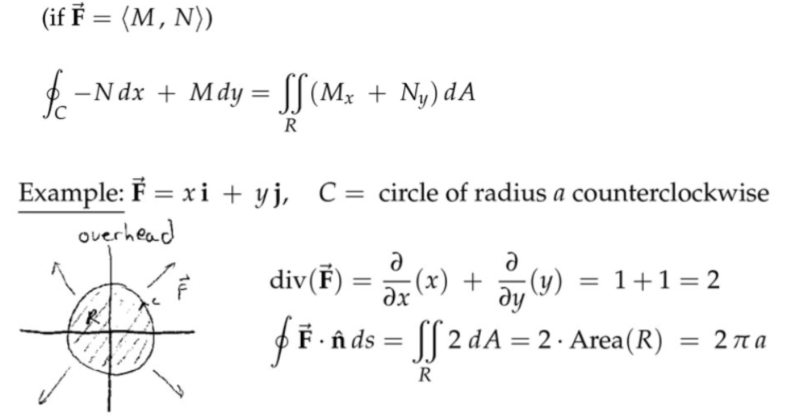
 注:
注:
(1) 无论将上述半径为\( 1 \)的圆放在向量场的哪个位置,得到的散度都是\(2 \),而不只是圆心的处圆的散度为\( 2 \)。
(2) 形象理解就是在平面上任意位置都安装有一个“冒出流量”的泵,而不只是圆心处有一个泵。各处泵的功率都一样。
(3) 如果只有圆心处有一个泵,那么越往外流速(向量场的模)应该越小(不包围圆心的圆,散度为零,只有包围的才为正数),类似点光源发出的光,越远处,单位面积上受到的辐照强度越小(平方反比),但是从我们的向量场来看,越远离圆心,流速越大,因此必须在远离圆心的地方都安上水泵,才能维持单位圆的散度(圆内流出的流量)为\( 2 \)。
(3) 对纯平移关系的向量场,散度为零;对纯旋转关系的向量场,散度也为零。总而言之,散度对平移和旋转都不敏感。散度只对伸缩变化敏感。(平移+旋转+伸缩 都是线性变换,对应矩阵的操作)
(4) 散度度量了流体膨胀后要占据的空间。
(5) 散度的源头是“冒出率”(source rate)。

(Extended Green's Theorem: Boundaries with Multiple Pieces)
 注:求通量的式子用散度来表达,形式上更容易记忆。其实是因为\( \hat{\mathbf{n}}\)相对于\( \hat{\mathbf{T}} \)就会产生路径微分的交换以及负号的出现,那么再按照格林公式作用又变换回去了,因此最后的形式很简洁,数学上直观。
注:求通量的式子用散度来表达,形式上更容易记忆。其实是因为\( \hat{\mathbf{n}}\)相对于\( \hat{\mathbf{T}} \)就会产生路径微分的交换以及负号的出现,那么再按照格林公式作用又变换回去了,因此最后的形式很简洁,数学上直观。 注:两种积分,加法和减法的等价性
注:两种积分,加法和减法的等价性
简单连通区域和保守场(Simply Connected Regions and Conservative Fields)

 注:要求解上面右图,外面大圈的路径积分,则必须知道内部孔洞的向量场分布,才能利用格林公式,而且这个时候的路径积分就不再只是外面的大圈了。另外,连通问题,从某种意义上来讲就是“拓扑学”的起点。拓扑学是研究区域形状的一个数学分支。
注:要求解上面右图,外面大圈的路径积分,则必须知道内部孔洞的向量场分布,才能利用格林公式,而且这个时候的路径积分就不再只是外面的大圈了。另外,连通问题,从某种意义上来讲就是“拓扑学”的起点。拓扑学是研究区域形状的一个数学分支。
 复习
复习

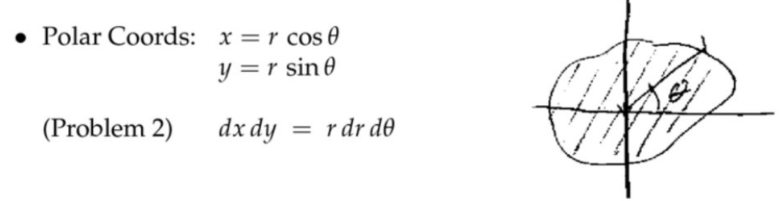
 \(I_o=I_x+I_y \)
\(I_o=I_x+I_y \)


