MIT-多变量微积分-1 – 历史的进程

网友笔记-不全配套视频习题视频 [mathjax] 多变量微积分(推荐) MIT官方资料

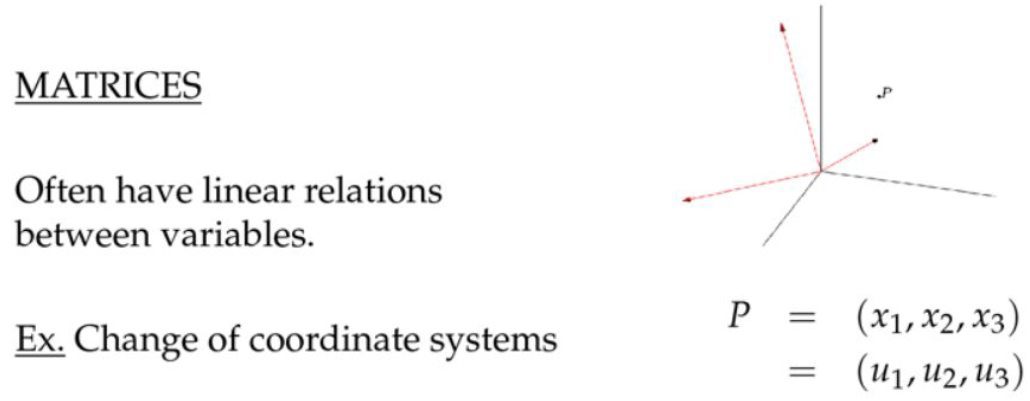
向量和点乘

向量的表示

$$\vec{A}=a_{1} \hat{i}+a_{2} \hat{j}+a_{3} \hat{k}=\left\langle a_{1}, a_{2}, a_{3}\right\rangle$$向量的方向$ \operatorname{dir}(\vec{A}) $

向量的加法：几何意义和数值计算。

向量乘以一个标量：直接放大或者缩小。

点乘定义和几何意义

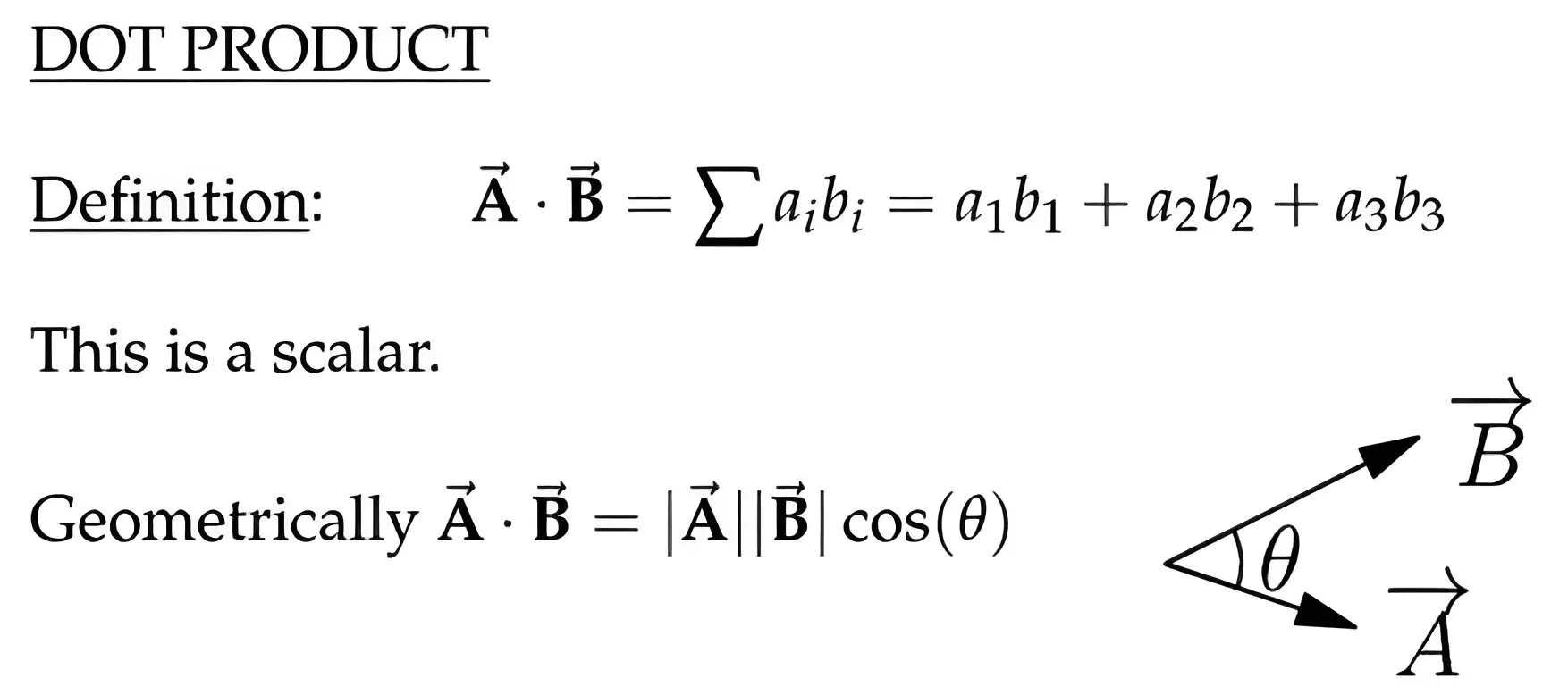
余弦定理和点乘的等价性

$$\begin{array}{l} \text { Law of cosines } \\ \qquad|\vec{C}|^{2}=|\vec{A}|^{2}+|\vec{B}|^{2}-2|\vec{A}||\vec{B}| \cos \theta \end{array}$$而$$\begin{aligned} |\vec{C}|^{2}=\vec{C} \cdot \vec{C} &=(\vec{A}-\vec{B}) \cdot(\vec{A}-\vec{B}) \\ &=\vec{A} \cdot \vec{A}-\vec{A} \cdot \vec{B}-\vec{B} \cdot \vec{A}+\vec{B} \cdot \vec{B}\\ &=|\vec{A}|^{2}+|\vec{B}|^{2}-2 \vec{A} \cdot \vec{B} \end{aligned}$$因此$$\vec{A} \cdot \vec{B}=|\vec{A}||\vec{B}| \cos \theta$$即通过余弦定理推导出了矩阵叉乘的定义；同样可以由矩阵叉乘的定义反向推导余弦定理。

点乘的应用

(1) 求解空间中任意两个向量之间的夹角(判断垂直关系)；求解向量长度。
(2) 说明$ x+2 y+3 z=0$是一个平面？
答：可以看成是与向量$ <1, 2, 3> $垂直并且过原点的一个平面。
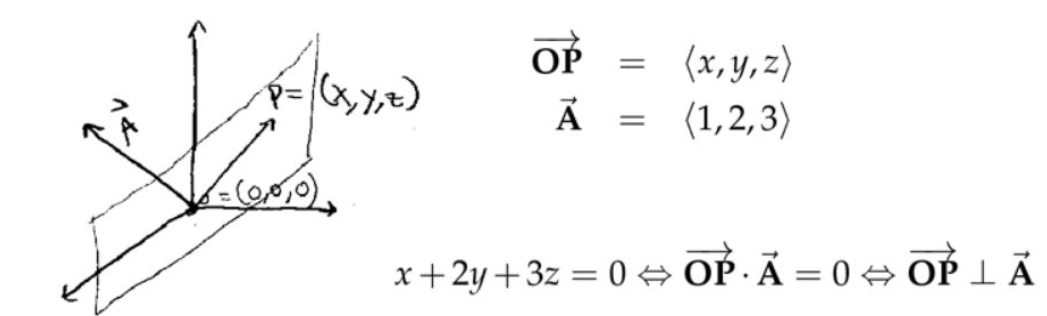(3) 求解一个向量在某个方向上的投影分量。
(4) 求解平面图形的面积
首先看一种比较容易想到的方法：
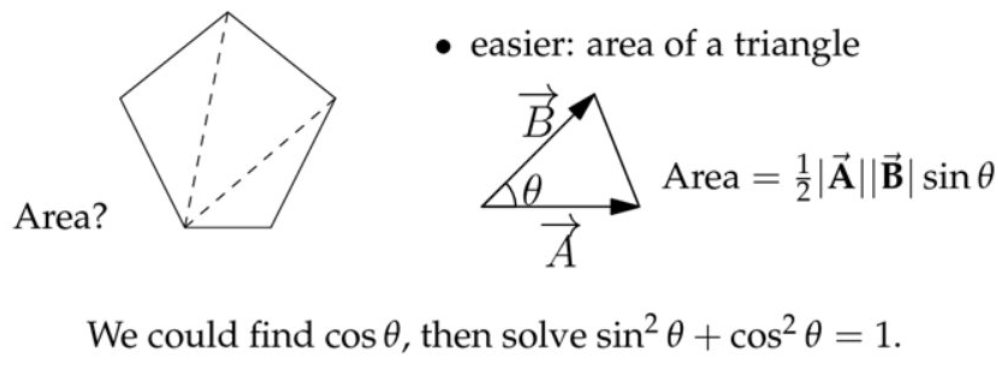接下来看如何利用点乘来计算(实现正余弦转换)
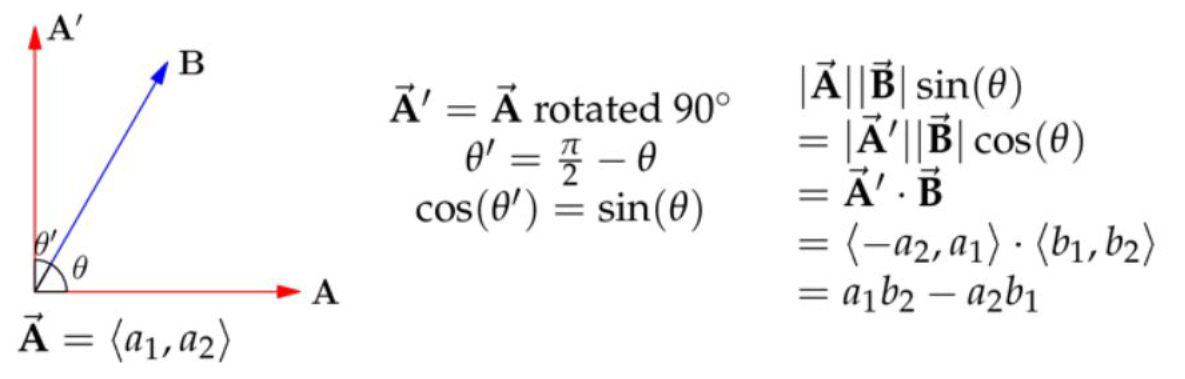先求出$\overrightarrow{\mathbf{A}^{\prime}} $，它和$\overrightarrow{\mathrm{A}} $垂直，但是大小一样。那么对$\overrightarrow{\mathbf{A}^{\prime}} $和$\overrightarrow{\mathrm{B}} $做点乘的绝对值，就是$\overrightarrow{\mathrm{A}} $和$\overrightarrow{\mathrm{B}} $围城的平行四边形的面积，如果乘以二分之一，那么就是对应三角形的面积。

求解$\overrightarrow{\mathbf{A}^{\prime}} $：
注意我们是利用$$\overrightarrow{\mathbf{A}^{\prime}} \cdot \overrightarrow{\mathbf{B}}=\langle-a_{2}, a_{1}\rangle \cdot\left\langle b_1, b_{2}\right\rangle=a_{1} b_{2}-a_{2} b_{1}$$而这个结果正好对应行列式$\left|\begin{array}{ll} a_{1} & a_{2} \\ b_{1} & b_{2} \end{array}\right| $的值。当然，如果值出现负数，那么就要取绝对值符号，小问题。
面积求解总结一下：

补充(六面体体积)

三个三维向量组成的行列式计算$$\operatorname{det}(\overrightarrow{\mathbf{A}}, \overrightarrow{\mathbf{B}}, \overrightarrow{\mathbf{C}})=\left|\begin{array}{lll} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{array}\right|=a_{1}\left|\begin{array}{ll} b_{2} & b_{3} \\ c_{2} & c_{3} \end{array}\right|-a_{2}\left|\begin{array}{ll} b_{1} & b_{3} \\ c_{1} & c_{3} \end{array}\right|+a_{3}\left|\begin{array}{ll} b_{1} & b_{2} \\ c_{1} & c_{2} \end{array}\right|$$三个向量组成的平行六面体的体积计算

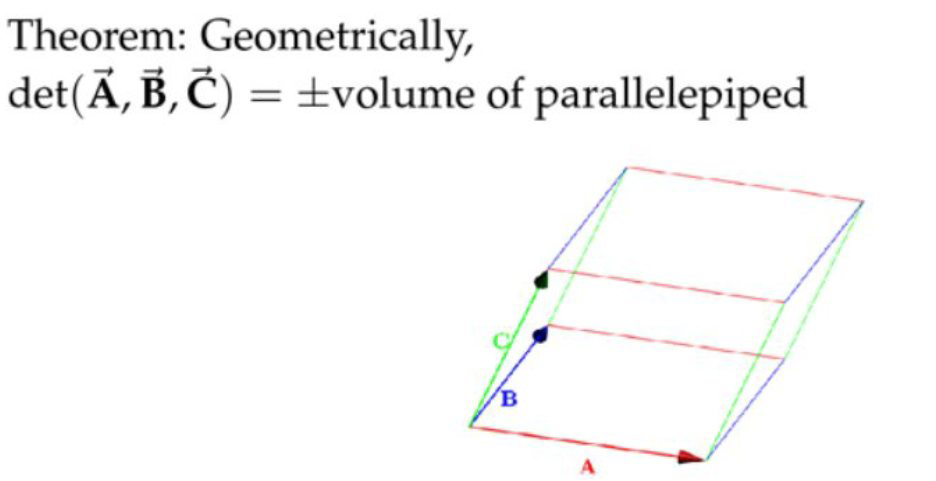
叉乘

定义

$$\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=\left|\begin{array}{rrr} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{array}\right|=\left|\begin{array}{ll} a_{2} & a_{3} \\ b_{2} & b_{3} \end{array}\right| \mathbf{i}-\left|\begin{array}{ll} a_{1} & a_{3} \\ b_{1} & b_{3} \end{array}\right| \mathbf{j}+\left|\begin{array}{ll} a_{1} & a_{2} \\ b_{1} & b_{2} \end{array}\right| \mathbf{k}$$其实上面不是真正意义上的行列式，因为计算出的结果是一个向量，但是我们借助了行列式计算的规则。从定义上来说，应该直接写成$\left|\begin{array}{ll} a_{2} & a_{3} \\ b_{2} & b_{3} \end{array}\right| \mathbf{i}-\left|\begin{array}{ll} a_{1} & a_{3} \\ b_{1} & b_{3} \end{array}\right| \mathbf{j}+\left|\begin{array}{ll} a_{1} & a_{2} \\ b_{1} & b_{2} \end{array}\right| \mathbf{k} $，但是$ \left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{array}\right|$这样写有助于记忆而已。

定理

右手定则计算

$$\begin{aligned} &\mathbf{i} \times \mathbf{j}=\mathbf{k}\\ &\left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right|=0 \mathbf{i}-0 \mathbf{j}+1 \mathbf{k} \end{aligned}$$

再探平行六面体体积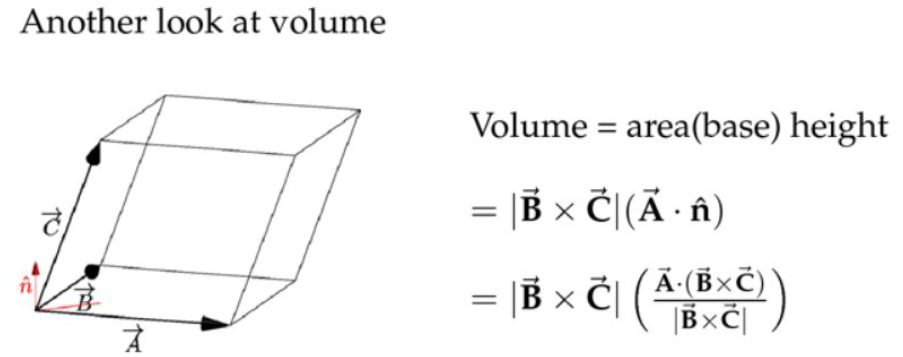

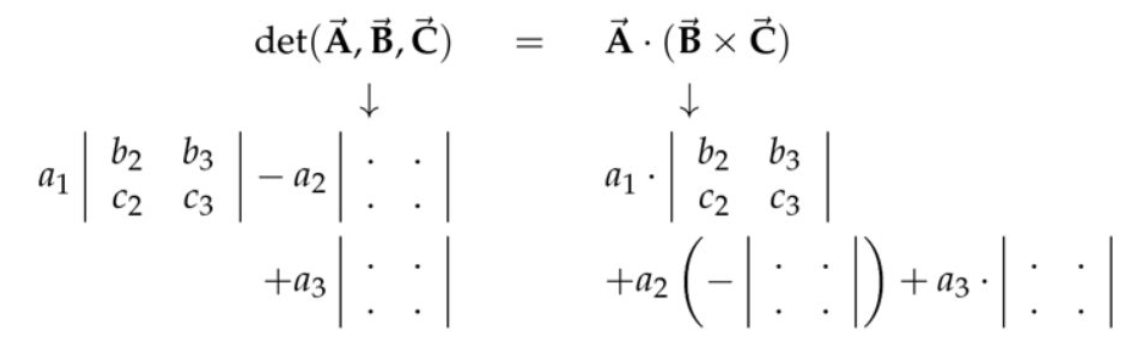
上面右侧，其实是按照点乘的定义($ \sum a_{i} b_{i}=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3} $)进行计算的；三个行列式对应着三个维度的值，是我们从“叉乘定义”那里得到的。

应用

(1) 已知三个点，判断任意一个点是否在这三个点组成的平面内。
方法1：三个向量围成的平行六面体的体积为零。
方法2：原来的三个点组成的平面的法向量$\overrightarrow{\mathbf{N}} $垂直于$\overrightarrow{\mathrm{P_{1}P}} $
法向量$ \overrightarrow{\mathrm{N}}=\overrightarrow{\mathrm{P}_{1} \mathrm{P}_{2}} \times \overrightarrow{\mathrm{P}_{1} \mathrm{P}_{3}} $
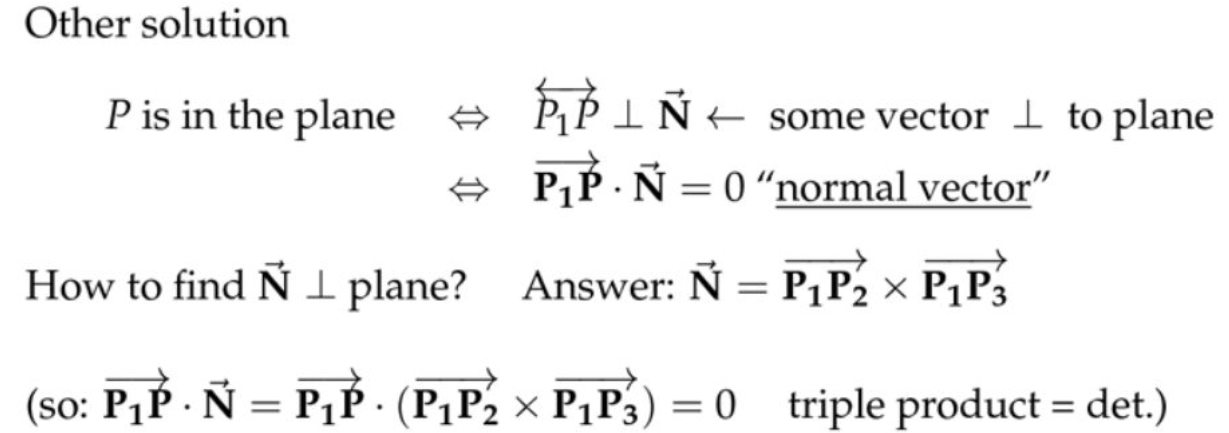注：
(1)$ \vec{A} \times \vec{A}=0 $。
(2) 前面的点乘和叉乘的混合叫作“混合积”，这是和行列式一样的东西。

矩阵

基本知识

1. 改变坐标系，其实就是线性变换。
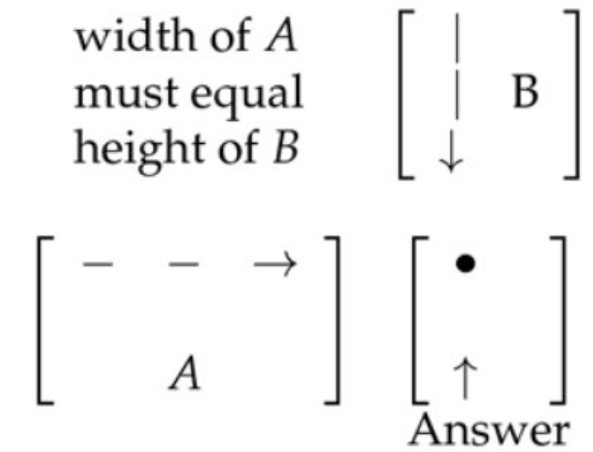
2. 两个矩阵相乘，我们可以这样思考运算规则：
3. 线性变换$A B $的先后顺序

4. 向量逆时针旋转90度
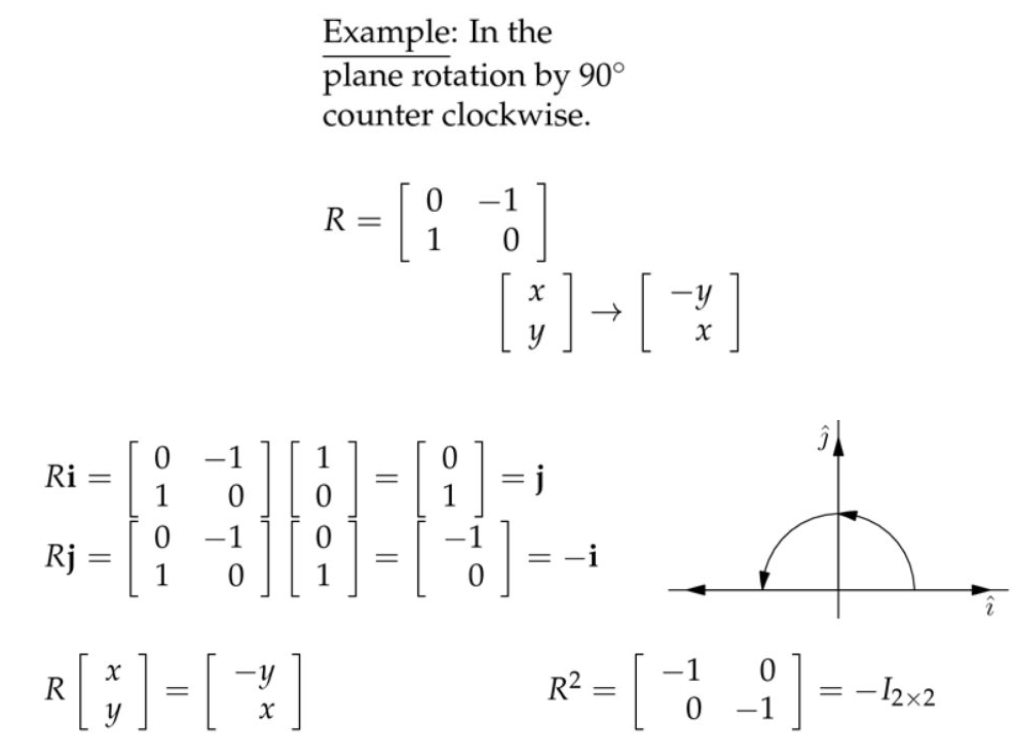横轴线性变换之后，变成了原来纵轴的方向；纵轴线性变换，变成了原来横轴的负方向。总的效果就是整个坐标轴逆时针旋转了90度。$ R^{2} $表示逆时针旋转了两次90度，最终效果就是$x $和$ y $前面都加一个负号。

计算逆矩阵

第一步：计算余子式矩阵；
第二步：计算代数余子式矩阵；(特定元素变号)
第三步：将代数余子式的转置；
第四步：将第三步的矩阵除以原矩阵的行列式的值。

解特定法向量的平面

例：求解法向量为$ \overrightarrow{\mathbf{N}}=\langle 1,5,10\rangle $而且过原点的平面？
解：
如果不是要求过原点，而是过特定点，比如
$ \text { Plane through } P_{0}=(2,1,-1) \text { and } \perp \overrightarrow{\mathbf{N}}=\langle 1,5,10\rangle$？
解：这里利用的是对该平面上任意一点$ P$，它和平面上已知点组成的向量一定在该平面上，所以垂直于给定的法向量。注：这里的$ -3 $除以法向量的模长就是原来过零点的该平面沿着法向量方向移动的距离。

平面的线性系统

三个平面交于一点：唯一解(系数矩阵可逆)；
交于一条线：无数组解(系数矩阵行列式为零)；
不相交：无解(系数矩阵不可逆，行列式也等于零)。

判断到底是无数组解还是无解，要通过消元法。

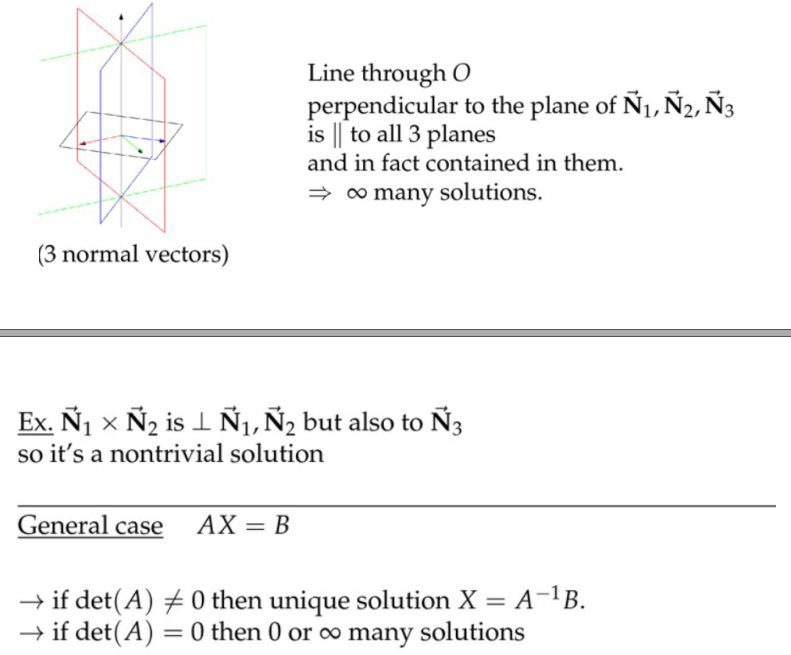
齐次方程组

零解是trivial solution(平凡解)
(a) $ \operatorname{det}(A) \neq 0$，那么只有零解；
(b) $ \operatorname{det}(A)=0 $，那么$\begin{aligned} &\Leftrightarrow \operatorname{det}\left(\overrightarrow{\mathbf{N}}_{1}, \overrightarrow{\mathbf{N}}_{2}, \overrightarrow{\mathbf{N}}_{3}\right)=0\\ &\Leftrightarrow \overrightarrow{\mathbf{N}}_{1}, \overrightarrow{\mathbf{N}}_{2}, \overrightarrow{\mathbf{N}}_{3} \text { coplanar } \end{aligned} $三个平面的法向量共面，而垂直于这个面而且过原点的直线就是方程组的解。这条直线一方面垂直这些法向量，那么和这些面都平行，另一方面，这条线过原点，因此这条线必然同时处在三个平面之内。

参数方程(直线/摆线/弧长/开普勒第二定律)

参数方程表示空间中的直线

已知三维空间中两个点的坐标，求解两点连成的直线上的所有点的位置坐标？
解：将这条直线看作是“移动的点的轨迹”
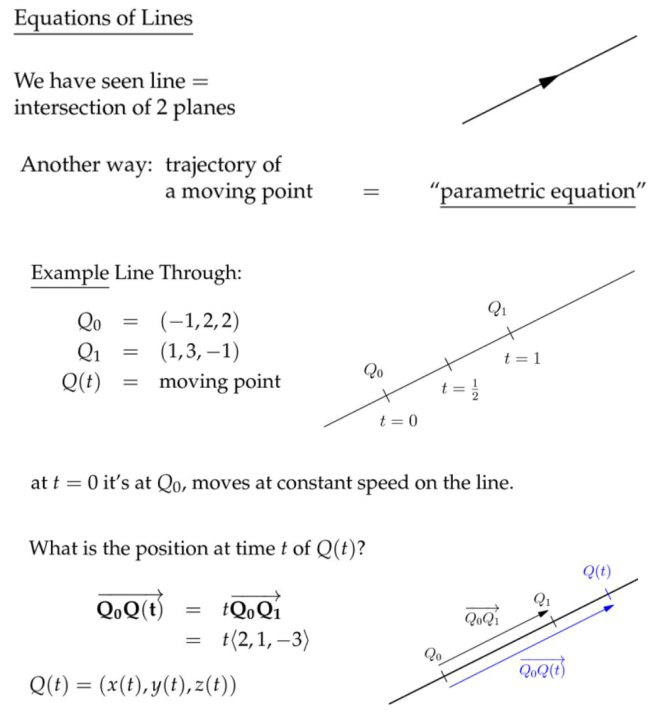$$\begin{aligned} &\left\{\begin{array}{ll} x(t)+1 & =t \cdot 2 \\ y(t)-2 & =t \\ z(t)-2 & =-3 t \end{array} \quad\left\{\begin{array}{l} x(t)=-1+2 t \\ y(t)=2+t \\ z(t)=2-3 t \end{array}\right.\right.\\ &\overrightarrow{\mathbf{Q}_{0} \mathbf{Q}(\mathbf{t})}=t \overrightarrow{\mathbf{Q}_{0} \mathbf{Q}_{1}} \quad \quad \mathbf{Q}(t)=\mathbf{Q}_{0}+t \overrightarrow{\mathbf{Q}_{0} \mathbf{Q}_{1}} \end{aligned}$$

平面和直线的交点

给定平面$ x+2 y+4 z=7$，上面谈的直线和这个平面的交点坐标是多少？
解：

摆线的参数方程

以摆线为例(Cycloid)，晚上自行车车轮上固定的灯的轨迹就是摆线。特点就是无论这个轮子的转速是快是慢，都不影响轨迹线，因此我们不采用时间$ t$作为变量参数，那么可以采用车轮水平移动的距离或者车轮转动的角度。下面我们以车轮转动的角度$ \theta$作为参数，构建摆线的参数方程。摆线的演示动画。
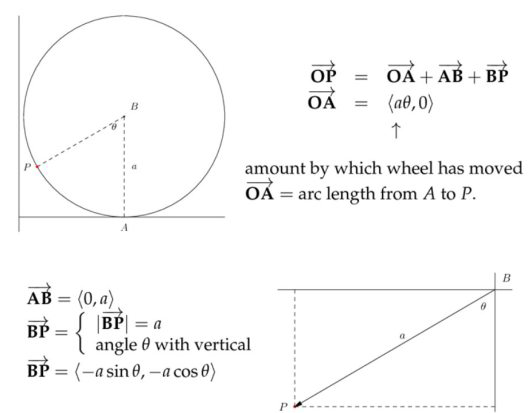最终的参数方程为$$\overrightarrow{\mathbf{O P}}=\langle\underbrace{a \theta-a \sin \theta}_{x(\theta)}, \underbrace{a-a \cos \theta}_{y(\theta)}\rangle$$问题：Question What happens near bottom?
答：在$ \theta=0$处进行泰勒展开(简单起见，让$a=1 $)，取几个高阶项，那么$$\begin{array}{l} x(\theta) \approx \theta-\left(\theta-\displaystyle\frac{\theta^{3}}{6}\right) \approx \displaystyle\frac{\theta^{3}}{6} \\ y(\theta) \approx 1-\left(1-\displaystyle\frac{\theta^{2}}{2}\right) \approx \displaystyle\frac{\theta^{2}}{2} \end{array}$$显然$ \theta=0 $处摆线的切线斜率无穷大。

摆线运动的速度和加速度

我们前面求解的是关于角度$ \theta$的参数方程，现在我们要求速度和加速度，那么必须将摆线方程转变成和时间有关的方程。假设这个轮子的半径为$ 1$，运动速度是$ 1 $个单位长度每单位时间，轮子和地面接触的痕迹的长度就是轮子水平方向移动的距离。换句话说，轮子转动的角速度，为每单位时间转动$1 $个角度，那么对应的弧长正好就是$ 1$。

所以摆线时间的参数方程为$$\overrightarrow{\mathbf{r}}(t)=\langle t-\sin t, 1-\cos t\rangle$$速度矢量的求解方式为$${\text { Velocity vector }} \overrightarrow{\mathbf{v}}=\frac{d \overrightarrow{\mathbf{r}}}{d t}=\left\langle\frac{d x}{d t}, \frac{d y}{d t}, \frac{d z}{d t}\right\rangle$$因此速度矢量的参数方程为$$\begin{aligned} &\overrightarrow{\mathbf{v}}=\langle 1-\cos t, \sin t\rangle\\ &(\text { at } t=0 \quad \overrightarrow{\mathbf{v}}=0 !) \end{aligned}$$速度的大小为$$\begin{aligned} &\begin{array}{l} |\overrightarrow{\mathbf{v}}|=\sqrt{(1-\cos t)^{2}+\sin ^{2} t} \\ =\sqrt{1-2 \cos t+\cos ^{2} t+\sin ^{2} t} \end{array}\\ &=\sqrt{2-2 \cos t} \end{aligned}$$加速度$$\begin{aligned} &\overrightarrow{\mathbf{a}}=\frac{d \overrightarrow{\mathbf{v}}}{d t}\\ &\text { e.g. cycloid } \overrightarrow{\mathbf{a}}=\langle\sin t, \cos t\rangle \end{aligned}$$
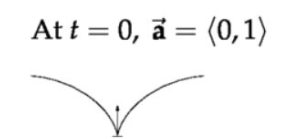上图表示上一个周期运动突然结束，然后速度突然变为零，同时在该瞬间获得一个向上的加速度。注意下式不成立$$\left|\frac{d \overrightarrow{\mathbf{r}}}{d t}\right| \neq \frac{d|\overrightarrow{\mathbf{r}}|}{d t}$$$\left|\displaystyle\frac{d \overrightarrow{\mathbf{r}}}{d t}\right| $表示的是速度矢量的模长，而后者就是表示位置向量$ \langle t-\sin t, 1-\cos t\rangle $取模长对时间求导而已，没有很好的物理内涵。

弧长(Arc length)

s= distance travelled along trajectory，弧长对时间求导就是速度矢量的模长$$\left|\frac{d s}{d t}\right|=\text { speed }=|\overrightarrow{\mathbf{v}}|$$
这里引入一个新的概念“单位正切矢量”$\hat{\mathbf{T}} $，从轨迹上看，每一个点的单位正切矢量表示的是质点在该处的速度方向，那么点乘在该点移动的微小距离(标量)，那么得到的就是移动前后位移矢量的微小变化。

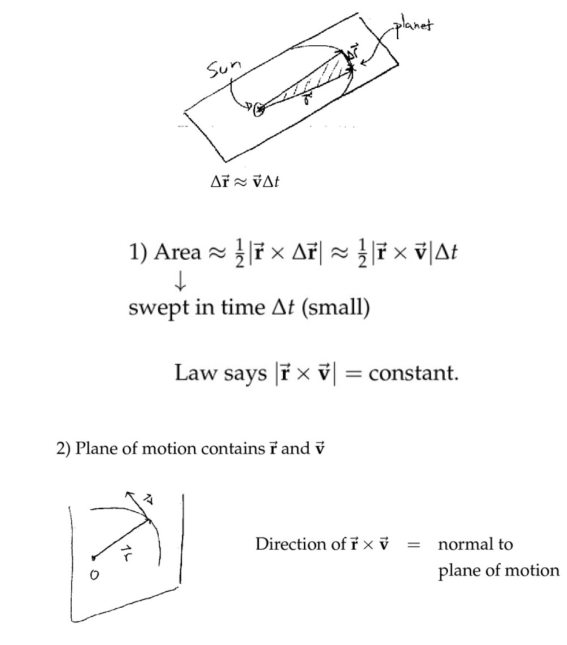
开普勒第二定律

【开普勒定律】(Kepler's laws of planetary motion)是开普勒1609年发表的成果，其中的开普勒第二定律描述的是：
Motion of planets in a plane, and the area is swept out by the line from sun to planet at a constant rate. 就是单位时间内行星和太阳的连线扫过的面积相等。后来，牛顿用万有引力定律科学上解释了这一现象。下面的推导，发现要实现上述定律，只需要位移矢量和加速度矢量的叉乘为零，换句话说二者的方向共线，这显然满足，因为星星运动的加速度只来自于和太阳之间的万有引力，所以这个加速度的方向和位移矢量的方向恰好共线而且反向。矢量运算真强大！

拓展资料：
(1) 行星的运动—上海八中
(2) 行星轨道为什么是椭圆—科普时报