列维-奇维塔符号
预备知识
(1) 爱因斯坦求和约定:如果在一个表达式中,某个下标重复出现两次,那么这个下标就是哑指标(dummy index),否则就是自由指标(free index)。比如\( a_{i} b_{j}=0\)里面的\( i\)和\( j \)都是自由指标,得到的是九个方程。\(a_{i} a_{i}= 0\)中的\( i \)是哑指标,要求和的,对应于一个方程即\( a_{i} a_{i}=a_{1} a_{1}+a_{2} a_{2}+a_{3} a_{3}=0\)。更复杂的比如\( \sigma_{i j} b_{j}+f_{i}=0 \)其中\( j \)是哑指标,要求和的,而\( i\)是自由指标,一个\( i\)的取值对应一个方程,于是这个表达式等价于\( 3 \)个独立的方程。[mathjax]
哑指标:重复两次(挨在一起),要求和;
自由指标:重复一次(即使重复也是在不同的子式子中),对应方程个数。$$\begin{array}{l} \mathbf{u}=u_{1} e_{1}+u_{2} e_{2}+u_{3} e_{3}=\sum_{i=1}^{3} u_{i} e_{i}=u_{i} e_{i} \\ \mathbf{a} \cdot \mathbf{b}=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}=\sum_{i=1}^{3} a_{i} b_{i}=a_{i} b_{i} \end{array}$$
(2) 约定:\( \mathbf{e}_{i}\)、\( \mathbf{e}_{j} \)、\( \mathbf{e}_{k} \)对应三维空间,\( \mathbf{e}_{1}\)、\( \mathbf{e}_{2}\)、\( \mathbf{e}_{3}\)任取;而\( \mathbf{e}_{\alpha }\)、\( \mathbf{e}_{\beta} \)对应二维平面,\( \mathbf{e}_{1} \)、\( \mathbf{e}_{2} \)任取。
例子-柯西应力张量(Cauchy stress tensor)
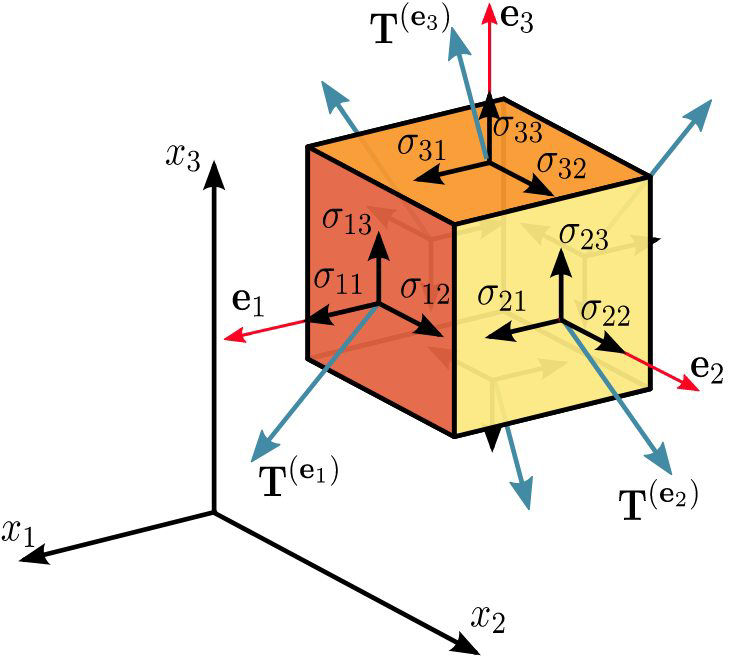
立方微元三个不同的面(平行的面看作一个)受到不同的力,然后这些力分别往三个轴上投影,得到的就是\( 9\)个分量。如下,写成了矩阵的形式,从每一行来看,一整行表示同一个面的受力分解,整个矩阵三行分别对应三个面;每行又又三列,对应该面力矢量在三个方向的投影大小。 柯西应力张量为$$\boldsymbol{\sigma}=\left[\begin{array}{ccc} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{array}\right] \equiv\left[\begin{array}{ccc} \sigma_{x x} & \sigma_{x y} & \sigma_{x z} \\ \sigma_{y x} & \sigma_{y y} & \sigma_{y z} \\ \sigma_{z x} & \sigma_{z y} & \sigma_{z z} \end{array}\right] \equiv\left[\begin{array}{ccc} \sigma_{x} & \tau_{x y} & \tau_{x z} \\ \tau_{y x} & \sigma_{y} & \tau_{y z} \\ \tau_{z x} & \tau_{z y} & \sigma_{z} \end{array}\right]$$设\( \mathbf{n} \)为单位矢量的方向,那么\( \mathbf{T}^{(\mathbf{n})}\)为通过与\( \mathbf{n} \)垂直平面的应力矢量。存在如下关系$$\mathbf{T}^{(\mathbf{n})}=\mathbf{n} \cdot \boldsymbol{\sigma} \quad \text { or } \quad T_{j}^{(\mathbf{n})}=\sigma_{i j} n_{i}$$具体展开就是$$\begin{array}{l} \mathbf{T}^{\left(\mathbf{e}_{1}\right)}=T_{1}^{\left(\mathbf{e}_{1}\right)} \mathbf{e}_{1}+T_{2}^{\left(\mathbf{e}_{1}\right)} \mathbf{e}_{2}+T_{3}^{\left(\mathbf{e}_{1}\right)} \mathbf{e}_{3}=\sigma_{11} \mathbf{e}_{1}+\sigma_{12} \mathbf{e}_{2}+\sigma_{13} \mathbf{e}_{3} \\ \mathbf{T}^{\left(\mathbf{e}_{2}\right)}=T_{1}^{\left(\mathbf{e}_{2}\right)} \mathbf{e}_{1}+T_{2}^{\left(\mathbf{e}_{2}\right)} \mathbf{e}_{2}+T_{3}^{\left(\mathbf{e}_{2}\right)} \mathbf{e}_{3}=\sigma_{21} \mathbf{e}_{1}+\sigma_{22} \mathbf{e}_{2}+\sigma_{23} \mathbf{e}_{3} \\ \mathbf{T}^{\left(\mathbf{e}_{3}\right)}=T_{1}^{\left(\mathbf{e}_{3}\right)} \mathbf{e}_{1}+T_{2}^{\left(\mathbf{e}_{3}\right)} \mathbf{e}_{2}+T_{3}^{\left(\mathbf{e}_{3}\right)} \mathbf{e}_{3}=\sigma_{31} \mathbf{e}_{1}+\sigma_{32} \mathbf{e}_{2}+\sigma_{33} \mathbf{e}_{3} \end{array}$$index notation is $$\mathbf{T}^{\left(\mathbf{e}_{i}\right)}=T_{j}^{\left(\mathbf{e}_{i}\right)} \mathbf{e}_{j}=\sigma_{i j} \mathbf{e}_{j}$$汇总一下,柯西应力张量可以写成$$\boldsymbol{\sigma}=\sigma_{i j}=\left[\begin{array}{l} \mathbf{T}^{\left(\mathbf{e}_{1}\right)} \\ \mathbf{T}^{\left(\mathbf{e}_{2}\right)} \\ \mathbf{T}^{\left(\mathbf{e}_{3}\right)} \end{array}\right]$$应力张量的分量可以表示为$$\begin{aligned} \mathbf{T}^{(\mathbf{n})} &=\mathbf{T}^{\left(\mathbf{e}_{1}\right)} n_{1}+\mathbf{T}^{\left(\mathbf{e}_{2}\right)} n_{2}+\mathbf{T}^{\left(\mathbf{e}_{3}\right)} n_{3} \\ &=\sum_{i=1}^{3} \mathbf{T}^{\left(\mathbf{e}_{i}\right)} n_{i} \\ &=\left(\sigma_{i j} \mathbf{e}_{j}\right) n_{i} \\ &=\sigma_{i j} n_{i} \mathbf{e}_{j} \end{aligned}$$
注:
(1) \(\mathbf{T}^{(\mathbf{n})} \)表示的是三个面受到的三个力矢量,这是非常简化的表达,\( \mathbf{T}\)加粗说明这是一个矢量。\( \mathbf{n}\)可以拆分成三个不同方向的单位正交矢量。
(2) \( T_{j}^{(\mathbf{n})} \),这里的\( T \)没有加粗,说明是一个标量,但是\( \mathbf{n}\)有三种取值,\( j \)也有三种取值(三列),因此\( T_{j}^{(\mathbf{n})} \)表示的是一个\( 3 \times 3 \)的系数矩阵。
(3) \( \mathbf{T}^{\left(\mathbf{e}_{i}\right)}\)不是表示\( \mathbf{e}_{i}\)方向力矢量的汇总,而是垂直于\( \mathbf{e}_{i} \)面的总受力矢量(可以分解成三个坐标方向)。
零/一/二阶张量
标量—零阶张量
标量(势函数)求梯度得到梯度场(向量场),升阶,但是向量场不一定对应一个势函数。
矢量—一阶张量
零阶张量求梯度升阶到一阶,二阶张量求散度降阶到一阶。
方矩阵—二阶张量
一阶张量求梯度得到二阶张量,三阶张量求散度得到二阶张量。
三种积
(1) 克罗内克积(Kronecker product)是两个任意大小的矩阵间的运算,表示为\(\otimes \)。克罗内克积是外积从向量到矩阵的推广,也是张量积在标准基下的矩阵表示。如果A是一个\( m \times n \)矩阵,B是一个\( p \times q\)矩阵,则克罗克内积\( A \otimes B\)是一个\( m p \times n q\)的分块矩阵。$$A \otimes B=\left[\begin{array}{ccc} a_{11} B & \cdots & a_{1 n} B \\ \vdots & \ddots & \vdots \\ a_{m 1} B & \cdots & a_{m n} B \end{array}\right]$$例子$$\left[\begin{array}{ll} 1 & 2 \\ 3 & 1 \end{array}\right] \otimes\left[\begin{array}{ll} 0 & 3 \\ 2 & 1 \end{array}\right]=\left[\begin{array}{llll} 1 \cdot 0 & 1 \cdot 3 & 2 \cdot 0 & 2 \cdot 3 \\ 1 \cdot 2 & 1 \cdot 1 & 2 \cdot 2 & 2 \cdot 1 \\ 3 \cdot 0 & 3 \cdot 3 & 1 \cdot 0 & 1 \cdot 3 \\ 3 \cdot 2 & 3 \cdot 1 & 1 \cdot 2 & 1 \cdot 1 \end{array}\right]=\left[\begin{array}{llll} 0 & 3 & 0 & 6 \\ 2 & 1 & 4 & 2 \\ 0 & 9 & 0 & 3 \\ 6 & 3 & 2 & 1 \end{array}\right]$$克罗内克积是张量积的特殊形式。
(2) 张量积\( \otimes\),向量、矩阵、张量、向量空间、代数、拓扑向量空间和模。在各种情况下这个符号的意义是同样的:最一般的双线性运算。
(3) 并矢积,对于选定的基\( \left\{\mathbf{e}_{i}\right\}\),并矢积\( \mathbb{P}=\mathbf{u} \otimes \mathbf{v} \)的分量\( P_{i j}\)可以定义为$$P_{i j}=u_{i} v_{j}$$这里的$$\mathbf{u}=\sum_{i} u_{i} \mathbf{e}_{i} \quad \mathbf{v}=\sum_{j} v_{j} \mathbf{e}_{j}$$于是$$\mathbb{P}=\sum_{i, j} P_{i j} \mathbf{e}_{i} \otimes \mathbf{e}_{j}$$
并矢(covector)
并矢这个概念其实是物理学家懒得学太多数学而做出的一个“阉割版”张量,按数学的处理,应该用\( \otimes\)符号来描述,物理直接简化为将矢量\( A \)和矢量\(B \)并在一起写\( AB \),便称之为“并矢”,来表示一个二阶张量。并矢的几种理解方式:
(1) 列向量右乘一个行向量得到一个矩阵,比如\( A=\left(A_{1}, A_{2}, A_{3}\right) \),\( B=\left(B_{1}, B_{2}, B_{3}\right) \),那么$$AB=\left[\begin{array}{l} A_{1} \\ A_{2} \\ A_{3} \end{array}\right]\left[\begin{array}{lll} B_{1} & B_{2} & B_{3} \end{array}\right]=\left[\begin{array}{lll} A_{1} B_{1} & A_{1} B_{2} & A_{1} B_{3} \\ A_{2} B_{1} & A_{2} B_{2} & A_{2} B_{3} \\ A_{3} B_{1} & A_{3} B_{2} & A_{3} B_{3} \end{array}\right]$$于是\( C \cdot(A B) \)可以看作是行矢量右乘上述矩阵,\( (A B) \cdot C\)可以看作列向量左乘上述矩阵。并矢\(AB \)的散度为$$\begin{array}{l} \left.\nabla \cdot(A B)=[\begin{array}{lllll} \partial_{1} & \partial_{2} & \partial_{3} \end{array}\right]\left[\begin{array}{lll} A_{1} B_{1} & A_{1} B_{2} & A_{1} B_{3} \\ A_{2} B_{1} & A_{2} B_{2} & A_{2} B_{3} \\ A_{3} B_{1} & A_{3} B_{2} & A_{3} B_{3} \end{array}\right]= \\ {\left[\partial_{1}\left(A_{1} B_{1}\right)+\partial_{2}\left(A_{2} B_{1}\right)+\partial_{3}\left(A_{3} B_{1}\right) \quad \partial_{1}\left(A_{1} B_{2}\right)+\partial_{2}\left(A_{2} B_{2}\right)+\partial_{3}\left(A_{3} B_{2}\right) \quad \partial_{1}\left(A_{1} B_{3}\right)+\partial_{2}\left(A_{2} B_{3}\right)+\partial_{3}\left(A_{3} B_{3}\right)\right]} \end{array}$$最终得到的是一个矢量,这是参考一个知乎网友写的,这种表达不是很好,下面用另一种表示。首先我们要知道并矢\( A B\)的每个元素\( A_i B_j\)在写成矩阵的时候其实是一种系数表达,\( A_i B_j \)其实对应的是\( A_i B_j\mathbf{e}_{i}\mathbf{e}_{j}\),想想我们在计算\( AB\)的时候把每个元素的\( \mathbf{e}_{i} \)或\(\mathbf{e}_{j} \)带入就知道了。于是$$\begin{aligned} \nabla \cdot \boldsymbol{\tau} \equiv \nabla \cdot \overline{\bar{\tau}}=&\left(\mathbf{e}_{1} \frac{\partial}{\partial x_{1}} \quad \mathbf{e}_{2} \frac{\partial}{\partial x_{2}} \quad \mathbf{e}_{3} \frac{\partial}{\partial x_{3}}\right)\left(\begin{array}{ccc} \tau_{11} & \tau_{12} & \tau_{13} \\ \tau_{21} & \tau_{22} & \tau_{23} \\ \tau_{31} & \tau_{32} & \tau_{33} \end{array}\right) \\ =&\left[\frac{\partial \tau_{11}}{\partial x_{1}}+\frac{\partial \tau_{21}}{\partial x_{2}}+\frac{\partial \tau_{31}}{\partial x_{3}}\right] \mathbf{e}_{1}+\left[\frac{\partial \tau_{12}}{\partial x_{1}}+\frac{\partial \tau_{22}}{\partial x_{2}}+\frac{\partial \tau_{32}}{\partial x_{3}}\right] \mathbf{e}_{2} \\ &+\left[\frac{\partial \tau_{13}}{\partial x_{1}}+\frac{\partial \tau_{23}}{\partial x_{2}}+\frac{\partial \tau_{33}}{\partial x_{3}}\right] \mathbf{e}_{3} \end{aligned}$$忽略标记符号不同,因为直接是复制别人的公式,配上下面公式就很好理解了$$\nabla=\mathbf{e}_{i} \frac{\partial}{\partial x_{i}}\\\nabla \cdot \overline{\bar{\tau}}=\mathbf{e}_{i} \frac{\partial}{\partial x_{i}} \cdot \tau_{i j} \mathbf{e}_{i} \mathbf{e}_{j}=\mathbf{e}_{i} \cdot \mathbf{e}_{i} \frac{\partial \tau_{i j}}{\partial x_{i}} \mathbf{e}_{j}=\frac{\partial \tau_{i j}}{\partial x_{i}} \mathbf{e}_{j}$$
按照电动力学老师讲义里面,有$$\partial_{i}\left(A_{i} B_{j}\right) \hat{e}_{j}=\left(\partial_{i} A_{i}\right) B_{j} \hat{e}_{j}+A_{i}\left(\partial_{i} B_{j}\right) \hat{e}_{j}$$于是得到$$\nabla \cdot(\overrightarrow{A B})=(\nabla \cdot \vec{A}) \vec{B}+(\vec{A} \cdot \nabla) \vec{B}$$注:
(1) 其中的\( \partial_{i}\left(A_{i} B_{j}\right) \hat{e}_{j}\)其实是\( \partial_{i} \hat{e}_{i} \left(A_{i} B_{j}\right) \hat{e}_{i} \hat{e}_{j}\);
(2) 注意这里的\( A\)和\( B \)都是随着时间和空间变化的向量,不考虑时间变化,那么\( \partial_{i}\left(A_{i} B_{j}\right) \hat{e}_{j}\)是一个随着位置坐标而变化的量。
希尔伯特空间矢量描述
回顾一下以前的量子力学,狄拉克把\( \langle\alpha | \beta\rangle\)劈成两半,变成左矢\( \langle\alpha| \)和右矢\(|\beta\rangle \)来进行计算。我们可以把左矢想成一个行向量,右矢想成一个列向量,“左右”正好和“行列”对应。于是内积\( \langle\alpha | \beta\rangle \)得到的是一个数,外积\( |\beta\rangle\langle\alpha| \)得到的是一个矩阵(其实就是克罗内克积),类似我们得到两个向量的并矢量,于是得到一个矩阵。
学习动机
广义相对论
广义相对论(General Relativity)的时空弯曲(space-time is curved)或者宇宙大爆炸(Universe is expanding)。
爱因斯坦场方程$$R_{\mu \nu}-\frac{1}{2} R g_{\mu \nu}+\Lambda g_{\mu \nu}=\frac{8 \pi G}{c^{4}} T_{\mu \nu}$$这里面包含了16个方程,解释了时空弯曲和宇宙大爆炸。方程中,带有下表的几个量都是张量,其中\(g_{\mu \nu} \)是metric tensor最重要,它是一个四阶矩阵。
量子力学+量子计算
量子叠加态\( \vec{\psi} =a \vec{v}+b \vec{w}\)其实是不同物理状态(本征态)的线性组合。量子纠缠\(\vec{\psi} \otimes \vec{\phi} \)中间的符号是张量积(tensor product),表示的含义是两个不同的geometrical space张量积作用之后,形成一个更复杂的geometrical space,这就是纠缠系统的由来。
参考资料:
1. 知乎:并矢是什么? 如何运算?
2. 知乎:并矢,外积与二阶张量
3. 维基百科:柯西应力张量
4. USEFUL VECTOR AND TENSOR OPERATIONS
5. 小木虫
6. Tensor for beginners--第一季
杂乱
张量
问:看了这个TED视频之后的总结?
答:这个视频给出了一个很形象的解释来描述一种“不变性”,即不以参考系的变化而变化的特性。比如我们要用语言表达“狗”这个概念,我们首先必须指定是何种语言,然后指定是该种语言中什么词。(狗)(中文)=(dog)(English)=(hond)(Dutch)。
一个人从A点(0, 0)移动到B点(2, 3),那么如何用数学的语言描述该过程呢?如果把人想象成一个质点,那么向量\(2\vec{i}+3\vec{j}\)表示该移动过程。但实际情况是人不是质点,如果以人的正前方为y轴正方向,正右方为x轴正方向,那么人在(0, 0)这一点的朝向,决定了相对于自身的参考系他该怎么移动到绝对参考系的(2, 3)这一点。具体如下图所示(左边是正对着站,右边是背对着)


 对两种运动方式来说,它们的数组不同,基向量不同,但是最后表示的是同一个矢量。总而言之,对个人来说,即使坐标系变化了,但是乘以对应坐标系的基向量,仍然得到一个和个人坐标系无关的矢量。
对两种运动方式来说,它们的数组不同,基向量不同,但是最后表示的是同一个矢量。总而言之,对个人来说,即使坐标系变化了,但是乘以对应坐标系的基向量,仍然得到一个和个人坐标系无关的矢量。
模拟水流:力的方向和大小都相同,但是如果作用点不一样,那么造成的效果也是完全不同的。当矢量力与另一个描述作用点的矢量结合我们就有一个叫“应力”的物理量(二阶张量的例子)。
