- 数学物理方法-姜颖-视频 对应课本[mathjax]
- 北京大学-邓卫真-讲义
- 复变函数中最令你惊艳的结论是什么?为什么?
- 学习复变函数与积分变换有什么用途?学习复变函数与积分变换有什么用途?—知乎
- 对物理学而言,哪些数学是重要的?
复变函数论
复数
复数的除法$$ z=\frac{z_{1}}{z_{2}}=\frac{x_{1}+i y_{1}}{x_{2}+i y_{2}} $$将分母实数化,然后计算$$ z=\frac{z_{1}}{z_{2}}=\frac{z_{1} z_{2}^{*}}{z_{2} z_{2}^{*}}=\frac{\left(x_{1} x_{2}+y_{1} y_{2}\right)+i\left(x_{2} y_{1}-x_{1} y_{2}\right)}{x_{2}^{2}+y_{2}^{2}} $$
有两个复数\(z_1\)和\(z_2\),证明(几何法和代数法都可以)$$ \left|z_{1}\right|-\left|z_{2}\right| \leq\left|z_{1}+z_{2}\right| \leq\left|z_{1}\right|+\left|z_{2}\right| $$推广\(\left|z_{1}+z_{2}+\cdots+z_{n}\right| \leq\left|z_{1}\right|+\left|z_{2}\right|+\cdots+\left|z_{n}\right|\)
欧拉公式:$$ e^{i x}=\cos x+i \sin x $$
欧拉公式的简单证明:
(1) 方法-1
指数函数的泰勒级数展开\(e^{a x}=\displaystyle\sum_{n=0}^{\infty} \displaystyle\frac{a^{n} x^{n}}{n !}\)
当把\(a=i\)以及\(x=\theta\)代入上述展开式并对实部和虚部进行归并后,我们有$$ e^{i \theta}=\left[1-\frac{\theta^{2}}{2}+\frac{\theta^{4}}{4 !}-\frac{\theta^{6}}{6 !}+\cdots\right]+i\left[\theta-\frac{\theta^{3}}{3 !}+\frac{\theta^{5}}{5 !}-\frac{\theta^{7}}{7 !}+\cdots\right]$$等式右边的实部正好是三角函数\( \cos \theta\)的泰勒展开式,而虚部正是\(\sin \theta\)的泰勒级数展开式。(2) 方法-2
由于\(\displaystyle\frac{d\left(e^{a x}\right)}{d x}=a e^{a x}\),所以有\(\displaystyle\frac{d e^{i \theta}}{d \theta}=i e^{i \theta}\),另外作为复数,\(e^{i \theta}\)一定可以一般性地表示为\(e^{i \theta}=r(\cos \alpha+i \sin \alpha)\),对该式子的两边同时对\( \theta \)求导,然后对比对应的系数,待定系数法求解证明。
【棣美弗定理】:\((\cos (x)+i \sin (x))^{n}=\cos (n x)+i \sin (n x)\)或者写成指数的形式\(z^{n}=\rho^{n} e^{i n \theta}\)
棣美弗定理应用实例:
\(\cos (5 \varphi)+i \sin (5 \varphi)=e^{i 5 \varphi}=\left(e^{i \varphi}\right)^{5}=(\cos (\varphi)+i \sin (\varphi))^{5}\),等式右侧展开,然后让实部与实部相等,虚部与虚部相等,即可以得到\(\cos (5 \varphi)=\cos ^{5} \varphi-10 \cos ^{3} \varphi \sin ^{2} \varphi+5 \cos \varphi \sin ^{4} \varphi\)
复球与无穷远点:
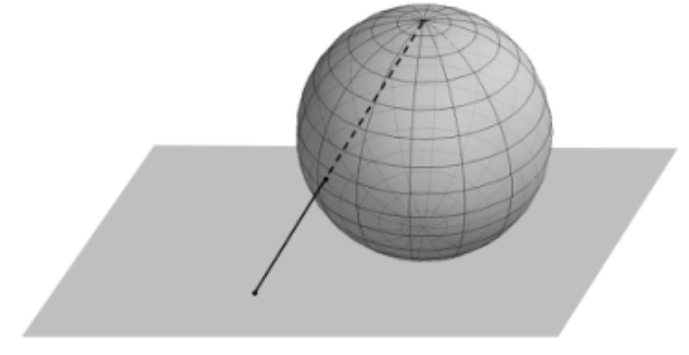 我们建立一个球面,然后让此球面与复平面在复平面的原点处相切,即球面的南极与复平面的原点重合。如图所示。之后将球面的北极与复平面上的任意一点直线相连,该直线必与球面相交于一点。这说明我们可以将球面上的点与复平面上的点也即整个复数域作对应。因此,这个球面我们就称之为复球面。从图上不难看出,复平面上所有距原点无穷远的点都对应于复球面上的北极点,从这个意义上讲,我们就把复平上无穷远处的点看作一个点,称为无穷远点。补充黎曼球面
我们建立一个球面,然后让此球面与复平面在复平面的原点处相切,即球面的南极与复平面的原点重合。如图所示。之后将球面的北极与复平面上的任意一点直线相连,该直线必与球面相交于一点。这说明我们可以将球面上的点与复平面上的点也即整个复数域作对应。因此,这个球面我们就称之为复球面。从图上不难看出,复平面上所有距原点无穷远的点都对应于复球面上的北极点,从这个意义上讲,我们就把复平上无穷远处的点看作一个点,称为无穷远点。补充黎曼球面
复变函数的概念

复变函数和实变函数类似,都要满足单值性。
复变函数区域的定义:
复平面上的一个点集\(D\),如果满足以下两个条件就可以称为区域。
开集性-(1) 对于点集\(D\)中的任何一点\(z_{0}\),总可以找到一个大于零的\(\varepsilon>0\),使得所有满足\(\left|z-z_{0}\right|<\varepsilon\)的点\(z\)都包含在该点集内;
连通性-(2) 点集内任何两点都可用由点集内的点构成的曲线连接起来。
注:有时我们也会考虑包含边界的情况,这个时候我们会用到闭区域的概念,它是由区域连同区域的所有边界一起构成的,写作\(\bar{D}=D+\partial D\)
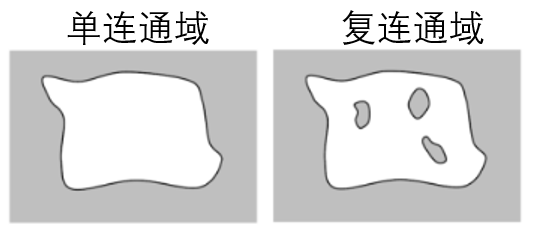
区域的分类:依据其连通性
复变函数的定义
\(z=\rho e^{i(\theta+2 n \pi)}\)辐角的多值性有可能造成 表达式的多值性$$ w=\sqrt{z}=\sqrt{\rho} e^{i\left(\frac{\theta}{2}+n \pi\right)}= \begin{cases}\sqrt{\rho} e^{i \frac{\theta}{2}}, & n=0,2,4,6, \cdots \\ -\sqrt{\rho} e^{i\frac{\theta}{2}}, & n=1,3,5, \cdots\end{cases} $$
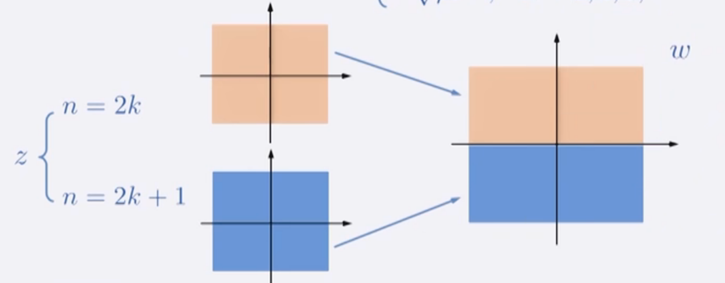 注:明明是一个点,开方后成了两个点。
注:明明是一个点,开方后成了两个点。
支点: 当自变量\(z\)围绕某点\(z_{0}\)转一圈回到原处后函数值变了,\(z_{0}\)即为该函数的支点。
 (1) \(w=\sqrt{z} \quad\) 支点: \(\quad z_{1}=0, \quad z_{2}=\infty\)
(1) \(w=\sqrt{z} \quad\) 支点: \(\quad z_{1}=0, \quad z_{2}=\infty\)
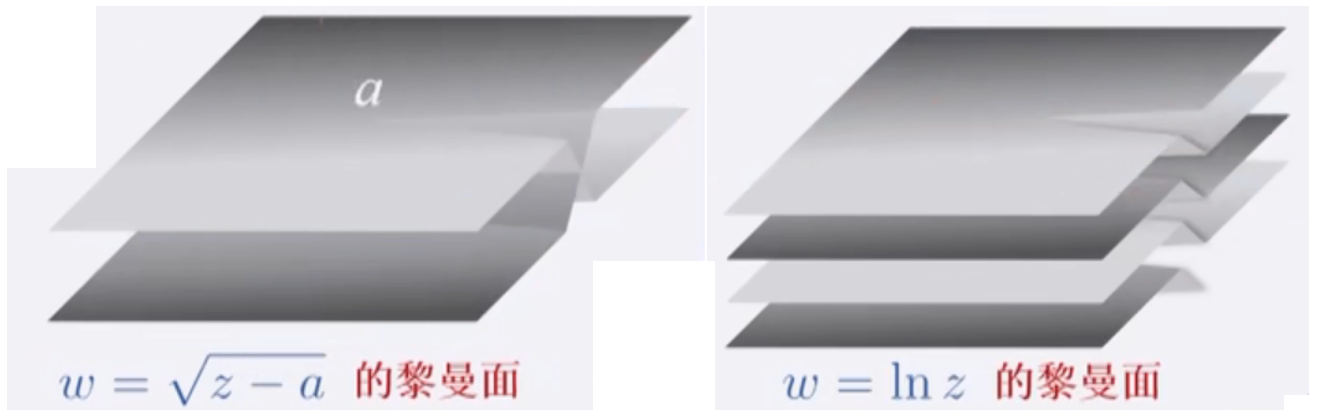
(2) \(w=\sqrt{z-a}\) 支点: \(\quad z_{1}=a, \quad z_{2}=\infty\)
(3) \(w=\ln z=\ln \left[\rho e^{i(\theta+2 n \pi)}\right]=\ln \rho+i(\theta+2 n \pi)\)
支点: \(\quad z_{1}=0, \quad z_{2}=\infty\)
黎曼面的分支个数由复变函数本身的性质决定。
复变函数的微分及解析函数的定义
复变函数 \(f(z)=u(x,y)+i v(x,y)\)
连续性:\(f(z)\)在\(z_{0}\)点及其邻域上有定义,且当沿任何路径\(z \rightarrow z_{0}\)时有$$\lim _{z \rightarrow z_{0}} f(z)=f\left(z_{0}\right) \quad f(z)$$则称函数在 \(z_{0}\)点连续。
如果\(f(z)\)在其定义域内处处连续\(\rightarrow f(z)\)为连续函数。
可导性:\(f(z)\)在\(z_{0}\)点连续,且当以任何方式\(\Delta z \rightarrow0\)时$$f^{\prime}\left(z_{0}\right) \equiv \lim _{\Delta z \rightarrow 0} \frac{f\left(z_{0}+\Delta z\right)-f\left(z_{0}\right)}{\Delta z}$$存在且唯一,那么我们说它是\(f(z)\)在\(z_{0}\)点的导数。
解析性:\(f(z)\) 在 \(z_{0}\)点及其邻域上各点均可导 \(\rightarrow f(z)\)在\(z_{0}\)点解析。
解析函数: \(f(z)\)在区域\(D\)上处处解析\(\rightarrow f(z)\) 为区域\(D\)上的解析函数。
导数计算:实变函数中关于导数的所有的公式都可用在复变函数上,只需将对应的公式中的自变量由实变量\(x\)替换为复变量\(z\)即可。
柯西黎曼条件:(函数可导或解析的必要条件)$$\left\{\begin{array}{l} \displaystyle\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y} \\ \displaystyle\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x} \end{array}\right.$$ 沿着第一条路径时\(\Delta z=\Delta x\)$$ f^{\prime}(z)=\lim _{\Delta x \rightarrow 0} \frac{[u(x+\Delta x,y)-u(x,y)]+i[v(x+\Delta x,y)-v(x,y)]}{\Delta x}=\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x} $$沿着第二条路径时\(\Delta z=i \Delta y\)$$ f^{\prime}(z)=\lim _{\Delta x \rightarrow 0} \frac{[u(x,y+\Delta y)-u(x,y)]+i[v(x,y+\Delta y)-v(x,y)]}{i \Delta y}=-i \frac{\partial u}{\partial y}+\frac{\partial v}{\partial y} $$由于此复变函数在该点可导, 这两个极限结果必须相等,于是我们可以推出直角坐标系下的柯西-黎曼条件。
沿着第一条路径时\(\Delta z=\Delta x\)$$ f^{\prime}(z)=\lim _{\Delta x \rightarrow 0} \frac{[u(x+\Delta x,y)-u(x,y)]+i[v(x+\Delta x,y)-v(x,y)]}{\Delta x}=\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x} $$沿着第二条路径时\(\Delta z=i \Delta y\)$$ f^{\prime}(z)=\lim _{\Delta x \rightarrow 0} \frac{[u(x,y+\Delta y)-u(x,y)]+i[v(x,y+\Delta y)-v(x,y)]}{i \Delta y}=-i \frac{\partial u}{\partial y}+\frac{\partial v}{\partial y} $$由于此复变函数在该点可导, 这两个极限结果必须相等,于是我们可以推出直角坐标系下的柯西-黎曼条件。
函数可导(或者解析)的充分必要条件:
(1) 函数的实部和虚部均为二元可微实函数;
(2) 满足柯西-黎曼条件。
证明:如果函数满足上述条件,那么在\(\displaystyle\lim _{\Delta x, \Delta y \rightarrow 0} \epsilon_{i}=0\)情况下$$ \begin{aligned} \Delta u &=\frac{\partial u}{\partial x} \Delta x+\frac{\partial u}{\partial y} \Delta y+\epsilon_{1} \Delta x+\epsilon_{2} \Delta y \\ \Delta v &=\frac{\partial v}{\partial x} \Delta x+\frac{\partial v}{\partial x} \Delta y+\epsilon_{3} \Delta x+\epsilon_{4} \Delta y \end{aligned} $$于是(用了柯西黎曼条件改写了\(i \Delta y\)前面的系数)$$ \begin{aligned} \Delta f &=\Delta u+i \Delta v \\ &=\left[\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x}\right] \Delta x+\left[\frac{\partial u}{\partial y}+i \frac{\partial v}{\partial y}\right] \Delta y+\left(\epsilon_{1}+i \epsilon_{3}\right) \Delta x+\left(\epsilon_{2}+i \epsilon_{4}\right) \Delta y \\ &=\left[\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x}\right] \Delta x+\left[\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x}\right] i \Delta y+\left(\epsilon_{1}+i \epsilon_{3}\right) \Delta x+\left(\epsilon_{2}+i \epsilon_{4}\right) \Delta y \\ &=\left[\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x}\right] \Delta z+\left(\epsilon_{1}+i \epsilon_{3}\right) \Delta x+\left(\epsilon_{2}+i \epsilon_{4}\right) \Delta y \end{aligned} $$最终得到(无论以任何方式趋近,这个比值都将存在,且唯一)$$ \lim _{\Delta z \rightarrow 0} \frac{\Delta f}{\Delta z}=\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x} $$
解析函数的特性-1:实部和虚部是调和函数。
对于解析函数\( f(z)=u(x,y)+i v(x,y)\),将柯西黎曼条件\( \displaystyle\frac{\partial u(x,y)}{\partial x}=\frac{\partial v(x,y)}{\partial y} \quad \displaystyle\frac{\partial u(x,y)}{\partial y}=-\frac{\partial v(x,y)}{\partial x}\)两个式子分别再对\(x\)和\(y\)做偏导数,得到\(\displaystyle\frac{\partial^{2} u(x,y)}{\partial x^{2}}=\frac{\partial^{2} v(x,y)}{\partial x \partial y} \quad \frac{\partial^{2} u(x,y)}{\partial y^{2}}=-\displaystyle\frac{\partial^{2} v(x,y)}{\partial x \partial y}\),于是得到拉普拉斯方程(第二个拉普拉斯方程也采用类似的方法得到)$$ \begin{aligned} &\frac{\partial^{2} u(x,y)}{\partial x^{2}}+\frac{\partial^{2} u(x,y)}{\partial y^{2}}=0 \\ &\frac{\partial^{2} v(x,y)}{\partial x^{2}}+\frac{\partial^{2} v(x,y)}{\partial y^{2}}=0 \end{aligned} $$解析函数的实部和虚部为满足柯西-黎曼条件的调和函数。如果随便给我们一个函数,怎么样非常简单地去判断它是不是解析函数,我们可以看看其实部和虚部是否满足调和函数,如果不满足的话,一定不是解析函数。
注:调和函数
解析函数的特性-2:解析函数与其自变量的复共轭无关\(\displaystyle\frac{\partial f(z)}{\partial z^{*}}=0\)。
对解析函数\(f(z)=u(x,y)+i v(x,y) \),其中的\(x=\displaystyle\frac{z+z^{*}}{2} \quad y=\displaystyle\frac{z-z^{*}}{2 i} \),那么将该表达式带入到原来的解析函数,似乎该解析函数同时是\( z\)和\(z^{*}\)的函数,即\( f(z) \equiv f\left(z,z^{*}\right)\)?$$\begin{aligned} \frac{\partial f}{\partial z^{*}} &=\frac{\partial f}{\partial x} \frac{\partial x}{\partial z^{*}}+\frac{\partial f}{\partial y} \frac{\partial y}{\partial z^{*}}=\frac{1}{2}\left[\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x}\right]+\frac{i}{2}\left[\frac{\partial u}{\partial y}+i \frac{\partial v}{\partial y}\right] \\ &=\frac{1}{2}\left[\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\right]+\frac{i}{2}\left[\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right]=0 \end{aligned}$$
解析函数的确定:由部分(实部或虚部)确定整个解析函数
仅仅已知了一个解析函数的实部 \(u(x,y)\) 以及该解析函数在某点 \(z_0\) 的取值 \(f(z_0)\), 如何确定该解析函数?
(1) 方法-1

(2) 方法-2
利用柯西-黎曼条件先找到解析函数的导数
对于\(f(z)=u(x,y)+i v(x,y)\),其中\(z=x+i y\),既然函数沿着任意方向对\( z\)求导都能得到相同且唯一的导数,那么我们就可以直接选取沿着实轴\(x\)方向去求导,$$ \frac{d f}{d z}=\frac{\partial f}{\partial x}=\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x}=\frac{\partial u}{\partial x}-i \frac{\partial u}{\partial y} \equiv g(z) $$因此\( f(z)=\displaystyle\int g(z) d z+C\)
实例:已知一个解析函数 \(f(z)\) 的实部 为 \(u(x,y)=2 x y\) 且 \(f(0)=0\), 求该解析函数的表达式。根据上述方法有$$\begin{array}{l} \displaystyle\frac{d f}{d z} =\frac{\partial u}{\partial x}-i \frac{\partial u}{\partial y}=2 y-2 i x=-i 2(x+i y)=-i 2 z \\ f =-i z^{2}+C \end{array}$$
(3) 方法-3 (没看懂)$$\begin{array}{l} f(z)=u(x,y)+i v(x,y) \\ [f(z)]^{*}=u(x,y)-i v(x,y) \\ u(x,y)=\displaystyle\frac{f(z)+[f(z)]^{*}}{2} \\ v(x,y)=\displaystyle\frac{f(z)-[f(z)]^{*}}{2 i} \end{array}$$于是(加上\( iC \)是赋予一定的自由度)$$u(x,y)=u\left(\frac{z+z^{*}}{2}, \frac{z-z^{*}}{2 i}\right)=h(z)+g\left(z^{*}\right)=h(z)+[h(z)]^{*}=[h(z)+i C]+[h(z)+i C]^{*}$$其实部对应于\(u(x,y)\)的实部即\( \displaystyle\frac { f(z)}{2 } \),因此$$ f(z)=2 h(z)+i C $$求解前面的例子$$ u(x,y)=2 x y=2 \frac{z+z^{*}}{2} \frac{z-z^{*}}{2 i}=\frac{z^{2}+\left(z^{*}\right)^{2}}{2 i} \quad f(z)=-i z^{2}+i C $$
复变函数的积分
单连通区域上柯西积分定理
对于一般函数的积分(之前学过的),积分结果一般依赖于积分路径。
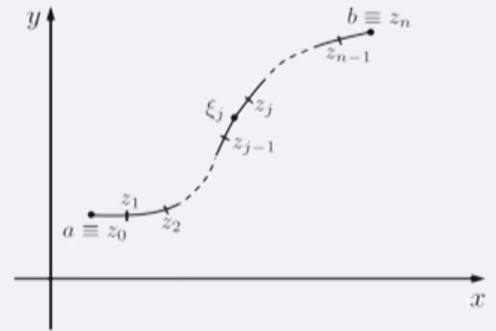 $$\begin{array}{l} \displaystyle\int_{L} f(z) d z \equiv \lim _{n \rightarrow \infty} \sum_{j=1}^{n} f\left(\xi_{j}\right)\left(z_{j}-z_{j-1}\right) \\ \displaystyle\int_{L}\left[f_{1}(z)+f_{2}(z)\right] d z=\int_{L} f_{1}(z) d z+\int_{L} f_{2}(z) d z \\ \displaystyle\int_{-L} f(z) d z=-\int_{L} f(z) d z \\ \displaystyle\int_{L_{1}} f(z) d z+\int_{L_{2}} f(z) d z=\int_{L_{1}+L_{2}} f(z) d z \end{array}$$单连通区域上柯西积分定理:$$\oint_{C} f(z) d z=0$$
$$\begin{array}{l} \displaystyle\int_{L} f(z) d z \equiv \lim _{n \rightarrow \infty} \sum_{j=1}^{n} f\left(\xi_{j}\right)\left(z_{j}-z_{j-1}\right) \\ \displaystyle\int_{L}\left[f_{1}(z)+f_{2}(z)\right] d z=\int_{L} f_{1}(z) d z+\int_{L} f_{2}(z) d z \\ \displaystyle\int_{-L} f(z) d z=-\int_{L} f(z) d z \\ \displaystyle\int_{L_{1}} f(z) d z+\int_{L_{2}} f(z) d z=\int_{L_{1}+L_{2}} f(z) d z \end{array}$$单连通区域上柯西积分定理:$$\oint_{C} f(z) d z=0$$ 解析函数在其单连通解析区域的积分,约定的方向是逆时针。$$\begin{aligned} \oint_{C} f(z) d z &=\oint_{C}[u(x,y)+i v(x,y)](d x+i d y) \\ &=\oint_{C}[u d x-v d y]+i \oint_{C}[u d y+v d x]\\ &= \iint_{\Sigma}[-\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}] d x d y+i \iint_{\Sigma}[\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}] d x d y \\& = 0\end{aligned}$$注:
解析函数在其单连通解析区域的积分,约定的方向是逆时针。$$\begin{aligned} \oint_{C} f(z) d z &=\oint_{C}[u(x,y)+i v(x,y)](d x+i d y) \\ &=\oint_{C}[u d x-v d y]+i \oint_{C}[u d y+v d x]\\ &= \iint_{\Sigma}[-\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}] d x d y+i \iint_{\Sigma}[\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}] d x d y \\& = 0\end{aligned}$$注:
(1) 线积分变面积分用到了格林公式\(\displaystyle\oint_{C}[P d x+Q d y]=\displaystyle\iint_{\Sigma}\left[-\frac{\partial P}{\partial y}+\frac{\partial Q}{\partial x}\right] d x d y\)
(2) 最后一步用到了柯西-黎曼条件\(\displaystyle\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y} \quad \quad \displaystyle\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}\)
(3) 单连通域上解析函数的积分只决定于起止位置而与路径无关。
复连通域上解析函数的柯西积分定理
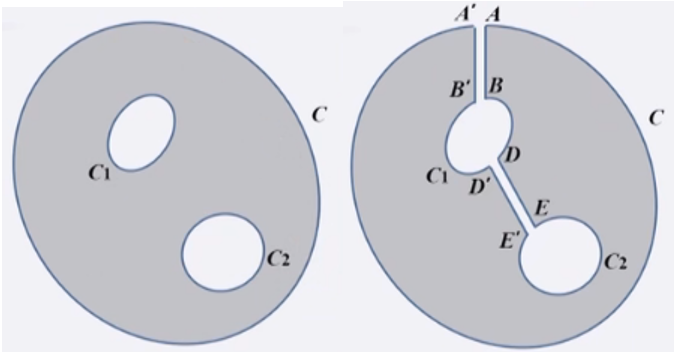 重新构造积分积分回路
重新构造积分积分回路
\(L=A^{\prime} A+A B+B D+D E+E E^{\prime}+E^{\prime} D^{\prime}+D^{\prime} B^{\prime}+B^{\prime} A^{\prime}\)
L构成了单连通域的边界\(\int_{L} f(z) d z=0\)
函数在解析区域的连续性$$ \int_{A}^{B} f(z) d z+\int_{B^{\prime}}^{A^{\prime}} f(z) d z=0, \quad \int_{D}^{E} f(z) d z+\int_{E^{\prime}}^{D^{\prime}} f(z) d z=0 $$ $$ \int_{B}^{D} f(z) d z+\int_{D^{\prime}}^{B^{\prime}} f(z) d z=\oint_{C_{1}} f(z) d z, \quad \int_{E}^{E^{\prime}} f(z) d z=\oint_{C_{2}} f(z) d z, \quad \int_{A^{\prime}}^{A} f(z) d z=\oint_{C} f(z) d z $$根据前面的单连通区域上柯西积分定理,可以知道沿着\( L\)回路积分的结果为零,因此得到$$ \oint_{C} f(z) d z=\oint_{C_{1}} f(z) d z+\oint_{C_{2}} f(z) d z $$更一般的情况$$ \oint_{C} f(z) d z=\sum_{n=1}^{N} \oint_{C_{n}} f(z) d z $$
柯西积分公式
$$f\left(z_{0}\right)=\frac{1}{2 \pi i} \oint_{C} \frac{f(z)}{z-z_{0}} d z$$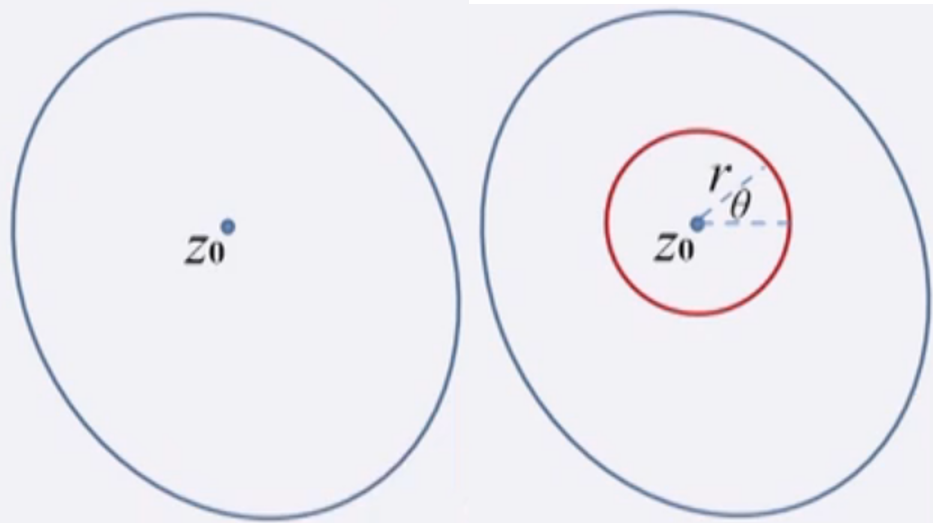
\(C\) 所包周区域为\(f(z)\)单连通解析区域,\(z_0\)为区域内一点。由于分母的存在,上式中的被积函数在积分回路\(C\)所包围的区域内不解析,存在奇点\(z_{0}\),因此,被积函数的解析区域是一个多连通域。于是,如图利用上述多连通域上的柯西积分定理,我们可以将积分回路连续形变到一个以\(z_{0}\)为圆心半径为\(r\)的圆\(C^{r}\)上,即$$ \begin{aligned} \oint_{C} \frac{f(z)}{z-z_{0}} d z &=\oint_{C_{r}} \frac{f(z)}{z-z_{0}} d z \quad z \in C_{r} \quad z=z_{0}+r e^{i \theta} \\ &=\int_{0}^{2 \pi} \frac{f\left(z_{0}+r e^{i \theta}\right)}{r e^{i \theta}} i r e^{i \theta} d \theta=i \int_{0}^{2 \pi} f\left(z_{0}+r e^{i \theta}\right) d \theta \end{aligned} $$无限缩小\(r\),得到$$ \oint_{C} \frac{f(z)}{z-z_{0}} d z=\lim _{r \rightarrow 0} \oint_{C_{r}} \frac{f(z)}{z-z_{0}} d z=i \lim _{r \rightarrow 0} \int_{0}^{2 \pi} f\left(z_{0}+r e^{i \theta}\right) d \theta=2 \pi i f\left(z_{0}\right) $$如果\(f(z)\)是常数\(1\),那么有下面很常用的关系式(其中 \(\Sigma_{C}\) 为 \(C\)所包围的区域)$$ \frac{1}{2 \pi i} \oint_{C} \frac{1}{z-z_{0}} d z= \begin{cases}1, & z_{0} \in \Sigma_{C} \\ 0, & z_{0} \notin \Sigma_{C}\end{cases} $$对于一个解析函数\(f(z)=\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\xi-z} d \xi\),其xx\( \)阶导数为$$f^{(n)}(z)=\frac{n !}{2 \pi i} \oint_{C} \frac{f(\xi)}{(\xi-z)^{n+1}} d \xi$$解析函数是任意阶可导的!解析函数的任何阶导数也均是解析函数。
最大模定理
设复变函数\(f(z)\)在闭区域\( \bar{D}\)上解析,则该复变函数的模\(|f(z)|\)的最大值只能出现在该区域的边界上,除非这个函数是常数。
证明:因为\(f(z)\)是解析函数,因此\([f(z)]^{n}\)也是解析函数,关于它的柯西积分公式为$$ [f(z)]^{n}=\frac{1}{2 \pi i} \oint_{C} \frac{[f(\xi)]^{n}}{\xi-z} d \xi $$其中积分回路\(C\)为该闭区域的边界,\(z\)为该区域内的一点。设点\(z\)到边界的最短距离为\(d\),即式中 \(|\xi-z| \geq d\), 复变函数 \(f(\xi)\)在边界\(C\)上的最大模为\(M\),于是有$$ \begin{aligned} |f(z)|^{n} &=\left|[f(z)]^{n}\right|=\left|\frac{1}{2 \pi i} \oint_{C} \frac{[f(\xi)]^{n}}{\xi-z} d \xi\right| \\ & \leq \frac{1}{2 \pi} \oint_{C} \frac{\left|[f(\xi)]^{n}\right|}{|\xi-z|}|d \xi| \leq \frac{1}{2 \pi} \oint_{C} \frac{M^{n}}{d}|d \xi|=\frac{M^{n} \ell}{2 \pi d} \end{aligned} $$其中 \(\ell\) 为该区域边界的长度。对上式结果两边同时开\(n\)次方,得$$ |f(z)| \leq M\left(\frac{\ell}{2 \pi d}\right)^{1 / n} $$因为上面的讨论对于任意的\(n\)均成立,因此令\(n \rightarrow \infty\),我们就得到\(|f(z)| \leq M\)
解析函数的幂级数展开
一般复变函数回路积分最终结果的计算方法,需要我们对复变函数在特定区域上作级数展开。级数展开不论在工程实际应用中还是科学理论研究方面都有者十分重要的意义。
幂级数及其收敛半径
$$ \sum_{n=0}^{\infty}a_{n}\left(z-z_{0}\right)^{n}=a_{0}+a_{1}\left(z-z_{0}\right)+a_{2}\left(z-z_{0}\right)^{2}+\cdots+a_{k}\left(z-z_{0}\right)^{k}+\cdots $$其中复常数\(a_{n}\)称为幂级数系数,而复常数\(z_{0}\)称为该幂级数的中心。
无穷级数最重要的性质就是其敛散性,一个函数如果在某点展开成无穷级数的话,则必须要求该级数能在此点收敛,否则这样的展开就毫无意义。下面讨论一下无穷级数的敛散性。
对于一个一般性的函数项级数\(\displaystyle\sum_{n=0}^{\infty} w(z)\),如果在某点\(z\)它的部分和的极限存在,即$$ \lim _{k \rightarrow \infty} \sum_{n=0}^{k} w(z)=S $$则称该级数在\(z\)点收敛,否则称该级数在此点发散;
补充
泰勒级数
\(f(z)\) 在以\(z_0\)为圆心的圆域内解析,则对于该圆域内任点\(z\), 有泰勒级数展开$$ \begin{aligned} &f(z)=\sum_{n=0}^{\infty} a_{n}\left(z-z_{0}\right)^{n} \\ &a_{n}=\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\left(\xi-z_{0}\right)^{n+1}} d \xi=\frac{f^{(n)}\left(z_{0}\right)}{n !} \end{aligned} $$(1) 展开中心点\(z_0\)必须是函数的解析点;
(2) 展开区域必须是以\(z_0\)为圆心的解析圆域;
(3) 级数没有非负幂次项。
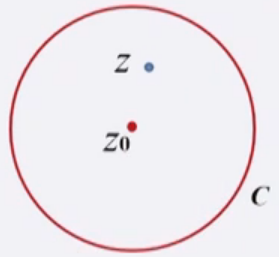 证明:$$ \begin{aligned} f(z) &=\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\xi-z} d \xi=\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\left(\xi-z_{0}\right)-\left(z-z_{0}\right)} d \xi \\ &=\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\xi-z_{0}} \frac{1}{1-\frac{z-z_{0}}{\xi-z_{0}}} d \xi \\ &=\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\xi-z_{0}} \sum_{n=0}^{\infty} \frac{\left(z-z_{0}\right)^{n}}{\left(\xi-z_{0}\right)^{n}} d \xi \\ f(z) &=\sum_{n=0}^{\infty}\left[\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\left(\xi-z_{0}\right)^{n+1}} d \xi\right]\left(z-z_{0}\right)^{n} \end{aligned} $$注:
证明:$$ \begin{aligned} f(z) &=\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\xi-z} d \xi=\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\left(\xi-z_{0}\right)-\left(z-z_{0}\right)} d \xi \\ &=\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\xi-z_{0}} \frac{1}{1-\frac{z-z_{0}}{\xi-z_{0}}} d \xi \\ &=\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\xi-z_{0}} \sum_{n=0}^{\infty} \frac{\left(z-z_{0}\right)^{n}}{\left(\xi-z_{0}\right)^{n}} d \xi \\ f(z) &=\sum_{n=0}^{\infty}\left[\frac{1}{2 \pi i} \oint_{C} \frac{f(\xi)}{\left(\xi-z_{0}\right)^{n+1}} d \xi\right]\left(z-z_{0}\right)^{n} \end{aligned} $$注:
(1) 幂级数展开\(\displaystyle\frac{1}{1-t}=\displaystyle\sum_{n=0}^{\infty} t^{n}, \quad|t|<1\)
(2) 交换求和和积分的顺序。
泰勒级数展开的收敛半径$$\begin{aligned} &R=\lim _{n \rightarrow \infty} \frac{1}{\sqrt[n]{\left|a_{n}\right|}} \\ &R=\lim _{n \rightarrow \infty}\left|\frac{a_{n}}{a_{n+1}}\right| \end{aligned}$$以上泰勒级数展开讨论的唯一条件是\(f(z)\)在以\(z_0\)为圆心的圆域内解析。
\(R=\left|z_{0}-z_{1}\right|\),其中\(z_1\)为离\(z_0\)最近的函数\(f(z)\)的奇点。
泰勒级数讨论最大模定理和刘维尔定理
Kronecker-\(\delta\) 符号$$ \frac{1}{2 \pi} \int_{0}^{2 \pi} e^{i(n-m) \theta} d \theta=\left\{\begin{array}{cc} 0, & m \neq n \\ 1, & m=n \end{array}\right\} \equiv \delta_{m n} $$具有挑选性$$ \sum_{m,n=0}^{\infty} a_{m} b_{n} \delta_{m n}=\sum_{n=0}^{\infty} a_{n} b_{n} $$最大模定理:设复变函数 \(f(z)\) 在闭区域\( \bar{D}\)上解析, 则该复变函数的模\(|f(z)|\) 的最大值只能出现在该区域的边界上, 除非这个函数是常数。
证明:反证法,假设(\( z_0\)在区域内,不在边界上)$$\left|f\left(z_{0}\right)\right|=\max |f(z)|, \quad z_{0} \in \Sigma, \quad z_{0} \notin \partial \Sigma $$以\( z_0\)为中心做泰勒级数展开
\(f(z)=\displaystyle\sum_{n=0}^{\infty} a_{n}\left(z-z_{0}\right)^{n}, \quad a_{0} \equiv f\left(z_{0}\right)\) $$ \begin{aligned} \left|a_{0}\right|^{2} &=\frac{1}{2 \pi} \int_{0}^{2 \pi}\left|a_{0}\right|^{2} d \theta=\frac{1}{2 \pi} \int_{0}^{2 \pi}\left|f\left(z_{0}\right)\right|^{2} d \theta \geq \frac{1}{2 \pi} \int_{0}^{2 \pi}|f(z)|^{2} d \theta=\frac{1}{2 \pi} \int_{0}^{2 \pi} f^{*}(z) f(z) d \theta \\ &=\frac{1}{2 \pi} \int_{0}^{2 \pi} \sum_{m=0}^{\infty} a_{m}^{*}\left[\left(z-z_{0}\right)^{*}\right]^{m} \sum_{n=0}^{\infty} a_{n}\left(z-z_{0}\right)^{n} d \theta \\ &=\sum_{m,n=0}^{\infty} a_{m}^{*} a_{n} r^{m+n} \frac{1}{2 \pi} \int_{0}^{2 \pi} e^{i(n-m) \theta} d \theta=\sum_{m,n=0}^{\infty} a_{m}^{*} a_{n} r^{m+n} \delta_{m n}=\sum_{n=0}^{\infty} a_{n}^{*} a_{n} r^{2 n} \end{aligned} $$因此和假设矛盾$$ \left|a_{0}\right|^{2} \geq \sum_{n=0}^{\infty}\left|a_{n}\right|^{2} r^{2 n} \longrightarrow a_{n}=0, \quad n \neq 0 $$注:\(z-z_{0}=r e^{i \theta}\)
刘维尔定理: 在全复平面内解析且有界(即最大模)的复变函数必为常函数。

解析函数的零点及其孤立性
解析函数零点的定义:\(f(z)\)在\(z_0\)点有 \(f(z_0)=0\),且\(f(z)\)在以\(z_0\)为圆心的圆域内的泰勒级数展开式最低幂次为\(k\)次$$ f(z)=\sum_{n=k}^{\infty} a_{n}\left(z-z_{0}\right)^{n} $$\(z_0\) 为 \(f(z)\)的 \(k\)阶零点$$f\left(z_{0}\right)=f^{\prime}\left(z_{0}\right)=f^{\prime \prime}\left(z_{0}\right)=\cdots f^{(k-1)}\left(z_{0}\right)=0, \quad f^{(k)}\left(z_{0}\right) \neq 0 $$非常函数的解析函数的零点必定是孤立的!
\(f(z)\)在\(z_0\)点有一定存在一个\(r\),使得在\(|z-z_0|<r\) 的区域内除了\(z_ 0\)点外函数\(f(z)\)不存在其他零点。
洛朗级数
由上面看到,如果\(z\)点包含在以\(z_{0}\)点为圆心的函数\(f(z)\)的单连通解析圆域内,则\(f(z)\)在此点可展开成以\(z_{0}\)为中心的泰勒级数。如果\(z\)点包含在以\(z_{0}\)点为圆心的函数\(f(z)\)的解析环域内的话,即如果\(z_{0}\)点本身是\(f(z)\)的奇点,或以\(z_{0}\)为圆心的圆向\(z\)点扩张时需扫过\(f(z)\)的非解析区域的话,则函数在此点需展开成洛朗级数。
洛朗定理: \(f(z)\)在以\(z_{0}\)为圆心、内半径和外半径分别为\(R_{1}\)和\(R_{2}\)的环域内解析,则在此区域内\(f(z)\)可展为洛朗级数$$ f(z)=\sum_{n=-\infty}^{\infty} a_{n}\left(z-z_{0}\right)^{n}, \quad a_{n}=\frac{1}{2 \pi i} \oint_{C}\left(\xi-z_{0}\right)^{-n-1} f(\xi) d \xi $$其中\(C\)为此解析环域内任意一个闭合曲线。我们看到,洛朗级数就是一个双边幂级数。
证明:$$\begin{array}{l} f(z)=\displaystyle\frac{1}{2 \pi i} \oint_{L} \frac{f(\xi)}{\xi-z} d \xi=\frac{1}{2 \pi i} \oint_{C_{2}} \frac{f(\xi)}{\xi-z} d \xi-\frac{1}{2 \pi i} \oint_{C_{1}} \frac{f(\xi)}{\xi-z} d \xi\\ \displaystyle\frac{1}{2 \pi i} \oint_{C_{2}} \frac{f(\xi)}{\left(\xi-z_{0}\right)-\left(z-z_{0}\right)} d \xi=\frac{1}{2 \pi i} \oint_{C_{2}} \frac{f(\xi)}{\xi-z_{0}} \sum_{n=0}^{\infty} \frac{\left(z-z_{0}\right)^{n}}{\left(\xi-z_{0}\right)^{n}} d \xi\\ -\displaystyle\frac{1}{2 \pi i} \oint_{C_{1}} \frac{f(\xi)}{\left(\xi-z_{0}\right)-\left(z-z_{0}\right)} d \xi=\frac{1}{2 \pi i} \oint_{C_{2}} \frac{f(\xi)}{z-z_{0}} \frac{1}{1-\frac{\xi-z_{0}}{z-z_{0}}} d \xi=\frac{1}{2 \pi i} \oint_{C_{2}} \frac{f(\xi)}{z-z_{0}} \sum_{n=0}^{\infty} \frac{\left(\xi-z_{0}\right)^{n}}{\left(z-z_{0}\right)^{n}} d \xi\\ f(z)=\displaystyle\sum_{n=0}^{\infty}\left[\frac{1}{2 \pi i} \oint_{C_{2}} \frac{f(\xi)}{\left(\xi-z_{0}\right)^{n+1}} d \xi\right]\left(z-z_{0}\right)^{n}+\sum_{n=-\infty}^{-1}\left[\frac{1}{2 \pi i} \displaystyle\oint_{C_{1}} \displaystyle\frac{f(\xi)}{\left(\xi-z_{0}\right)^{n+1}} d \xi\right]\left(z-z_{0}\right)^{n} \end{array}$$
留数定理在实变函数积分中的应用
复变函数的色散关系
