英语词汇学习:[mathjax]
sideway force 侧向力
parallelepiped [pærəle'lepɪped] 平行六面体
parallelogram [ˌpærəˈleləɡræm] 平行四边形
contour [ˈkɒntʊə(r)] plot 等值线
Earth's gravitational field 地球重力场 [ˌɡrævɪˈteɪʃənl]
breadth n. 宽度 [bredθ] (length/breadth/height)
perturbation [ˌpɜːtəˈbeɪʃn] (尤指不寻常的)小变化,微扰
rectangular box 长方形盒子
expanding and contracting 扩张(膨胀)和压缩
heat transfer and wave motion热传递和波动
vorticity [vɔr'tɪsɪti] 旋量
vortex [ˈvɔːrteks] n. [航][流] 涡流;漩涡;(动乱,争论等的)中心;旋风
irrotational 无旋的;无漩涡的
cumbersome [ˈkʌmbərsəm] adj. 笨重的;累赘的;难处理的
suffix [ˈsʌfɪks] n. 后缀,词尾
summation convention 爱因斯坦求和约定
substitution tensor 替换张量
cyclic permutation 循环置换
neat and elegant expression 简介和优雅的表达
suffix notation
前面我们已经学过了张量的一些最基本的内容(电动力学-张量补充),但是对于如何将向量微积分运用到梯度、散度、旋度、三重积(混合积)等的运算还没有详细学习。这里运用suffix notation的好处一个是让向量微积分的表达式更加简洁,更重要的是可以让向量微积分的一些运算或者证明公式变得更加容易。工具很重要!
前面已经学过了哑指标(求和)和自由指标,这里不赘述。
向量加法
\( \boldsymbol{c}=\boldsymbol{a}+\boldsymbol{b}\)等价于\( c_{i}=a_{i}+b_{i}\),当然写成\( c_{j}=a_{j}+b_{j}\)或者\( c_{k}=a_{k}+b_{k}\)都可以。
向量点乘
\( \boldsymbol{a} \cdot \boldsymbol{b}=\sum_{j=1}^{3} a_{j} b_{j}=a_{j} b_{j}\)
\((\boldsymbol{a} \cdot \boldsymbol{b})(\boldsymbol{c} \cdot \boldsymbol{d})=a_{j} b_{j} c_{k} d_{k} \)因为每一项的顺序都是任意的,说以又可以写成\( c_{k} a_{j} d_{k} b_{j}\)。
例子
(1) \( a_{j} b_{i} c_{j}=\sum_{j=1}^{3} a_{j} b_{i} c_{j}=(\boldsymbol{a}\cdot \boldsymbol{c}) b_{i} =(\boldsymbol{a} \cdot \boldsymbol{c}) \boldsymbol{b}\)
(2) 对于\( \boldsymbol{u}+(\boldsymbol{a} \cdot \boldsymbol{b}) \boldsymbol{v}=|\boldsymbol{a}|^{2}(\boldsymbol{b} \cdot \boldsymbol{v}) \boldsymbol{a}\),我们先写成$$u_{i}+(\boldsymbol{a} \cdot \boldsymbol{b}) v_{i}=(\boldsymbol{a} \cdot \boldsymbol{a})(\boldsymbol{b} \cdot \boldsymbol{v}) a_{i}$$然后引入哑指标写成$$u_{i}+a_{j} b_{j} v_{i}=a_{j} a_{j} b_{k} v_{k} a_{i}$$(3) 对于两个\( N \)阶方阵\( A\)和\( B \),有\(C=A B \),可以表示为$$C_{i j}=A_{i 1} B_{1 j}+A_{i 2} B_{2 j} \ldots+A_{i N} B_{N j}=\sum_{k=1}^{N} A_{i k} B_{k j}=A_{i k} B_{k j}$$矩阵的迹可以表示为$$\operatorname{Tr}(A B)=\operatorname{Tr}\left(A_{i k} B_{k j}\right)=A_{j k} B_{k j}$$和\( BA\)的迹相等,证明如下:$$\begin{aligned} \operatorname{Tr}(B A) &=B_{j k} A_{k j} \\ &=A_{k j} B_{j k} \\ &=A_{j k} B_{k j} \\ &=\operatorname{Tr}(A B) \end{aligned}$$注意:\( j \leftrightarrow k\)交换不影响。
Kronecker delta (置换张量)
$$\delta_{i j}=\left\{\begin{array}{ll} 1 & \text { if } i=j \\ 0 & \text { if } i \neq j \end{array}\right.$$\( \delta_{i j}\)可以看作是一个非常简单的张量,对应的是一个三阶单位阵$$\delta_{i j}=\left(\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right)$$根据对称性,很容易知道\( \delta_{i j}=\delta_{j i}\)。
置换张量
前面提到的\(\delta_{i j} \)其实是一个substitution tensor,特点如下$$\delta_{i j} a_{j}=a_{i}$$作用于\( a_{j}\)之后可以把下标换成\(i \),证明如下$$\delta_{i j} a_{j}=\sum_{j=1}^{3} \delta_{i j} a_{j}=\delta_{i 1} a_{1}+\delta_{i 2} a_{2}+\delta_{i 3} a_{3}$$置换张量和点积的关系$$\delta_{i j} a_{i} b_{j}=\sum_{i=1}^{3} \sum_{j=1}^{3} \delta_{i j} a_{i} b_{j}=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}=a \cdot b$$当然\( \boldsymbol{a} \cdot \boldsymbol{b}=a_{i} b_{i}=a_{i} \delta_{i j} b_{j}=\delta_{i j} a_{i} b_{j}\)
例子
(1) 计算\( \delta_{j j} \)$$\delta_{j j}=\sum_{j=1}^{3} \delta_{j j}=\delta_{11}+\delta_{22}+\delta_{33}=3$$
(2) 简化\( \delta_{i j} \delta_{j k}\)$$\delta_{i j} \delta_{j k}=\sum_{j=1}^{3} \delta_{i j} \delta_{j k}=\delta_{i 1} \delta_{1 k}+\delta_{i 2} \delta_{2 k}+\delta_{i 3} \delta_{3 k}=\delta_{i k}$$注:置换张量这里的作用就是将\( \delta_{j k} \)的下标\( j \)变成\( i \)。
Alternating tensor \( \epsilon_{i j k}\) (交错张量)
这个张量的好处是让叉乘和旋度的求解变得更加方便。交错张量的定义为$$\epsilon_{i j k}=\left\{\begin{array}{ll} 0 & \text { if any of } i, j, k \text { are equal } \\ +1 & \text { if }(i, j, k)=(1,2,3),(2,3,1) \text { or }(3,1,2) \\ -1 & \text { if }(i, j, k)=(1,3,2),(2,1,3) \text { or }(3,2,1) \end{array}\right.$$交错张量的对称性特点:
(1) \( \epsilon_{i j k}=\epsilon_{j k i}=\epsilon_{k i j}\)
(2) 交换一次变号\( \epsilon_{i j k}=-\epsilon_{j i k}\)
交错张量和叉乘/混合积的关系$$(\boldsymbol{a} \times \boldsymbol{b})_{i}=\epsilon_{i j k} a_{j} b_{k}$$取\( i=1\),那么$$\epsilon_{1 j k} a_{j} b_{k}=\sum_{j=1}^{3} \sum_{k=1}^{3} \epsilon_{1 j k} a_{j} b_{k}$$考虑两种非零的情况\( j=2, k=3\)和\(j=3, k=2 \),于是上式最终的结果为\( \epsilon_{123} a_{2} b_{3}+\epsilon_{132} a_{3} b_{2}=a_{2} b_{3}-a_{3} b_{2}\)。
三阶矩阵行列式的值可以表示为$$|M|=\epsilon_{i j k} M_{1 i} M_{2 j} M_{3 k}$$,里面出现的\( 123\)表示已经限定从第一、二、三行各挑出一个元素进行相乘。与之相关的公式为$$\epsilon_{p q r}|M|=\epsilon_{i j k} M_{p i} M_{q j} M_{r k}$$三重积(混合积)可以表示为\( \boldsymbol{a} \cdot \boldsymbol{b} \times \boldsymbol{c}=a_{i}(\boldsymbol{b} \times \boldsymbol{c})_{i}=a_{i} \epsilon_{i j k} b_{j} c_{k}=\epsilon_{i j k} a_{i} b_{j} c_{k}\)
例子
(1) $$\begin{aligned} \boldsymbol{a} \cdot \boldsymbol{b} \times \boldsymbol{c} &=\epsilon_{i j k} a_{i} b_{j} c_{k} \\ &=\epsilon_{kij} a_{i} b_{j} c_{k} \\ &=(\boldsymbol{a} \times \boldsymbol{b})_{k} c_{k} \\ &=\boldsymbol{a} \times \boldsymbol{b} \cdot \boldsymbol{c} \end{aligned}$$注:这里用到了\(\epsilon_{i j k}=\epsilon_{k i j} \)
(2)
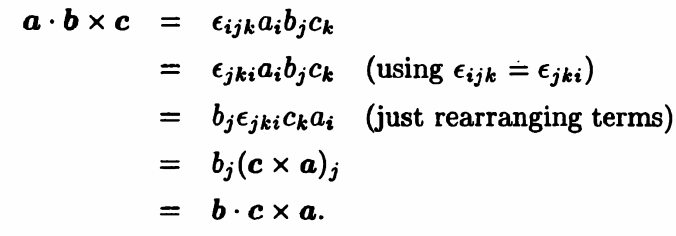 (3) 计算\( \epsilon_{i i k}=0\)
(3) 计算\( \epsilon_{i i k}=0\)
(4) 计算$$\epsilon_{i j k} \epsilon_{i j k}=\epsilon_{123}^{2}+\epsilon_{132}^{2}+\epsilon_{213}^{2}+\epsilon_{231}^{2}+\epsilon_{312}^{2}+\epsilon_{321}^{2}=6$$
\( \epsilon_{i j k}\)和\( \delta_{i j}\)之间的关系
$$\epsilon_{i j k} \epsilon_{k l m}=\delta_{i l} \delta_{j m}-\delta_{i m} \delta_{j l}$$这个公式主要用于两个叉乘的运算。
例子:用上面的公式推导双叉乘运算

梯度/散度/旋度的后缀表示
梯度
本来的写法为\( \nabla f=\left(\frac{\partial f}{\partial x_{1}}, \frac{\partial f}{\partial x_{2}}, \frac{\partial f}{\partial x_{3}}\right)\),后缀表示法$$[\nabla f]_{i}=\frac{\partial f}{\partial x_{i}}$$梯度算子可以改写为$$[\nabla]_{i}=\frac{\partial}{\partial x_{i}}$$散度$$ \boldsymbol{\nabla} \cdot \boldsymbol{u}=\frac{\partial u_{1}}{\partial x_{1}}+\frac{\partial u_{2}}{\partial x_{2}}+\frac{\partial u_{3}}{\partial x_{3}}=\frac{\partial u_{j}}{\partial x_{j}} $$旋度
运用后缀表示法,第一个分量可以写成$$[\nabla \times \boldsymbol{u}]_{1}=\frac{\partial u_{3}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{3}}=\epsilon_{1 j k} \frac{\partial u_{k}}{\partial x_{j}}$$其中\( jk\)都是哑指标,有两种组合方式,然后求和。总的表示方法为$$[\nabla \times \boldsymbol{u}]_{i}=\epsilon_{i j k} \frac{\partial u_{k}}{\partial x_{j}}$$注:散度公式其实可以直接借用\( (\boldsymbol{a} \times \boldsymbol{b})_{i}=\epsilon_{i j k} a_{j} b_{k} \)和\( [\nabla]_{i}=\frac{\partial}{\partial x_{i}}\)推导出来。
例子
位置向量\( \boldsymbol{r}=\left(x_{1}, x_{2}, x_{3}\right)\),利用suffix notationq求解\( \nabla \boldsymbol{r}, \nabla \cdot \boldsymbol{r} \text { and } \nabla \times \boldsymbol{r}\)?
解:先有$$\begin{aligned} \frac{\partial x_{i}}{\partial x_{j}} &=\left\{\begin{array}{ll} 1 & \text { if } i=j \\ 0 & \text { if } i \neq j \end{array}\right.\\ &=\delta_{i j} \end{aligned}$$而\( r=|\boldsymbol{r}|=(\boldsymbol{r} \cdot \boldsymbol{r})^{1 / 2}=\left(x_{j} x_{j}\right)^{1 / 2}\),则有$$\begin{array}{l} [ \nabla \boldsymbol{r}]_{i} =\frac{\partial}{\partial x_{i}}\left(x_{j} x_{j}\right)^{1 / 2} \\ =\frac{1}{2}\left(x_{j} x_{j}\right)^{-1 / 2} \frac{\partial}{\partial x_{i}}\left(x_{j} x_{j}\right) \\ =\frac{1}{2 r} 2 x_{j} \frac{\partial x_{j}}{\partial x_{i}} \\ =\frac{1}{r} x_{j} \delta_{i j}=\frac{x_{i}}{r} \end{array}$$因此$$\nabla \boldsymbol{r}=\boldsymbol{r}/ r$$散度$$\nabla \cdot \boldsymbol{r}=\frac{\partial x_{j}}{\partial x_{j}}=\delta_{j j}=3$$旋度$$[\nabla \times \boldsymbol{r}]_{i}=\epsilon_{i j k} \frac{\partial x_{k}}{\partial x_{j}}=\epsilon_{i j k} \delta_{j k}=0$$
梯度/散度/旋度的组合
虽然不用suffix notation也能推导出梯度、散度、旋度的组合,但是往往用suffix notation能更快地推导出结果。
梯度的散度$$\nabla \cdot(\nabla f)=\frac{\partial}{\partial x_{j}}\left([\nabla f]_{j}\right)=\frac{\partial}{\partial x_{j}}\left(\frac{\partial f}{\partial x_{j}}\right)=\frac{\partial^{2} f}{\partial x_{j} \partial x_{j}}=\nabla^{2} f$$注:我们完全可以把\( \nabla \cdot(\nabla f) \)看作是点乘;最后得到的其实是函数\( f\)的Laplacian。
梯度的旋度

散度的梯度$$[\nabla(\nabla \cdot \boldsymbol{u})]_{i}=\frac{\partial}{\partial x_{i}}\left(\frac{\partial u_{j}}{\partial x_{j}}\right)=\frac{\partial^{2} u_{j}}{\partial x_{i} \partial x_{j}}$$注:无法再化简了。
旋度的散度$$\begin{aligned} \boldsymbol{\nabla} \cdot(\boldsymbol{\nabla} \times \boldsymbol{u}) &=\frac{\partial}{\partial x_{i}} \epsilon_{i j k} \frac{\partial u_{k}}{\partial x_{j}} \\ &=\epsilon_{j i k} \frac{\partial}{\partial x_{j}} \frac{\partial u_{k}}{\partial x_{i}} \quad(\text { relabelling } i \leftrightarrow j) \\ &=-\epsilon_{i j k} \frac{\partial}{\partial x_{j}} \frac{\partial u_{k}}{\partial x_{i}}\\&=-\epsilon_{i j k} \frac{\partial}{\partial x_{i}} \frac{\partial u_{k}}{\partial x_{j}} \\& =0 \end{aligned}$$旋度的旋度
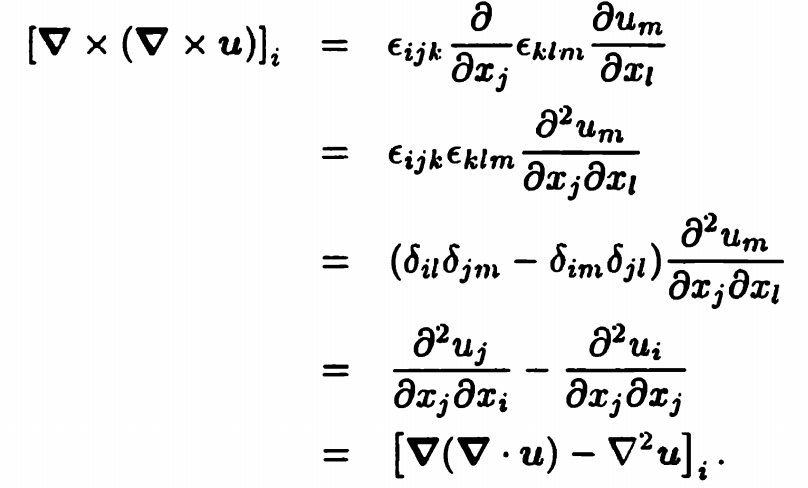 注:(1)这个结果提供了\( \nabla^{2}\)作用于向量的物理定义,从上面的结果我们可以推导出$$\nabla^{2} \boldsymbol{u}=\nabla(\nabla \cdot \boldsymbol{u})-\nabla \times(\nabla \times \boldsymbol{u})$$(2)只有上面的组合方式,其他组合方式不make sense(似乎没考虑张量)。
注:(1)这个结果提供了\( \nabla^{2}\)作用于向量的物理定义,从上面的结果我们可以推导出$$\nabla^{2} \boldsymbol{u}=\nabla(\nabla \cdot \boldsymbol{u})-\nabla \times(\nabla \times \boldsymbol{u})$$(2)只有上面的组合方式,其他组合方式不make sense(似乎没考虑张量)。
例子
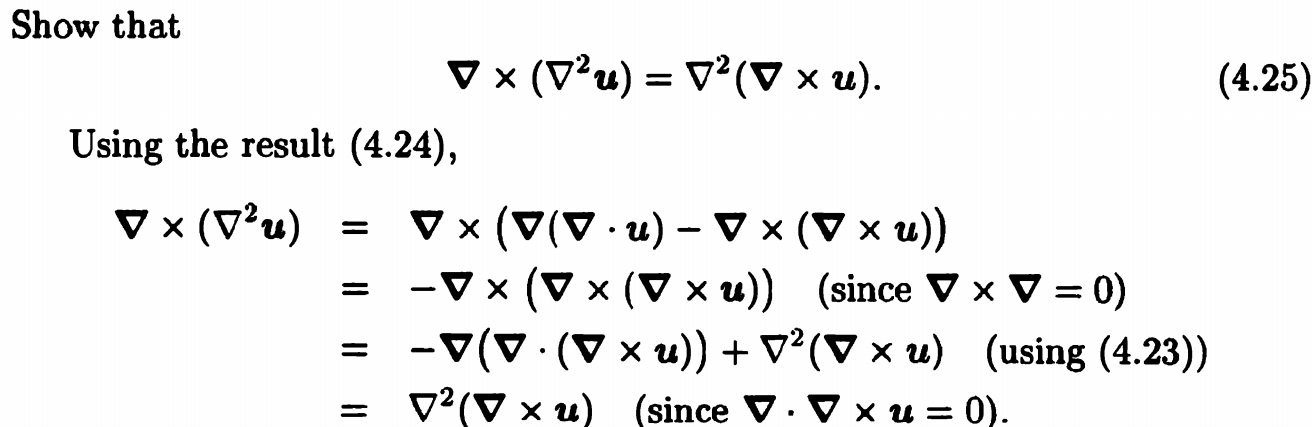 注意:
注意:
(1) \( \nabla^{2}\)和\( \)这两个算子数commute(互易的,即可以交换顺序);
(2) \( \nabla \times \nabla=0\)试想一下,如果对一个标量先做梯度再做旋度,而我们知道势函数的梯度场是无旋的,故结果为零,按照周磊老师讲的,梯度是径向,而旋度是切线,前后作用一下结果就为零;
(3) \( \nabla \cdot \nabla \times \boldsymbol{u}=0\) 向量场旋一下就没了散度。
梯度/散度/旋度作用于函数的乘积
对向量函数乘积(点乘/叉乘)、标量函数乘积、标量和向量乘积进行梯度/散度/旋度运算,有的根据微分运算的法则,很容易求解出来,但是大多数时候不是那么容易看出来,这个时候用suffix notation就展现出其威力,推导起来简单、快捷。
假设\(f \)和\( g\)是 differentiable scalar field,\( \boldsymbol{u} \)和\( \boldsymbol{v}\)是differentiable vector field,那么有:
(1) 梯度$$\begin{array}{c}
{[\nabla(f g)]_{i}=\frac{\partial}{\partial x_{i}}(f g)=f \frac{\partial g}{\partial x_{i}}+g \frac{\partial f}{\partial x_{i}}=[f \nabla g+g \nabla f]_{i}} \\
\nabla(f g)=f \nabla g+g \nabla f
\end{array}$$(2) 散度$$\begin{aligned}
\boldsymbol{\nabla} \cdot(f \boldsymbol{u}) &=\frac{\partial}{\partial x_{i}}\left(f u_{i}\right) \\
&=\frac{\partial f}{\partial x_{i}} u_{i}+f \frac{\partial u_{i}}{\partial x_{i}} \\
&=\nabla f \cdot \boldsymbol{u}+f \nabla \cdot \boldsymbol{u}
\end{aligned}$$(3) 旋度
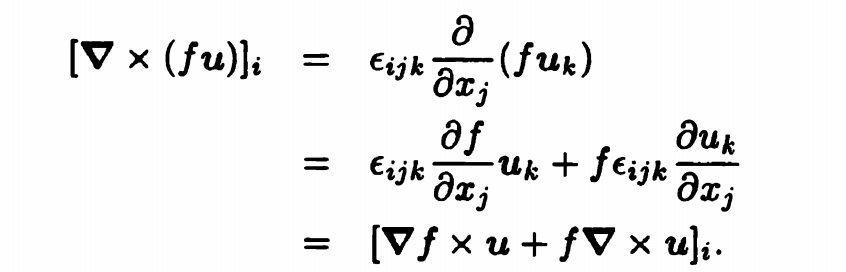 (4) 向量叉乘的散度$$\begin{aligned}
(4) 向量叉乘的散度$$\begin{aligned}
\boldsymbol{\nabla} \cdot(\boldsymbol{u} \times \boldsymbol{v}) &=\frac{\partial}{\partial x_{i}}\left(\epsilon_{i j k} u_{j} v_{k}\right) \\
&=\epsilon_{i j k} \frac{\partial u_{j}}{\partial x_{i}} v_{k}+\epsilon_{i j k} u_{j} \frac{\partial v_{k}}{\partial x_{i}} \\
&=\left(\epsilon_{k i j} \frac{\partial u_{j}}{\partial x_{i}}\right) v_{k}-\left(\epsilon_{j i k} \frac{\partial v_{k}}{\partial x_{i}}\right) u_{j} \\
&=(\nabla \times \boldsymbol{u}) \cdot \boldsymbol{v}-(\boldsymbol{\nabla} \times \boldsymbol{v}) \cdot \boldsymbol{u}
\end{aligned}$$(5) 向量叉乘的旋度
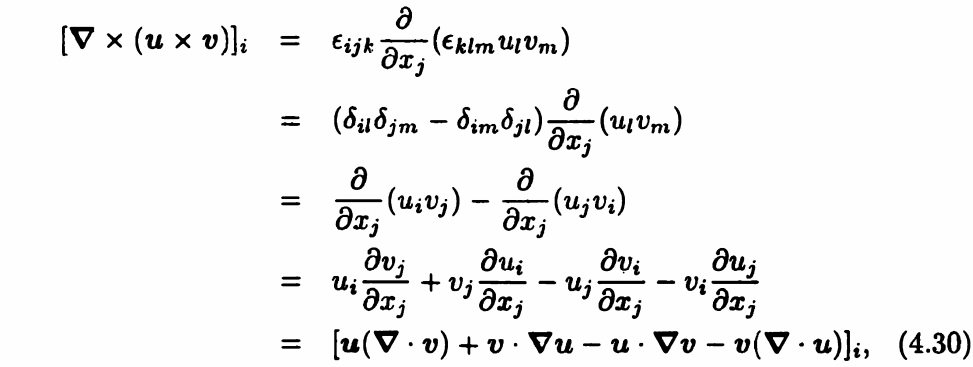 其中\( \boldsymbol{u} \cdot \boldsymbol{\nabla}\)定义为$$\boldsymbol{u} \cdot \boldsymbol{\nabla}=u_{j} \frac{\partial}{\partial x_{j}}$$可以作用于标量或者向量。
其中\( \boldsymbol{u} \cdot \boldsymbol{\nabla}\)定义为$$\boldsymbol{u} \cdot \boldsymbol{\nabla}=u_{j} \frac{\partial}{\partial x_{j}}$$可以作用于标量或者向量。
(6) 向量点乘的梯度
先有

后有(将\( \boldsymbol{u} \)和\( \boldsymbol{v} \)交换)$$[\boldsymbol{v} \times(\boldsymbol{\nabla} \times \boldsymbol{u})]_{i}=v_{j} \frac{\partial u_{j}}{\partial x_{i}}-v_{j} \frac{\partial u_{i}}{\partial x_{j}}$$两个式子相加得到
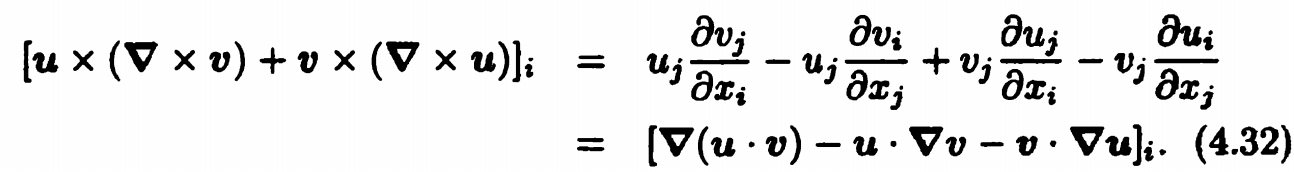
整理一下得到
![]()
例子
(1) 用两种方法求解\( \nabla \cdot(f g \boldsymbol{u})\)
第一种方法:
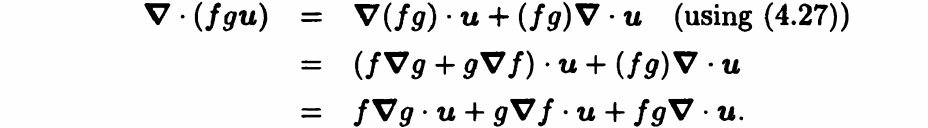 第二种方法(用 suffix notation ):
第二种方法(用 suffix notation ):
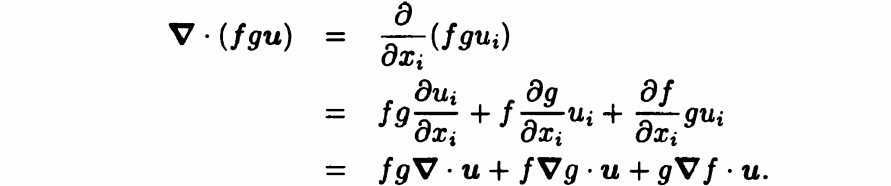 (2)
(2)
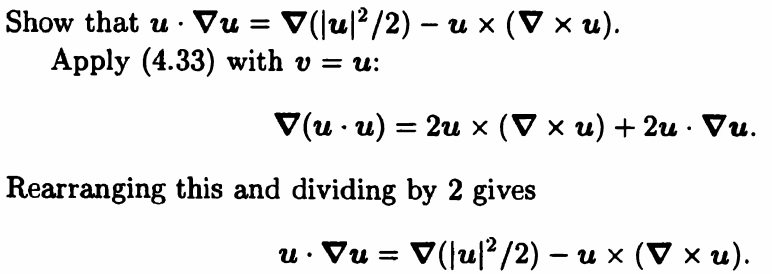 注:借用的是
注:借用的是
![]() (3)
(3)

汇总
(1) \( \delta_{i j} a_{j}=a_{i} \)
(2) \( [\boldsymbol{a} \times \boldsymbol{b}]_{i}=\epsilon_{i j k} a_{j} b_{k}\)
(3) $$[\nabla f]_{i}=\frac{\partial f}{\partial x_{i}}, \quad \nabla \cdot \boldsymbol{u}=\frac{\partial u_{j}}{\partial x_{j}}, \quad[\nabla \times \boldsymbol{u}]_{i}=\epsilon_{i j k} \frac{\partial u_{k}}{\partial x_{j}}$$
(4)
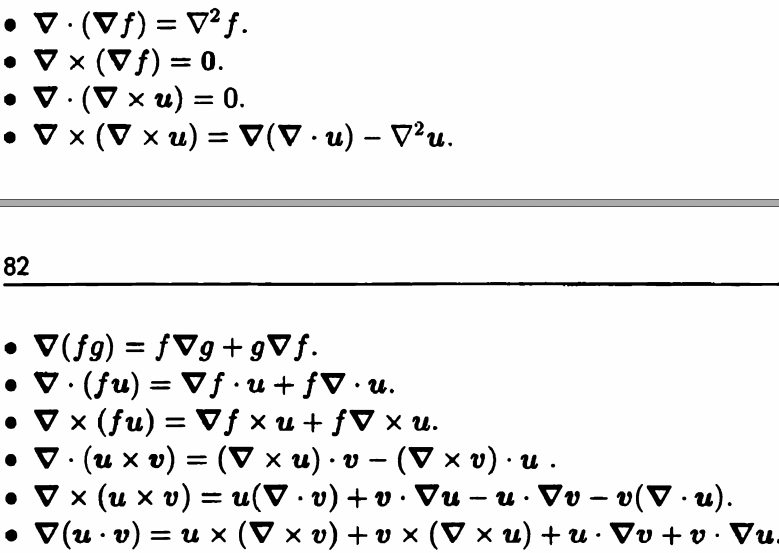 下面的内容是知乎上学习的:
下面的内容是知乎上学习的:
Nabla算符同时具有微分性和矢量性
(1) 微分性体现在乘积的微分导数公式\( \frac{d}{d x}(f g)=\frac{d f}{d x} g+f \frac{d g}{d x} \)变形;
(2) 相当于已经考虑完了微分的性质.化简就是想办法利用标量矢量混合运算让 \( \nabla \)作用在该作用的地方
Nabla算符和张量
标量势零阶张量,矢量是一阶张量,并矢是二阶张量。
梯度运算是升阶运算:标量(势函数)求梯度得到的是一阶张量(向量),向量(场)求梯度就得到二阶张量。
散度运算是降阶运算:向量场求散度就得到标量场,二阶张量求散度就得到矢量。
旋度是平阶运算:向量场求旋度还是向量场,好像没有旋度算符作用在二阶张量/标量的例子。
向量混合积具有负轮换性$$\boldsymbol{A} \cdot(\boldsymbol{B} \times \boldsymbol{C})=\left|\begin{array}{lll}
A_{x} & A_{y} & A_{z} \\
B_{x} & B_{y} & B_{z} \\
C_{x} & C_{y} & C_{z}
\end{array}\right|$$如果交换\(A \)和\( B\)的位置,那么行列式的行交换显然导致了结果变号。但是如果交换偶数次,那么不变号。所以才有如下等式$$A \cdot(B \times C)=B \cdot(C \times A)=C \cdot(A \times B)\\A \cdot(C \times B)=B \cdot(A \times C)=C \cdot(B \times A)$$引伸到如下混合积运算$$\nabla \cdot(\vec{f} \times \vec{g})=\nabla \cdot\left(\vec{f} \times \vec{g}_{c}\right)+\nabla \cdot\left(\vec{f}_{c} \times \vec{g}\right)=(\nabla \times \vec{f}) \cdot \vec{g}-(\nabla \times \vec{g}) \cdot \vec{f}$$上式中\( (\nabla \times \vec{g}) \cdot \vec{f} \)三个符号的排序发生了基数次交换,所以前面必须有个负号。
参考资料:
1. Nabla算符∇的运算律以及常用公式
2. 电动通:数学部分(2)微分运算
3. 费曼物理学讲义第二卷-前三章[mathjax]
4. 高等数学引论》杂记(一)