基/坐标变换和图像压缩
基变换
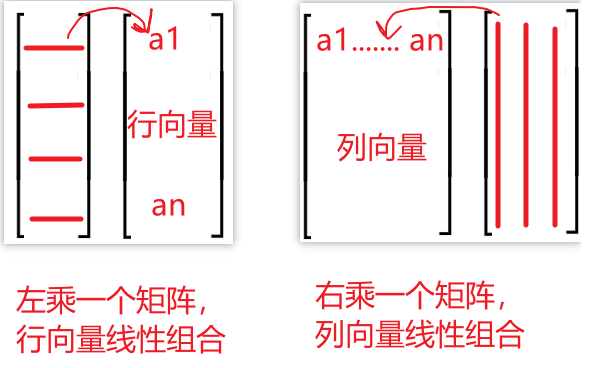
- 对一个行向量组成的矩阵,左乘一个矩阵,就是对行向量进行线性组合;
- 对一个列向量组成的矩阵,右乘一个矩阵,就是对列向量进行线性组合;
- 对上面两种情形,各自转置,那么行向量的线性组合变为列向量的线性组合,列向量的线性组合变成了行向量的线性组合。
已知两组基\(\boldsymbol{m}_1, \boldsymbol{m}_2, \ldots, \boldsymbol{m}_s\)以及\(\boldsymbol{n}_1, \boldsymbol{n}_2, \ldots, \boldsymbol{n}_s\),当且仅当它们是同一个向量空间的基时,那么存在唯一的矩阵\(P\),使得下式成立:$$ \left(\boldsymbol{n}_1, \boldsymbol{n}_2, \ldots, \boldsymbol{n}_s\right)=\left(\boldsymbol{m}_1, \boldsymbol{m}_2, \ldots, \boldsymbol{m}_s\right) P $$矩阵\(P\)称为由基\(\boldsymbol{m}_1, \boldsymbol{m}_2, \ldots, \boldsymbol{m}_s\)到基\(\boldsymbol{n}_1, \boldsymbol{n}_2, \ldots, \boldsymbol{n}_s\)的【过渡矩阵】(Transition Matrix),而上述公式称为【基变换公式】(Change of basis formula)。
$$ P_{s \times s}=\left(\begin{array}{cccc} p_{11} & p_{12} & \cdots & p_{1 s} \\ p_{21} & p_{22} & \cdots & p_{2 s} \\ \vdots & \vdots & \ddots & \vdots \\ p_{s 1} & p_{s 2} & \cdots & p_{s s} \end{array}\right) \quad\left\{\begin{array}{l} \boldsymbol{n}_1=p_{11} \boldsymbol{m}_1+p_{21} \boldsymbol{m}_2+\cdots+p_{s 1} \boldsymbol{m}_{\boldsymbol{s}} \\ \boldsymbol{n}_2=p_{12} \boldsymbol{m}_1+p_{22} \boldsymbol{m}_2+\cdots+p_{s 2} \boldsymbol{m}_{\boldsymbol{s}} \\ \cdots \cdots \cdots \\ \boldsymbol{n}_{\boldsymbol{s}}=p_{1 s} \boldsymbol{m}_1+p_{2 s} \boldsymbol{m}_2+\cdots+p_{s s} \boldsymbol{m}_{\boldsymbol{s}} \end{array}\right. $$等价描述:
- 当且仅当向量\(\boldsymbol{n}_1, \boldsymbol{n}_2, \ldots, \boldsymbol{n}_s\)是基\(\boldsymbol{m}_1, \boldsymbol{m}_2, \ldots, \boldsymbol{m}_s\)的线性组合时,或者说向量\(\boldsymbol{n}_1, \boldsymbol{n}_2, \ldots, \boldsymbol{n}_s\)在基\(\boldsymbol{m}_1, \boldsymbol{m}_2, \ldots, \boldsymbol{m}_s\)张成的空间中时,上述方程才有解;
- 当这两个基是同一个向量空间的基时,才有过渡矩阵\(P\)。
基变换的几何意义:比如\(P\)为由基\(\boldsymbol{m}_1, \boldsymbol{m}_2\)到基\(\boldsymbol{n}_1, \boldsymbol{n}_2\)的过渡矩阵,其实就是将前者变换为了后者: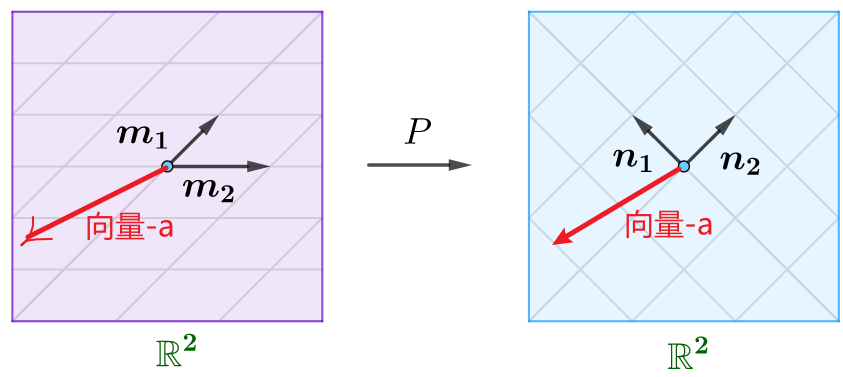
注意上图中,基变换前后,向量\(\boldsymbol{a}\)的位置并不发生变换,即向量的位置是绝对的,不随着基的变化而变化。基变换,使得向量\(\boldsymbol{a}\)在两个基下的坐标发生了变化,但是基向量乘以对应的坐标都可以复刻出向量\(\boldsymbol{a}\)的位置。即基变换只是Changing Representations of Vectors。
从映射的角度看基变换:同一个向量空间内的基变换,并不改变原来向量的位置。下面的箭头描述的是不同基表示下,向量空间的【identity map】,即the map which assigns every member of a set \(A\) to the same element.

基变换的可逆性:过渡矩阵一定是满秩矩阵,所以矩阵必然可逆,即可用过渡矩阵在不同基之间来回变换。
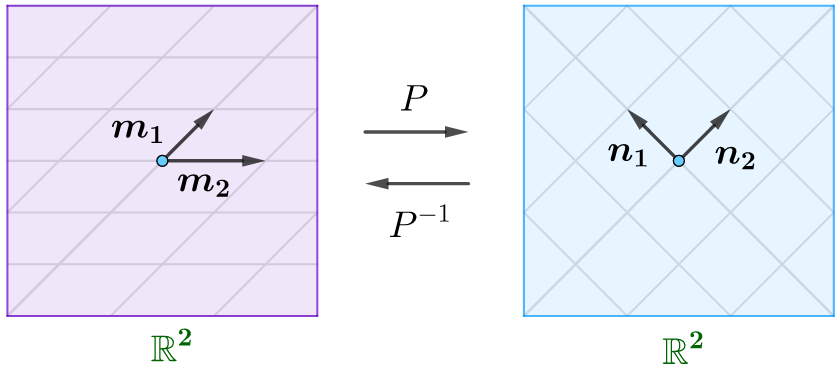
坐标变换
已知\(P\)为由基\(\mathcal{M}=\left\{\boldsymbol{m}_{\mathbf{1}}, \boldsymbol{m}_{\mathbf{2}}, \ldots, \boldsymbol{m}_s\right\}\)到基\(\mathcal{N}=\left\{\boldsymbol{n}_1, \boldsymbol{n}_2, \ldots, \boldsymbol{n}_s\right\}\)的过渡矩阵$$\left(\boldsymbol{n}_1, \boldsymbol{n}_2, \ldots, \boldsymbol{n}_s\right)=\left(\boldsymbol{m}_1, \boldsymbol{m}_2, \ldots, \boldsymbol{m}_s\right) P$$又知向量\(\boldsymbol{x}\)在基\(\mathcal{M}\)下的坐标为\([\boldsymbol{x}]_{\mathcal{M}}\)以及在基\(\mathcal{N}\)下的坐标为\([\boldsymbol{x}]_{\mathcal{N}}\),则有【坐标变换公式】(Change of coordinates formula)$$ [\boldsymbol{x}]_{\mathcal{N}}=P^{-1}[\boldsymbol{x}]_{\mathcal{M}}, \quad[\boldsymbol{x}]_{\mathcal{M}}=P[\boldsymbol{x}]_{\mathcal{N}} $$于是有$$ \begin{aligned} \left(\boldsymbol{n}_1, \boldsymbol{n}_2, \ldots, \boldsymbol{n}_s\right)[\boldsymbol{x}]_{\mathcal{N}} &=\left(\boldsymbol{m}_1, \boldsymbol{m}_2, \ldots, \boldsymbol{m}_s\right) P[\boldsymbol{x}]_{\mathcal{N}} \\ &=\left(\boldsymbol{m}_1, \boldsymbol{m}_2, \ldots, \boldsymbol{m}_s\right) P P^{-1}[\boldsymbol{x}]_{\mathcal{M}} \\ &=\left(\boldsymbol{m}_1, \boldsymbol{m}_2, \ldots, \boldsymbol{m}_s\right)[\boldsymbol{x}]_{\mathcal{M}} \end{aligned} $$ 注:傅里叶变换其实也是一种坐标变换(基变换),即频域和时域之间的变换,实空间和倒空间的变换,位置空间和动量空间的变换。
注:傅里叶变换其实也是一种坐标变换(基变换),即频域和时域之间的变换,实空间和倒空间的变换,位置空间和动量空间的变换。
补充
设定阈值,有些系数(向量)扔掉或者保留。肉眼感知不到的差异。对于元素全为\(1\)的列向量,是低频信号,频率为\(0\);\(1\)和\(-1\)交替的列向量属于高频信号,可能对应于噪音或者抖动(jitter),对于平缓的讲课来说,很少有噪音。
好的基向量要求:
- 可以快速求逆矩阵:
- 比如FFT矩阵为复数域上的酉矩阵(正交矩阵),所以其共轭转置就是逆矩阵;
- 小波基,也是正交矩阵,所以转置一下就是其逆矩阵,JPEG2000用的就是这种;
- 少量的基向量就可以得到近似信号,可压缩的比例就比较高。
相似矩阵和若尔当标准型
相似矩阵
矩阵\(\boldsymbol{A} \)和\( \boldsymbol{B}\)均是阶方阵,若存在可逆矩阵\( \boldsymbol{M}\)使得下式成立,则\( \boldsymbol{A}\)和\(\boldsymbol{B} \)为【相似矩阵】(Similar matrices)。$$\boldsymbol{B}=\boldsymbol{M}^{-1} \boldsymbol{A} \boldsymbol{M}$$首先我们直观感觉是,矩阵\( \boldsymbol{A}\)和\(\boldsymbol{B} \)的行列式一定相等,因为因为将矩阵\( \boldsymbol{A}\)左乘的矩阵和右乘的矩阵的行列式互为倒数,所以最终矩阵\( \boldsymbol{A} \)的行列式值不变。另外在研究矩阵的对角化的时候我们知道如果矩阵\(\boldsymbol{A} \)具有\(n \)个线性无关的特征向量,那么可进行对角化\( \boldsymbol{A} =\boldsymbol{\Lambda} \boldsymbol{S}^{-1} \),换一种写法有\( \boldsymbol{S}^{-1} \boldsymbol{A} \boldsymbol{S}=\boldsymbol{\Lambda}\)。很显然矩阵\(\boldsymbol{A} \)和\( \boldsymbol{\Lambda}\)满足前面说的相似矩阵的定义,因此二者是相似矩阵(矩阵\( \boldsymbol{\Lambda} \)是矩阵\(\boldsymbol{A} \)所有相似矩阵中最简洁的)。对于任意同阶可逆方阵\( \boldsymbol{M}\)来说,矩阵\(\boldsymbol{A} \)和\( \boldsymbol{M}^{-1} \boldsymbol{A} \boldsymbol{M}\)一定是相似的。
相似矩阵最重要的性质是:具有相同的特征值。这一点很容易证明。根据\( A M M^{-1} \mathbf{x}=\lambda \mathbf{x}\)很容易知道\( B M^{-1} \mathbf{x}=\lambda M^{-1} \mathbf{x}\)。也就是是说如果矩阵\( A\)具有特征值\( \lambda\),那么相似矩阵\( B\)也具有同样的特征值\(\lambda \),只是对应的特征向量发生了变化,变成了\(M^{-1} \mathbf{x} \)。细细体会一下这里面的变与不变。
根据前面有关韦达定理和矩阵特征值的笔记,我们知道所有特征值的和 = 主对角线元素之和,所有特征值的乘积 = 行列式的值。而相似矩阵的特征值都一样,因此相似矩阵:特征多项式相同;行列式相同;迹相同。
矩阵\(\boldsymbol{A} \)和\( \boldsymbol{B}\)相似,那么两者实际上是同一个线性映射在不同基下的代数表示:
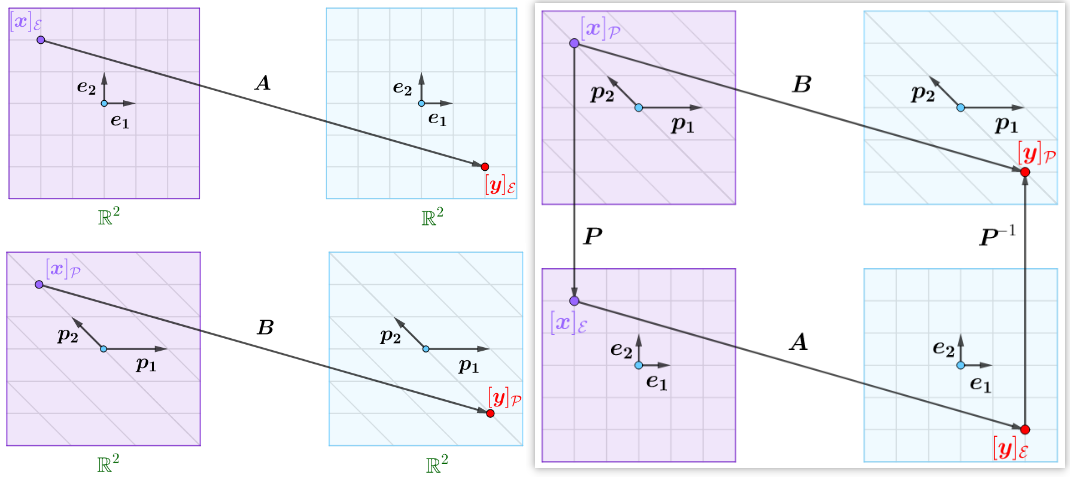
在自然基下,线性映射可以用矩阵\(\boldsymbol{A} \)来表示,即有\(\boldsymbol{A}[\boldsymbol{x}]_{\mathcal{E}}=[\boldsymbol{y}]_{\mathcal{E}}\)。如果不采用自然基,而是采用基\(\mathcal{P}\),注意定义域和到达域的空间不变,那么上述线性映射可以用矩阵\(\boldsymbol{B} \)来表示,即有\(\boldsymbol{B}[\boldsymbol{x}]_{\mathcal{P}}=[\boldsymbol{y}]_{\mathcal{P}}\)。
如果存在可逆矩阵\(\boldsymbol{P}\),也就是存在过度矩阵\(\boldsymbol{P}\),通过坐标变换公式有:$$ [\boldsymbol{x}]_{\mathcal{E}}=\boldsymbol{P}[\boldsymbol{x}]_{\mathcal{P}}, \quad[\boldsymbol{y}]_{\mathcal{P}}=\boldsymbol{P}^{-1}[\boldsymbol{y}]_{\mathcal{E}}$$那么矩阵\(\boldsymbol{A}\)和矩阵 \(\boldsymbol{B}\)就可通过过渡矩阵\(\boldsymbol{P}\)联系起来,此时\(\boldsymbol{A}\)和\(\boldsymbol{B}\)就是相似矩阵。
在我先前总结的张量的文章中,提到描述“狗”这个动物的时候,我们选定的“语言参考系(坐标系)”不同,那么描述的方式也不同,但是最终都是指向“狗”,比如(狗)(中文)=(dog)(English)=(hond)(Dutch)。类似地,相似矩阵的特征值是其本征的属性,不随外界参考系的变化而变化,参考系的变化只是让特征向量发生改变。
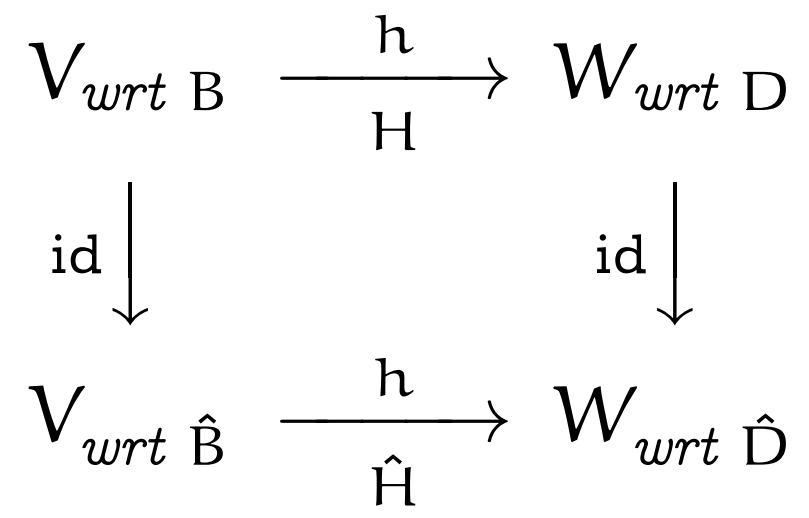
注:在一般线性群中,相似性 = 共轭。回忆一下群论中的共轭:设有群\(G\),对于\(f, h \in G\),若\(\exists g \in G\),使得\(g f g^{-1}=h\),则称\(f, h\)共轭,记为\(f \sim h\)。显然,群论中的共轭也具有传递性。
矩阵的分类—对角化
- 特征值都没有重根,矩阵很容易对角化并且找到对应的特征向量。
- 特征值有重根,如果一个矩阵的特征值\(\lambda_{1}=\lambda_{2}=4 \),那么可能存在下面两种情况:
- 可对角化,存在两个特征向量 (small family的情况)。\( \left[\begin{array}{ll} 4 & 0 \\ 0 & 4 \end{array}\right]\)只和自己相似,任意相似变换都得到自己\(M^{-1}\left[\begin{array}{ll} 4 & 0 \\ 0 & 4 \end{array}\right] M=4 M^{-1} I M=\left[\begin{array}{ll} 4 & 0 \\ 0 & 4 \end{array}\right] \)。
- 不能对角化,只有一个特征向量,也就是我们之前提到的退化矩阵 (big family 的情况,除上面情况之外的所有情形)。比如最典型和简洁的就是\( \left[\begin{array}{ll} 4 & 1 \\ 0 & 4 \end{array}\right]\),元素\(1 \)的位置换成其他数值仍是相似矩阵。
对于不能对角化的情形,我们可以将矩阵改写成【若尔当标准型】(Jordan form),即得到"almost" diagonal matrix (近似对角化矩阵),然后根据【Generalized eigenvector】的概念得到退化矩阵缺失的那个特征向量。
在不改变迹和行列式的前提下,有矩阵\(\left[\begin{array}{cc} 5 & 1 \\ -1 & 3 \end{array}\right] ,\left[\begin{array}{cc} 4 & 0 \\ 17 & 4 \end{array}\right] ,\left[\begin{array}{cc} a & * \\ * & 8-a \end{array}\right] \)等,都是不能对角化的情况,但都和前面提到的矩阵\( \left[\begin{array}{ll} 4 & 1 \\ 0 & 4 \end{array}\right]\)相似。如果能够对角化,那么一定会和特征值构成的对角矩阵\(4I \)相似,但是这种矩阵只和自己相似,不带别人玩。
注:在有重根的前提下判定到底属于哪种情形,可以从矩阵的秩来理解,减去\(\lambda I \)的到的矩阵的维数为\( r\),那么对应的\( n-r\)就是零空间的维数,也就是特征向量的维数。
若尔当标准型的作用
从实际计算的角度看,很少会出现特征值相同的情形,因为这里特征值相同指的是完全相同(非常严格的要求),显然在实际问题计算中很难碰到。假设在某种理想情况下你碰到了特征值相同的情形,那么在此基础上,假如矩阵的元素稍有偏差,特征值将不可避免地改变,秩也不可避免地改变,因此对于数值计算来说,不是什么好事。
先前我们知道不是所有的矩阵都能进行对角化,特征值都不同的,当然特征向量都不不相关,可以进行对角化,另外就是我们前面提到的,在特征值相同的情况下,有一小部分可对角化,大部分不能对角化。若尔当标准型的作用就是让所有的矩阵都可以对角化,传统意义上能够对角化的情况只是若尔当标准型的一个子类(特殊情况)。
下面举例子说明,一个四阶矩阵具有四重特征值\( \lambda_{1}=\lambda_{2}=\lambda_{3}=\lambda_{4}=0\)。
矩阵\(\boldsymbol{A}=\left[\begin{array}{ccc|c} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 \end{array}\right] \)的秩为\( 2\),因此零空间的维数为\( 4-2=2\),所以对应的特征向量的个数是\( \)个。若尔当指出,上对角线每增加一个\(1 \),矩阵就减掉一个特征向量,所以本例中特征向量的个数是\( 4-2=2\)。
矩阵\(\boldsymbol{B}=\left[\begin{array}{lll|l} 0 & 1 & 7 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 \end{array}\right] \)和矩阵\(\boldsymbol{A}=\)是相似矩阵。但是矩阵\( \boldsymbol{C}=\left[\begin{array}{ll|ll} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array}\right]\)和矩阵\( \boldsymbol{A}\)不是相似矩阵,因为具有不同的若尔当块。
若尔当块\( J_{i}=\left[\begin{array}{ccccc} \lambda_{i} & 1 & 0 & \cdots & 0 \\ 0 & \lambda_{i} & 1 & \ddots & \vdots \\ 0 & 0 & \ddots & \ddots & 0 \\ \vdots & & \ddots & \ddots & 1 \\ 0 & 0 & \cdots & 0 & \lambda_{i} \end{array}\right]\)对角线上为重复的特征值\(\lambda_{i} \),上对角线为\(1\),其他为\(0 \)。每个若尔当块只有一个特征向量,若干个若尔当块拼成一个若尔当矩阵$$J=\left[\begin{array}{cccc} J_{1} & 0 & \cdots & 0 \\ 0 & J_{2} & \cdots & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \cdots & J_{d} \end{array}\right]$$
两个矩阵具有相同的特征值和特征向量个数,但是其若尔当块的尺寸不同,两者也并不是相似矩阵,如前面说的矩阵\(\boldsymbol{A} \)和\(\boldsymbol{B} \)并不相似。
【若尔当理论】:任意\( n\)阶矩阵\(\boldsymbol{A} \)都与一个若尔当矩阵\(\boldsymbol{J} \)相似。若尔当矩阵的每一个若尔当块对应一个特征向量。若矩阵具有\( n\)个不同的特征向量,则可以对角化,此时其若尔当标准型\(\boldsymbol{J} \)就是对角阵\( \boldsymbol{\Lambda}\)。若出现重特征值,则特征向量个数变少。
参考资料:
(1) Jordan 标准形—朝花夕拾
(2) Generalized eigenvector—Wiki
AI与线性代数
SVD
【奇异值分解】(singular value decomposition):对于任意矩阵\( A=U \Sigma V^{T}\),分解结果为列正交矩阵\( U\),对角阵\(\Sigma \)和行正交矩阵\(V \);对任意矩阵SVD分解的结果是最终也是最好的分解。
\(n\)阶方阵\(A\)能否SVD分解:
- 如果方阵\(A\)具有\(n\)个线性无关的特征向量,那么显然有\(A=S \Lambda S^{-1} \),其中\(\Lambda\)为特征值矩阵,\(S\)为特征向量矩阵,特征向量线性无关不能保证正交,因此不能保证能够SVD分解;
- 如果\(A\)为对称阵:
- 如果存在\(n\)个不同的特征值,显然不同特征值的特征向量相互正交,即\(S\)和\(S^{-1}\)都为正交矩阵,显然一定满足SVD分解;
- 如果特征值有重根,那么可以在该特征空间挑选合适的特征向量,使得最终的特征向量集合中的向量相互正交,即选取适当特征向量就可以满足SVD分解;
SVD分解的实现过程
将矩阵\( A\)视为一种线性变换,比如\( A \mathbf{x}=\mathbf{b}\)通过\( A\)的作用将向量\( \mathbf{x}\)变成了向量\( \mathbf{b}\)。如下图所示,SVD分解就是要在行空间寻找一组正交基,将其通过矩阵\(A \)的线性变换生成列空间的一组正交基\( A \mathbf{v}_{i}=\sigma_{i} \mathbf{u}_{i}\)。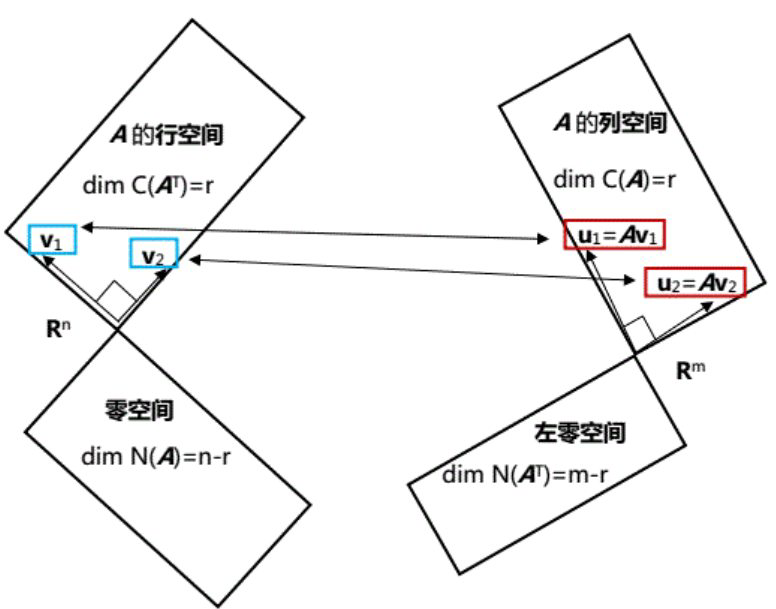
找出矩阵\(A\)行空间中相互正交的基向量很容易,格拉姆-施密特正交化的方法。但是经过矩阵\(A \)的线性变换之后得到的两个向量不一定是正交的,因此满足要求的行空间的正交基非常特殊。
用矩阵数学语言来描述这一过程:问题的核心就是在行空间找到一组特殊的正交基,使得$$ \begin{aligned} A\left[\begin{array}{llll} \mathbf{v}_1 & \mathbf{v}_2 & \cdots & \mathbf{v}_r \end{array}\right] &=\left[\begin{array}{lllll} \sigma_1 \mathbf{u}_1 & \sigma_2 \mathbf{u}_2 & \cdots & \sigma_r \mathbf{u}_r \end{array}\right] \\ &=\left[\begin{array}{lllll} \mathbf{u}_1 & \mathbf{u}_2 & \cdots & \mathbf{u}_r \end{array}\right]\left[\begin{array}{llll} \sigma_1 & & & \\ & \sigma_2 & & \\ & & \ddots & \\ & & & \sigma_r \end{array}\right] \end{aligned} $$我们现在进行的是将“行空间”通过矩阵\(A \)的线性变换转化成“列空间”,其实从更大的picture来看,将矩阵\(A \)作用于“零空间”会得到零向量。零空间的正交基\( \mathbf{v}_{r+1} \ldots \ldots\mathbf{v}_{n}\)线性变换有\(A \mathbf{x}=0 \)。要知道,正交矩阵是标准正交方阵,所以我们必须把零空间的基向量补齐,当然还有线性变换后的左零空间补齐,以及特征值补齐(都是零)。补齐之后等式变为\(A V=U \Sigma \),于是有\(A=U \Sigma V^{-1}=U \Sigma V^{\mathrm{T}} \)。
接下里是求解\( U\)、\(\Sigma \)和\(V \)。我们知道正交矩阵\( U\)和\(V \)有一个牛逼的性质就是\(Q^{-1}=Q^{\mathrm{T}} \),我们需要好好利用这个性质,然后我们知道了对于对称矩阵的分解\(A=S \Lambda S^{-1}=Q \Lambda Q^{-1}=Q \Lambda Q^{\mathrm{T}} \)。结合这两个知识点,我们进行下面的转换$$\begin{aligned} A^{\mathrm{T}} A &=V \Sigma^{\mathrm{T}} U^{\mathrm{T}} U \boldsymbol{\Sigma} V^{\mathrm{T}} \\ &=V \Sigma^{\mathrm{T}} \Sigma V^{\mathrm{T}} \\ &=V\left[\begin{array}{cccc} \sigma_{1}^{2} \\ & \sigma_{2}^{2} \\ & & \ddots \\ & & & \sigma_{r}^{2} \end{array}\right] V^{\mathrm{T}} \end{aligned}$$上面就变成了正定矩阵(对称矩阵的特例)\(A^{\mathrm{T}} A \)的正交分解,其对应的特征值为\( \sigma_{i}^{2}\),特征向量为\(\mathbf{v}_{i} \)。同理,也可以求得\(U \)。
SVD分解的例子-1
求矩阵\(A=\left[\begin{array}{cc} 4 & 4 \\ -3 & 3 \end{array}\right] \)的SVD分解。矩阵是可逆矩阵,秩为\(2 \),则需在行空间求得\(\mathbf{v}_{1} \)和\( \mathbf{v}_{2}\),列空间中求得\( \mathbf{u}_{1}\)和\(\mathbf{u}_{2} \),以及伸缩因子\(\sigma_{1} \)和\(\sigma_{2} \)。
(1)求\( V\):计算\( A^{\mathrm{T}} A=\left[\begin{array}{cc} 4 & -3 \\ 4 & 3 \end{array}\right]\left[\begin{array}{cc} 4 & 4 \\ -3 & 3 \end{array}\right]=\left[\begin{array}{cc} 25 & 7 \\ 7 & 25 \end{array}\right]\),它的特征向量为\( \left[\begin{array}{l} 1 \\ 1 \end{array}\right]\)和\( \),标准化后得到\(\left[\begin{array}{cc} 1 \\ -1 \end{array}\right] \),求得\(\sigma_{1}^{2}=32, \sigma_{2}^{2}=18 \)。
(2)求\( U\):用\(A A^{\mathrm{T}} \)可得相同的特征值(伸缩系数的平方)\(\sigma_{1}^{2}=32, \sigma_{2}^{2}=18 \),特征向量为\( \left[\begin{array}{l} 1 \\ 0 \end{array}\right]\)和\(\left[\begin{array}{l} 0 \\ 1 \end{array}\right] \)。
(3)根据\( A=U \Sigma V^{T}\)求解出\(A=U \Sigma V^{T}=\left[\begin{array}{cc} 4 & 4 \\ 3 & -3 \end{array}\right] \)。显然这个结果是错误的,问题在于这里的结果满足前面的四个子空间图的关系,也就是说行空间的基向量\(\mathbf{v}_{1} \)和\(\mathbf{v}_{2} \)是标准正交的,通过矩阵\( A\)坐标变换得到的列空间的基向量\( \mathbf{u}_{1}\) 和\( \mathbf{u}_{2}\)也是正交的(扣掉伸缩系数的话,就是标准正交)。但是“手系发生了变化”,也就是说行空间的\(\mathbf{v}_{1} \)到\(\mathbf{v}_{2} \)时逆时针,但是转换到列空间的\(\mathbf{u}_{1} \)到\( \mathbf{u}_{2}\)是顺时针旋转。
SVD分解的例子-2
前面的例子是满秩的情况,也就是不存在零空间。我们现在举的例子是存在零空间的情况。求奇异矩阵\( A=\left[\begin{array}{ll} 4 & 3 \\ 8 & 6 \end{array}\right]\)的SVD分解。
显然,矩阵的行空间和列空间都是一维的,而零空间和左零空间也是一维的。我们可以在二维坐标系上画出来。行空间和列空间分别是两条直线,对应的零空间和左零空间也是两条直线。
很容易直接看出来\( \mathbf{v}_{1}=\left[\begin{array}{c} 0.8 \\ 0.6 \end{array}\right], \mathbf{v}_{2}=\left[\begin{array}{r} 0.6 \\ -0.8 \end{array}\right], \mathbf{u}_{1}=1 / \sqrt{5}\left[\begin{array}{l} 1 \\ 2 \end{array}\right], \mathbf{u}_{2}=1 / \sqrt{5}\left[\begin{array}{r} 2 \\ -1 \end{array}\right]\)。根据\(A^{m\mathrm{T}} A=\left[\begin{array}{ll} 4 & 8 \\ 3 & 6 \end{array}\right]\left[\begin{array}{ll} 4 & 3 \\ 8 & 6 \end{array}\right]=\left[\begin{array}{cc} 80 & 60 \\ 60 & 45 \end{array}\right] \),由于秩为\( 1\),所以很容易看出特征值为\( \sigma_{1}^{2}=125, \sigma_{2}^{2}=0\)。因此矩阵的SVD分解为$$ A=1 / \sqrt{5}\left[\begin{array}{cc} 1 & 2 \\ 2 & -1 \end{array}\right]\left[\begin{array}{cc} \sqrt{125} & 0 \\ 0 & 0 \end{array}\right]\left[\begin{array}{cc} 0.8 & 0.6 \\ 0.6 & -0.8 \end{array}\right]$$总结一下做奇异值分解就是在矩阵的四个子空间中寻找到合适的基:
(1) \(\mathbf{v}_{1}, \mathbf{v}_{2} \dots \dots \mathbf{v}_{r} \)为行空间的标准正交基。
(2) \(\mathbf{u}_{1}, \mathbf{u}_{2} \ldots \ldots \mathbf{u}_{r} \)为列空间的标准正交基。
(3) \(\mathbf{v}_{r+1}, \mathbf{v}_{r+2} \ldots \ldots \mathbf{v}_{n} \)为零空间的标准正交基。
(4) \(\mathbf{u}_{r+1}, \mathbf{u}_{r+2} \ldots \ldots \mathbf{u}_{m} \)为左零空间的标准正交基。
SVD分解在最小二乘法问题的应用:奇异值分解在最小二乘法问题中有重要应用,因为在实际问题中常碰到矩阵\(A\)不是列满秩的状态,因此\(A^{T} A\)不可逆,无法用之前的方法求最优解。即使是列满秩的情况当矩阵是超大型矩阵时,\(A^{\mathrm{T}}A\)的计算量太大,用奇异值分解的办法会降低计算量。
二阶方阵SVD的几何意义
\(A=\left[\begin{array}{ll}\mathbf{u}_1 & \mathbf{u}_2\end{array}\right]\left[\begin{array}{ll}\sigma_1 & 0 \\ 0 & \sigma_2\end{array}\right]\left[\begin{array}{c}\mathbf{v}_1^\mathrm{T} \\ \mathbf{v}_2^\mathrm{T}\end{array}\right]\)其中\(\sigma \)是奇异值,替代了对角化中的特征值\( \lambda \)。
奇异值分解的几何意义为:旋转-拉伸-旋转。
注:二阶旋转矩阵形式为\( \left[\begin{array}{cc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array}\right] \),任何二阶正交矩阵都可以写成这样旋转角度的形式。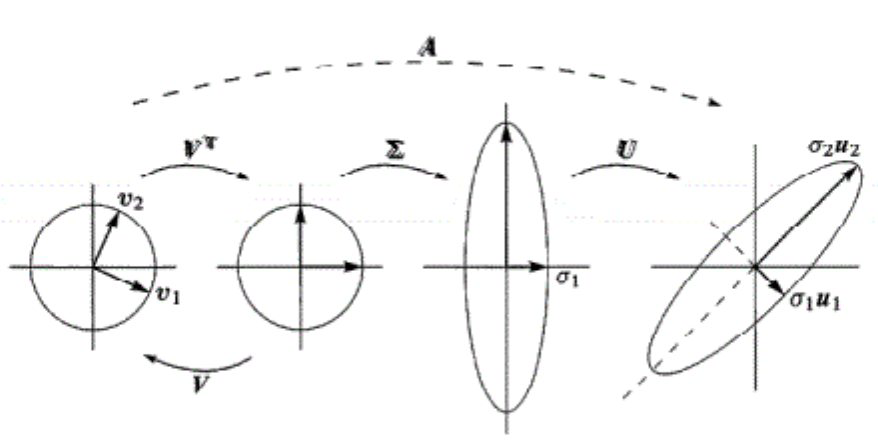
PCA
XX
SVM
循环矩阵与卷积
线性变换及其对应矩阵
【线性变换】(Linear transformation or linear map)
线性变换是一个函数\(T: \mathbf{R}^{n} \rightarrow \mathbf{R}^{m}\)满足$$ \begin{aligned} T(\mathbf{v}+\mathbf{w}) &=T(\mathbf{v})+T(\mathbf{w}) \\ T(c \mathbf{v}) &=c T(\mathbf{v}) \end{aligned} $$对任意向量\(\mathbf{v}, \mathbf{w} \in \mathbf{R}^{n}\)和标量\(c \in \mathbf{R}\)都成立。注意\( \mathbf{R}^{n}\)是向量空间,它是具有\( n\)个实数分量的所有向量的集合。当然了上面的两个式子的组合可以得到$$T(c \mathbf{v}+d \mathbf{w})=c T(\mathbf{v})+d T(\mathbf{w})$$另外,根据\(T(c \mathbf{v})=c T(\mathbf{v})\),如果取\(c=0\),显然\( c \mathbf{v}\)为零向量,而\(c T(\mathbf{v})\)也为零向量,即必有$$T(\mathbf{0})=\mathbf{0}$$线性变换可以在脱离具体坐标和具体数值的情况下进行讨论,但是对于实际应用的科学计算,我们还是要回到坐标系中。每一个线性变换都对应一个矩阵,矩阵概念的背后就是线性变换的概念。相似矩阵描述的是同一种线性变换,GS教授说理解线性变换的本质就是找到它背后的矩阵。矩阵侧重于实际应用,而线性变换侧重于抽象思维,学习线性代数,要讲二者结合起来理解。
线性变换的例子
(1)投影(Projection)
我们以前知道的投影有平面内向量的投影,比如将力投影到运动方向上;还有三维空间的投影,比如立体几何中,将一个空间三角形,投影到坐标平面上。现在我们抛开矩阵,从线性变换的概念来讨论“投影”。通过线性变换使得平面内的一个向量变为平面内的另一个向量,这种变换关系通常称之为“映射”(mapping)。$$T: \mathbf{R}^{2} \rightarrow \mathbf{R}^{2}$$ \(T(\mathbf{v}) \)就像一个函数,给一个输入,进行线性变换后得到一个输出,而且输入和输出的内容都在\( \mathbf{R}^{2}\)空间内,比如将二维平面的向量投影到一条直线上。其实这里的\(T \)是一个【线性算子】。
(2)旋转45度(rotation by 45 degree)
这是个线性变换\(T: \mathbf{R}^{2} \rightarrow \mathbf{R}^{2} \),加法数乘都满足。
(A)向量旋转示意图 (B)二维平面图像旋转示意图
(B)二维平面图像旋转示意图 这里其实是通过\( T(\mathbf{v})=A \mathbf{v}\)左乘一个矩阵\( A\)进行线性变换,对于旋转操作,这个矩阵为\( \left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\)。如果想让这个房子上下颠倒(沿着\( x\)轴翻转或者说镜像),那就不是旋转操作,不过也还是线性操作,对应的矩阵为\( \left[\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right]\)。
这里其实是通过\( T(\mathbf{v})=A \mathbf{v}\)左乘一个矩阵\( A\)进行线性变换,对于旋转操作,这个矩阵为\( \left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\)。如果想让这个房子上下颠倒(沿着\( x\)轴翻转或者说镜像),那就不是旋转操作,不过也还是线性操作,对应的矩阵为\( \left[\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right]\)。
注:实数二维平面旋转群SO(2)和一维复数空间的旋转群U(1)同构。
(3)\( T(\mathbf{v})=A \mathbf{v}\)
对某一线性变换\( T: \mathbf{R}^{3} \rightarrow \mathbf{R}^{2}\),输入一个三维向量而输出一个二维向量。变成矩阵的形式,则矩阵\( A\)是一个\(2 \times 3 \)矩阵。
非线性变换的例子
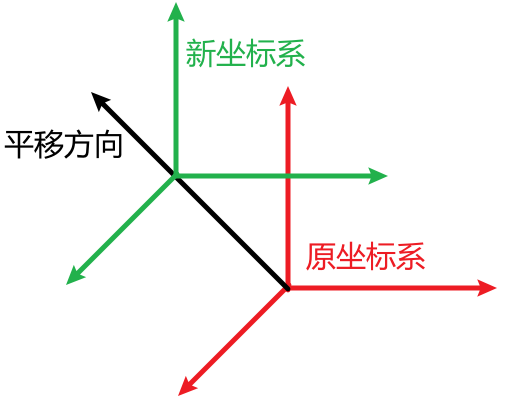
(1) 平面平移(Shift whole plane)
沿着某方向\(\mathbf{v}_{0} \)平移一个平面,这就不是线性变换,两条法则都违反。更简单的验证方法是线性运算规则的特例\( T(0)=0\),“平移”不符合这个规则的特例。
拓展:【平移矩阵】(Translation Matrix)
注意,对于三维空间中的平移操作,我们要用四阶矩阵来描述,具体过程如下:$$ \left[\begin{array}{c} x+\text { Translation. } x \\ y+\text { Translation. } y \\ z+\text { Translation. } z \\ 1 \end{array}\right]=\left[\begin{array}{cccc} 1 & 0 & 0 & \text { Translation. } x \\ 0 & 1 & 0 & \text { Translation. } y \\ 0 & 0 & 1 & \text { Translation. } z \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right] $$如果从空间变换的角度看,假设translation是沿着过原点的某个直线平移一定距离,那么显然在原坐标空间中该直线上的向量,将会继续沿着该直线平移,即原空间上,该直线上的所有向量是translation变换的特征向量。注意从上面这个四阶Translation Matrix似乎看不出直观的特征向量/特征值。
(2) 求长度\( T(\mathbf{v})=\|\mathbf{v}\|\)
输入一个三维向量,得到一个数值,或者说一维向量\( T: \mathbf{R}^{3} \rightarrow \mathbf{R}^{1}\)。这个变换可以满足\( T(0)=0\),但是数乘负数就不满足规则。
线性变换的描述
如果我们想了解线性变换对整个输入空间的影响,只需要确定它的一组基\( \mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{\mathbf{n}}\)线性变换的结果。$$\begin{array}{c} \mathbf{v}=\mathrm{c}_{1} \mathbf{v}_{1}+\mathrm{c}_{2} \mathbf{v}_{2}+\ldots \ldots+\mathrm{c}_{n} \mathbf{v}_{n} \\ \left.T(\mathbf{v})=\mathrm{c}_{1} \boldsymbol{T}\left(\mathbf{v}_{1}\right)+\mathbf{c}_{2} \boldsymbol{T}\left(\mathbf{v}_{2}\right)+\ldots \ldots+\mathbf{c}_{n} \boldsymbol{T} \mathbf{( v}_{\mathbf{n}}\right) \end{array}$$最简单的,比如对于二维平面而言,我们任意选取两个非零的线性无关的向量\(\mathbf{v}_{1} \)和\( \mathbf{v}_{2} \),如果我们知道线性变换后的\( T(\mathbf{v}_{1} )\)和\( T(\mathbf{v}_{2} )\),那么我们就可以确定线性变换的方式,换句话说,对于平面上的任意向量,我们就都可以给出其线性变换后的结果(见微知著)。
线性变换与坐标无关,而矩阵与坐标有关。选定一组基,则对于一位向量而言\( \mathrm{c}_{1},\mathrm{c}_{2}\)等等就是一组坐标值,给定了将向量表示为基向量线性组合的唯一的表达式。因此可以说坐标源自于基,\( \mathrm{c}_{1}, \mathrm{c}_{2} \ldots \ldots \mathrm{c}_{\mathrm{n}}\)等就是向量的一组坐标值。通常给出空间的坐标是标准坐标,即一组标准基。例如$$\mathbf{v}=\left[\begin{array}{l} 3 \\ 2 \\ 4 \end{array}\right]=3\left[\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right]+2\left[\begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right]+4\left[\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right]$$其实我们已经默认向量\( \mathbf{v}\)是由三个基向量线性组合而成。
如果用矩阵\(A \)来表示线性变换\( \boldsymbol{T}: \mathbf{R}^{n} \rightarrow \mathbf{R}^{m}\),则需要两组基,即输入空间的一组基(\( n\)个)和输出空间的一组基(\( m\)个)。
从线性变换角度理解投影
处理二维平面内的向量向某条直线投影的问题。假设两个基向量中的\( \mathbf{v}_{1}\)正好是投影方向的向量,而\( \mathbf{v}_{2}\)是垂直于投影方向。输出空间的基向量选择和输入空间一样的。于是对于输入空间中的任意向量\( \mathbf{v}\)有\(\mathbf{v}=\mathbf{c}_{1} \mathbf{v}_{1}+\mathbf{c}_{2} \mathbf{v}_{2} \),输出为\(T(\mathbf{v})=c_{1}\mathbf{v}_{1} \)。线性变换矩阵为\( A=\left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right]\),输入\( \left[\begin{array}{l} c_{1} \\ c_{2} \end{array}\right]\)得到\( \left[\begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array}\right]\left[\begin{array}{cc} c_{1} \\ c_{2} \end{array}\right]=\left[\begin{array}{cc} c_{1} \\ 0 \end{array}\right]\)。
我们知道,对于投影矩阵\( \)来说,对本来就在投影方向上的向量进行投影有得到的是自身,同样地,对垂直于投影方向的向量进行投影得到的是零,也就是说\(1 \)和\( 0\)一定是投影矩阵的两个特征值。特征值\( \)对应的特征向量就是沿着投影方向上的向量,而特征值\( \)对应的特征向量就是沿着投影的垂直方向。
如果我们以标准坐标作为基,那么\(\mathbf{w}_{1}=\mathbf{v}_{1}=\left[\begin{array}{l} 1 \\ 0 \end{array}\right], \mathbf{w}_{2}=\mathbf{v}_{2}=\left[\begin{array}{l} 0 \\ 1 \end{array}\right] \)。对应的投影矩阵\(P=\displaystyle\frac{a a^{T}}{a^{T} a}\),对于投影到斜\( 45\)度的直线,\( P=\left[\begin{array}{ll} 1 / 2 & 1 / 2 \\ 1 / 2 & 1 / 2 \end{array}\right]\)。
确定线性变换矩阵\( A\)(Rule to find A)
矩阵\( A\)的列实际上描述输入原空间的基向量得到的列空间线性组合的系数:$$\begin{array}{l} T\left(\mathbf{v}_{1}\right)=a_{11} \mathbf{w}_{1}+a_{21} \mathbf{w}_{2}+\ldots \ldots+a_{m 1} \mathbf{w}_{m} \\ T\left(\mathbf{v}_{2}\right)=a_{12} \mathbf{w}_{1}+a_{22} \mathbf{w}_{2}+\ldots \ldots+a_{m 2} \mathbf{w}_{m}\\\ldots \ldots \end{array}$$这样矩阵\(A \)就满足“A[输入向量的坐标]=[输出空间的坐标]”。
\( A\left[\begin{array}{c} 1 \\ 0 \\ \vdots \\ 0 \end{array}\right]=\left[\begin{array}{c} a_{11} \\ a_{21} \\ \vdots \\ a_{m 1} \end{array}\right]\)所得结果就是输出空间的坐标,即输出空间的基进行线性组合所需的系数。
一个特殊的线性变换-求导(\(T=\displaystyle\frac{d}{d x} \))
输入—函数:\( c_{1}+c_{2} x+c_{3} x^{2}\)
输入—基:\( 1, x, x^{2}\)
输出—函数:\(c_{2}+2 c_{3} x\)
基:\(1, x \)
这是一个\( T: \mathbf{R}^{3} \rightarrow \mathbf{R}^{2}\)的线性变换。矩阵\(A \)满足\(A\left[\begin{array}{cc} c_{1} \\ c_{2} \\ c_{3} \end{array}\right]=\left[\begin{array}{cc} c_{2} \\ 2 c_{3} \end{array}\right] \)求得\(A=\left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 2 \end{array}\right] \)。
更普遍的来讲,矩阵的逆矩阵就是线性变换的逆变换,矩阵的乘积就是线性变换的乘积,矩阵的乘法源自于线性变换。
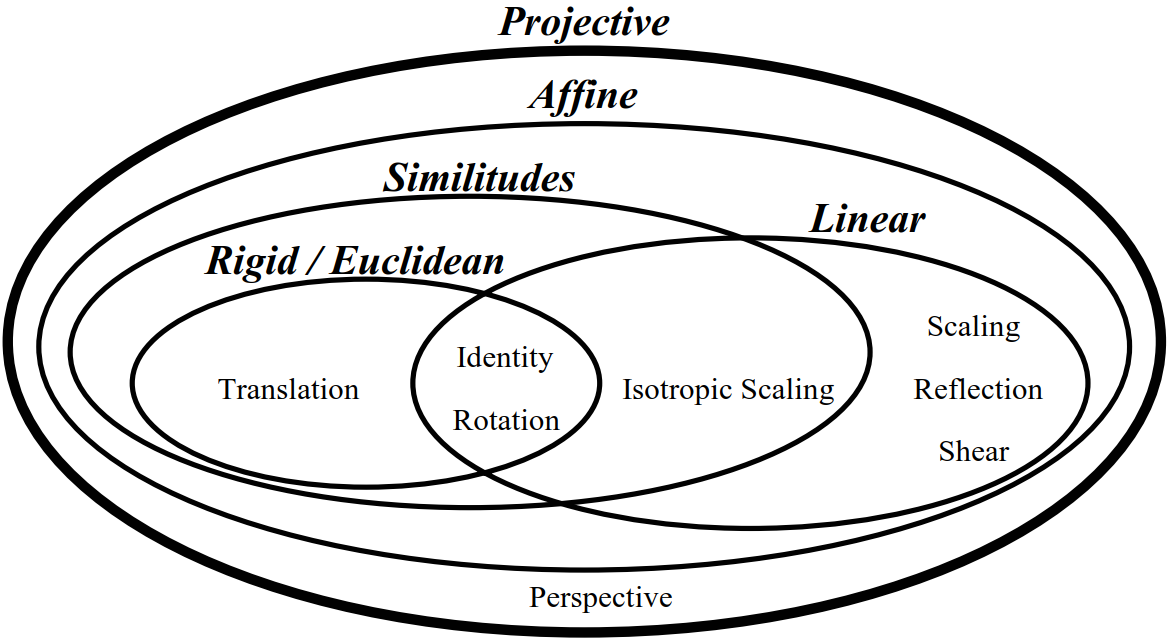
仿射变换
【仿射变换】(Affine transformation),又称仿射映射,是指在几何中,对一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。对一个向量 \(\vec{x}\)平移\(\vec{b}\),与旋缩放\(A\) 的仿射映射为\(\vec{y}=A \vec{x}+\vec{b}\)
xxx补充
参考资料:
(1) 如何通俗地讲解「仿射变换」这个概念?—知乎
(2) 仿射变换及其变换矩阵的理解
(3) 计算机图形学—中科大
射影变换
xx
坐标系变换
坐标系变换是一个很重要的内容,涉及到多方面的知识,比如(偏)倒数求解,极坐标的变换,矩阵和行列式的计算等等,总而言之可以同时把微积分和线性代数以及对应的几何图像联系起来,有助于我们图像化地理解相关知识。具体来讲,在我们的极坐标中,就是坐标系的变换,在处理发射光谱的波长波数转化的时候,也涉及坐标系变换的知识。不仅要会用坐标系变换,更要理解其中的精髓。[mathjax]$$\begin{aligned} &I=\int_{0}^{+\infty} e^{-x^{2}} d x\\ &I^{2}=\int_{0}^{+\infty} \int_{0}^{+\infty} e^{-\left(x^{2}+y^{2}\right)} d x d y=\int_{0}^{\pi / 2} \int_{0}^{+\infty} e^{-\rho^{2}}\rho d \rho d \theta=\frac{\pi}{4} \end{aligned}$$上面是一种简单的方法求解特殊积分的值,如果对第一个式子,我们把积分区间变成负无穷到正无穷,那么最终积分得到的值是\(\sqrt{π}\)。可以看出\( x-y\)坐标变换成极坐标计算的好处,那么为什么可以这样变换呢?$$\iint_{S} f(x, y) d x d y=\iint_{S^{*}} f(\rho \cos \theta, \rho \sin \theta) \rho d \rho d \theta$$原来的积分区间是\(S\),变换坐标之后的积分区间是\(S^{*}\),但是\(S\)的面积是不等于\(S^{*}\)的面积的,或者进一步说\(S\)中任意微小区域的面积和与之对应的\(S^{*}\)上的区域的面积不相等,但是f的值没有变化,其实就是\(dS^{*}\)对\(dS\)进行了缩放处理,为了修正这一部分的,所以我们用了我们在\( f\)之后乘了\( \rho\),这里的\( \rho\)就是雅各比系数。$$\begin{array}{l}{d x=d(\rho \cos \theta)=\cos \theta d \rho+(-\rho \sin \theta) d \theta} \\ {d y=d(\rho \sin \theta)=\sin \theta d \rho+\rho \cos \theta d \theta} \\ {d x d y=\left[\begin{array}{cc}{\cos \theta} & {-\rho \sin \theta} \\ {\sin \theta} & {\rho \cos \theta}\end{array}\right]\left[\begin{array}{c}{d \rho} \\ {d \theta}\end{array}\right]}\end{array}$$我们容易得到如下的行列式关系,前面的行列式就相当于对ρ-θ轴上的向量逆时针旋转一定的角度,而且旋转前后的模长不变,所以这个变换矩阵的行列式的模长是\(1\),但是对于第二个行列式,我们得到的模长\( \rho\),相当于把原来的向量(面积)扩大了\( \rho\)倍。所以这里的\( \rho\) 就是雅各比系数。就上面的等式来说,就是必须把dρdθ的面积扩大\( \rho\)倍才能恢复成原来的\(dxdy\)的面积。$$\left|\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right|=1\quad\quad\left|\begin{array}{cc} \cos \theta & -\rho \sin \theta \\ \sin \theta & \rho \cos \theta \end{array}\right|=\rho$$对于下面的等式,我们可以将任何一点 \(\left[\begin{array}{l}{x} \\ {y}\end{array}\right] \)想象成 \(x\vec { i }+y\vec { i } \),相当于说对原来的\(x\)轴和\(y\)轴都做一定的变换。其中的\(\vec{i}\)等于\(\left[\begin{array}{cc}{1}\\{0}\end{array}\right] \),\(\vec{j}\)等于\(\left[\begin{array}{cc}{0}\\{1} \end{array}\right]\)$$ \left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} a x+b y \\ c x+d y \end{array}\right]=x\left[\begin{array}{l} a \\ c \end{array}\right]+y\left[\begin{array}{l} b \\ d \end{array}\right] $$下面我们来思考一下这个2*2矩阵对原有坐标系的影响。 \(a=1,\quad c=0\)相当于原有的\( x\)轴不发生变化; \(b=0,\quad d=1\)相当于原有的\( y\)轴不发生变化; 进一步地,实际上原来的\(x\),或者说\(x\vec{i}\)已经变成了\(a\vec{i}+c\vec{j}\);而\(y\vec{i}\)已经变成了\(b\vec{i}+d\vec{j}\) 很容易知道原来的点到原点的距离,或者说模长是\( \sqrt{x^2+y^2}\),我们能直接平方和开根号的基础是两个基向量的相互垂直的,而新得到的坐标/向量的长度不能采用类似的方法,也就是说\( \sqrt{(ax+by)^2+(cx+dy)^2}\)是错误的,因为我们不知道新的基向量是否垂直。新的基向量垂直的条件是\( ab+cd=0\) 将新的基向量转化成极坐标的形式\( \left[\begin{array}{cc}{a}\\{c}\end{array}\right]\)=\( \rho_1\left[\begin{array}{cc}{\cos\alpha}\\{\sin\alpha}\end{array}\right]\),\( \left[\begin{array}{cc}{b}\\{d}\end{array}\right]\)=\( \rho_2\left[\begin{array}{cc}{\cos(\beta+\pi/2)}\\{\sin(\beta+\pi/2)}\end{array}\right]\)。也就是说将原来\(x\)轴的基向量逆时针旋转了\(\alpha \)度,同时大小扩展为原来的\(\rho_1\)倍,而y轴的基向量逆时针旋转了\( \beta\)度,大小扩展为原来的\(\rho_2\)倍,注意这里\(\pi/2\)的处理,因为\(y\)轴的基向量的方向就相当于从x轴方向顺时针旋转了\(\pi/2\)度。如果\(\alpha \)和\( \beta\)一样大,就意味着整个坐标轴是一起沿着原点逆时针旋转,然后基向量分别在各自纬度上伸缩。我们先只考虑旋转操作,如果\(\alpha = \beta\),那么我们可以得到:$$ \begin{aligned} &\cos (\beta+\pi / 2)=-\sin (\beta)=-\sin (\alpha) \\ &\sin (\beta+\pi / 2)=\cos (\beta)=\cos (\alpha) \end{aligned} $$所以有:$$ \left[\begin{array}{ll} a & b \\ c & d \end{array}\right]=\left[\begin{array}{cc} \rho_{1} \cos \alpha & -\rho_{2} \sin \alpha \\ \rho_{1} \sin \alpha & \rho_{2} \cos \alpha \end{array}\right] $$如果没有伸缩操作,那么\( \rho_1=\rho_2=1\),也就是纯坐标轴旋转操作。 再回顾我们先前\( x-y\)坐标系变换为极坐标系,其实这不是一个简单的旋转+伸缩的变换。取一个特定的\(\rho\)和\( \theta\),这一组数对应的点/向量,必须将\(\rho\)轴旋转\( \theta\)度,然后将\( \theta\)所在的轴旋转\( \theta\)度,然后仅对旋转之后的\( \theta\)轴进行比例为\(\rho\)的伸缩变换,这样得到的点/向量正好对应到原来的\(x-y\)坐标系,需要记住旋转操作并不改变大小,最后一步的缩放操作解释了极坐标变换的雅各比系数\(\rho\)。 这里还是有点不明白(把\(du\)和\(dv\)展开就知道了,然后等式右边整理为\(dx\)和\(dy\)的线性组合,由于\(dx\)只和\(dx\)有关,所以右侧\(dx\)前面的系数是\(1\),\(dy\)前面的系数是\(0\))
参考PPT-Jacobian
复习三
左右逆和伪逆
拉普拉斯矩阵
补充
Tikhonov正则化
从谱的分布来说的话,如果矩阵是病态的,就会有几个很小的本征值(接近0),那么迭代计算逆矩阵的算法表现出数值不稳定性。Tikhonov正则化方法就相当于在本征值上加上了一个常数,从而提高了矩阵迭代计算的稳定性。
参考资料:
(1) Revealing trap depth distributions (thermal barrier)-PRB
向量空间-群-映射
交换图
xx
不变子空间
(1) \(\{0\}\),因为每个线性映射都必有映射\(0 \mapsto 0\);
(2) \(V\),显然\(\mathbf{v} \in V \Longrightarrow T(\mathbf{v}) \in V\);
(3) 令 \(\mathbf{v}\) 为 \(T\) 的一个特征向量,也即 \(T \mathbf{v}=\lambda \mathbf{v}\) 。则 \(W=\operatorname{span}\{\mathbf{v}\}\) 是 \(T\) 不变的。
线性空间的直和分解
- \(W=\sum V_{i}\)是直和;
- 零向量的表法唯一;
- \(V_{i} \cap \displaystyle\sum_{j \neq i} V_{j}=\{0\}(i=1,2, \cdots, s)\)
- \( \text { dim }(W)=\sum \text { dim }\left(V_{i}\right)\)
从集合的角度理解:
- 子空间的和对应集合中的并集;
- 子空间的直和对应集合中的不交并;
- 子空间的\(0\)(零向量)对应集合中的空集;
- 向量空间中直和与和的区别 正如集合中并集和不交并的区别。
从【分治】(divide-and-conquer)的角度看:线性空间的直和分解,就是将线性空间分成不相交的子空间,这些子空间唯一的交集就是零向量,或者说将该线性空间分解为几个子空间的直和。线性空间中的问题,可以投影到不同的子空间(分)去分别解决,再把结果汇总合并起来就得到原问题的解(治)。各个子空间,相互独立,互不干扰。这种分治的思想在求解线性方程组、微分方程组的结构、拓扑基等等都存在。
线性空间不变子空间直和分解:对于很大一类算子\(T: V \rightarrow V\) (normal operator),我们可以找到一个\( V\)的直和分解\(V=\oplus_{i=1}^{n} E_{i}\),使得$$ T x=\sum_{i=1}^{n} \lambda_{i} P_{E_{i}} x $$这里 \(P_{E_{i}}\) 是 \(V\)到\(E_{i}\)的投影。也就是说,对于\(V\)中的任意一个向量\( x\),经过投影矩阵\(P_{E_{i}}\)作用后,分别投影到了不同子空间上得到一组\(x_i\),用线性变换\(T\)作用在这些\(x_i\),得到的结果分别为\(\lambda_i x_i \),即线性变换后的结果仍处在各自子的子空间\(E_i\)中,也即\(E_{i}\)是线性变换\(T\)下的不变子空间。那么算子\(T\)作用在\( x\)恰好是\(\lambda_i x_i \)的和。特殊地,如果 \(x\) 恰好在某个\(E_{k}\)中,那么\(T x=\lambda_{k} x\),此时这个算子近似一个简单的数乘(multiplicative operator)算子。
- 这其实是算子对角化的,推广到无限维空间也是成立的,比如拉普拉斯算子也可以进行这样的分解;
- 其实上面的直和分解的不变子空间就是各个特征向量所在的子空间,它们也是不变子空间;
- 矩阵的特征值要想说清楚还要从线性变换入手,把一个矩阵当作一个线性变换在某一组基下的矩阵,最简单的线性变换就是数乘变换,求特征值的目的就是看看一个线性变换对一些非零向量的作用是否能够相当于一个数乘变换,特征值就是这个数乘变换的变换比,这样的一些非零向量就是特征向量,其实我们更关心的是特征向量,希望能把原先的线性空间分解成一些和特征向量相关的子空间的直和,这样我们的研究就可以分别限定在这些子空间上来进行,这和物理中在研究运动的时候将运动分解成水平方向和垂直方向的做法是一个道理!
- 本质就是约化,把高维的问题约化到低维,把复杂的变换约化成简单的变换,降维过程往往和特征值/特征向量有关;
- 比方说随便写一个乱七八糟的方阵,你不知道怎么处理,事实上数学家a priori也不知道怎么处理(a priori不知道怎么翻译比较好,“先验”?)但是给你一个对角阵,你的思路估计会清晰很多,你知道对角阵代表的就是在不同的特征方向上做不同的伸缩变换(当然伸缩的系数可能是复数,这种情形对应到实平面里面的旋转+伸缩)的一个复合。然后有一个奇迹出现了:很多矩阵,在你换一个角度(换一套坐标系)去观察以后,它其实就是个对角阵。你去把一个矩阵对角化的过程,就是去找那些特征方向,也就是一维的不变子空间的过程,也就是你去寻找最佳的“观察角度”的过程。
当然你不可能总是这么幸运。有些矩阵是不可对角化的,本质原因是他们有2维以上的“不可约”不变子空间(这里的不可约和表示论里面的不可约是一个意思)。在这种情形下,如果是复矩阵,你就应该去考虑所谓的Jordan标准型。非平凡的Jordan块当然比对角阵麻烦一点,但是比起原来那个乱七八糟的矩阵总是方便太多。在这种情形下你还是要去找所有的“不可约”不变子空间(Jordan标准型里的根子空间),然后考虑这个矩阵在每个不变子空间上长什么样(Jordan块)。这个过程就好像你面对一个复杂的机器(让你不知所措的一个矩阵),你先观察它的内在结构(寻找它的特征空间/不变子空间),然后拿锤头起子或者别的什么工具(特征值、(广义)特征向量等知识)把它拆卸成一个个你可以理解的零件(把大矩阵分解成你可以理解的小矩阵块,比如Jordan块),然后你就对原来那个机器的运作机理有所了解了。本质上是一种“分析”的思维方式(这里的分析不是数学分析意义上的分析,而是跟“综合”相对的那个分析)。—Yuhang Liu
参考资料:
(1) 向量空间的子空间的“和”与“直和”,这两个概念的区别是什么?—知乎
(2) 把线性空间分解为不变子空间的直和有何用处?—知乎
(3) 重修线性代数7—相似—应行仁
等待继续补充
【代数结构】(Algebraic structure) = 集合 + 运算
- 集合里的元素,可能是数字,也可能是数组等;
- 运算,比如加法,乘法运算。
由于集合的不同,以及运算的不同,还有关于集合和运算的规则有异,就形成了不同的代数结构(群、环、域、和格)。群是最基本的代数结构,它有一个集合,一种运算(二元运算,最简单的比如加法、乘法等);向量空间则比较复杂些,有两个集合,两种运算(加法和数乘)。
向量空间= 集合+线性变换 (linear mappings)
线性代数研究的对象是向量空间,群论的研究对象是群”,群和向量空间都属于代数结构。
同构(Isomorphism)
群的角度:从群G到群F上,存在一一对应的满映射Φ,且这个映射本身保持群的乘法运算规律不变,也就是说G中两个元素乘积的映射,等于群G中两个元素映射的乘积,则称群G与群F同构,记作G≅F。映射Φ称为同构映射,它的作用是:(同构示意图)
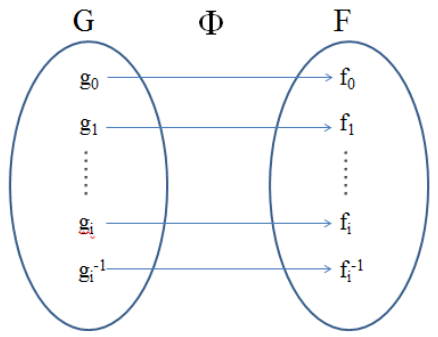
- 从数学角度,两个同构的群有完全相同的结构,没有本质的区别;
- 空间反演群{E、I}与二阶循环群{e、a}完全同构。
- 三阶置换群与 D3 群完全同构。
- 数二维空间的旋转群SO(2)和一维复数空间的旋转群U(1)同构的。
向量空间的角度:群同构就是向量空间的线性同构(Linear isomorphism)。Linear isomorphisms between vector spaces; they are specified by invertible matrices.
线代启示录链接补充
线性空间之间的同构就是保持线性运算的双射。
xxxxxx
同态(Homomorphism)
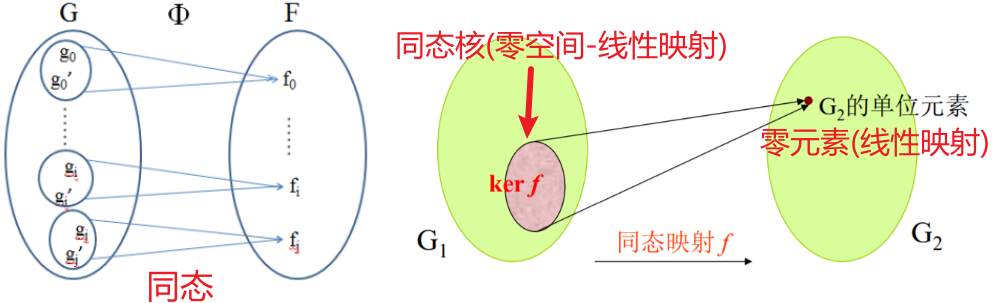
- Homomorphisms of vector spaces are also called linear maps(线性映射)。
- 群同态在向量空间上的体现是线性映射。
- 群同态的核kernel体现为线性映射(矩阵)的零空间Null Space。
映射
【线性映射】(Linear map):线性映射是从一个向量空间\(V\)到另一个向量空间\(W\)的映射且保持加法运算和数量乘法运算(两个线性空间域相同),而【线性变换】(linear transformation)是线性空间\(V\)到其自身的线性映射,不过有时候人们并不区分,people use them interchangeably。比如在我的笔记线性变换及其对应矩阵章节的例子,对于某一线性变换\(T: \mathbf{R}^{3} \rightarrow \mathbf{R}^{2}\) ,表达式为\(T(\mathbf{v})=A \mathbf{v}\),其中\(A\) 是一个 \(2 \times 3\) 矩阵,那么输入一个三维向量而输出一个二维向量。
例子:(线性变换及其对应矩阵中的例子这里就不列举了)
- 函数\(f: \mathbb{R} \rightarrow \mathbb{R}: x \mapsto c x\),the graph is a line through the origin.
- \(T(\boldsymbol{v})=\boldsymbol{v}+\boldsymbol{u}_{0}\)不是线性变换,因为\(T(\mathbf{0})\neq\mathbf{0}\)。
- The zero map \(\mathbf{x} \mapsto \mathbf{0}\) between two vector spaces (over the same field) is linear.
- For real numbers, the map \(x \mapsto x^{2}\) is not linear.
- Differentiation defines a linear map from the space of all differentiable functions to the space of all functions. It also defines a linear operator on the space of all smooth functions$$ \frac{d}{d x}\left(c_{1} f_{1}(x)+c_{2} f_{2}(x)+\cdots+c_{n} f_{n}(x)\right)=c_{1} \frac{d f_{1}(x)}{d x}+c_{2} \frac{d f_{2}(x)}{d x}+\cdots+c_{n} \frac{d f_{n}(x)}{d x} $$
- A definite integral over some interval \(I\) is a linear map from the space of all real-valued integrable functions on \(I\) to \(\mathbb{R}\). For example,$$ \int_{a}^{b}\left[c_{1} f_{1}(x)+c_{2} f_{2}(x)+\cdots+c_{n} f_{n}(x)\right] d x=c_{1} \int_{a}^{b} f_{1}(x) d x+c_{2} \int_{a}^{b} f_{2}(x) d x+\cdots+c_{n} \int_{a}^{b} f_{n}(x) d x $$
如果线性映射是双射,则称线性同构。
【双线性映射】(Bilinear map):补充xxx
【线性算子】A linear operator is a linear transformation that maps a vector space \(V\) into itself. (来自Linear Algebra with Applications 9th edition)。
【双射】(Bijection):one-to-one correspondence的映射,也叫invertible function。
- 函数 \(f: \mathbb{R} \rightarrow \mathbb{R}\) ,其形式为 \(f(x)=2 x+1\) ,是双射的。
- 指数函数 \(g: \mathbb{R} \rightarrow \mathbb{R}\) ,其形式为 \(g(x)=e^{x}\) ,不是双射。因为不存在一 \(\mathbb{R}\) 内的 \(x\) 使得 \(g(x)=-1\) ,故 \(g\) 非为双射。但若其陪域(Codomain,也叫到达域)改成正实数 \(\mathbb{R}^{+}=(0,+\infty)\) ,则 \(g\) 便是双射,其反函数为自然对数函数 \(\ln\)。
【保距映射】(Isometry):在度量空间之中保持距离不变的同构关系,几何学中的对应概念是【全等变换】。
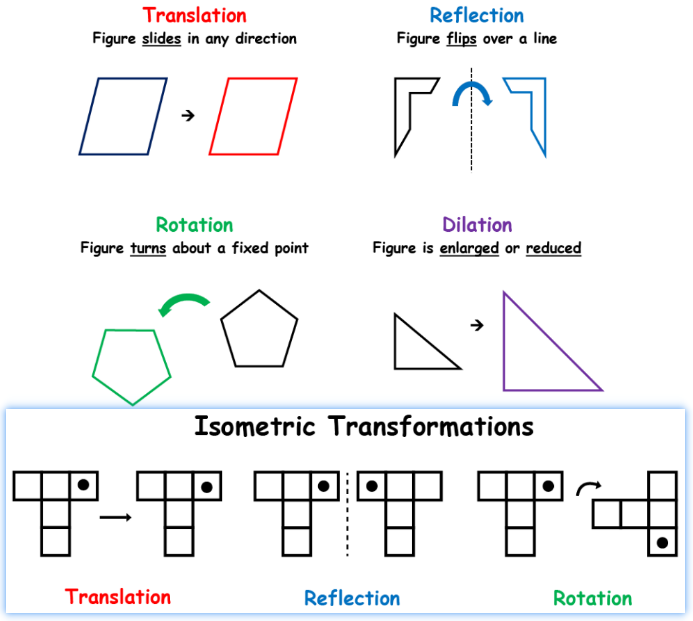
对于the four major types of transformations:只有其中的Translation/Reflection/Rotation是isometric transformations。
- Translation (figure slides in any direction)
- Reflection (figure flips over a line)
- Rotation (figure turns about a fixed point)
- Dilation (figure is enlarged or reduced)
【保角映射】
范德堡方法+保角映射
不同拓扑结构下半导体电阻率特性研究
参考资料:
(1) 同构的向量空间—线代启示录
(2) 保長、保角與共形映射—线代启示录
(2) 如何理解同构的向量空间?—知乎
(3) 浅谈线性代数与群论的一致性-A -B