混沌

气象学家洛伦兹发现稍微修改计算的条件，比如“输入数据”中小数点后保留的位数，或者计算的起始点稍微变化，都会导致随着时间的延长，后一次模拟的结果和前一次模拟的结果之间差别越来越大。他抓住这突发的事件，经过反复思考，后来这个地方就产生了一门新的学问。洛伦兹是混沌理论的少有几位创立者之一，他在1963年发表的关于混沌理论的开创性研究在被冷落了12年之久以后才得到广泛承认，并很快引发对混沌研究的热潮，由此诞生和发展起了一门新兴学科—混沌理论，成为现代新兴学科的代表。

【混沌理论】是关于非线性系统在一定参数条件下展现分岔、周期运动与非周期运动相互纠缠，以至于通向某种非周期有序运动的理论。

• 【蝴蝶效应】(初始值的微小变化极大影响结果)；
• 【非线性现象】(多个因素相互影响/约束，未知函数有非线性项)，其实就是蝴蝶效应的原因；
• 典型的混沌现象：
  • 天气预报，长期天气预报注定失败(微小的变化会影响很远很远)。
  • 三体问题。
• 混沌和随机运动的差异：外在表现和纯粹的随机运动很相似，即都不可预测。但和随机运动不同的是，混沌运动在动力学上是确定的，它的不可预测性是来源于运动的不稳定性，或者说混沌系统对无限小的初值变动和微扰也具有敏感性，无论多小的扰动在长时间以后，也会使系统彻底偏离原来的演化方向。

物理学家们喜欢想，人们要做的全部事情就是说：这些是条件，下一步将发生什么？— 费曼
(这句话是说必然性、确定性的思维方式，而混沌与分形在思想方法上对我们来说是一个冲击。)

To see a World in a Grain of Sand And a Heaven in a Wild Flower, Hold Infinity in the palm of your hand And Eternity in an hour. — William Blake

单摆来回摆动的轨迹是一样的，但是【双杆摆】(Double-compound-pendulum)将呈现混沌行为。 从开始略微不同的初始条件摆杆将导致一个完全不同的轨迹。双杆摆是具有混沌方案最简单的动力系统之一。

【洛伦兹吸引子】，以其双纽线形状而著称，映射展示出动力系统(三维系统的三个变量)的状态是如何以一种复杂且不重复的模式，随时间的推移而演变的，对应方程组(第二个和第三个方程非线性)如下。(交互动画参考Lorenz System—geogebra)
$$\begin{aligned} &\frac{d x}{d t}=10(x-y) \\ &\frac{d y}{d t}=28 x-y-x z \\ &\frac{d z}{d t}=x y-\frac{8}{3} z \end{aligned}$$

• 其中\(x\)、\(y\)和\(z\)分别表示对流强弱、上升部分和下降部分的温差、水平方向的温差；
• 上图表示的其实是一个相空间；
• 吸引子是动态系统的归宿。归宿，比如往天上扔个东西，或者树上的苹果，最后都会落到地上，这就是归宿。对于洛伦兹吸引子来说，归宿就是蝴蝶；对于地球围绕太阳转，由于没有摩擦力，只有万有引力，系统没有耗散，所以吸引子是一个极限环。
• 分形维数大约2.06；
• 分形是混沌在空间中的描述，混沌是分形在时间上的体现。混沌现象可以看作由连续空间(时域)向分形流形(频域/空域)的映射。

吸引子

补充

迭代是有广泛应用的数学方法，例如大学牛顿求根迭代法$$x_{n+1}=x_{n}-P\left(x_{n}\right) / P^{\prime}\left(x_{n}\right)$$当\(P(x)=x^{4}-1\)时$$x_{n+1}=x_{n}-\left(x_{n}^{4}-1\right) /\left(4 x_{n}^{3}\right)$$
下面举一个更简单的迭代例子：
Logistic映射(驱动力和耗散力)，这个例子类似“种群”的增长/衰退，\(x_{n}\)表示种群在第\(n\)代时的数量：$$x_{n+1}=f\left(x_{n}\right)=\mu x_{n}\left(1-x_{n}\right)$$存在定常解\(x_{*}=0\)和\(x_{*}=1-\displaystyle\frac{1}{\mu}\)。

如果迭代到某一步，左边带入\(a\)，右边得到\(b\)；左边带入\(b\)，右边得到\(  a\)；则得到周期为\(2\)的解，这时\(a\)和\(b\)满足：$$\left.\begin{array}{l} a=f(b) \\ b=f(a) \end{array}\right\} \Rightarrow\left\{\begin{array}{l} a=f(f(a)) \\ b=f(f(b)) \end{array}\right.$$对于前面的Logistic映射，我们现在有$$x=f(f(x))=\mu[\mu x(1-x)][1-\mu x(1-x)]$$可解得除了两个不动点的解之外，还有两个解$$x_{3,4}=\frac{(\mu-1) \pm \sqrt{(\mu+1)(\mu-3)}}{2 \mu}$$当\(\mu=3.2\)时，这两个解分别为\(x_{3}=0.513\)和\(x_{4}=0.799\)。

可以考虑多次迭代：\(f^{k}(x)=f(f \cdots(f(x))\)：
(1) 如果有\(a\)使得\(f(a)=a\)，则称\(a\)为不动点。
(2) 如果有\(a\)使得\(f^{k}(a)=a\)，则称\(a\)为周期点;
(3) 使得上式成立的最小的\(k\)，称为周期。

混沌解：计算表明，当参数达到某一临界值\(\mu = 3.57\)，则从有限周期变成周期无限的混沌状态。下图是单峰映射的分叉图Bifurcation diagram for the logistic map。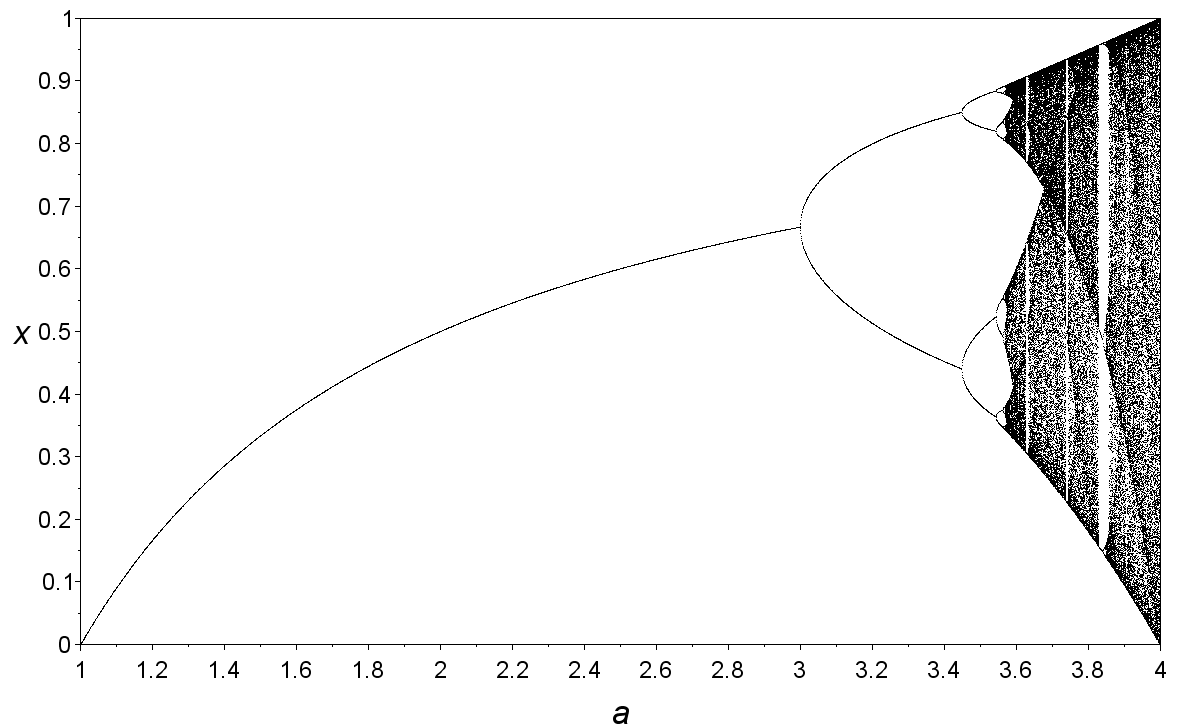

参考资料：
1. 《蝴蝶效应之谜：走近分形与混沌》(张天蓉)
2. 书的读书笔记-CSDN
3. 从刘徽割圆谈起
4. 妈咪说MommyTalk视频-混沌与分形专题
5. 雪花周长和地球直径谁更大？1.26维空间啥样？李永乐老师讲分形几何

分形

A fractal is a way of seeing infinity.——Benoit Mandelbrot

非线性系统其实也是有规律的，那么我们是否可以采取一些手段，透过复杂，混乱和不规则的形态来探寻他们背后的规律呢，为了解决这个问题分形理论应运而生。

1967年，英国工程师在科学杂志上发表文章《英国的海岸线有多长》，他提到从一定的意义上来说，英国的海岸线是无限长，量的尺子越小，最终的结果是海岸线测量结果越长。

生理学分形(Fractals in Physiology)以及生活中的分形

Some of the most visually striking examples of fractal forms are found in physiology: The respiratory, circulatory, and nervous systems are remarkable instances of fractal architecture, branches subdividing and subdividing and subdividing again. 上图画了肺的分形结构。大脑不是分形的，但是mind可以产生分形结构的思考过程；从人工智能和机器学习的角度看，some of the most successful of these deep neural networks operate on a principle where they're processing information over and over again, while periodically feeding back in the original information to keep the process going. And that might sound a little bit familiar, because it actually is quite similar to the way that Mandelbrot's fractal equation works. It's an engine for generating fractal levels of complexity. And perhaps that's why these fractal images resonate so deeply with us. It's because when we're looking at them, in a way, we're seeing a reflection of ourselves.

• 利希滕贝格图；
• 树木、蕨类植物、菜花；
• 身体中的血管，神经；

【科赫雪花】(Koch snowflake)：也叫科赫曲线，单位长的正三角形，每三分之一中端擦掉，然后拱起一个小三角形，不断重复。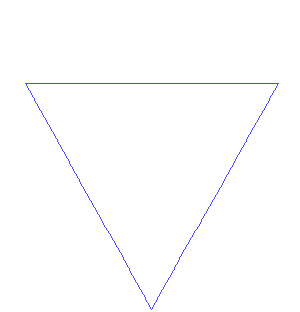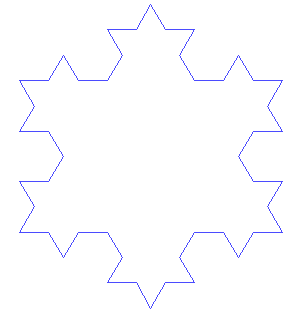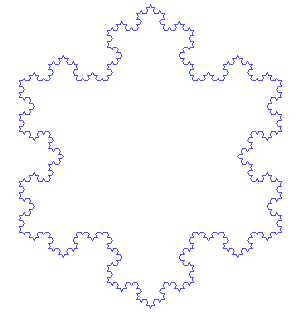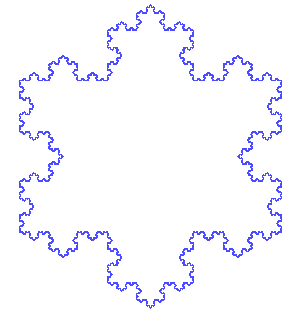总长度：\(\displaystyle\lim _{n \rightarrow \infty} 3 \times\left(\frac{4}{3}\right)^{n}=\infty\)虽然曲线长度无限，但是所围成的面积有限(显然不可能超过初始三角形外接圆的面积)。其构造是“自相似性”。

【谢尔宾斯基三角形/谢尔宾斯基地毯】
分形常被理解为“分数维图形”。一般来说是复杂而似乎没有规则的，就像前面提到的Julia集。分形是一个非线性过程中复杂现象的几何特征。

【朱利亚集合】(Julia set)
朱利亚集合可以由\(f_{c}(z)=z^{2}+c\)进行反复迭代得到。对于固定的复数\(c\)，取某一\(z\)值比如\(z=z_{0}\)，可以得到序列$$ z_{0}, f_{c}\left(z_{0}\right), f_{c}\left(f_{c}\left(z_{0}\right)\right), f_{c}\left(f_{c}\left(f_{c}\left(z_{0}\right)\right)\right), \ldots $$这一序列可能发散于无穷大或始终处于某一范围之内并收敛于某一值。我们将使其不扩散的\(z\)值的集合称为朱利亚集合。不同\(c\)值时所得到的不同的朱利亚集合在复平面上的图像参考这里。

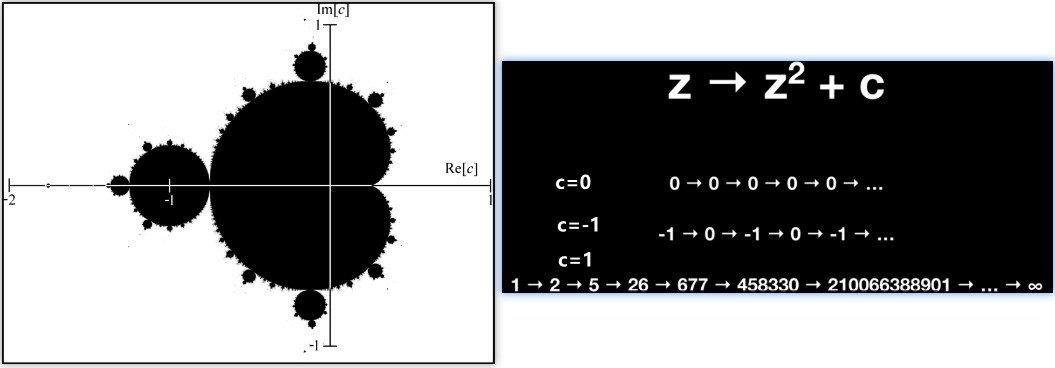
【曼德博集合】(Mandelbrot set)
曼德博是分形之父，他首次提出分形Fractal的概念。
曼德博集合可以用复二次多项式来定义：\(f_{c}(z)=z^{2}+c\)，其中\(c\)是一个复数参数，从\(z=0\)开始对\(f_{c}(z)\)进行迭代：$$ \begin{aligned} &z_{n+1}=z_{n}^{2}+c, n=0,1,2, \ldots \\ &z_{0}=0 \\ &z_{1}=z_{0}^{2}+c=c \\ &z_{2}=z_{1}^{2}+c=c^{2}+c \end{aligned} $$每次迭代的值依序如序列所示：\(\left(0, f_{c}(0), f_{c}\left(f_{c}(0)\right), f_{c}\left(f_{c}\left(f_{c}(0)\right)\right), \ldots\right)\)不同的参数\(c\)可能使序列的绝对值逐斩发散到无限大，也可能收敛在有限的区域内。曼德博集合\(M\)就是使序列不延伸至无限大的所有复数\(c\)的集合。曼德博集虽然存在有限面积，但是目前只能通过蒙特卡洛方法来计算。

分形的特点：
(1) 任意小的尺度上都具有精细结构；
(2) 无法用传统的欧式几何来描述；
(3) 具有自相似性(self-similarity)，其实就是套娃；
(4) 具有简单的递归定义；
(5) 一般情况下分形维数会大于拓扑维数，且可以是分数(皮亚诺曲线和希尔伯特曲线就是例外)；

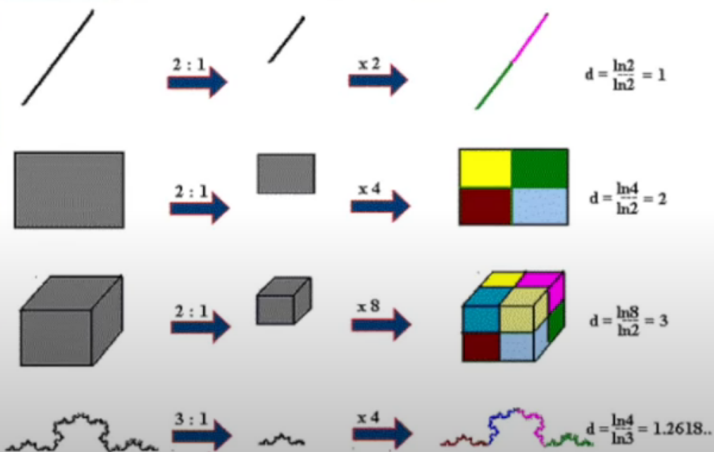
【分形维数】(Hausdorff维数)

• 传统维数：我们传统的线是一维，面是二维，体是三维，这些是拓扑维度，从这个角度讲上面画的科赫雪花和谢尔宾斯基地毯都是二维的；
• 豪斯多夫维数是专门用来研究分形结构的；
• 皮亚诺曲线和希尔伯特曲线的分形维数是2；
• 科赫雪花维数的计算：将科赫曲线的尺寸缩小至原来的三分之一；然后，用4个这样的小科赫曲线，便能构成与原来一模一样的科赫曲线。因此，我们得到科赫曲线的维数为\(d=\frac{\ln 4}{\ln 3}=1.2618 \cdots\)。

测度：一般来讲，就是集合的长度、面积、体积。

Hausdorff测度：

【Lebesgue测度】：设\(E\)是\(\mathbf{R}^{n}\)上的一点集，设\(\left\{U_{k}\right\}\)是\(E\)的开覆盖，定义直径：$$diaU=\sup \{d(x, y) \mid \forall x, y \in U\}$$定义\(\inf \displaystyle\sum_{k}\left(diaU_{k}\right)^{n}\)为集合\(E\)的Lebesgue外测度。(注：可能相差一个正常数)

【希尔伯特曲线】：

拓展资料：
(1) Fractals: a world in a grain of sand | Ben Weiss | TEDxVeniceBeach
(2) Fractals in Physiology—Yale Math
(3) Are Humans Fractals? Biology and Behavior (multiple studies)—Conscious Vibe
(4) 《蝴蝶效应之谜：走近分形与混沌》— 张天蓉
(5) 《大自然的分形几何学》—Mandelbrot