Radiometric到Photometric的转换
Radiometry- deals with the detection and measurement of electromagnetic radiation across the total spectrum.
Photometry - subfield of radiometry; radiometric power scaled by the spectral response of the human eye.
下标"e"表示energetic;下标"v"表示visual。

- 上面是scotopic and the photopic curves of spectral luminous efficacy (non-normalized values),我们常说的Luminous efficiency function是归一化后的值,而且是没有量纲的;
- scotopic vision (暗视觉),photopic vision (明视觉),暗视觉是眼睛在完全暗适应的条件下的灵敏曲线,由于应用发光的材料一般多要求较强的量度,暗视觉用的很少;
- Luminous efficiency function = Luminosity function = 标准光度函数 = 相对视见函数,代表的是the average spectral sensitivity of human visual perception of light. It is based on subjective judgements of which of a pair of different-colored lights is brighter, to describe relative sensitivity to light of different wavelengths. It is not an absolute reference to any particular individual, but is a standard observer representation of visual sensitivity of theoretical human eye.
- 标准光度函数分布在380nm到780nm之间,也表示仅有此区段的光谱能够被转换为亮度,这亦表示仅此区段的光谱为可见光。
- Power (Watts) is converted to luminous flux (lumens) via the relation$$\Phi_{\mathrm{v}}=683.002 \mathrm{~lm} / \mathrm{W} \cdot \int_{0}^{\infty} V(\lambda) \Phi_{\mathrm{e}, \lambda}(\lambda) \mathrm{d} \lambda$$
- 555.016nm处的强度最高,此点的强度被定义为683 lm/W,或者说1W 该波长的单色光对应683 lm;
- 相对视见函数\(V(\lambda)\)是无量纲量,555.016nm处的值为1,也是最大值;
- \(\Phi_{\mathrm{v}}\)表示的是luminous flux (光通量), 单位是流明lumen;
- \(\Phi_{\mathrm{e}, \lambda}(\lambda)\)表示的是spectral radiant flux (光谱辐射功率分布),单位是W/nm;
- 更准确地说是将光谱的功率分布(纵轴单位为W/nm,积分即为总功率,单位W)转化为单一数值——光通量;即函数到单一数值的映射。
计算100 W白炽灯的光通量:The radiant flux (\(\Phi_e\)) of a 100W incandescent lightbulb is about 80W, with the remaining 20W being converted directly to non-radiated heat.\(\Phi_e^{\mathrm{bulb}}=\displaystyle\int_0^{\infty} \Phi_{e, \lambda}^{\mathrm{bulb}}(\lambda) d \lambda=80 \mathrm{W}\) 即对灯泡的spectral flux (\(\Phi_{e, \lambda}\))进行积分,spectral flux of an object is radiant flux per unit wavelength, and is typically measured in Watts/nanometer.
如果只对可见光区积分:\(\displaystyle\int_{380 \mathrm{~nm}}^{750 \mathrm{~nm}} \Phi_{e, \lambda}^{\text {bulb }}(\lambda) d \lambda=8.7 \mathrm{W}\),即效率只有\(8.7 \%\)。
进一步地,考虑人眼相对视见函数,$$ \Phi_{\mathrm{v}}=683.002 \mathrm{~lm} / \mathrm{W} \cdot \int_0^{\infty} V(\lambda) \Phi_{e, \lambda}^{\mathrm{bulb}}(\lambda) d \lambda=683.002 \frac{\mathrm{lm}}{\mathrm{W}} \cdot 2.4 \mathrm{~W} \approx 1600 \mathrm{~lm} $$The luminous flux of our 100W incandescent lightbulb is a measly 2.4 W or 1600lm.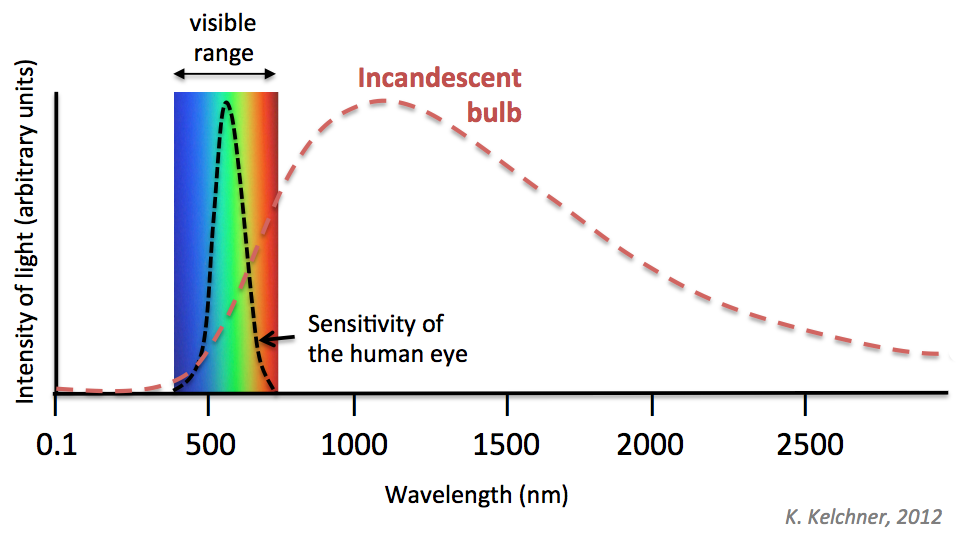 参考资料:Color: From Hexcodes to Eyeballs
参考资料:Color: From Hexcodes to Eyeballs
Plane/(Projected)Solid Angle
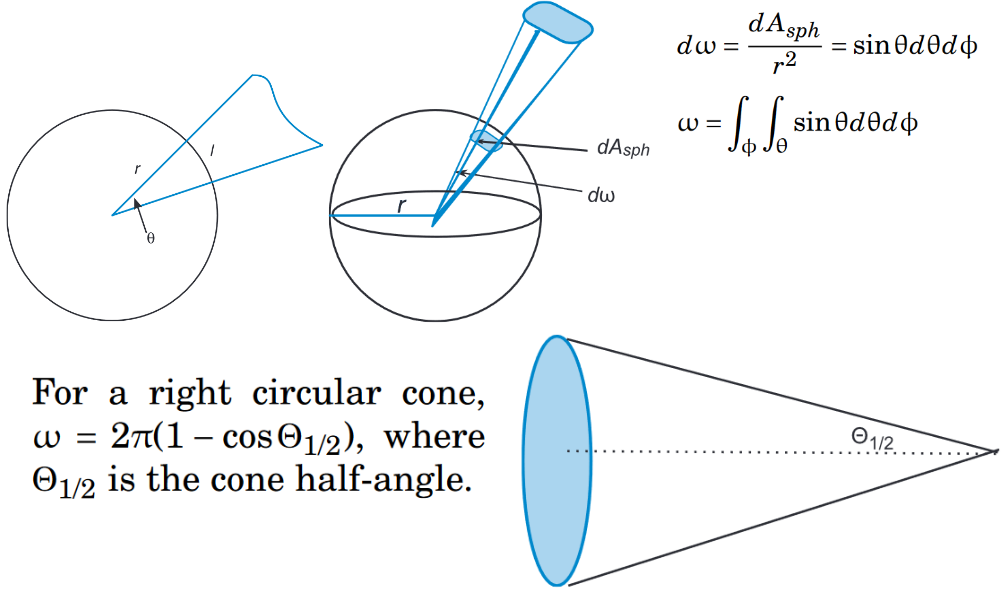
- 平面角\(\theta\) is defined as the ratio of the arc length to the circle's radius \( \theta = l/r\)
- 立体角\(\omega \) is the ratio of a subtended spherical surface area to the square of the sphere radius. Its unit is the steradian (sr), the solid angle with vertex at the center of a sphere, subtending an area on the surface of the sphere whose sides have length equal to the sphere radius. The solid angle of a hemisphere is \(2\pi\) sr, and the solid angle of a sphere is \(4\pi\) sr.
- 投影立体角
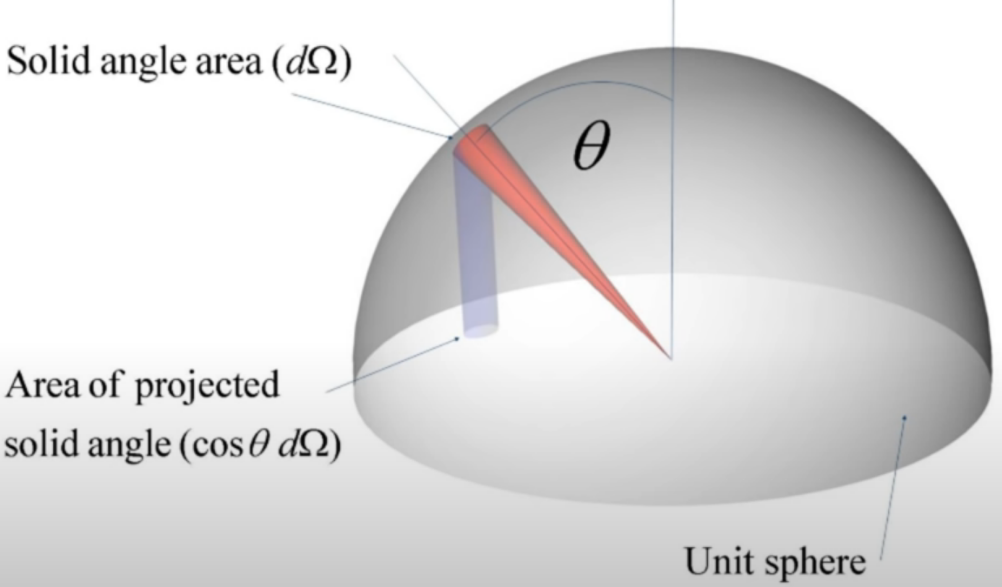
- A hemisphere has \(2\pi\) steradians (solid angle) but \(\pi\) projected steradians (projected solid angle).
- 类似平面角和立体角,单纯的投影立体角对应的面积是没有意义的,有意义的是该面积/\(r^2\),其中\(r\)表示投影面大圆的半径。
- 整个半球面的投影面积就是平面上圆的大小,除以半径的平方,就得到\(\pi\) projected steradians。
- 投影立体角与立体角之间的关系为\(\mathrm{d} \omega^{\perp}=|\cos \theta| \mathrm{d} \omega \)
Photometric Units and Symbols
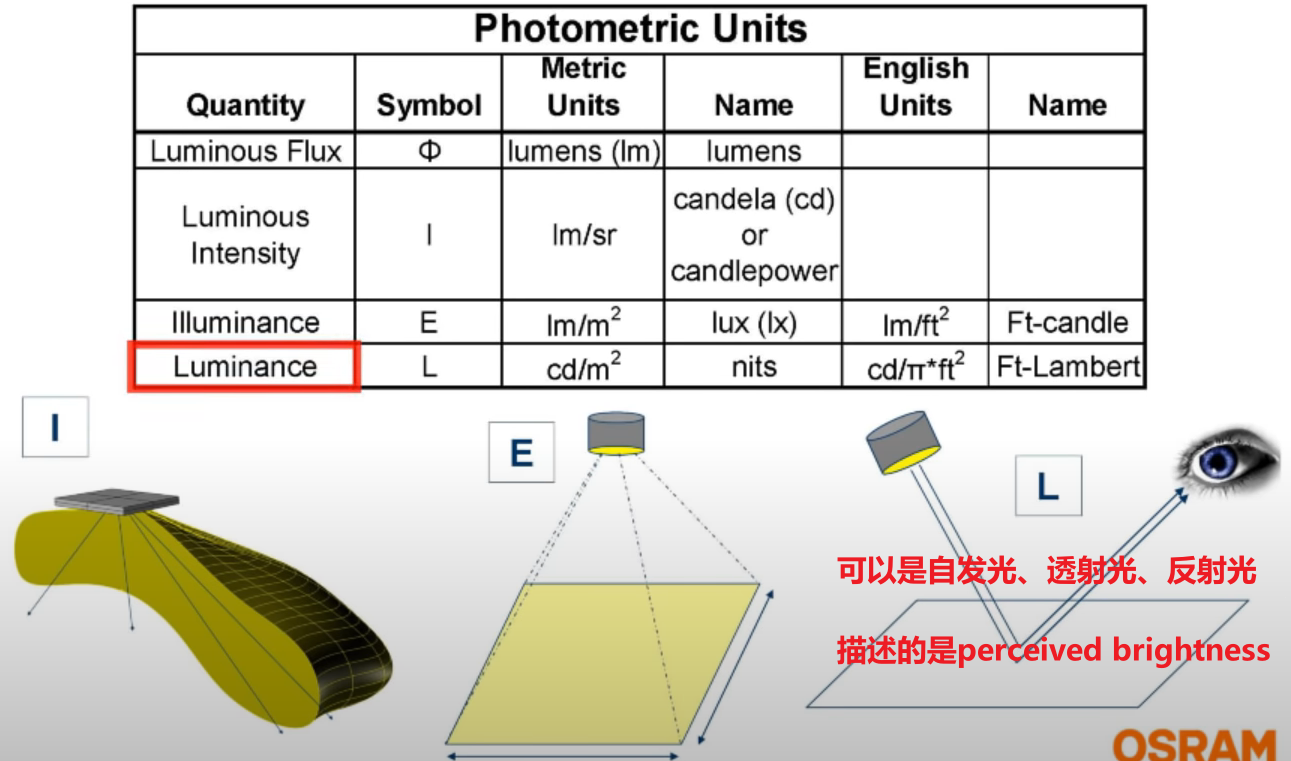
亮度
- Luminance(亮度) is a photometric measure of the luminous intensity per unit area of light travelling in a given direction. It describes the amount of light that passes through, is emitted from, or is reflected from a particular area, and falls within a given solid angle.
- 小米电视6 OLED屏幕峰值亮度为800nit,说的也是亮度;
- 人眼photopic vision下能感知到的最低亮度为0.3 mcd/m2,长余辉材料的有效长余辉发光时间也是据此来计算。
发光强度
- Luminous intensity (发光强度)的单位是坎德拉 (cd),国际单位制七个基本单位之一;
- cd是有方向性的,是指光在一个特定方向的一个单位立体角内的光通量;
- 一只普通蜡烛的发光强度约为1 cd;
- 555.016nm单色光源,在某个方向的辐射强度为1/683 W每球面度,则该辐射源在该方向的辐射强度(Radiation intensity)为1 cd。
- 1cd的点光源,所有立体角的光通量加和为\(4\pi\) lm。
形状的影响
- 点光源,发射各向同性;
- 对于一个平面光源或者平面反射体,它的发光强度完全可以有方向性。因为反射体的反射能力和发射体的发射能力可以有方向性。这种物体从不同方向看有着不同的亮度。但是通常的粉末发光器件,如果是平面型的,则一般不会有方向性。因为粉末包含的是微晶,是杂乱排列的,就和标准的反射体如粉末状硫酸钡一样,它的反射基本上是没有方向性的。对于这种发射体或反射体,则从任何方向看其亮度都是一样的。因此如果一个发光面在垂直方向的发光强度是1cd,按朗伯体处理,其他立体角的发光强度为\(\cos \theta\) cd,所有的发光面积分(对立体角积分)得到的总发光通量为\(\pi\) lm。这里的\(\pi\)其实就是前面谈到的投影立体角(整个半球面立体角的投影)。
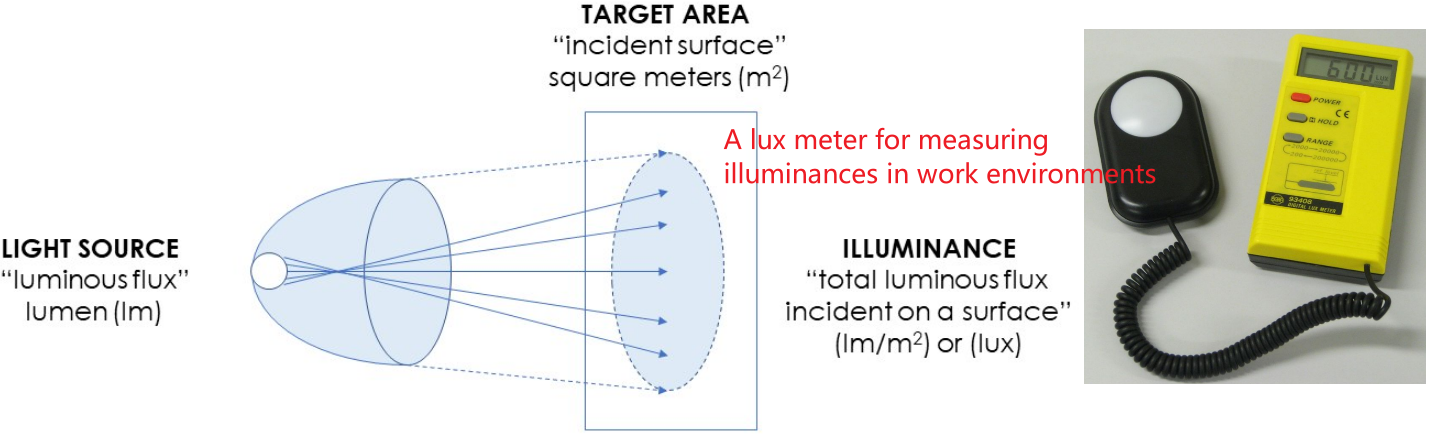
照度(Illuminance)
- 单位面积所接收到的光通量(lm/m2);可理解为:单位面积内获得多少光(不是光子数,因为里面考虑了人眼敏感函数)。
- 居家的一般照度建议在300 ~ 500勒克斯之间 (1 lx = 1 lm/m2 = 1 cd·sr/m2) ;
- 照度是照射在某一单位面积表面上的入射光的总量;而亮度是指从某一单位面积表面上反射到人眼中的反射光总量。照度和亮度,一个是指单位面积内获得的光有多少,一个是指单位面积内看上去有多亮。
- 照度和被照物是无关的,拿我们的手掌举例,无论是手心还是手背,在同等条件下,得到的光是一样多的,即照度是一样的。但是,我们肉眼看上去是不一样的,手心总是会比手背感觉上亮一点,这就是亮度不一样。这是因为手心手背的反射率不一样。
Lambertian Source
 The radiant intensity of a Lambertian emitter, as shown in polar coordinates here, is proportional to \( \cos \theta\)
The radiant intensity of a Lambertian emitter, as shown in polar coordinates here, is proportional to \( \cos \theta\) - Intensity falls off as \(\cos \theta\);
- Brightness (luminance) is independent of angle,发光强度降低的同时,肉眼感知到的发光面积也在等比例地减小,所以最终的效果是亮度不变;
- Many LEDs are very nearly Lambertian sources.
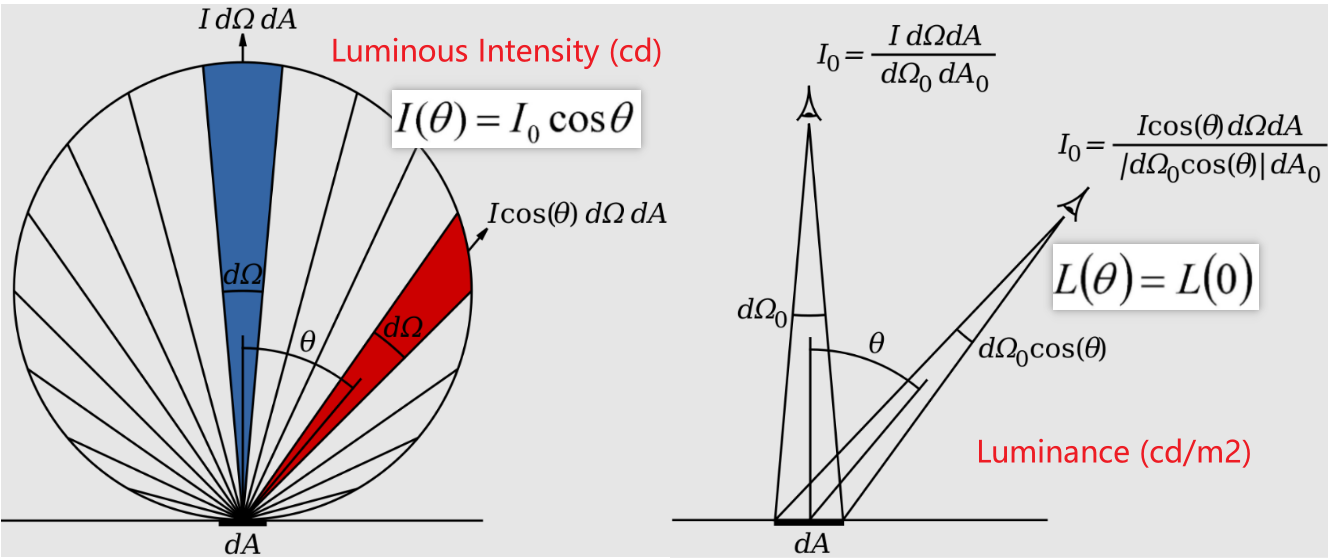
- 注意上面的图为了简化,\(I_0\)的单位是photons/(s·m2·sr). The number of photons/sec directed into any wedge is proportional to the area of the wedge.
-
Peak luminous intensity and luminous flux
In general, the luminous intensity of a point on a surface varies by direction; for a Lambertian surface, that distribution is defined by the cosine law, with peak luminous intensity in the normal direction. Thus when the Lambertian assumption holds, we can calculate the total luminous flux$$\begin{aligned} F_{\text {tot }} &=\int_{0}^{2 \pi} \int_{0}^{\pi / 2} \cos (\theta) I_{\max } \sin (\theta) d \theta d \phi \\ &=2 \pi \cdot I_{\max } \int_{0}^{\pi / 2} \cos (\theta) \sin (\theta) d \theta \\ &=2 \pi \cdot I_{\max } \int_{0}^{\pi / 2} \frac{\sin (2 \theta)}{2} d \theta \\ &=\pi \,\mathrm{sr} \cdot I_{\max } \end{aligned}$$比如一个显示器的亮度为 100 cd/m2 (= 100 nits, typical PC monitor),显示器面积为0.1 m2,那么最大的发光强度为10 cd或者10 lm/sr(垂直方向),根据前面的计算系数\(\pi \,\mathrm{sr}\)可以得到光通量luminous flux为31.4 lm。这里的\(\pi\)其实也是前面讨论的投影立体角。
参考资料:
(1) Lambert's cosine law-Wiki
(2) Lambertian Emitters and Scatterers-RP-photonics
(3) 99.9%的人不知道亮度和照度的区别
(4)
(5) Optics for Energy Radiometry, Photometry Color
(6)
(1)
拓展:
(1) Physically Based Rendering
xx'
视锥细胞(cone cell)
- 人眼有红、绿、蓝三种视锥细胞,正是这些基本的"三原色视觉细胞"赋予人类感知色彩世界的能力,人眼对颜色的感知和叠加是线性的(格拉斯曼定律)。
- 大部分鸟类天生就具有四种视锥细胞。
- 皮皮虾具有十六种视锥细胞。
视杆细胞(rod cell):
格拉斯曼定律
内在光敏视网膜神经节细胞(ipRGC):
薄暮现象(Purkinje effect):
Scotopic vision:
Photopic vision:
色盲:色盲基因仅存在X染色体上,而且是隐形(recessive)基因,Y染色体上没有相关基因片段,所以对于女性来说,必须两条X染色体上同时存在该隐形色盲基因才表现色盲,而男性只要其X染色体上携带该基因那么就表现为色盲。因此色盲在男性中的比例远高于女性。
动物的眼睛和视觉
猫
- 眼睛反光是因为有Retroreflector;
- 视锥细胞只有绿色和蓝色两种;
参考资料:
(1) 为什么会有紫红色这一种矛盾的颜色?—知乎
(2) 色彩空间基础—章佳杰
(3) 色彩空间表示与转换—章佳杰
(4) 光谱渲染的几个例子—章佳杰
(5) 色温、白平衡与色彩恒常性—章佳杰
(6) 饶毅谈“色”
(7) 都世民-科学网