由于单变量微积分的知识以前掌握得还可以，但是想感受一下MIT教学的内容，进一步夯实对于单变量微积分的理解，所以精选出知乎网友的笔记-1 笔记-2，帮助我查漏补缺。对应视频地址。
导数、斜率、速率、变化率、极限和连续
导数的表示法：微积分的发展是很多人同时开展研究并推动的，这也导致了导数有多种记法。若\( y=f(x) \)，则有\( \Delta y=\Delta f=f(x)-f\left(x_{0}\right)=f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)\)。
(1) 牛顿表示法\(f^{\prime} \)；
(2) 莱布尼兹表示法\( \displaystyle\frac{d f}{d x}=\displaystyle\frac{d y}{d x}=\displaystyle\frac{d}{d x} f=\frac{d}{d x} y \)
比较有意思的是，英国人觉得他们在微积分领域进展比欧洲大陆慢的一个重要原因就是采用了牛顿的表达式。我觉得这也有一定道理，微积分比较核心的内容就是函数与函数之间的关系，而莱布尼兹的表达式确实更加有效地体现了这一点。
\( O\left((\Delta x)^{2}\right)\)的含义：\( O\left((\Delta x)^{2}\right) \)包含\( (\Delta x)^{2} \)和\((\Delta x)^{3} \)乃至\((\Delta x)^{n} \)各高阶项的缩写。
导数的“变化率”解释：\( \Delta x \rightarrow 0\)则有\(\displaystyle\frac{\Delta y}{\Delta x} \rightarrow \displaystyle\frac{d y}{d x} \)注意这两个相等的条件。当\( \Delta x \)趋于零，平均速度趋近于瞬时速度，那么差商趋近于导数。
物理学解释实例：
(1) \(q= \)电荷，\(\displaystyle\frac{d q}{d t}= \)电流；
(2) \( s= \)距离，\( \displaystyle\frac{d s}{d t}= \)速度；
(3) \(T= \)温度，\( \displaystyle \frac{d T}{d t}=\)温度梯度；
(4) 测量灵敏度
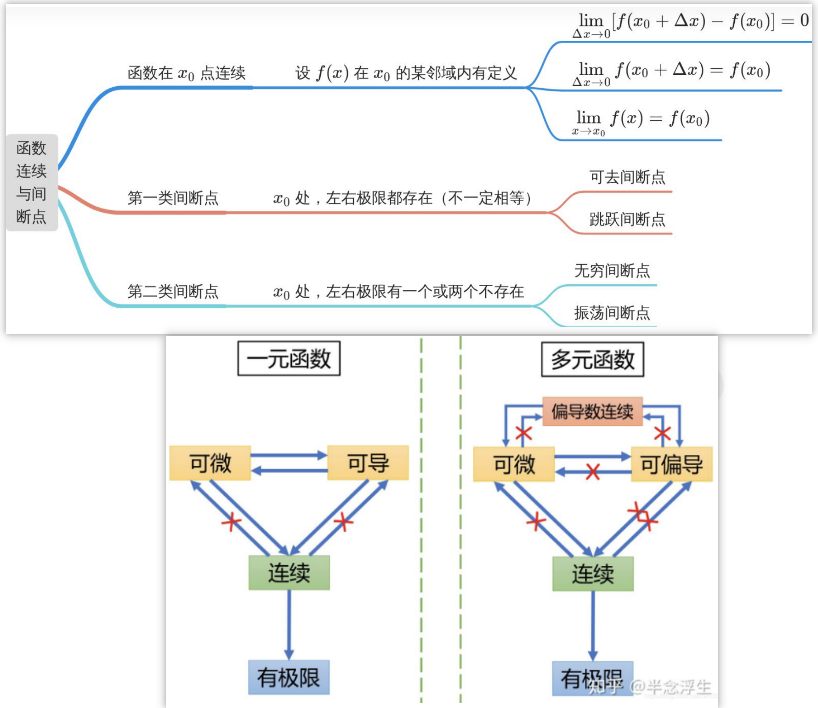
函数的连续性：函数在\( x_{0} \)处连续，那么一定有左极限等于右极限等于函数值。
讨论不连续的情况：
(1) 跳跃间断点，左右极限都存在但是不相等；
(2) 可去间断点，“补上”该点，一切就完美；
(3) 无穷间断点，比如\( y=1 / x \)；
(4) 另类间断点，比如\( y=\sin \displaystyle\frac{1}{x} \)，\( x \)趋近于零的时候，无线震荡，没有左右极限。
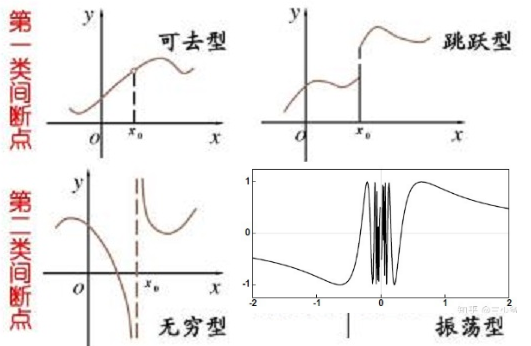
第一类间断点：左极限及右极限都存在。
第二类间断点：指函数的左右极限至少有一个不存在。第二类间断点有非常多种，如：
- 无穷间断点；
- 振荡间断点；
- 单侧间断点；
- 狄利克雷函数间断点；
- 黎曼函数间断点等等。
可导必连续(一元函数)
证明如下：$$\lim _{x \rightarrow x_{0}} f(x)-f\left(x_{0}\right)=\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}\left(x-x_{0}\right)=f^{\prime}\left(x_{0}\right) \cdot 0=0$$极限值等于函数值。
正余弦函数的导函数的推导
以正弦函数为例：\( \displaystyle\frac{d}{d x} \sin x=\cos x\)处理方法是求差商(借助三角函数和差化积)$$\frac{\sin (x+\Delta x)-\sin x}{\Delta x}=\frac{\sin x \cos \Delta x+\cos x \sin \Delta x-\sin x}{\Delta x}\\=\sin x\left(\frac{\cos \Delta x-1}{\Delta x}\right)+\cos x\left(\frac{\sin \Delta x}{\Delta x}\right)$$A: \(\Delta x \rightarrow 0\)时，\((\cos \Delta x-1) / \Delta x \rightarrow 0\)
B: \(\Delta x \rightarrow 0\)时，\(\sin \Delta x / \Delta x \rightarrow 1\)
因此\(\Delta x \rightarrow 0\)时，\(\displaystyle\frac{d}{d x} \sin x=\cos x\)。对于余弦函数也有类似推导。下面论述A，B两个极限值的正确性。
按照定义可知：$$ \begin{aligned} \left.\frac{d}{d x} \cos x\right|_{x=0} &=\lim _{\Delta x \rightarrow 0} \frac{\cos \Delta x-1}{\Delta x}=0 \\ \left.\frac{d}{d x} \sin x\right|_{x=0} &=\lim _{\Delta x \rightarrow 0} \frac{\sin \Delta x}{\Delta x}=1 \end{aligned} $$因此利用正弦和余弦函数在 \(x=0\) 处的导数值可以给出 \(\displaystyle\frac{d}{d x} \sin x\) 和 \(\displaystyle\frac{d}{d x} \cos x\) 在定义域上其它点的数值。
这里用几何法进行讨论A，B两个极限值：连接图中红色弧长的两个端点，可以得到一个很小的三角形，当这里的弧长对应的角度很小的时候，弧长就约等于这个小三角形的斜边，而斜边在角度很小的时候，其实约等于大角度(接近90度)对应的长边。
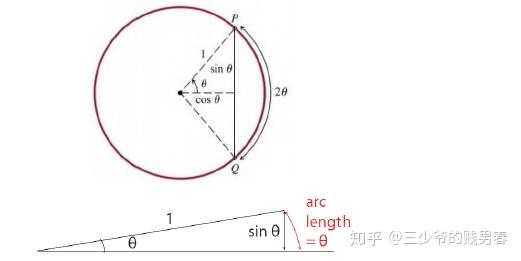
这里可以采用类似的方法，同样连接弧长的两个点，得到小三角形的斜边，那么非常小的角度所对应的直角边除以小三角形的斜边的值必然很小，在小角度逼近零度的时候必然对应于二者的比值逼近零。
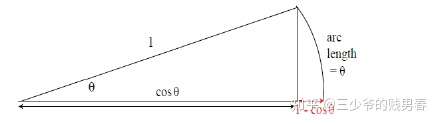
正弦函数导数的几何证明: \(\displaystyle\frac{d}{d x} \sin x=\cos x\)
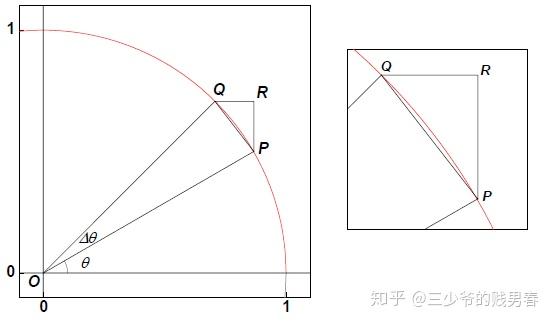
$$\lim _{\Delta \theta \rightarrow 0} \frac{\Delta y}{\Delta \theta}=\lim _{\Delta \theta \rightarrow 0} \frac{\Delta \sin \theta}{\Delta \theta}=\cos \theta$$
求导公式
\(y=\tan ^{-1} x=\arctan x \)的求导公式
首先写成\( \tan (y)=x \)，然后等式两边对\(x \)求导得到$$\begin{aligned} &\Rightarrow\left(\frac{d}{d y} \tan y\right) \frac{d y}{d x}=1\\ &\Rightarrow \frac{1}{\cos ^{2} y} y^{\prime}=1\\ &\Rightarrow y^{\prime}=\cos ^{2} y \end{aligned}$$通过三角函数关系化简
由上图可知\( \cos y=\displaystyle \frac{1}{\sqrt{1+x^{2}}}\)，所以$$\frac{d}{d x} \tan ^{-1} x=\frac{1}{1+x^{2}}$$
任意指数函数\( a^{x}\)的求导公式
方法1：\( a^{x}=\left(e^{\ln a}\right)^{x}=e^{x \ln a}\)
方法2：令\( u(x)= a^{x}\)，利用$$\frac{d}{d x} \ln u=\left(\frac{d}{d u} \ln u\right) \frac{d u}{d x}=\frac{1}{u} \frac{d u}{d x}$$
求导\(\boldsymbol{v}=\boldsymbol{x}^{\boldsymbol{x}} \)$$\begin{aligned} &\Rightarrow \ln v=x \ln x\\ &\Rightarrow(\ln v)^{\prime}=\ln x+x \cdot \frac{1}{x}\\ &\Rightarrow \frac{v^{\prime}}{v}=1+\ln x\\ &\Rightarrow v^{\prime}=x^{x}(1+\ln x) \end{aligned}$$
求\(\displaystyle\lim _ {n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n} \)$$n \ln \left(1+\frac{1}{n}\right)=\frac{1}{\Delta x} \ln (1+\Delta x)=\frac{1}{\Delta x}(\ln (1+\Delta x)-\ln (1))$$其中\(\Delta x=\displaystyle \frac{1}{n} \rightarrow 0 \)，上式即为求\(\ln x \)在\( x=1\)的导数，即$$\left.\frac{d}{d x} \ln x\right|_{x=1}=\left.\frac{1}{x}\right|_{x=1}=1$$
线性近似和二阶近似、相关变率
线性近似(Linear and Quadratic Approximations)：$$f(x) \approx f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)$$描述的“切线近似”
卫星上的时间\( T \)地面时间 \( T^{\prime} \)之间的关系符合狭义相对论，称为时间膨胀：$$T^{\prime}=\frac{T}{\sqrt{1-v^{2} / c^{2}}}$$用\(u\)替换 \( v^{2} / c^{2}, \)则有 \((1-u)^{-1 / 2} \approx 1+u / 2 \quad, \) 因此有 $$T^{\prime}=T\left(1-\frac{v^{2}}{c^{2}}\right)^{-1 / 2} \approx T\left(1+\frac{1}{2} \frac{v^{2}}{c^{2}}\right)$$误差比率与\(v^{2} / c^{2}\)成正比，系数为\(\displaystyle\frac {1}{2} \)。线性近似在工程中应用广泛，人们关心“输入改变量”和“输出改变量”之间的线性关系。用线性代数去替代复杂的方程非常必要，比如此问题中实际上还要考虑卫星的速度变化、观察视角、加速度、广义相对论效应、卫星重力与地表差异等等，叠加形成的公式要复杂得多，但取近似公式就相对简单。
二阶近似(抛物线近似 Quadratic Approximations)：在线性近似精度不够的时候才会使用二阶近似$$f(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2}\left(x-x_{0}\right)^{2}$$几个常见函数的二阶近似公式：$$ \begin{aligned} &\cos x \approx 1-\frac{1}{2} x^{2} \\ &e^{x} \approx 1+x+\frac{1}{2} x^{2} \\ &\ln (1+x) \approx x-\frac{1}{2} x^{2} \\ &(1+x)^{r} \approx 1+r x+\frac{r(r-1)}{2} x^{2} \end{aligned}$$函数的凹凸性：利用二阶导数的正负可以知道函数的凹凸性，Convex function指的是凸函数(二阶导数大于零)，Concave function指的是凹函数(二阶导数小于零)，这里的定义和同济高数不同(不采用这本书的内容)。或者用concave upward 和concave downward分别表示凸函数和凹函数，参考下图
二阶导数的几何定义是函数曲线的弯曲状态，二阶导数大的地方，曲线的峰陡峭尖锐，二阶导数导数小的地方，曲线变化平缓。
相关变率：
例子-1，一条长度为1的绳子，裁成两段，分别围城两个正方形，求面积之和的最大值。
面积之和\(A=(\displaystyle \frac{x}{4})^{2}+(\displaystyle \frac{1-x}{4})^{2}\)，极值点的导数为零，然后将该点对应的面积之和与两个极端(边界)情况的面积之和作比较，即可确认最终结果。
例子-2，一个固定容积的没有顶盖的长方体盒子，求其表面积最小值。简化条件下，底为正方形(简化条件下，底为正方形)。
长方体的体积为\(V=x^{2} y\)，表面积\(A=x^{2}+4 x y\)，有两种方法求解：
(1) 用\( x\)和已知的\(V\)去表示\( y\)，这样表面积就是一个一元函数；
(2) 隐函数求导的方法，\( V=x^{2} y\)左右两边对\(x\)求导，得到\(2 x y+x^{2} y^{\prime}=0\)，于是有\(y^{\prime}=-\displaystyle \frac{2 x y}{x^{2}}=-\displaystyle \frac{2 y}{x}\)，因此面积的极值点$$\frac{d}{d x} A=2 x+4 y+4 x y^{\prime}=2 x+4 y+4 x\left(\frac{2 y}{-x}\right)=2 x-4 y=0$$
牛顿迭代法
牛顿迭代法：求\(x^{2}=5\)的解，这相当于求\(f(x)=x^{2}-5=0\)的解。从一个猜测点\( x_0\)出发，\(x_{0}=2\)离所求方程的解很近。在\((2, \quad f(2))\)点做函数曲线的切线，与\(x\)轴相较于一点\(x_1\)，则\(x_1\)是新的猜测点，它距离方程的解更近了一些，然后重复这个过程。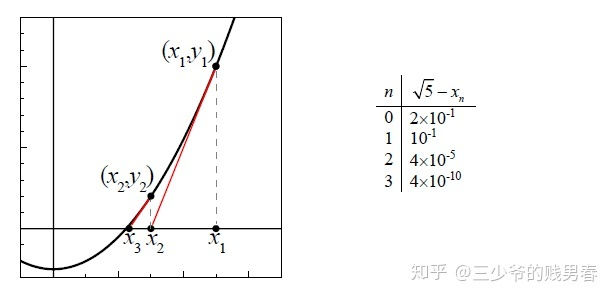
切线的表达式为\(y-y_{0}=m(x-x_{0})\)，与\(x\)轴交点即为\(x_1\)满足\(0-y_{0}=m(x_{1}-x_{0})\)。整理得到\(x_{0}-\displaystyle\frac{y_{0}}{m}=x_{1}\)，即\(x_{1}=x_{0}-\displaystyle\frac{f(x_{0})}{f^{\prime}(x_{0})}\)。牛顿迭代的通项公式为$$x_{n+1}=x_{n}-\frac{f(x_{n})}{f^{\prime}(x_{n})}$$本例中\(x_0\)，\(f(x)=x^{2}-5\)，$$f^{\prime}(x)=2 x, \quad x_{n+1}=x_{n}-\frac{x_{n}{ }^{2}-5}{2 x_{n}}=\frac{x_{n}}{2}+\frac{5}{2 x_{n}}$$带入得到$$\begin{aligned} &x_{1}=\frac{1}{2} \cdot 2+\frac{5}{4}=\frac{9}{4} \\ &x_{2}=\frac{1}{2} \cdot \frac{9}{4}+\frac{5}{2} \cdot \frac{4}{9}=\frac{161}{72} \ldots \ldots . \end{aligned}$$
牛顿迭代法的误差分析：设\(x\)是真正的零点值，\(E_{n}=|x-x_{n}|\)，\(E_{n+1}=|x-x_{n+1}|\)，通常情况下，牛顿法都很有效，能保证误差满足下面关系$$E_{n+1} \approx E_{n}^{2}$$一言以蔽之，牛顿法误差减小的速度非常快，且有广泛的应用，但有两个条件：
(1) \(|f^{\prime}|\)不能太小，\(|f^{\prime \prime}|\)不能太大；
(2) 初值\(x_0\)要在\(x\)附近，不能离太远。
(1) 二阶导数决定了曲线的弯曲程度，也表明切线和函数曲线的差异(二阶近似中的二次项系数)，因此如果二阶导数太大对于通过切线逼近函数值的牛顿迭代法很不利；弯曲的程度影响到准确度，如果弯曲程度为\(0\)，即二阶导为\(0\)时，切线在\(x\)轴上的截距\(x_{n+1}\)是精确的，即为\(x\)，弯曲程度不大，切线能够比较贴近曲线。
(2) 如果一阶导太小，取极限的话，一阶导为\( 0\)，则与\( x\)轴无交点，不能得到截距，总之一阶导太小的话，牛顿法会失效。
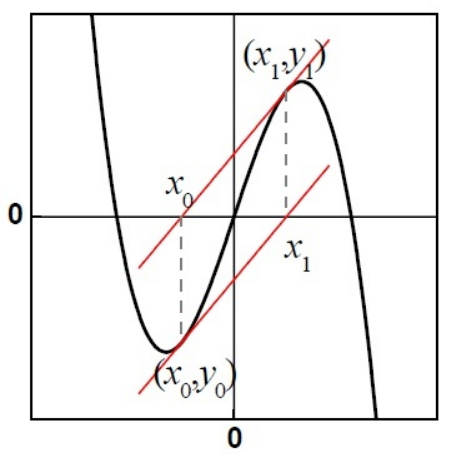牛顿法不适用的情况：
(1) 如果\(x_0\)距离\(x\)太远，可能会得到另一个根，尽量选取你想求解的那个根附近的初始点；
(2) 有一种更棘手的情况，\(x_n\)和\(x_{n+1}\)会彼此循环迭代，再也不能向前迭代。