矢量分析
三重积(混合积)
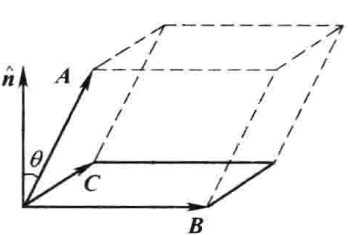平行六面体的体积可以表示为$$A \cdot(B \times C)=B \cdot(C \times A)=C \cdot(A \times B)$$负号的三重积$$A \cdot(C \times B)=B \cdot(A \times C)=C \cdot(B \times A)$$混合积的行列式计算法$$\boldsymbol{A} \cdot(\boldsymbol{B} \times \boldsymbol{C})=\left|\begin{array}{lll} A_{x} & A_{y} & A_{z} \\ B_{x} & B_{y} & B_{z} \\ C_{x} & C_{y} & C_{z} \end{array}\right|$$混合积的可交换性$$A \cdot(B \times C)=(A \times B) \cdot C$$矢量三重积$$A \times(B \times C)=B(A \cdot C)-C(A \cdot B)\\(\boldsymbol{A} \times \boldsymbol{B}) \times \boldsymbol{C}=-\boldsymbol{C} \times(\boldsymbol{A} \times \boldsymbol{B})=-\boldsymbol{A}(\boldsymbol{B} \cdot \boldsymbol{C})+\boldsymbol{B}(\boldsymbol{A} \cdot \boldsymbol{C})$$单位方向矢量$$\hat{r}=\frac{r}{r}=\frac{x \hat{x}+y \hat{y}+z \hat{z}}{\sqrt{x^{2}+y^{2}+z^{2}}}$$三维向量绕着\( x \)轴旋转的线性变换$$\left(\begin{array}{l} \bar{A}_{y} \\ \bar{A}_{z} \end{array}\right)=\left(\begin{array}{cc} \cos \phi & \sin \phi \\ -\sin \phi & \cos \phi \end{array}\right)\left(\begin{array}{l} A_{y} \\ A_{z} \end{array}\right)$$绕任意轴旋转的线性变换$$\left(\begin{array}{l} \bar{A}_{x} \\ \bar{A}_{y} \\ \bar{A}_{z} \end{array}\right)=\left(\begin{array}{lll} R_{x x} & R_{x y} & R_{x z} \\ R_{y x} & R_{y y} & R_{y z} \\ R_{z x} & R_{z y} & R_{x z} \end{array}\right)\left(\begin{array}{c} A_{x} \\ A_{y} \\ A_{z} \end{array}\right)$$
梯度
温度\( T(x, y, z) \)的偏导数为$$\mathrm{d} T=\left(\frac{\partial T}{\partial x}\right) \mathrm{d} x+\left(\frac{\partial T}{\partial y}\right) \mathrm{d} y+\left(\frac{\partial T}{\partial z}\right) \mathrm{d} z$$写成点积的形式$$\begin{aligned} \mathrm{d} T &=\left(\frac{\partial T}{\partial x} \hat{x}+\frac{\partial T}{\partial y} \hat{y}+\frac{\partial T}{\partial z} \hat{z}\right) \cdot(\mathrm{d} x \hat{x}+\mathrm{d} y \hat{y}+\mathrm{d} z \hat{z}) \\ &=(\nabla T) \cdot(\mathrm{d} l) \end{aligned}$$梯度具有大小和方向，为了进行几何解释，可以写成$$\mathrm{d} T=\nabla T \cdot \mathrm{d} \boldsymbol{l}=|\nabla T||\mathrm{d}\boldsymbol{l}| \cos \theta$$当\( |\mathrm{d} l| \)固定时，只有当\( \nabla T\)和\( \mathrm{d} \boldsymbol{l}\)方向相同时，\( \mathrm{d} T\)的变化才最大。
(1) 梯度\(\nabla T \)所指方向是函数\( T \) 有最大增加的方向
(2) \( |\nabla T| \)给出沿这个最大增加方向的增率(增加速率)
(3) 一个点梯度为零的意义：移动一点点，\( dT=0 \)，一阶近似的系数为零。
\(\nabla \)算子$$\nabla T=\left(\hat{\boldsymbol{x}} \frac{\partial}{\partial x}+\hat{\boldsymbol{y}} \frac{\partial}{\partial y}+\hat{z} \frac{\partial}{\partial z}\right) T$$
$$\begin{aligned} \nabla \cdot \boldsymbol{v} &=\left(\hat{x} \frac{\partial}{\partial x}+\hat{y} \frac{\partial}{\partial y}+\hat{z} \frac{\partial}{\partial z}\right) \cdot\left(v_{x} \hat{x}+v_{y} \hat{y}+v_{z} \hat{z}\right) \\ &=\frac{\partial v_{x}}{\partial x}+\frac{\partial v_{y}}{\partial y}+\frac{\partial v_{z}}{\partial z} \end{aligned}$$
散度
$$\begin{aligned} \nabla \cdot \boldsymbol{v} &=\left(\hat{x} \frac{\partial}{\partial x}+\hat{y} \frac{\partial}{\partial y}+\hat{z} \frac{\partial}{\partial z}\right) \cdot\left(v_{x} \hat{x}+v_{y} \hat{y}+v_{z} \hat{z}\right) \\ &=\frac{\partial v_{x}}{\partial x}+\frac{\partial v_{y}}{\partial y}+\frac{\partial v_{z}}{\partial z} \end{aligned}$$
旋度
$$\begin{aligned} \nabla \times \boldsymbol{v} &=\left|\begin{array}{ccc} \hat{\boldsymbol{x}} & \hat{\boldsymbol{y}} & \hat{\boldsymbol{z}} \\ \partial / \partial x & \partial / \partial y & \partial / \partial z \\ v_{x} & v_{y} & v_{z} \end{array}\right| \\ &=\hat{\boldsymbol{x}}\left(\frac{\partial v_{z}}{\partial y}-\frac{\partial v_{y}}{\partial z}\right)+\hat{\boldsymbol{y}}\left(\frac{\partial v_{x}}{\partial z}-\frac{\partial v_{z}}{\partial x}\right)+\hat{\boldsymbol{z}}\left(\frac{\partial v_{y}}{\partial x}-\frac{\partial v_{x}}{\partial y}\right) \end{aligned}$$
梯度/散度/旋度的积规则
二阶微分
(1) 梯度的散度：\(\nabla \cdot(\nabla T) \)
(2) 梯度的旋度：\( \nabla \times(\nabla T) \)
(3) 散度的梯度：\( \nabla(\nabla \cdot \boldsymbol{v})\)
(4) 旋度的散度：\( \nabla \cdot(\nabla \times \boldsymbol{v})\)
(5) 旋度的旋度：\(\nabla \times(\nabla \times \boldsymbol{v}) \)
讨论：
(1) \(\nabla \cdot(\nabla T) \)简写为\(\nabla^{2} T \)，称为\(T \)的拉普拉斯；矢量的拉普拉斯\( \nabla^{2} \boldsymbol{v} \)，$$\nabla^{2} \boldsymbol{v} \equiv\left(\nabla^{2} v_{x}\right) \hat{\boldsymbol{x}}+\left(\nabla^{2} v_{y}\right) \hat{\boldsymbol{y}}+\left(\nabla^{2} v_{z}\right) \hat{\boldsymbol{z}}$$(2) 梯度的旋度总是零$$\nabla \times(\nabla T)=0$$对势函数求梯度，然后再求旋度，可以理解为既要沿着一个方向走，又要沿着这个方向的垂直方向走，结果就是动不了了。
(3) \( \nabla(\nabla \cdot \boldsymbol{v})\)物理上用得很少，注意它不是矢量的拉普拉斯。
(4) \( \nabla \cdot(\nabla \times \boldsymbol{v})=0\)，证明见视频
形象上理解，想想一下磁偶极子，一圈电流环路上套着很多磁场的小环，因为电流产生的磁场是有旋场，而磁场的旋度正好对应电流。如果我们先对磁场作一个旋度，那么得到的就是电流，而这个电流和这里的磁场环一样，都是没有源的，找不到“头”和“尾”，因此再对电流做散度，结果为零。
(5) \( \nabla \times(\nabla \times \boldsymbol{v})=\nabla(\nabla \cdot \boldsymbol{v})-\nabla^{2} \boldsymbol{v} \)
注：这一条结合我们先前\( A \times(B \times C)=B(A \cdot C)-C(A \cdot B) \)这个公式很容易推导出来，注意这个公式是老师要求记住的。
(6) 思考：我们上面提到了不仅可以将拉普拉斯算子作用在标量上，也可以将这个算子作用在矢量上。拉普拉斯算子作用在标量上，最终得到的是一个标量；我们可以将原始的标量看作是零阶张量，然后求梯度，相当于升阶到一阶张量(向量)，然后求散度，相当于降阶到零阶张量，即最终结果同样是标量。拉普拉斯算子作用在矢量上，同样地，先是对矢量求梯度，那么升阶到二阶张量，然后求散度，降阶到一阶张量。其实拉普拉斯算子无论是作用在标量还是矢量上，作用过程都是先升阶再降阶，于是最终结果的阶数和原始数据的阶数是一致的。
综上：真正有用的是拉普拉斯(梯度的散度)和散度的梯度(很少用)。
\( \nabla\)算符同时具有矢量性和微分性
\( \nabla\)算符同时具有微分性和矢量性。
微分性：不可以随便移动位置，并且它如果作用在两个量的组合上，那么它就要分别作用到两个量上(类似求导)。
矢量性：它是一个矢量，不能像常数那样随意提前提后，要有一定的规律，这个规律包括：
(1) 点乘叉乘是矢量与矢量之间的运算，而微分算符只能作用到标量上
(2) 混合积的轮转公式和三重积公式
梯度的基本定理$$\int_{a }^{b}(\nabla T) \cdot \mathrm{d} \boldsymbol{l}=T(b)-T(a)$$势函数的梯度的路径积分，和路径无关。
几何解释：假设你想测量埃菲尔铁塔的高度。你可以攀限塔梯，用一把尺子测量每一阶梯的高度，然 后把它们加在一起，或者你可以用一个测高仪测量塔顶和塔底的读数，然后把 两个读数相减 ;两种方法的结果应该一样(这就是基本定理)。
散度的基本定理$$\int_{V}(\nabla \cdot \boldsymbol{v}) \mathrm{d} \tau=\oint_{S} \boldsymbol{v} \cdot \mathrm{d} a$$几何解释：如果\( \boldsymbol{v} \)代表一个不可压缩流体的流，那么它的通量就是单位时间内流出表面的总的流量。现在散度是矢量从某点“散出”的量度，即一个具有高散度的地方像一个“水龙头”，向外流出液体。如果在一个体积内存在大量的水龙头，那么这个体积边界流出的总通量就等于这些水龙头流出量的和。实际上，我们有两种方法计算总的流出量：(1) 把所有龙头的流出量加在一起；(2) 在边界的每一点测流量，然后相加。
旋度的基本定理
传统分部积分延伸到矢量微积分
传统的分部积分\( \int_{a}^{b} f\left(\frac{\mathrm{d} g}{\mathrm{d} x}\right) \mathrm{d} x=-\int_{a}^{b} g\left(\frac{\mathrm{d} f}{\mathrm{d} x}\right) \mathrm{d} x+\left.f g\right|_{a} ^{b} \)借助散度定理，对一个体积有$$\nabla \cdot(f \boldsymbol{A})=f(\nabla \cdot \boldsymbol{A})+\boldsymbol{A} \cdot(\nabla f)$$进行积分$$\int \nabla \cdot(f \boldsymbol{A}) \mathrm{d} \boldsymbol{\tau}=\int f(\nabla \cdot \boldsymbol{A}) \mathrm{d} \tau+\int \boldsymbol{A} \cdot(\nabla f) \mathrm{d} \tau=\oint f \boldsymbol{A} \cdot \mathrm{d} \boldsymbol{a}$$即$$\int_{V} f(\nabla \cdot \boldsymbol{A}) \mathrm{d} \tau=-\int_{V} \boldsymbol{A} \cdot(\nabla f) \mathrm{d} \tau+\oint_{S} f \boldsymbol{A} \cdot \mathrm{d} \boldsymbol{a}$$
极坐标系
\( \left\{\begin{array}{l} x=r \cos \theta \\ y=r \sin \theta \end{array}\right.\)，坐标为\( (r, \theta) \)的任意点的位置矢量为$$\vec{R}=r \cos \theta \hat{x}+r \sin \theta \hat{y}$$新坐标系的基矢$$\begin{aligned} \hat{r} &=\frac{\partial \vec{R}}{\partial r}=\cos \theta \hat{x}+\sin \theta \hat{y} \\ \hat{\theta}=& \frac{\partial \vec{R}}{\partial \theta} \frac{1}{r}=-\sin \theta \hat{x}+\cos \theta \hat{y} \end{aligned}$$于是$$\Rightarrow\left\{\begin{array}{l} \hat{r}=\cos \theta \hat{x}+\sin \theta \hat{y} \\ \hat{\theta}=-\sin \theta \hat{x}+\cos \theta \hat{y} \end{array}\right.$$用矩阵的形式表示为\( \left[\begin{array}{l} \hat{r} \\ \hat{\theta} \end{array}\right]=\left[\begin{array}{rr} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{l} \hat{x} \\ \hat{y} \end{array}\right] \)也就是通过矩阵\( A\)作用，将原来的直角坐标的基矢量转变成极坐标系下的基矢量。那么通过矩阵\( A \)的逆矩阵，也可以将极坐标系下的基矢量转换回去，由于\( A \)本身是正交矩阵，所以它的逆矩阵就是它的转置。于是有$$\left[\begin{array}{l} \hat{x} \\ \hat{y} \end{array}\right]=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c} \hat{r} \\ \hat{\theta} \end{array}\right]$$注意，变换前后都是模长为一的基矢量，这种变换矩阵并不反映变换前后实际矢量的大小变化。如果我们将\(\left\{\begin{array}{l} x=r \cos \theta \\ y=r \sin \theta \end{array}\right. \)都写成全微分的形式，那么\( \begin{array}{l} d x=d(r \cos \theta)=\cos \theta d r+(-r \sin \theta) d \theta \\ d y=d(r \sin \theta)=\sin \theta d r+r \cos \theta d \theta \end{array}\)，写成矩阵的形式就是$$\left[\begin{array}{l} dx \\ dy \end{array}\right]=\left[\begin{array}{cc} \cos \theta & -r\sin \theta \\ \sin \theta & r\cos \theta \end{array}\right]\left[\begin{array}{c} dr \\ d{\theta} \end{array}\right]$$
球坐标系(参考知乎)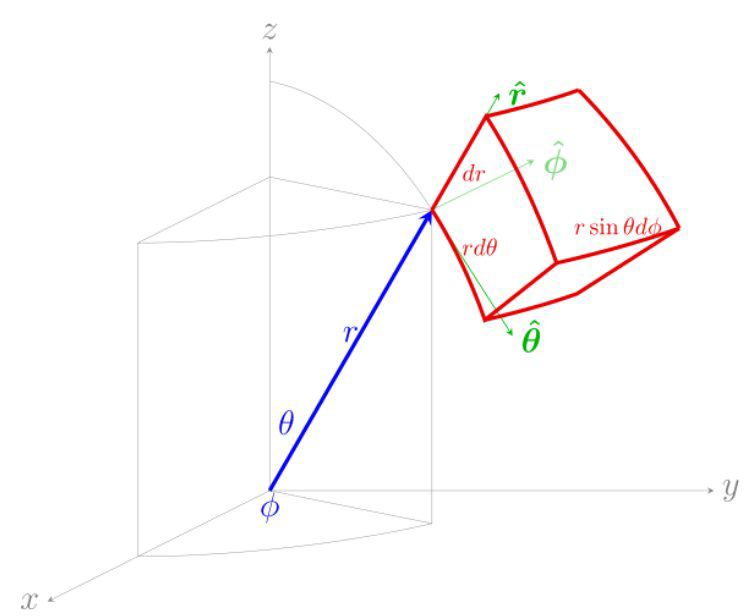
也可以通过类似极坐标的处理方法，我们有\( \left\{\begin{array}{l} x=r \sin \theta \cos \phi \\ y=r \sin \theta \sin \phi \\ z=r \cos \theta \end{array}\right. \)那么坐标为\( (r, \theta, \phi) \)的任意点的位置矢量为\( \vec{R}=r \sin \theta \cos \phi \hat{x}+r \sin \theta \sin \phi \hat{y}+r \cos \theta \hat{z} \)$$\begin{array}{lll} \hat{r}=\frac{\partial \vec{R}}{\partial r}=\sin \theta \cos \phi \hat{x}+\sin \theta \sin \phi \hat{y}+\cos \theta \hat{z} \\ \hat{\theta}=\frac{\partial \vec{R}}{\partial \theta} \frac{1}{r}=\cos \theta \cos \phi \hat{x}+\cos \theta \sin \phi \hat{y}-\sin \theta \hat{z} \\ \hat{\phi}=\frac{\partial \vec{R}}{\partial \phi} \frac{1}{r \sin \theta}=-\sin \phi \hat{x}+\cos \phi \hat{y} \end{array}$$注：上式我们根据图，然后投影，再归一化也能得到一样的结果。
用矩阵表示为$$\left[\begin{array}{c} \hat{r} \\ \hat{\theta} \\ \hat{\phi} \end{array}\right]=\left[\begin{array}{ccc} \sin \theta \cos \phi & \sin \theta \sin \phi & \cos \theta \\ \cos \theta \cos \phi & \cos \theta \sin \phi & -\sin \theta \\ -\sin \phi & \cos \phi & 0 \end{array}\right]\left[\begin{array}{c} \hat{x} \\ \hat{y} \\ \hat{z} \end{array}\right]$$对线性变换矩阵取逆，那么逆变换为$$\left[\begin{array}{l} \hat{x} \\ \hat{y} \\ \hat{z} \end{array}\right]=\left[\begin{array}{ccc} \sin \theta \cos \phi & \cos \theta \cos \phi & -\sin \phi \\ \sin \theta \sin \phi & \cos \theta \sin \phi & \cos \phi \\ \cos \theta & -\sin \theta & 0 \end{array}\right]\left[\begin{array}{c} \hat{r} \\ \hat{\theta} \\ \hat{\phi} \end{array}\right]$$即\( \Rightarrow\left\{\begin{array}{l} \hat{x}=\sin \theta \cos \phi \hat{r}+\cos \theta \cos \phi \hat{\theta}-\sin \phi \hat{\phi} \\ \hat{y}=\sin \theta \sin \phi \hat{r}+\cos \theta \sin \phi \hat{\theta}+\cos \phi \hat{\phi} \\ \hat{z}=\cos \theta \hat{r}-\sin \theta \hat{\theta} \end{array}\right.\)
直角坐标的全微分\(\mathrm{d} \boldsymbol{l}=\mathrm{d} x \hat{\boldsymbol{x}}+\mathrm{d} y \hat{\boldsymbol{y}}+\mathrm{d} z \hat{\boldsymbol{z}} \)换成球坐标，写成$$\mathrm{d} \boldsymbol{l}=\mathrm{d} r \hat{ \boldsymbol{r}}+r \mathrm{d} \theta \hat{\boldsymbol{\theta}}+r \sin \theta \mathrm{d} \phi \hat{\boldsymbol{ \boldsymbol{\phi}}}$$所以微小体积元$$\mathrm{d} \tau=\mathrm{d} l_{r} \mathrm{d} l_{\theta} \mathrm{d} l_{\phi}=r^{2} \sin \theta \mathrm{d} r \mathrm{d} \theta \mathrm{d} \phi$$注：这里表示空间中任意一点，移动\( \mathrm{d} \boldsymbol{l} \)对应的直角坐标系和求坐标系中的体积变化的比例关系。
柱坐标系
狄拉克函数
具体描述：一个物体，除了某个质点外，密度处处为零，这个质点的密度是无限大，但是对这个物体的进行密度积分则是有限的，为这个物体的质量。
例子：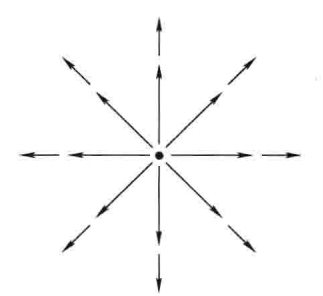
矢量函数\( \boldsymbol{v}=\frac{1}{r^{2}} \hat{r} \)，散度为零(这里用到了前面提到的球坐标系中的散度公式)$$\nabla \cdot \boldsymbol{v}=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{1}{r^{2}}\right)=\frac{1}{r^{2}} \frac{\partial}{\partial r}(1)=0$$选定半径\( R \)，利用高斯定理，积分结果不为零$$\begin{array}{l} \oint \boldsymbol{v} \cdot \mathrm{d} \boldsymbol{a}=\int\left(\frac{1}{R^{2}} \hat{\boldsymbol{r}}\right) \cdot\left(R^{2} \sin \theta \mathrm{d} \theta \mathrm{d} \boldsymbol{\phi} \hat{\boldsymbol{r}}\right) \\ =\left(\int_{0}^{\pi} \sin \theta \mathrm{d} \theta\right)\left(\int_{0}^{2 \pi} \mathrm{d} \boldsymbol{\phi}\right)=4 \pi \end{array}$$注：实际上所有的贡献都来自\(r=0 \)的点，该点的散度无穷大，后面会有讨论。
两种图形化理解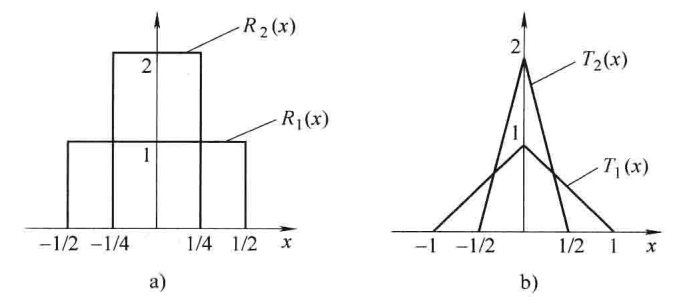
摘出特定函数值的性质：$$\int_{-\infty}^{\infty} f(x) \delta(x-a) \mathrm{d} x=f(a)$$总把\( \delta\)想象成跟在积分符号后面比较容易理解其含义。
三维\( \delta \)函数$$\delta^{3}(\boldsymbol{r})=\delta(x) \delta(y) \delta(z)$$其中\(\boldsymbol{r}\equiv x \hat{x}+y \hat{y}+z \hat{z} \)$$\int_{\text {整个空间}} \delta^{3}(\boldsymbol{r}) \mathrm{d} \tau=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \delta(x) \delta(y) \delta(z) \mathrm{d} x \mathrm{d} y \mathrm{d} z=1$$推广$$\int_{\text {整个空间 }} f(\boldsymbol{r}) \delta^{3}(\boldsymbol{r}-\boldsymbol{a}) \mathrm{d} \tau=f(\boldsymbol{a})$$于是我们再思考前面例子的矛盾之处，散度的正确结果为$$\nabla \cdot\left(\frac{\hat{\boldsymbol{r}}}{r^{2}}\right)=4 \pi \delta^{3}(\boldsymbol{r})$$
矢量场理论
亥姆霍兹定理
讨论的问题是，如果一个向量场的散度和旋度都确定了，那么这个向量场是否是唯一的。参考这里
势函数
