课程网站-Chris Mack-The University of Texas at Austin
Youtube-视频合集
NIST/SEMATECH e-Handbook of Statistical Methods
Six Sigma-Response Surface Modeling
Response Surface Methodology-荧光粉
Data and Measurement
What is Data? (Data = the results of a measurement)
- Definition of the thing being measured
- Measurement value (number plus units)
- Estimate of the uncertainty of each measurement
- Experimental context (measurement method + environment)
- Context uncertainty (uncertainty of controlled and uncontrolled input parameters)
- Measurement model (theory, assumptions and definitions used in making the measurement)
几乎所有的测量都是indirect,我们实际是不是测量我们真正想要的东西,而是测量something else and then we're relating the thing we measure to the thing we want.
The Measurement Model
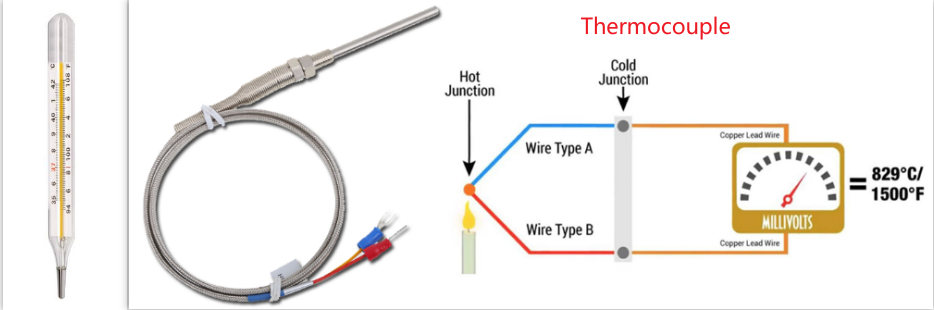
- Virtually all measurements are indirect
— We have a set of theories that relate what is actually being measured to what we want to measure (measurement model) - Ex: Measuring temperature with a thermometer
-
- Thermal expansion of mercury (or spirits) turns length measurement into temperature measurement
- Theory: linear model of liquid thermal expansion
-
- Ex: Measuring temperature with a thermocouple
-
- Junction of dissimilar metals turns temperature change into voltage change (Seebeck effect)
- Theory: polynomial model of voltage versus temperature, coupled with digital (or analog) voltage measurement.
-
Measurement is not a Passive Act
- Measurement can change the thing you are measuring
— Measurement is often not observation without disturbance - Example: SEM measurement
-
- Sample charging
- Physical and chemical changes of sample due to electron bombardment 电子轰击 (carbon deposition, etc.)
- Effects can be current and voltage dependent
-
All Measurements are Uncertain
- Measurement error exists, but we do not know what it is
-
- If we knew the measurement error, we would subtract it out!
- Unknown errors are called uncertainties
-
- Our goal is to estimate the uncertainty in our measurements
-
- Random errors can be estimated using repeated measurements
- Systematic errors require a sophisticated understanding of the measurement process (and the measurement model)
-
Measurement Stability
- We often make assumptions of spatial and/or temporal stability of measurements.
-
- Repeated measurements are taken at different times, locations, conditions, etc.
- How constant is the sample?
- How constant is the measurement process?
- How constant is the measurement context?
-
Measurement Terms
- 【Metrology】(计量学/ 量测学/ 量衡学): the science of measurement.
- 【Measurand】(被测物): the thing being measured.
- 【True Value】: the unknown (and unknowable) thing we wish to estimate.
- 【Error】: true value – measured value.
- 【Measurement Uncertainty】: an estimate of the dispersion of measurement values around the true value.
Uncertainty Components
- 【Systematic errors】
-
- Produce a bias in the measurement result.
- We look for and try to correct for all systematic errors, but we are never totally successful.
- We try to put an upper limit on how big we expect systematic errors could be.
-
- 【Random errors】
— Can be evaluated statistically, through repeated measurements.
Other Measurement Terms

- 【Accuracy】(准确度): the same as error, it can never be known, but is estimated as the maximum systematic error that might reasonably exist
- 【Precision】(精密度): the standard deviation of repeated measurements (random error component). 精密仪器Precision Instrument
-
- 【Repeatability】: standard deviation of repeated measurements under conditions as nearly identical as possible. 侧重于自己在原来的仪器(样品)上重复试验。
- 【Reproducibility】: standard deviation of repeated measurements under conditions that vary in a typical way (different operators, instruments, days). 侧重比如自己观察到的实验现象,别人是否能在他自己的仪器上观察到。
-
- 对于上面右侧的图,Wiki给的说明是Accuracy is the proximity of measurement results to the accepted value; precision is the degree to which repeated (or reproducible) measurements under unchanged conditions show the same results.
Measurement Model Example
- How wide is this feature?

- Most critical dimension measurement tools use a trapezoidal (梯形的) feature model
-
- What criterion should be used to best fit a trapezoid to this complicated shape?
- Accuracy of the width measurement is a strong function of the appropriateness of the feature model (not a good fit means not a good measurement)
-
- The measurement model of an SEM = the feature model + a model for how electrons interact with the sample
Data Example
Chemical vapor deposition (CVD) is used to deposit a tungsten film on a silicon wafer
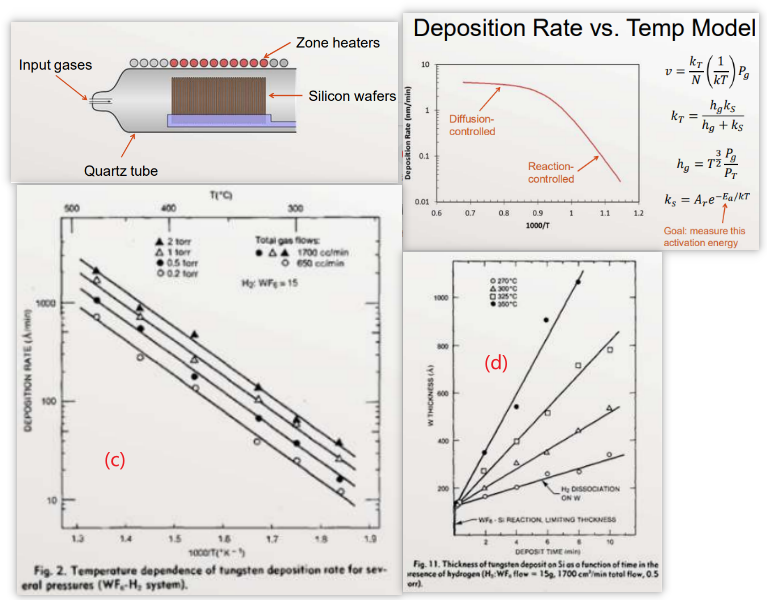
图(c)
- There is no mention of deposition rate measurement error
- "The temperature was controlled to within ± 2ºC of the desired value within the deposition zone."
- The context of the experiment is well described
- There was no mention of context uncertainty (ex: pressure, flow rates)
- "From the Arrhenius plots an activation energy, Ea, of 0.71 eV/atom (69,000 J/mol) was calculated."实际上不同的线拟合的结果应该有差异。
图(d)
- Deposition rate is the slope of these lines (presumably determined by ordinary least squares regression)
- What is the uncertainty (standard error) in the slopes?
- What assumptions are being made here? Can the assumptions be tested? (指的是沉积厚度和沉积时间的线性关系)
Process Modeling
Introduction
- Introduction to Process Modeling-NIST
- Process modeling is the concise description of the total variation in one quantity \(y\) (called the response variable) by partitioning (分割,分开) it into
-
-
- A deterministic component (确定性的成分) given by a mathematical function of one or more other quantities, \(x_{1}, x_{2}, \ldots\) and possibly unknown coefficients \(\beta_{0}, \beta_{1}, \ldots\)
- A random component \(\varepsilon\) that follows a particular probability distribution $$ y=f(\boldsymbol{x}, \boldsymbol{\beta})+\varepsilon \quad \boldsymbol{x}=\left(x_{1}, x_{2}, \ldots\right) ; \boldsymbol{\beta}=\left(\beta_{0}, \beta_{1}, \ldots\right) $$
-
-
- Generally, we require \(\mathrm{E}[\varepsilon]=0\).
— Thus \(f(\boldsymbol{x}, \boldsymbol{\beta})\) describes the average response, \(\mathrm{E}[y]\), if the experiment is repeated many times, not the actual response for a given trial - Our three tasks in modeling:
-
- Find the equation from \(f(\boldsymbol{x}, \boldsymbol{\beta})\) that meets our goals
- Find the values of the coefficients \(\beta\) that are "best" in some sense
- Characterize the nature of \(\varepsilon\) (distribution of errors)
-
- The 【perfect model】 has
-
- The correct set of input variables \(x_{1}, x_{2}, \ldots\)
- The correct model form \(f(\boldsymbol{x}, \boldsymbol{\beta})\)
- The correct values for the coefficients \(\beta_{0}, \beta_{1}, \ldots\)
- The correct probability distribution for \(\varepsilon\), including parameters such as its standard deviation \(\sigma\)
-
- Picking the right model (form and predictor variables) is called 【modeling building】
- Finding the best estimate of the parameter values and the properties of the random variable \(\varepsilon\) is called 【regression】
Model Generalizability
\(y=f(\boldsymbol{x}, \boldsymbol{\beta})+\varepsilon\)
- The three aspects of our model (equation, coefficients, and errors) can have different levels of generalizability
— We often want to know the levels of generalizability - Example: model of thermal stress on polymer
-
- The equation form applies to all materials (under certain conditions)
- The parameters change for different materials
- The errors are a function of measurement and experimental methods, independent of materials
-
Some Terminology
- \(y=\) response variable, response, dependent variable
- \(x=\) predictor variable, explanatory variable, independent variable, predictor, regressor
- Our "model" is both the function \(f(\boldsymbol{x}, \boldsymbol{\beta})\) and the assumed distribution of \(\varepsilon\)
Regression
- Regression involves three things:
-
- Data (a response variable as a function of one or more predictor variables)
- Model (fixed form and predictor variables, but with unknown parameters)
- Method (a statistical regression technique appropriate for the model and the data to find the “best” values of the model parameters)
-
- High quality regression requires high quality in all three items
The Model
- Statistical Relationship: \(y_{i}=f\left(x_{i}, \beta\right)+\varepsilon_{i}=\hat{y}_{i}+\varepsilon_{i}\)
- Functional Relationship: \(\hat{y}=f(x, \beta)\) or \(E[Y \mid X]=f(X, \beta)\)
\(X, Y=\) random variables (probability terminology)
\(\hat{y}=\) predicted (mean) response
\(y_{i}=\) measured response for \(\mathrm{i}^{\text {th }}\) data point
\(x_{i}=\) value of explanatory variable for \(\mathrm{ith}^{\text {th }}\) data point
\(X, Y=\) random variables (probability terminology)
\(\hat{y}=\) predicted (mean) response
\(Y_{i}=\) measured response for \(\mathrm{i}^{\text {th }}\) data point
\(X_{i}=\) value of 【explanatory variable】 (解释变量,其实就是自变量) for \(\mathrm{i}^{\text {th }}\) data point
\(\beta_{k}=\) true model parameters (can never be known)
\(b_{k}=\) best fit model parameters for this data set (sample); our estimate for \(\beta_{k}\).
\(\varepsilon_{i}=\) true value of \(\mathrm{i}^{\text {th }}\) residual (from true model, not known)
\(e_{i}=\) actual ith residual for the current model
Example Model
- Straight line model:$$ \begin{aligned} &f(x, \beta)=\beta_{0}+\beta_{1} x \\ &\hat{y}_{i}=\beta_{0}+\beta_{1} x_{i} \\ &y_{i}=\beta_{0}+\beta_{1} x_{i}+\varepsilon_{i} \end{aligned} $$
- Regression produces the "best" estimate of the model given the data \(\left(x_{i}, y_{i}\right)\) :$$ y_{i}=b_{0}+b_{1} x_{i}+e_{i} $$
Models for Linear Regression
- We use linear regression for 【linear parameter models】: \(\hat{y}\) is directly proportional to each unknown model coefficient
-
- \(\hat{y}=\sum_{k} \beta_{k} f_{k}(x)\) for bivariate data (双变量数据)
- Example: \(\hat{y}=\beta_{0}+\beta_{1} x+\beta_{2} x^{2}+\beta_{3} \ln (x)\)
-
- Multivariate data: two or more explanatory variables (we'll call them \(x_{1}, x_{2}\), etc.)
Nonlinear Regression
- We call our regression nonlinear if it is nonlinear in the coefficients
-
- Linear regression: \(\hat{y}=\beta_{0}+\beta_{1} \ln (x)+\beta_{2} x^{3}\)
- Nonlinear regression: \(\hat{y}=\beta_{0} e^{\beta_{1} x}\)
- (非)线性回归,其实就是说应变量能不能表示为多个待定系数的线性组合,其中每一个待定系数都和一个含有自变量\(x \)的表达式相乘。比如函数\(f(x, \boldsymbol{\beta})=\displaystyle\frac{\beta_{1} x}{\beta_{2}+x}\)是非线性的,因为它不能表示为两个\(\beta\)的线性组合。非线性函数的其他示例包括指数函数 , 对数函数 , 三角函数 , 幂函数 , 高斯函数和洛伦兹曲线 。 某些函数(如指数函数或对数函数)可以进行转换,以使它们是线性的。 如此转换,可以执行标准线性回归,但必须谨慎应用。
-
- Linear regression is relatively easy
— Numerically stable with unique solution given a reasonable definition of "best" fit - Nonlinear regression is relatively hard
Regression Review
Vocabulary
- Experiment — explanatory variables are manipulated (controlled), all other inputs are held constant, and the response variable is measured
但是对于observation来说,我们测试inputs和outputs,也不控制inputs - Model — a mathematical function that approximates the data and is useful for making predictions
- Regression — a method of finding the best fit of a model to a given set of data through the adjustment of model parameters (coefficients)
— What do we mean by “best fit”? - Residual: \(\varepsilon_{i}=y_{i}-f\left(\boldsymbol{x}_{\boldsymbol{i}}, \boldsymbol{\beta}\right), e_{i}=y_{i}-f\left(\boldsymbol{x}_{\boldsymbol{i}}, \boldsymbol{b}\right)\)
residual可能是error in the mdel and/or model;这里的\(\boldsymbol{\beta}\)是model理论上参数,我们无法知道,但是可以用\(\boldsymbol{b}\)去估计。 - A "good" model has small residuals
-
- Small mean, \(|\bar{\varepsilon}|\)
- Small variance (方差), \(\sigma_{\varepsilon}^{2}\)
-
- Much of our model and regression checking will involve studying and plotting residuals
— Plot \(e_{i} v s . \hat{y}_{i}\) (works for multiple regression)
What Do We Mean by “Best Fit”?
- First, assume \(\varepsilon\) is a random variable that does not depend on \(x\)
-
- There are no systematic errors
- The model is perfect
-
- Desired properties of a "best fit" estimator
-
- Unbiased, \(\sum \varepsilon_{i}=\sum e_{i}=0\left(\right.\) and \(\left.E\left[b_{k}\right]=\beta_{k}\right)\)(其实就是实验次数无穷大时的收敛值)
- Efficient, minimum variance \(\sigma_{e}^{2}\left(\right.\) and \(\left.\operatorname{var}\left(b_{k}\right)\right)\)
- Maximum likelihood (for an assumed pdf of \(\varepsilon\) )
- Robust (to be discussed later)
鲁棒性,if I have a or a few bad data point(s), how much does it screw up answer。
-
Maximum Likelihood Estimation
- 【Likelihood function】: the probability of getting this exact data set given a known model and model parameters
— To calculate the likelihood function, we need to know the joint probability distribution function (pdf) of \(\varepsilon\) - 【Maximum Likelihood】: what parameter values maximize the likelihood function?
-
- Take the partial derivative of the likelihood function (or more commonly the log-likelihood function) with respect to each parameter, set it equal to zero
- Solve resulting equations simultaneously
-
MLE Example – straight line
- Let \(y_{i}=\beta_{0}+\beta_{1} x_{i}+\varepsilon_{i}, \varepsilon_{i} \sim N\left(0, \sigma_{\varepsilon}\right)\), iid
- Since each \(\varepsilon_{i}\) is independent, the likelihood function for the entire data set is$$ L=\prod_{i=1}^{n} \mathbb{P}\left(y_{i}\right)=\prod_{i=1}^{n} \mathbb{P}\left(\varepsilon_{i}\right) $$
- Since the residuals are iid Normal,$$ L=\left(\frac{1}{\sqrt{2 \pi} \sigma_{\varepsilon}}\right)^{n} \exp \left[-\frac{1}{2} \sum_{i=1}^{n} \frac{\varepsilon_{i}^{2}}{\sigma_{\varepsilon}^{2}}\right] $$
- Define chi-square as$$ \chi^{2}=\sum_{i=1}^{n} \frac{\varepsilon_{i}^{2}}{\sigma_{\varepsilon}^{2}} \quad \text { (also called weighted SSE) } $$
- Maximizing \(L\) is the same as minimizing \(\chi^{2}\)
- Solve these equations simultaneously$$ \frac{\partial \chi^{2}}{\partial \beta_{k}}=0 \text { for all } k \text { (all coefficients) } $$
- For our line model, \(\varepsilon_{i}=y_{i}-\left(\beta_{0}+\beta_{1} x_{i}\right)\)

- Substitute our estimate for \(\beta_{0}\) into \(\chi^{2}\)
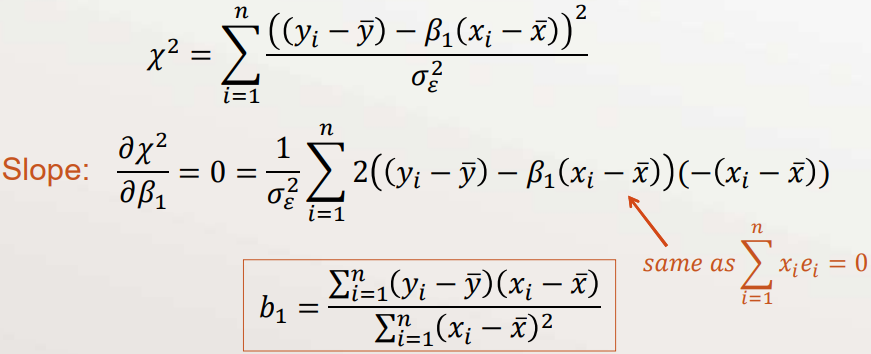
Assumptions for this MLE
- We assumed three things:
- Each residual (and \(y_{i}\) ) is independent
- Each residual (and \(y_{i}\) ) is identically distributed
- Each \(\varepsilon_{i} \sim N\left(0, \sigma_{\varepsilon}\right)\), and thus \(y_{i} \sim N\left(\hat{y}, \sigma_{\varepsilon}\right)\)
- We call this 【ordinary least squares】 (OLS)
- If any of these assumptions are invalid, then our least-squares estimates will not be the maximum likelihood estimates
Properties of our OLS Solution
- The parameters are unbiased estimators of the true parameters, with minimum variance compared to all other unbiased estimators (if our assumptions are correct)
- \(\displaystyle\sum_{i=1}^{n} e_{i}=0\)
- \(\displaystyle\sum_{i=1}^{n} y_{i}=\displaystyle\sum_{i=1}^{n} \hat{y}_{i}\), so that \(\bar{y}=\overline{\hat{y}}\)
- \(\displaystyle\sum_{i=1}^{n} \hat{y}_{i} e_{i}=0\)
- \(\displaystyle\sum_{i=1}^{n} x_{i} e_{i}=0\)
- The best fit line goes through the point \((\bar{x}, \bar{y})\)
OLS Matrix Formulation
When we have multivariate data, it is most convenient to formulate the OLS/MLE problem using matrix math
- \(i=1,2,3, \ldots, n\) data point index
- \(k=0,1,2, \ldots, p-1\) predictor variable index
- \(x_{i, k}=i^{t h}\) value for the \(k^{t h}\) predictor variable
- \(y_{i}=i^{t h}\) response data value
- \(\hat{y}=\beta_{0}+\beta_{1} x_{1}+\beta_{2} x_{2}+\cdots+\beta_{p-1} x_{p-1}\)
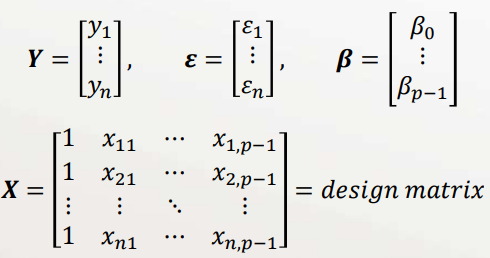
Model in matrix form: \(\boldsymbol{Y}=\boldsymbol{X} \boldsymbol{\beta}+\boldsymbol{\varepsilon}\)
(each row in \(X\) and \(\boldsymbol{Y}\) is a "data point")
Sum of square errors$$ S S E=\sum_{i=1}^{n} \varepsilon_{i}^{2}=\boldsymbol{\varepsilon}^{T} \boldsymbol{\varepsilon}=(\boldsymbol{Y}-\boldsymbol{X} \boldsymbol{\beta})^{T}(\boldsymbol{Y}-\boldsymbol{X} \boldsymbol{\beta}) $$
Maximum Likelihood estimate (minimum SSE): $$ \frac{\partial \chi^{2}}{\partial \beta_{k}}=0=\sum_{i=1}^{n} x_{i, k} \varepsilon_{i} \text { giving } \boldsymbol{X}^{\boldsymbol{T}} \boldsymbol{\varepsilon}=\mathbf{0} $$Using the definition of the residual, \( \boldsymbol{X}^{T} \boldsymbol{X} \boldsymbol{\beta}=\boldsymbol{X}^{T} \boldsymbol{Y}\)
Minimum SSE occurs when the coefficients are estimated as $$ \begin{gathered} \widehat{\boldsymbol{\beta}}=\left(\boldsymbol{X}^{T} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{T} \boldsymbol{Y} \\ \widehat{\boldsymbol{Y}}=\boldsymbol{X} \widehat{\boldsymbol{\beta}}=\boldsymbol{X}\left(\boldsymbol{X}^{T} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{T} \boldsymbol{Y}=\boldsymbol{H} \boldsymbol{Y} \\ \boldsymbol{H}=\boldsymbol{X}\left(\boldsymbol{X}^{T} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{T}=\text { hat matrix } \\ \boldsymbol{e}=\boldsymbol{Y}-\widehat{\boldsymbol{Y}}=(\boldsymbol{I}-\boldsymbol{H}) \boldsymbol{Y} \end{gathered} $$注意\(\boldsymbol{I}\)表示的是identity matrix;\(\boldsymbol{H}\)和\(\boldsymbol{I}-\boldsymbol{H}\)都是symmetric;common alternate notation: \(b_{k}=\hat{\beta}_{k}\)
We can use our solution to calculate the covariance matrices:$$ \begin{gathered} \operatorname{cov}(\boldsymbol{e})=s_{e}^{2}(\boldsymbol{I}-\boldsymbol{H}), \quad \operatorname{var}\left(e_{i}\right)=s_{e}^{2}\left(1-h_{i i}\right) \\ \operatorname{cov}\left(e_{i}, e_{j}\right)=-s_{e}^{2} h_{i j} \\ \operatorname{cov}(\widehat{\boldsymbol{Y}})=s_{e}^{2} \boldsymbol{H}, \quad \operatorname{var}\left(\hat{y}_{i}\right)=s_{e}^{2} h_{i i} \\ \operatorname{cov}(\widehat{\boldsymbol{\beta}})=s_{e}^{2}\left(\boldsymbol{X}^{T} \boldsymbol{X}\right)^{-1} \end{gathered} $$其中\(s_{e}^{2}\)是Variance of the residuals。
MLE Straight-Line Regression
- Our model: \(E[Y \mid X]=\beta_{0}+\beta_{1} X\)$$ \begin{aligned} &\beta_{1}=\frac{\operatorname{cov}(X, Y)}{\operatorname{var}(X)} \\ &\beta_{0}=E[Y]-\beta_{1} E[X] \end{aligned} \quad \rho=\frac{\operatorname{cov}(X, Y)}{\sqrt{\operatorname{var}(X) \operatorname{var}(Y)}} $$
- Ordinary least squares (OLS) estimators:$$ b_{1}=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \quad b_{0}=\bar{y}-b_{1} \bar{x} $$
Uncertainty of Fit Parameters
- The regression fit is based on a sample of data$$ \text { Population Model: } y_{i}=\beta_{0}+\beta_{1} x_{i}+\varepsilon_{i} $$
- To create confidence intervals for \(b_{0}, b_{1}\), and \(\hat{y}_{i}\), we need to know their sampling distributions
— Given the assumption of \(\varepsilon_{i} \sim N\left(0, \sigma_{\varepsilon}^{2}\right)\), the parameter sampling distributions are unbiased and t-distributed (DF = n-2) degrees of freedom) - $$ \begin{gathered} \operatorname{var}\left(b_{1}\right)=\frac{\operatorname{var}(\varepsilon)}{n \operatorname{var}(X)} \quad \operatorname{var}\left(b_{0}\right)=\frac{\operatorname{var}(\varepsilon)}{n}\left(1+\frac{\bar{x}^{2}}{\operatorname{var}(X)}\right) \\ \operatorname{cov}\left(b_{0}, b_{1}\right)=-\bar{x} \operatorname{var}\left(b_{1}\right) \end{gathered} $$
- Estimators: (其中\(p\)表示number of model parameters)$$ \begin{gathered} s_{e}^{2}=\frac{1}{n-p} \sum_{i=1}^{n} e_{i}^{2} \\ s_{b 1}^{2}=\frac{s_{e}^{2}}{(n-1) s_{x}^{2}} \quad s_{b 0}^{2}=\frac{s_{\varepsilon}^{2}}{n}+s_{b 1}^{2} \bar{x}^{2} \end{gathered} $$
Confidence Intervals
- The sampling distributions are Student's t with DF = n – 2
- Slope CI: \(b_{1} \pm t_{n-2, \alpha} s_{b 1} \quad s_{b 1}^{2}=\displaystyle\frac{s_{\varepsilon}^{2}}{(n-1) s_{x}^{2}}\)
- Intercept CI: \(b_{0} \pm t_{n-2, \alpha} s_{b 0} \quad s_{b 0}^{2}=\displaystyle\frac{s_{\varepsilon}^{2}}{n}+s_{b 1}^{2} \bar{x}^{2}\)
其中\(n\)是Critical t-value,\(\alpha=\)是significance level (e.g., 0.05)
Uncertainty of Predictions
- Uncertainty in \(\hat{y}_{i}\) comes from the spread of the residuals and from uncertainty in the best fit parameters \(b_{1}\) and \(b_{0}\)$$ \begin{aligned} \operatorname{var}\left(\hat{y}_{i}\right) &=\frac{\operatorname{var}(\varepsilon)}{n}\left(1+\frac{\left(x_{i}-\bar{x}\right)^{2}}{\operatorname{var}(X)}\right) \\ s_{\hat{y}_{i}}^{2} &=\frac{s_{\varepsilon}^{2}}{n}+s_{b 1}^{2}\left(x_{i}-\bar{x}\right)^{2} \end{aligned} $$
- Uncertainty in a predicted new measurement \(\hat{y}_{\text {new }}\) adds additional uncertainty of a single measurement$$ s_{\hat{y}_{n e w}}^{2}=s_{\hat{y}_{i}}^{2}+s_{\varepsilon}^{2} $$
Uncertainty of Correlation Coefficient
$$ \rho=\frac{\operatorname{cov}(X, Y)}{\sqrt{\operatorname{var}(X) \operatorname{var}(Y)}} \quad r=\frac{1}{n-1} \sum_{i=1}^{n}\left(\frac{x_{i}-\bar{x}}{s_{x}}\right)\left(\frac{y_{i}-\bar{y}}{s_{y}}\right) $$
- The sampling distribution for \(r\) is about Student's t (D F=n-2) only for \(\rho=0\). For this case$$ S_{r}=\frac{s_{\varepsilon}}{\sqrt{n-1} s_{y}} $$
- For \(\rho \neq 0\), the sampling distribution is complicated
- We’ll use the Fisher z-transformation: $$ z=\frac{1}{2} \ln \left(\frac{1+r}{1-r}\right) $$
- When \(n>25, z\) is about normal with$$ E[z]=\frac{1}{2} \ln \left(\frac{1+\rho}{1-\rho}\right) \quad \operatorname{var}(z)=\frac{1}{n-3} $$
Assumptions in OLS Regression
- \(\varepsilon\) is a random variable that does not depend on \(x\) (i.e., the model is perfect, it properly accounts for the role of \(x\) in predicting \(y\) )
- \(\mathrm{E}\left[\varepsilon_{l}\right]=0\) (the population mean of the true residual is zero); this will always be true for a model with an intercept
- All \(\varepsilon_{i}\) are independent of each other (uncorrelated for the population, but not for a sample)
- All \(\varepsilon_{j}\) have the same probability density function (pdf), and thus the same variance (called homoscedasticity)
- \(\varepsilon \sim \mathrm{N}\left(0, \sigma_{\varepsilon}\right)\) (the residuals, and thus the \(y_{i}\), are normally distributed)
- The values of each \(x_{i}\) are known exactly
Checking the Assumptions
- Do the assumptions in OLS regression hold?
— Which assumptions can you validate?
— If an assumption is violated, how far off is it? - If one or more assumptions do not hold, does the observed violation invalidate the statistical procedure used?
— If so, what next?
Failed Assumptions – the Anscombe Problems
F. J. Anscombe, “Graphs in Statistical Analysis”, The American Statistician, Vol. 27, No. 1
(Feb., 1973) pp. 17 – 21.
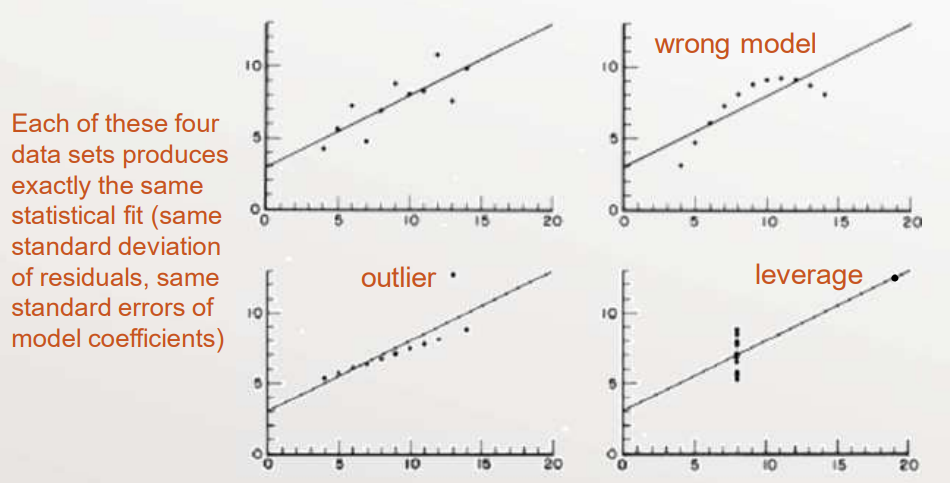
What Happens When OLS Assumptions are Violated?
- At best, the regression becomes inefficient
— Do the assumptions in OLS regression holdThe uncertainty around the estimates is larger than you think: \(\operatorname{var}[\hat{\theta}]\) for some parameter \(\theta\) - At worst, the regression becomes biased
— The results may be misleading: bias \([\hat{\theta}]\) - We want small mean square error (MSE)$$\operatorname{MSE}(\hat{\theta})=\operatorname{var}[\hat{\theta}]+(\operatorname{bias}[\hat{\theta}])^{2}$$
Checking Our Assumptions
- Regression Diagnostics: checking for violations in any of the OLS assumptions
- Topics we'll address:
- Normality of residuals
- Outliers (identically distributed)
- Leverage and influence
- Heteroscedasticity (variation in variance)
- Error in predictor variables
- The wrong model
- Correlated residuals
Fixing Problems
- Regression Remediation: changing our regression to address diagnostic problems
- Topics we'll address:
- Outlier removal or adjustment
- Data transformation
- Weighted regression
- Total regression
- Model building
- Autocorrelation analysis
Response surface methodology