[mathjax]
在固态物体中，少数价电子因为受到的束缚力较弱，将变得自由，在固体当中晃来晃去。对它产生作用的不再仅仅是单个的“母”原子，而变成了整个晶格形成的势场。有两种相当重要的简化模型：第一种是索末非的电子气理论，该理论忽略所有力的作用(除了限制性边界)，把晃来晃去的电子看作是一个盒子里的自由粒子(可看作是三维情况下的无线深方势阱)；第二种是布洛赫理论，它引入了一种周期性势场来表示这种规则化排列并且带正电的核的吸引作用(但仍然忽略了电子间的排斥作用)。这两种模型虽然仅仅是简历固体量子理论崎岖之路上迈出的第一步，但它却成功地揭示了泡利不相容原理在固体理论中的重要地位，并且为理解导体、半导体、绝缘体的重要电学性质提供了极具启发性的思路。
自由电子气模型
假设我们讨论的是一块方形固体，边长分别是\(\begin{array}{lll} l_{x}, & l_{y}, & l_{z} \end{array} \)，且固体中的电子在阱内没有收到任何力的作用。按照三维无线深势阱的处理，采用笛卡尔坐标很容易求解，这一部分在球坐标这一章节给出了解法，只是当时讨论的是正方体。这里直接给出结果：$$ \psi_{n_{x} n_{y} n_{z}}=\sqrt{\frac{8}{l_{x} l_{y} l_{z}}} \sin \left(\frac{n_{x} \pi}{l_{x}} x\right) \sin \left(\frac{n_{y} \pi}{l_{y}} y\right) \sin \left(\frac{n_{z} \pi}{l_{z}} z\right)$$其中\( n_{x}=1,2,3, \ldots, n_{y}=1,2,3, \ldots, n_{z}=1,2,3, \ldots \)允许的能量值为$$E_{n_{x} n_{y} n_{z}}=\frac{\hbar^{2} \pi^{2}}{2 m}\left(\frac{n_{x}^{2}}{l_{x}^{2}}+\frac{n_{y}^{2}}{l_{y}^{2}}+\frac{n_{z}^{2}}{l_{z}^{2}}\right)=\frac{\hbar^{2} k^{2}}{2 m}$$其中\( \mathbf{k} \equiv\left(k_{x}, k_{y}, k_{z}\right)\)
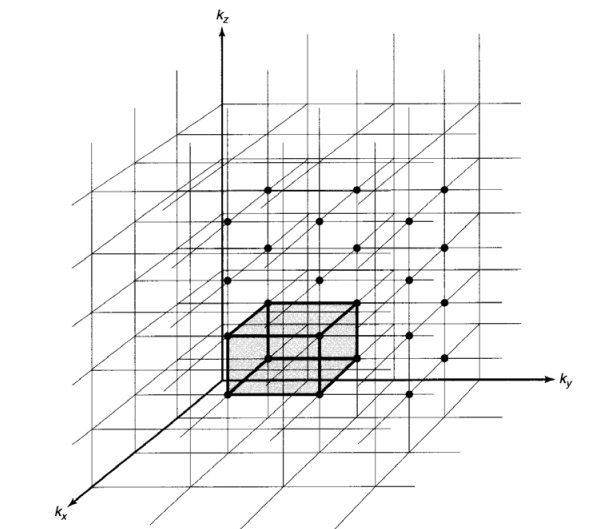用\(k_{x}=\left(\pi / l_{x}\right),\left(2 \pi / l_{x}\right),\left(3 \pi / l_{x}\right), \ldots \)和\( k_{y}=\left(\pi / l_{y}\right),\left(2 \pi / l_{y}\right),\left(3 \pi / l_{y}\right), \ldots \)以及\( k_{z}=\left(\pi / l_{z}\right),\left(2 \pi / l_{z}\right),\left(3 \pi / l_{z}\right), \ldots \)分别画平面，每一个交点表示不同的定态，它在上图中占有(平句化)空间大小为\( k_{z}=\left(\pi / l_{z}\right),\left(2 \pi / l_{z}\right),\left(3 \pi / l_{z}\right), \ldots \)，其中的\( V\)即为宏观固体的体积。假设该固体有\( N \)个原子，每个原子贡献\( q \)个电子(价电子)。如果电子是玻色子，那么所有的电子都将处在基态\( \psi_{111} \)；但是实际上电子是费米子，因而满足泡利不相容原理，所有每一个态(上图中不同的交点)只能容纳两个电子。要想知道电子可以占据的最高能量位置，其实就是去求解上图中形成的八分之一球的最大半径\( k_F\)，注意形成的是球，所以在球和坐标轴的交点处得到\(n_{x} \)或\( n_{y} \)或\(n_{z} \)的取值最大值是不一样的。我们有八分之一球的体积除以每一个状态的体积就得到状态数，然后乘以二即为所有的电子数目：$$\frac { 2\frac{1}{8}\left(\frac{4}{3} \pi k_{F}^{3}\right) }{\left(\frac{\pi^{3}}{V}\right) } =Nq$$于是有\( k_{F}=\left(3 \rho \pi^{2}\right)^{1 / 3} \)，其中\( \rho \equiv \frac{N q}{V}\)为自由电子密度(单位体积内自由电子的数目)。
\( \mathbf{k} \)空间中，电子被占据和没有被占据的分界面为“费米面”，对应的能量为费米能量\( E_{F}=\frac{\hbar^{2}}{2 m}\left(3 \rho \pi^{2}\right)^{2 / 3}\)。
电子气体的总能量很容易通过积分得到$$ E_{\mathrm{tot}}=\frac{\hbar^{2} V}{2 \pi^{2} m} \int_{0}^{k_{F}} k^{4} d k=\frac{\hbar^{2} k_{F}^{5} V}{10 \pi^{2} m}=\frac{\hbar^{2}\left(3 \pi^{2} N q\right)^{5 / 3}}{10 \pi^{2} m} V^{-2 / 3} $$这个能量所扮演的角色和正常气体内能\( U\)的角色很相似。这个固体中的自由电子气似乎想往外跑，但是被固体边界限制住了，所以只能对固体的内壁施加一个“压力”；如果这个固体(盒子)的体积扩大了，总能量就会下降，类似气体对外做功。到此，我们就可以部分地理解为什么低温固体不会简单地塌缩(往内部坍塌，密度增大)：固体受到一个内部的稳定压力，这个压力和电子间的排斥力和热运动无关(我们都忽略了)，它属于一种量子效应，来源于全同费米子的波函数反对称条件，我们把它称为“简并压”(或者排斥压力)。
价带结构
现在我们考虑固体中除去价电子之外的部分，这部分形成了周期性势场。定性来看，电子的行为，很大程度上取决于这个势场，势场的具体形状仅对细节有关。比如一维狄拉克梳，它由无数个平均分布的狄拉克函数峰组成(这在斯坦福傅里叶变换的笔记中有具体讲)。但首先，我们要介绍一个强大的定理，它可以大大地简化周期势的分析过程。
周期势的定义是每经过一个固定的具体\( a\)就会重复自身的势场$$V(x+a)=V(x)$$布洛赫定理告诉我们，对于含周期势的薛定谔方程\( -\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}+V(x) \psi=E \psi \)，它的解必定有如下形式：$$\psi(x+a)=e^{i K a} \psi(x)$$其中\( K\)为某些适当的常数(这里我们称之为常数是因为它和\( x\)无关，但是可能和能量\( E\)有关)。
下面我们证明为什么周期性势场中波函数的解是上述形式：令\( D\)为“位移”算符：$$D f(x)=f(x+a)$$对于一个周期势，\( D\)和哈密顿算符对易：\( [D, H]=0\)，因此我们可以任意选择\( H \)的本征函数使它同时是\( D \)的本征函数，即\( D \psi=\lambda \psi\)或\( \psi(x+a)=\lambda \psi(x)\)，\( \lambda \)显然非零，所以可以写成指数形式\(\lambda=e^{i K a} \)(其中\( K \)为适当的常数，这也满足了归一化条件\( |\psi(x+a)|^{2}=|\psi(x)|^{2}\))，证毕。
当然，某个固体物质不可能无限大，它的边界一定会破坏周期势\( V(x) \)，导致布洛赫不再适用。但是，对于任何宏观的晶体，它都具有很大数量级的原子数目(无数个梳子的齿)，很难想像边界效应对于固体内部深处的电子有明显影响(意思到底是啥？)。这就启示我们可以用下面的方法来修正布洛赫定理：以\( N \approx 10^{23} \)为周期，我们把\( x\)轴首位相连成一个圆，这样形式上我们可以加上边界条件：$$\psi(x+N a)=\psi(x)$$由它可以推出$$e^{i N K a} \psi(x)=\psi(x)$$所以\( e^{i N K a}=1 \)，或者\( N K a=2 \pi n \)，因此有：$$K=\frac{2 \pi n}{N a}, \quad(n=0,\pm 1,\pm 2, \ldots)$$特别地，对于这种排列方式，\(K \)一定是实数。布洛赫定理的优点就是我们仅需要求解一个晶格内(比如\(0 \leq x<a \))的薛定谔方程；递推方程\(\psi(x+a)=e^{i K a} \psi(x) \)给出了固体各处的解。
现在我们假设势场是由狄拉克梳组成的：$$V(x)=\alpha \sum_{j=0}^{N-1} \delta(x-j a)$$(我们可以想象一下，将\( x=Na \)的尾端和\( x=0\)的首端连接起来，那么原来的\( x=Na\)等价于现在的\( x=-a \))在\( 0<x<a \)内势能为零，所以：$$-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}=E \psi$$或者$$\frac{d^{2} \psi}{d x^{2}}=-k^{2} \psi$$其中\( k \equiv \frac{\sqrt{2 m E}}{\hbar} \)(波矢的平方和能量成正比)。通解为：$$\psi(x)=A \sin (k x)+B \cos (k x), \quad(0<x<a)$$根据布洛赫定理，紧邻原点左侧的晶胞的波函数为$$\psi(x)=e^{-i K a}[A \sin k(x+a)+B \cos k(x+a)], \quad(-a<x<0)$$由于波函数在的连续性，同时取上述两个波函是的\( x=0 \)，因此有$$B=e^{-i K a}[A \sin (k a)+B \cos (k a)]$$\( x=0\)处左右两侧波函数的微分并不相等，但是存在如下的关系(参考前面\(\delta \)势函数的笔记)$$k A-e^{-i K a} k[A \cos (k a)-B \sin (k a)]=\frac{2 m \alpha}{\hbar^{2}} B$$联立上面两个方程可以得到$$\left[e^{i K a}-\cos (k a)\right]\left[1-e^{-i K a} \cos (k a)\right]+e^{-i K a} \sin ^{2}(k a)=\frac{2 m \alpha}{\hbar^{2} k} \sin (k a)$$进一步化简得到$$\cos (K a)=\cos (k a)+\frac{m \alpha}{\hbar^{2} k} \sin (k a)$$上式决定了\( k \)可能的取值，因而也决定了允许的能量值。令\(z \equiv k a \quad \beta \equiv \frac{m \alpha a}{\hbar^{2}} \)，那么前面那个复杂的式子可以化简为$$f(z) \equiv \cos (z)+\beta \frac{\sin (z)}{z}$$
常数\( \beta\)是表征狄拉克函数“强度”的一个无量纲量，\( f(z)\)即为\( \cos (K a) \)。下图是\( \beta=10 \)时\( f(z)\)的图像。需要特别注意的是\( f(z)\)存在超过\( (-1,+1)\)的范围，但是实际上\( f(z)= \cos (K a)\)，不可能超过该范围，所以超出的部分实际上是无解的。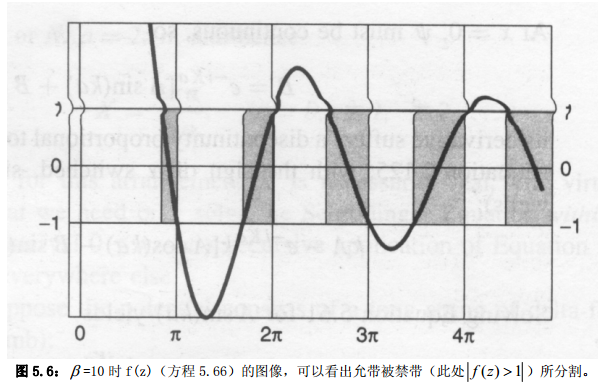
这些间隙表示被禁止的能量，称为能隙：它们被允许能量的能带所分离。在一个给定的能带中，实际上所有的能量都是允许的，因为根据\( K a=2 \pi n / N \)，\(N \)是一个很大的数，\( n \)为任意整数。你可能会想在上图中画\( N \)条垂直的线，取值是\( \cos (2 \pi n / N)\)从\( (+1,-1)\)的所有值 (即从\( n=0 \)到\( n=N / 2\))，然后再到\( +1\)(\( n=N-1\))—在这一点，布洛赫因子\( e^{i K a}\)完成一个振荡周期，因此不会因为\( n\)继续增加而产生新解。这些线与\( f(z) \)的每个交点表示一个允许的能量。显然每个能带中有\( N\)个状态，因为这些线相距很近，在很多情况下它们都可以被视为是连续的。
注：
1. 上述的处理方法，我们只将周期性作为为唯一考虑的因素，其实这不是现实中的情景，也就是说真实的周期性势场不是这种简化的狄拉克梳子，用狄拉克梳子其实忽略了每一个势场的形状，只保留了周期性的特征。有些书籍采用了周期性矩形势场来处理布洛赫定理，但是不改变最终的结果的主要特性。
到目前为止，我们仅仅在势场中放入了一个电子。在实际中，这个值将是\( Nq\)，其中\( q \)是每个原子具有的“自由”电子数。因为泡利不相容原理的存在，只有两个电子可以占据一个相同的空间态，所以如果\( q=1\)，它们将填充第一能带的一半，如果\(q=2 \)，它们将完全填满第一能带，如果\( q=3\)，它们将填满第二能带的一半，以此类推。这些都是在一维基态的情况，在三维中，对于实际情况下的势能场，能带结构会更加复杂，但是仍满足禁带分割允带—这种能带结构正是周期性势场的标致。
绝缘体：如果一个能带被完全填满，此时如果要激发一个电子就需要一个较大的能量，因为电子需要跳过一个禁带，这样的材料称之为绝缘体。
导体：相反地，如果一个(高)能带是部分填充的，激发一个电子只需要一个很小的能量，这种材料通为导体。
半导体：如果我们对绝缘体进行掺杂，加一些\( q\)偏小或偏大的原子，这些杂质原子将会产生一些“多余”的电子进入高能带，或者在原来被占满的能级中产生一些空穴，这两种情况都会在绝缘体中产生微弱的电流，这种材料我们称为半导体。
在自由电子模型中，所有的固体都应当是很好的导体，因为在允带中没有很大的带隙，只有应用了能带理论我们才成功解释了固体中电子的导电性。
参考资料：(拓展补充，上面的不详细)
1. 导带、价带、禁带、允带都是什么逻辑关系？
2. 绝缘体、半导体、良导体、超导体这些材料的内在不同是什么？