Hamiltonian Mechanics Sequence
Lagrangian and Hamiltonian Mechanics

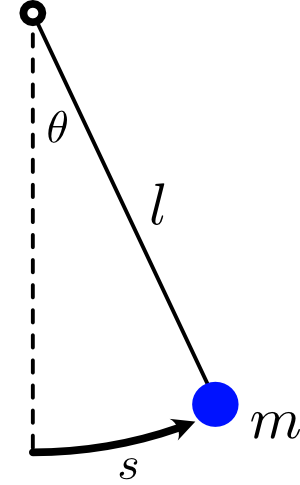
Newton's Approach
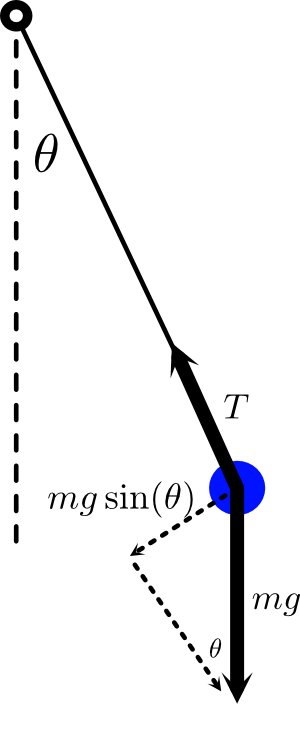
物体受到重力\( mg\)和tension \(T\),牛顿力学告诉我们the equation of motion\(\sum \vec{F}=m \vec{a}\),则是一个vector equation,但是我们只需要关注tangential component—that is, the component of the force and acceleration along the circle where the particle is constrained to move. $$\begin{array}{l} m \ddot{s}=-m g \sin \theta \\ s=l \theta \end{array}$$得到最终的结果为$$ \ddot{\theta}=-\frac{g}{l} \sin \theta $$It's actually pretty complicated—too complicated to write down a simple expression for the solution \(\theta(t)\). 在小角度近似下可以用\(\theta\)去替代\( \sin \theta\),于是系统就可以对应于简谐振动的模型。不同初始状态下的\(\theta(t)\)的样子参考动画。
Lagrange's Approach
牛顿力学是写出总的受力\(\sum \vec{F}\),但是拉格朗日力学tells us to start by writing down the kinetic energy \(K\) and potential energy \(U\), and then to take their difference: (注意这里的负号)$$L=K-U$$其中\(L\) is called the Lagrangian. 简单计算知动能\(K=\displaystyle\frac{1}{2} m l^{2} \dot{\theta}^{2}\)。以中心圆点作为ground level,于是势能为\(U=-m g l \cos \theta\)。Then the Lagrangian for the pendulum is$$ L(\theta, \dot{\theta})=\frac{1}{2} m l^{2} \dot{\theta}^{2}+m g l \cos \theta $$Newton told us to compute the total force \(\sum \vec{F}\) and then write the equation \(\sum \vec{F}=m \vec{a}\). Lagrange instructs us to compute the Lagrangian \(L\), and then write down the Euler-Lagrange equation: $$ \frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{\partial L}{\partial \dot{\theta}}\right)=\frac{\partial L}{\partial \theta} $$ Euler-Lagrange equation is the condition for the action \( S\) which is the integral of the Lagrangian, to be minimized: $$ \text { minimize } \quad S=\int \mathrm{d} t L \Longleftrightarrow \text { Euler-Lagrange eqn } $$The claim is that of all the paths a particle could follow, the one it actually chooses is the path that minimizes (or more precisely extremizes) the action. This is known as the principle of least action, and the implication is that the trajectory satisfies the Euler-Lagrange equation because that's the condition for extremizing the action. 欧拉-拉格朗日方程为变分法中的一条重要方程。它是一个二阶偏微分方程。它提供了求泛函的临界值(平稳值)函数,换句话说也就是求此泛函在其定义域的临界点的一个方法,与微积分差异的地方在于,泛函的定义域为函数空间而不是\(\mathbb{R}^{n}\)。
将pendulum Lagrangian带入到Euler-Lagrange equation,那么等式右边改写为$$ \frac{\partial L}{\partial \theta}=\frac{\partial}{\partial \theta}(m g l \cos \theta)=-m g l \sin \theta $$注意动能项\(\displaystyle\frac{1}{2} m l^{2} \dot{\theta}^{2}\)没有贡献,因为它只是\( \dot{\theta} \)的函数,和\(\theta\)无关,等于说我们将\( \dot{\theta} \)和\(\theta\)当作independent variables when we take these derivatives。等式左边改写为$$ \frac{\partial L}{\partial \dot{\theta}}=m l^{2} \dot{\theta} \Longrightarrow \frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{\partial L}{\partial \dot{\theta}}\right)=m l^{2} \ddot{\theta} $$Euler-Lagrange equation等式左右两边可以改写为$$ m l^{2} \ddot{\theta}=-m g l \sin \theta $$which is the same thing we found earlier from \(F=m a\).
广义动量(generalized momentum):\(\displaystyle\frac{\partial L}{\partial \dot{\theta}}=m l^{2} \dot{\theta}\)共轭(conjugate to) 广义坐标\(\theta\),想一想相空间的笔记就知道了。
广义力(generalized force):\(\displaystyle\frac{\partial L}{\partial \theta}\), because the Euler-Lagrange equation then resembles Newton's second law: rate of change of momentum = force.
拉格朗日方法的好处:不用处理\(\sum \vec{F}=m \vec{a}\)中的向量,选择我们喜欢的坐标系(包括非惯性参考系non-inertial coordinates)去描述这个系统,写下拉格朗日量\( L=K-U\),将其带入到基于所选坐标系的Euler-Lagrange equation。It also makes it much easier to deal with constraints(约束) and to understand symmetries
Hamilton's Approach
不同于拉格朗日量\(L=K-U\)的写法,哈密顿量描述用\(E=K+U\)来描述系统总能量$$ E=\frac{1}{2} m l^{2} \dot{\theta}^{2}-m g l \cos \theta $$记住动量\( p=m l^{2} \dot{\theta}\),因此我们可以将上述方程改写为$$ H(\theta, p)=\frac{p^{2}}{2 m l^{2}}-m g l \cos \theta $$其中\(H\) is called the Hamiltonian,对于上述简单的单摆系统,哈密顿量就是总能量。More generally, it's defined by$$ H=\dot{\theta} \frac{\partial L}{\partial \dot{\theta}}-L $$如果根据\(-p=m l^{2} \dot{\theta}\),用\(\dot{\theta}\)来代替式子中的\(p\)的话,很容易验证上述公式的正确性。
之前我们used the Lagrangian to write down the Euler-Lagrange equation—we use the Hamiltonian to write down Hamilton's equations: $$ \dot{\theta}=\frac{\partial H}{\partial p}, \quad \dot{p}=-\frac{\partial H}{\partial \theta} $$Euler-Lagrange equation gave us a single 2nd order differential equation, Hamilton gives us a pair of 1st order equations for \(\theta\) and \(p\). 简单求导可以得到Hamilton's equations for the pendulum are$$ \dot{\theta}=\frac{p}{m l^{2}}, \quad \dot{p}=-m g l \sin \theta $$第一个方程其实就是动量的定义\(p=m l^{2} \dot{\theta}\),将其对时间求导可得\(\dot{p}=m l^{2} \ddot{\theta}\),配合上面的第二个方程我们可以得到$$m l^{2} \ddot{\theta}=-m g l \sin \theta$$which is once again the original equation of motion! So Hamilton's equations are equivalent to \(F=m a\) and the Euler-Lagrange equation; they just split the single 2nd order equation into a pair of 1st order equations.
哈密顿方法的好处:事实上,Hamilton's 1st order equations并不一定比二阶运动方程更容易求解,但是我们可以从哈密顿量一阶方程得到new geometric perspective on the mechanics of the pendulum: as the pendulum moves, we trace out a curve in the \(\theta-p\) plane known as a flow on phase space.
To specify what the pendulum is doing at any given instant, 我们需要知道位置和速度,或者等价地知道位置和动量\((\theta_{0}, p_{0})\),通过初始条件就可以借助哈密顿量\((\theta(t), p(t))\)求解算出后面任意时刻的运动状态
\(\theta-p\)相平面中的曲线\((\theta(t), p(t))\)叫作a flow on the phase space。这些flows很特别,they won't travel along any old curve in the plane。因为单摆的能量守恒,如果我们在某个flow curve的任意时刻去evaluate the Hamiltonian,we're guaranteed to always get the same number— \(H\) is a constant of the flow. 这意味着不管初始的哈密顿量\(H_0\)是多少,the flow will be trapped on the curve in the \(\theta-p\) plane where the energy is \(H(\theta, p)=H_{0}\)。参考动画
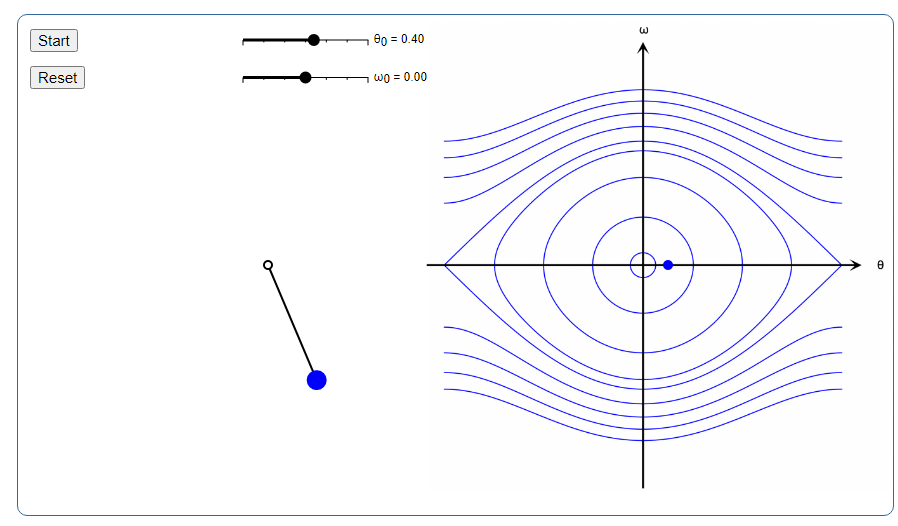
相图中的曲线可以分为两类,the closed loops near the middle and the wavy (波浪形的) lines at the top and bottom。二者过渡的边界状态是:将小球放在最高处,初始角速度为零。
This is only the tip of the iceberg for Lagrangian and Hamiltonian mechanics. Not only are these fascinating and extremely useful approaches to classical mechanics, they are fundamental to the way we think about quantum mechanics. For example, functions on phase space in classical mechanics turn into operators on the space of quantum states in quantum mechanics. If you know the state \(|\psi\rangle\) of a quantum system at \(t=0\), the Schrödinger equation says that the state at a later time \(t\) will be \(e^{-\frac{i}{\hbar} H t}|\psi\rangle\), where \(H\) is the operator versior of the classical Hamiltonian function. The Lagrangian, meanwhile, appears in the path-integral (路径积分) formulation of quantum mechanics.
Principle of Least Action
最小作用量原理是物理中的profound and far-reaching idea,
如果有一个粒子从1点运动到2点,那么它的轨迹应该是怎样的?牛顿的方法是将粒子所受的各种力加和,然后利用\(F=m \ddot{x}\) (equation of motion)求解,\(x(t)\)就是我们要求的结果。It's a different way of looking at things that underlies a huge amount of what we humans have learned about the world in the last few hundred years—from Newtonian mechanics, to relativity, to quantum mechanics, and quantum field theory.
力\(F(x)\)和势能函数\(U(x)\)的关系$$ F(x)=-\frac{\mathrm{d} U}{\mathrm{~d} x} $$比如对于重力场acting on a projectile the potential is \(U=m g x\),斜率就是\( mg\),那么力就是其负数,\(F=-m g\) ;对于a mass on a spring,势能为\(U=\displaystyle\frac{1}{2} k(x-l)^{2}\),斜率为\(k(x-l)\),于是spring force为\( F=-k(x-l)\)。
In terms of the potential energy then, we can write the equation of motion as$$ m \ddot{x}=-\frac{\mathrm{d} U}{\mathrm{~d} x} $$动能\(K=\displaystyle\frac{1}{2} m \dot{x}^{2}\),总能量\(E=K+U\)。但是现在我们想写出二者的difference \(K-U\) $$ L=\frac{1}{2} m \dot{x}^{2}-U(x) $$This combination is called the Lagrangian function, and right now it might look like it's coming out of left field, but let's see where it leads us. For any path \(x(t)\) between the particle's starting position \(x\left(t_{1}\right)=x_{1}\) and its ending position \(x\left(t_{2}\right)=x_{2}\), define a number \(S\) by integrating the Lagrangian along the curve: $$ S=\int_{t_{1}}^{t_{2}} \mathrm{~d} t\left(\frac{1}{2} m \dot{x}(t)^{2}-U(x(t))\right) $$\(S\) is called the action of the path. So far \(x(t)\) can be any curve connecting the two given endpoints. We want to use the action to figure out the actual trajectory that the particle will follow.
Claim: 粒子的轨迹就是那个action \( S\)最小的那个。因此这叫作principle of least action (最小作用量原理)。注意可能求解出的是一个saddle point,但是这里我们只focus on the typical case。