球坐标中的薛定谔方程
薛定谔方程$$i \hbar \frac{\partial \Psi}{\partial t}=H \Psi$$三维形式下的哈密顿算符为$$\frac{1}{2} m v^{2}+V=\frac{1}{2 m}\left(p_{x}^{2}+p_{y}^{2}+p_{z}^{2}\right)+V$$其中$$p_{x} \rightarrow \frac{\hbar}{i} \frac{\partial}{\partial x}, \quad p_{y} \rightarrow \frac{\hbar}{i} \frac{\partial}{\partial y}, \quad p_{z} \rightarrow \frac{\hbar}{i} \frac{\partial}{\partial z}$$其中动量写成算符的形式有$$\mathbf{p} \rightarrow \frac{\hbar}{i} \nabla$$而拉普拉斯算子\(\nabla^{2} \equiv \displaystyle\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}} \)则有$$i \hbar \frac{\partial \Psi}{\partial t}=-\frac{\hbar^{2}}{2 m} \nabla^{2} \Psi+V \Psi$$
注：\( p_{x}^{2} \)就是作用两次算符，也就是得到二阶偏微分。
令\( \mathbf{r}=(x, y, z) \)，微小体积元\( d^{3} \mathbf{r}=d x d y d z \)，归一化条件$$\int |\Psi|^{2} d^{3} \mathbf{r}=1$$如果势函数不随时间变化，空间波函数满足的薛定谔方程为$$-\frac{\hbar^{2}}{2 m} \nabla^{2} \psi+V \psi=E \psi$$波函数最终的解为$$\Psi(\mathbf{r}, t)=\sum c_{n} \psi_{n}(\mathbf{r}) e^{-i E_{n} t / \hbar}$$线性组合的系数由初态波函数确定。
上面的是笛卡尔坐标的表示，另外还有球坐标的表示方法\( \mathbf{r}=(r, \theta, \phi) \)，到底用什么坐标表示方便，要依据具体情况而定，下面先介绍用笛卡尔坐标的情况。
求解三维无线深位能阱的波函数
空间波函数的薛定谔方程为\( H \psi(\vec{r})=E\psi(\vec{r}) \)，在盒子里面势场为零，则有$$-\frac{\hbar^{2}}{2 m}\left(\frac{\partial^{2} \psi}{\partial x^{2}}+\frac{\partial^{2} \psi}{\partial y_{2}}+\frac{\partial^{2} \psi}{\partial z^{2}}\right)=E \psi$$边界条件(六个面上的波函数都是零)$$\begin{aligned} & \psi(x, y, 0)=\psi(x, y, a) \\ =& \psi(x, 0, z)=\psi(x, a, z) \\ =& \psi(0, y, z)=\psi(a, y, z) \\ =& 0 \end{aligned}$$遇到偏微分方程的第一件事情就是做分离变数法$$\psi(x, y, z)=X(x) Y(y) Z(z)$$于是可以得到下面的方程组(其实就是三个向量方向的方程)$$\begin{array}{l} -\displaystyle\frac{\hbar^{2}}{2 m} \frac{d^{2} X}{d x^{2}}=E_{x} X \\ -\displaystyle\frac{\hbar^{2}}{2 m} \frac{d^{2} Y}{d y^{2}}=E_{y} Y \\ -\displaystyle\frac{\hbar^{2}}{2 m} \frac{d^{2} Z}{d z}=E_{z} Z \\ E_{x}+E_{y}+E_{z}=E \end{array}$$上面其实是三个一维的情况，变成求解一维无限深势阱的问题，令\(k \equiv \displaystyle\frac{\sqrt{2 m E}}{\hbar} \)，原方程可以写成$$\frac{d^{2} \psi}{d x^{2}}=-k^{2} \psi$$同时套三个方向，于是有$$E_{x}=\frac{\hbar^{2} k_{x}^{2}}{2 m} \quad E_{y}=\frac{\hbar^{2} k_{y}^{2}}{2 m} \quad E_{y}=\frac{\hbar^{2} k_{y}^{2}}{2 m} $$而\( X(x)=A \cos {kx} +B \sin {kx} \)边界条件(\( X(0)=0\)和\(X(a)=0 \))使得\( k_{x} a=n_{x} \pi \quad n_{x}=1,2,3 \)，而且\( A=0 \)，同样可以得到\( Y(z) \)和\( Z(z)\)。解得本征函数为$$\psi_{n_{x}, n_{y}, n_{z}}(x, y, z)=\left(\frac{2}{a}\right)^{\frac{3}{2}} \sin \frac{n_{x} \pi x}{a} \sin \frac{n_{y} \pi y}{a} \sin \frac{n_{z} \pi z}{a}$$本征值为$$E_{n_{x} n_{y}, n_{z}}=\frac{\pi^{2} \hbar^{2}}{2 m a^{2}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right) \quad n_{x}, n_{y}, n_{z}=1,2,3, \ldots$$对于一维无限深势阱的问题，quantum number只需要一个，这里三维的情况，需要三个quantum number(三个方向的quantization)。基态就是三个quantum number都取\( 1\)的情况，则基态波函数为$$\psi_{111}(x, y, z)=\left(\frac{2}{a}\right)^{\frac{3}{2}} \sin \frac{\pi x}{a} \sin \frac{\pi y}{a} \sin \frac{\pi z}{a}$$三维立方体的情况，有很多“degenerate state”，比如$$(1,1,2),(1,2,1),(2,1,1)\quad \psi_{112}\quad \psi_{121}\quad \psi_{211}$$虽然量子数不同(本征函数不同)，但是本征值(能量)相同。如果三个维度不相等，那么简并的情况就不一样了，正是因为立方体的高对称性，才有很多波函数的简并态。
对称性和简并态在物理上是相连的，很多物理系统都是如此。
注：
(1) 一维无限深势阱中\( E_{n}=\displaystyle\frac{\hbar^{2} k_{n}^{2}}{2 m}=\displaystyle\frac{n^{2} \pi^{2} \hbar^{2}}{2 m a^{2}}\)，\( \psi(x)=A \sin k x+B \cos k x\)，\(k_{n}=\displaystyle\frac{n \pi}{a}, \quad n=1,2,3, \dots \)，边界条件得\( B=0 \)。
(2) 半导体中等效质量在各个方向可能不一定相同，所以对称性也会被破坏，简并也会被破坏。
(3) 笛卡尔坐标在多数实际情况下不是很好，比如三五族半导体量子点，一般是锥形，笛卡尔坐标不合适，应该用柱坐标。中心场则适合球坐标，交互作用(大小)只和距离有关，和方位无关，比如氢原子的电子云波函数。
球坐标表示\((r, \theta, \phi) \)
球坐标很适合中心力场对称的情况。
拉普拉斯算符$$\nabla^{2}=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial}{\partial r}\right)+\frac{1}{r^{2}} \frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)+\frac{1}{r^{2}} \frac{1}{\sin ^{2} \theta} \frac{\partial}{\partial \theta}\left(\frac{\partial^{2}}{\partial \phi^{2}}\right)$$于是定态薛定谔方程可以写成$$-\frac{\hbar^{2}}{2 m}\left[\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial \psi}{\partial r}\right)+\frac{1}{r^{2}} \frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial \psi}{\partial \theta}\right)+\frac{1}{r^{2}} \frac{1}{\sin ^{2} \theta} \frac{\partial}{\partial \theta}\left(\frac{\partial^{2} \psi}{\partial \phi^{2}}\right)\right]+V \psi=E \psi$$
分离变数法$$\psi(r, \theta, \phi)=R(r) Y(\theta, \phi)$$于是得到两个方程$$\begin{array}{r} \displaystyle\frac{1}{R} \frac{d}{d r}\left(r^{2} \frac{d R}{d r}\right)-\frac{2 m r^{2}}{\hbar^{2}}[V(r)-E]=l(l+1) \\ \displaystyle\frac{1}{Y}\left\{\frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial Y}{\partial \theta}\right)+\frac{1}{\sin \theta^{2}} \frac{\partial^{2} Y}{\partial \phi^{2}}\right\}=-l(l+1) \end{array}$$注意这里的\(l(l+1) \)和\( -l(l+1) \)都是事后才知道可以写成相邻两个整数的乘积，这里假装我们已经知道了；严格来讲等式右边应该是两个常数，而且是复数域的。
角动量方程(任何球对称问题都适用)
前面推导的\( \displaystyle\frac{1}{Y}\left\{\frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial Y}{\partial \theta}\right)+\frac{1}{\sin \theta^{2}} \frac{\partial^{2} Y}{\partial \phi^{2}}\right\}=-l(l+1) \)对任何球对称的问题都成立，也就是说不仅适用这里求解薛定谔方程，其他涉及到球对称的电磁学(电动力学)、流体力学等问题都用的是相同的公式，因为这里不涉及势场的任何问题，描述的仅仅是球对称的一般特性，\( Y(\theta, \phi) \)也叫作球谐函数。方程两边乘以\( Y \sin ^{2} \theta\)，得到$$\sin \theta \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial Y}{\partial \theta}\right)+\frac{\partial^{2} Y}{\partial \phi^{2}}=-l(l+1) \sin ^{2} \theta Y$$然后继续分离变量\( \mathrm{Y}(\theta, \phi)=\Theta(\theta) \Phi(\phi) \)(这已经是第三次分离变量了)，等式两边同时除以\( \Theta \Phi \)得到$$\left\{\frac{1}{\Theta}\left[\sin \theta \frac{d}{d \theta}\left(\sin \theta \frac{d \Theta}{d \theta}\right)\right]+l(l+1) \sin \theta^{2}\right\}+\frac{1}{\Phi} \frac{\mathrm{d}^{2} \Phi}{\mathrm{d} \phi^{2}}=0$$左侧第一项仅仅是\( \theta\)的函数，而第二项仅仅是\( \phi \)的函数，要想等式相等，这两项必须都等于常数，而且两个常数互为相反数，我们称它为分离常数“\( m^{2} \)”。因此有$$\begin{array}{c} \displaystyle\frac{1}{\Theta}\left[\sin \theta \frac{d}{d \theta}\left(\sin \theta \frac{d \Theta}{d \theta}\right)\right]+l(l+1) \sin \theta^{2}=m^{2} \\ \displaystyle\frac{1}{\Phi} \frac{d^{2} \Phi}{d \phi^{2}}=-m^{2} \end{array}$$(1) 关于\( \phi\)的方程
第二个式子看起来是弹簧振子模型的微分方程，但问题是这里的\( m\)我们并没有限定它必须是实数，换句话说可能为复数(当然求解之后我们发现确实是实数)，我们将解函数表述为复指数的形式$$\Phi(\phi)=e^{i m \phi}$$而周期性边界条件(转一圈回到自己)要求$$\Phi(\phi+2 \pi)=\Phi(\phi)$$即\( \exp [i m(\phi+2 \pi)]=\exp (i m \phi)\)，于是求得$$m=0,\pm 1,\pm 2, \dots$$
注：
对于弹簧振子模型\( y^{\prime \prime}+\omega_{n}^{2} y=0 \)，方程的解除了用正余弦函数线性组合\(y_{n}=C_{1} \cos \left(\omega_{n} t\right)+C_{2} \sin \left(\omega_{n} t\right) \)，还可以用两个指数项线性组合(线性组合的系数很可能是复数)\(y_{n}=c_{1} e^{i \omega_{n} t}+c_{2} e^{-i \omega_{n} t} \)。上面关于\( \Phi(\phi) \)的方程也是两个解\( \exp (i m \phi)\)和\(\exp (-i m \phi) \)的线性组合，但是我们只选了一个\( \exp (i m \phi)\)，主要是因为负的也包含在里面了，至于前面的系数，我们把它融合到\(\Theta \)中了。电动力学中也有类似\( \frac{1}{\Phi} \frac{d^{2} \Phi}{d \phi^{2}}=-m^{2} \)的方程，那个时候是用正余弦表示函数的解，因为那个时候电势一定是实数，所以可以这样求解。量子力学则没有这种约束，所以写成更一般的指数形式。
(2) 关于\( \theta\)的方程$$\sin \theta \frac{d}{d \theta}\left(\sin \theta \frac{d \Theta}{d \theta}\right)+\left[l(l+1) \sin ^{2}\theta-m^{2}\right] \Theta=0$$令\( \cos \theta \equiv x\)，于是\( \sin ^{2} \theta=1-x^{2} \quad -\sin \theta d \theta=d x \)，那么原方程可以变化为(\( dx \)替换\( d \theta\)，那么所有\( \sin { \theta} \)的项都变成二次)$$\left(1-x^{2}\right) \frac{d}{d x}\left[\left(1-x^{2}\right) \frac{d f}{d x}\right]+\left[\left(l(l+1)\left(1-x^{2}\right)-m^{2}\right] f=0\right.$$这个式子就是associated Legendre equation(associatedpolynomials在于含有\(m^2 \)这一项)，中文叫作“伴随勒让德方程”。
下面先求解最简单的情况\( m=0 \)
上式变为$$\left(1-x^{2}\right) \frac{d}{d x}\left[\left(1-x^{2}\right) \frac{d f}{d x}\right]+l(l+1)\left(1-x^{2}\right) f=0$$把两个微分整合在一起，然后稍微化简得到(Legendre's differential equation)$$\left(1-x^{2}\right) \frac{d^{2} f}{d x^{2}}-2 x \frac{d f}{d x}+l(l+1) f=0$$令\( f(x)=\displaystyle\sum_{n=0}^{\infty} a_{n} x^{n} \)，那么$$ f^{\prime}(x)=\sum_{n=0}^{\infty} n a_{n} x^{n-1} \quad f^{\prime \prime}(x)=\sum_{n=0}^{\infty} n(n-1) a_{n} x^{n-2} $$将这三个式子带入后，然后将同样次幂的\( x \)项放在一起，重新整理，可以得到$$a_{n+2}=-\frac{(l-n)(l+n+1)}{(n+1)(n+2)} a_{n}$$对于\( n>>1 \)，会有\( a_{n+2}=a_{n} \)，显然当\( x=\pm 1\)的时候，\( f(x) \)有无穷项，那么最终会爆掉，因此\(\psi \) is not normalizable. 注意无论是\(n \)取奇数还是偶数都会有相同的结论。下面讨论\( f(x) \)不会爆掉的解：
(1) \( a_0 \)对应的偶序列是finite有限的，同时\(a_1=0 \);
(2) \( a_1 \)对应的奇序列是finite有限的，同时\(a_0=0 \)
要想满足上面奇序列或者欧序列有限的条件，那么必有\( l\)是一个非负整数，即让\( l-n=0\)时序列中止(如果采用\( (l+n+1)=0\)的条件，最终会得到相同的解\( f(x)\)，只是号码的定义不一样，我们只解\( l \)为非负整数的情况)。
(1) 对于\( l=0 \)则\( a_2=0\)，而且\( a_{1}=a_{3}=a_{5}=\dots=0 \)
因此\(P_{0}(x)=a_{0} \)，我们用\( P(x)\)替代\(f(x) \)
(2) 对于\( l =1\)则\(a_3=0 \)，而且\( a_{0}=0=a_{2}=a_{4}= \dots=0 \)
因此\( P_{1}(x)=a_{1} x \)
(3) 对于\( l =2 \)而且连\( a_{1}=a_{3}=a_{5}=\dots=0\)
得到\( a_{2}=-3a_{0} \)，\( a_{4}=0\)，因此\( P_2(x)=a_0(1-x^2) \)其中的常数\( a_0\)用归一化条件确定。
实际中，归一化得到的最终解可以写成$$P_{0}(x)=1\quad P_{1}(x)=x \quad P_{2}(x)=\frac { 1}{ 2 }(1-3x^2) \dots $$多项式呈现奇偶交替的特点。这就是“勒让德多项式”。注意这里的量子数\(l \)的取值为\( 0,\,1,\,2,\,3\dots \)，如果取负值，得到的是相同的解(波函数)。
注：
(1) 另一种证明
首先引出Rodrigues' formula，这是产生\( m=0 \)时\(P_{i}(x) \)的一个式子(不需要知道怎么来的，会用就行，它就是求解Legendre’s differential equation的结果)，$$P_{l}(x)=\frac{1}{2^{l} l !}\left(\frac{d}{d x}\right)^{l}\left(x^{2}-1\right)^{l}$$其中的\( \left(\frac{d}{d x}\right)^{l}\left(x^{2}-1\right)^{l} \)表示对\( \left(x^{2}-1\right)^{l}\)微分\( l\)次。
可以证明\( P_{l}(x) \)是方程\( \left(1-x^{2}\right) \frac{d}{d x}\left[\left(1-x^{2}\right) \frac{d f}{d x}\right]+l(l+1)\left(1-x^{2}\right) f=0 \)的解。令\( v=\left(x^{2}-1\right)^{l} \)，根据微分的二项式定理$$\left(\frac{d}{d x}\right)^{m}(u v)=\sum C_{m}^{n}\left(\frac{d}{d x}\right)^{n-m} u\left(\frac{d}{d x}\right)^{m} v$$带入就可证明。
(2) 当\(m=0 \)，对应的\( l=0\)，求得\( P_{0}(x)=1 \)为常数，因此此时的波函数的角度方向是完全球对称的。(其实就是化学中的\(s \)轨道电子)
下面讨论\( m\neq 0 \)的情况(基于\( m=0\)的结果来推导)
对于\( \left(1-x^{2}\right) \displaystyle\frac{d}{d x}\left[\left(1-x^{2}\right) \frac{d f}{d x}\right]+\left[\left(l(l+1)\left(1-x^{2}\right)-m^{2}\right] f=0\right. \)
令\(f(x)=\left(1-x^{2}\right)^{\left|\frac{m}{2}\right|} u(x) \)，带入上式会得到$$\left(1-x^{2}\right) u^{\prime \prime}-2(m+1) x u^{\prime}+[l(l+1)-m(m+1)] u=0$$整个式子再微分一次有$$\left(1-x^{2}\right)\left(u^{\prime}\right)^{\prime \prime}-2(m+2) x\left(u^{\prime}\right)^{\prime}+[\ell(l+1)-(m+1)(m+2)]\cdot(u)^{\prime}=0$$通过归纳法(多微分一次\( u \)，就让\( m\)加\( 1\))可知如果\( P_{l}(x)\) is a solution for \( m=0\)，那么\( P_{l}^{m}(x)\) is a solution for \( m =m \) 其中\( P_{l}^{m}(x)=\left(1-x^{2}\right)^{\left|\frac{m}{2}\right|}\left(\displaystyle\frac{d}{d x}\right)^{m} P_{l}(x)\)。这里的\(\left(\displaystyle\frac{d}{d x}\right)^{m} P_{l}(x) \)就是对\( u(x) \)微分\( m\)次(应该加绝对值符号，因为\( m\)可能为负)。\(P_{l}(x) \)就是我们上面提到的产生\(m=0 \)解的Rodrigues' formula。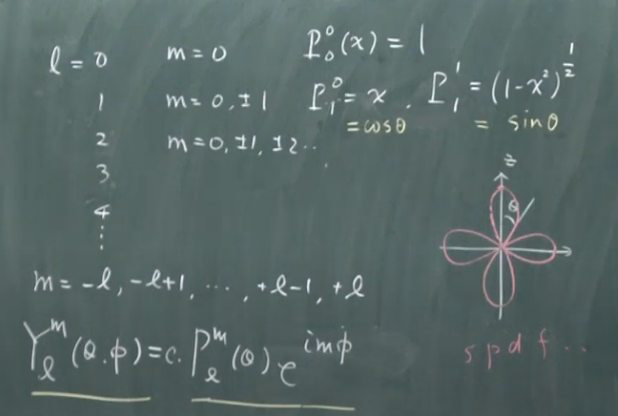
(1) \(P_{l}(x) \)中\( x \)的最高次数为\( l\)次
(2) 下面的常数\( c\)是用来归一化的常数
(3) \( P_{l}^{m}(x)\)中\( m\)的绝对值一定不大于\( l\)
(4) \(m=1 \)和\( m=-1 \)虽然得到相同的\( P_{l}^{m}(x)\)，但是\(e^{i m \phi} \)这一部分不同，因此最终的波函数也不同。(比如\( P_{1}^{1}\,\text{and}\,P_{1}^{-1}\))
(5) \( Y_{\ell}^{m}(\theta, \phi)=c \cdot P_{l}^{m}(\theta) e^{i m \phi}\)
(6) 这是\( P_{1}^{0}=x= \cos \theta \)的图像，因为复指数项目共轭相乘为1，而\( \cos \theta \)共轭相乘就是平方。躺着的就是\( P_{1}^{1}=\sin \theta \)对应的波函数。
上面只是求解角度方向上的波函数，没有确定径向，但是已经可以给出波的分布空间，但是在各处波函数出现的几率大小还没有确定(具体来说，比如电子出现的概率大小)，需要通过求解径向函数来确定。
球谐函数的正交性$$\int_{0}^{2 \pi} \int_{0}^{\pi}\left[Y_{l}^{m}(\theta, \phi)\right]^{*}\left[Y_{l^{\prime}}^{m^{\prime}}(\theta, \phi)\right] \sin \theta d \theta d \phi=\delta_{l l^{\prime}} \delta_{m m^{\prime}} $$即$$\left\langle\ell^{\prime}, m^{\prime} | \ell, m\right\rangle=\delta_{l l^{\prime}} \delta_{m m^{\prime}}$$首先证明\( m \neq m^{\prime} \)的情况$$\int_{0}^{2 \pi} e^{-i m^{\prime} \phi} e^{i m \phi} d \phi=\left.\frac{1}{i\left(m-m^{\prime}\right)} e^{i(m-m^{\prime}) \phi}\right|_{0}^{2\pi}=0$$接下来证明当\(m=m^{\prime} \)，但\( l \neq l^{\prime} \)时，同样正交。其实就是证明$$\int_{0}^{\pi} P_{l^{\prime}}^{m}(\theta) P_{l}^{m}(\theta) \sin \theta d \theta=0$$这里的证明比较复杂省略。
求无线深球势阱的径向函数
无线深球势阱的条件为$$V(r)=\left\{\begin{array}{ll} 0, & r<a \\ \infty, & r>a \end{array}\right.$$求解之前谈一下球对称波函数的归一化条件，求坐标系的体积微元为$$d^{3} \mathbf{r}=r^{2} \sin \theta d r d \theta d \phi$$所以归一化方程为$$\int|\psi|^{2} r^{2} \sin \theta d r d \theta d \phi=\int|R|^{2} r^{2} d r \int|Y|^{2} \sin \theta d \theta d \phi=1$$对\( R \)和\( Y\)分别归一化得到$$\int_{0}^{\infty}|R|^{2} r^{2} d r=1 \quad \text { 和 } \int_{0}^{2 \pi} \int_{0}^{\pi}|Y|^{2} \sin \theta d \theta d \phi=1$$径向方程$$\frac{d}{d r}\left(r^{2} \frac{d R}{d r}\right)-\frac{2 m r^{2}}{\hbar^{2}}[V(r)-E] R=l(l+1) R$$变量代换令\( u(r) \equiv r R(r) \)，则有$$R=u / r, \quad d R / d r=[r(d u / d r)-u] / r^{2}, \quad(d / d r)\left[r^{2}(d R / d r)\right]=r d^{2} u / d r^{2}$$于是$$-\frac{\hbar^{2}}{2 m} \frac{d^{2} u}{d r^{2}}+\left[V+\frac{\hbar^{2}}{2 m} \frac{l(l+1)}{r^{2}}\right] u=E u$$这个在形式上和一维薛定谔方程是一样的，只是等效势为$$V_{e f f}=V+\frac{\hbar^{2}}{2 m} \frac{l(l+1)}{r^{2}}$$第二项为离心项，使粒子有向外的倾向。另外归一化条件变为$$\int_{0}^{\infty}|u|^{2} d r=1$$在势阱里面$$\frac{d^{2} u}{d r^{2}}=\left[\frac{l(l+1)}{r^{2}}-k^{2}\right] u$$其中\(k \equiv \displaystyle\frac{\sqrt{2 m E}}{\hbar} \)。
下面分两种情况讨论：
(1) \( l=0\)，于是$$\frac{d^{2} u}{d r^{2}}=-k^{2} u \Rightarrow u(r)=A \sin (k r)+B \cos (k r)$$实际的径向波函数\( R(r)=u(r) / r\)，所以当\(r \)趋近于零时\( [\cos (k r)] / r \)趋于无穷大，因此必有\(B=0 \)，边界条件要求\( \sin (k a)=0\)，因此$$E_{n 0}=\frac{n^{2} \pi^{2} \hbar^{2}}{2 m a^{2}}, \quad(n=1,2,3, \ldots .)$$归一化\( u(r) \)得到\(A=\sqrt{2 / a} \)，于是$$R(r)=\sqrt{\frac{2}{a}} \frac{\sin \left(\frac{n \pi r}{a}\right)}{r}$$取个\( m=l=0\)的特例有波函数为$$\psi_{n 00}=R(r) Y_{0}^{0}(\theta, \phi)=\sqrt{\frac{2}{a}} \frac{\sin \left(\frac{n \pi r}{a}\right) * \frac{1}{\sqrt{4 \pi}}}{r}=\frac{1}{\sqrt{2 a \pi}} \frac{\sin (n \pi r / a)}{r}$$
(2) \( l\)是一个正整数，解函数为$$u(r)=\operatorname{Arj}_{l}(k r)+B r n_{l}(k r)$$其中\( j_{l}(x)\)是\( l\)阶的球贝塞尔函数，\( n_{l}(x) \)是\( l \)阶的诺依曼函数。$$j_{l}(x) \equiv(-x)^{l}\left(\frac{1}{x} \frac{d}{d x}\right) \frac{\sin x}{x} ; \quad n_{l}(x) \equiv-(-x)^{l}\left(\frac{1}{x} \frac{d}{d x}\right) \frac{\cos x}{x}$$
显然对于\( n_{l}(x)\)来说，当\(x \)趋近于零的时候，为无穷大，故\( B=0 \)，即$$u(r)=\operatorname{Arj}_{l}(k r) \quad R(r)=A j_{l}(k r)$$边界条件\(R(a)=0 \)，因此\( k \)必须满足\( j_{l}(k a)=0 \)，即\( (k a) \)是第\( l\)阶球Bessel函数的零点，而这种函数虽然也像正余弦函数一样振荡，但是其零点只能通过数值方法求解，即不能写出零解的表达式。令\( \beta_{n l}\)为\( l\)阶球Bessel函数的第\( n\)个零点，那么根据边界要求有$$k=\frac{1}{a} \beta_{n l}$$允许的能量值为$$E_{n l}=\frac{\hbar^{2}}{2 m a^{2}} \beta_{n l}^{2}$$径向函数为$$\left[\begin{array}{l} u(r)=\operatorname{Arj_l}(k r) \\ u(r) \equiv r R(r) \end{array} \Rightarrow R(r)=A j_{l}(k r) \Rightarrow R(r)=A j_{l}\left(\frac{\beta_{n l} r}{a}\right)\right.$$最终的波函数为$$\psi_{n l m}(r, \theta, \phi)=A_{n l} j_{l}\left(\beta_{n l} r / a\right) Y_{l}^{m}(\theta, \phi)$$常数\( A_{n l} \)是由归一化条件确定的。
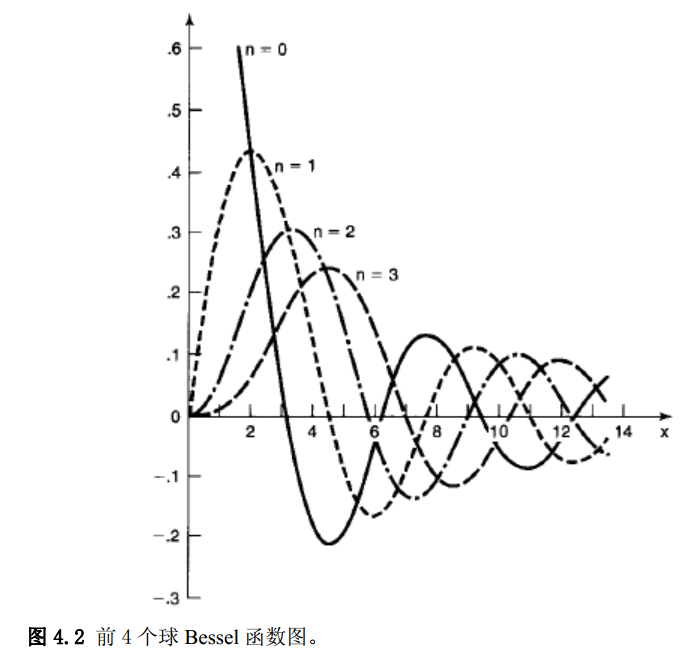
讨论：
(1) 因为Bessel函数不可能出现相同的零点，即任意\( \beta_{n l} \)只能表示唯一的\( l \)阶函数的第\( n \)个零点。所以能量\( E_{n l} \)不会重复。
(2) 能量只由径向函数决定，即径向部分确定了\( n\)和\(l \)的取值；角度部分根据\(l \)的取值可以取对应的几种\(m \)值，但是只是角度旋转的作用，不改变能量。
(3) 每个能级都是\( (2 l+1) \)重简并的，因为每个\(l \)值，都有\( (2 l+1) \)个不同的\( m \)值。比如\( \psi_{211}\)、\( \psi_{21-1}\)和\( \psi_{210}\)的能量都是\( E_{21} \)。
(4) 要比较\( E_{23} \)和\( E_{32}\)要由图中看出来，或者说数值解出来，否则不能直接比较出大小。
(5) 化学中sp杂化以及chemcial-bond其实都是特定波函数的线性组合。
(6) 角动量\( \mathbf{L}=\mathbf{r} \times \mathbf{p}=\mathbf{r} \times(m \mathbf{v})\)，如果不考虑方向，那么\( L= mvr\)(其中\( v \)是垂直径向的速度)。那么转动动能$$E_{\text {rotation}}=\frac { L^2}{ 2m } =\frac{1}{2} m v^{2}$$但是对这里的球对称量子力学模型中，角动量为\( L^{2}=\ell(l+1) \hbar^{2}\)，因此\( \displaystyle\frac{\hbar^{2}}{2 m} \displaystyle\frac{l(l+1)}{r^{2}}\)这一项其实是转动动能，只是这里写在的势能项里面，和传统的势能一起组合成\(V_{eff } \)。
氢原子
有确定的势函数\(V(r)=-\displaystyle\frac{1}{4 \pi \epsilon_{0}} \displaystyle\frac{e^{2}}{r} \)(类氢原子都很类似，如果有两个电子，就是三体问题，不能有解析解，只能数值求解)，于是径向方程为(注意：\( u(r) \equiv r R(r) \))$$-\frac{\hbar^{2}}{2 m} \frac{d^{2} u}{d r^{2}}+\left[-\frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{1}{r}+\frac{\hbar^{2}}{2 m} \frac{l(l+1)}{r^{2}}\right] u=u E$$对于束缚态电子，能量\( E<0\)，令\( \kappa \equiv \displaystyle\frac{\sqrt{-2 m E}}{\hbar} \)，径向方程化为$$\frac{1}{\kappa^{2}} \frac{d^{2} u}{d r^{2}}=\left[1-\frac{m e^{2}}{2 \pi \varepsilon_{0} \hbar^{2} \kappa} \frac{1}{(\kappa r)}+\frac{l(l+1)}{(\kappa r)^{2}}\right] u$$引入\( \rho \equiv \kappa r\)和\( \rho_{0} \equiv \displaystyle\frac{m e^{2}}{2 \pi \varepsilon_{0} \hbar^{2} \kappa}\)，于是$$\frac{d^{2} u}{d \rho^{2}}=\left[1-\frac{\rho_{0}}{\rho}+\frac{l(l+1)}{\rho^{2}}\right] u$$
考察渐进形式的解：
(1) 当\( \rho \rightarrow \infty \)时，方程变为$$\frac{d^{2} u}{d \rho^{2}}=u $$一般解为\(u(\rho)=A e^{-\rho}+B e^{\rho} \)，因为\( \rho\)是正数，为了防止波函数爆掉，因此\( B=0 \)，即$$u(\rho) \sim A e^{-\rho}$$
(2) 当\( \rho \rightarrow 0 \)时，离心项起主要作用，近似方程为$$\frac{d^{2} u}{d \rho^{2}}=\frac{l(l+1)}{\rho^{2}} u$$一般解为(知道答案就行)$$u(\rho)=C \rho^{l+1}+D \rho^{-l}$$为了防止波函数爆掉，最终结果为$$u(\rho) \sim C \rho^{l+1}$$
(3) 分离出渐近形式，引入新的函数\(v(\rho) \)$$u(\rho)=\rho^{l+1} e^{-\rho} v(\rho)$$对\( \rho \)进行二次微分(比较耗时麻烦)，带入原来的径向方程，整理得到$$2(l+1-\rho) \frac{d v}{d \rho}+\rho \frac{d^{2} v}{d \rho^{2}}+\left[\rho_{0}-2(l+1)\right] v=0$$令\( v(\rho)=\displaystyle\sum_{j=0}^{\infty} c_{j} \rho^{j} \)于是一阶导数$$\frac{d v}{d \rho}=\sum_{j=0}^{\infty} j c_{j} \rho^{j-1}=\sum_{j=0}^{\infty}(j+1) c_{j+1} \rho^{j}$$二阶导数$$\frac{d^{2} v}{d \rho^{2}}=\sum_{j=0}^{\infty} j(j+1) c_{j+1} \rho^{j-1}$$结果带入先前的方程$$\begin{array}{l}
\displaystyle\sum_{j=0}^{\infty} j(j+1) c_{j+1} \rho^{j}+2(l+1) \sum_{j=0}^{\infty}(j+1) c_{j+1} \rho^{j} \\
\quad-2 \sum_{j=0}^{\infty} j c_{j} \rho^{j}+\left[\rho_{0}-2(l+1)\right] \displaystyle\sum_{j=0}^{\infty} c_{j} \rho^{j}=0
\end{array}$$同幂次的合并一下$$j(j+1) c_{j+1}+2(l+1)(j+1) c_{j+1}-2 j c_{j}+\left[\rho_{0}-2(l+1)\right] c_{j}=0$$于是递归公式$$c_{j+1}=\left\{\frac{2(j+l+1)-\rho_{0}}{(j+1)(j+2 l+2)}\right\} c_{j}$$当\( j \)很大时，递推公式为$$c_{j+1} \cong \frac{2 j}{(j+1) j} c_{j}=\frac{2}{j+1} c_{j}$$假定这个式子严格成立，那么$$c_{j}=\frac{2^{j}}{j !} c_{0}$$则$$v(\rho)=c_{0} \sum_{j=0}^{\infty} \frac{2^{j}}{j !} \rho^{j}=c_{0} e^{2 \rho}$$从而$$u(\rho)=c_{0} \rho^{l+1} e^{\rho}$$显然当\( \rho \)很大时爆掉。因此\( c_j \)必须在某一项终止(\( \rho_0\)被quantize，即能量\( E\)被quantize)。对某个最大的整数\( j_{\max }\)，必有$$c_{\left(j_{\max }+1\right)}=0$$因此$$2\left(j_{\max }+l+1\right)-\rho_{0}=0$$定义主量子数$$n \equiv j_{\max }+l+1$$于是\( \rho_{0}=2 n \)，而\( \rho_{0} \equiv \displaystyle\frac{m e^{2}}{2 \pi \varepsilon_{0} \hbar^{2} \kappa}\)，即\( \rho_{0} \)决定了\(\kappa \)，而\( \kappa \)决定了能量\( E \)，因此最终能量\( E \)也被quantize了。将\( \rho_{0}=2 n\)带入$$E=-\frac{\hbar^{2} \kappa^{2}}{2 m}=-\frac{m e^{4}}{8 \pi^{2} \varepsilon_{0}^{2} \hbar^{2} \rho_{0}^{2}}$$得到允许的能量值为$$E=-\left[\frac{m}{2 \hbar^{2}}\left(\frac{e^{2}}{4 \pi \varepsilon_{0}}\right)^{2}\right] \frac{1}{n^{2}}=\frac{E_{1}}{n^{2}}, \quad n=1,2,3, \ldots$$这就是著名的“波尔公式”。或者$$E=-13.6 \mathrm{eV} \cdot \frac{1}{n^{2}}$$
注：
(1)对于氢原子谱线，瑞士高中老师发现\( \lambda=C \displaystyle\frac{n^{2}}{n^{2}-2^{2}}\)，而Walther Ritz倒过来发现波长\(\displaystyle\frac{1}{\lambda}=R\left[\frac{1}{2^{2}}-\frac{1}{n^{2}}\right] \)(巴耳末系)。如果这里的\( \frac{1}{2^{2}} \)换成\( \frac{1}{1^{2}}\)，就是莱曼系，在紫外区。更比一般的氢原子光谱公式是里德伯公式\(\frac{1}{\lambda}=R\left(\frac{1}{n^{2}}-\frac{1}{n^{\prime 2}}\right) \)。
(2) 我们前面写的\( u(\rho)=c_{0} \rho^{l+1} e^{\rho} \)是针对\( c_j \)可以无限延续的情况，事实上是不可能的，所以其实这个等式是不成立的。我们研究\( u(\rho) \)还是得用\(u(\rho)=\rho^{l+1} e^{-\rho} v(\rho) \)。
由\( \rho_{0} \equiv \displaystyle\frac{m e^{2}}{2 \pi \varepsilon_{0} \hbar^{2} \kappa}\)和\(\rho_{0}=2 n \)得到\(\displaystyle\frac{m e^{2}}{2 \pi \varepsilon_{0} \hbar^{2} \kappa}=2n \)，因此$$\kappa=-\left(\frac{m e^{2}}{4 \pi \varepsilon_{0} \hbar^{2}}\right) \frac{1}{n}=\frac{1}{a n}$$其中的\( a\)为“波尔半径”$$a=\frac{4 \pi \varepsilon_{0} \hbar^{2}}{m e^{2}}=0.529 \times 10^{-10} \mathrm{m}$$而$$\rho=\frac{r}{a n}$$氢原子的空间波函数用三个量子数\((n, l, m) \)来表示$$\psi_{n l m}(r, \theta, \phi)=R_{n l}(r) Y_{l}^{m}(\theta, \phi)$$
注：氢原子很特殊，正好在可见光区有这么些谱线，而且恰好证实了这些量子数的存在。以后仪器更精密，发现谱线还可以再细分。
讨论具体波函数：
首先有\( n=l+j_{\max }+1 \)，那么
(1) \( n=1 \quad \Rightarrow \ell=0 \Rightarrow m=0\)，那么$$\begin{aligned} \psi_{100}(r, \theta \cdot \phi) &=R_{10}(r) Y_{0}^{0}(\theta, \phi) \\ &=\frac{1}{\sqrt{4 \pi}} R_{10}(r) \end{aligned}$$而$$C_{1}=\frac{2(0+0+1)-2}{(0+1)(0+0+2)} C_{0}=0$$所以\(v(\rho)=c_0 \)，因此$$u(\rho)=e^{-\rho} \rho^{l+1} v(\rho)=e^{-\rho} \cdot \rho \cdot c_0$$那么径向波函数为$$R_{10}(r)=\frac{u(\rho)}{r}=\frac{1}{r} \cdot e^{-\kappa r}(\kappa r) \cdot c_{0}=c_{0} e^{-\frac{r}{a}}$$所以最终结果为$$\psi_{100}(r, \theta \cdot \phi)=c_{0} e^{-\frac{r}{a}}$$平方一下就是径向分布的几率(\( 1s \) state)，是随着径向距离指数衰减，中间的(靠近正电)的地方电子云分布最密集。
(2) \( n=2 \quad \Rightarrow \ell=0 \Rightarrow m=0 \)
求解一通有\( R_{20}(r)=\displaystyle\frac{c_{0}}{2 a}\left(1-\frac{r}{2 a}\right) e^{-r / 2 a} \)
注：
(a) \( 2s \)电子的波函数(没平方)，平方之后，显然在\( r=2a \)处电子云密度为零。
(b) 对于\( ns \)电子，\(e^{-\frac{r}{na}} \)表明，\( n \)越大，衰减越慢，也就是说中心的分布密度和外围的分布密度差别不是很大，那么电子云就可以覆盖到更远的地方。电子云离原子核越远，能量越高，无穷远处能量取零，而最靠近中心(原子核)的\( 1s\)电子轨道能量最小。
(c) 同样的，\( n \)越大，\(e^{-\frac{r}{na}} \)前面的多项式次数更多，那么零点就更多。
(d) 求解时利用的公式\( P_{l}^{m}(x)=\left(1-x^{2}\right)^{\left|\frac{m |}{2}\right|}\left(\displaystyle\frac{d}{d x}\right)^{m} P_{l}(x)\) (\(m \)应该是绝对值阶微分)
(3) \( n=2 \quad \Rightarrow \ell=1 \Rightarrow m=0,\pm 1 \)
\( p_x\)(两个图的乘积)
\( p_y\)和\( p_z \)(二者的线性组合，欧拉展开)