参考1：固体物理导论  图床 Solid-state physics-img/
参考2：李威仪固体物理
参考3：复旦大学车静光教学网站
参考4：中科大王冠中教学网址
参考5：蔡家麒固体物理笔记
参考6：Ashcroft & Mermin《固体物理》笔记
固体物理研究方式的特点：近似模型  →  近似规律  →  修正模型 →  螺旋上升

金属自由电子气体模型

Drude模型

Drude(自由电子气)模型的基本假定:
(1)  独立电子近似：电子和电子之间无相互作用
(2)  自由电子近似：除碰撞的瞬间外，电子与离子无相互作用
(3)  弛豫时间近似：一给定电子在单位时间内受一次碰撞的几率为\( 1 / \tau \)，为泊松过程，\(dt\)时间内发生碰撞的概率为\(\displaystyle\frac{d t}{\tau}\)；换句话说，平均下来每隔\(  \tau\)时间碰撞一次，存活寿命\( \tau \)，然后马上再次投胎。

欧姆定律(李威仪chapter 23 )

自由电子在外场下的动力学方程

假定\(  t\)时刻电子的平均动量为\( \boldsymbol{p}(t)\)，经过\(  dt\)时间，电子没有受到碰撞的概率为\(1-d t / \tau  \)，这部分电子对平均动量的贡献为\(  \boldsymbol{p}(t+d t)=\left(1-\displaystyle\frac{d t}{\tau}\right)[\boldsymbol{p}(t)+\boldsymbol{F}(t) d t]\)，其中\( \boldsymbol{F}(t) \)为\(  t\)时刻感受到的作用力。涉及到\(  (d t)^{2}\)的高阶小量可以忽略，那么在一级近似的条件下有：$$\frac{d \boldsymbol{p}(t)}{\mathrm{d} t}=\boldsymbol{F}(t)-\frac{\boldsymbol{p}(t)}{\tau}$$进一步改写有$$m \frac{d \boldsymbol{v}(t)}{d t}=\boldsymbol{F}(t)-m \frac{\boldsymbol{v}(t)}{\tau}$$相当于在通常的运动方程中引入一个依赖于速度的阻尼项(我们先前学的弹簧-粘壶模型，粘壶造成的阻力也和速度大小成正比)。

散射图像

电子在电场作用下加速运动，经过过\(  \tau\)时间，和原子实发生了碰撞(散射)，速度瞬间归零，但是下一时刻由于热作用，还会瞬间获得一个“热运动速度”，同时开始在电场作用下慢慢加速(沿着导电方向)。在研究电子的平均运动时，前面的每个电子的热运动速度汇总之后为零，所以我们只需要讨论电场作用下的“漂移速度”，同时也即只考虑这个方向的动量。平衡时有\(  \displaystyle\frac {\mathrm{d} \boldsymbol{p}(t)  }{  dt}=0 \)，所以$$0=-\frac{\boldsymbol{p}(t)}{\tau}-e \boldsymbol{E} \Rightarrow \frac{m \boldsymbol{v}_{\text {漂移 }}}{\tau}=-e \boldsymbol{E}$$于是得到\(  \boldsymbol{v}_{\text {漂移 }}=-\displaystyle\frac{e \tau}{m} \boldsymbol{E}\)，这里其实也很好理解，漂移速度来源于电场对电子的加速作用，而加速的力和加速的时间都知道，所以平均下来的漂移速度很容易求出。电流密度(单位截面上的电流大小)\(  \boldsymbol{j}=-n e \boldsymbol{v}_{\text {漂移 }}\)，于是有\( \boldsymbol{j}=n e \displaystyle\frac{e \tau}{m} \boldsymbol{E} \)。先前我们已经知道欧姆定律的另一种形式为\( \boldsymbol{j}=\sigma \boldsymbol{E} \)，因此电导率为：$$\sigma=\frac{n e^{2} \tau}{m}$$由于电阻率非常方便测量，我们大部分时候都是用上面这个公式去求弛豫时间，于是也可以算出平均自由程，还可以用它去求霍尔效应系数，交流电阻等等问题。

自由电子气模型的失败之处：
(1)  电导率\( \sigma \)和温度的关系
根据前面的推导，我们知道单位体积的价电子密度、电子质量和电子带电量都不会变化，位移能让\( \sigma \)变化的就是弛豫时间\( \tau \)，而这个由等于平均自由程除以\(v_{\mathrm{RMS} }\)，\(v_{\mathrm{RMS}}=\left(3 {k} {T} / {m}\right)^{1 / 2}  \)，因此最终有\( \sigma \propto {T}^{-1 / 2} \)，但是实验测得\(\sigma \propto {T}^{-1}  \)。这里的RMS表示root mean square方均根。

(2)  比热容
上述模型得到的比热容为常数\( 3 / 2 R \)，实验测到的比热容和温度成正比\(  10^{-4} RT\)，而且比模型值小两个数量级。说明在该模型中，电子对热容的贡献被严重高估。

注：
1. 我们上面谈的平均动量\(  \boldsymbol{p}(t)\)，电子的速度可以分为由电场造成的漂移速度(沿着“导线”方向)和自由运动产生的速度(方向杂乱无章，和电场无关，是一种热运动)。后者为\(v_{\mathrm{RMS}}=(3 k T / m)^{1 / 2}\)注\((1 / 2 m \overline{v^{2}}=3 / 2 k T)\)。后者的大小远大于前者，但是平均之后的速度就“看不见”\( v_{\mathrm{RMS}} \)，只看得见电场漂移速度drift velocity \(   v_{d}\)。
2. 李威仪是通过微观电流圆柱体，得到\(  J = QNv_d\)。
3. 理想气体模型的假设：
(1) 气体分子本身不占有体积
(2) 气体分子持续以直线运动，并且与容器器壁间发生弹性碰撞，因而对器壁施加压强
(3)  气体分子间无作用力，亦即不吸引也不排斥
(4)  气体分子的平均能量与开尔文温度成正比
4. 拓展
(1) 什么是 Drude 模型？它在固体物理中的意义是什么？

索末菲模型

(1)  将自由电子用量子力学的观点来处理(电子气能量量子化&泡利不相容原理)
(2)  修正电子能量的分布函数(玻尔兹曼分布到费米狄拉克分布)

先看一维导体的情况：将电子看作自由电子放在一维无限深势阱中，电子的能量是会被量子化的，得到了一个量子数。
实际上对于金属导体来说，肯定是三维的情况: (得到了三个量子数，这部分在量子力学中也有笔记)，简单分析就知道\( \mathrm{E}_{0} \)是一个很小的值(主要是普朗克常数太小了)。

经典理论：电子可以占据相同的状态和能量，玻尔兹曼分布表明，绝对零度的时候，所有电子的能量都为零

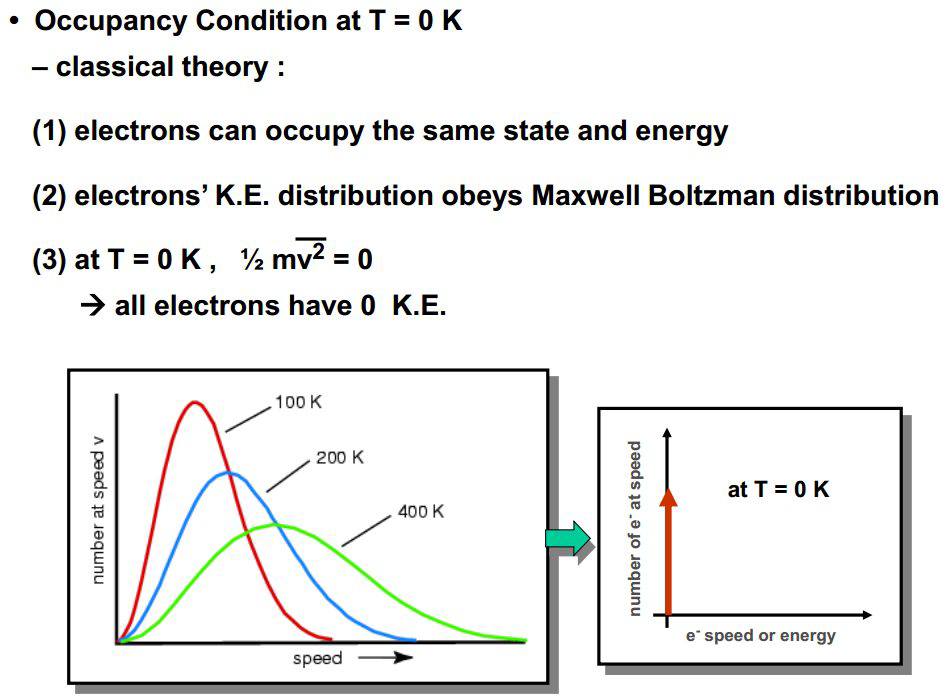引入量子力学的理论后：存在简并态(不同量子数，但是能量一样)，电子从低能级往上填充，\( T=0 \mathrm{K} \)时，填充的最后一个电子对应的能级(能填充的最高能级)即为费米能级。注意填充的能级是量子化的，\( E_0 \)非常小，所以相邻能级之间的距离其实非常近，以至于我们的仪器无法分辨，所以看起来似乎是“连续的”。李老师用“幼儿园抢马桶”来形象比喻。

下面问题来了：(1) 能填充到的最高能级，即费米能级的能量是多少？(2)  每增加一段能量范围，到底存在多少量子态？
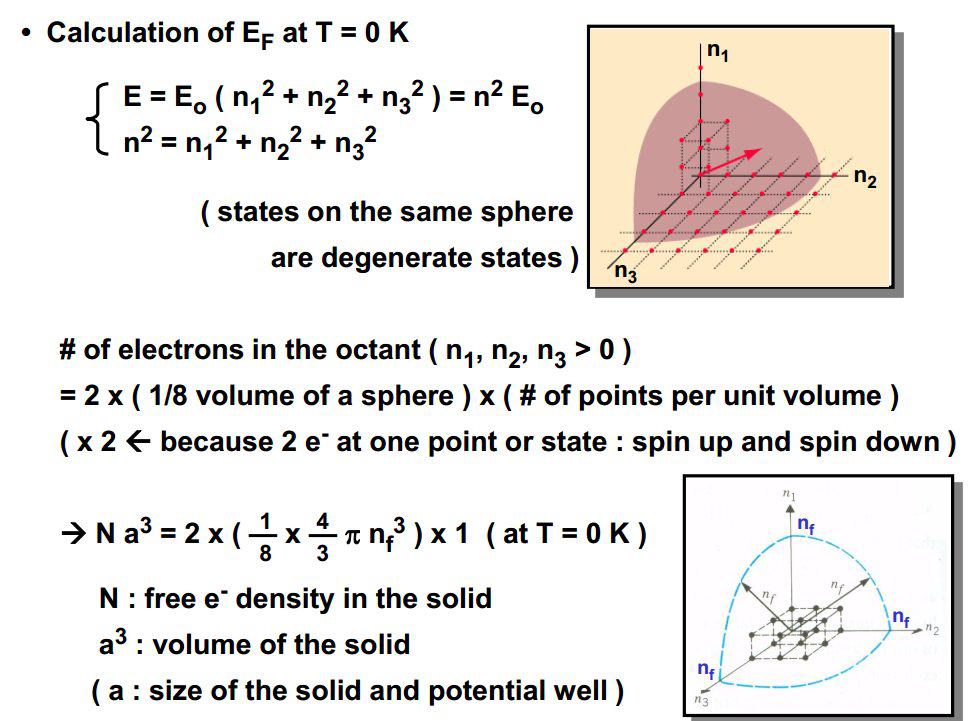
即有，对于金属导体而言，费米能级的大小只和自由电子密度有关，知道了自由电子密度，即可知道费米能级。上面计算铜的例子，古典模型中电子的平均能量应该是\(  3 / 2 kT\)。

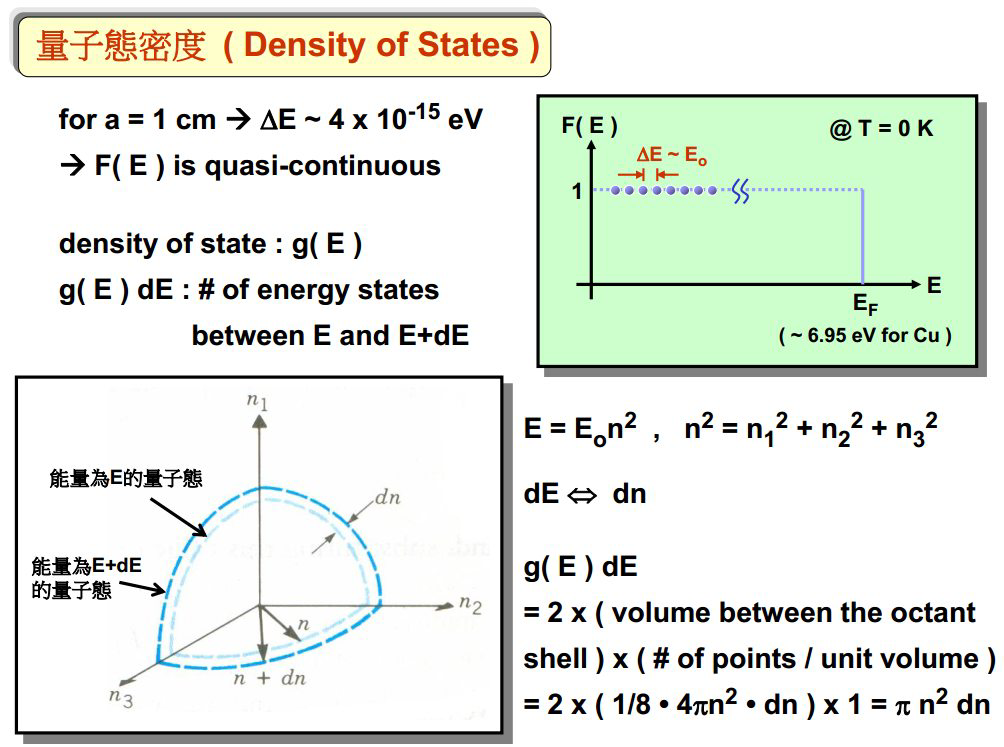
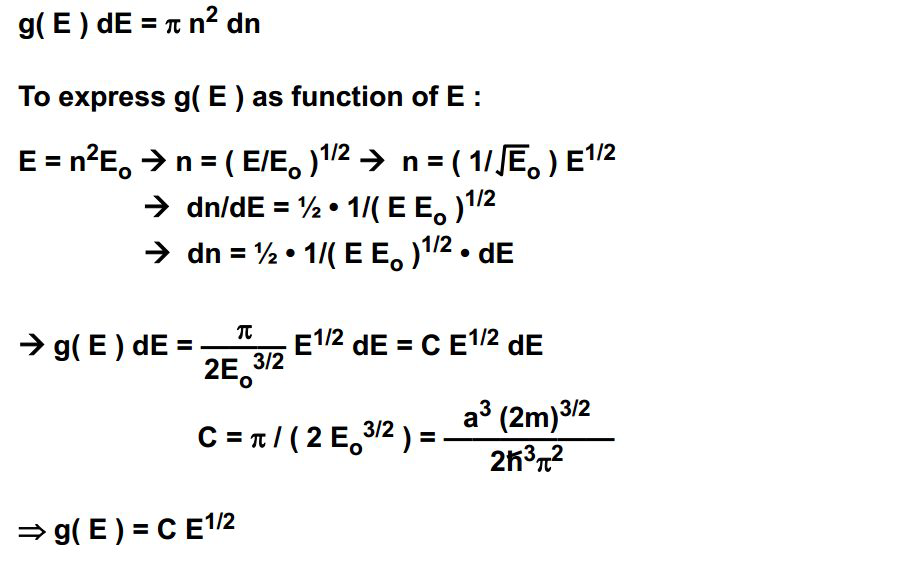
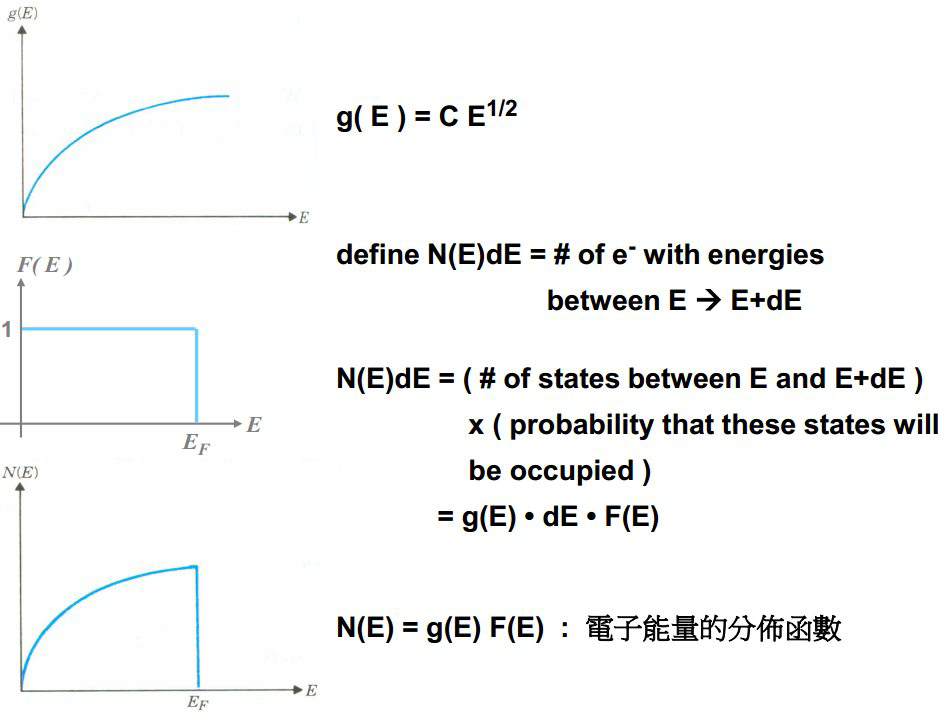
以上求解费米能级和态密度是李威仪老师的讲法，但是基尔和车老师都是采用“玻恩-冯·卡门边界条件”来求解，求解的方式还是很相似的。以下是推导求解过程：

Drude模型采用的是经典统计，在温度为\(  T\)的平衡态下是满足麦克斯韦-玻尔兹曼分布的\( f(E)=n\left(\displaystyle\frac{m}{2 \pi kT}\right)^{3 / 2} e^{-E / kT} \)。事实上，电子是费米子，满足的是费米-狄拉克统计分布：$$f(E)=\frac{1}{e^{\left(E-E_{F}\right) / k T}+1}$$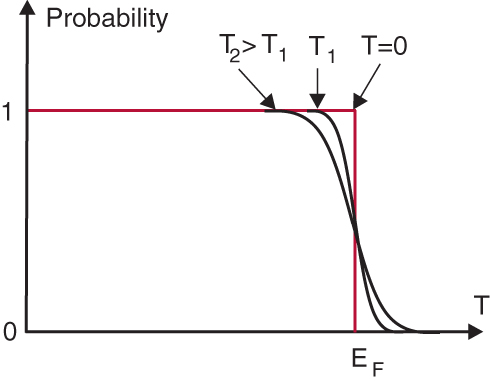上式描述的是在温度\(  T\)下，能量为\( E \)的状态被占据的几率，其中\(E_F  \)称为化学势，是温度的函数(李威仪说可以认为其不随温度变化)。温度为绝对零度时，电子所能占据的最高能级就是费米能级，此时的化学势 \(  E_F \)就是费米能级；在任意温度下，电子占据概率恰好为\(  50 \%\)的能级就是化学势(按照李的说法，也是费米能级)。

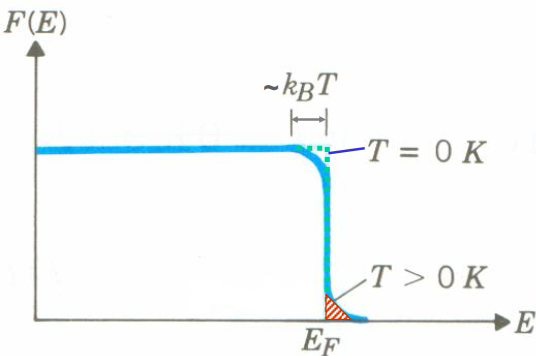
在零度时，电子都处于费米能级以下，随着温度的升高，某些稍微高于费米能级的位置将被占据，同时稍微低于费米能级的位置将空出来。事实上这部分变化的比例其实很小：$$\begin{array}{l}  E=E_{F}+2 k T \rightarrow F(E)=0.12  \\    E=E_{F}-2 k T \rightarrow F(E)=0.88\end{array} $$室温下的\(k T\)仅为\(  26 \mathbf{mA}\)，远小于\(  E_F\)。按照车/李老师的估算，只有\( k T / E_{F}  \)比例的电子发生了能级变化。电子被加热，不像经典粒子每个电子都能得到\(  kT\)的能量，而仅仅费米能级附近的电子被激发，所以Drude模型高估了对热容有贡献的电子数。\(  kT/ E_{F} \propto T\)正好也和实验结果热容和温度成正比对应上了。

参考和注释
1. 在室温下，化学势与费米能很接近，常把化学势也称为费米能。(阎守胜)
2. 知乎谁能通俗地讲述一下「费米能级」的概念
3. hyperphysics对于不同分布的形象解释
4. 硅火燎原》-10-费米能级
5. \(  E_{F}=T_{F} k\)中\( T_{F} \)为费米温度

自由电子气的其他性质

自由电子气模型的局限及修正

整数和分数化量子霍尔效应

晶体结构

原子的周期性阵列

半导体的性质依赖于基体材料的晶体结构，这是因为电子具有较短的波长，使其对样品中原子的周期性规则排布非常敏感。X射线的波长和晶体结构单元的长度相当，所以X射线可以作为“尺子”，通过衍射(其实也是干涉)来实现对晶体结构的探测。

一组不共面的平移矢量\(  \left(a_{1}, a_{2}, a_{3}\right)\)，那么\(  \boldsymbol{r}^{\prime}=\boldsymbol{r}+u_{1} \boldsymbol{a}_{1}+u_{2} \boldsymbol{a}_{2}+u_{3} \boldsymbol{a}_{3}\)的集合就定义了一个晶格(或称为“空间点阵”或者Bravias格子)，其中\( \boldsymbol{r} \)为晶格中观察点的位置(想作一个起始位置)。\(  \boldsymbol{a}_{i}\)为初基平移矢量/“基矢”(常用来定义晶轴)；\(  a_{1} \cdot a_{2} \times a_{3}\)为最小“晶胞”，就是基础“砌块”。

注：车老师的资料，\(  \mathbf{R}_{{i}}=l_{1} \mathbf{a}_{1}+l_{2} \mathbf{a}_{2}+l_{3} \mathbf{a}_{3}\)，那么\(\mathbf{a}_{i}  \)称为基矢，用整数\(l_{1}, l_{2}, l_{3}  \)和基矢组成的矢量称为“(正)格矢”。任何一个格矢可以由另外两个格矢来表示\( \mathbf{R}_{\mathbf{1}}=\mathbf{R}_{\mathbf{m}}+\mathbf{R}_{\mathbf{n}} \)。

晶体结构 = 晶格 + 结构基元(原胞)

结构基元可以是一个原子，也可以是多个。结构基元重复排列就构成了晶体。将结构基元数学抽象成几何上的点(得到格点)，那么这些格点的集合构成的就是晶格。晶格是晶体结构的数学表示；晶格中的每个格点代表基元，不要和代表原子的小球混淆。结构基元中，第\(  j\)个原子的中心位置相对于一个格点，可以用\( \boldsymbol{r}_{j}=x_{j} \boldsymbol{a}_{1}+y_{j} \boldsymbol{a}_{2}+z_{j} \boldsymbol{a}_{3} \)来表示，其中\( 0 \leqslant x_{j}, \quad y_{j}, \quad z_{j} \leqslant 1 \)(注意不要求是在整数)。

对于一个晶体来说，体积最小的基本结构单元(不一定是平行六面体，但我常取平行六面体)就是“原胞”，当然即使是平行六面体选取方式也不止一种(即不同的基矢下得到不同的原胞，但是体积都一样)，每一个原胞所占据的空间等于一个格点平均分配到的空间，即我们可以认为每个原胞中只包含一个格点。原胞通过平移操作即可构建出整个晶体。

既然点阵是等同点的集合，我们只要绘出一个点阵的最小周期单元（一个阵点及相应空间）即可，这个最小的周期重复单元称作点阵的原胞。(王冠中)

除了上述上述原胞的取法，还有一种不依赖于基矢的取法：维格纳－赛兹原胞，当然也只包含一个格点。倒格子中(晶格可称为正格子)，与W-S原胞对应的称为布里渊区，构造方法与W-S原胞相同。

晶体中任何一个原子的位置，都可以用格矢和原胞内原子位置矢量表示。

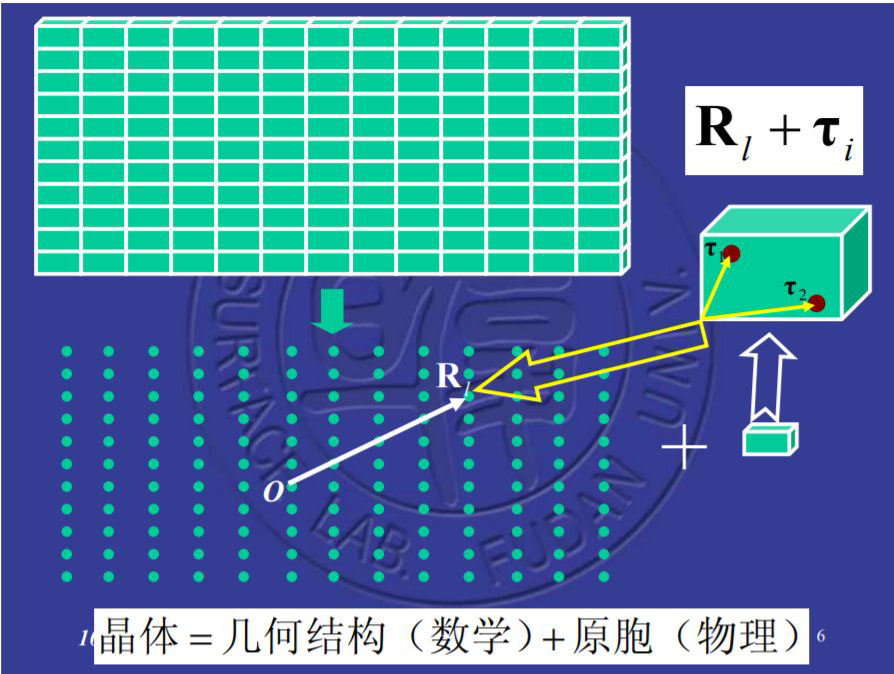
知识总结：

• 点阵和晶胞对比：点阵单位和晶胞都是用来描述晶体周期性结构的。点阵是抽象的，只反映晶体结构周期重复的方式；晶胞是按晶体实际情况(反映了周期性)划分出来的，它包含原子在空间的排布等内容。
• 晶胞参数 = 点阵参数，通过在空间点阵中选取三个不互相平行的单位矢量，它们的长度及相应的夹角称为点阵参数或晶胞参数。

考资料：
1. 科学网：晶体学中几个基本概念的辨析
2. 知乎：《结构化学基础》，周公度 段连运，2008(推荐书籍)
3. 为什么晶体只有 230 种空间结构？-知乎

晶格的基本类型、晶面指数系统、简单晶体结构

可以参考车老师PPT或者北航固态物理
特别强调：晶面指的是格点所在平面。

倒格子和第一布里渊区

我们首先需要知道，什么是正格子(正空间)，什么是倒格子(倒空间)，二者是如何联系的。本科的时候老师水平有限，无法让学生理解，现在我自己的数学基础慢慢上来了，可以理一理了。

下面汇总一下各个思考的角度(来源知乎)：
1. 傅里叶变换都是\(  e^{i p q}\)的形式，其中\(p  \)和\(  q\)是共轭物理量(指在量子力学中其算符不对易的物理量，注意不是复数的共轭，量子力学是从分析力学而来的，所以可以将这一概念推广)。举个例子\(  [\hat{A}, \hat{B}] \neq 0\)，两个算符不对易，那么物理量\(  A\)和\( B \)就是共轭物理量。从量纲上来分析，显然指数上的\(  i p q\)必须是一个无量纲数，所以如果\( f(p) \)中的\(  p\)是时间，那么\(q  \)对应的量纲就是\(  \displaystyle\frac {  1}{\text {time} } \)，也就是频率的量纲。而如果\( f(p) \)中的\( p \)是坐标，那么\(  q\)就应该是\( \displaystyle\frac{1}{\text {length}} \)的量纲，也就是与波矢\( k \)的量纲相同，根据德布罗意波\(  p=\hbar k\)，其中\( \hbar \)是一个有量纲的常数，于是我们认为坐标空间傅里叶变换之后得到的波矢空间，也可以“认为是”动量空间(毕竟乘以一个常数就好了)。

2. 平面波的表达式\( e^{i(k x-\omega t)} \)，其中的频域空间(\( \omega \))和时域空间(\(t  \))之间是傅里叶变换，那么它们的隔壁，波矢空间(\( k \))和坐标空间(\(  x\))之间也是满足傅里叶变换。

3.   知乎: 倒格子的引入及其在晶体结构研究中的作用
知乎: 倒空间和动量空间

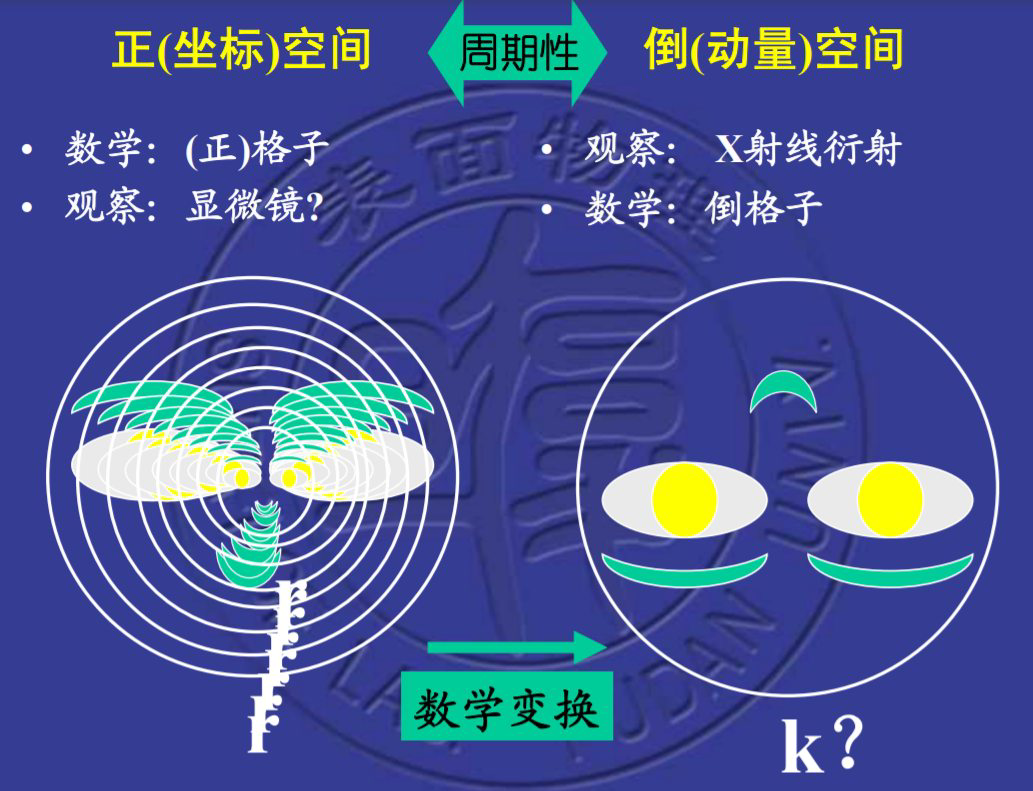(1)  坐标空间中用格矢\( \mathbf{R}_{l} \)来描写晶体的平移周期性，那么在动量空间呢？

势能、电荷密度等满足叠加原理的物理量：
\(  V(\mathbf{r})=\displaystyle\sum_{l} V_{\text {atom }}\left(\mathbf{r}-\mathbf{R}_{l}\right) \quad  \rho(\mathbf{r})=\displaystyle\sum_{l} \rho_{\text {atom }}\left(\mathbf{r}-\mathbf{R}_{l}\right) \quad F(\mathbf{r})=\displaystyle\sum_{l} f\left(\mathbf{r}-\mathbf{R}_{l}\right)\)
如果晶体具有平移周期性，则上述物理量都是\(\mathrm{R}_{l}  \)的周期函数：$$F\left(\mathbf{r}+\mathbf{R}_{l}\right)=F(\mathbf{r})$$对其进行傅里叶展开：$$F(\mathbf{r})=\sum_{h} F_{\mathbf{K}_{h}} e^{i \mathbf{K}_{h} \cdot \mathbf{r}}$$\(  e^{-i \mathbf{K}_{h} \cdot \mathbf{r}}\)称为傅里叶系数，上式两边乘以共轭因子\(e^{-i \mathbf{K}_{h} \cdot \mathbf{r}}  \)后积分可以得到这个系数：$$\begin{array}{l}   \displaystyle\frac{1}{V} \displaystyle\int F(\mathbf{r}) e^{-i \mathbf{K}_{h} \cdot \mathbf{r}} d \mathbf{r}=\sum_{h^{\prime}} F_{\mathbf{K}_{h^{\prime}}} \displaystyle\frac{1}{V} \displaystyle\int e^{i\left(\mathbf{K}_{h^{\prime}}-\mathbf{K}_{h}\right) \cdot \mathbf{r}} d \mathbf{r} \\ \displaystyle\frac{1}{V} \displaystyle\int F(\mathbf{r}) e^{-i \mathbf{K}_{h} \cdot \mathbf{r}} d \mathbf{r}=F_{\mathbf{K}_{h}}\end{array}$$仅当\( \mathbf{K}_{h^{\prime}}=\mathbf{K}_{h} \)时，上面的式子(顶上的)，这个积分不为零，且等于\(  V\)。

由周期性条件\(  F(\mathbf{r})=F\left(\mathbf{r}+\mathbf{R}_{l}\right)\)，即等式两端表示的波函数是重合的，那么对两侧分别做傅里叶变换，得到的波矢空间的函数也必然是相等的。注意类比时域/频域傅里叶变换的“时延性”\(  f(t \pm b) \leftrightarrow e^{\pm 2 \pi i s b} F(s)\)(\( 2 \pi \)是否要，看需求，可以融合进频率\(  s\)里面得到\(  \omega \))，设等式左边的傅里叶变换结果为\(F_{\mathbf{K}_{h}}  \)，那么右边傅里叶变换的结果为\(  F_{\mathbf{K}_{h}} e^{i \mathbf{K}_{h} \cdot \mathbf{R}_{l}}\)，根据前面的分析，二者相等，于是有\( F_{\mathbf{K}_{h}}=F_{\mathbf{K}_{h}} e^{i \mathbf{K}_{h} \cdot \mathbf{R}_{l}} \)，即：$$F_{\mathbf{K}_{h}}\left(1-e^{i \mathbf{K}_{h} \bullet \mathbf{R}_{l}}\right)=0$$\(  F_{\mathbf{K}_{h}} \neq 0\)，所以只可能\( e^{i \mathbf{K}_{h} \cdot \mathbf{R}_{l}}=1 \)，即有\(  \mathbf{K}_{h} \bullet \mathbf{R}_{l}=2 \pi m\)，\(  m\)为整数。

总结一下，如果有平移周期性，那么一定在傅里叶空间存在\( \mathbf{K}_{h} \)矢量满足\(\mathbf{K}_{h} \bullet \mathbf{R}_{l}=2 \pi m  \)。

(2)  \( \mathbf{K}_{h} \)矢量有什么物理含义?

傅里叶变换的笔记中(山函数)那一节，我们谈到“离散对周期，周期对离散。时域如果是离散的，频域就是周期的；如果频域离散，时域就要周期。如果时域既是离散又是周期，那么频域也既是离散又是周期。” 这对我们的晶格来说当然也适用，即由于我们的晶格是离散的点组成的同时也具有周期性，那么必然其傅里叶变换之后的波矢空间也是既离散又周期。下面用车老师的PPT具体谈谈这个问题。

我们可以用\(  \delta\)函数来描写格点\(  \rho(\mathbf{r})=\displaystyle\sum_{\mathbf{R}_{l}} \delta\left(\mathbf{r}-\mathbf{R}_{l}\right)\)，这是周期函数，因此可以对其进行傅里叶变换$$\rho_{\mathbf{k}}=\int \rho(\mathbf{r}) e^{-i \mathbf{k} \cdot \mathbf{r}} d \mathbf{r}=\sum_{\mathbf{R}_{l}} \int \delta\left(\mathbf{r}-\mathbf{R}_{l}\right) e^{-i \mathbf{k} \cdot \mathbf{r}} d \mathbf{r}=\sum_{\mathbf{R}_{l}} e^{-i \mathbf{k} \cdot \mathbf{R}_{l}}$$格点满足平移周期性，即\( \mathbf{K}_{h} \bullet \mathbf{R}_{l}=2 \pi m \)，那么乘上不变因子有$$\rho_{\mathbf{k}}=\sum_{\mathbf{R}_{l}} e^{-i\left(\mathbf{k}-\mathbf{K}_{h}\right) \cdot \mathbf{R}_{l}}$$利用泊松求和公式即可得$$\rho_{\mathbf{k}}=\sum_{\mathbf{R}_{l}} e^{-i\left(\mathbf{k}-\mathbf{K}_{h}\right) \cdot \mathbf{R}_{l}}=\sum_{\mathbf{K}_{h}} \delta\left(\mathbf{k}-\mathbf{K}_{h}\right)$$

即当矢量\( \mathbf{K}_{h}\)与\(  \mathbf{R}_{l} \)乘积是\( 2 \pi \)的整数倍时，在坐标空间\( \mathbf{R}_{l} \)处的\( \delta  \)函数的傅里叶变换为在动量空间以\(  \mathbf{K}_{\mathbf{h}}\)为中心的\( \delta \)函数！

这告诉了我们什么信息，\( \mathbf{K}_{h} \)对应什么？
1. 坐标空间里，\( \delta(\mathbf{r}-\mathbf{R}_{l})  \)函数表示在\(  \mathbf{R}_{l} \)的格点，当满足上述条件时，其傅里叶变换也是\(\mathbf{k}-\mathbf{K}_{h}\)函数，表示坐标空间几何点的傅里叶变换也是几何点！
2.  或者说前面\(  \mathbf{K}_{h} \)与\(\mathbf{R}_{l}   \)的关系定义了倒空间矢量，\( \mathbf{K}_{h} \)的量纲为\(  \mathbf{R}_{l}\)的倒数。

(3)  在正空间中，格矢\(  \)端点(格点)的集合就是格子，那么，矢量\( \mathbf{K}_{h} \)端点的集合是什么呢？

倒格子

倒格子定义：对布拉菲格子中所有的格矢\( \mathbf{R}_{l}  \)，有一系列动量空间矢量\(\mathbf{K}_{h}\)，满足\( e^{i \mathbf{K}_{h} \cdot \mathbf{R}_{l}}=1 \)和\(  \mathbf{K}_{h} \cdot \mathbf{R}_{l}=2 \pi m\)(\(m  \)为整数)的全部端点\( \mathbf{K}_{h} \)的集合，构成该布拉菲格子的倒格子，这些点称为倒格点，\(  \mathbf{K}_{h}\)称为倒格矢。

布拉菲格子也称为正格子；我们知道了倒格子或正格子中的任意一个，就可以推出另一个；正格子和倒格子满足傅里叶变换关系，所以倒空间也称为傅里叶空间。

倒格子基矢：对正格子\(  \mathbf{R}_{l}=l_{1} \mathbf{a}_{1}+l_{2} \mathbf{a}_{2}+l_{3} \mathbf{a}_{3}\)，根据正倒格子的关系，有$$\mathbf{K}_{h} \cdot \mathbf{R}_{l}=l_{1} \mathbf{K}_{h} \cdot \mathbf{a}_{1}+l_{2} \mathbf{K}_{h} \cdot \mathbf{a}_{2}+l_{3} \mathbf{K}_{h} \cdot \mathbf{a}_{3}=2 \pi m$$如果选择一组\( \mathbf{b} \)，使得\(  \mathbf{b}_{i} \cdot \mathbf{a}_{j}=2 \pi \delta_{i j}\)，那么矢量\( \mathbf{K}_{h}\)就可以由\( \mathbf{b} \)组成$$\mathbf{K}_{h}=h_{1} \mathbf{b}_{1}+h_{2} \mathbf{b}_{2}+h_{3} \mathbf{b}_{3}$$这就定义了倒格子基矢，它可以满足正、倒格矢之间的\( \mathbf{K}\cdot \mathbf{R}=2\pi m \)的关系。这样形式上就与正格矢一样，\( \mathbf{K}_{h} \)也具有平移对称性，即可用基矢\(  \mathbf{b}_{i}\)和整数来表示平移周期性。

(4)  \( \mathbf{b}_{i} \cdot \mathbf{a}_{j}=2 \pi \delta_{i j} \)表示什么？

是正交关系! 这里面的\(  \delta_{i j}\)表示克罗内可德尔塔，我们在量子力学中见过，所以\(  \mathbf{b}_{1}\)与\( \mathbf{a}_{1} \)和\( \mathbf{a}_{2} \)同时正交，即\(  \mathbf{b}_{1}\)垂直于\( \mathbf{a}_{1} \)和\( \mathbf{a}_{2} \)确定的平面，或者说\(  \mathbf{b}_{1} \)平行于\(  \mathbf{a}_{2} \times \mathbf{a}_{3}\)。可以设$$\mathbf{b}_{1}=\eta\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)$$而正交关系有\( \mathbf{a}_{1} \bullet \mathbf{b}_{1}=\eta \mathbf{a}_{1} \cdot\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)=2 \pi \)，因此(\(  \Omega\)就是正格子原胞的体积)$$\eta=\frac{2 \pi}{\mathbf{a}_{1} \cdot\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)}=\frac{2 \pi}{\Omega} \quad \mathbf{b}_{1}=\frac{2 \pi}{\Omega}\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right) \quad \Omega=\left|\mathbf{a}_{1} \cdot\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)\right|$$

(5)  总结一下倒格子？

• \(  \mathbf{K}_{h}\)的端点构成倒空间中的布拉菲格子
• 倒格矢\(\mathbf{K}_{h}=h_{1} \mathbf{b}_{1}+h_{2} \mathbf{b}_{2}+h_{3} \mathbf{b}_{3}  \)
• 满足平移对称性\( \mathbf{K}_{h}=\mathbf{K}_{h^{\prime}}+\mathbf{K}_{h^{\prime \prime}} \)
• 倒格子原胞体积是正格子原胞体积的导数\(  \Omega^{*}=\left|\mathbf{b}_{1} \cdot\left(\mathbf{b}_{2} \times \mathbf{b}_{3}\right)\right|=\displaystyle\frac{(2 \pi)^{3}}{\Omega}\)   (注：这里的\( 2 \pi \)是因为我们选择倒空间的时候，是以“角频率”，而不是以频率作为倒格子波矢，那样的话，就没有体积关系中的\(  (2 \pi)^{3}\))。

晶体结构衍射理论和实验观测

固体结合

Bloch(布洛赫)定理

思考：

• 周期性势场中运动的电子波应该具有什么形式？
• 这样形式的波函数意味着什么？
• 离子实为什么好像对电子没有作用？

能带理论是固体物理最核心的内容，而布洛赫定理是能带理论的基础。它解释了电子自由程很长的问题！但是未对金属、绝缘体做出解释(这一部分由Wilson完成，但是基础是布洛赫定理)

空晶格模型

能带结构解读

近自由电子近似

 

超导

 

Cooper pair

How can electrons form pairs while they should be repelling each other? Indeed, electrons are electrically negative, and two negative  charges repel each other. Cooper gives the following explanation:

At a low temperature, when an electron moves, it slightly attracts the surrounding atoms. The reason is that the electron has a negative electric charge and the atoms a positive one, since the latter is missing one of its electrons (we should say "positive ions" rather than "atoms"). A negative charge attracts a positive charge. If a second electron appears at that moment, it experiences two atoms at a closer range than usual for a short period of time, and it will be pulled between them. Two atoms closer together create a more electricly positive zone, thus being more attractive to the electron. The second electron naturally follows the first due to the oscillation of atoms. This is called "attraction via network vibrations" (or "phonons").

At high temperatures, atoms vibrate more and the path of the first electron is obscured preventing the second electron from following it and forming a Cooper pair. This is why conventional superconductivity only happens at very low temperatures.