• Math 21b Spring 2018

• 特征向量和特征值的应用-油管

 

正交矩阵和施密特正交化

正交矩阵及其性质

【标准正交】(Orthonormal vectors)：满足如下条件的向量 \(\mathbf{q}_{1} ， \mathbf{q}_{2} \ldots \ldots \mathbf{q}_{n}\) 标准正交 : $$ \mathbf{q}_{i}^{\mathrm{T}} \mathbf{q}_{j}= \begin{cases}0 & \text { if } i \neq j \\ 1 & \text { if } i=j\end{cases} $$标准正交向量是线性无关的，很多线性代数的计算都建立在标准正交的基础上，可以将一些复杂问题简化，降低运算律。

比如如果\( \boldsymbol{Q}\)的列向量为标准正交向量(\(\boldsymbol{Q} \)不一定是方阵)，那么\(\boldsymbol{Q}^{\mathrm{T}} \boldsymbol{Q}=\boldsymbol{I}\)单位阵。
对于投影矩阵\( \boldsymbol{P}=\boldsymbol{Q}\left(\boldsymbol{Q}^{\mathrm{T} } \boldsymbol{Q}) ^{-1}\boldsymbol{Q}^{\mathrm{T} }\right.\)分两种情况讨论：
(1) \(\boldsymbol{Q} \)不是方阵，那么\( \boldsymbol{P}=\boldsymbol{Q}\boldsymbol{Q}^{\mathrm{T} }\)；
(2) \(\boldsymbol{Q} \)是方阵，那么投影矩阵就是单位阵\( \boldsymbol{P}=\boldsymbol{I}\)，因为\(\boldsymbol{Q} \)的列向量张成了整个空间，所以投影过程不会对向量有任何改变(已经在空间内，再往该空间投影，投影前后向量不变)。

Recall：我们先前提到的最小二乘法求解，将\(\boldsymbol{A} \mathbf{x}=\mathbf{b}\)转化为求解\(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} \hat{\mathbf{x}}=\boldsymbol{A}^{\mathrm{T}} \mathbf{b}\)，如果\(\boldsymbol{A}\)的列向量都是标准正交，那么\(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}=\boldsymbol{I}\)，于是我们要求解的问题变为了\( \hat{\mathbf{x}}=\boldsymbol{A}^{\mathrm{T} }\mathbf{b}\)。此处的\( \boldsymbol{A}\)和上面讨论的\( \boldsymbol{Q}\)是一个东西。

【(标准)正交矩阵】(orthogonal matrix)：标准正交的方阵即为正交矩阵。比如$$ \boldsymbol{Q}=\left[\begin{array}{lll} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] \quad \boldsymbol{Q}^{\boldsymbol{\mathrm{T}}}=\left[\begin{array}{lll} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array}\right] $$上面两个置换矩阵都是正交矩阵，并且二者的乘积为单位阵。

再比如\(\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right]\)为正交矩阵，但是\(\left[\begin{array}{rr}1 & 1 \\ 1 & -1\end{array}\right]\)不是正交矩阵，因为没有归一化。

再比如\(\displaystyle\frac{1}{2}\left[\begin{array}{rrrr}1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1\end{array}\right]\)这个矩阵叫作【Hadamard矩阵】，是由\( -1\)和\(1\)组成的正交矩阵，不同阶数的矩阵性质不同且没有规律，无从判断几阶的阿达玛矩阵为正交矩阵。

长方形矩阵\(\displaystyle\frac{1}{3}\left[\begin{array}{rr}1 & -2 \\ 2 & -1 \\ 2 & 2\end{array}\right]\)的列向量标准正交，我们可以将其拓展为正交矩阵\(\displaystyle\frac{1}{3}\left[\begin{array}{rrr}1 & -2 & 2 \\ 2 & -1 & -2 \\ 2 & 2 & 1\end{array}\right]\)

正交矩阵的性质：

• \(\boldsymbol{Q}^{\mathrm{T}} \boldsymbol{Q}=\boldsymbol{I}\)，\(\boldsymbol{Q}^\mathrm{T}=\boldsymbol{Q}^{-1}\)，最典型的比如置换矩阵；
• 行列式的值必为\(+1\) 或 \(-1\)；
  • 为\(+1\)时，称为特殊正交矩阵，即【旋转矩阵】；
  • 为\(-1\)时，称为【瑕旋转矩阵】(improper rotation matrix)，即旋转+镜射。从化学结构对称性的角度看，就是\(S_n\) symmetry，即\(S_{n}=\) rotation of \(360^{\circ} / n+\) perpendicular mirror reflection。我理解的话，此时的正交矩阵等于纯旋转矩阵乘以一个纯镜射矩阵，而这里的纯旋转矩阵、镜射矩阵也都是正交矩阵。更具体的例子，比如将unchanged point放在三维坐标原点，那么沿着\(Z\)轴旋转\(\varphi\)，然后做\(x-y\)面的反射，这样的旋转反射可以表示为矩阵$$ A=\left(\begin{array}{ccc} \cos \varphi & -\sin \varphi & 0 \\ \sin \varphi & \cos \varphi & 0 \\ 0 & 0 & -1 \end{array}\right) $$
    
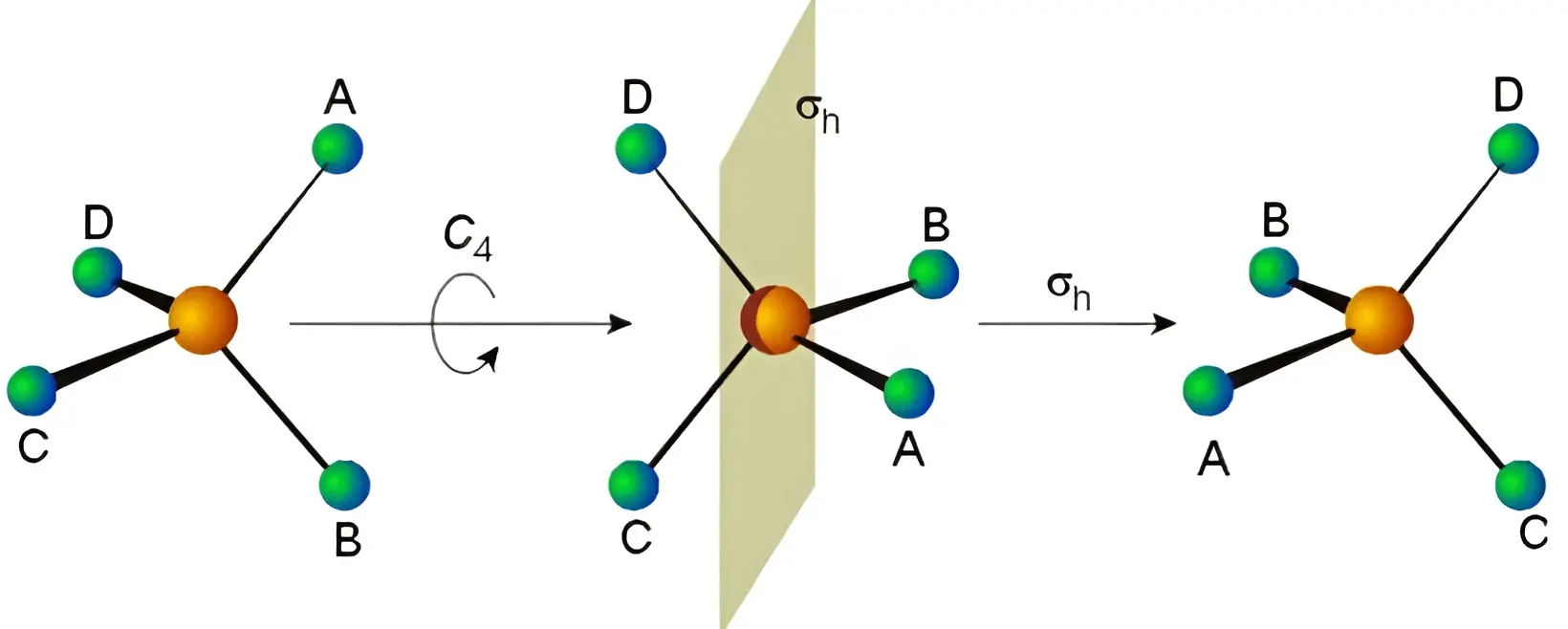
  • 注意，瑕旋转矩阵的旋转角度可能为零(360度)，那么此时瑕旋转矩阵等同于【镜射矩阵】。
• 作为一个线性变换，是【保距映射】，具体例子为旋转与镜射，此处是指欧式距离。
• 正交矩阵乘一个向量的结果是：把这个向量反射到某个平面并且/或者旋转它，不会改变向量的长度。
• 复特征值模长必为\(1\)。

正交矩阵与群：

xx补充

正交矩阵与矩阵分解：

• SVD分解中，两次旋转操作，都对应正交矩阵。
  
• 补充xxxx

 

Gram–Schmidt process

【格拉姆-施密特正交化】：两个线性无关的向量\( \mathbf{a}\)和\( \mathbf{b}\)它们张成了一个向量空间，我们现在要做的是找到两个标准正交的向量\( \mathbf{q_{1}}\)和\( \mathbf{q_{2}}\)使它们张成的空间和先前的空间一样。

施密特的贡献：如果我们有一组正交基\( \mathbf{a}\)和\( \mathbf{b}\)，那么我们让它们除以各自的模长，得到的就是标准正交基。$$\mathbf{q}_{1}=\frac{\mathbf{a}}{||\mathbf{a}||}, \mathbf{q}_{2}=\frac{\mathbf{b}}{||\mathbf{b}||}$$格拉姆的贡献：

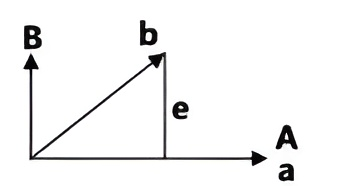
将\( \mathbf{a}\)和\( \mathbf{b}\)转化成相互垂直的\( \mathbf{A}\)和\( \mathbf{B}\)(前者\(\mathbf{A}=\mathbf{a}\)，变化后者)，$$\mathbf{B}=\mathbf{b}-\mathbf{p}=\mathbf{b}-\frac{\mathbf{A^\mathrm{T} } \mathbf{b}}{\mathbf{A^T} \mathbf{A}} \mathbf{A}$$ 等式两端同时乘以\( \mathbf{A^{T}}\)可以得到\( \mathbf{A}^{\mathrm{T} } \mathbf{B}=0\)。这里的\(\mathbf{A} \)和\( \mathbf{B}\)都是一维(列)向量，但是不限制\(  \mathbf{R}^n\)中的\(  n\)，即不限制每个向量中包含的元素个数。

如果多出来一个线性无关的向量\( \mathbf{c}\)，我们可以通过\( \mathbf{c}\)中减去其在\( \mathbf{A}\)和\( \mathbf{B}\)两个方向的投影来得到\( \mathbf{C}\)。$$\mathbf{C}=\mathbf{c}-\frac{\mathbf{A}^{\mathrm{T}} \mathbf{c}}{\mathbf{A}^{\mathrm{T}} \mathbf{A}} \mathbf{A}-\frac{\mathbf{B}^{\mathrm{T}} \mathbf{c}}{\mathbf{B}^{\mathrm{T}} \mathbf{B}} \mathbf{B}$$

注：正交化本质就是扣掉该向量在所有其他向量上的分量，这个分量可以通过投影矩阵的形式(最简单的形式，分母是数字，杀鸡用牛刀)，也可以直接想成向量内积的形式去计算。总而言之，扣除分量之后得到的新向量和其他向量张成空间垂直，或者说新向量与其他向量每一个都垂直。这样将每个向量都这样处理，然后归一化，即可得到正交化的向量组，即一组标准正交基。

例如 : \(\mathbf{a}=\left[\begin{array}{l}1 \\ 1 \\ 1\end{array}\right], \mathbf{b}=\left[\begin{array}{l}1 \\ 0 \\ 2\end{array}\right]\)，则有 \(\mathbf{A}=\mathbf{a}, \mathbf{B}=\left[\begin{array}{l}1 \\ 0 \\ 2\end{array}\right]-\displaystyle\frac{3}{3}\left[\begin{array}{l}1 \\ 1 \\ 1\end{array}\right]=\left[\begin{array}{c}0 \\ 1 \\ -1\end{array}\right]\)，验证计算得 \(\mathbf{A}^{\mathbf{T}} \mathbf{B}=0\)。写出 \(\boldsymbol{q}_{1}\)，\(\boldsymbol{q}_{2}\) 所组成的矩阵为：$$ \boldsymbol{Q}=\left[\begin{array}{ll} \mathbf{q}_{1} & \mathbf{q}_{2} \end{array}\right]=\left[\begin{array}{rr} 1 / \sqrt{3} & 0 \\ 1 / \sqrt{3} & -1 / \sqrt{2} \\ 1 / \sqrt{3} & 1 / \sqrt{2} \end{array}\right] $$\(\boldsymbol{Q}\)列向量的空间就是\( \mathbf{a}\)和\(\mathbf{b}\)张成的空间。 因此矩阵\(\boldsymbol{Q}\)和矩阵\(\left[\begin{array}{ll}1 & 1 \\ 1 & 0 \\ 1 & 2\end{array}\right]\)有相同的列空间。

QR分解

换一种思路理解线性无关向量的标准正交化
前面我们是用施密特正交化公式的方法来将多个线性无关的向量进行标准正交化(不改变列空间)，但是真正学习线性代数的可不喜欢这种方法。我们先前学习了\( \mathbf{A}=\mathbf{LU}\)分解，而在对\( \mathbf{A}\)做施密特正交化的过程可以用矩阵运算的方式表示为\( \mathbf{A}=\mathbf{Q R}\)，此处\(\mathbf{R} \)为上三角矩阵。上一问中，对\(\mathbf{A} \)其实进行的是列操作得到\(\mathbf{R}\)，同样地，如果对\( \mathbf{R}\)进行列操作也可以得到矩阵\( \mathbf{A}\)。$$\left[\begin{array}{cc} \mathbf{a}_{1} & \mathbf{a}_{2} \end{array}\right]=\left[\begin{array}{ll} \mathbf{q}_{1} & \mathbf{q}_{2} \end{array}\right]\left[\begin{array}{cc} \mathbf{a}_{1}^{\mathrm{T}} \mathbf{q}_{1} & \mathbf{a}_{2}^{\mathrm{T}} \mathbf{q}_{1} \\ \mathbf{a}_{1}^{\mathrm{T}} \mathbf{q}_{2} & \mathbf{a}_{2}^{\mathrm{T}} \mathbf{q}_{2} \end{array}\right]$$\( \mathbf{R}\)为上三角矩阵，\( \mathbf{a}_{1}^{\mathrm{T}} \mathbf{q}_{2}=0\)，因为\(\mathbf{a}_{1} \)和\( \mathbf{q}_{1}\)的方向一致，于是和\( \mathbf{q}_{2}\)正交。

采用\(\mathbf{QR} \)分解来帮助求解\( \mathbf{A} \mathbf{x}=\mathbf{b}\)的问题，最大的又是是提高了数值的稳定性。

 

 

行列式和代数余子式

行列式的初等性质
(1)  \(\operatorname{det}(I)=1\)，\(\left|\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right|=+1 \)

(2)  交换行列式的两行，得到的行列式值要变号。也就是说对于置换矩阵来说，如果行交换的总次数为偶数，那么最终不变号，如果行交换的总次数为奇数，那么行列式值就要变号。\(\left|\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right|=-1 \)

(3)
(3-a)如果在矩阵的一行乘以\(t\)，那么行列式的值就要乘以\(t\)。$$\left|\begin{array}{cc} t a & t b \\ c & d \end{array}\right|=\mathrm{t}\left|\begin{array}{ll} a & b \\ c & d \end{array}\right|$$
(3-b)  行列式是“行列式的行”的线性函数(每次只能在一行上做线性变换)$$\left|\begin{array}{cc} a+a^{\prime} & b+b^{\prime} \\ c & d \end{array}\right|=\left|\begin{array}{ll} a & b \\ c & d \end{array}\right|+\left|\begin{array}{ll} a^{\prime} & b^{\prime} \\ c & d \end{array}\right|$$行列式的推导性质(基于前面三条性质)
(4)  含有相同行的行列式值为\(0\)。从性质(2)推导而来，行交换，本来应该变号，但是实际是不变号的，唯一的可能就是行列式的值为\(0\)。
(5)  矩阵的\(k\)行减去第\(i\)行的倍数，并不改变行列式的值。换句话说，我们在用这个进行消元的时候，并不改变矩阵对应的行列式的值。
(6)  如果矩阵的某一行全部都是\(0\)，那么其行列式为\(0\)。在性质(3)a中取\(t=0\)即可证明。
(7)  三角阵的行列式的值等于其对角线上的数值(主元)的乘积。$$\left|\begin{array}{ccccc} d_{1} & * & * & \dots & * \\ 0 & d_{2} & * & \dots & * \\ 0 & 0 & \ddots & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & \cdots & \cdots & d_{n} \end{array}\right|=\left|\begin{array}{ccccc} d_{1} & 0 & 0 & \cdots & 0 \\ 0 & d_{2} & 0 & \cdots & 0 \\ 0 & 0 & \ddots & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & \cdots & \cdots & d_{n} \end{array}\right|=d_{1} d_{2} \cdots d_{n}\left|\begin{array}{cccccc} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & \ddots & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & \cdots & \cdots & 1 \end{array}\right|=d_{1} d_{2} \cdots d_{n}$$ 证明：消元不改变行列式值(性质5)+性质3(a)。
(8)  当且仅当矩阵\( A\)为奇异矩阵时，其行列式为\( 0\)。
我们先前理解的奇异矩阵就是消元操作之后，会有某一行全为零，于是行列式肯定等于零；另一方面，如果不是奇异矩阵，那么按照性质\( 7\)的变换(不会出现全为零的行)，我们得到的行列式的值肯定不是零。
(9)   \(\operatorname{det}(\boldsymbol{A} \boldsymbol{B})=\operatorname{det}(\boldsymbol{A}) \operatorname{det}(\boldsymbol{B}) \)尽管矩阵的和的行列式不等于行列式的和，但是矩阵乘积的行列式等于矩阵行列式的乘积。

如果\(A \)是可逆矩阵，那么\(\operatorname{det}\left(\boldsymbol{A}^{-1}\right)=\displaystyle\frac{1}{\operatorname{det}(\boldsymbol{A})} \)，此外\( \operatorname{det}\left(A^{2}\right)=\operatorname{det}(A)^{2}\)，\( \operatorname{det}(2 A)=2^{n} \operatorname{det}(A)\)，类似三维体积问题，每一个维度上翻倍，那么新的体积是原有体积的\(2^{3}=8 \)倍。
(10)  \(\operatorname{det}\left(\boldsymbol{A}^{\mathrm{T}}\right)=\operatorname{det}(\boldsymbol{A}) \)   主要是利用\(A=L U \)分解，而\(L \)和\( U\)都是三角阵，利用性质\( 7\)。

计算机计算行列式的方法：并不是按照显示的方式计算的，而是消元转化为三角阵，然后将主元相乘。例如(不考虑\(a=0 \))$$\left[ \begin{array}{ll} a & b \\ c & d \end{array} \right] \rightarrow \left[ \begin{array}{ll} a & b \\ 0 & d-\frac { c }{ a } \end{array} \right] \quad \Rightarrow \left| \begin{array}{ll} a & b \\ c & d \end{array} \right| =a\left( d-\frac { c }{ a } b \right) =ad-bc$$

 

推导行列式的计算方法(推导)
计算方法是基于前面性质的推论，特别是前三条性质。对于二阶矩阵$$\begin{aligned} \left|\begin{array}{lll} a & b \\ c & d \end{array}\right| &=\left|\begin{array}{ll} a & 0 \\ c & d \end{array}\right|+\left|\begin{array}{ll} 0 & b \\ c & d \end{array}\right| \\ &=\left|\begin{array}{ll} a & 0 \\ c & 0 \end{array}\right|+\left|\begin{array}{ll} a & 0 \\ 0 & d \end{array}\right|+\left|\begin{array}{ll} 0 & b \\ c & 0 \end{array}\right|+\left|\begin{array}{ll} 0 & b \\ 0 & d \end{array}\right| \\ &=0+a d-c b+0 \\ &=a d-b c \end{aligned}$$对于三阶矩阵$$\begin{aligned} \left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{22} \\ a_{31} & a_{32} & a_{33} \end{array}\right| &=\left|\begin{array}{ccc} a_{11} & 0 & 0 \\ 0 & a_{22} & 0 \\ 0 & 0 & a_{33} \end{array}\right|+\left|\begin{array}{ccc} a_{11} & 0 & 0 \\ 0 & 0 & a_{23} \\ 0 & a_{22} & 0 \end{array}\right|+\left|\begin{array}{ccc} 0 & a_{12} & 0 \\ a_{21} & 0 & 0 \\ 0 & 0 & a_{33} \end{array}\right| \\ &+\left|\begin{array}{ccc} 0 & a_{12} & 0 \\ 0 & 0 & a_{22} \\ a_{31} & 0 & 0 \end{array}\right|+\left|\begin{array}{ccc} 0 & 0 & a_{13} \\ a_{21} & 0 & 0 \\ 0 & a_{22} & 0 \end{array}\right|+\left|\begin{array}{ccc} 0 & 0 & a_{13} \\ 0 & a_{22} & 0 \\ a_{31} & 0 & 0 \end{array}\right| \\ &=a_{11} a_{22} a_{33}-a_{11} a_{23} a_{33}-a_{12} a_{21} a_{33} \\ &+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-a_{13} a_{22} a_{31} \end{aligned}$$总之，总体的思路是先拆个稀巴烂，每次拆一行，总共拆\( n\)行，类似于\(n \)个循环嵌套，一层层剥离，就可以得到所有可能的\( n^{n}\)种情况。但是其中很多行列式的值为零，实际需要计算的量就会减少(计算\(n! \)个行列式即可)，这就要求不同行所取的元素的对应的列数不同(所在的列如果相同，那么通过性质\( 5\)，消元使得这一行的所有元素都为零，而消元不改变行列式大小，所以最终推出行列式等于零)。计算的时候，通过行交换都换成三角阵，那么根据前面性质七就很好算，但是要注意行交换了多少次(变号情况)。

代数余子式(cofactor formula)的应用
代数余子式是用较小的矩阵的行列式来写出\(n \)阶行列式的公式，有点降阶的意思。例子$$\begin{aligned} \operatorname{det}(\boldsymbol{A}) &=a_{11}\left(a_{22} a_{13}-a_{22} a_{12}\right)+a_{12}\left(-a_{21} a_{33}+a_{23} a_{31}\right)+a_{13}\left(a_{21} a_{32}-a_{22} a_{31}\right) \\ &=\left|\begin{array}{lll} a_{11} & 0 & 0 \\ 0 & a_{22} & a_{22} \\ 0 & a_{32} & a_{33} \end{array}\right|+\left|\begin{array}{lll} 0 & a_{12} & 0 \\ a_{21} & 0 & a_{22} \\ a_{31} & 0 & a_{33} \end{array}\right|+\left|\begin{array}{lll} 0 & 0 & a_{13} \\ a_{21} & a_{22} & 0 \\ a_{31} & a_{22} & 0 \end{array}\right| \end{aligned}$$需要注意的是符号的变化。对于二阶矩阵，我们同样可以采用相同的方法$$\left|\begin{array}{ll} a & b \\ c & d \end{array}\right|=a d+b(-c)$$代数余子式的核心是通过降阶来讲原来的行列式展开为更简单的行列式。

原矩阵去掉\(a_{i j} \)所在的行和列得到的\( n-1\)阶行列式叫作【余子式】，记为\(M_{i j} \)；记\(A_{i j}=(-1)^{i+j} M_{i j} \)，叫作元素\(a_{i j} \)的【代数余子式】。

【拉普拉斯展开】(Laplace expansion)：\(\operatorname{det}(A)=\displaystyle\sum_{j=1}^n(-1)^{i+j} M_{i, j} a_{i, j}\)

【伴随矩阵】(Adjugate matrix)
代数余子式\(A_{i j}\)组成的矩阵，然后进行转置得到的就是伴随矩阵。$$A^{*}=\left(\begin{array}{cccc} A_{11} & A_{21} & \cdots & A_{n 1} \\ A_{12} & A_{22} & \cdots & A_{n 2} \\ \cdots & \cdots & \cdots & \cdots \\ A_{1 n} & A_{2 n} & \cdots & A_{m n} \end{array}\right)=\left(A_{i j}\right)^{\mathrm{T}}$$伴随矩阵最大的用处是用来计算逆矩阵\(A^{-1}=\displaystyle\frac{1}{\operatorname{det}(A)} A^*\)

三种计算行列式值的方法的复杂程度：消元法 < 代数余子式 < 行列式展开

【三对角阵】
它除对角线和对角线两侧相邻的元素之外，其他元素全为零。比如计算由1组成的4阶三对角阵$$A_{4}=\left[\begin{array}{llll} 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 \end{array}\right]$$我们可以从1阶开始算起$$ \left|A_{1}\right|=1,\left|A_{2}\right|=\left|\begin{array}{ll} 1 & 1 \\ 1 & 1 \end{array}\right|=0,\left|A_{3}\right|=\left|\begin{array}{lll} 1 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{array}\right|=-1 $$ $$ \Rightarrow \quad\left|\boldsymbol{A}_{1}\right|=1\left|\begin{array}{lll} 1 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{array}\right|-1\left|\begin{array}{lll} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 1 & 1 \end{array}\right|=\left|\boldsymbol{A}_{3}\right|-1\left|\boldsymbol{A}_{2}\right|=-1 $$从矩阵的特殊结构我们可以知道\( |A_{n}|=\left|A_{n-1}\right|-1\left|A_{n-2}\right|\)。

由1组成的n阶级三对角阵的行列式从1阶开始按照1、0、-1、-1、0、1进行循环。

三对角线性方程组,对于熟悉数值分析的同学来说，并不陌生，它经常出现在微分方程的数值求解和三次样条函数的插值问题中，具体参考这里。

【柯西-比内公式】(Cauchy–Binet formula)：补充xx$$ \begin{aligned} &A=\left(\begin{array}{ccc} 1 & 1 & 2 \\ 3 & 1 & -1 \end{array}\right) \quad B=\left(\begin{array}{ll} 1 & 1 \\ 3 & 1 \\ 0 & 2 \end{array}\right)\\ &\operatorname{det}(A B)=\left|\begin{array}{cc} 1 & 1 \\ 3 & 1 \end{array}\right| \cdot\left|\begin{array}{cc} 1 & 1 \\ 3 & 1 \end{array}\right|+\left|\begin{array}{cc} 1 & 2 \\ 1 & -1 \end{array}\right| \cdot\left|\begin{array}{cc} 3 & 1 \\ 0 & 2 \end{array}\right|+\left|\begin{array}{cc} 1 & 2 \\ 3 & -1 \end{array}\right| \cdot\left|\begin{array}{cc} 1 & 1 \\ 0 & 2 \end{array}\right| \end{aligned} $$

 

 

克莱姆法则/逆矩阵/体积

二阶矩阵求逆矩阵的方法如下：$$\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]=\frac{1}{a d-b c}\left[\begin{array}{cc} d & -b \\ -c & a \end{array}\right]$$我们根据这样的特例，能否找到通行的求解任意阶矩阵的逆矩阵的方法。

求解逆矩阵的公式(formula for \( A^{-1}\))的通用办法
先给出答案(这里的\( A^{*} \)就是伴随矩阵，或者说\( \left(A_{i j}\right)^{\mathrm{T}} \))$$A^{-1}=\frac{1}{\operatorname{det}(A)} A^{*}$$我们知道$$A A^{*}=\left[\begin{array}{ccc} a_{11} & \dots & a_{1 n} \\ \vdots & \ddots & \vdots \\ a_{n 1} & \cdots & a_{m n} \end{array}\right]\left[\begin{array}{ccc} C_{11} & \dots & C_{n 1} \\ \vdots & \ddots & \vdots \\ C_{1 n} & \cdots & C_{m n} \end{array}\right]$$于是有$$AA^{*}=\left[\begin{array}{ccccc} \operatorname{det} A & 0 & 0 & \cdots & 0 \\ 0 & \operatorname{det} A & 0 & \cdots & 0 \\ 0 & 0 & \ddots & & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & \operatorname{det} A \end{array}\right]=\operatorname{det}(A) I$$我们很容易知道对角线上的元素都是\(\operatorname{det} A \)，但是如何理解非对角线上的元素都是零呢？

比如我们用\( A\)的第\( i\)行去乘伴随矩阵的第\( j\)列(其实就是矩阵\( A\)第\(j\)行的代数余子式)，可以看作将原行列式的第\(i \)行赋值给第\(j\)行，这样做的话不改变第\(j \)行的代数余子式，而新得到的行列式展开结果为零，因为行列式中存在相同的两行。

【克莱姆法则】(Cramer's rule for \( \mathbf{x}=\boldsymbol{A}^{-1} \mathbf{b}\))
如果\(A \)可逆，那么方程必然有解$$\mathbf{x}=\boldsymbol{A}^{-1} \mathbf{b}=\frac{1}{\operatorname{det}(\boldsymbol{A})} \boldsymbol{C}^{\mathrm{T}} \mathbf{b}$$我们可以这样思考$$\mathbf{x_{j}}=\frac{\operatorname{det}\left(\boldsymbol{B}_{j}\right)}{\operatorname{det}(\boldsymbol{A})}$$其中$$\boldsymbol{B}_{1}=\left[\begin{array}{ccccc} b_{1} & a_{12} & \cdots & \cdots & a_{1 n} \\ b_{2} & a_{22} & \cdots & \cdots & a_{2 n} \\ b_{3} & a_{32} & \ddots & & a_{3 n} \\ \vdots & & & \ddots & \vdots \\ b_{n} & a_{n 2} & \cdots & \cdots & a_{n n} \end{array}\right], \boldsymbol{B}_{n}=\left[\begin{array}{ccccc} a_{11} & \cdots & \cdots & a_{1 n-1} & b_{1} \\ a_{21} & \cdots & \cdots & a_{2 n-1} & b_{2} \\ \vdots & & \ddots & \vdots & \vdots \\ \vdots & & & a_{n-1 n-1} & b_{n-1} \\ a_{n 1} & a_{n 2} & \cdots & a_{n n-1} & b_{n} \end{array}\right]$$将矩阵\(B_{j} \)的行列式的数值从第\( j\)列用代数余子式展开计算，正好是伴随矩阵\(A^{*}\)的第\( j\)行和向量\(\mathbf{b} \)点积的结果。这里我们用到了性质\( 10，\) \(\operatorname{det}\left(\boldsymbol{A}^{\mathrm{T}}\right)=\operatorname{det}(\boldsymbol{A}) \)。

注：
(1) 相比消元法，这种克莱姆法则的计算效率更低。
(2) 克莱姆法则的应用实例见维基百科，可以更好地帮助理解。

矩阵行列式和体积的关系
以三阶为例，\( |\operatorname{det}(\mathbf{A})|=\text { volume of box }\)。行列式的绝对值就是平行六面体的体积，行列式的正负对应左手系和右手系。

(1) 如果矩阵\( A\)是单位矩阵，那么就像性质1说的，行列式等于1，体积也是1。
(2)如果矩阵\( A\)是正交矩阵，那么其构成也是三个相互垂直且长度为1的正方体，体积同样等于行列式的值的绝对值。
(3)交换矩阵的行，不会改变体积，因为行列式只是变号，绝对值是不变的，这对应于性质2。
(4)对于长方体，将其中一条边的长度翻倍，那么体积翻倍，正好对应于性质3a。
(5) 对于二阶行列式，其行列式的绝对值就是对应的平行四边形的体积。其二分之一，就是对应三角形的面积。考虑不过原点的情况$$\frac{1}{2}\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|$$可以这样思考，第三列的代数余子式展开，可以得到过原点的大三角形面积减去过原点的两个小三角形的面积。
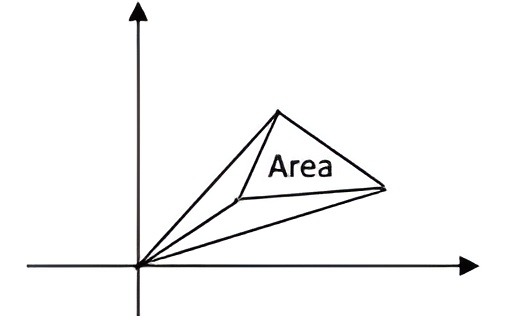行列式是将矩阵的信息压缩成一个数，可以将“体积”视为它压缩后给出的信息。更多几何意义参见书籍。(参考线性代数的几何意义)

 

特征值和特征向量

$$A \mathbf{x}=\lambda \mathbf{x}$$矩阵\(A \)相当于算符，作用于输入函数\( \mathbf{x}\)，得到输出\(\lambda \mathbf{x} \)。特征向量即在特定的向量\( \mathbf{x}\)方向上输出的\( A \mathbf{x}\)与\(\mathbf{x} \)平行；特征值\(\lambda\)就是缩放因子。

如果\( A\)是不可逆矩阵，那么\(0\)一定是其特征值之一，即$$A \mathbf{x}=0 \mathbf{x}=0$$特征值\( 0\)对应的特征向量张成了矩阵\( A\)的零空间。

• 一般定义里面特征向量不能是零向量；
• 【特征子空间】：属于\(  \lambda_i\)的全体特征向量与零向量构成的集合，有的地方也叫【特征空间】；
• 【主特征向量】：特征值最大的特征向量；
• 【谱】：矩阵特征值的集合；
• 【迹】(trace)：对于\( n \times n\)矩阵\(A \)，它具有\( n\)个特征值(包含重复的特征值)，并且它们的和等于矩阵对角线上元素的和，这个数值称为矩阵的迹。

 

常见矩阵的特征值/向量

(1)【投影矩阵】
如果矩阵\( P\)是朝向某平面的投影矩阵，那么对于该平面内的向量\(\mathbf{x} \)，有\(P \mathbf{x} =\mathbf{x}\)，也就是是说\( 1\)是矩阵\(P \)的特征值，对应的特征向量张成了投影矩阵\(P \)对应的投影平面(空间)，或者说投影矩阵的行空间。

        另一方面，对于垂直于该空间的向量\(\mathbf{x} \)，显然，经过投影矩阵\(P \)的作用后得到的是零向量，也就是说\( P \mathbf{x}=0 \mathbf{x}=0\)，于是特征值\(0\)对应于该特征向量\( \mathbf{x}\)。所有满足要求的特征向量构成的是投影矩阵的零空间。

        上面的投影空间和零空间，也就是两类特征向量各自张成的空间，这两个空间相互垂直。总而言之，投影矩阵\(P \)的特征向量张成了整个左侧空间(四个子空间的正交关系图)，由于投影矩阵是对称阵，所以左侧空间和右侧空间相同。

(2)【交换矩阵】
\(A=\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right] \)具有特征向量\( \mathbf{x}=\left[\begin{array}{l} 1 \\ 1 \end{array}\right]\)，对应于特征值\(1 \)；另一个特征向量\( \mathbf{x}=\left[\begin{array}{c} 1 \\ -1 \end{array}\right]\)，对应于特征值\( -1\)。这两个特征向量张成了整个空间。因为是对称矩阵，所以两个特征向量相互垂直(具体原因后面的问答中有解释)。

(3) 【反射矩阵】(Reflection matrix)
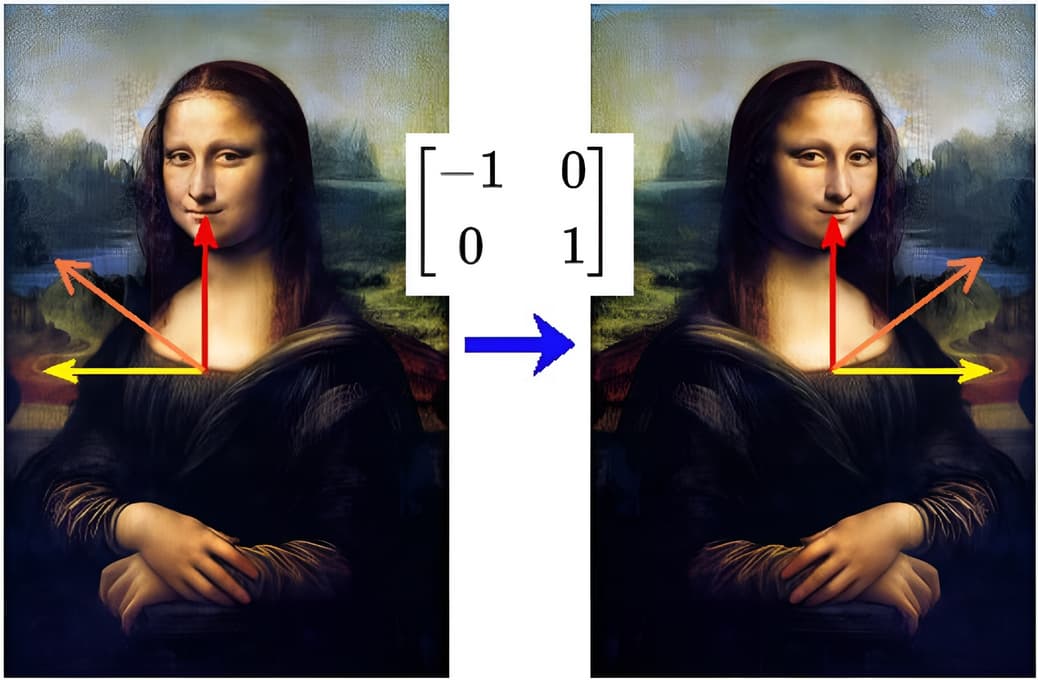当蒙娜丽莎的图像左右翻转时，中间垂直的红色向量方向保持不变。而水平方向上黄色的向量的方向完全反转，因此它们都是左右翻转变换的特征向量。红色向量长度不变，其特征值为1。黄色向量长度也不变但方向变了，其特征值为-1。橙色向量在翻转后和原来的向量不在同一条直线上，因此不是特征向量。

下图给出了分别沿着\(x\)轴、坐标原点、\(y\)轴、\(y=x\)轴进行reflection transformation操作对应的矩阵。

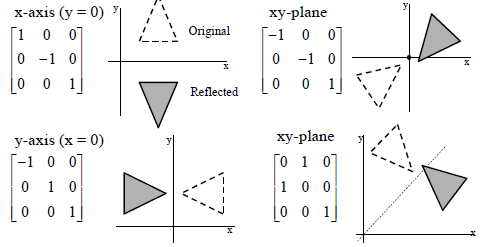
(4)【旋转矩阵】(Rotation Matrix)
二维旋转(沿着原点)$$\left[\begin{array}{c} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]$$相当于对\( \left[\begin{array}{l} x \\ y \end{array}\right]\)沿着原点，逆时针旋转\( \theta\)得到\( \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]\)。根据旋转矩阵的性质，我们就知道，对于实数的坐标向量而言，旋转之后，除了少数几个特定的旋转角度，其他旋转操作之后都不会与原来的方向相同或者相反，除非原始的坐标向量就是零向量。

如果我们取\(  \theta=90^{\circ}\)，根据通用的求解方式有$$\operatorname{det}(Q - \lambda I)=\left|\begin{array}{cc} -\lambda & -1 \\ 1 & -\lambda \end{array}\right|=\lambda^{2}+1=0\quad \Rightarrow \quad \lambda _{ 1 }=i,\quad \lambda _{ 2 }=-i$$如果一个矩阵具有复数特征值\(a+bi \)，则它的共轭复数\(a-bi \)也是矩阵的特征值。实数特征值让特征向量伸缩，而虚数让其旋转(类似小杂音)。

实例：逆时针90度旋转矩阵\(Q=\left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right]=\left[\begin{array}{cc} \cos 90^{\circ} & -\sin 90^{\circ} \\ \sin 90^{\circ} & \cos 90^{\circ} \end{array}\right] \)，根据前面推导的性质，知道对于这个矩阵的两个特征值有\(\lambda_{1}+\lambda_{2}=0, \lambda_{1} \lambda_{2}=1\)，那么实数特征向量只有零向量，因为其它任何向量乘以旋转矩阵，方向都会发生变化。

三维旋转(沿着轴)
比如沿着\(Z\)轴旋转\( \theta\)的矩阵为\(R_{z}(\theta)=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1\end{array}\right]\)，实际例子如下$$ R_{z}\left(90^{\circ}\right)\left[\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right]=\left[\begin{array}{ccc} \cos 90^{\circ} & -\sin 90^{\circ} & 0 \\ \sin 90^{\circ} & \cos 90^{\circ} & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right]=\left[\begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right]=\left[\begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right] $$向量\((1,0,0)\)沿着\( Z\)轴旋转\(90 \)度得到向量\((0,1,0)\)。

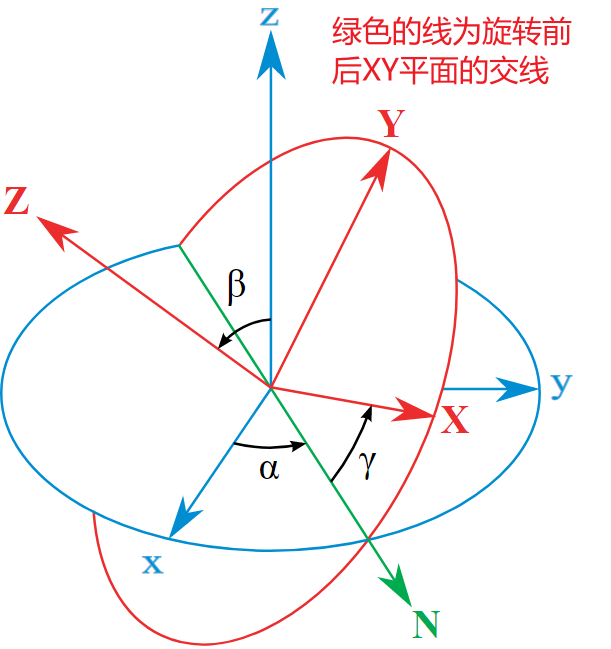
当然对于更复杂的旋转操作，可以分解为三个Basic rotations的合成：$$ R=R_{z}(\alpha) R_{y}(\beta) R_{x}(\gamma)=\left[\begin{array}{ccc} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{array}\right]\left[\begin{array}{llll} 1 & 0 & 0 \\ 0 & \cos \gamma & -\sin \gamma \\ 0 & \sin \gamma & \cos \gamma \end{array}\right] $$represents a rotation whose yaw, pitch, and roll angles are \(\alpha, \beta\) and \(\gamma\), respectively.

(5)【伸缩矩阵】(Scaling Matrix)：薄金属板关于一个固定点(看作原点)均匀伸展，使得板上每一个点到该固定点的距离翻倍。这个伸展是一个有特征值\(2\)的变换。从该固定点到板上任何一点的向量是一个特征向量，而相应的特征空间是所有这些向量的集合。显然这里任意特征值对应的特征空间都是一维的。表达如下$$\left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{cc}2 & 0 \\ 0 & 2\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right]$$

三维情况，比如三阶方阵，对角线上的元素分别为\( 3\)、\( 2\)、\( 2\)，其他元素为零，如果被作用的空间是原点以及\( (1,1,1)\)和三个坐标轴组成的小立方体，那么对于特征值\( 2 \)来说，它有两个特征向量\((0,1,0)\)和\((0,0,1)\)，显然该特征值对应的特征空间为二维。经过这个矩阵的变换之后，原来的小立方体变成了更大的长方体了。

(6) 【剪切变换】(shear transformation)：拓展，参考wiki

(7) 【挤压变换】(squeeze transformation)：拓展，参考wiki

(6) 地球自转：地球的自转，每个从地心往外指的箭头都在旋转，除了在转轴上的那些箭头。考虑地球在一小时自转后的变换，地心指向地理南极的箭头是这个变换的一个特征向量，但是从地心指向赤道任何一处的箭头不会是一个特征向量。因为指向极点的箭头没有被地球的自转拉伸，它的特征值是1。

(7) 驻波——多维向量空间：一个两端固定的弦上的驻波可以视为特征向量的一个例子，振动弦的原子到它们在弦静止时的位置之间的带符号那些距离视为一个空间中的一个向量的分量，那个空间的维数就是弦上原子的个数。驻波的形状，或者更精确地表达，弦上每个原子位置的向量(垂直于弦的方向)组成的高维向量，随着时间的流逝不断变化。以任意时刻作为起点，经过时间\(T\)后(时间变换函数作用)，恰好和起始状态的形状重叠，弦的形状函数(\(t=0 \)时刻，变\(x\))经过时间\(T\)变换后得到自己(\(t=T\)，变\(x\))，于是特征值就是\(1\)，如果存在阻尼，那么特征值就会小于\( 1\)。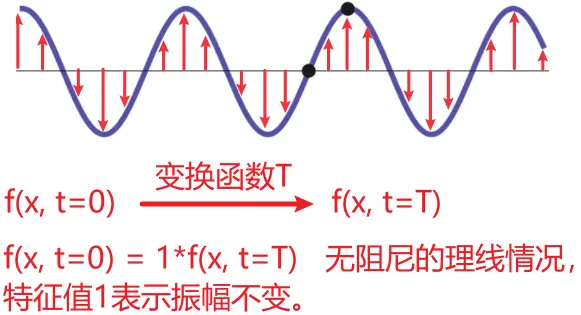

(8) 【Differential Operators】：见本页谈线性空间和线性算子章节，补充，，，，以及深入理解傅里叶变换-Tracholar

(9) 【特征函数-傅里叶变换】：补充，，，参考Eigenfunctions of the Fourier Transform-Caltech

(9) 【特征向量—特征脸是特征变量的例子】：在图像处理中，脸部图像的处理可以看作分量为每个像素的辉度的向量。该向量空间的维数是像素的个数。一个标准化面部图形的一个大型数据集合的协变矩阵的特征向量称为特征脸。它们对于将任何面部图像表达为它们的线性组合非常有用。特征脸提供了一种用于识别目的的数据压缩的方式。在这个应用中，一般只取最大那些特征值所对应的特征脸。

(10) 【特征向量—因子分析】：在因素分析中，一个协变矩阵的特征向量对应于因素，而特征值是因素负载。因素分析是一种统计学技术，用于社会科学和市场分析、产品管理、运筹规划和其他处理大量数据的应用科学。其目标是用称为因素的少量的不可观测随机变量来解释在一些可观测随机变量中的变化。可观测随机变量用因素的线性组合来建模，再加上“残差项。

(11) 【特征向量—分子轨道】：在量子力学中，特别是在原子物理和分子物理中，在Hartree-Fock理论下，原子轨道和分子轨道可以定义为Fock算子的特征向量。相应的特征值通过Koopmans定理可以解释为电离势能。在这个情况下，特征向量一词可以用于更广泛的意义，因为Fock算子显式地依赖于轨道和它们地特征值。如果需要强调这个特点，可以称它为隐特征值方程。这样地方程通常采用迭代程序求解，在这个情况下称为自洽场方法。在量子化学中，经常会把Hartree-Fock方程通过非正交基集合来表达。这个特定地表达是一个广义特征值问题称为Roothaan方程。

参考资料：
第一性原理计算的理论基础——赵纪军
怎样理解 Hartree-Fock Method？—知乎

(9) 【Hermitian Operators】，也叫自伴算子，其实就是复对称矩阵，其特征值都是实数，本征函数(向量)相互正交，而且本征函数是完备的。与物理系统的每一个可测量相对应的是量子力学算符。 算符之所以出现在量子力学中，是因为在量子力学里，我们需要用波函数来描述系统的运动状态。 常用算符 (参考：算符及其运算规则—知乎)

用更简单的话来说，量子力学中，矩阵代表力学量，矩阵的特征向量代表定态波函数(eigenstate)，矩阵的特征植代表力学量的某个可能的观测值。

特征值的思想：很多人会问矩阵的特征值特征向量为什么这么神奇，可以把矩阵的操作变成一个简单的参数\(\lambda\)。还有人会问道为什么特征值在物理中出现非常频繁。对此我只能简单解释一下，物理中常见的被研究物体都有一个自身的内禀结构，这个内在结构的方向往往和观察者也就是外场的坐标有区别。当我们给物体施加一个外场刺激的时候，比如说外力或者电场极化等等，物体沿着其内在结构的取向来响应外场，但是观察者从外场坐标下采集反馈。实际上矩阵在不同坐标之间实现变换，特征向量显示了物体内结构的方向，特征向量则是在这个主方向上物体对外场的响应参数。在有的领域直接将特征值称为伸缩系数，实际上它反应了在其所对应的特征向量方向上，内结构与外场之间的相互关系。

特征值还有一个应用是作为降维的判据，比如在图像压缩过程中，极小的特征值会被赋值为0，以此节省存储空间，也便于其它操作。反映在图像上，降维后的图像基本轮廓依旧清晣，图像细节有所牺牲。

思想要点：矩阵的特征值要想说清楚还要从线性变换入手，把一个矩阵当作一个线性变换在某一组基下的矩阵，最简单的线性变换就是数乘变换，求特征值的目的就是看看一个线性变换对一些非零向量的作用是否能够相当于一个数乘变换，特征值就是这个数乘变换的变换比，这样的一些非零向量就是特征向量，其实我们更关心的是特征向量，希望能把原先的线性空间分解成一些和特征向量相关的子空间的直和，这样我们的研究就可以分别限定在这些子空间上来进行，这和物理中在研究运动的时候将运动分解成水平方向和垂直方向的做法是一个道理！参考特征值和特征向量的物理意义——数理溯源

特征值的求解

根据矩阵迹的特点，对于一个二阶矩阵，在已知一个特征值的条件下，由此可以得到另一个特征值。

对于一般情况\( A \mathbf{x}=\lambda \mathbf{x}\)，我们转化成\( (A-\lambda I) \mathbf{x}=0\)。下面通过两个方式说明\(A-\lambda I \)为奇异矩阵，或者说行列式等于\( 0\)。
(1) 我们要求的\(\mathbf{x} \)肯定是非零向量，不然没意义。如果有解，说明\(A-\lambda I \)的零空间至少是一维的，于是矩阵\(A-\lambda I \)不可能是满秩矩阵，因此其行列式等于零。
(2) 方程有非零解，说明矩阵\(A-\lambda I \)列向量的某些线性组合结果可以为零，于是这些列向量不是线性无关的，矩阵就不是满秩，因此行列式等于零。

于是根据\( \operatorname{det}(A-\lambda I)=0\)，我们可以解得\( n\)个特征值，但是方程可能有重根，重根对应的不一定是重复的特征向量。得到特征值，可以根据消元法解\(A-\lambda I \)，这一矩阵零空间中的向量为矩阵\(A \)的特征向量。

Example-1: 一般方法求解特征值和特征向量的例子\(A=\left[\begin{array}{ll} 3 & 1 \\ 1 & 3 \end{array}\right]\)？
根据行列式等于零$$\operatorname{det}(A-\lambda I)=\left|\begin{array}{cc} 3-\lambda & 1 \\ 1 & 3-\lambda \end{array}\right|=(3-\lambda)^{2}-1=\lambda^{2}-6 \lambda+8$$很容易看出两个特征值分别是\( 2\)和\( 4\)，它们俩的和正好就是矩阵迹。下面求特征向量$$\begin{aligned} &A-4 I=\left[\begin{array}{cc} -1 & 1 \\ 1 & -1 \end{array}\right],(A-4 I) \mathbf{x}_{1}=0, \mathbf{x}_{1}=\left[\begin{array}{cc} 1 \\ 1 \end{array}\right]\\ &A-2 I=\left[\begin{array}{ll} 1 & 1 \\ 1 & 1 \end{array}\right],(A-2 I) \mathbf{x}_{2}=0, \mathbf{x}_{2}=\left[\begin{array}{l} -1 \\ 1 \end{array}\right] \end{aligned}$$与前面的例子\(A=\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right] \)相比，特征向量不变，但是特征值平移了三个单位。

Example-2: 设 3 阶实矩阵 \(A\) 的特征多项式为 \(f(x)=x^{3}-3 x^{2}+4 x-2\) ，证明: \(A\)既不是正交矩阵，也不是实对称矩阵。参考castelu的B站视频

(反)对称矩阵和矩阵转置

对称矩阵的特征向量正交(主动选择)

设\( \lambda_{1}\)和\( \lambda_{2}\)是一个对称矩阵的特征值，对应的特征向量分别是\(\mathbf{x}_{1} \)和\(\mathbf{x}_{2} \)。于是\( A \mathbf{x}_{1}=\lambda \mathbf{x}_{1}\)，两边同时乘以\(\mathbf{x}_{2} \)，于是\(\mathbf{x}_{2}^{\mathrm{T}} \boldsymbol{A} \mathbf{x}_{1}=\lambda_{1} \mathbf{x}_{2}^{\mathrm{T}} \mathbf{x}_{1} \)，而\(\mathbf{x}_{2}^{\mathrm{T}} \boldsymbol{A} \mathbf{x}_{1}=\left(\boldsymbol{A}^{\mathrm{T}} \mathbf{x}_{2}\right)^{\mathrm{T}} \mathbf{x}_{1}=\lambda_{2} \mathbf{x}_{2}^{\mathrm{T}} \mathbf{x}_{1} \)。因此有\( \left(\lambda_{1}-\lambda_{2}\right) \mathbf{x}_{2}^{\mathrm{T}} \mathbf{x}_{1}=0\)，而两个特征值不相等，因此只会是两个特征向量相互正交。

• 对称矩阵永远有实数的特征值；
• 而反对称矩阵，即满足\(\boldsymbol{A}^{\mathrm{T}}=-\boldsymbol{A} \)的矩阵，具有纯虚数的特征值，旋转矩阵就是反对称阵。

转置之后矩阵特征值和特征向量的变化
我们前面提到的行列式的第十条性质有\(\operatorname{det}\left(\boldsymbol{A}^{\mathrm{T}}\right)=\operatorname{det}(\boldsymbol{A}) \)，转置前后矩阵的行列式值不变。于是可以推出\(\operatorname{det}(\boldsymbol{A}-\lambda \boldsymbol{I})=\operatorname{det}((\boldsymbol{A}-\lambda \boldsymbol{I})^{\mathrm{T}})=\operatorname{det}\left(\boldsymbol{A}^{\mathrm{T}}-\lambda \boldsymbol{I}\right)\)，因此如果\(\lambda \)是矩阵\( \boldsymbol{A}\)的特征值，则有\(\operatorname{det}\left(\boldsymbol{A}^{\mathrm{T}}-\lambda \boldsymbol{I})=0\right. \)，因此\(\lambda \)也是转置矩阵\( \boldsymbol{A}^{\mathrm{T}}\)的特征值。

特征向量，如果我们知道矩阵\( \boldsymbol{A}\)的特征值\(\lambda \)，于是\( (\boldsymbol{A}-\lambda \boldsymbol{I}) \mathbf{x}=0\)，其中的特征向量\( \mathbf{x}\)对应于矩阵\( (\boldsymbol{A}-\lambda \boldsymbol{I})\)的零空间，换句话说，对应于\( \lambda \)的特征向量一定在该零空间内，同时该零空间的任意向量也满足\( (A-\lambda \boldsymbol{I}) \mathbf{x}=0 \)。同理，转置矩阵\( \boldsymbol{A}^{\mathrm{T}}\)的特征向量对应于矩阵\((\boldsymbol{A}^{\mathrm{T}} -\lambda \boldsymbol{I})\)的零空间，或者说\((\boldsymbol{A}-\lambda \boldsymbol{I}) \)的左零空间。注意$$(\boldsymbol{A}-\lambda \boldsymbol{I}) ^{\mathrm{T}}=\boldsymbol{A}^{\mathrm{T}}-\lambda \boldsymbol{I}$$

韦达定理和矩阵特征值

【韦达定理】
先回顾一下我们初中学的韦达定理$$ax^{ 2 }+bx+c=0(a,b,c\in R,a\neq 0)\quad \Rightarrow \begin{matrix} & x_{ 1 }+x_{ 2 }=-\frac { b }{ a } \\ & x_{ 1 }x_{ 2 }=\frac { c }{ a } \end{matrix}$$推广到复数系一元\(n \)次方程$$a_{n} x^{n}+a_{n-1} x^{x-1}+\cdots+a_{1} x+a_{0}=0$$通过因式分解可以得到$$\begin{aligned} &x_{1}+x_{2}+\cdots+x_{n}=\sum_{i=1}^{n} x_{i}=-\frac{a_{n-1}}{a_{n}}\\ &x_{l} x_{2} \cdots x_{n}=\prod_{i=1}^{n} x_{i}=(-1)^{n} \frac{a_{0}}{a_{n}} \end{aligned} $$所有特征值的和 = 主对角线元素之和
如果矩阵的阶数是偶数，那么\( a_{n}\) 就为\(1 \)，\( a_{n-1}\)就是原行列式主对角线上元素之和的负数，那么根据前面的韦达定理，特征值的加和就是\(- a_{n-1}\)，也就是主对角线上元素之和。考虑奇数阶矩阵，最后也得到同样的结果。因此我们说所有特征值的和就是主对角线上所有元素之和。

所有特征值的乘积 = 行列式的值
首先我们很容易知道矩阵的行列式等于\( a_{0}\)。如果矩阵的阶数是偶数的话，\((-1)^{n} \)就是\(1 \)，\( a_{n}\)也是\(1 \)，同样地，阶数是奇数的话，\((-1)^{n} \)就是\(-1\)，\( a_{n}\)也是\(-1 \)。总而言之，无论怎么变化，特征值的乘积一定是\( a_{0}\)，也就是行列式的值。其实通过因式分解我们也能感觉出来。

退化矩阵

对于三角阵，特征值就是对角线上的元素。比如\(A=\left[\begin{array}{cc} 3 & 1 \\ 0 & 3 \end{array}\right] \)得到$${ \text{det} }(A-\lambda I)=\left| \begin{array}{cc} 3-\lambda & 1 \\ 0 & 3-\lambda \end{array} \right| =(3-\lambda )(3-\lambda )=0\quad \Rightarrow \quad \lambda _{ 1 }=\lambda _{ 2 }=3$$于是\( (A-\lambda I){ \mathbf{x} }=\left[ \begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array} \right] { \mathbf{x} }=0\quad \Rightarrow \quad \mathbf{x}_{1}=\left[\begin{array}{l} 1 \\ 0 \end{array}\right]\)，没有线性无关的\( \mathbf{x}_2\)，说明矩阵\( A\)是一个【退化矩阵】，对应相同的特征值，而特征向量短缺。

补充xxx
我似乎在网上看到，有人说奇异矩阵就是退化矩阵，但是这里GS老师讲的是特征向量缺失的矩阵叫作退化矩阵，下面是GS老师举的退化矩阵的例子，显然这个矩阵并不是奇异矩阵$$A=\left[\begin{array}{ll} 3 & 1 \\ 0 & 3 \end{array}\right]$$计算得到特征值\( \lambda_{1}=\lambda_{2}=3\)，很容易发现，三角矩阵的特征值就是主对角线上的元素。带入特征值，得到$$(A-\lambda I) \mathbf{x}=\left[\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right]\left[\begin{array}{l} x_{1} \\ x_{2} \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \end{array}\right]$$算出特征向量\( \left[\begin{array}{l} 1 \\ 0 \end{array}\right]\)，带入另一个特征值也得到了相同的特征向量，无法得到另一个与这个特征向量线性无关的新特征向量。关于退化矩阵特征向量的求解，需要用【若尔当标准型】和【广义特征向量】(Generalized eigenvector)的概念和方法去求解，我们将这部分的讨论放在笔记线性代数—3。

 

 

对角化和矩阵的幂

可对角化矩阵与对角阵

矩阵对角化的条件(Diagonalizing a matrix \(S^{-1} A S=\Lambda \))

如果矩阵\( A\)具有\(n \)个线性无关的特征向量(可以进行对角化的条件，很少数不满足)，将它们作为列向量可以组成一个可逆方阵\(S \)，称为【模态矩阵】(modal matrix)，并且有：$$\begin{aligned} A S &=A\left[\mathbf{x}_{1} \quad \mathbf{x}_{2} \quad \cdots \quad \mathbf{x}_{\mathbf{n}}\right] \\ &=\left[\lambda_{1} \mathbf{x}_{1} \quad \lambda_{2} \mathbf{x}_{2} \quad \cdots \quad \lambda_{\mathbf{n}} \mathbf{x}_{\mathbf{n}}\right] \end{aligned}=S\left[\begin{array}{cccc} \lambda_{1} & 0 & \cdots & 0 \\ 0 & \lambda_{2} & & 0 \\ \vdots & & \ddots & \vdots \\ 0 & \cdots & 0 & \lambda_{n} \end{array}\right]=S \Lambda$$这里的矩阵\( \Lambda\)为对角矩阵，他的非零元素就是矩阵\( A\)的特征值。因为矩阵\(S \)列向量线性无关，所以其逆矩阵\( S^{-1}\)一定存在。于是有$$ \begin{aligned} A &=S \Lambda S^{-1} \\ \Lambda &=S^{-1} A S \end{aligned} $$

• 矩阵\(A\)和特征值构成的对角阵\(\Lambda\)相似，而且具有相同的特征值和特征向量；
• 矩阵\(A\)和和其任意相似矩阵\(B\)一定具有相同的特征值，但是特征向量一般不同。

总结各种分解

• 消元法，\( LU\)分解；
• 施密特正交化，\(QR \)分解；
• 对角化，\(S \Lambda S^{-1}\)分解。

特殊情况分析：对角化的条件是有\(n \)个线性无关的特征向量，那么是不是说矩阵有\( n\)个不重复的特征值呢？显然，当特征值不同的时候，特征向量一定不同，这也是大多数矩阵的情况。但是少数矩阵的特征值有重复，但是重复的特征值可能对应多个不同的特征向量，比如单位矩阵，我们知道特征值只有\( 1\)，但是特征向量有\( n\)个，而且都是线性无关的，这样的情况同样可以进行矩阵的对角化。

总结：

• 所有特征值不重复，则所有的特征向量线性无关，可以对角化；
• 有重复的特征值，那么可能特征向量线性无关，也可能线性相关，于是可能可以对角化，也可能不行。(可以对角化的例子就是单位矩阵；不可以对角化的例子就是我们前面提到的退化矩阵)
• 对于对角阵，一定可以对角化，而且对角化之后得到的矩阵\(\Lambda \)就是它自身。
• 对角化的好处：Diagonal matrices are much easier to work with than non-diagonal matrices. They're easier to multiply, easier to invert, and easier to understand how they'll affect the respective coordinates.

矩阵\( A\)左乘和右乘对角矩阵

• 右边乘以对角阵，我们要把矩阵\(A \)看作是一个个列向量，右边的对角阵同样切割成一列一列，每使用一列，相当于\(A\mathbf{x}\)，也就是对矩阵\(A \)的列向量进行线性组合。最终得到的新矩阵，就是将矩阵\(A \)的每一个列向量前面乘上对应的系数。
• 左边乘以对角阵，我们把矩阵\(A \)看做是一个个行向量，左边的对角阵同样地切割成一行一行。用对角阵的每一行去乘以\( A\)，相对于用那一行对矩阵\( A\)进行所有行向量的线性组合，然后得到新的行向量替代原来的那一行。于是最终得到的新矩阵，就是将矩阵\( A\)的每一行乘以对应的系数。
• 矩阵\( A\)是列向量或者行向量的情况：
  • • 如果是列向量，那么只能左乘对角阵，得到的是列向量，相当于将同一行的对角阵元素和\(A\)中的元素相乘，然后推到右边只留下一列。
    • 如果是行向量，那么只能右乘对角阵，得到的是行向量。相当于把行向量套在对角阵上，然后将二者压缩成一行，每一列上的两个元素相乘得到对应位置的新元素。

 

矩阵的幂运算(Powers of \( A\))

如果我们进行的是\(LU \)分解或者其他分解，显然进行幂运算很麻烦。但是如果将矩阵\(A \)对角化之后，再进行幂运算就简单很多。首先我们知道$$A\mathbf{x}=\lambda \mathbf{x}\, \Rightarrow \, A^{ 2 }{ \mathbf{x} }=\lambda A{ \mathbf{x} }=\lambda ^{ 2 }{ \mathbf{x} }\,\Rightarrow\, A^{n}\mathbf{x}=\lambda^{n}\mathbf{x}$$表明矩阵\(A^{2} \)的特征值是\( \lambda^{2}\)，推广之后，就是矩阵\(A^{n} \)的特征值是\( \lambda^{n}\)。

如果进行对角化，则有$$A^{2}=S \Lambda S^{-1} S A S^{-1}=S \Lambda^{2} S^{-1}\quad\Rightarrow \quad A^{k}=S \Lambda^{k} S^{-1}\quad$$

差分方程—利用对角化后的幂运算
从给定的一个向量\(\mathbf{u}_{0} \)出发，我们可以通过前一项乘以矩阵\( A\)得到下一项的方式，得到一个向量序列：\(\mathbf{u}_{k+1}=A \mathbf{u}_{k} \)。这个序列可以是一阶差分方程，而\(\mathbf{u}_{k+1}=A^{k} \mathbf{u}_{0} \)就是方程的解。但是这种简洁形式并没有给出足够的信息，我们需要通过特征向量和矩阵的幂运算给出真实的解的结构。

我们将\(\mathbf{u}_{0} \)写成特征向量线性组合的形式：$$\begin{array}{l} \mathbf{u}_{0}=\mathrm{c}_{1} \mathbf{x}_{1}+\mathrm{c}_{2} \mathbf{x}_{2}+\ldots+\mathrm{c}_{n} \mathbf{x}_{n}=\mathbf{S}{\mathbf{c}} \\ A \mathbf{u}_{0}=\mathrm{c}_{1} \lambda_{1} \mathbf{x}_{1}+\mathrm{c}_{2} \lambda_{2} \mathbf{x}_{2}+\ldots+\mathrm{c}_{n} \lambda_{n} \mathbf{x}_{n} \\ \mathbf{u}_{\mathbf{k}}=A^{\mathbf{k}} \mathbf{u}_{0}=\mathrm{c}_{1} \lambda_{1}^k\mathbf{x}_{1}+\mathrm{c}_{2} \lambda_{2}^k \mathbf{x}_{2}+\ldots+\mathrm{c}_{n} \lambda_{n}^{k} \mathbf{x}_{n}=\mathbf{S}\Lambda^{k} {\mathbf{c}} \end{array}$$我们再仔细分析一下最下面的那个式子，首先我们知道根据矩阵的幂运算有\( A^{k}=\mathbf{S} \Lambda^{k} \mathbf{S}^{-1}\)；根据克莱姆法则有\(如果\mathbf{Sc}=\mathbf{u_{0}} \)，则有\( \mathbf{c}=\mathbf{S}^{-1}\mathbf{u_{0}}\)，因此有$$\mathbf{u}_{\mathbf{k}}=\mathbf{S} \Lambda^{k} \mathbf{S^{-1}}\mathbf{u_{0}}=\mathbf{S} \Lambda^{k} (\mathbf{S^{-1}}\mathbf{u_{0}})=\mathbf{S} \Lambda^{k} \mathbf{c}$$

【斐波拉契数列】：\( 0,1,1,2,3,4,8,13 \dots\)，通项公式为\(\mathrm{F}_{\mathrm{k}+2}=\mathrm{F}_{\mathrm{k}+1}+\mathrm{F}_{\mathrm{k}} \)，求\( \mathrm{F}_{100} \)？

如果我们使用计算机编程的方法，就是不断使用for循环，循环100次就得到最后的结果。但是我们其实可以从矩阵的角度去理解这个问题，似乎一下子不好想到，因为我们在前面的问题的讨论中是给出了相邻两项的矩阵关系，但是这里新的一项与前面的两项都有关系，不能直接套用，于是我们需要巧妙地构造新的项，也就是用\(\mathbf{u}_{\mathbf{k+1}}=\left[\begin{array}{c} \mathrm{F}_{k+2} \\ \mathrm{F}_{k+1} \end{array}\right] \)。于是$$\begin{array}{c} \mathrm{F}_{\mathrm{k}+2}=\mathrm{F}_{\mathrm{k}+1}+\mathrm{F}_{\mathrm{k}} \\ \mathrm{F}_{\mathrm{k}+1}=\mathrm{F}_{\mathrm{k}+1} \end{array} \, \Rightarrow \,\mathbf{u}_{\mathbf{k}+1}=\left[\begin{array}{ll} 1 & 1 \\ 1 & 0 \end{array}\right] \mathbf{u}_{\mathbf{k}}$$令\( A=\left[\begin{array}{ll} 1 & 1 \\ 1 & 0 \end{array}\right]\)，于是\( \mathbf{u}_{\mathbf{k}}=A \mathbf{u}_{\mathbf{k-1}}=A^{\mathbf{k}}\mathbf{u}_{0}=\mathrm{c}_{1} \lambda_{1}^k\mathbf{x}_{1}+\mathrm{c}_{2} \lambda_{2}^k \mathbf{x}_{2}\)，因为\(\mathbf{x}_{1} \)和\(\mathbf{x}_{2} \)是矩阵\( A\)的两个特征向量，那么它们的线性组合覆盖整个\( \mathbf{R}^{2}\)空间，也就是说\(\mathbf{u}_{0} \)一定可以用这两个特征向量的线性组合来表示，取的系数分别是\( c_{1}\)和\( c_{2}\)。我们很容易求得两个特征值为\(\lambda_{1}=\displaystyle\frac{1+\sqrt{5}}{2} \quad\lambda_{2}=\displaystyle\frac{1-\sqrt{5}}{2} \)，特征向量为\( \mathbf{x}_{1}=\left[\begin{array}{l} \lambda_{1} \\ 1 \end{array}\right] \quad \mathbf{x}_{2}=\left[\begin{array}{l} \lambda_{2} \\ 1 \end{array}\right]\)而$$\mathbf{u}_{0}=\left[\begin{array}{l} \mathrm{F}_{1} \\ \mathrm{F}_{0} \end{array}\right]=\left[\begin{array}{l} 1 \\ 0 \end{array}\right]=\mathrm{c}_{1} \mathbf{x}_{1}+\mathrm{c}_{2} \mathbf{x}_{2}\,\Rightarrow \,c_{1}=-c_{2}=\frac{1}{\sqrt{5}}$$ $$\left[\begin{array}{l} \mathrm{F}_{100} \\ \mathrm{F}_{99} \end{array}\right]=A^{99}\left[\begin{array}{l} \mathrm{F}_{1} \\ \mathrm{F}_{0} \end{array}\right]=\left[\begin{array}{ll} \lambda_{1} & \lambda_{2} \\ 1 & 1 \end{array}\right]\left[\begin{array}{ll} \lambda_{1}^{99} & \\ & \lambda_{2}^{99} \end{array}\right]\left[\begin{array}{l} c_{1} \\ c_{2} \end{array}\right]=\left[\begin{array}{l} c_{1} \lambda_{1}^{100}+c_{2} \lambda_{2}^{100} \\ \end{array}\right]\, \Rightarrow \,\mathrm{F}_{100} \approx \mathrm{c}_{1} \lambda_{1}^{100} $$绝对值大于\(1 \)的\( \lambda_{1}\)在控制着斐波拉契数列的增长，当\(k \)很大的时候，显然\( \lambda_{2}\)那一项可以忽略。

 

 

微分方程和\(e^{A t}\)

微分方程和\(e^{A t} \)的关系
前面我们利用矩阵的对角化解决了差分问题，现在我们进一步学习用矩阵对角化(特征值+特征向量)来求解微分方程。我们首先讨论的是一阶常系数微分方程，将其转化为线性代数的问题进行处理。主要思路基于常系数线性微分方程的解是指数形式，而寻找其指数和系数就是线代主要研究的问题，会涉及到矩阵指数的运算\(e^{A t} \)。$$\frac{d \mathbf{u}}{d t}=\boldsymbol{A} \mathbf{u}, \boldsymbol{A}=\left[\begin{array}{cc} -1 & 2 \\ 1 & -2 \end{array}\right], \mathbf{u}(0)=\left[\begin{array}{1} u_{1} \\ u_{2} \end{array}\right]=\left[\begin{array}{l} 1 \\ 0 \end{array}\right]$$这里的\( \mathbf{u}(0)\)是初始值，我们如果把这里的\(\displaystyle\frac{d \mathbf{u}}{d t}=\boldsymbol{A} \mathbf{u} \)里面的向量和矩阵全部看作单一的数字，就是我们在高数里面学的很简单的微分方程，因变量\( \mathbf{u}\)的变化速率和自身的大小成正比，而这个\( \boldsymbol{A}\)类似比例系数，这就是我们常见的指数形式函数。虽然这里的\(\boldsymbol{A} \)是一个矩阵，但是作用形式是类似的，分析矩阵\(\boldsymbol{A} \)是要追踪\( \mathbf{u}\)随时间的变化。由于矩阵\( \boldsymbol{A}\)是奇异矩阵(列向量一定不是线性无关，零空间一定存在，于是必有一个特征值是\( 0\)，根据矩阵的迹就可以推出另一个特征值)，我们很容易知道\( \lambda_{1}=0, \lambda_{2}=-3 \)。上述方程的通解形式是$$\mathbf{u}(t)=c_{1} e^{\lambda_{1}t } \mathbf{x}_{1}+c_{2} e^{\lambda_{2} t} \mathbf{x}_{2}$$其中含有\( \lambda_{1}=0\)的一项使得这一部分是不随时间变化的，对于含有\(\lambda_{2}=-3 \)的那一项来说，随着时间的增长，这一部分越来越小，当时间趋近无穷大的时候，这一部分可以忽略，因此整个解趋于平稳，而且这个解最终只和第一项有关，或者说和\(c_{1} \mathbf{x}_{1} \)有关。这里和前面求解斐波拉契数列的在\(k \)很大的情况，神似。根据特征值求得特征向量于是有$$\mathbf{x}_{1}=\left[\begin{array}{l} 2 \\ 1 \end{array}\right]\quad \mathbf{x}_{2}=\left[\begin{array}{l} 1 \\ -1 \end{array}\right] \, \Rightarrow \,\mathbf{u}(\mathrm{t})=\mathrm{c}_{1} \mathrm{e}^{\lambda_{1} t} \mathbf{x}_{1}+\mathrm{c}_{2} \mathrm{e}^{\lambda_{2} t} \mathbf{x}_{2}=c_{1} \mathrm{e}^{0}\left[\begin{array}{l} 2 \\ 1 \end{array}\right]+\mathrm{c}_{2} \mathrm{e}^{-3 t}\left[\begin{array}{c} 1 \\ -1 \end{array}\right]$$根据初始态条件，可以推导出\( c_{1}=c_{2}=1 / 3\)于是$$\mathbf{u}(\mathrm{t})=\frac{1}{3}\left[\begin{array}{l} 2 \\ 1 \end{array}\right]+\frac{1}{3} e^{-3 t}\left[\begin{array}{c} 1 \\ -1 \end{array}\right]$$前一项为稳态状态，后一项随着时间衰减。

        特征向量给出的是方向，前面的系数\( c\)给出的是在不同方向上所占的权重，而特征值给出的就是矩阵操作在特征向量方向的操作效果，在上一讲差分方程里它就是一个倍数即线性增长能力，而在微分方程中它代表在该方向上的指数增长能力，因此两者稳定性的评价并不相同。

重新理解微分方程
对于微分方程\(\displaystyle\frac{d^{2} y}{d x^{2}}+y=0 \)，求解该方程可以视为求解它的列空间。我们可以得到的解为：$$y=\cos x, y=\sin x, y=e^{i x}$$这三个解不是线性无关的，只有其中任意一个都可以被另外两个解线性表示。事实上，通解为\(y=c_{1} \cos x+c_{2} \sin x \)，其中\( c\)可以为任意复数。也将解的线性组合构成的空间称为解空间，其维数为\( 2\)。\(\cos x \)和\(\sin x \)可以成为解空间的一组基。这些不是向量，而是函数，但是同样可以对其进行线性运算，在线性代数的讨论范围之类。

【耦合】和【解耦】
耦合就是couple，解耦就是decouple。下面我们通过耦合和解耦表达式来反推上面的求解步骤。$$\left[\begin{array}{l} u_{1}^{\prime} \\ u_{2}^{\prime} \end{array}\right]=A\left[\begin{array}{l} u_{1} \\ u_{2} \end{array}\right] \Rightarrow\left[\begin{array}{l} v_{1}^{\prime} \\ v_{2}^{\prime} \end{array}\right]=\Lambda\left[\begin{array}{l} v_{1} \\ v_{2} \end{array}\right]$$上面左边部分为耦合状态，\(A \)就是原始的系数矩阵，也就是说无论是\(u_{1}^{\prime} \)还是\(u_{2}^{\prime} \)都需要同时用\(u_{1} \)和\(u_{2} \)这两个元素来表示，也就是说函数关系混叠在一起。而右边的部分为解耦的状态，\(\Lambda \)为对角阵，\(v_{1}^{\prime} \)只需要用\(v_{1}\)乘以一个常数来表示，而\(v_{2}^{\prime} \)也是只需要用\(v_{2}\)乘以一个常数来表示，这种解耦状态就相当于两个独立的微分方程，我们很容易进行各自单独求解。

下面我们来探求如何将上面左边部分和右边部分联系起来。一般来说，我们可以将这里的\(u_{1} \)和\(u_{2} \)看作是\(\mathbf{R}^{2} \)空间的基向量，同时\(v_{1} \)和\(v_{2} \)也是该空间的基向量，于是两组基向量之间肯定能够通过一个线性变换相互转化，假设这个线性变化矩阵为\( P\)，于是有如下关系\(\begin{aligned} {\left[\begin{array}{c} u_{1} \\ u_{2} \end{array}\right]=P\left[\begin{array}{l} v_{1} \\ v_{2} \end{array}\right] \Rightarrow\left[\begin{array}{l} u_{1}^{\prime} \\ u_{2}^{\prime} \end{array}\right]=P\left[\begin{array}{l} v_{1}^{\prime} \\ v_{2}^{\prime} \end{array}\right] } \\ {\left[\begin{array}{l} v_{1}^{\prime} \\ v_{2}^{\prime} \end{array}\right]=\Lambda\left[\begin{array}{c} v_{1} \\ v_{2} \end{array}\right] } \\ {\left[\begin{array}{l} u_{1} \\ u_{2} \end{array}\right]=P\left[\begin{array}{l} v_{1} \\ v_{2} \end{array}\right] \Rightarrow\left[\begin{array}{l} v_{1} \\ v_{2} \end{array}\right]=P^{-1}\left[\begin{array}{l} u_{1} \\ u_{2} \end{array}\right] } \end{aligned}\) \( \Rightarrow\left[\begin{array}{l} u_{1}^{\prime} \\ u_{2}^{\prime} \end{array}\right]=P \Lambda P^{-1}\left[\begin{array}{l} u_{1} \\ u_{2} \end{array}\right] \Rightarrow A=P \Lambda P^{-1} \)

因为先前我们讨论矩阵对角化的问题中，将矩阵\( A\)进行对角化的方式是写成\(A=S \Lambda S^{-1} \)，其中矩阵\(S \)是由矩阵\( A\)的特征向量构成，而\( \Lambda \)是对角阵，对角线上的元素就是特征值。于是上面的矩阵\( P\)就是特征向量矩阵\( S\)。因此现在我们需要做的就是求解矩阵\( A\)的特征值和特征向量。然后先求出\( \left[\begin{array}{l} v_{1} \\ v_{2} \end{array}\right]\)，接着用矩阵\( P\)进行线性变换就得到\(\left[\begin{array}{l} u_{1} \\ u_{2} \end{array}\right] \)求解顺序如下$$\left[ \begin{array}{l} v_{ 1 }^{ \prime } \\ v_{ 2 }^{ \prime } \end{array} \right] =\Lambda \left[ \begin{array}{l} v_{ 1 } \\ v_{ 2 } \end{array} \right] \quad \Rightarrow \quad \left[ \begin{array}{l} u_{ 1 } \\ u_{ 2 } \end{array} \right] =P\left[ \begin{array}{l} v_{ 1 } \\ v_{ 2 } \end{array} \right] \quad $$

再谈解耦
我们已知的是\(  \displaystyle\frac{d \mathbf{u}}{d t}=A \mathbf{u} \)，其中\(\mathbf{u} \)的第一行的那个元素就是\( u_{1}\)，第二行的元素就是\( u_{2}\)。接下来我们令\( \mathbf{u}=\mathbf{S} \mathbf{v}\)，其中\( \mathbf{S}\)是矩阵\( A\)的特征向量，由于其组成是线性无关的特征向量，于是通过一定的线性组合可以覆盖整个\(\mathbf{R}^{2} \)空间，也就是说，无论\(\mathbf{u} \)，在\(\mathbf{S} \)固定的情况下，肯定能找到一个\( \mathbf{v} \)使得\(\mathbf{u} \)可以用\( \mathbf{Sv} \)来表示。于是有$$\begin{gathered} \boldsymbol{S} \frac{d \mathbf{v}}{d t}=\boldsymbol{A} S \mathbf{v} \\ \Rightarrow \frac{d \mathbf{v}}{d t}=\boldsymbol{S}^{-1} \boldsymbol{A} \boldsymbol{S} \mathbf{v}=\boldsymbol{\Lambda} \mathbf{v} \end{gathered}$$新的方程不在耦合。我们先前讨论过，左乘一个对角阵，相当于把对象矩阵切割成一行一行，然后根绝左乘矩阵每一行的性质进行线性组合。由于对角阵的特殊性质，因此左乘一个对角阵，相当于将对角阵上每一行元素作为系数乘在对象矩阵的每一行上。将解耦后的矩阵方程组切成一行一行，于是有\(  \displaystyle\frac{d v_{i}}{d t}=\lambda_{i} v_{i}\)，于是方程的通解为$$\begin{array}{c} \mathbf{v}(\mathrm{t})=e^{\mathbf{\Lambda} t} \mathbf{v}(0) \\ \mathbf{u}(\mathrm{t})=\boldsymbol{S} e^{\mathbf{\Lambda} t} \boldsymbol{S}^{-1} \mathbf{u}(0)=e^{\boldsymbol{A} t} \mathbf{u}(0) \end{array}$$

一阶线性微分方程的稳定性
(1)    特征值既可以是实数，也可以是复数范围，但是如果从复数范围考虑，实部必须小于零\(\operatorname{Re}(\lambda)<0 \)，这样才有\(\mathbf{u}(t) \)不发散。(支配稳定性的是实部，虚部的效果是在单位圆上转圈)
(2)    (非零)稳态：至少有一个特征值为\(0 \)，并且其他所有的特征值实部都为负数。
(3)     至少有一个特征值满足\( \operatorname{Re}(\lambda)>0\)，则解是发散的。

阵指数函数(Matrix exponential\(e^{A t} \))
根据指数的幂级数(这里也是泰勒级数)的公式：$$e^{x}=\sum_{n=0}^{\infty} \frac{x^{n}}{n !}=1+x+\frac{x^{2}}{2}+\frac{x^{3}}{6}+\cdots$$来定义矩阵型指数运算$$e^{A t}=I+A t+\frac{(A t)^{2}}{2}+\frac{(A t)^{3}}{6}+\cdots$$其实不止可以进行矩阵指数函数的运算，对于其他函数同样适用。比如对于几何级数展开$$\frac{1}{1-x}=\sum_{n=0}^{\infty} x^{n}=1+x+x^{2}+\cdots+x^{n}+\cdots \quad \forall x:|x|<1$$我们进行矩阵运算有$$(I+A t)^{-1}=I+A t+(A t)^{2}+(A t)^{3}+\cdots \quad if \,|\lambda(\boldsymbol{A} t)|<1$$如果\(\boldsymbol{A} t \)的特征值的绝对值很小很小，都小于\(1 \)，那么我们可以省去级数后面的很多项，只取前面几项作为近似值，而且这也是一个求解逆矩阵的方法之一(特定情况)。

前面我们已经写出了矩阵指数的公式\(e^{A t}=S e^{\Lambda t} S^{-1} \)。如果矩阵\(A \)具有\(n \)个线性无关的特征向量，我们可以从幂级数定义的矩阵指数公式来再次验证：$$\begin{aligned} e^{A t} &=I+A t+\frac{(A t)^{2}}{2}+\frac{(A t)^{3}}{6}+\cdots \\ &=S S^{-1}+S \Lambda S^{-1} t+\frac{S \Lambda^{2} S^{-1}}{2} t^{2}+\frac{S \Lambda^{3} S^{-1}}{6} t^{3}+\cdots \\ &=S\left(I+\Lambda t+\frac{\Lambda^{2}}{2} t^{2}+\frac{\Lambda^{3}}{6} t^{3}+\cdots\right) S^{-1} \\ &=S e^{\Lambda t} S^{-1} \end{aligned}$$能够对角化的矩阵都能够表示为上式。$$e^{\Lambda t}=\left[\begin{array}{cccc} e^{\lambda_{1} t} & 0 & \cdots & 0 \\ 0 & e^{\lambda_{2} t} & & 0 \\ \vdots & & \ddots & \vdots \\ 0 & \cdots & 0 & e^{\lambda_{n} t} \end{array}\right]$$

二阶微分方程的矩阵表示
我们可以将二阶微分方程\( y^{\prime \prime}+b y^{\prime}+k y=0\)转化为\( 2 \times 2\)的一阶问题进行处理，构造方法类似先前的斐波拉契数列的处理方法。令\(\mathbf{u}=\left[\begin{array}{l} y^{\prime} \\ y \end{array}\right] \)，则有$$\mathbf{u}^{\prime}=\left[\begin{array}{l} y^{\prime \prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{cc} -b & -k \\ 1 & 0 \end{array}\right]\left[\begin{array}{l} y^{\prime} \\ y \end{array}\right]$$如果是\( k\)阶微分方程，那么需要一个\(k \times k \)矩阵，除了第一行和下面一排斜线上的元素之外，这个系数矩阵的其他元素都是零。以\( 5\)阶为例子，\(\begin{bmatrix} 1 & 1 & 1 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{bmatrix} \)，其中的\( 1\)表示可能有非零元素。

 

再谈线性空间和线性算子

【Linear Spaces】 拓展补充   xxx

A linear space \(V\) is any set that has a zero element and where elements can be added and scalar multiplied.

• (zero) \(0\) is in \(V\).
• (addition) if \(f\) and \(g\) are in \(V\) then so is \(f+g\).
• (scalar multiplication) if \(f\) is in \(V\) and \(c\) is a scalar then \(c f\) is in \(V\).

线性空间的例子： (注：zero function is the function \(z\) where \( z(t) -0\))

(1) \(C^{\infty}\) the set of smooth functions \(f: \mathbb{R} \rightarrow \mathbb{R}\)
Recall that a function is smooth if it is continuous and every derivative of it is also continuous We know from calculus that$$ \frac{d^{n}}{d t^{n}}(f+g)=\frac{d^{n} f}{d t^{n}}+\frac{d^{n} g}{d t^{n}} $$so if both of the derives on the right are continuous, so is the one on the left. This shows that a sum of two functions is again smooth. Similarly we can show a scalar multiple of a smooth function is smooth. The zero function is smooth, because it is a constant function.

(2) \(P\) the set of polynomials
Constant functions, and in particular the zero function, are polynomials. The sum of two polynomials is a polynomial, and a scalar multiple of a polynomial is a polynomial.

(3) \(C_{\text {per }}^{\infty}\) the set of smooth functions \(f: \mathbb{R} \rightarrow \mathbb{R}\) which are \(2 \pi\)-periodic (that is, \(f(t+2 \pi)=f(t)\))
We already showed the set of smooth functions is a linear space. so we just need to deal with the periodicity requirement. The zero function is constant, so it is \(2\pi\)-periodic. The sum of periodic functions is periodic, as is a scalar multiple of a periodic function.

(4) \(V\) the set of smooth functions \(f:[0,2 \pi] \rightarrow \mathbb{R}\) with \(f(0)=f(2 \pi)\)
In fact, it is equivalent to the space of \(2\pi\)-periodic functions—we are just focusing on one period.

【Differential Operators】:A differential operator is a linear transformation \(T: C^{\infty} \rightarrow C^{\infty}\) of the form$$ T(f)=f^{(n)}+a_{n-1} f^{(n-1)}+\cdots+a_{1} f^{\prime}+a_{0} f $$where \(a_{0}, a_{1}, \ldots, a_{n-1}\) are (possibly complex) constants. The order of \(T\) is \(n\), the highest derivative in the above expression.将\(f^{(n)}\)的系数设定为\( 1\)是为了方便。In practice, we can always scale things to make this happen.

微分算子和矩阵类似。对矩阵来说，它是有限维的，其作用对象—向量也是有限维的，我们可以求解其特征项值和特征向量；对于微分算子来说，我们可以将其看作是一个"无限维的向量"(严格来说不是向量，而是某种线性变换)，其作用对象也是无限维的函数，我们同样可以求解其特征值和特征向量。

微分算子的线性特性

• \(T(f+g)=T(f)+T(g)\)
• \(T(c f)=c T(f)\)

求解下面实例的kernel及其dimension

• \(T(f)=f^{\prime}\)
  A function \(f\) is in the kernel of \(T\) precisely when \(f^{\prime}=0\). So, the kernel is the space of constant functions. This is one dimensional.
• \(T(f)=f^{\prime}-\lambda f\)
  核对应的满足\(f^{\prime}-\lambda f\)的\(f\)组成的集合，显然\(f(t)=b e^{\lambda t}\)，其中\(b\)为任意常数。This is again one dimensional.
• \(T(f)=f^{\prime \prime}+k^{2} f\)
  核对应的满足\(f^{\prime \prime}+k^{2} f\)的\(f\)组成的集合。The kernel of \(T\) consists of solutions to the harmonic oscillator, so \(f(t)=a \cos (k t)+b \sin (k t)\). It is two dimensional, since \(\cos (k t)\) and \(\sin (k t)\) form a basis for ker \(T\).

定理—kernel的阶数：The kernel of an \(n\)-th order differential operator \(T\) is \(n\)-dimensional. It consists of solutions to the differential equation \(T(f)=0\). Differential equations of this form are called homogeneous.

【特征函数】
微分算子\(T\)的特征值和特征函数：其中\(f\)为a non-zero function，特征值\(\lambda\)为常数。$$T(f)=\lambda f$$

习题实例：有两个微分算子\(T(f)=f^{\prime \prime \prime}-6 f^{\prime \prime}-4 f^{\prime}+24 f\) and \(D(f)=f^{\prime}\)

(1) 求解\(D\)的特征值和特征函数：
即求解\(f^{\prime}=\lambda f\)，对任意\(\lambda\)来说，其特征函数为\(f(t)=b e^{\lambda t}\)

(2) Suppose \(f\) is an eigenfunction for \(D\) with eigenvalue \(\lambda\). What is \(T(f)\) ?
Suppose \(f(t)=b e^{\lambda t}\) is a \(\lambda\)-eigenfunction for \(D\). Then 带入到\(T(f)\)得到$$T\left(b e^{\lambda t}\right)=\left(\lambda^{3}-6 \lambda^{2}-4 \lambda+24\right) b e^{\lambda t}$$换句话说\(f(t)=b e^{\lambda t}\)也是\(T\)的特征函数，对应的特征值为\(\lambda^{3}-6 \lambda^{2}-4 \lambda+24\)。

(3) Use your answer to part (2) to find all functions of the form \(f(t)=e^{\lambda t}\) which solve the differential equation \(f^{\prime \prime \prime}-6 f^{\prime \prime}-4 f^{\prime}+24 f=0\)
The functions \(f(t)=e^{\lambda t}\) are eigenfunctions of \(T\) with eigenvalue \(\lambda^{3}-6 \lambda^{2}-4 \lambda+24\).
\(f^{\prime \prime \prime}-6 f^{\prime \prime}-4 f^{\prime}+24 f=0\)解得\(\lambda=\pm 2\) or \(\lambda=6\). Then according to \(f(t)=e^{\lambda t}\), the final solutions are \(e^{2 t}, e^{-2 t}\) and \(e^{6 t}\).

(4) Find the generic solution to \(f^{\prime \prime \prime}-6 f^{\prime \prime}-4 f^{\prime}+24 f=0\)
Solution. The solutions to this differential equation are the same as ker \(T\), which is 3dimensional, as \(T\) has order 3 . But in part (3) we found three linearly independent solutions \(e^{2 t}, e^{-2 t}\) and \(e^{6 t}\) (they are linearly independent because eigenfunctions with different eigenvalues are linearly independent). These solutions then span ker \(T\) and so the generic solution to the differential equation is $$ f(t)=c_{1} e^{2 t}+c_{2} e^{-2 t}+c_{3} e^{6 t} $$ for constants \(c_{1}, c_{2}, c_{3}\)

【特征多项式】(Characteristic Polynomial)
The characteristic polynomial of a differential operator \(T(f)=f^{(n)}+\) \(a_{n-1} f^{(n-1)}+\cdots+a_{1} f^{\prime}+a_{0} f\) is$$ p_{T}(\lambda)=\lambda^{n}+a_{n-1} \lambda^{n-1}+\cdots+a_{1} \lambda+a_{0} $$

定理—微分算子的特征值/特征向量：Suppose \(T\) is an order \(n\) differential operator and \(p_{T}(\lambda)\) its characteristic polynomial.
(1) The function \(e^{\lambda t}\) is an eigenfunction for \(T\) with eigenvalue \(p_{T}(\lambda)\), i.e., \(T\left(e^{\lambda t}\right)=p_{T}(\lambda) e^{\lambda t}\)
(2) If \(p_{T}(\lambda)\) has \(n\) distinct roots then the functions \(e^{\lambda_{1} t}, \ldots, e^{\lambda_{n} t}\) is a basis for ker \(T\).
(3) 对于齐次微分方程，即\(T(f)=0\)的情况，求求解算子\(T\)的特征值，即等价于求解\(p_T(\lambda)=0\)对应的\(\lambda\)。
(4) 对于最简单的情形\(\displaystyle\frac{d N}{d t}=\lambda N\)，特征方程的解为\(N=\exp (\lambda t)\)，如果\(\lambda \)为负数，那么\(N\)的演变为一个指数衰减，如果为正数，那么称指数增长。\( \lambda\)可以是任意复数，\(d/dt \)算子的作用空间是单变量可微函数的空间，该空间有无穷维(因为不是每个可微函数都可以用有限的基函数的线性组合来表达)。但是每个特征值所对应的特征空间是一维的，它就是所有形为\(N=N_{0} \exp (\lambda t)\)的函数集合，\(N_{0} \)为\(  t=0\)时刻的数量。

 

习题实例：Consider the differential equation \(f^{\prime \prime}+4 f^{\prime}+4 f=0\).

(1) Find the solutions of the form \(f(t)=e^{\lambda t}\).
特征多项式为\(p_{T}(\lambda)=\lambda^{2}+4 \lambda+4=(\lambda+2)^{2}\) which has a single root \(\lambda=-2\) with multiplicity \(2\). So the only solution of the form \(e^{\lambda t}\) is \(e^{-2 t}\).

(2) Show that \(f(t)=t e^{\lambda t}\) is also a solution.
\(f^{\prime \prime}+4 f^{\prime}+4 f=\left(12 e^{-2 t}-8 t e^{-2 t}\right)+4\left(-4 e^{-2 t}+4 t e^{-2 t}\right)+4\left(e^{-2 t}-2 t e^{-2 t}\right)=0\)

(3) What is the general solution to the differential equation?
The differential operator \(D^{2}+4 D+4\) has order 2, so its kernel is 2-dimensional. The functions \(e^{-2 t}\) and \(t e^{-2 t}\) are linearly independent and in the kernel, so are a basis for it. Therefore the general solution is $$ f(t)=c_{1} e^{-2 t}+c_{2} t e^{-2 t} . $$

Recap. Suppose \(T\) is an order \(n\) differential operator and \(p_{T}(\lambda)\) its characteristic polynomial.
(1) If \(p_{T}(\lambda)\) has \(n\) distinct roots \(\lambda_{1}, \ldots, \lambda_{n}\) then the functions \(e^{\lambda_{1} t}, \ldots, e^{\lambda_{n} t}\) are linearly independent solutions to the differential equation \(T(f)=0\).
(2) If \(\lambda\) is a repeated root of \(p_{T}(\lambda)\) with multiplicity \(m\), then the functions \(e^{\lambda t}, t e^{\lambda t}, t^{2} e^{\lambda t}, \ldots, t^{m-1} e^{\lambda t}\) are linearly independent solutions to the differential equation \(T(f)=0\).

参考资料：Math 21b