Quantum Physcis—Basic Concepts

videos lecture notes 图床Quantum Physcis-img/

Key Features of Quantum Mechanics

Quantum physics is the result of applying the framework of quantum mechanics to different physical phenomena.[mathjax]

Quantum Optics—applied to light and optical devices
Quantum Electrodynamics—applied to elelctromagnetism
Quantum Gravity—applied to gravitation

The era of quantum physics begins in 1925.

Linearity of the Equations of Motion

Nolinear theories: more complex, like Einstein’s theory of general relativity, classical mechanics.

Actually, for most cases of classical mechanics, they are linear. The only exceptions are , for example, simple harmonic oscillator. Here, we will show a few exmples for the nolinearity in classcial mechanics. $$F=\frac{d p}{d t} \quad where\quad F(x)=x^{3}$$ or the example from the notes: consider the equation of motion for a particle on a line under the a time-independent potential $ V(x)$, which is in general an arbitrary of $ x $. $$m \frac{d^{2} x(t)}{d t^{2}}=-V^{\prime}(x(t)) \quad where \quad \left.V^{\prime}(x(t)) \equiv \frac{\partial V(x)}{\partial x}\right|_{x=x(t)}$$

Linear theories: simple, straight-forward, like Maxwell’s theory of electromagnetism and quantum mechanics.

The linearity of Maxwell’s theory accounts for the fact that a single transatlantic cable can carry simultaneously millions of different kinds of information. Regarding linearity, the key properties are scaling and adding. For example, solution $ (\mathbf{E}, \mathbf{B}, \rho, \mathbf{J})$ gives the solution set $ (\alpha \mathbf{E}, \alpha \mathbf{B}, \alpha \rho, \alpha \mathbf{J}) $. Two solutions $ \left(\mathbf{E}_{1}, \mathbf{B}_{1}, \rho_{1}, \mathbf{J}_{1}\right) $ and $ \left(\mathbf{E}_{2}, \mathbf{B}_{2}, \rho_{2}, \mathbf{J}_{2}\right) $, give the solution $\left(\mathbf{E}_{1}+\mathbf{E}_{2}, \mathbf{B}_{1}+\mathbf{B}_{2}, \rho_{1}+\rho_{2}, \mathbf{J}_{1}+\mathbf{J}_{2}\right) $.

The characteristic of linearity can be expressed by linear operator $ L $($ L u=0 $), then here comes$$L\left(u_{1}+u_{2}\right)=L u_{1}+L u_{2}, \quad L(a u)=a L u$$ which implies $ L\left(\alpha u_{1}+\beta u_{2}\right)=\alpha L u_{1}+\beta L u_{2}$ as well. Note that $ \alpha u_{1}+\beta u_{2}$ is the general superposition of the solutions $ u_1 $ and $ u_2 $. Here, an simple example will help us have a better feeling of this operator:$$\frac{d u}{d t}+\frac{1}{\tau} u=0$$We can rewrite it as the form of operator: $$L u \equiv \frac{d u}{d t}+\frac{1}{\tau} u \equiv (\frac{d }{d t}+\frac{1}{\tau}){u}$$ Actually, due to the simplicity from linearity, in some sense, QM is simpler than CM. We can also write the Schr¨odinger equation as the form of linear operator: $$L \Psi \equiv i \hbar \frac{\partial \Psi}{\partial t}-\hat{H} \Psi$$

Complex Numbers are Essential

Quantum mechanics is the first physics theory that truly makes use of complex numbers.

All measurements in physics result in real numbers. In quantum mechanics, however, complex numbers are fundamental.
The measurable quantity in wave fucntion $\Psi $ is not a typical direct physical variable, and Born gave it probabilities interpretation with $ |\Psi|^{2} $.
It's useful to think of the wavefunction $ \Psi$ as a vector in some complex vector space.

Loss of Determinism

God does not play dice.—Einstein
Einstein, stop telling God what to do.—Niels Bohr

Getting a simple feeling of particles of light/photons:

A small laser pulse can contain many billions of photons.
Our eyes are very good photon detectors(see 10 photons in dark).
Light behaves like a particle. But it has nothing to do with a classcial zero-size object with definite position and velocity. A quantum mechanical particle: a packet of energy and momentum that is not composed of smaller packets.
In classcial physics, the results of an experiment can be determined by the conditions. While for photon invovled quantum mechanical, it is not deterministic.

Consider a polarizer whose preferential direction is aligned along the $ \hat{\mathbf{x}}$ direction, and light polarized along a direction forming an angle $ \alpha $ with the x-axis. Thinking of the light as a propagating wave, the incident electric field $$\mathbf{E}_{\alpha}=E_{0} \cos \alpha \hat{\mathbf{x}}+E_{0} \sin \alpha \hat{\mathbf{y}}$$So beyond the polarizer, $\mathbf{E}=E_{0} \cos \alpha \hat{\mathbf{x}} $, which means s means that the fraction of the beam’s energy that goes through the polarizer is $ (\cos \alpha)^{2}$. Meanwhile, the same frequency as the incident light. Since all the photons in the incident beam are identical and do not interact with each other(premise), whether one photon goes through or is absorbed should be determined/predicted. One goes, then all goes; one is absorbed, then all are absorbed. But this is not the case so that a loss of determinism appears. What we can really talk about is probability, and in our case, a probability of $ (\cos \alpha)^{2} $ is for "go through", and $ 1-(\cos \alpha)^{2} $ for "absorption". Einstein and others suggested the existence of hidden variable that classify the "identical photons" as we discussed before, which was proven wrong by John Bell. Superposition of the two states: $$\mid \text { photon } ; \alpha\rangle=\cos \alpha \mid \text { photon } ; x\rangle+\sin \alpha \mid \text { photon } ; y\rangle$$ Note that ket is a state/vector, and $ \mid \text { photon } ; x\rangle$ is the state beyong the polarizer.

Quantum Suerpositions

Mach-Zehnder interferometer

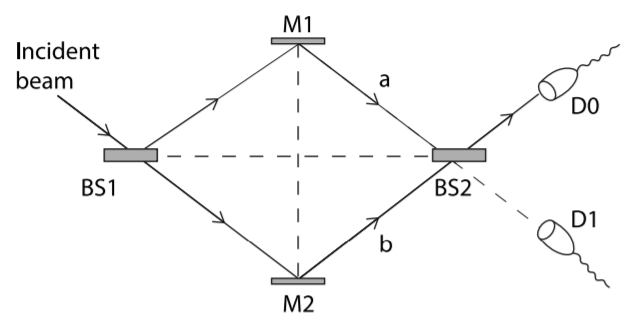Constructive interference happens on the top of BS2, giving a beam going into D0, while destructive interference happens on the bottom of BS2 with no beam for D1. Or, vice versa(the other way around). We should keep it in mind that where there is constructive interference, there should be destructive interference somewhere. Otherwise, the energy is not conservative. If we think of the incoming photon is sent one by one, then this is what is going to happen. Each photon is in superposition of two states: upper beam(M1) and lower beam(M2). Then, it interferes constructively with itself on the top/bottom of BS2.

Notes:
1. If two different photons interfere constructively on the top of BS2, then e total energy is four times. Or for destructive interference, two photons end up giving no photon. (a litte bit confused)
2. The projection of the polarized light along $ x$ and $ y$ axis as we discussed above is also an example of quantum superposition. That is to say, every polarized light photon can be seen as the result of the combination of two quantum states.
3. wavefunction = quantum state = vector

Physical state is the super position: $$|\Psi\rangle=\alpha|A\rangle+\beta|B\rangle, \quad \alpha, \beta \in \mathbb{C}$$If we measure it, we either get $a $ or $ b $, not the intermediate value between $ a$ and $ b $. $$\text { Probability }(a) \sim|\alpha|^{2}, \quad \text { Probability }(b) \sim|\beta|^{2}$$

Quantum mechanics assumption: Superposing a state with itself doesn’t change the physics.$$|A\rangle \cong 2|A\rangle \cong i|A\rangle \cong-|A\rangle$$

A superposition of a spin up and a spin down state$$|\Psi\rangle=|\uparrow ; z\rangle+|\downarrow ; z\rangle$$The probability for an electron with spin up or an electron with spin down is equal if we measure it.

Entanglement

Entangled states of two particles are those in which we can’t speak separately of the state of each particle.

Particle 1: a set of states $ \left\{\left|u_{1}\right\rangle,\left|u_{2}\right\rangle, \ldots\right\}$
Particle 2: a set of states $ \left\{\left|v_{1}\right\rangle,\left|v_{2}\right\rangle, \ldots\right\}$
Particle 1&2 system: a set of states (not entangled)$\left|u_{i}\right\rangle \otimes\left|v_{j}\right\rangle, \quad i, j \in \mathbb{N} $
Particle 1&2 system: (entangled) $ \left|u_{1}\right\rangle \otimes\left|v_{1}\right\rangle+\left|u_{2}\right\rangle \otimes\left|v_{2}\right\rangle$

Experiments with Photons

Mach-Zehder Interferometer

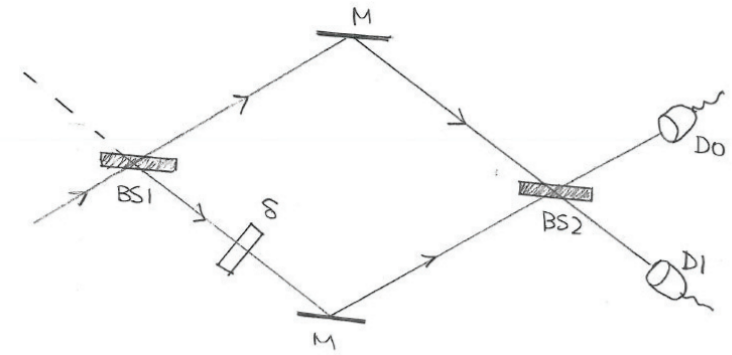For the incident beams, now it can comes either from the top or from the bottom of BS1. Here, we use the vector $ \left(\begin{array}{l} \alpha \\ \beta \end{array}\right)$ to encode the information about the probabilities of finding on the top ($ |\alpha|^{2} $) and on the bottom ($ |\beta|^{2}$). Since the photon must be found in either one of the beams we must have$$|\alpha|^{2}+|\beta|^{2}=1$$We use two different vectors to describe the state of upper beam and lower beam: $$\text{photon on upper beam: }\left(\begin{array}{l}1 \\ 0\end{array}\right) \quad \text{photon on bottom beam :} \left(\begin{array}{l}0 \\ 1\end{array}\right)$$Therefore$$\left(\begin{array}{l} \alpha \\ \beta \end{array}\right)=\left(\begin{array}{l} \alpha \\ 0 \end{array}\right)+\left(\begin{array}{l} 0 \\ \beta \end{array}\right)=\alpha\left(\begin{array}{l} 1 \\ 0 \end{array}\right)+\beta\left(\begin{array}{l} 0 \\ 1 \end{array}\right)$$In the lower branch, there is a phase shifter of phase factor $ e^{i \delta}$. The amplitude gets multiplied by the phase.

Phase-shifter does not change the probability to find the photon.
For example, if $\delta = \pi $, π the effect of the phase shifter is to change the sign
of the wavefunction since $ e^{i \pi}=-1$.

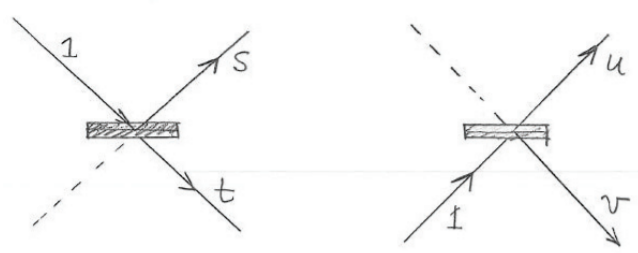The effect of the beam splitter is to give an output wavefunction for each of the two cases: $$\text { Left BS: }\left(\begin{array}{l} 1 \\ 0 \end{array}\right) \rightarrow\left(\begin{array}{l} s \\ t \end{array}\right), \quad \text { Right BS: } \quad\left(\begin{array}{l} 0 \\ 1 \end{array}\right) \rightarrow\left(\begin{array}{l} u \\ v \end{array}\right)$$Therefore, an incident photon state $ \left(\begin{array}{l} \alpha \\ \beta \end{array}\right) $ would give $$\left(\begin{array}{l} \alpha \\ \beta \end{array}\right)=\alpha\left(\begin{array}{l} 1 \\ 0 \end{array}\right)+\beta\left(\begin{array}{l} 0 \\ 1 \end{array}\right) \rightarrow \alpha\left(\begin{array}{l} s \\ t \end{array}\right)+\beta\left(\begin{array}{l} u \\ v \end{array}\right)=\left(\begin{array}{l} \alpha s+\beta u \\ \alpha t+\beta v \end{array}\right)=\left(\begin{array}{ll} s & u \\ t & v \end{array}\right)\left(\begin{array}{l} \alpha \\ \beta \end{array}\right)$$In summary, the BS1 produces the followin effect$$\left(\begin{array}{l} \alpha \\ \beta \end{array}\right) \rightarrow\left(\begin{array}{ll} s & u \\ t & v \end{array}\right)\left(\begin{array}{l} \alpha \\ \beta \end{array}\right)$$The constarints on operator(BS matrix) are as follows $$\begin{aligned} |s|^{2}+|t|^{2} &=1 \\ |u|^{2}+|v|^{2} &=1 \end{aligned}$$Here, the beam splitters are balanced, so we get $$|s|^{2}=|t|^{2}=|u|^{2}=|v|^{2}=\frac{1}{2}$$In order to keep the vector normalized after the effect of operator, the following must holds$$((\alpha s+\beta u)^2+(\alpha t+\beta v)^2=1)$$which results in $ su+tv =0$. Then, we can guess$$\left(\begin{array}{ll} s & u \\ t & v \end{array}\right)=\left(\begin{array}{lr} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array}\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\right)$$The minus sign in the bottom right means that a photon incident from below, as it is reflected, will have its amplitude changed by a sign or equivalently a phase shift by $ \pi $. Actually, the coating with middle refractive index between glass and air is on the bottom side, so there exist half-wave loss. Another possibility for a beam splitter (a dielectric coating on the top side) matrix is with left top minus. For our case, BS1 have its coating on the top side, while BS2 bottom side. $$\mathrm{BS} 1: \frac{1}{\sqrt{2}}\left(\begin{array}{rr} -1 & 1 \\ 1 & 1 \end{array}\right), \quad \text { BS } 2: \quad \frac{1}{\sqrt{2}}\left(\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\right)$$Therefore$$\text { input : }\left(\begin{array}{l} \alpha \\ \beta \end{array}\right) \quad \text { output: } \frac{1}{\sqrt{2}}\left(\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\right) \frac{1}{\sqrt{2}}\left(\begin{array}{rr} -1 & 1 \\ 1 & 1 \end{array}\right)\left(\begin{array}{l} \alpha \\ \beta \end{array}\right)=\frac{1}{2}\left(\begin{array}{cc} 0 & 2 \\ -2 & 0 \end{array}\right)\left(\begin{array}{l} \alpha \\ \beta \end{array}\right)=\left(\begin{array}{c} \beta \\ -\alpha \end{array}\right)$$For example, the incident photon beam $ \left(\begin{array}{l} 0 \\ 1 \end{array}\right) $, then the output from the interferometer is $ \left(\begin{array}{l} 1 \\ 0 \end{array}\right) $.
If we put conceret between BS1 and lower mirror(input the same), then for the BS1, the first matrix still works, which gives$$\frac{1}{\sqrt{2}}\left(\begin{array}{rr} -1 & 1 \\ 1 & 1 \end{array}\right)\left(\begin{array}{l} 0 \\ 1 \end{array}\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{l} 1 \\ 1 \end{array}\right)$$Because of the block, the lower element becoms zero, but BS2 matrix works for the upper path as well, which gives$$\frac{1}{\sqrt{2}}\left(\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\right)\left(\begin{array}{c} \frac{1}{\sqrt{2}} \\ 0 \end{array}\right)=\left(\begin{array}{l} \frac{1}{2} \\ \frac{1}{2} \end{array}\right)$$ It is noteworthy that before blocking the lower path we could not get a photon to D1. The probability to reach D1 is now 1/4 and was increased by blocking a path.

Elitzur-Vaidman Bombs

Particle Nature of Light and Wave Nature of Matter

Photoelectric Effect

quanta是爱因斯坦用的，photon是化学剂lewis发明的。h是密立根测出来的，个普朗克在拟合黑体辐射也用到

Compton Scattering, Matter Waves (PDF)