视频 课程官网 别人的笔记1 笔记2 263 and 278 两门课 语言不同,但是有重叠,有融合。
傅里叶级数与傅里叶变换
傅里叶级数的简单可视化
從三角求和公式到 Fourier 級數
值得学习的笔记1 为什么要进行傅立叶变换
需要补充的内容
- 补充狄利克雷条件
- 吉布斯现象
- 负频率,参考珂学原理,和电路设计漫谈之66: 负频率是怎么来的?
性质和公式汇总
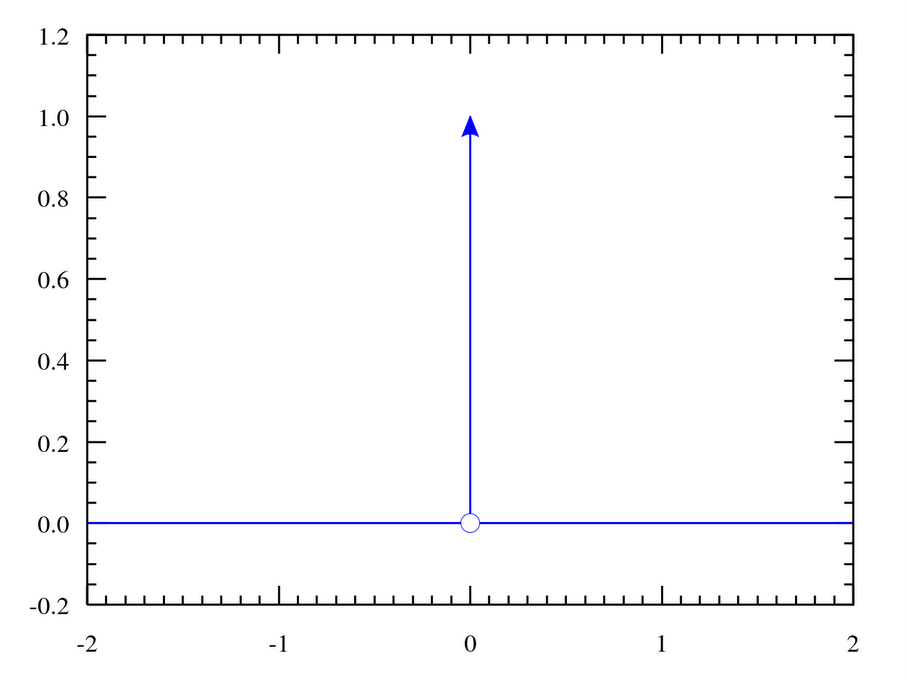
狄拉克函数的性质
先回顾一下基本定义,满足\( \delta(x)=\left\{\begin{array}{ll} +\infty, & x=0 \\ 0, & x \neq 0 \end{array}\right. \),而且\(\displaystyle\int_{-\infty}^{\infty} \delta(x) d x=1 \),它是一个广义函数,在物理学中常用其表示质点、点电荷等理想模型的密度分布。
 具有如下性质:
具有如下性质:
(1) 挑选性$$\int_{-\infty}^{\infty} f(x) \delta\left(x-x_{0}\right) d x=f\left(x_{0}\right)$$上式表示\(f(x)\)和\(\delta\left(x-x_{0}\right)\)的乘积积分即精确挑出\(f(x)\)在\(x=x_0\)处的函数值\( f(x_0)\)。当我们将\(x_0\)看作变化的量,那么\(f(x_0)=f(x_0) * \delta(x_0)=\displaystyle\int_{-\infty}^{\infty} f(x) \delta\left(x_0-x\right) d x\)卷积,由于\( \delta \)函数的特殊性,该式子右侧部分和上式左侧部分虽然写法不同,但是结果相同。从卷积的角度看,就是将原函数拆成一个个无穷多个连续冲激的形式,冲激的幅度是原函数在这一点的函数值,以此来重新复刻原函数。在信号处理中,\( f(t)=\displaystyle\int_{-\infty}^{\infty} f(\tau) \delta(t-\tau) d \tau=\int_{-\infty}^{\infty} \delta(\tau) f(t-\tau) d \tau\),这个式子的表达更加清晰,第二个等号利用的是卷积的Commutativity性质(参考[珂学原理-视频])。
(2) 频谱为常数
根据傅里叶变换我们可以得到频谱$$F(k)= \int_{-\infty}^{\infty} \delta(x-0) e^{-i k x} d x= e^{-i k \cdot 0}=1$$为一个常数,说明函数的频率是均匀分布的,即个频率分量所占的比例相同!
从频谱的逆变换定义\(\delta\)函数$$\delta(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{i k x} d k$$
(3) 泛函
在性质(1)中,我们提到"从卷积的角度看,就是将原函数拆成一个个无穷多个连续冲激的形式,冲激的幅度是原函数在这一点的函数值,以此来重新复刻原函数"。这其实就是泛函的思想,\(f(t)=\displaystyle\int_{-\infty}^{\infty} f(\tau) \delta(t-\tau) d \tau\),即输入不同的\(\delta(t-\tau)\)函数,然后通过\(f(\tau)\)的作用(先相乘,然后积分),得到不同的数值,所有的数值最后按照对应\(t\)的大小排列,最后重新复刻出\(f(t)\)。
(4) 电动力学中的相关公式
\(\nabla \cdot\left(\displaystyle\frac{\hat{\boldsymbol{r}}}{r^2}\right)=4 \pi \delta(\boldsymbol{r})\),\(\nabla^2(1 / r)=-4 \pi \delta(\boldsymbol{r})\),其中\(\delta(\boldsymbol{r})=\delta(x) \delta(y) \delta(z)\)。
(5) 卷积核,扩散,高斯波包等等,待补充
参考资料:
(1) delta 函数及其性质—知乎
(2) delta函数及其性质—进阶版
(3) Dirac delta function—Wiki
傅里叶变换的性质
回顾一下连续傅里叶变换和逆变换:(注:保证变换和逆变换前面系数乘积为\( 1\)即可)
数学家的写法$$\begin{aligned} &F(k)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} f(x) e^{-i k x} d x\\ &f(x)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} F(k) e^{i k x} d k \end{aligned}$$物理和工程师的写法$$\begin{aligned} &F(k)= \int_{-\infty}^{+\infty} f(x) e^{-i k x} d x\\ &f(x)=\frac{1}{2 \pi} \int_{-\infty}^{+\infty} F(k) e^{i k x} d k \end{aligned}$$可以参考网友笔记:傅里叶变换的性质
(1) 周期为\(1\)的函数的傅里叶系数:$$\begin{aligned} f(t) &=\sum_{k=-n}^{n} \hat{f}(k) e^{2 \pi i k t} \\ \hat{f}(k) &=\int_{0}^{1} e^{-2 \pi i k t} f(t) d t \end{aligned}$$
(2) 非周期函数的傅里叶级数:$$\begin{aligned} C_{k} &=\frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) e^{-2 \pi i \frac{k}{T} t} d t \\ f(t) &=\sum_{k=-\infty}^{\infty} C_{k} e^{2 \pi i \frac{k}{T} t} \end{aligned}$$
(3) 连续傅里叶变换:如果\( f(t)\)的周期被定为在整个实数域中,即\( -\infty<T<\infty \),那么其傅里叶变换为$$ \mathcal{F} f(s)=\int_{-\infty}^{\infty} e^{-2 \pi i s t} f(t) d t $$
(4) 傅里叶变换的对偶性$$F(-s)=\mathcal{F} f(-s)=\int_{-\infty}^{\infty} e^{2 \pi i s t} f(t) d t=\mathcal{F}^{-1} f(s)$$
$$(\mathcal{F} f)^{-}=\mathcal{F}^{-} f=\mathcal{F}\left(f^{-}\right)$$
$$\mathcal{F} \mathcal{F} f=\mathcal{F}(\mathcal{F} f)=\mathcal{F}\left(\mathcal{F}^{-}\left(f^{-}\right)\right)=f^{-}$$
$$\mathcal{F} \operatorname{sinc}=\mathcal{F} \mathcal{F} \pi=\pi^{-}=\pi$$
(5) 奇偶虚实性:一般情况下\(f(t)\)是复函数,因而可以把它表示成模与相位或者实部与虚部两部分,即$$F(s)=|F(s)| e^{ i \varphi(s)}=R(s)+i X(s)$$(5-1)如果\( f(t)\)为实数:$$F(s)=\int_{-\infty}^{\infty} f(t) e^{-2\pi i s t}dt=\int_{-\infty}^{\infty} f(t) \cos (2\pi s t) d t-i \int_{-\infty}^{\infty} f(t) \sin (2\pi s t) d t$$显然此时的频谱实部\( R(s)\)为偶函数,虚部\(X(s)\)为奇函数。根据\(|F(s)|=\sqrt{R^2(s)+X^2(s)}\)可知,此时的幅度谱也是偶函数。当\(f(t)\)为实偶函数,则频谱函数为实偶函数;当\(f(t)\)为实奇函数,则频谱函数为虚奇函数。比如余弦函数的傅里叶变换就是实偶函数\(\mathcal{F} \cos (2 \pi a x)=\displaystyle\frac{1}{2}\left(\delta_a+\delta_{-a}\right)\);上面讨论的\( \delta (x)\)也是实偶函数,其傅里叶变换为常数(实偶函数);正弦函数的傅里叶变换就是虚奇函数\(\mathcal{F} \sin (2 \pi a x)=\displaystyle\frac{1}{2 i}\left(\delta_a-\delta_{-a}\right)\)。
(5-2) 如果\(f(t)\)为虚函数,令\(f(t)=j g(t)\),则有$$ \left\{\begin{array}{l} R(s)=\displaystyle\int_{-\infty}^{\infty} g(t) \sin (2\pi s t) d t \\ X(s)=\displaystyle\int_{-\infty}^{\infty} g(t) \cos (2\pi s t) d t \end{array}\right. $$此时\(R(s)\)是奇函数,\(X(s)\) 是偶函数,而 \(|F(s)|\) 仍然为偶函数,\(\varphi(s)\)仍然为奇函数。
(9) 时延迟性(delayed)$$f(t \pm b) \leftrightarrow e^{\pm 2 \pi i s b} F(s)$$这在频谱上并不体现出了,因为模长没变,变的是相位。从相位移动角度$$F(s)=|F(s)| e^{2 \pi i \theta(s)}$$
(10) 尺度变化$$f(a t) \leftrightarrow \frac{1}{|a|} F\left(\frac{s}{a}\right)$$
(11) 线性(linearity)性质$$\mathcal{F} (\alpha f)+\mathcal{F} (\beta g)=\alpha \mathcal{F}f+\beta\mathcal{F}g$$
(12) 卷积(convolution)定理:\( (g * f)(x)=\displaystyle\int_{-\infty}^{\infty} g(x-y) f(y) d y\)
时域卷积:(例子\( \mathcal{F}(\Pi * \Pi)=(\mathcal{F} \Pi)(\mathcal{F} \Pi)=\operatorname{sinc}^{2}=\mathcal{F} \Lambda\))$$\mathcal{F}(g * f)=(\mathcal{F} g)(\mathcal{F} f)$$频域卷积$$\mathcal{F}(f \cdot g)=\mathcal{F}(f) * \mathcal{F}(g)$$
(13) 滤波:\(G(s)=F(s) H(s) \) 其中\( H(s)\)是传递函数,\( F(s) \)是原始信号的频谱,\( G(s) \)是滤波后的频谱,对\( G(s) \)做傅里叶逆变换就得到滤波后的时域信号。
(14) 傅里叶导数定理:$$\mathcal{F}\left(f^{\prime}\right)(s)=2 \pi i s(\mathcal{F} f)(s)$$推广:$$\mathcal{F}\left(f^{n}\right)(s)=(2 \pi i s)^{n}(\mathcal{F} f)(s)$$
(15) 概率分布与卷积:同分布独立随机变量的和的密度函数为他们各自密度函数的卷积$$p\left(x_{1}+x_{2}+\ldots+x_{n}\right)=p_{1} * p_{2} * \ldots * p_{n}$$如果是同分布的,卷积四五次就非常接近高斯分布的形状了。
(16) Parseval定理$$\int_{-\infty}^{\infty}|\mathcal{F} f(s)|^{2} d s=\int_{-\infty}^{\infty}|f(x)|^{2} d x$$该等式表明信号在时域与频域的能量(功率)相等。其一般形式为:
设有\( f(x), g(x) \in S\),则$$\int_{-\infty}^{\infty} \mathcal{F} f(s)\overline{ \mathcal{F}g(s) } d s=\int_{-\infty}^{\infty} f(x) \overline{ g(x)} d x$$
(17) \( \delta\)函数的极限定义:$$\delta(x)=\lim _{\epsilon \rightarrow 0} \frac{1}{\epsilon} f\left(\frac{x}{\epsilon}\right)$$其中\( f\)满足\( \displaystyle\int_{-\infty}^{\infty} f(x) d x=1\)
(18) 广义函数/分布$$\left\langle T_{f}, \phi\right\rangle=\int_{-\infty}^{\infty} f(x) \phi(x) d x$$重新定义脉冲函数:\( \langle\delta, \varphi\rangle=\varphi(0) \)
推广得到新的分布\( \delta_{a}\):\( <\delta_{a}, \varphi>=\varphi(a)\)
傅里叶变换可以看作是一个广义函数\( e^{-2 \pi i s x}\)(测试函数的集合是\( S\)):$$\mathcal{F} f(x)=\left\langle e^{-2 \pi i s x}, f(x)\right\rangle=\int_{-\infty}^{\infty} e^{-2 \pi i s x} f(x) d x$$
(19) 广义函数/分布$$\left\langle T_{f}, \phi\right\rangle=\int_{-\infty}^{\infty} f(x) \phi(x) d x$$重新定义脉冲函数:\( \langle\delta, \varphi\rangle=\varphi(0) \)
推广得到新的分布\( \delta_{a}\):\( <\delta_{a}, \varphi>=\varphi(a)\)
傅里叶变换(正余弦、常数函数同样可以)可以看作是一个广义函数\( e^{-2 \pi i s x}\)(测试函数的集合是\( S\)):$$\mathcal{F} f(x)=\left\langle e^{-2 \pi i s x}, f(x)\right\rangle=\int_{-\infty}^{\infty} e^{-2 \pi i s x} f(x) d x$$
(20) 缓增分布\( T \)的傅里叶变换:$$\langle\mathcal{F} T, \varphi\rangle=\langle T, \mathcal{F} \varphi\rangle$$逆变换$$<\mathcal{F}^{-1} T, \varphi>=<T, \mathcal{F}^{-1} \varphi>$$
例子:
- \(<\mathcal{F} \delta, \varphi>=<1, \varphi>\)
- \(<\mathcal{F} e^{2 \pi i a x}, \varphi>=\left\langle\delta_{a}, \varphi\right\rangle \)
- \( \mathcal{F} \cos (2 \pi a x)=\displaystyle\frac{1}{2}\left(\delta_{a}+\delta_{-a}\right)\)
- \( \mathcal{F} \sin (2 \pi a x)=\displaystyle\frac{1}{2 i}\left(\delta_{a}-\delta_{-a}\right)\)
(21) 分布的导数\( T^{\prime}\) $$<T^{\prime}, \varphi>=-<T, \varphi^{\prime}>$$
分布的导数的傅里叶变换/分布的傅里叶变换的导数$$\begin{array}{c}
\mathcal{F}\left(T^{\prime}\right)=2 \pi i s \mathcal{F} T \\
(\mathcal{F} T)^{\prime}=\mathcal{F}(-2 \pi i t T)
\end{array}$$
(22) 分布的乘积(要求\( f \varphi \in S\))$$<T f, \varphi>=\int_{-\infty}^{\infty} T(x) f(x) \varphi(x) d x=<T, f \varphi>$$利用这个可以推导出\( \delta\)函数的抽样性\( f \delta_{a}=f(a) \delta_{a}\)
(23) 分布的卷积 $$<S * T, \varphi>=<S(x),<T(y), \varphi(x+y)>>$$注:成立条件为\( <T(y), \varphi(x+y)>\)是一个测试函数。
利用这个推导出\( f * \delta=f \) 和\( f(x) * \delta_{a}(x)=f(x-a)\)以及\(\delta_{a} * \delta_{b}=\delta_{a+b} \)
(24) \(\delta(x) \)函数的缩放特性$$\delta(a x)=\frac{1}{|a|} \delta$$
(25) 狄拉克梳子$$\mathrm{III}_{p}=\sum_{k=-\infty}^{\infty} \delta(x-k p)$$三个性质:采样、周期和傅里叶变换 $$f(x) \Pi I_{p}(x)=\sum_{k=-\infty}^{\infty} f(k p) \delta(x-k p)$$ $$\left(f * \Pi I_{p}\right)(x)=\sum_{k=-\infty}^{\infty} f(x-k p)$$ $$\begin{aligned} \mathcal{F} \mathrm{III}_{p} &=\frac{1}{p} \mathrm{III}_{\frac{1}{p}} \\ \mathcal{F}^{-1} \mathrm{III}_{p}&=\frac{1}{p} \mathrm{III}_{\frac{1}{p}} \end{aligned}$$对于标准梳子\( \mathcal{F} \mathrm{III}=\mathrm{III}\)
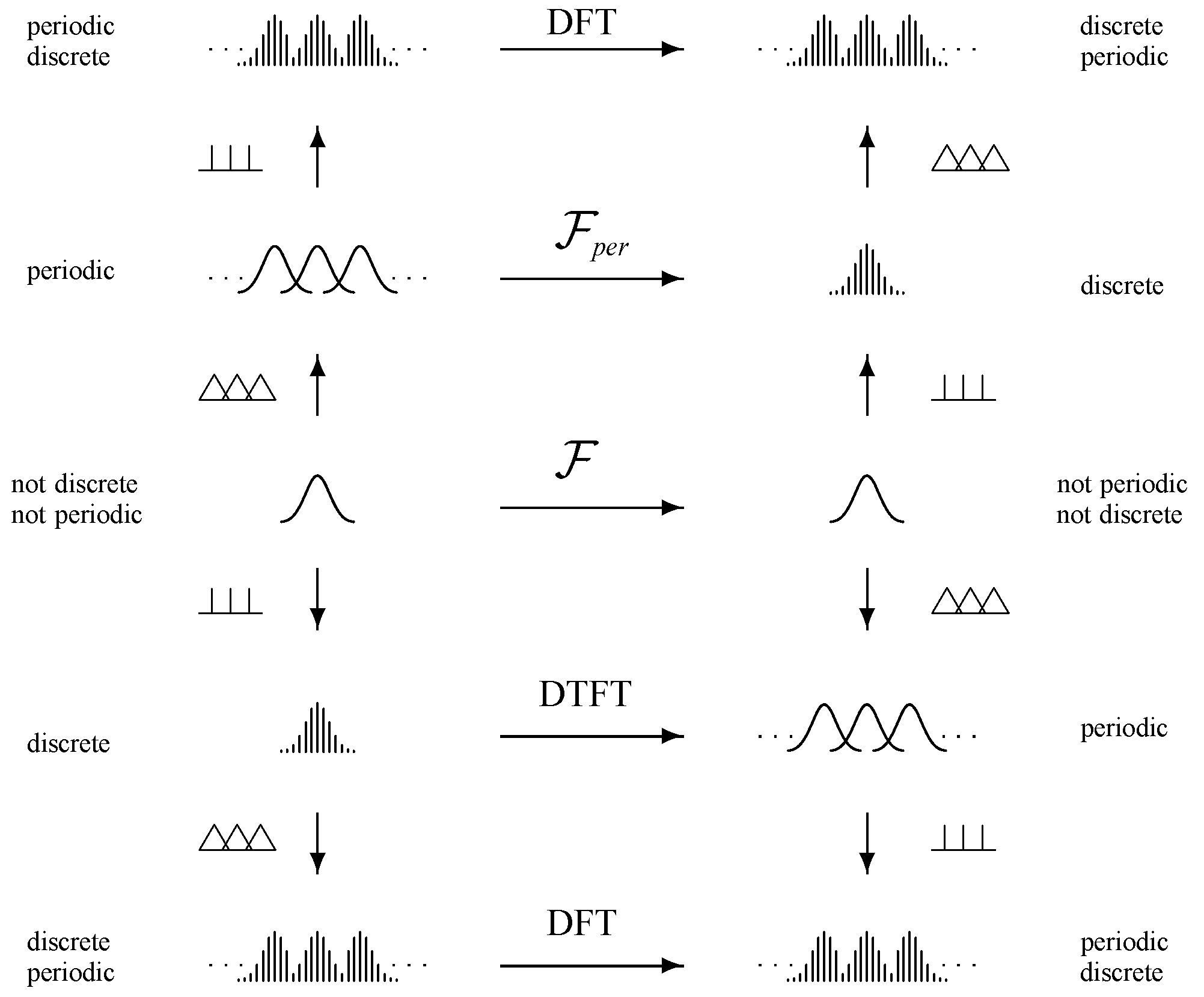
(26) 信号与系统里面有一个重要的口诀: 离散对周期,周期对离散。时域如果是离散的,频域就是周期的;如果频域离散,时域就要周期。如果时域既是离散又是周期,那么频域也既是离散又是周期。
下图是Four Fourier transforms and the links ⊥⊥⊥ and △△△ between them. In the tempered distributions(缓增分布) sense, all four transforms \(\mathcal{F}\), \( \mathcal{F}_{p e r}\), DTFT and DFT reduce to only one Fourier transform, the Fourier transform on tempered distributions. (来自文献Four Particular Cases of the Fourier Transform)