MIT-多变量微积分-2

原来的求解极值的方法，得到的结果，很可能不满足约束条件。[mathjax]

多元函数及其微分

二元函数及其切线逼近和优化

多元函数比如$ f(x,y)=$temperature at point $ x,y)$，我们这里只讨论二元和三元的情况，更多元的情况分析方法类似。

1. 变量的函数图像

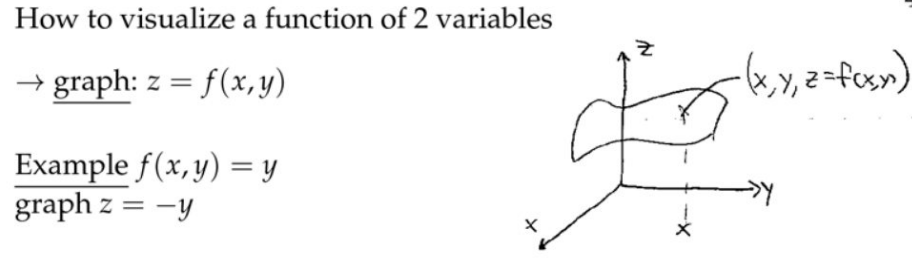
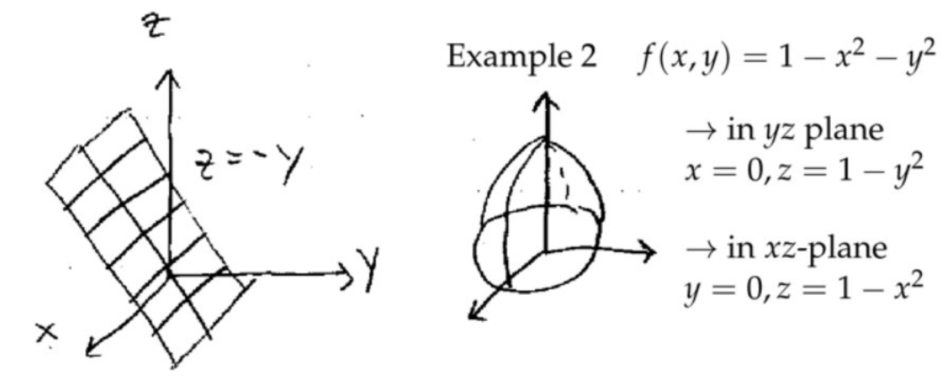
所以对$ f(x, y)=1-x^{2}-y^{2}$最终就是沿着$ z$轴旋转一圈。

2. 等高线图(Contour plot)
3. 等值线(level curve)

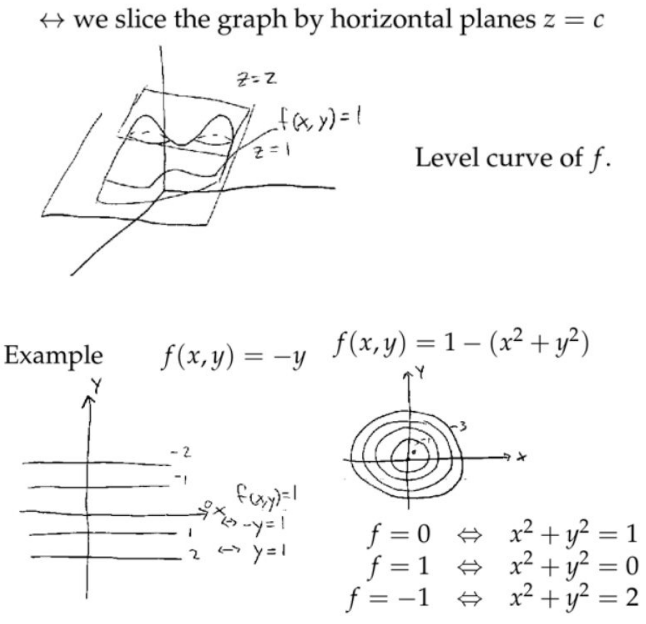
如果从$ f=1 $变化到$f=2 $，$ x-y$平面中的两条线相距很近(线的分布很密)，表示从$ z $轴上看，高度变化很剧烈，或者说“山峰很陡峭”。

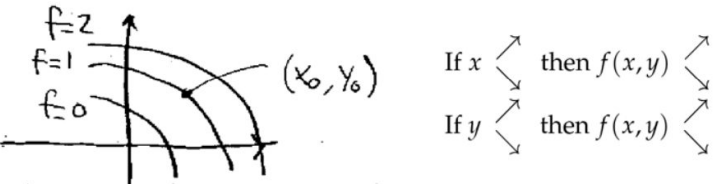
4. 偏导数(Partial derivatives)
从切平面的角度看偏导数
$$\begin{aligned}&\text { Example: } f(x, y)=x^{3} y+y^{2} \quad \frac{\partial f}{\partial x}=3 x^{2} y+0\\ &\frac{\partial f}{\partial y}=x^{3}+2 y\end{aligned}$$
5. 近似公式(Approximation Formula)
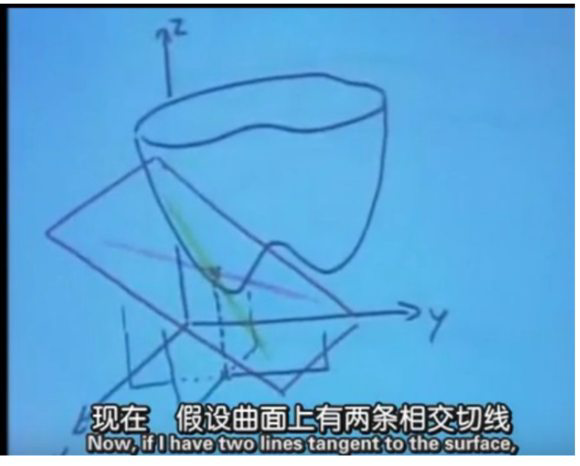
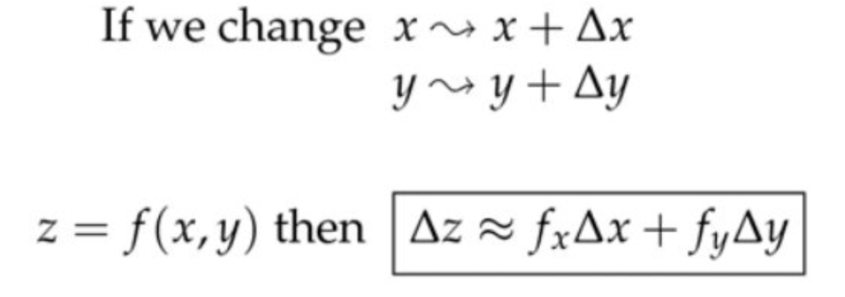证明：对于$z=f(x, y) $，我们可以确定任意点的沿着在$ y-z$和$ x-z $平面上的两条切线，对应的斜率为$ f_x $和$ f_y$。那么根据这两个切线我们就可以确定一个平面，在该平面内，微小移动或者$y $，都满足$$\Delta z \approx f_{x} \Delta x+f_{y} \Delta y$$例子
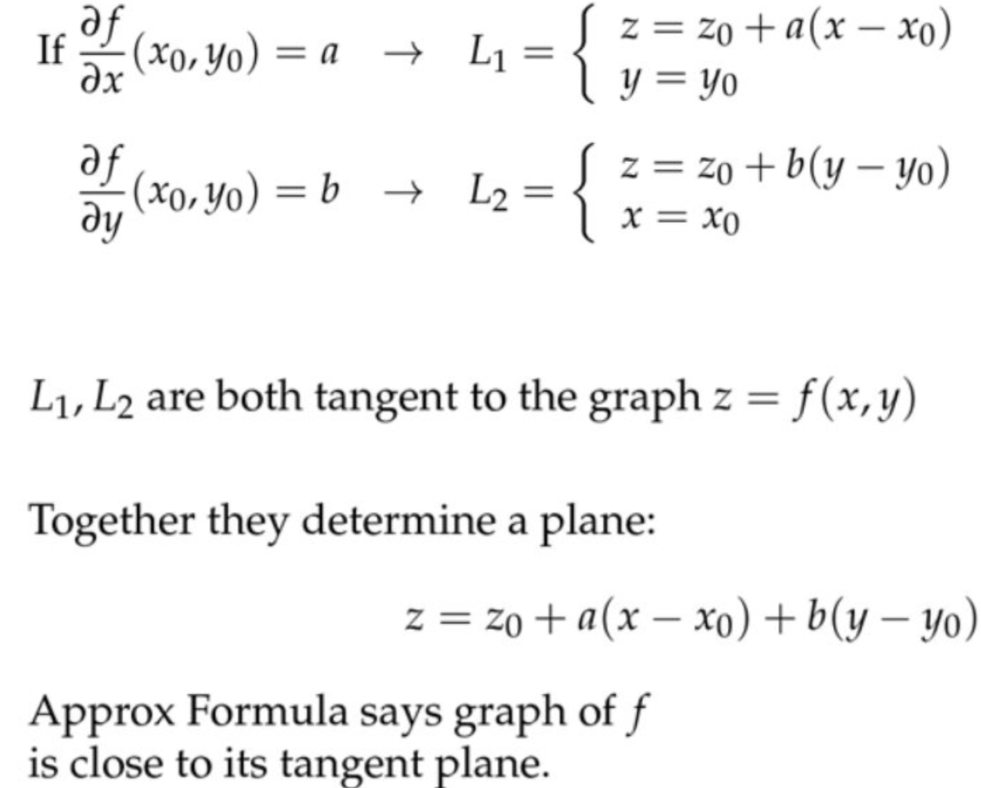对该平面方程$ z=z_{0}+a\left(x-x_{0}\right)+b\left(y-y_{0}\right) $来说，如果固定$x=x_0 $，显然就得到了$ f_{y} $对应的切线$ L_2 $；如果固定$y=y_0 $，显然就得到了$ f_{x} $对应的切线$ L_1 $。说白了就是平面退化成直线。
注：$$L_{1}=\left\{\begin{array}{l}
z=z_{0}+a\left(x-x_{0}\right) \\
y=y_{0}
\end{array}\right.$$(a) 这种表示表示直线的方法是写出了两个平面的方程，那么它们的组合就是两个平面的交线方程。我们在前面是将所求直线上的点看作moving point，然后用参数方程求解的。

(b) 对于极小值或者极大值点，$ \Delta z \approx f_{x} \Delta x+f_{y} \Delta y=0$，实际是，从偏导数都为零的点，稍微移动一下，变动的函数值是$ \Delta x$或者$ \Delta y$的高阶无穷小。(可以对比一下一元函数的泰勒一阶展开的近似处理)

另外的方法得到平面方程：
用参数方程表示这两条切线，让后做向量的外积，得到所求平面的法向量，可以先写出过原点的所求平面的方程，即$$ax+by-z=0$$然后将该平面沿着法向量方向平移到过$(x_0,y_0,z_0) $，即
$z=z_{0}+a\left(x-x_{0}\right)+b\left(y-y_{0}\right) $。
具体方法为，将切线$L_1 $上的点看作moving points，将其方程看作是关于$ x$的参数方程，那么由切点$ (x_0,y_0,z_0)$出发的沿着该切线方向的方向向量为$ <x-x_0,0, a(x-x_0)>$；同理可以得到另一条切线的方向向量为$ <0,y-y_0, b(y-y_0)>$。二者外积$$\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=\left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x-x_0 & 0 & a(x-x_0)\\ 0 & y-y_0 & b(y-y_0) \end{array}\right|$$化简一下就知道切平面的法向量方向为$ <a,b,-1> $再带入$(x_0,y_0,z_0) $即可得到该点切平面的方程。

6. 偏导数的应用
(a) find min/max of a function of $ f(x,y)$
当$f_{x}=0 \text { and } f_{y}=0 $时，上面提到的切平面(tangent plane) is horizontal(水平的)。
例子：$ f(x, y)=x^{2}-2 x y+3 y^{2}+2 x-2 y $

$$f(x, y)=[(x-y)+1]^{2}+2 y^{2}-1 \geq-1=f(-1,0), \text { so minimum }$$

(b) 最小二乘法
$$\begin{aligned} &\text { Want: } \frac{\partial D}{\partial a}=\sum_{i=1}^{n} 2\left(y_{i}-\left(a x_{i}+b\right)\right)\left(-x_{i}\right)=0\\ &\frac{\partial D}{\partial b}=\sum_{i=1}^{n} 2\left(y_{i}-\left(a x_{i}+b\right)\right)(-1)=0 \end{aligned}$$ $$\Leftrightarrow\left\{\begin{array}{l} \displaystyle\sum_{i=1}^{n}\left(x_{i}^{2} a+x_{i} b-x_{i} y_{i}\right)=0 \\ \displaystyle\sum_{i=1}^{n}\left(x_{i} a+b-y_{i}\right)=0 \end{array}\right.$$从下面的线性方程组很容易求解出$ a$和$ b $$$\Leftrightarrow\left\{\begin{array}{l} \left(\displaystyle\sum_{i=1}^{n} x_{i}^{2}\right) a+\left(\displaystyle\sum_{i=1}^{n} x_{i}\right) b=\displaystyle\sum_{i=1}^{n} x_{i} y_{i} \\ \left(\displaystyle\sum_{i=1}^{n} x_{i}\right) a+n b=\displaystyle\sum_{i=1}^{n} y_{i} \end{array}\right.$$推广：
(a) Best exponential fit $$y=c e^{a x}\Leftrightarrow \ln (y)=\ln (c)+a x$$ 从而求出最佳拟合直线(指数函数)
(b) 二次型$ y=a x^{2}+b x+c $拟合：其实和拟合出直线一样，按照前面的步骤，会得到三阶线性方程组(让三个偏导数都为零)，即可确定这三个参数。

7. 寻找最值点(二次型)
前面我们提到，对于所有偏导数都为零的点，有三个情况，一个是local min，一个是local max，还有就是saddle point鞍点(既不是极小值又不是极大值)。至于局域极小值或者局域极大值是不是全局的最小或者最大呢？这就需要和边界或者无穷远处的函数值进行比较。

我们先考虑这种形式$ w=a x^{2}+b x y+c y^{2} $，如果$ a \neq 0 $，那么$$w=a\left(x^{2}+b / a x y\right)+c y^{2}=a\left(x+\frac{b}{2 a} y\right)^{2}+\left(c-\frac{b^{2}}{4 a}\right) y^{2}$$稍微整理一下有$$w=\frac{1}{4 a}\left[4 a^{2}\left(x+\frac{b}{2 a} y\right)^{2}\right.\left.+\left(4 a c-b^{2}\right) y^{2}\right]$$下面分三种情况讨论：

还可以从二次公式的角度来理解(一元二次函数)，等价的：
注：如果不理解鞍点的情况，看一下下图，对于函数$z=y^{2}-x^{2} $，我们在$ x-z$平面，看到的是函数$ z=-x^{2}$，而我们在$ y-z$平面，看到的是函数$ z=y^{2} $。$ b^{2}-4 a c<0$的情况，可以把$ x+\frac{b}{2 a} y $看作一个整体$ u$。$4 a c-b^{2}=0 $是无法判断的情况。
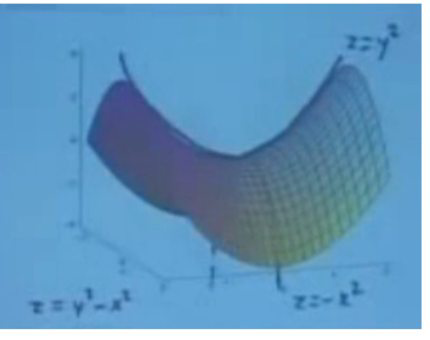8. 寻找最值点(一般情况，二阶偏导数)$$\frac{\partial^{2} f}{\partial x^{2}}=f_{x x}, \quad f_{x y}=\frac{\partial^{2} f}{\partial x \partial y}=\frac{\partial^{2} f}{\partial y \partial x}=f_{y x}\quad \frac{\partial^{2} f}{\partial y^{2}}=f_{y y}$$ 以$ w=a x^{2}+b x y+c y^{2}$为例子，$$\begin{array}{l} w_{x}=2 a x+b y \quad w_{y}=b x+2 c y \\ w_{x x}=2 a \quad W_{x y}=b=b=w_{y x} \quad w_{y y}=2 c \\ A=2 a \quad B=b \quad C=2 c \quad A C-B^{2}=4 a c-b^{2} \end{array}$$和我们前面的方法得到的判定公式是一致的。

为什么能够用二阶导数来推断极值点情况？
答：因为当我们用一阶近似$ \Delta z \approx f_{x} \Delta x+f_{y} \Delta y$的时候，由于两个一阶偏导数都为零，所以得到一阶近似的变化$ \Delta z $为$ \Delta x$和$\Delta y $的高阶无穷小，因此我们得不到有用的判断极值情况的信息。现在我们引入二阶近似(根据泰勒展开)：
最终得到的效果和我们之前按照二次型的方法处理得到的结果是完全一样的。都要注意的是，对于鞍点，也就是degenerate case，我们需要根据实际情况进行判断；当然，我们基本上在应用中不会碰到鞍点这种比较复杂的情况。

注：这里用到的小技巧是二元函数的泰勒展开，我们之前接触的都是一元函数的泰勒展开。
For example, for a function $f(x,y)$ that depends on two variables, $x$ and $y$, the Taylor series to second order about the point $(a,b)$ is $$ f(a, b)+(x-a) f_{x}(a, b)+(y-b) f_{y}(a, b)+\frac{1}{2 !}\left((x-a)^{2} f_{x x}(a, b)+2(x-a)(y-b) f_{x y}(a, b)+(y-b)^{2} f_{y y}(a, b)\right)$$例子：

全微分/链式法则/梯度/方向导数

(Total Differentials/Chain rules/Gradient/ Directional Derivatives)

1. 全微分和链式法则
一元函数的隐式微分对于$ y=f(x) $有$$d y=f^{\prime}(x) d x$$比如下面的例子$$\begin{aligned} y=\sin ^{-1} x & \\ x=\sin y \rightarrow & d x=\cos y d y \\ & \frac{d y}{d x}=\frac{1}{\cos (y)}=\frac{1}{\sqrt{1-x^{2}}} \end{aligned}$$多元函数$f(x, y, z) $的全微分$$\begin{aligned} d f &=f_{x} d x+f_{y} d y+f_{z} d z \\ &=\frac{\partial f}{\partial x} d x+\frac{\partial f}{\partial y} d y+\frac{\partial f}{\partial z} d z \end{aligned}$$特别注意$ df$不是$ \Delta f $。$ \Delta f $表示的是一个数，当自变量有些许变化的时候，$ \Delta f $就是变化的量值；$ \Delta x \Delta y \Delta z $都是实实在在的数量，所以$ \Delta f $也是数。$ df$不是特定值，只能用其他的微分去解释它，更像一种符号，或者不是很确切地说，是当自变量变化趋于零的状态时，$ df $的变化特点，也就是描述的是更纯粹的该点的信息。

下面的第一条其实解释的是什么是微分。老师特别强调$ d $和$\Delta $生活在不同的世界，它们看不到对方。下面用更好的方法说明为什么$\displaystyle\frac{d f}{d t}=f_{x} \displaystyle\frac{d x}{d t}+f_{y} \displaystyle\frac{d y}{d t}+f_{z} \displaystyle\frac{d z}{d t}$成立。
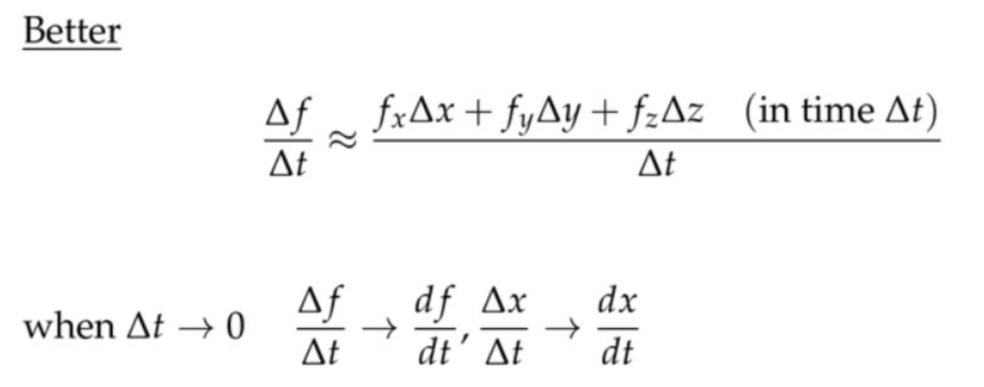$ \approx \text { becomes }=\text { in } \operatorname{limit} \Delta t \rightarrow 0 $时$ \displaystyle\frac{d f}{d t}=f_{x} \frac{d x}{d t}+f_{x} \frac{d y}{d t}+f_{z} \frac{d z}{d t} $成立(严格证明需要用数学分析的方法，没必要，这里只是理解就行)。
例子：$ w=x^{2} y+z \quad x=t, y=e^{t}, z=\sin (t) $
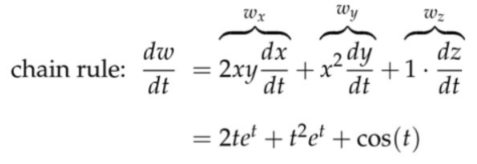直接开始的时候就全部用$ t$代换也会得到完全相同的结果$$ \begin{aligned} &w(t)=t^{2} e^{t}+\sin (t) \\ &\frac{d w}{d t}=2 t e^{t}+t^{2} e^{t}+\cos (t) \end{aligned}$$应用：证明两个函数相乘/相除的求导法则$$\begin{aligned} &f=u v \quad u=u(t), v=v(t)\\ &\frac{d u v}{d t}=f_{u} \frac{d u}{d t}+f_{v} \frac{d v}{d t}=v \frac{d u}{d t}+u \frac{d v}{d t} \end{aligned}$$ $$\begin{aligned} &g=\frac{u}{v} \quad u=u(t), v=v(t)\\ &\frac{d u / v}{d t}=\frac{1}{v} \frac{d u}{d t}+\left(\frac{-u}{v^{2}}\right) \frac{d v}{d t}=\frac{u^{\prime} v-v^{\prime} u}{v^{2}} \end{aligned}$$Chain rule with more variables! $$\begin{aligned} w &=f(x, y) \text { where } \begin{array}{l} x=x(u, v) \\ y=y(u, v) \end{array} \\ &=f(x(u, v), y(u, v)) \end{aligned}$$ $$\text { Question: what are } \frac{\partial w}{\partial u}, \frac{\partial w}{\partial v} \text { in terms of } \frac{\partial w}{\partial x}, \frac{\partial w}{\partial y}, x_{u}, x_{v}, y_{u}, y_{v}$$ 求解方法是先将$ d w$写成由$d x $和$d y $组成的全微分的形式，然后同样地将$ d x $和$ d y $用$ du$和$ dv $展开成全微分的形式。$$\begin{aligned} d w &=f_{x} d x+f_{y} d y \\ &=f_{x}\left(x_{u} d u+x_{v} d v\right)+f_{y}\left(y_{u} d u+y_{v} d v\right) \\ &=\underbrace{\left(f_{x} x_{u}+f_{y} y_{u}\right)}_{\frac{\partial w}{\partial u}} d u+\underbrace{\left(f_{x} x_{v}+f_{y} y_{v}\right)}_{\frac{\partial w}{\partial v}} d v \end{aligned}$$ 注意偏导数中上下的$ \partial x $ 不能消掉，而$ d x$可以消掉$$\begin{aligned} &\frac{\partial f}{\partial u}=\frac{\partial f}{\partial x} \frac{\partial x}{\partial u}+\frac{\partial f}{\partial y} \frac{\partial y}{\partial u}\\ &\frac{\partial f}{\partial v}=\frac{\partial f}{\partial x} \frac{\partial x}{\partial v}+\frac{\partial f}{\partial y} \frac{\partial y}{\partial v} \end{aligned}$$以上面的式子解释一下就是，$ u $的变化导致了$ x $的变化，$ x$的变化导致了$ f$的变化；$ u $的变化导致了$ y $的变化，$ y$的变化导致了$ f$的变化。
例子：极坐标

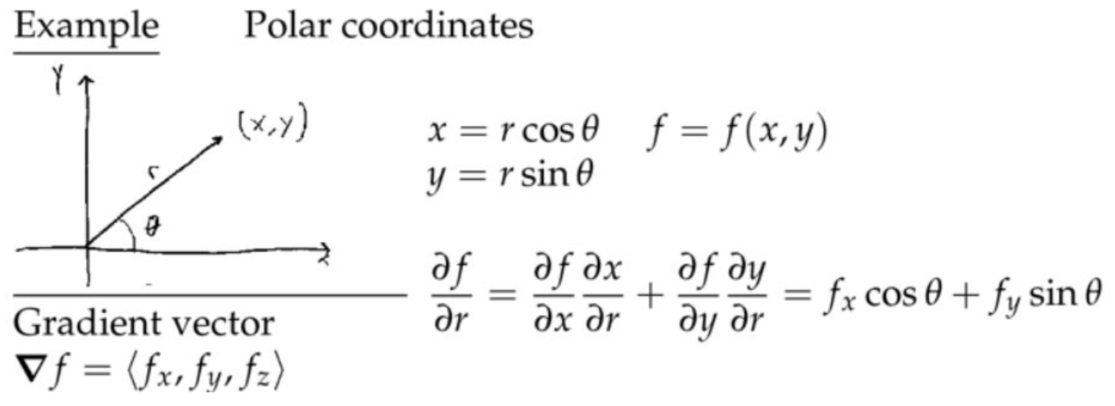
2. 梯度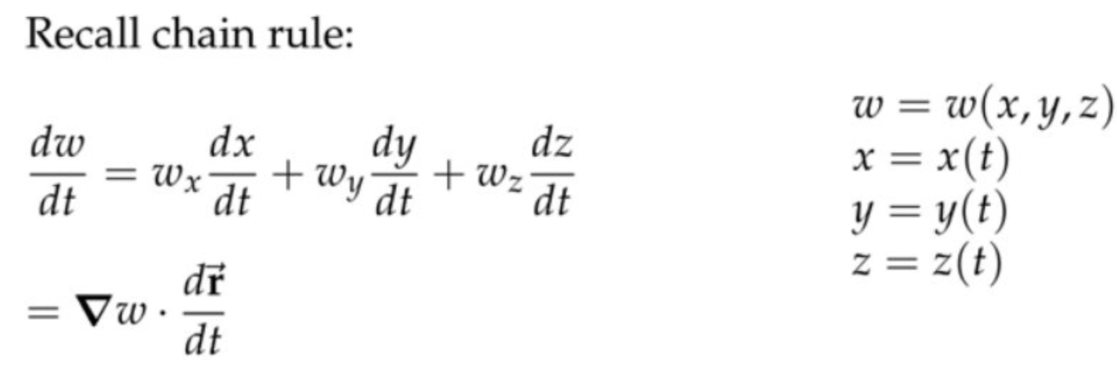$ \boldsymbol{\nabla} w=\left\langle w_{x}, w_{y}, w_{z}\right\rangle $表示的是$w $在$(x, y, z) $处的梯度向量。
速度向量$ \displaystyle\frac{\partial \overrightarrow{\mathbf{r}}}{\partial t}=\left\langle\frac{d x}{d t}, \frac{d y}{d t}, \frac{d z}{d t}\right\rangle$。
定理：梯度向量总是垂直于等值线(level curve)/等值面((level surface)。

上图是二元变量函数，对应的是等值线。
梯度向量总是指向函数值更高的地方。
例子1：三元变量函数，等值面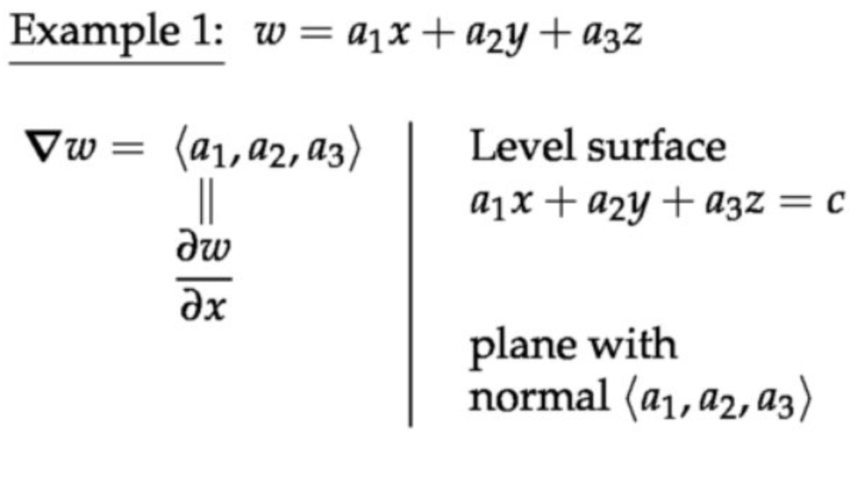
例子2：二元变量函数，等值线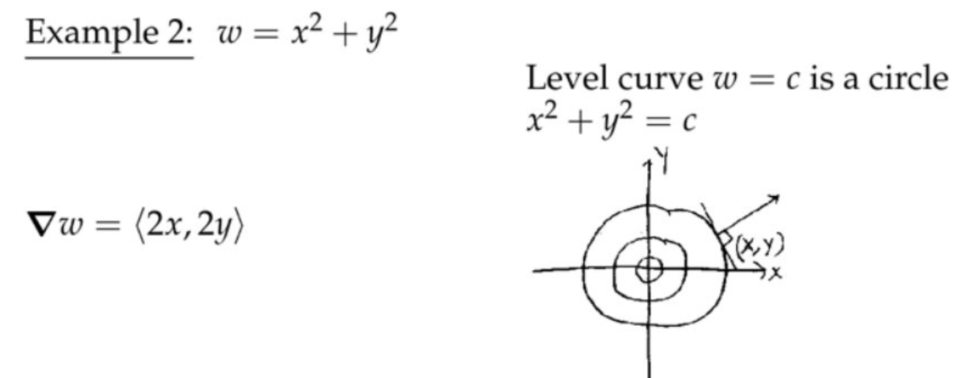

证明：

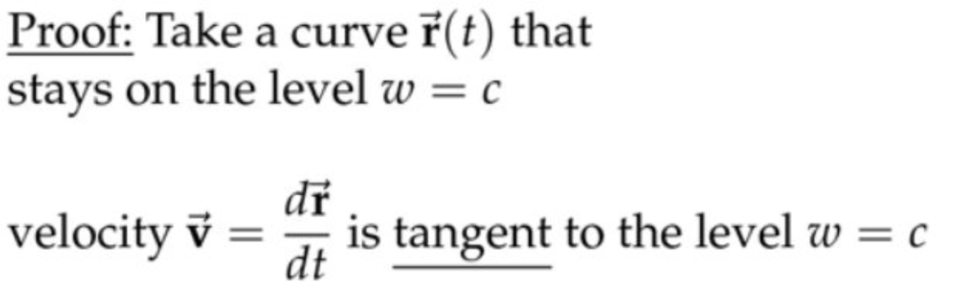
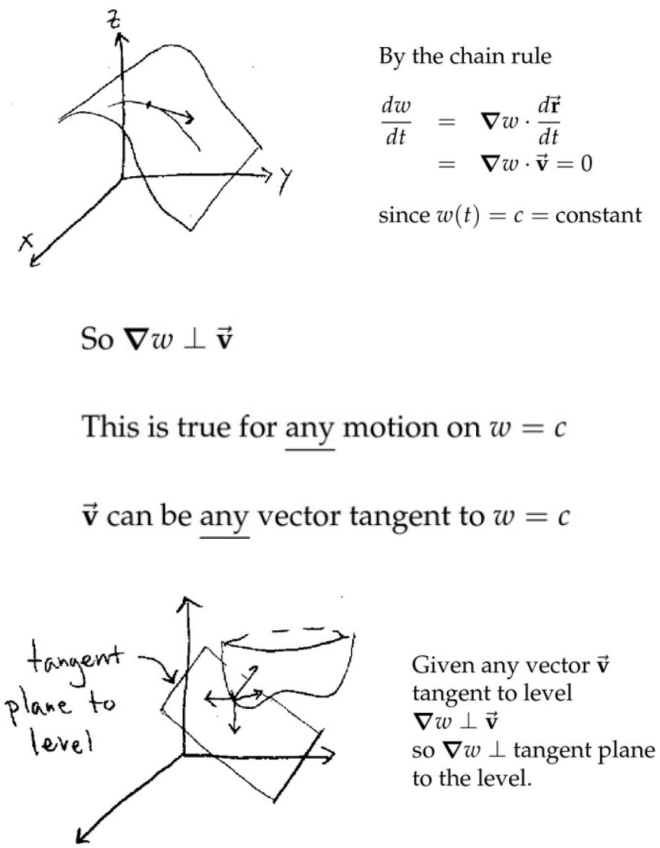对于二元函数，梯度向量垂直于等值线的的切线；对于三元函数，梯度向量垂直于等值面的切平面，当然必须先确定等值面上的一个切点(无论这个等值面是什么奇怪形状)。等值面上移动的点的速度一定是始终和等值面相切；换句话说速度方向一定在该点的切平面内，而梯度向量垂直于该切平面，所以梯度向量的方向一定和速度方向垂直。

例子：求$x^{2}+y^{2}-z^{2}=4 $在$ (2,1,1)$点处的切平面？

方法1：最原始最笨的办法，将上面的式子改写成用$ x$和$ y $来表示$z $的表达式，即按照二元函数的方式来处理。
这里的改写方法可能不那么难，但对其他更复杂的情况，改写起来就没那么容易了。仿照我们前面求两个切线$ L_1 $和$ L_12$的例子，先分别求出$ z$对$x $和$ y$的两个偏导数，假设结果分别为$ a$和$ b$，那么切平面就为$z=z_{0}+a\left(x-x_{0}\right)+b\left(y-y_{0}\right) $，其中的$\left(x_{0}, y_{0}, z_{0}\right) $就是我们条件中的给定点的数据。

方法2：按照三元函数的方法处理
令$ w=c $，其中$ w=x^{2}+y^{2}-z^{2}$
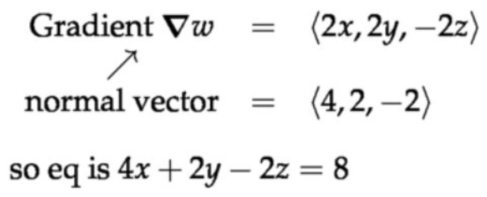方法3：全微分处理方法 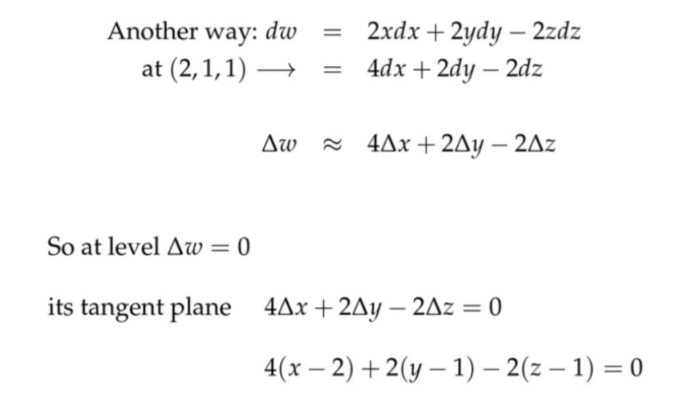11. 方向导数(Directional derivatives)
思考和总结：方向导数是一个数，描述的是函数的自变量沿着该方向变化时，函数值的变化快慢。一个点的梯度向量的方向，就是函数值变坏最快的方向，也就是说沿着这个方向走单位距离，函数值的增长最快(梯度向量指向的是函数值更大的地方)。所以求解一个点各个方向的的方向导数，可以发现，只有沿着梯度向量的方向，函数值增长就越快，沿着梯度向量的反方向的电话，函数值减小最快，而沿着垂直于梯度向量的方向(二元函数是切线方向；如果是三元函数，那么是切平面上的向量方向)，函数值的一阶近似变化为零。

注意：上面的$ \frac{d \overrightarrow{\mathbf{r}}}{d s}$，我们以前参数化的时候，都是用时间$ t $，这里用的是$ s $表示直线上的一段距离(其他情况也可能是弧长)。这是一个惯例，意味着把沿着直线运动经过的距离参数化了。

拉格朗日乘数法和约束微分

(Lagrange Multipliers and Constrained Differentials)

1. 拉格朗日乘数法

在约束条件$ g(x, y, z)=c $下(也就是说三个变量中只有两个是独立的，我们可以任意选取其中的两个作为自变量)，求函数$ P(x, y, z)$的极小值/极大值。

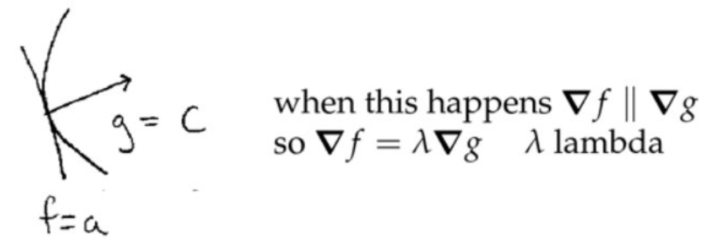
例子：证明拉格朗日乘数法：
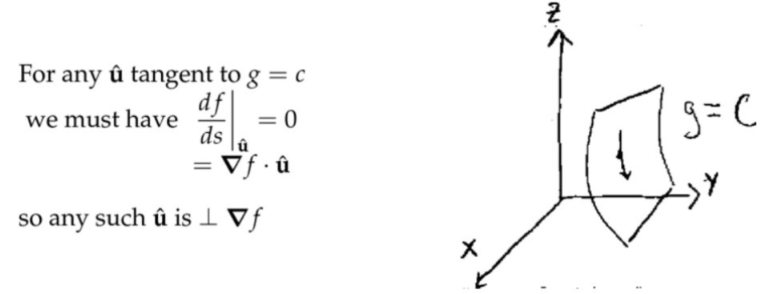注：在限制条件的等值面$ g=c $中，点移动的方向$\hat{\mathbf{u}} $必定和等值面相切，否则就会跑到等值面外边去了。那么在这样的限定条件下，要想要目标函数$ f$取得极小值/极大值，必然有等值面上点移动的方向正好和函数$ f$梯度向量的方向垂直，这样才能保证$ f$在该方向的变化速率为零(类似一元函数一阶导数为零的点)。
等值面中 $\hat{\mathbf{u}} $ 的方向必然在该点的切平面上，而且切平面上的任意方向都满足点的移动条件。接着，我们上面知道$ \nabla f$的方向一定是垂直于 $\hat{\mathbf{u}} $ 的方向。$\hat{\mathbf{u}} $ 是可以在切平面上任意选取的，因此唯一的情况就是$ \nabla f$垂直于该切平面。
注：先前多元函数求二阶偏导数来判断是不是极值点的方法在这里不奏效，需要带入几个解看看，或者从几何图像上判定。

例子：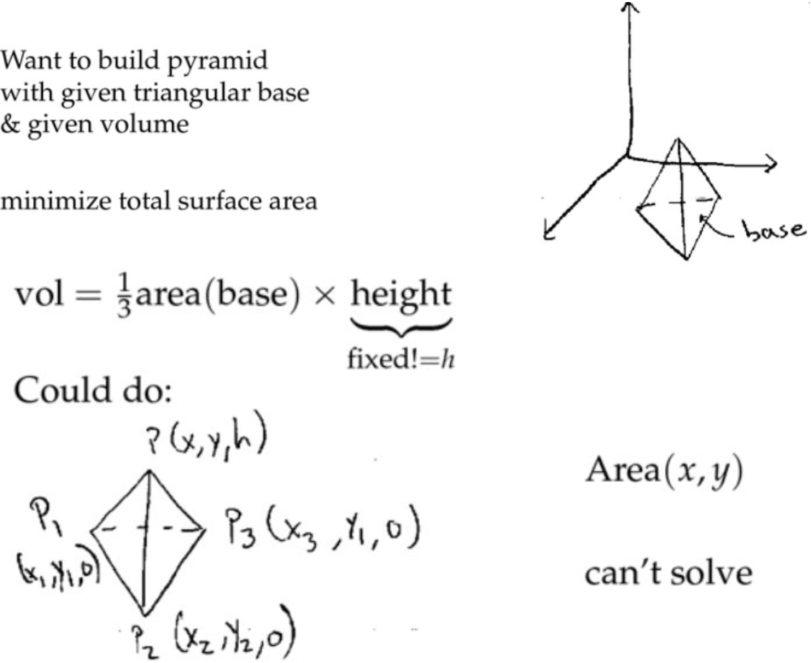

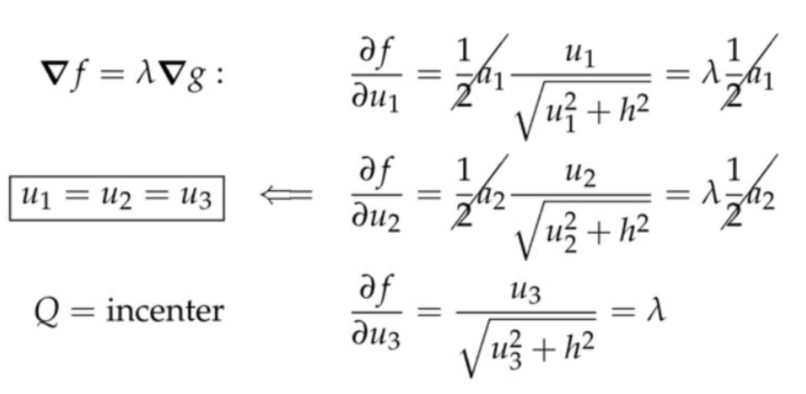
2. 非独立变量(Non-independent Variables)

比如对于函数$f(P, V, T) $来说，三个自变量不是相互独立的，因为存在$ P V=n R T$的限制条件。更普遍地来说，对于任意函数$ f(x, y, z)$，存在$ g(x, y, z)=c$的限制条件。$$\text { If } g(x, y, z)=c \text { then } z=z(x, y) \quad \text { How to find } \frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}?$$例子：$ \text { Ex. } \underbrace{x^{2}+y z+z^{3}=8}_{g} \text { at }(2,3,1)$
首先两边求偏微分(此时将三个自变量看作是相互独立)，等式右边是常数，于是偏微分得到$ 0$，于是有$$2 x d x+z d y+(y+3 z^{2}) d z=0$$在$ (2,3,1)$点，上式可以写成$$ 4 d x+d y+6 d z=0$$如果有$ z=z(x, y)$，那么有$ d z=-\frac{1}{6}(4 d x+d y)$(当$ y$不变的时候，设置$dy=0$，当$x$不变时，设置$dx=0$)，于是$$ \frac{\partial z}{\partial x}=-\frac{4}{6}=-\frac{2}{3} ; \quad \frac{\partial z}{\partial y}=-\frac{1}{6}$$一般情况：如果$ g(x, y, z)=c$，那么$ d g=g_{x} d x+g_{y} d y+g_{z} d z=0$，那么$$d z=-\frac{g_x}{g_z} d x-\frac{g_y}{g_z} d y$$求$ \displaystyle\frac{\partial z}{\partial x}$的时候，我们将$dy=0$，于是$ d z=-\displaystyle\frac{g_{x}}{g_{z}} d x$，因此有$ \displaystyle\frac{\partial z}{\partial x}=-\frac{g_{x}}{g_{z}}$。

注：
(1) 注意$d z=-\displaystyle\frac{g_x}{g_z} d x-\displaystyle\frac{g_y}{g_z} d y $中负号的由来；
(2) 很多情况下，不能直接地由$ g(x, y, z)=c$改写成$ z=z(x, y) $，或者即使改写，表达式也很复杂，那么再求偏导的话，就更麻烦了，所以这里采取的是将$d z=-\displaystyle\frac{g_x}{g_z} d x-\frac{g_y}{g_z} d y $的各个变量组合写成全微分的形式。带入特定点，就可以用$ dx $和$ dy$“线性表示”$ dz $，那么偏导数其实就是前面线性组合的系数。

3. 更清晰的标记方法(clearer notation)

对于函数$ f(x, y)=x+y$有$\displaystyle \frac{\partial f}{\partial x}=1$，如果设定$ x=u \quad y=u+v$，那么有$ f=x+y=2 u+v$，于是$\displaystyle\frac {f }{u}=0 $。那么问题来了，虽然$ u=x$，但是$ f$对它们分别求导得到的结果不一样。这是因为对$x$求导的时候，是设定$ y$为常数，而对$ u$求导的时候，是设定$v=y-x$为常数。因此，我们需要给出更清晰的表示方法：$$ \begin{aligned} &\left(\frac{\partial f}{\partial x}\right)_{y}=\text { keep } y \text { const. } \\ &\left(\frac{\partial f}{\partial u}\right)_{v}=\text { keep } v \text { const. } \end{aligned} \quad \underbrace{\left(\frac{\partial f}{\partial x}\right)_{y}}_{1} \neq \underbrace{\left(\frac{\partial f}{\partial x}\right)_{v}=\left(\frac{\partial f}{\partial u}\right)_{v}}_{2}$$

注：将$ x$和$ y$看作自变量的时候，对$ x$求偏导是默认$ y$不变；将$ u$和$ v $看作自变量的时候，对$ u $求偏导是默认$ v $不变。因此即使有$ x=u $，但是对$ x$和$ u $求偏导数的时候，默认不变的量是不同的，因此这两个偏导数不相同。为了更好地区分到底默认什么是不变的，我们把偏导数括起来，然后用下标标注什么是不变的量。

例子：