三重积分和三维空间的表面积分

三重积分

1. 三重积分矩形和圆柱坐标

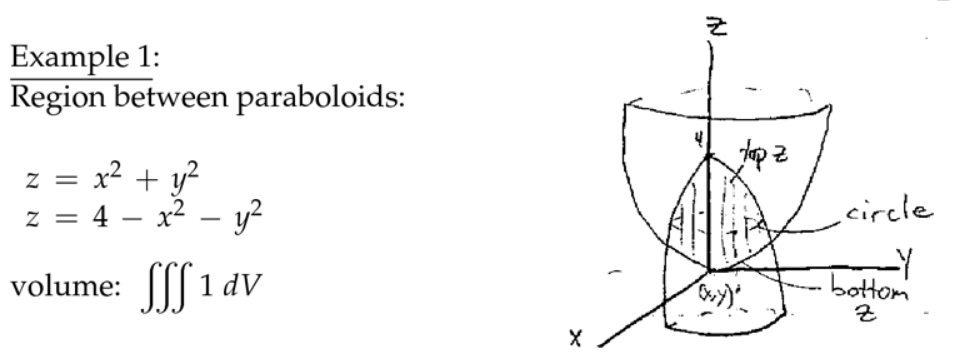
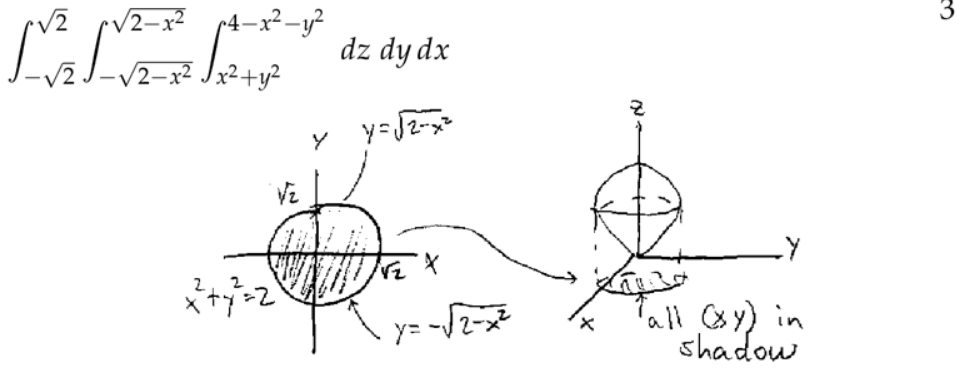
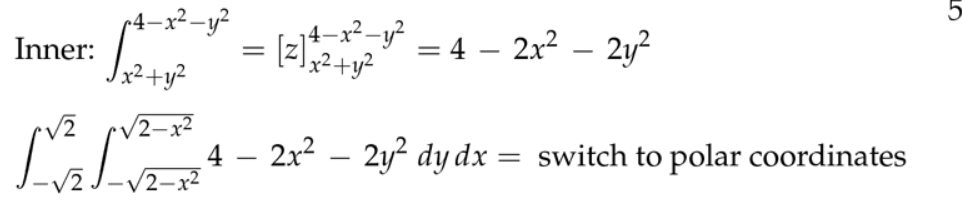
注：这里不是球坐标，而是三维空间下的极坐标，能这样变化是因为\( dz \)的积分可以用\(x  \)和\(  y\)来表示(\( 4-2 x^{2}-2 y^{2} \))。

注：一般来说，先对\(z \)积分比较简单，因为\(  z\)的值，直接由\( x \)和\(  y\)决定。

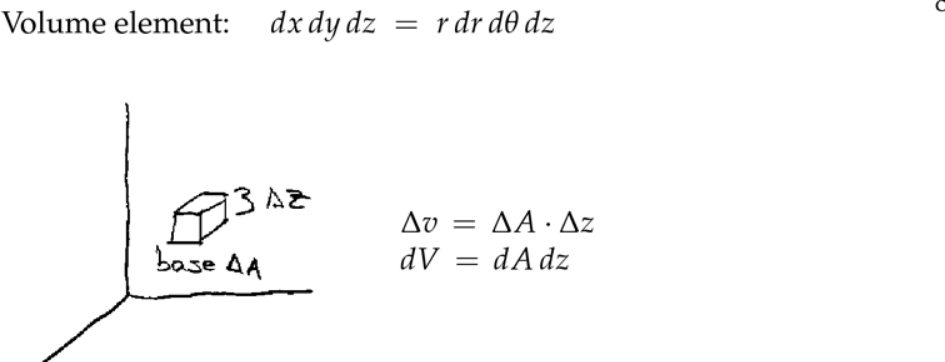
2. 应用和例子

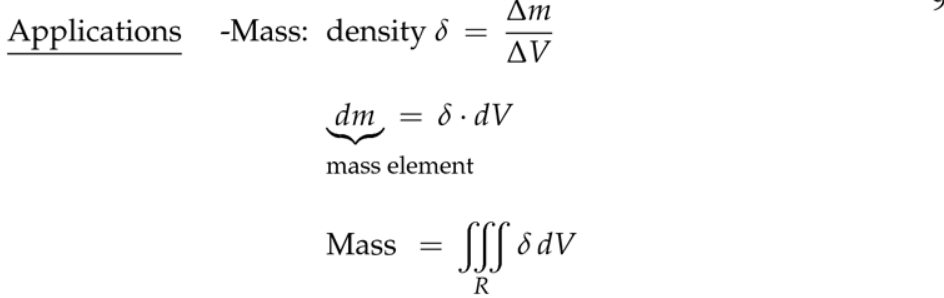
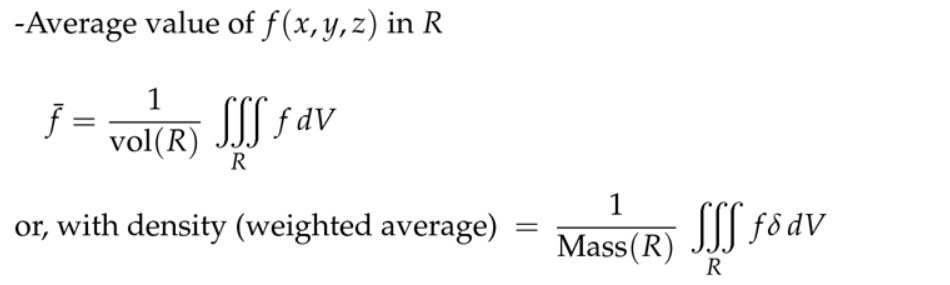
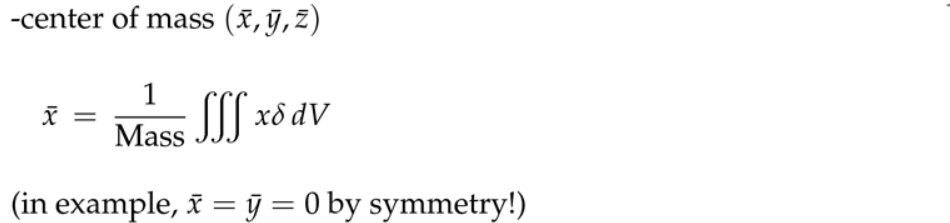
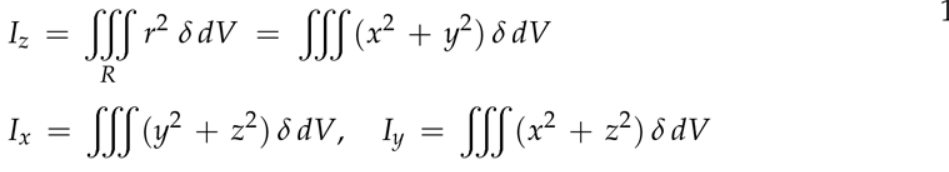
注：这里\( dz \)最后积分，那么里面的积分就相当于水平一刀一刀切过去。设计齿轮或者由类似旋转功能的机械零件，你要精确地知道，使它们转动，需要多大的力，引擎是否够等等来设计。

注：圆投影到\(  xy\)得到的是椭圆，上面画得不够椭圆。

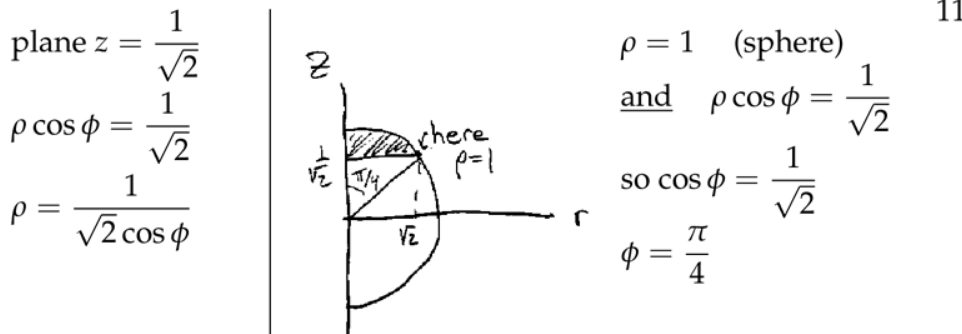
3. 球坐标(Spherical Coordinates)

注：这里的两个角度可以类比经纬度，但是不完全一样。赤道的维度为零。

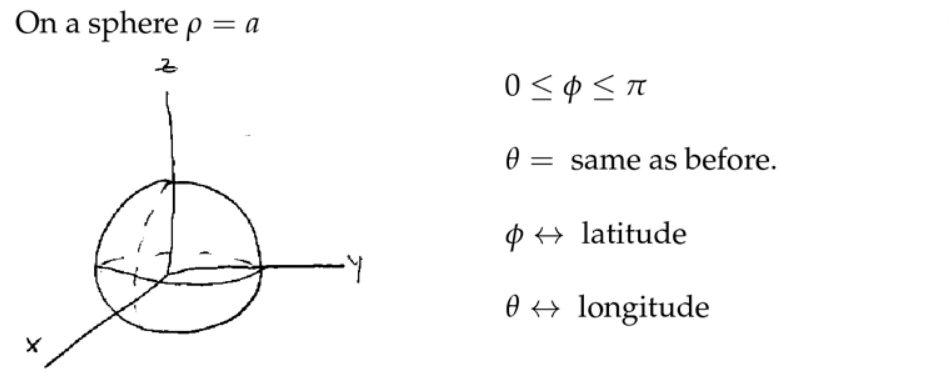
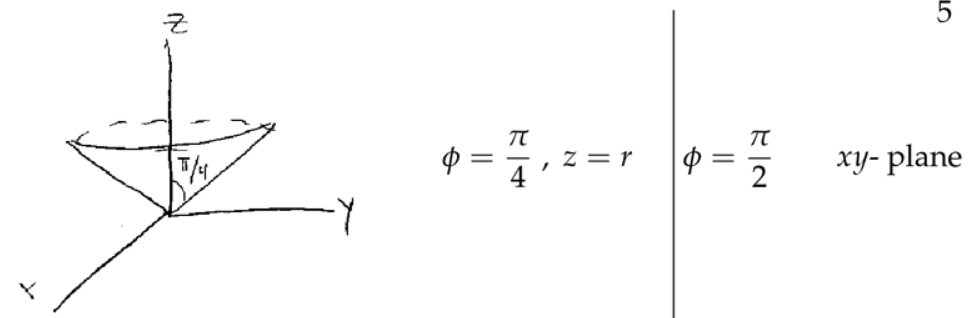
4. 球坐标中的三重积分

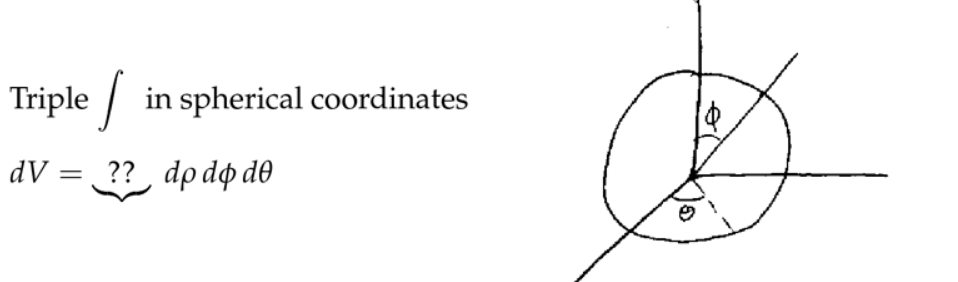
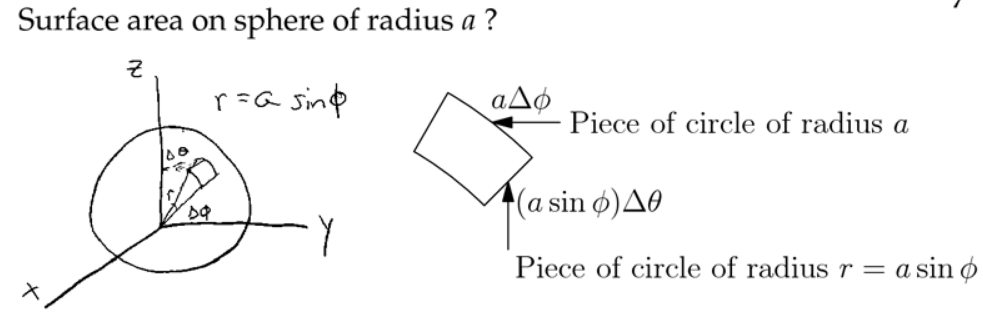
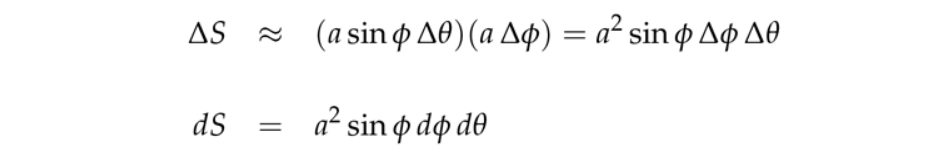
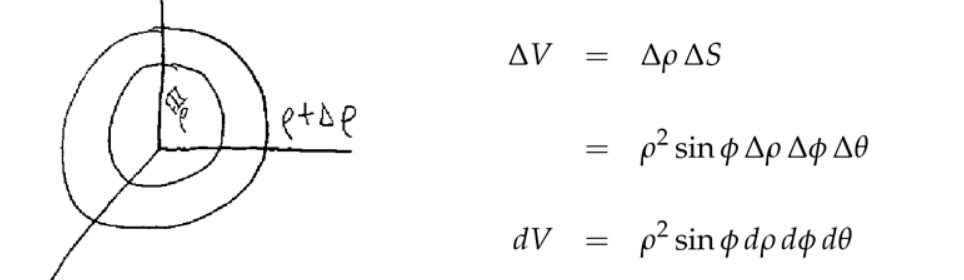
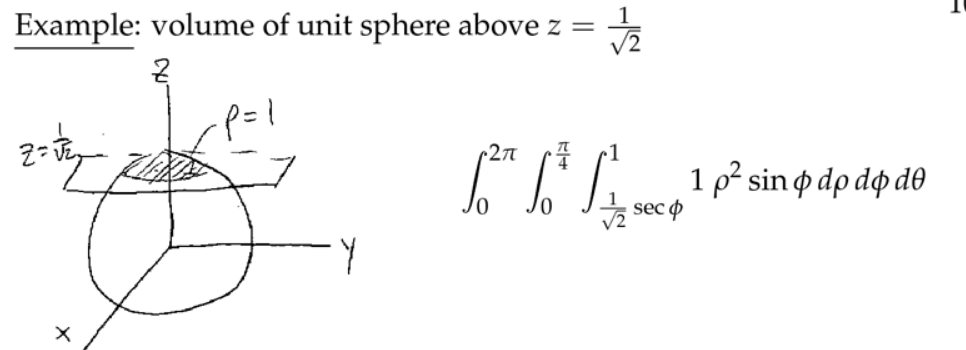
5. 应用：引力

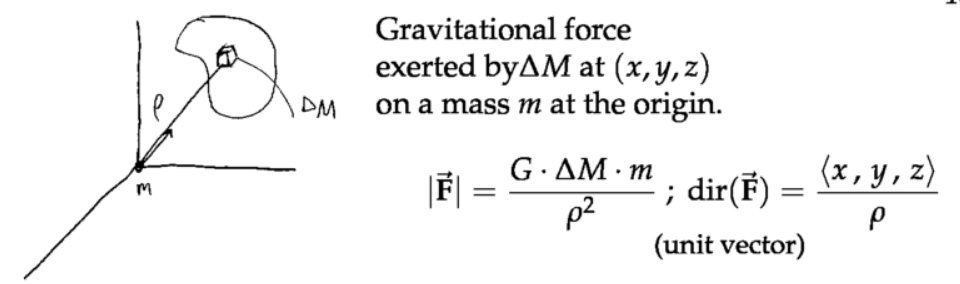
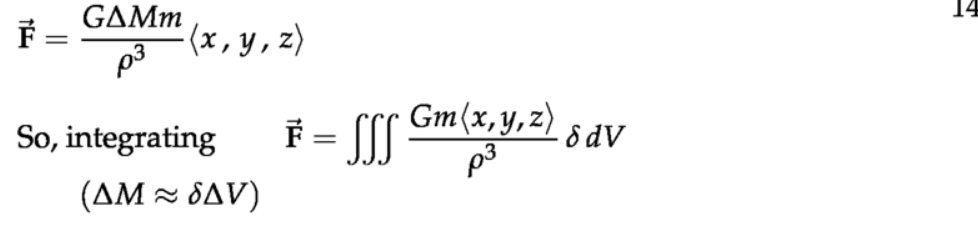
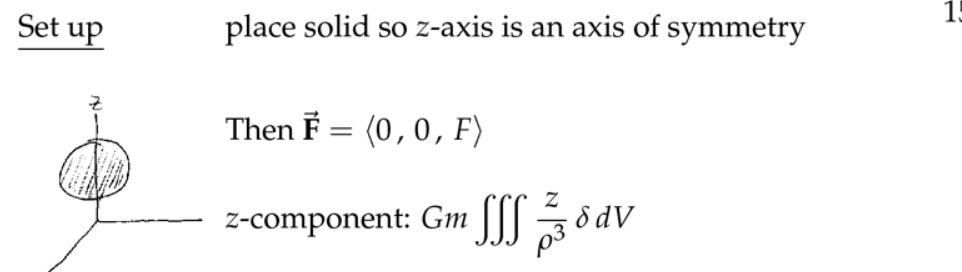
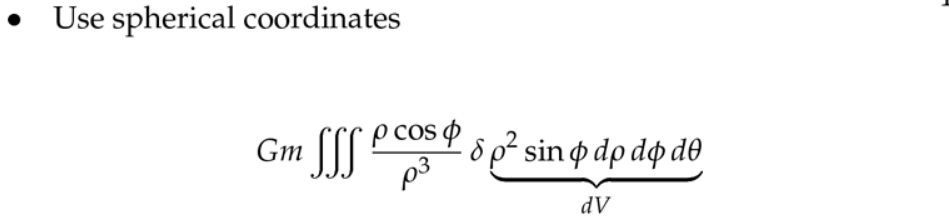
注意：满足行星(恒星)等效条件(牛顿证明了)的要求是：球形，而且是质量均匀分布的。地球近似满足条件，那么我受到的重力(地球引力)，近似认为地球的所有质量都集中在的地球球心，然后计算该质点对我的引力即为重力。

通量和散度定理

1. 空间中的向量场


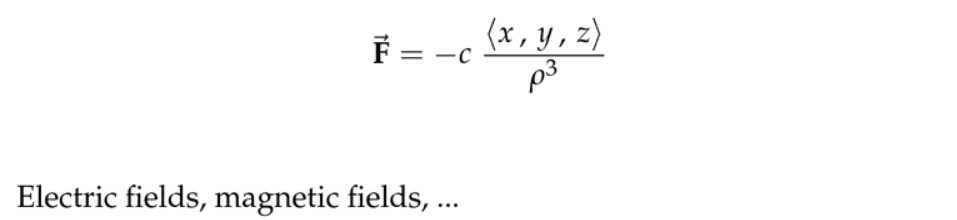
注：负号表示朝向原点方向，而\(  \langle x, y, z\rangle\)给出了场的向量方向，除以一个\(  \rho\)就是单位方向向量，因此最终表达式分母是三次方。这里表现的其实是平方反比关系，电/磁场都满足。

2. 通过曲面的通量

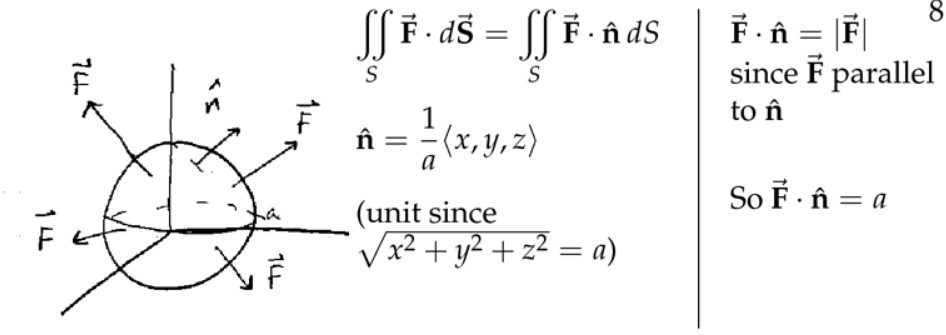
3. 计算通量，寻找ndS

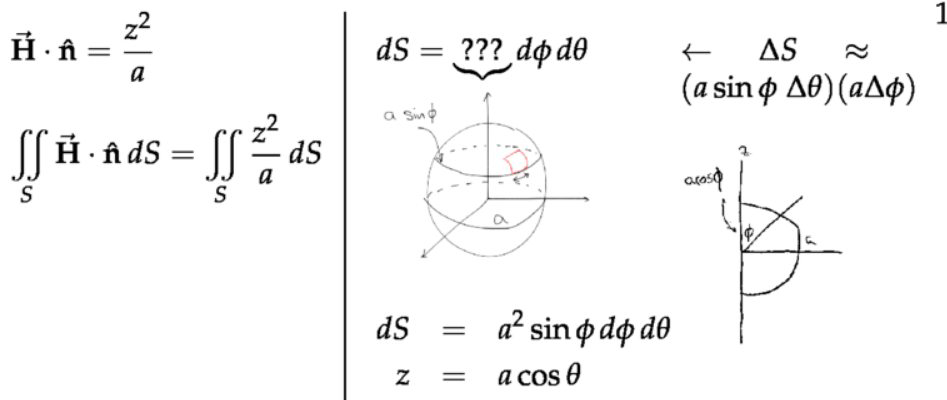
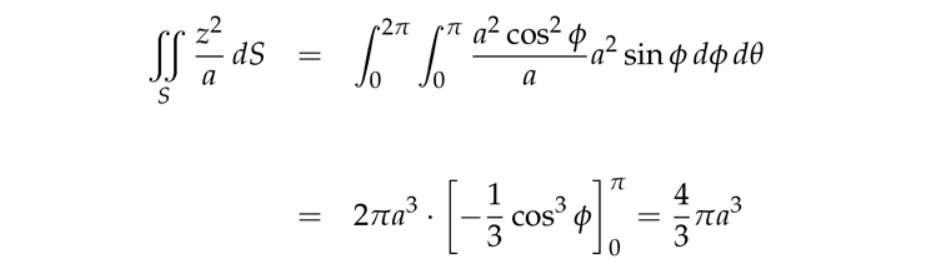
注：这里只是将球面参数化(类似圆周上的参数化，不考虑\(  r\)只考虑角度)，实际上不是球坐标，没有变量\(  \rho\)这一项。
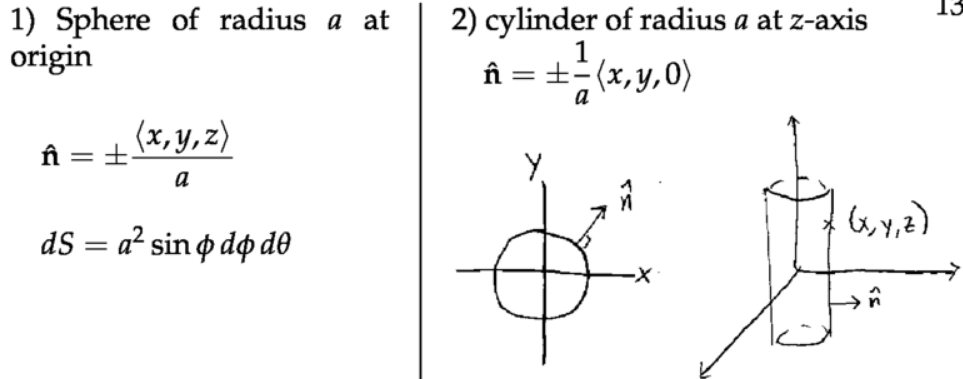
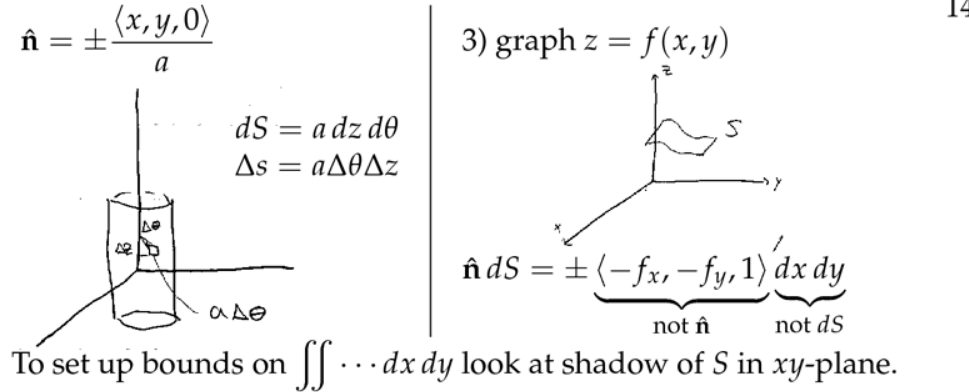注：正负号由选取的正方向决定。利用\(  \hat{\mathbf{n}} d S=\pm\left\langle-f_{x},-f_{y}, 1\right\rangle d x d y\)比直接求\( \hat{\mathbf{n}} \)和\(d S  \)更简单，后面我们将用向量叉乘的方法来说明这个等式。
注：底面积为\(\Delta \mathbf{S}  \)，高度为\(  \overrightarrow{\mathbf{F}} \cdot \hat{\mathbf{n}}\)。

4. ndS for a Surface z = f(x, y)
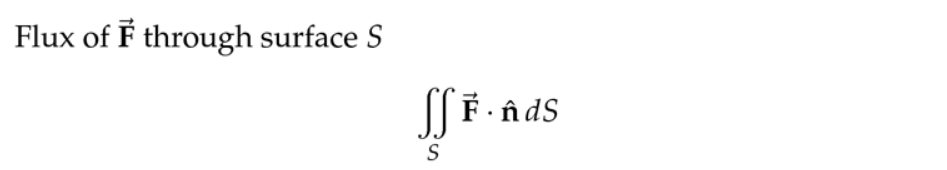
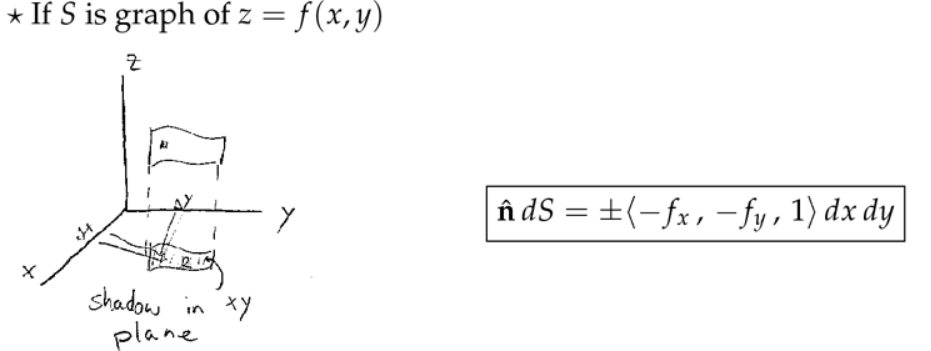注：如果\(  f_x=f_y=0\)，那么投影前后面积不变。这里的\( \hat{\mathbf{n}} d S=\pm\left\langle-f_{x},-f_{y}, 1\right\rangle d x d y \)其实是进行投影操作，当然搞复杂的话，我们可以用投影矩阵来操作。现在我们不从线性代数投影矩阵角度，而是从\(  \left\langle-f_{x},-f_{y}, 1\right\rangle\)模长角度来思考，我们知道对于二维平面上的直线，取其中一段的长度为\(l=\sqrt{1+k^2}(x_2-x_1) \)，只是现在这里的投影变成了面积，所以\( dS=\sqrt{1+f_x^2+f_y^2}(dS_{xy}) \)。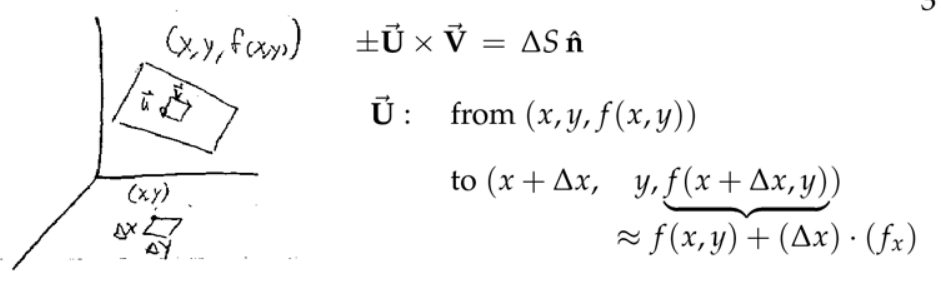

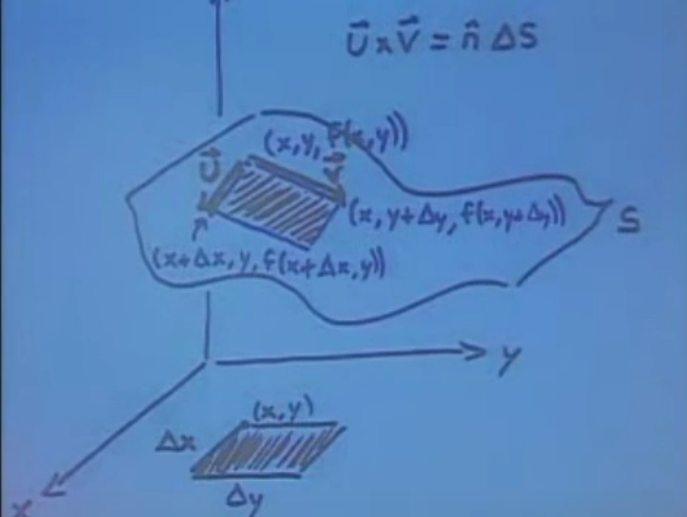
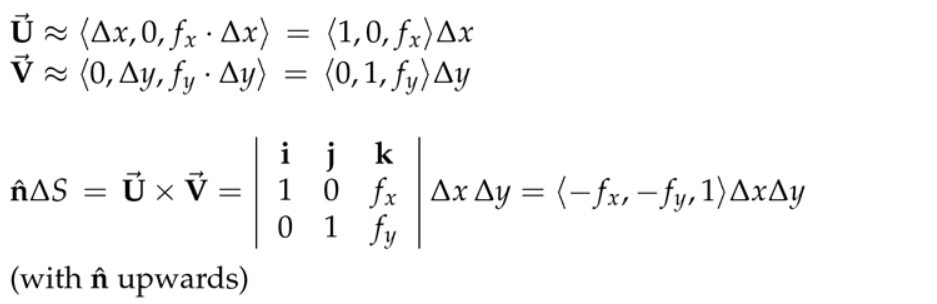
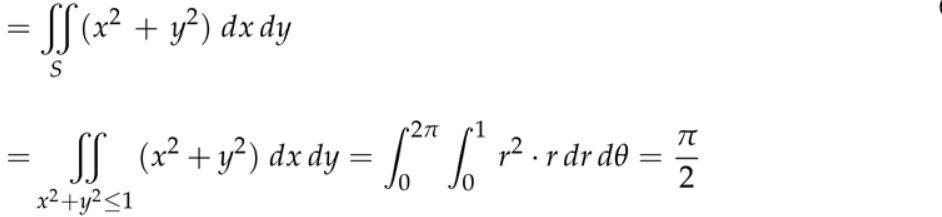
5. 其他方法来寻找ndS
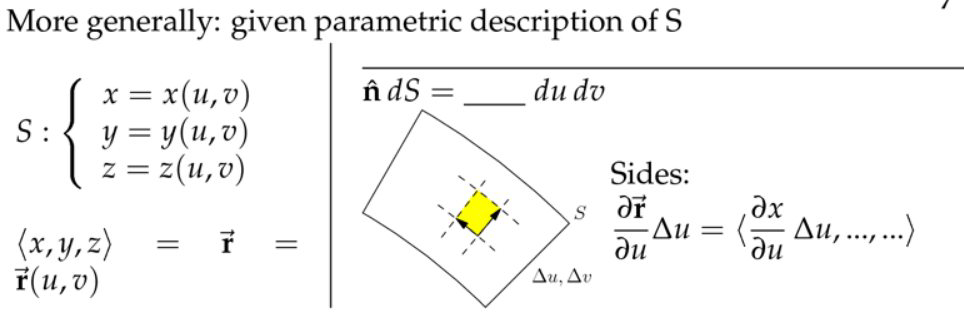
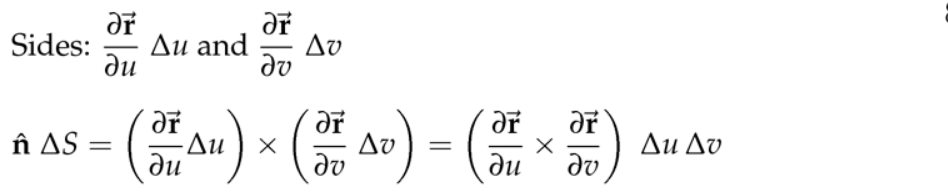注：前面的两个例子\( z=f(x,y) \)和固定半径的球面(两个角度参数化球面上的点)都是上面的特例。
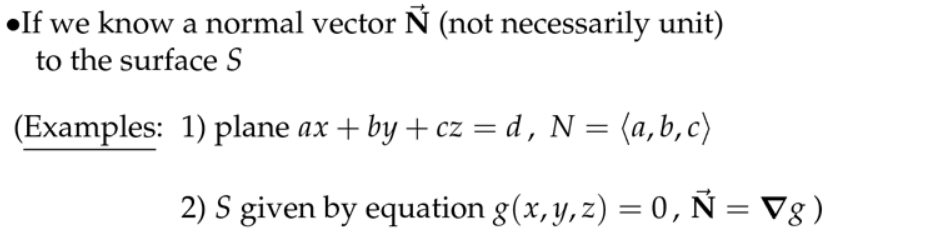注：表达式右侧的常数表面，表达式表示表示的是一个“等值面”，那么其法向量方向就是梯度方向。
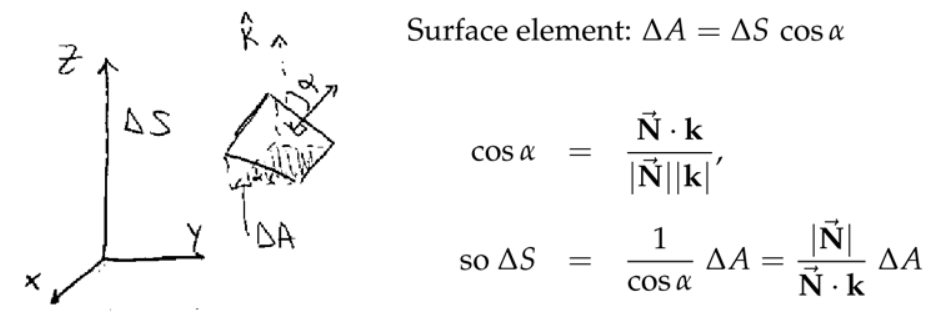注：两个平面的夹角其实就是二者法向量的夹角。
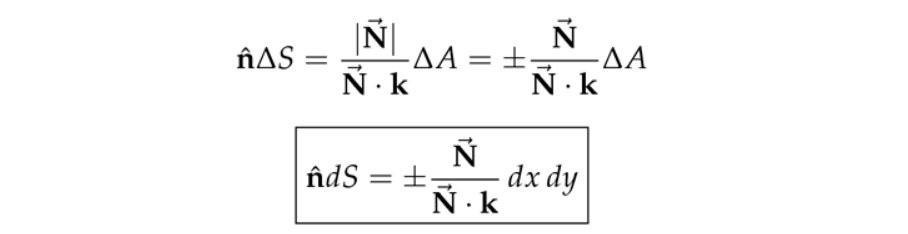
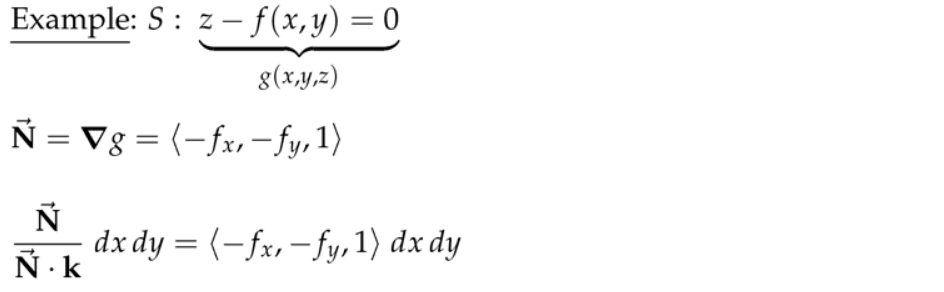注：\(  \overrightarrow{\mathrm{N}} \cdot \mathrm{k}=1\)，其实就是\(\overrightarrow{\mathrm{N}}  \)在\(\mathrm{k}  \)方向(\(  z\)轴方向)分量。

6. 散度定理(3D版通量格林公式)

7. 通量的物理意义：Del标记
注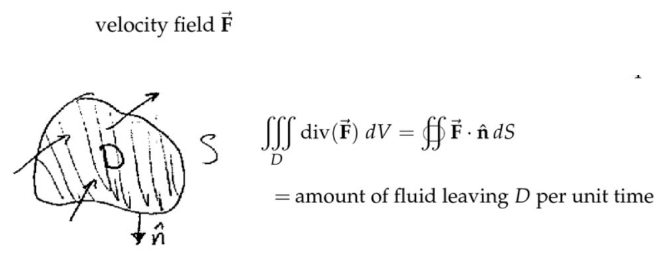特别注意，散度定理是针对不可压缩流体的，比如水，而气体属于可压缩流体，那么就不能用散度定理。散度描述的是空间中某个位置，单位体积内，冒出或者流失的量。

8. 证明散度定理

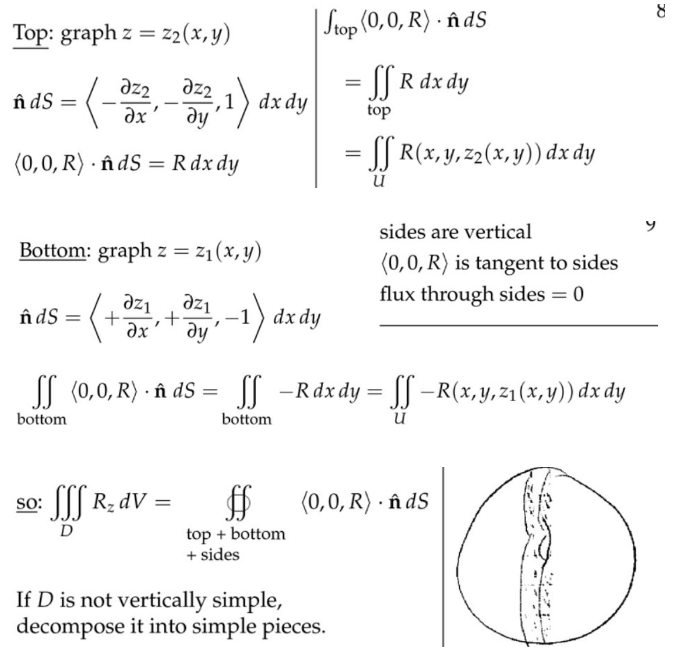
9. 扩散方程
注：势函数的梯度，是从小的地方指向大的地方，而烟雾流动的方向是从大的地方指向小的地方(高浓度向低浓度扩散)。因此，上面出现负号。
注：这里积分外对\(t  \)求导，等于积分里面对\( t \)求偏导。
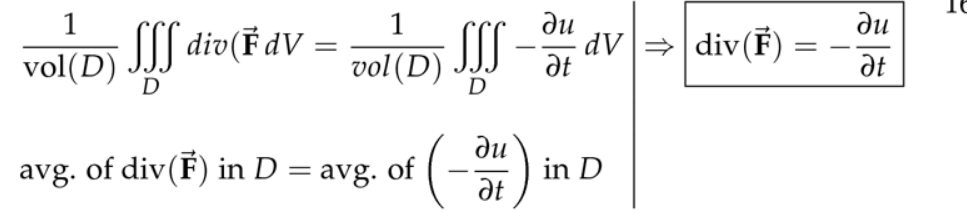注：
(1)  \( \operatorname{div}(\overrightarrow{\mathbf{F}})=-\displaystyle\frac{\partial u}{\partial t} \)描述的是空间某处，单位时间内单位体积内，物质增加或减少的速度，这里的物质既可以是某个浓度(不考虑流体流动的纯扩散)，也可以是含有的热量(温度作为表现形式)。
(2)  根据 \( \operatorname{div}(\overrightarrow{\mathbf{F}})=-\displaystyle\frac{\partial u}{\partial t} \)和\( \overrightarrow{\mathbf{F}}=-k \nabla u \)可以推出\( \displaystyle\frac{\partial u}{\partial t}=-\operatorname{div}(\overrightarrow{\mathbf{F}})=-k \operatorname{div}(\nabla u)=k \nabla^{2} u \)

线积分和斯托克斯定理

1.  空间中的线积分

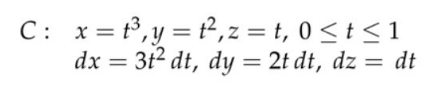注：参数方程表示路径。

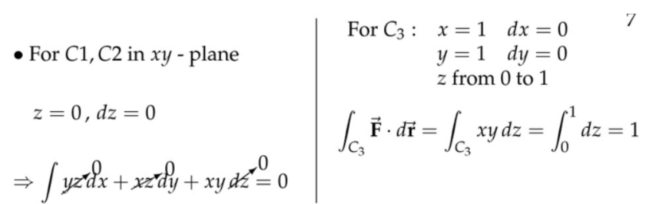
注：两种路径得到一样的结果，实际上这碰巧是一个保守力场（势场），所以做功与路径无关。

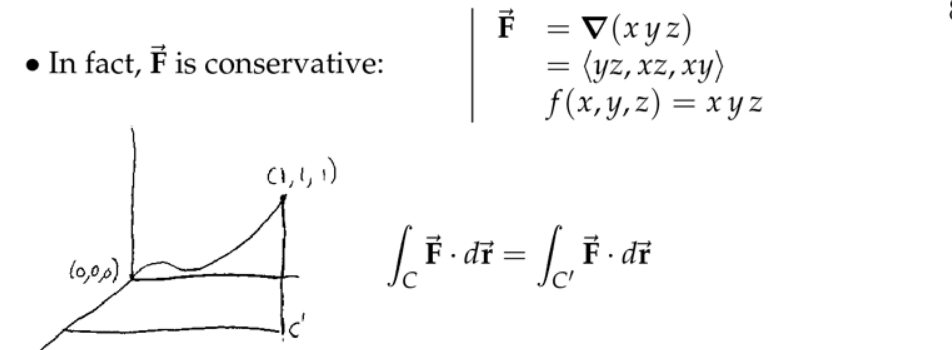
2. 梯度场和势函数

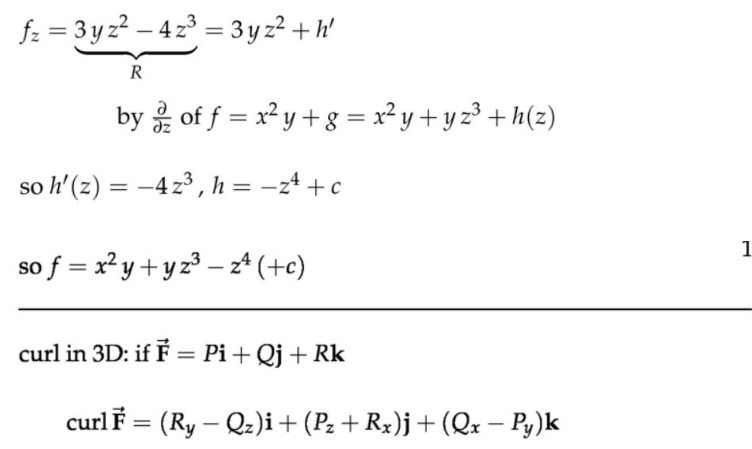
注：这个定理将取代“功”的格林公式，我们称之为斯托克斯公式。

3. 三维空间的旋度

注：保守场，三个方向向量前面的系数都为零。三维空间中向量场的旋度仍然是一个向量场，而二维平面中的旋度是一个标量。

注：这里的行列式写法不是规范的，而是为了便于记忆而已。
注：复杂运动的组成，平移、膨胀、旋转；膨胀对应的是散度，旋转对应的旋度。以流速场中的乒乓球为例子，旋度会告诉你乒乓球的旋转方向和转速，旋度的大小正好就是旋转角速度的两倍。旋转的方向不一定是沿着某个坐标轴，但是始终由旋度方向垂直于旋转平面，而且旋度模长为旋转角速度的两倍。

4. 斯托克斯定理(3D版做功格林公式)
注：平移/膨胀(伸缩)的旋度都是零，表征向量场伸缩的其实是散度。平移/伸缩/旋转，其实都可以用线性代数的语言来描述。
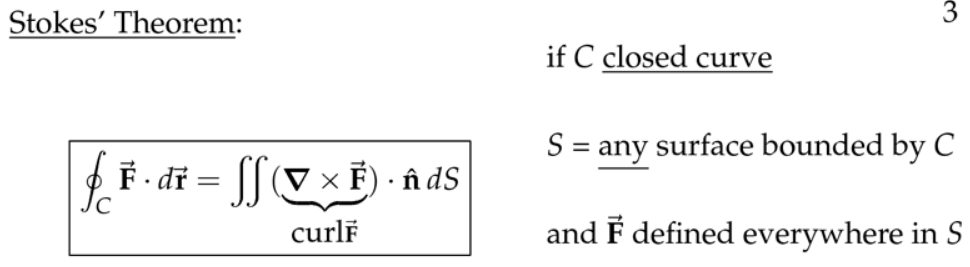注：等式的左边好理解，就是沿着闭合路径向量场做功的积分，这个闭合路径可想象成一圈绳子在空间中的状态；等式右边，积分区间是套在绳子上的布袋子，也可以是各种形状(形状的选取不影响最终结果)，可以把这个袋子切割成无数个小方块单元面，每一个小单元有一个“单位法向量”、“旋度”，这两个都是向量，那么将这个旋度向量投影到单位法向量方向，得到一个标量，然后和小方块的面积元相乘积分。

另外，散度定理是向量场往单位面积元的“单位法向量”上投影，斯托克斯定理是“旋度场”往单位面积的法向量方向投影。

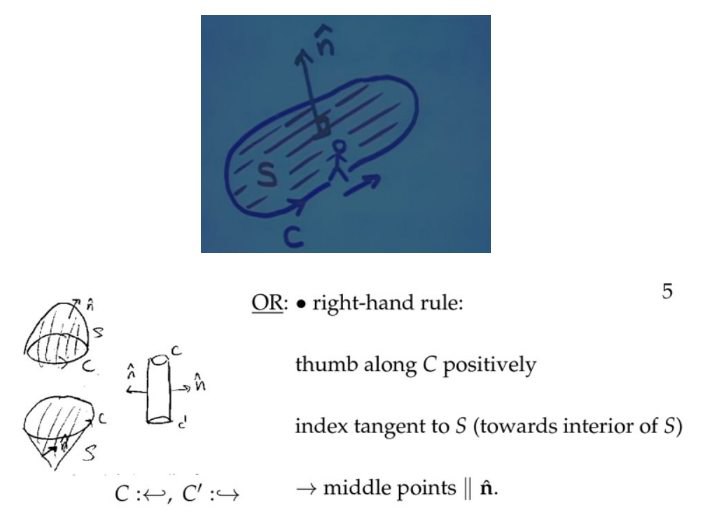
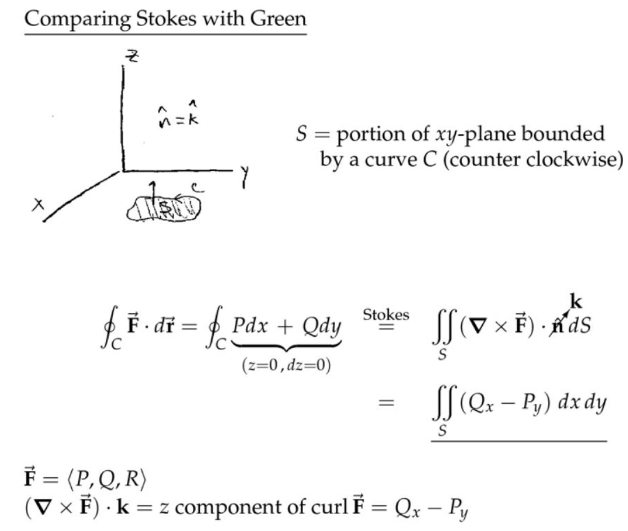
注：格林公式=斯托克斯公式在\(  xy\)平面的特例。

5. 斯托克斯定理的证明

注：做功、通量、旋度都make sense无论坐标系统怎么变。

注：图中大的环路可能不是在一个平面上，但是经过过无限分割后，我们可近似认为这些一个个小块是在一个平面上的。

6. 例子
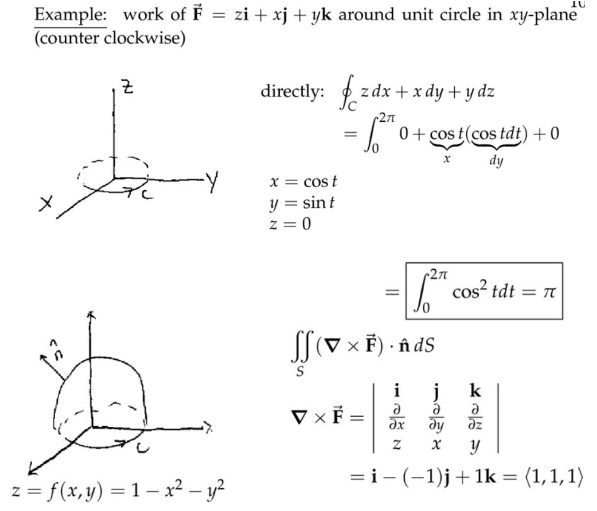注：通量的大小与选取的面无关，只要底部闭合线路径确定，当然选择平面时最简单的。

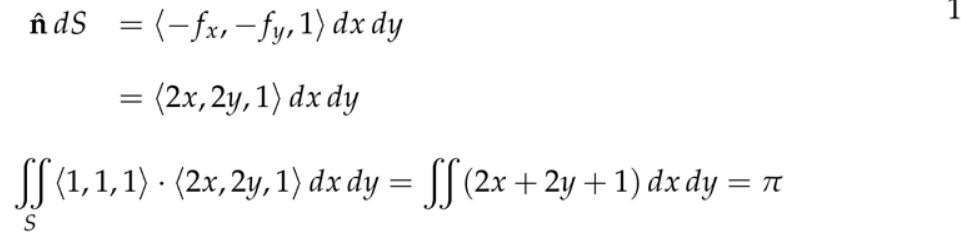
7. 简单连通区域和拓扑
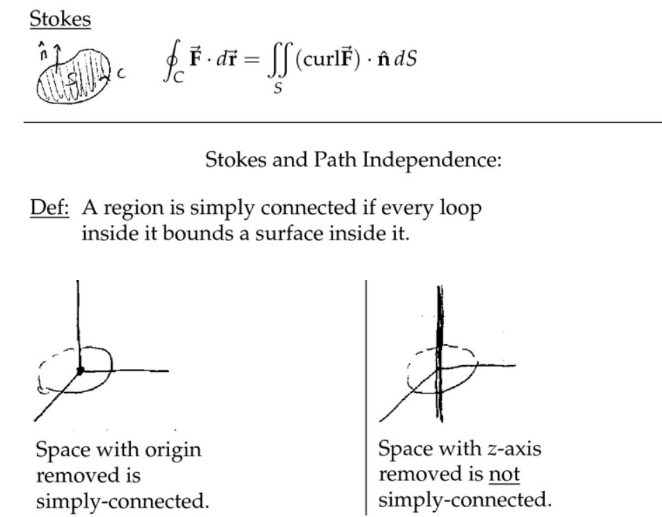注：上面左边的图，选择曲面的时候，可以绕过原点；但是右边的图，无论怎么选择面，总不可能绕过\(z  \)轴。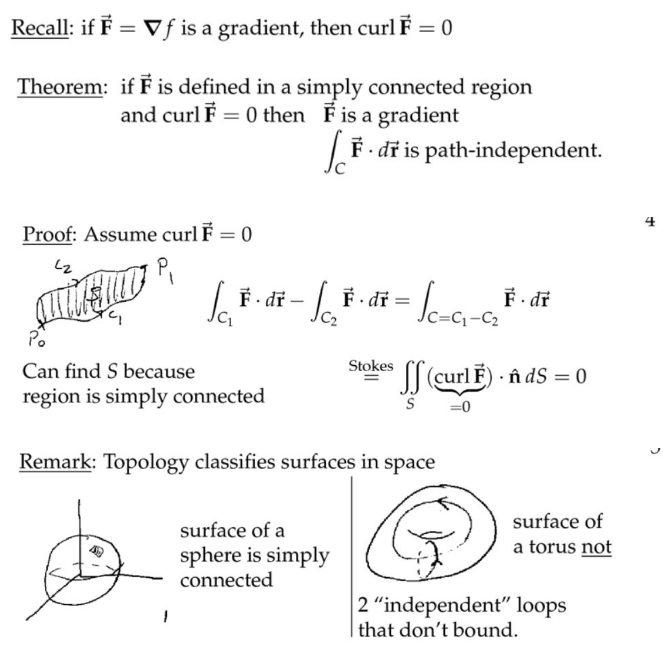

注：上面左侧的图，在球表面上，随便选取一个闭合曲线回路，总能在球上找到“盖子”盖住这个曲线回路；而右侧的图(甜甜圈)，比如选取包含中间孔洞的表面圆回路，或者图中的虚线圆，无法在这个甜甜圈表面找到一块面积能将这两个“洞”盖上。这是从拓扑学的角度来分类。

8. 斯托克斯定理和表面独立性

9. 多重积分汇总

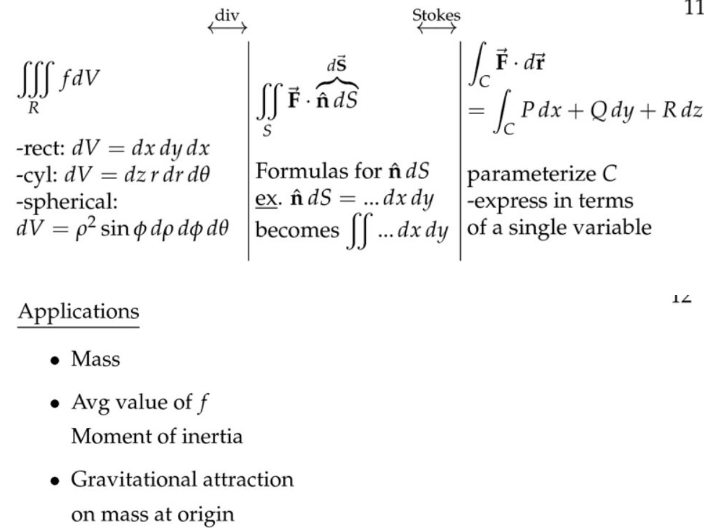
注：上面两个和下面一个，分别是：二重积分与三重积分，一重积分与二重积分，灵重积分与一重积分。特别注意上面右边的那个，是从一个向量场到另一个向量场(由前面的向量场得到的旋度场)。

物理应用

1. 散度和物理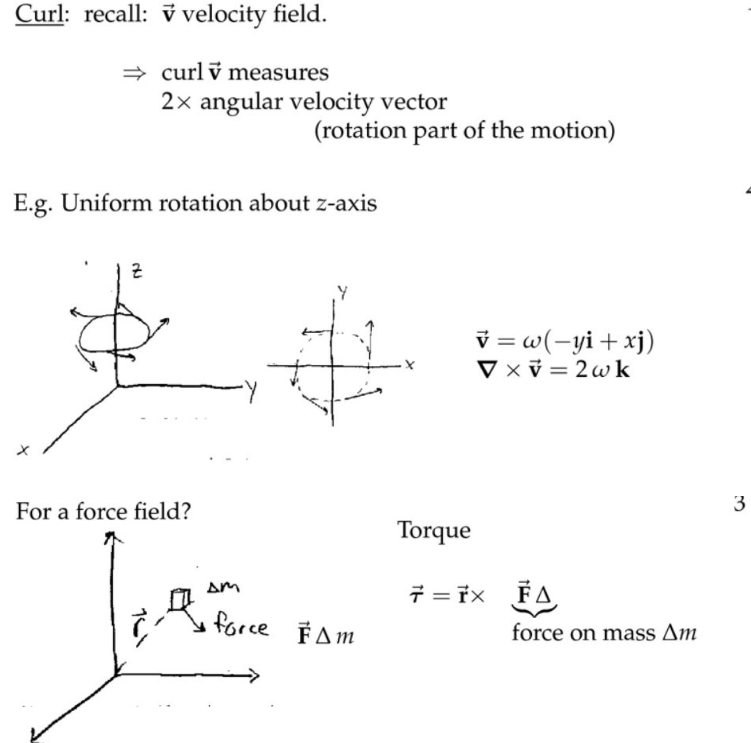

注：地球的公转是由于太阳的引力，但是自转不是因为太阳的引力，而是因为地球形成之初就在自转(it was formed spinning.)。以这种方式来理解万有引力，是纯数学的一个十分深刻的推论。地球、月球和所有东西，都是可以发生形变的，形变、摩擦、潮汐等作用使旋转慢慢变得相互同步起来，这也是月球总以同一面朝向地球的原因。如果是“刚体”，万有引力就不会影响旋转。

2. 麦克斯韦方程组

注：
(1)电荷密度就是电荷除以体积；
(2)传统的静电场，我们认为是电势函数的梯度，因此静电场是无旋场，那么\( \nabla \times \overrightarrow{\mathbf{E}} \)或者环路积分\(  \oint_{C} \overrightarrow{\mathbf{E}} \cdot d \overrightarrow{\mathbf{r}}\)结果为零；但是变化的磁场会产生感生电动势，那么现在的电场就不是传统的静电场了，旋度不为零了，环路积分也不为零了。
(3)  法拉第定律说明变化的磁场产生了电场，麦克斯韦-安培定律又表明电流的产生(或者电场的变化)又会产生变化的磁场，等于说是一个循环。