欧拉方法ODE1
问：什么是显式解(explicit solution)和隐式解(implicit solution)？
答：可以写成\( y=f(x)\)的叫作显式解；只能写成\(f(x, y)=C \)的叫作隐式解，隐式解是方程的形式，但这个方程能确定这个函数。
问：什么是ODE(Ordinary differential equation)和PDE(Partial differential equation)？
答：ODE是常微分方程，PDE是偏微分方程。这里我们将讨论的是ODE常微分方程。
问：什么是函数句柄(function handle)？
答：
(a) 例子
F=@(t,y).06*y-t %这里的.06就是0.06，我们输入t和y值，然后按公式计算
比如F(1,2) 得到的结果为0.06*1-2= -0.8800
(b) 例子(logisctic equation)
a=2;
b=3;
F=@(t, y)a*y-b*y^2
问：什么是欧拉方法ODE1？
答：
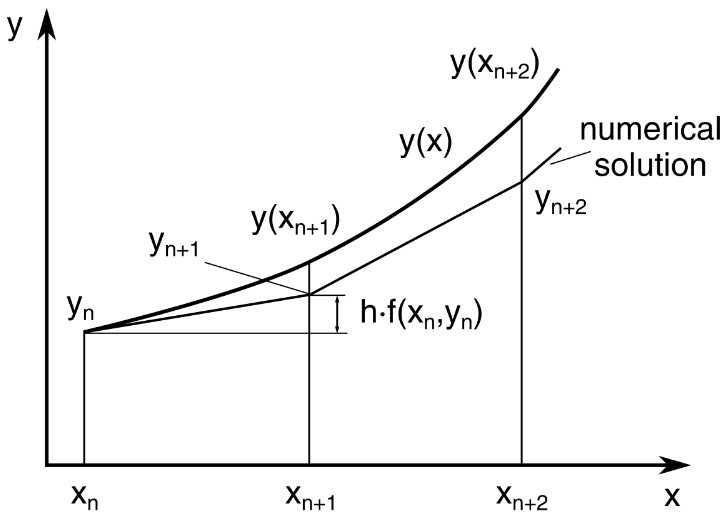欧拉方法$$y^{\prime}(t)=f(t, y(t)), \quad y\left(t_{0}\right)=y_{0}$$我们知道某一点的导数值和函数值，就可以按照类似泰勒展开形式，只保留一阶导数项。根据\( t_{n+1}=t_{n}+h\)有$$y_{n+1}=y_{n}+h f\left(t_{n}, y_{n}\right)$$
先展示一下ODE1的函数
function yout = ode1(F,t0,h,tfinal,y0)
% ODE1 A simple ODE solver.
% yout = ODE1(F,t0,h,tfinal,y0) uses Euler's
% method with fixed step size h on the interval
% t0 <= t <= tfinal
% to solve
% dy/dt = F(t,y)
% with y(t0) = y0.
% Copyright 2014 - 2015 The MathWorks, Inc.
y = y0;
yout = y;
for t = t0 : h : tfinal-h
s = F(t,y);
y = y + h*s;
yout = [yout; y]; %每次得到的新的y都放在yout后面拼接起来
end
例子1$$\begin{aligned} &y^{\prime}=2 y\\ &y(0)=10\\ &0 \leq t \leq 3 \end{aligned}$$求解的代码
F=@(t,y) 2*y; t0=0; h=1; tfinal=3; y0=10; ode1(F,t0,h,tfinal,y0)
例子2: 用ODE1求复利(compound interest )
假设条件为，初始存入100美元，每年的年利率为6%，每个月底取出所有的本息然后再存进去，如此操作总共12年，求每一个月底的账户金额。
代码如下：
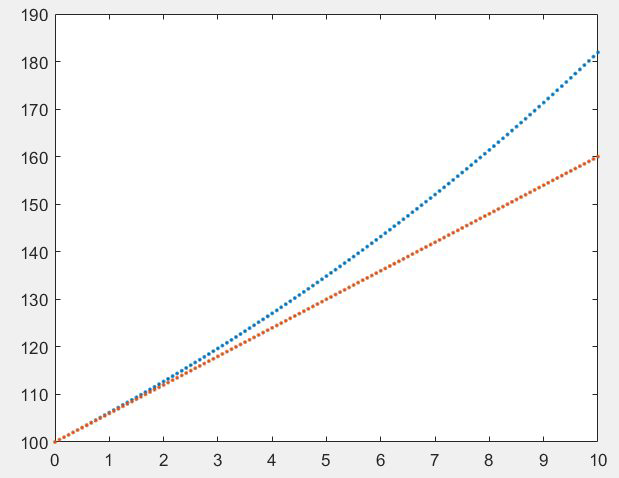
F=@(t,y) .06*y; % t0=0; h=1/12; tfinal=10; y0=100; compound=ode1(F,t0,h,tfinal,y0) format bank %取两位小数，分别对应美元和美分 t=(0:h:tfinal)'; %转置一下 simple=y0+100*0.06*t; plot(t,[compound,simple],'.') %对比两种存钱方法
中间点法ODE2
问：什么是ODE2方法(midpoint method)？
答：
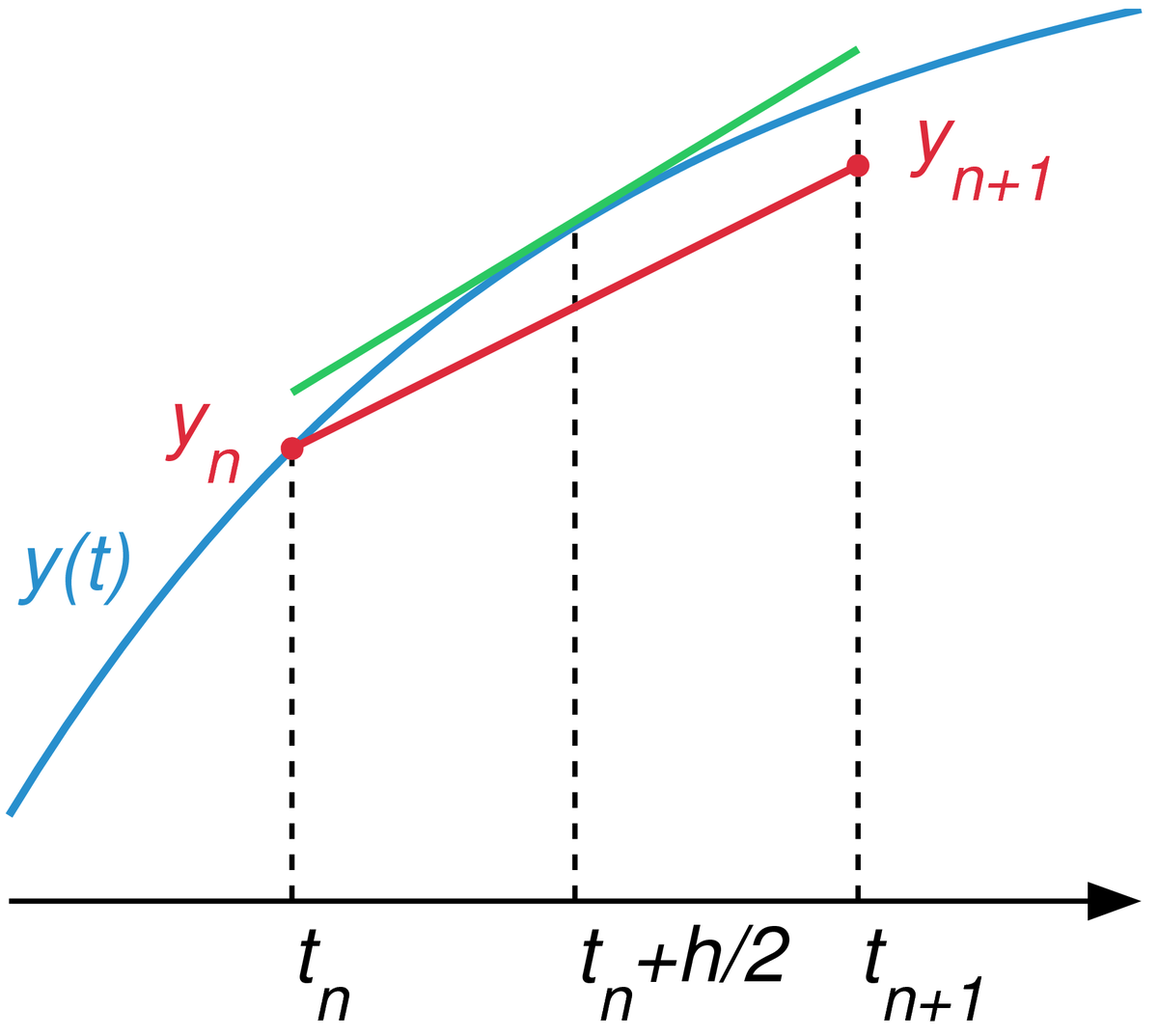ODE1的方法是用个所在点的斜率，推导下一个点的高度位置；ODE2是用相邻两个点中间的点的斜率确定下一个函数点的位置。方法为$$\begin{aligned} &s_{1}=f\left(t_{n}, y_{n}\right)\\ &s_{2}=f\left(t_{n}+\frac{h}{2}, y_{n}+\frac{h}{2} s_{1}\right)\\ &y_{n+1}=y_{n}+h s_{2} \end{aligned}$$
先展示一下ODE2的代码
function yout = ode2(F,t0,h,tfinal,y0)
% ODE2 A simple ODE solver.
% yout = ODE2(F,t0,h,tfinal,y0) uses a midpoint
% rule with fixed step size h on the interval
% t0 <= t <= tfinal
% to solve
% dy/dt = F(t,y)
% with y(t0) = y0.
% Copyright 2014 - 2015 The MathWorks, Inc.
y = y0;
yout = y;
for t = t0 : h : tfinal-h
s1 = F(t,y);
s2 = F(t+h/2, y+h*s1/2);
y = y + h*s2;
yout = [yout; y];
end
例子1：$$\begin{aligned} &\frac{d y}{d t}=\sqrt{1-y^{2}}\\ &y(0)=0\\ &0<=t<=\frac{\pi}{2} \end{aligned}$$其实很容易看出答案为\(y(t)=\sin t \)，不过我们用ODE2来计算。
代码如下
F=@(t,y) sqrt(1-y^2);
t0=0;
h=pi/32;
tfinal=pi/2;
y0=0;
y=ode2(F,t0,h,tfinal,y0);
t=(0:h:tfinal)'; %转置一下
simple=sin(t);
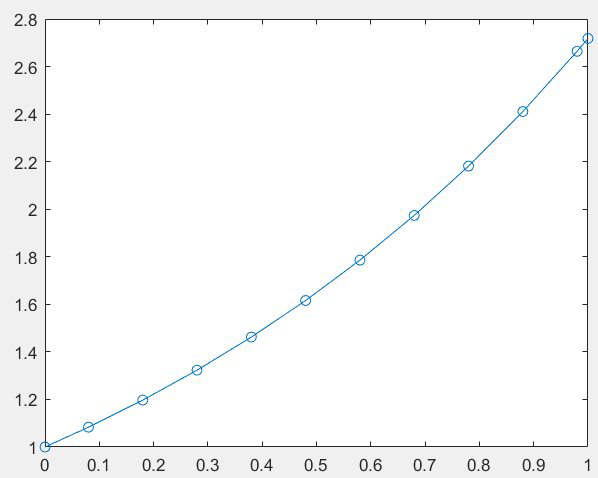
plot(t,[y,simple],'o-')
axis([0 pi/2 0 1])
set(gca,'xtick',[0:pi/8:pi/2],'xticklabel',{'0','\pi/8','\pi/4','3\pi/8','\pi/2'})
xlabel('t'),ylabel('y')
其实函数解和数值解的两个图像几乎重合，表面我们的数值解很好。
作业1：Modify ode2, creating ode2t, which implements the trapezoid(梯形) method, $$\begin{aligned} &s_{1}=f\left(t_{n}, y_{n}\right)\\ &s_{2}=f\left(t_{n}+h, y_{n}+h s_{1}\right)\\ &y_{n+1}=y_{n}+h \frac{s_{1}+s_{2}}{2} \end{aligned}$$
经典龙格-库塔法ODE4
问：什么是经典龙格-库塔法(Classical Runge-Kutta)ODE4？
答：这个是近100年最受欢迎的numerical method，特别是20世纪很流行，现在仍有人用。我们在ODE1中每一个新的点的计算只借助了上一个点的斜率值，而在ODE2中，我们每一个新的点的计算借助的是前\( \frac {h }{ 2} \)拟合点的斜率值，而这个斜率值是按照ODE1的方法推算的。
而龙格-库塔法，每一个新的点\( x_{n+1} \)的计算借助的是一个平均斜率，这个平均斜率是多个斜率值的加权平均值，选取的斜率值越多，那么误差越小，精度越高。比如最简单的取两个斜率值：$$\begin{aligned} &K_{1}=f\left(x_{n}, y_{n}\right)\\ &K_{2}=f\left(x_{n+1}, y_{n}+h K_{1}\right)\\ &y_{n+1}=y_{n}+\frac{h}{2}\left(K_{1}+K_{2}\right) \end{aligned}$$我们一般用四阶龙格-库塔方法来处理ODE。
四阶龙格-库塔方法$$\begin{aligned} &K_{1}=f\left(x_{n}, y_{n}\right)\\ &K_{2}=f\left(x_{n+\frac{1}{2}}, y_{n}+\frac{h}{2} K_{1}\right)\\ &K_{3}=f\left(x_{n+\frac{1}{2}}, y_{n}+\frac{h}{2} K_{2}\right)\\ &K_{4}=f\left(x_{n+1}, y_{n}+h K_{3}\right)\\ &y_{n+1}=y_{n}+\frac{h}{6}\left(K_{1}+2 K_{2}+2 K_{3}+K_{4}\right) \end{aligned}$$经典的四阶龙格-库塔格式每一步需要计算四次函数值 f，它具有四阶精度。
先展示一下ODE4的代码
function yout = ode4(F,t0,h,tfinal,y0)
% ODE4 Classical Runge-Kutta ODE solver.
% yout = ODE4(F,t0,h,tfinal,y0) uses the classical
% Runge-Kutta method with fixed step size h on the interval
% t0 <= t <= tfinal
% to solve
% dy/dt = F(t,y)
% with y(t0) = y0.
% Copyright 2014 - 2015 The MathWorks, Inc.
y = y0;
yout = y;
for t = t0 : h : tfinal-h
s1 = F(t,y);
s2 = F(t+h/2, y+h*s1/2);
s3 = F(t+h/2, y+h*s2/2);
s4 = F(t+h, y+h*s3);
y = y + h*(s1 + 2*s2 + 2*s3 + s4)/6;
yout = [yout; y];
end
例子1：点燃火柴棒，前面的ball的火焰快速增长直到达到critical size，然后保持这个size，因为ball内部消耗的氧气和ball表面available的氧气量达到平衡状态。对应的微分方程和条件为$$\begin{aligned} &\frac{d y}{d t}=y^{2}-y^{3}\\ &y(0)=y_{0}\\ &0 \leq t \leq \frac{2}{y_{0}} \end{aligned}$$
代码如下
F=@(t,y) y^2-y^3; t0=0; y0=0.01; tfinal=2/y0; h=0.4; y=ode4(F,t0,h,tfinal,y0); t=(0:h:tfinal)'; %转置一下 plot(t,y,'.')
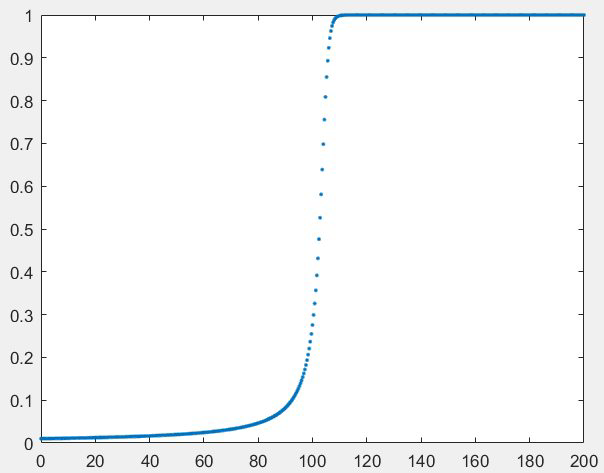图中在中点的位置附近，函数的增长率一下子变得非常快，也就是说在极短的时间内完成了从缓慢增长到稳定状态。那么在这个快速增长的区域，对于数值方法来说是一个很大的挑战，容易出现很大的误差，关于误差这部分我们后面将详述。
作业1：
If the differential equation$$\frac{d y}{d t}=f(t)$$only involves \( t, \) not \( y,\) then its solution is just an integral,$$y(t)=\int f(t) d t$$In this situation, the Runge-Kutta method becomes a classic method of numerical quadrature. It should be familiar if you have ever studied such methods. Do you recognize it?
作业2：
What is the solution to$$\frac{d y}{d t}=1+y^{2}$$with$$y(0)=0$$What happens if you try to use ode4 to solve this equation on the interval$$0 \leq t \leq 2$$
作业3：
What happens with ode4 if the length of the interval, tfinal-to, is not evenly divisible by the step size, h? For example, if t0=0, tfinal =p i, and h=0 .1. This is one of the hazards of a fixed step size.
作业4：
问：什么是误差阶数？什么是泰勒级数
答：
\(o(x^p) \)表示的是\(x^p \)的高阶无穷小，也就是当\( p \)趋近于零时，\( o(x^p) \)比\(x^p \)更快趋近于零。比如\(x^2 \)是\(x \)的高阶无穷小，可以表示为\(x^2=o(x) \)。回忆一下什么叫作“同阶无穷小”，什么叫作“等价无穷小”(比如\( \sin x\)和\( x \))。
将\( f(x)\)在\(x=a \)处泰勒展开，得到的是$$f(x)=f(a)+\frac{f^{\prime}(a)}{1 !}(x-a)+\frac{f^{\prime \prime}(a)}{2 !}(x-a)^{2}+\frac{f^{\prime \prime \prime}(a)}{3 !}(x-a)^{3}+o(x-a)^{3}$$
对于欧拉方法ODE1，相当于在\( y_{n} \)泰勒展开，于是 $$ y_{n+1}= y_{n}+\frac {f(t_{n},y_{n}) }{ 1 } h+o(h)$$注意这里的\( o(h)=m*h^2 \)(\( m\)是一个特定常数参见余项形式)。这就说每一步的的误差正比于步长的平方。
对于经典的四阶龙格-库塔法，每一步的local error(局部截断误差，或者说每一步的误差)为\(h^5 \)阶，总的global error为\(h^4 \)阶，如果让步长减半为\(\frac { h}{ 2} \)，那么误差将会减少\( 2^4 \)。对于ODE1欧拉方法是一个一阶方法，意味着其局部截断误差（每步误差）正比于步长的平方，并且其全局截断误差正比于步长。
命名：odepq uses methods of order p and q
作业：
Modify order x to do further experiments involving the order of our ODE solvers.
ODE23(估计误差，自动调整步长)
问：什么是modern numercial method？
答：
modern numercial method 不同于前面的ODE1欧拉方法或者四阶龙格-库塔方法，它的特点是：
(1) Error estimate and step size control;
(2) Fully accurate continuous interpolant(插值)
也就是不指定步长，而是指定你所需要的精度，程序根据所要求的误差自动调整步长。
Bogacki-Shampine Order 3(2) (ODE23的basis)$$\begin{aligned} s_{1} &=f\left(t_{n}, y_{n}\right) \\ s_{2} &=f\left(t_{n}+\frac{h}{2}, y_{n}+\frac{h}{2} s_{1}\right) \\ s_{3} &=f\left(t_{n}+\frac{3}{4} h, y_{n}+\frac{3}{4} h s_{2}\right) \\ t_{n+1} &=t_{n}+h \\ y_{n+1} &=y_{n}+\frac{h}{9}\left(2 s_{1}+3 s_{2}+4 s_{3}\right) \\ s_{4} &=f\left(t_{n+1}, y_{n+1}\right) \\ e_{n+1} &=\frac{h}{72}\left(-5 s_{1}+6 s_{2}+8 s_{3}-9 s_{4}\right) \end{aligned}$$每一步计算的误差都去和这里的\(e_{n+1} \)进行比较，如果实际误差比它大，那么减小步长(多插入点)。
先展示ODE23的代码(automatic step choice of ODE23)
function [tout,yout] = ode23tx(F,tspan,y0,arg4,varargin)
%ODE23TX Solve non-stiff differential equations. Textbook version of ODE23.
%
% ODE23TX(F,TSPAN,Y0) with TSPAN = [T0 TFINAL] integrates the system
% of differential equations dy/dt = f(t,y) from t = T0 to t = TFINAL.
% The initial condition is y(T0) = Y0.
%
% The first argument, F, is a function handle or an anonymous function
% that defines f(t,y). This function must have two input arguments,
% t and y, and must return a column vector of the derivatives, dy/dt.
%
% With two output arguments, [T,Y] = ODE23TX(...) returns a column
% vector T and an array Y where Y(:,k) is the solution at T(k).
%
% With no output arguments, ODE23TX plots the emerging solution.
%
% ODE23TX(F,TSPAN,Y0,RTOL) uses the relative error tolerance RTOL
% instead of the default 1.e-3.
%
% ODE23TX(F,TSPAN,Y0,OPTS) where OPTS = ODESET('reltol',RTOL, ...
% 'abstol',ATOL,'outputfcn',@PLOTFUN) uses relative error RTOL instead
% of 1.e-3, absolute error ATOL instead of 1.e-6, and calls PLOTFUN
% instead of ODEPLOT after each successful step.
%
% More than four input arguments, ODE23TX(F,TSPAN,Y0,RTOL,P1,P2,...),
% are passed on to F, F(T,Y,P1,P2,...).
%
% ODE23TX uses the Runge-Kutta (2,3) method of Bogacki and Shampine (BS23).
%
% Example
% tspan = [0 2*pi];
% y0 = [1 0]';
% F = @(t,y) [0 1; -1 0]*y;
% ode23tx(F,tspan,y0);
%
% See also ODE23.
% Copyright 2012 - 2015 The MathWorks, Inc.
% Initialize variables.
rtol = 1.e-3;
atol = 1.e-6;
plotfun = @odeplot;
if nargin >= 4 & isnumeric(arg4)
rtol = arg4;
elseif nargin >= 4 & isstruct(arg4)
if ~isempty(arg4.RelTol), rtol = arg4.RelTol; end
if ~isempty(arg4.AbsTol), atol = arg4.AbsTol; end
if ~isempty(arg4.OutputFcn), plotfun = arg4.OutputFcn; end
end
t0 = tspan(1);
tfinal = tspan(2);
tdir = sign(tfinal - t0);
plotit = (nargout == 0);
threshold = atol / rtol;
hmax = abs(0.1*(tfinal-t0));
t = t0;
y = y0(:);
% Initialize output.
if plotit
plotfun(tspan,y,'init');
else
tout = t;
yout = y.';
end
% Compute initial step size.
s1 = F(t, y, varargin{:});
r = norm(s1./max(abs(y),threshold),inf) + realmin;
h = tdir*0.8*rtol^(1/3)/r;
% The main loop.
while t ~= tfinal
hmin = 16*eps*abs(t);
if abs(h) > hmax, h = tdir*hmax; end
if abs(h) < hmin, h = tdir*hmin; end
% Stretch the step if t is close to tfinal.
if 1.1*abs(h) >= abs(tfinal - t)
h = tfinal - t;
end
% Attempt a step.
s2 = F(t+h/2, y+h/2*s1, varargin{:});
s3 = F(t+3*h/4, y+3*h/4*s2, varargin{:});
tnew = t + h;
ynew = y + h*(2*s1 + 3*s2 + 4*s3)/9;
s4 = F(tnew, ynew, varargin{:});
% Estimate the error.
e = h*(-5*s1 + 6*s2 + 8*s3 - 9*s4)/72;
err = norm(e./max(max(abs(y),abs(ynew)),threshold),inf) + realmin;
% Accept the solution if the estimated error is less than the tolerance.
if err <= rtol
t = tnew;
y = ynew;
if plotit
if plotfun(t,y,'');
break
end
else
tout(end+1,1) = t;
yout(end+1,:) = y.';
end
s1 = s4; % Reuse final function value to start new step.
end
% Compute a new step size.
h = h*min(5,0.8*(rtol/err)^(1/3));
% Exit early if step size is too small.
if abs(h) <= hmin
warning('Step size %e too small at t = %e.\n',h,t);
t = tfinal;
end
end
if plotit
plotfun([],[],'done');
end
例子1：
F=@(t,y)y; %微分方程，导函数等于函数值本身(其实是指数函数)
ode23(F,[0 1],1) % interval from 0 to 1, 初始值为1，没有output argument(输出参数)
结果为
例子2：
F=@(t,y)y;
[t,y]=ode23(F,[0 1],1) %对比上一个例子加入输出参数
plot(t,y,'o-') %的到的图和上面一样
注意，从0开始第一步选择的步长为0.08(自动调整，满足误差要求)，后面的步长都是0.1，然后最后一步的步长为0.02正好到1。程序的默认误差(default error)为\( 10^{-3}\)。
例子3：
代码
a=0.25; y0=15.9; F=@(t,y)2*(a-t)*y^2 [t,y]=ode23(F,[0 1],y0) plot(t,y,'-',t,y,'.','markersize',24)
图像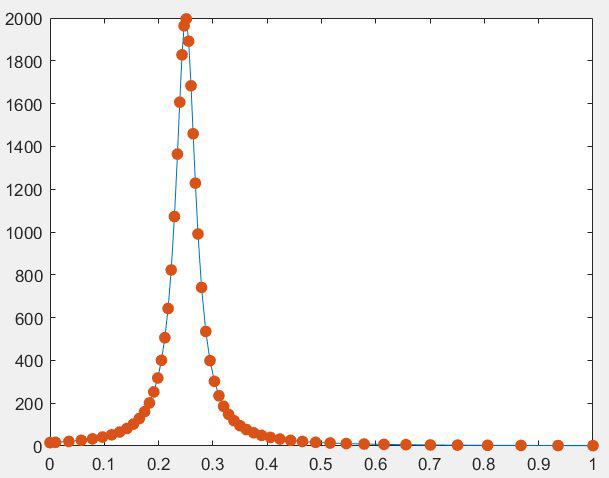
图像在0.25附近快速增长，然后又快速下降，这部分是容易出现误差较大的情况，所以ODE23程序自动调整了这一部分的步长，所以点从横轴来看比较密(步长小)，从0.5到1这一部分由于函数值本身变化很小，所以可以在取较大步长的情况下满足默认的误差范围。
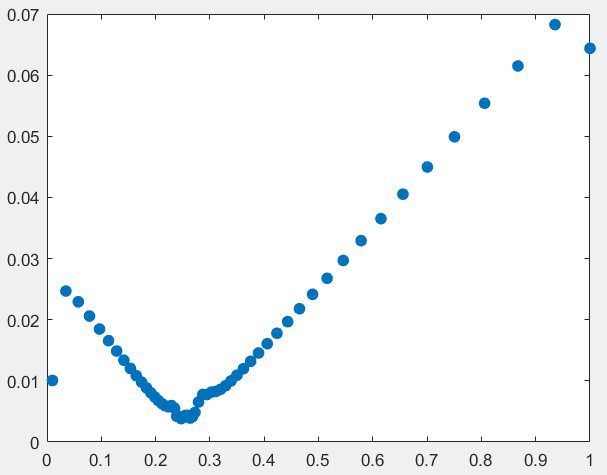
如果根据每一步的步长大小作图，即添加
h=diff(t);
plot(t(2:end),h,'.','markersize',24)这两行代码，可以得到如下图像
问：简单介绍一下各种插值法？
答：