MIT-微分方程 – Page 2 – 历史的进程

二阶微分方程

概述和无阻尼情况

【二阶常微分方程】(Second Order Equations)二阶常微分方程的典型方程式为$$A \frac{d^{2} y}{d t^{2}}+B \frac{d y}{d t}+C y=0$$二阶常微分方程在应用中特别广泛，二阶导数对应着加速度或者曲线的弯曲程度。我们先讨论三个系数$ A、B、C $均为常数，而且input为零的情况，也就是求解“零解”，这个时候解函数的形式均为指数形式，零解有两个(类似组成二维零空间)，通常写成$ y_{n}=c_{1} e^{s_{1} t}+c_{2} e^{s_{2} t}$的形式，其中的两个参数需要两个初始条件来确定，比如$y(0) $和$y^{\prime}(0)$。

注意这是在非共振情况下的通解，共振时的通解为$y_{n}=c_{1} e^{s t}+c_{2} te^{s t}$

无阻尼，input为零(free harmonic motion)

回忆无摩擦力的弹簧系统，滑块将一直运动下去。把坐标原点选在弹簧原长处，x轴沿弹簧方向$ \boldsymbol{F}=-k x \boldsymbol{i}=m \boldsymbol{a}=m \ddot{\boldsymbol{x}}$投影得标量微分方程$ m \ddot{x}-k x=0$。解得微分方程的通解为$$x=A \cos \left(\sqrt{\frac{k}{m}} t+t_{0}\right)$$

进入正题，在物理和工程中最常见的运动方程—简谐运动的方程，其形式为$$m y^{\prime \prime}+k y=0 $$其中因为没有阻尼项，所以没有一阶导数项。这个方程就是表示弹簧的简介振动或者钟摆(pendulum)的运动(只有在小角度下才能这样仅是处理)。现在我们为了计算简便，设定$ m=k=1$。于是有$ y^{\prime \prime}=-y$，立刻就会想到正余弦函数。如果$ m $和$ k$为实数，则二阶导数和原函数之间还差着参数$ k / m $，因此零解之一为$ y_{n}=c_{1} \cos (\sqrt{\displaystyle\frac{k}{m}} t) $，根号是因为求导两次提到外面就是一次了，而其零解表达式为两个零解之和：$$y_{n}=c_{1} \cos (\sqrt{\frac{k}{m}} t)+c_{2} \sin (\sqrt{\frac{k}{m}} t)$$令$ \omega_{n}= \sqrt{\displaystyle\frac{k}{m}}$，其中$\omega_{n} $表示【自然频率】(固有频率)，更严格地说应该是角频率，从量纲的角度看，$ kx=ma$，所以$ k/m=a/x $量纲为$ \mathbf{s}^{-2}$，开方之后就是角频率的量纲。如果对应的是LC系统，那么固有频率就是$ f=\displaystyle\frac{1}{2 \pi \sqrt{L C}}$。于是方程变为$$y^{\prime \prime}+\omega_{n}^{2} y=0$$解变为$y_{n}=C_{1} \cos \left(\omega_{n} t\right)+C_{2} \sin \left(\omega_{n} t\right) $。可以看出零解中的参数需要带入初始值来确定，带入$ y(0)$和$y^{\prime}(0) $，最终得到正余弦表达式$$y_{n}=y(0) \cos \left(\omega_{n} t\right)+\frac{y^{\prime}(0)}{\omega_{n}} \sin \left(\omega_{n} t\right)$$虚指数的表达式：$$ y_{n}=c_{1} e^{i \omega_{n} t}+c_{2} e^{-i \omega_{n} t}$$

这里的方程描述的是纯简谐运动，在正余弦表达式中只有无限延伸的纯周期振荡的量；而在虚指数表达式中，由于指数为纯虚数，也即信号还是在纯周期振荡而不会随着时间增长而缩放。因此这从一点来看，二者也是等价的。
可以用$ e^{i \omega_{n} t}$和$ e^{-i \omega_{n} t}$按一定形式线性组合(复数系数)可以分别得到$ \cos \left(\omega_{n} t\right)$和$ \sin \left(\omega_{n} t\right) $)，或者说两种基底所描述的两个空间可以相互转换。

无阻尼，input不为零(Forced Harmonic Motion)

$$m \frac{d^{2} y}{d t^{2}}+k y=f(t)$$与前面的自由状态的简谐运动不同，等式右边引入了外力作用。现在我们研究两个个相对简单的情况
(a) 输入余弦函数$ m \displaystyle\frac{d^{2} y}{d t^{2}}+k y=\cos \omega t $
解函数一定包含两种频率信息，一是自然频率$ \omega_{n}=\sqrt{\displaystyle\frac{k}{m}}$(对应于零解)，二是外力频率$ \omega $。这两者的匹配状态决定着运动的状态，在实际应用中甚至会决定桥梁是否会因为两频率相等$ \omega=\omega_{n} $导致共振状态而发生倒塌。

方程只有二次导函数和函数本身，再加上余弦输入，因此很容易想到特解形式为$ y_{p}=Y \cos \omega t$，这个解函数也称为【受迫响应】(forced response)。带入特解$$\begin{aligned} &-\omega^{2} m Y \cos \omega t+k Y \cos \omega t=\cos \omega t\\ &\Rightarrow\left(k-\omega^{2} m\right) Y=1\\ &\Rightarrow Y=\frac{1}{k-\omega^{2} m}, y_{p}=\frac{\cos \omega t}{k-\omega^{2} m} \end{aligned}$$带入自然频率$ \omega_{n}=\sqrt{\displaystyle\frac{k}{m}} $，然后加上零解就可以得到通解$$y(t)=\frac{\cos \omega t}{m\left(\omega_{n}^{2}-\omega^{2}\right)}+C_{1} \cos \omega_{n} t+C_{2} \sin \omega_{n} t$$可以看到当外力频率和自然频率接近时，对函数值的大小影响非常大，我们将因子$ Y(\omega)=\displaystyle\frac{1}{m\left(\omega_{n}^{2}-\omega^{2}\right)} $称为【频率响应】(frequecny response)。

(b) 输入Delta函数$ m \displaystyle\frac{d^{2} y}{d t^{2}}+k y=\delta(t) $
外力的作用只发生在最初的一瞬间，即在时刻给系统-比如蛋白或者弹簧一个外力冲击，这一瞬间给了系统一定的速度，但是还没有发生位移，该方程的解函数称为冲激响应。

将方程看作是齐次的$ m g^{\prime \prime}+k g=0 $，但是方程的初始条件因为冲激而发生了改变，位移不变$g(0)=0 $，速度发生变化$ g^{\prime}(0)=1 / m $(为什么这样写后面要讨论)。将初始条件带入我们先前得到的零解通式$ y_{n}=y(0) \cos \left(\omega_{n} t\right)+\displaystyle\frac{y^{\prime}(0)}{\omega_{n}} \sin \left(\omega_{n} t\right) $求得方程的解为$ g(t)=\displaystyle\frac{\sin \omega_{n} t}{m \omega_{n}}$。

有阻尼情况(冲激和阶跃响应)

非受迫阻尼运动(Unforced Damped Motion)

$$A \frac{d^{2} y}{d t^{2}}+B \frac{d y}{d t}+C y=0$$非受迫阻尼运动中，“非受迫”指外力为零，则方程是齐次的；有“阻尼”表示一阶导数的系数$ B\not=0$，对应着阻尼项。

物理模型

对力学模型而言，$ A $为质量mass，$B $是摩擦系数, damping constant，$ C $是弹簧常数, spring constant；
在电子电路中，$ B $通常是电阻，将能量以热的形式耗散。
解函数可以用参量的组合来表示：
- 【自然频率】$ \omega_{n}=\sqrt{\displaystyle\frac{C}{A}}=\sqrt{\displaystyle\frac{k}{m}} $
- 【阻尼比】(damping ratio) $Z E T A=\displaystyle\frac{B}{\sqrt{4 A C}}=\displaystyle\frac{b}{\sqrt{4 m k}} $(无量纲)

解函数的形式还是指数函数$ y=e^{s t} $的类型，对于常系数微分方程来说，解函数的结构往往包含指数函数。回代入微分方程，得到$\left(A s^{2}+B s+C\right) e^{s t}=0 $。因此转化成求解【特征方程】$$A s^{2}+B s+C=0$$其解为$s_{1}, s_{2}=\displaystyle\frac{-B \pm \sqrt{B^{2}-4 A C}}{2 A} $。

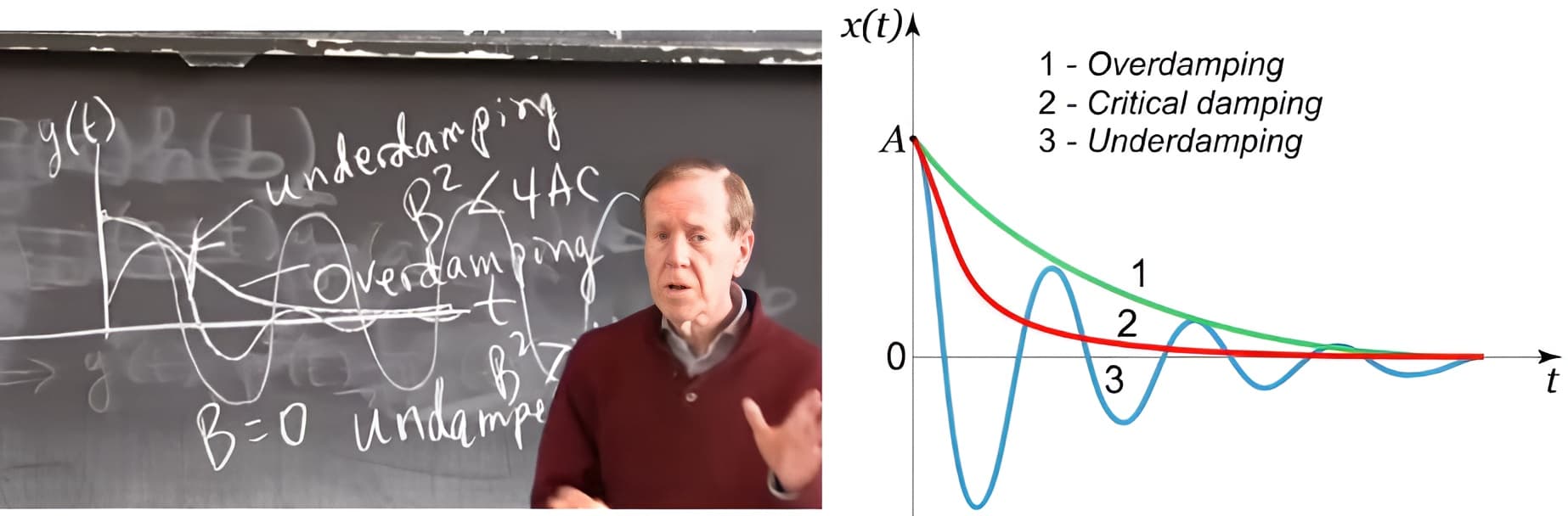
$B=0 $，对应于【无阻尼】，两个纯虚数根$ s=\pm i \omega_{n}$，方程退化为上一问的情况(自由简谐运动)，对应解为如下：(注意这里的系数项是复数)$$y_{n}=c_{1} e^{i \omega_{n} t}+c_{2} e^{-i \omega_{n} t}$$
$ B^{2}<4 A C $，对应于【欠阻尼】，方程的解$ s $中存在虚部，摩擦使得简谐振荡变得缓慢了，解函数中引入了指数衰减。设$s=r \pm \mathrm{i} \omega_n$，则$$y_{n}=c_{1} e^{s_1 t}+c_{2} e^{s_2 t}=c_{1} e^{(r+i\omega _n) t}+c_{2} e^{(r-i\omega _n) t}=e^r(c_{1} e^{i\omega _n t}+c_{2} e^{-i\omega _n t})$$
$ B^{2}=4 A C $，对应于【临界阻尼】(共振)，两个相同的实数根，特征值缺失，$s_{1}=s_{2}=-B / 2 A =-C/A=r $，通解为$$y_{n}=c_{1} e^{ r t}+c_{2} te^{ r t}$$
$ B^{2}>4 A C$，对应于【过阻尼】，$s_{1}, s_{2}<0 $，两个不同的实数根$r_1$和$r_2$，通解为$$y_{n}=c_{1} e^{ r_1t}+c_{2}te^{ r_2 t}$$

【阻尼铰链】：是一种利用液体的缓冲性能，缓冲效果理想的一种液压缓冲铰链，门在60°开始自行缓慢关闭，减低冲击力，形成关闭时的阻尼铰链舒适效果。

现实生活中，许多大楼内房间或卫生间的门上在装备自动关门的扭转弹簧的同时，都相应地装有阻尼铰链，使得门的阻尼接近临界阻尼，这样人们关门或门被风吹动时就不会造成太大的声响。当自动门上安装的阻尼铰链使门的阻尼达到过阻尼时，自动关门需要更长的时间。如记忆枕。

参考资料：
(1) 過阻尼, 欠阻尼, 臨界阻尼-台大物理系
(2) 简谐运动之阻尼振动
(3) hyperphysics-Damped Harmonic Oscillator
(4) 阻尼振动、受迫振动和共振-山东大学
(5) 二阶常系数齐次微分方程—小时百科
(6) 为什么临界阻尼比过阻尼衰减快?-知乎

冲激响应(Impulse Response )

$$g^{\prime \prime}+B g^{\prime}+C g=\delta(t)$$求解的关键点在于将方程转化为$g^{\prime \prime}+B g^{\prime}+C g=0 $，初始条件为$ g(0)=0, g^{\prime}(0)=1$。我们前面已经知道对于冲激响应，我们还是将其看成齐次微分方程，求解出通式然后带入特定的初始条件即可。先前我们已经研究了二阶齐次的情况，因此方程的解为$ g(t)=c_{1} e^{s_{1} t}+c_{2} e^{s_{2} t} $，带入初值条件得到$$ g(t)=\frac{e^{s_{1} t}-e^{s_{2} t}}{s_{1}-s_{2}} $$我们再次讨论阻尼情况：
(1) $B=0 $ No damping，$ s=\pm i \omega_{n} $，$ g(t)=\displaystyle\frac{\sin \omega_{n} t}{\omega_{n}} $

(2) $ B^{2}<4 C $ Under damping $ s=-\displaystyle\frac{B}{2} \pm i \omega_{d} $ $ g(t)=e^{-B t / 2} \displaystyle\frac{\sin \omega_{d} t}{\omega_{d}} $

(3) $ B^{2}=4 C $ Critical damping $ s=-B / 2 $ $g(t)=t e^{-B t / 2} $

(4) $ B^{2}>4 C $ Over damping $ s_{1}$ and $ s_{1} $ are two different real number $ g(t)=\displaystyle\frac{e^{s_{1} t}-e^{s_{2} t}}{s_{1}-s_{2}}$
可以看到随着阻尼系数越来越来大，相当于原来的free oscillation不断的拉平。当阻尼比较小的时候，$ s$的虚部存在，就会始终有振荡，另外阻尼越大振荡周期约大。当阻尼大到一定程度的时候，振荡就会消失，$ s $也只剩下实部，这也符合我们的物理实验直觉。(思考一下BC正负号)

阶跃响应(Step Response)

$$r^{\prime \prime}+B r^{\prime}+C r=H(t)$$初始条件$ r(0)=0, r^{\prime}(0)=0$。根据阶跃函数的特点，我们很容易知道常数函数符合要求，有时候为了简化数量和单位的问题，方程写作$ r^{\prime \prime}+B r^{\prime}+C r=C H(t) $，则特解的形式为$r(t)=1 $。

但是该特解并不复合初值条件，需要和某个“零解”线性组合才能得到符合初值的特解。将零解$ r(t)=c_{1} e^{s_{1} t}+c_{2} e^{s_{2} t} $构造为$ r(t)=c\left(s_{2} e^{s_{1} t}-s_{1} e^{s_{2} t}\right) $的形态，可以保证其一阶导数等于$0 $，而带入通解中使其满足$r(0)=0 $，可以得到$ r(t)=1+\displaystyle\frac{s_{2} e^{s_{1} t}-s_{1} e^{s_{2} t}}{s_{1}-s_{2}} $。

画出阶跃响应的函数图像，可以其从零点出发最终逼近稳态，很多工程问题就是研究其逼近稳态的速度。比如一个开关从关闭到突然打开，那么某个物理参数会从零不断增长到稳定值，我们经常研究到达稳定值的95 %需要多长的时间。

阶跃函数$ H(t) $是冲激函数$ \delta(t) $的积分，而阶跃响应也是冲激响应的积分。二者都是重要的解函数，冲激响应在理论和实际应用中经常出现，而阶跃响应在应用中更为重要，因为一个“开关”过程在工程应用中非常常见。

指数响应和可能的共振(Exponential Response - Possible Resonance)

(a) 指数响应$$A \frac{d^{2} y}{d t^{2}}+B \frac{d y}{d t}+C y=e^{s t}$$这是典型的指数响应，求解二阶的微分方程的方法和求解更高阶微分方程的方法其实是一样的，通用的$ n $阶常系数微分方程$$A_{N} \frac{d^{N} y}{d t^{N}}+\cdots+A_{1} \frac{d y}{d t}+A_{0} y=e^{s t}$$方程的求解方法是令解函数为$ y=Y e^{s t} $代回原方程得到，对于$ n $阶方程$ Y=\displaystyle\frac{1}{A_{N} s^{N}+\cdots+A_{1} s+A_{0}}$，对于二阶有$$Y=\frac{1}{A s^{2}+B s+C}$$这里的$ Y $称为【传递函数】(transfer function)，它表示了输出函数和输入函数之间的关系。(这里，输入一个指数函数，输出的也是一个指数函数)

(b) 共振
如果给定的输入函数中的$ s $恰好是齐次方程解—“零解” $ s_{1} $或者$ s_{2} $，则其满足$ A s^{2}+B s+C=0 $，因为分母 $ Y $为零，于是形成了【共振现象】，而$ s_{1} $和$ s_{2} $也称为函数传递的极点。这个时候函数特解$y_{p}=\displaystyle\frac{e^{s t}}{A s^{2}+B s+C} $的分母为$ 0 $，但是分子不是，因此整体不满足$\displaystyle\frac {0 }{ 0} $，即用我们求解一阶微分方程用到的洛必达法则。

解决办法：将先前的特解与“零解”做线性组合，使得当$ s\rightarrow s_{1} $时，分母分子都趋近于零，即$ \displaystyle\frac { 0 }{ 0 } $型，这个时候就可以用洛必达法则。最终构造的结果为$ y_{p}=\displaystyle\frac{e^{s t}-e^{s_{1} t}}{A s^{2}+B s+C}$，它满足$ y(0)=0 $以及前面的条件。用洛必达法则处理该极限$$\lim _{s \rightarrow s_{1}} \frac{e^{s t}-e^{s_{1} t}}{A s^{2}+B s+C}=\lim _{s \rightarrow s_{1}} \frac{t e^{s t}}{2 A s+B}=\frac{t e^{s_{1} t}}{2 A s_{1}+B}$$因此得到共振状态下的特解为$$y_{\text {resonant}}=\frac{t e^{s_{1} t}}{2 A s_{1}+B}$$

特殊情况：$ s_{1}$为原方程的重根，那意味着现在的分母仍旧是零，因此需要再次使用洛必达法则，但是这是极少见的情况。

正余弦响应

本讲讨论的是二阶常系数微分方程$$A \frac{d^{2} y}{d t^{2}}+B \frac{d y}{d t}+C y=\cos \omega t=\operatorname{Re}\left(e^{i \omega t}\right)$$解形式为$y=M \cos \omega t+N \sin \omega t $，GS老师将其称为【Rectangular Form】。代回原方程，然后对比系数，可以求得$$M=\frac{C-A \omega^{2}}{D}, N=\frac{B \omega}{D}$$其中$ D=\left(C-A \omega^{2}\right)^{2}+(B \omega)^{2}$。解函数可以写成极坐标的形式$$y(t)=G \cos (\omega t-\alpha) $$电子领域通常用$ G $表示增益，而$\alpha $表示相位角，写成这种形式的优点是我们可以直接从解析式中看到运动的形式，例如$ G$代表振荡的幅度$ G=\sqrt{M^{2}+N^{2}}=\displaystyle\frac{1}{\sqrt{D}} $，而相位角的正切为$ \tan \alpha=\displaystyle\frac{N}{M}=\frac{B \omega}{C-A \omega^{2}}$。

实例 $y^{\prime \prime}+y^{\prime}+2 y=\cos t $
求得 $D=2, M=N=1 / 2 $。直角坐标表示$ y=\displaystyle\frac{1}{2}(\cos t+\sin t) $；极坐标表示$y=\displaystyle\frac{1}{\sqrt{2}} \cos \left(t-\displaystyle\frac{\pi}{4}\right) $。

RLC电路求解

对于RLC电路，根据基尔霍夫电压定律，环路电压积分为$ 0$有$$L \frac{d I}{d t}+R I+\frac{1}{C} \int I \, d t=V e^{i \omega t}$$方程为二阶常系数微分方程，输入为指数函数，解函数也为指数函数的形式，因此有$I=W e^{i \omega t} $。对原方程求导可以使之变为常见的方程形式：$$L I^{\prime \prime}+R I^{\prime}+\frac{1}{C} I=i \omega V e^{i \omega t}$$在使用数字计算机之前，人们曾用实际的电路图然后通过测试电流等物理量直接运算，即通过模拟计算机中的电路来求解方程。将解函数回代，得到$$\left(i \omega L+R+\frac{1}{i \omega C}\right) Wi \omega e^{i \omega t}=Vi \omega e^{i \omega t} \Rightarrow W=\frac{V}{R+i\left(\omega L-\frac{1}{\omega C}\right)}$$其中的$ R+i\left(\omega L-{1}/{\omega C}\right) $被称为【复阻抗】，常用$Z$来表示。

方程的求解并没有新的思想，只是将我们通用的参数$ ABC $变成了这里的$LRC $，而它们同样地构成了一个传递函数的形式。电压的幅长出现在分子上位$ V$，而复阻抗幅长的平方为$|Z|^{2}=R^{2}+\left(\omega L-{1}/{\omega C}\right)^{2} $。

实际的电路远比这里的复杂，但是本质还是KVL和KCL的应用，分别对应“环”和“节点”，我们在GS老师的线性代数中也学习了相关的内容，通过关联矩阵将一系列物理量联系起来，构建线性方程组。如何对应起来？？？按道理这里的实部和WL老师的实部应该是对应的。

在Walter Lewin老师的视频中，认为RLC这种存在磁通量变化的电路，应该用法拉第定律而不是KVL，因为磁通量变化使得整个回路不是一个保守场，电感上的电压降为$0 $，其产生的反电动势(看似是电压降)是分布在整个电路中的，而不是加在电感$ L $两端的。根据法拉第定律(这里的电源就是普通余弦函数)，有$$V_{c}+0+I R-V_{0} \cos \omega t=-L \frac{d I}{d t}$$

待定系数法

(Methods of Undetermined Coefficients)
对于方程$$A \frac{d^{2} y}{d t^{2}}+B \frac{d y}{d t}+C y=f(t)$$如果输入函数是【好函数】，那么就可以用待定系数法快速求解。

(a) 好函数$ e^{s t} $
其指数响应为$Y e^{s t} $，求解过程就是将解函数回代从而确定系数$ Y$。比如$ y^{\prime \prime}+y^{\prime}+y=e^{s t} $，带入解函数有$ \left(s^{2}+s+1\right) Y e^{s t}=e^{s t} $，于是$Y=\displaystyle\frac{1}{s^{2}+s+1} $

(b) 多项式
比如多项式$ t $,其响应函数为$y_{p}=a+b t $。对于方程$ y^{\prime \prime}+y^{\prime}+y=t $，带入解函数有$ y_{p}=t-1 $。对于多项式都是同样的策略。

(c) 正余弦函数
响应函数$ y^{\prime \prime}+y^{\prime}+y=\sin t $，对于$ y_{p}=c_{1} \cos t+c_{2} \sin t$，将响应函数带入同样可以求得方程的特解。对于$\cos t $或者$ \sin t $来说，里面都包含了两个指数函数。

(d) 以上函数的某些乘积组合
比如方程$y^{\prime \prime}+y^{\prime}+y=t \sin t $，将两种响应函数的乘积组合$ y_{p}=(a+b t) \sin t+(c+d t) \cos t $作为试函数回代求解

特例-共振
$y^{\prime \prime}-y=e^{t} $，如果尝试特解$ y_{p}=Y e^{s t}$，那么左边等于零，这是因为$ e^{s t} $本身就是零解，这里实际上是发生了共振，这时要尝试的特解是$ y_{p}=Y te^{s t} $，然后确定参数$Y $，等于说特解多乘了一个extra factor $t $。

所谓的【好函数】实际上是求导后仍旧为同一类的函数，比如指数函数和特征多项式都是这种类型，并且后面的课程会看到它们更容易进行拉普拉斯变换。

简单谈一下微分方程的整体图像：对于非线性方程，只能用数值解法进行处理，这堂课的平行课程会讨论应用MATLAB来进行微分方程的数值求解。当方程是线性方程，并且是常系数的条件下总能求得方程的解析式，但有时解析式中会包含积分。当微分方程等式右侧的输入函数为几种特殊函数时，解函数的形式也非常简单明了。

例如方程$$y^{\prime \prime}-3 y^{\prime}+2 y=4 t $$(1)零解 我们先前已经讨论过零解的通式为$ y_{n}=c_{1} e^{s_{1} t}+c_{2} e^{s_{2} t} $，只需用$ e^{s t} $带入，就可以得到一个一元二次方程，即可以求得两个解$ s_{1}=1$和$ s_{2}=2$，即零空间的两个基为$ e^{t} $和$ e^{2t} $。
(2)特解 根据输入函数的特点，我们可以写出特解函数的基本结构，将其回代入方程，可以求出相应参数，于是$ y_{p}=3+2 t $
(3)通解 $ y(t)=y_{p}+y_{n}=y_{p}=3+2 t+ c_{1} e^{t}+c_{2} e^{2t} $

上面的方程，如果输入函数变为$ e^{s t}$，那么特解形式$ y_{p}=Y e^{s t} $，回代得$ \left(s^{2}-3 s+2\right) Y e^{s t}=e^{s t}$，于是$ Y=\displaystyle\frac{1}{s^{2}-3 s+2} $。需要强调两点：一是如果$ s $为虚数，那么可以根据欧拉公式输入函数可以表示为余弦和正弦函数加和，它们同样是容易处理的好函数；二是如果$ s$的值让$ Y $的分母为$ 0 $，则该表达式失效，即“共振”现象，需要改变特解形式，这里我们如前面所说，引入$y_{p}=Y te^{s t} $，然后再用洛必达法则得到特解为$y_{p}=\displaystyle\frac{t e^{s t}}{2 s-3} $。

实际应用中，遇到“好函数”的概率很大，总结如下：

常数变易法

Variations of Parameters$$y^{\prime \prime}+B(t) y^{\prime}+C(t) y=f(t)$$求解的关键是求出方程的特解，而在此之前需要知道两个零解，先前我们讨论的是常系数的情况，通过待定系数法很容易求出。这里系数现在随着时间变化，于是零空间不再是$ y=c_{1} y_{1}(t)+c_{2} y_{2}(t) $，而是新构造的函数$y=c_{1}(t) y_{1}(t)+c_{2}(t) y_{2}(t) $，注意这里的两个零解$ y_{1}(t) $和$ y_{2}(t) $必须是已知的。回代之后有$$\begin{aligned} &c_{1}^{\prime} y_{1}+c_{2}^{\prime} y_{2}=0\\ \\ &c_{1}^{\prime} y_{1}^{\prime}+c_{2}^{\prime} y_{2}^{\prime}=f(t) \end{aligned}$$可以求出$ c_{1}^{\prime} $和$ c_{2}^{\prime} $，将其进行积分然后线性组合即可得到$$y(t)=y_{1}(t) \int \frac{-y_{2} f(t) d t}{W(t)}+y_{2}(t) \int \frac{y_{1}(t) f(t) d t}{W(t)}$$其中$ W(t)=\left|\begin{array}{ll}
y_{1} & y_{2} \\
y_{1}^{\prime} & y_{2}^{\prime}
\end{array}\right|=y_{1} y_{2}^{\prime}-y_{2} y_{1}^{\prime} $。补充资料见这里，原始视频。

例子($B(t) $为常数)$$y^{\prime \prime}+B y^{\prime}+C y=f(t)$$(a) 先求零解，零空间的两个基解为$ y_{1}=e^{s_{1} t}, y_{2}=e^{s_{2} t} $，其中的$\mathcal{s}_{1} $和$ \mathcal{s}_{2} $为方程$s^{2}+B s+C=0 $的两个根。
(b) 求出$ W(t) $， $ W(t)=y_{1} y_{2}^{\prime}-y_{2} y_{1}^{\prime}=\left(s_{2}-s_{1}\right) e^{s_{1} t} e^{s_{2} t} $
(c) 带入$ y(t)=y_{1}(t) \displaystyle\int \displaystyle\frac{-y_{2} f(t) d t}{W(t)}+y_{1}(t) \displaystyle\int \displaystyle\frac{y_{1}(t) f(t) d t}{W(t)} $ 即$$\begin{aligned}
y(t) &=e^{s_{1} t} \int_{0}^{t} \frac{-e^{s_{2} T} f(T) d T}{\left(s_{2}-s_{1}\right) e^{s_{1} T} e^{s_{2} T}}+e^{s_{2} t} \int_{0}^{t} \frac{e^{s_{1} T} f(T) d T}{\left(s_{2}-s_{1}\right) e^{s_{1} T} e^{s_{2} T}} \\
&=\frac{-1}{s_{2}-s_{1}} \int_{0}^{t} e^{s_{1}(t-T)} f(T) d T+\frac{1}{s_{2}-s_{1}} \int_{0}^{t} e^{s_{2}(t-T)} f(T) d T \\
&=\int_{0}^{t} g(t-T) f(T) d T
\end{aligned}$$其中$g(t-T)=\displaystyle\frac{e^{s_{2}(t-T)}-e^{s_{1}(t-T)}}{s_{2}-s_{1}} $应用常数变易法求解常系数微分方程的结果告诉我们，响应函数实际上是输入函数$ f(t)$和一个增长因子$ g(t-T) $的乘积的积分，增长因子部分实际上就是冲激响应(见前面冲激响应的讨论)。着相当于在$T $时刻输入一个大小为$ f(T) $的冲激函数，这个函数造成的结果就是$f(T) $在$t-T $的时间内按照冲激响应的增长模式，将所有时刻的冲激响应累计起来就是这个积分$\displaystyle \int_{0}^{t} g(t-T) f(T) d T $，这也就是得到的函数的最终表达式。

回忆一下我们之前讨论，和这里联系起来
储蓄过程中(开始的时候账户没一分钱)，对于方程$ \displaystyle\frac{d y}{d t}=a y+q(t) $，我们的通解是$ y(t)=y(0) e^{a t}+\displaystyle\int_{s=0}^{s=t} e^{a(t-s)} q(s) d s$，对于后面一部分的特解，里面的$ q(s) $就是输入函数，$e^{a(t-s)} $就是增长因子，二者乘积的积分就是响应函数。

移位冲激函数，方程为$\displaystyle\frac{d y}{d t}=a y+\delta(t-T) $，$ t=T $时刻突然存进一块钱，于是冲激响应为$$y(t)=\left\{\begin{array}{cc} 0 & t<T \\ e^{a(t-T)} & t \geq T \end{array}\right.$$其中的输入函数就是$ 1 $，已经乘到了增长因子$e^{a(t-T)} $里面。

拉普拉斯变换

基本性质

定义：$\mathcal{L}\{f(t)\} \rightarrow F(s)$，计算方法$$ \mathcal{L}\{f(t)\}=\int_{0}^{\infty} e^{-s t} f(t) d t $$实例(利用分部积分)：

令$f(t)=1$，则$\mathcal{L}\{1\}=\displaystyle\int_{0}^{\infty} e^{-s t} d t=\frac { 1 }{ s} $。注：令$s>0$
令$f(t)=e^{at}$，则$$\mathcal{L}\left\{e^{at}\right\}=\int_{0}^{\infty} e^{-s t} e^{a t} d t=\int_{0}^{\infty}e^{(a-s) t} dt=1/(s-a)$$上式成立的条件是$a-s<0$；如果$a-s>0$，则我们可以说此时拉普拉斯变换没有被定义。
令$f(t)=\sin (\omega t)$，则通过多次分部积分可以得到$$\mathcal{L}\{\sin (\omega t)\}=\displaystyle\int_{0}^{\infty} e^{-s t} \sin (\omega t)d t=\displaystyle\frac{\omega}{s^{2}+\omega^{2}}$$

线性算子：根据拉普拉斯变换的定义，显然$$ \begin{aligned} \mathcal{L}\left\{c_{1} f(t)+c_{1} g(t)\right\} &=c_{1} \mathcal{L}\{f(t)\}+c_{2} \mathcal{L}\{g(t)\} \\ \mathcal{L}\left\{c_{3} f(t)\right\} &=c_{3} \mathcal{L}\{f(t)\} \end{aligned} $$

Laplace of derivatives：($e^{-s t}$减小得足够快，以压制可能的$f(t)$的增长)$$\mathcal{L}\left\{f^{\prime}(t)\right\}=\int_{0}^{\infty} e^{-s t} f^{\prime}(t) d f=\left[e^{-st} f(t)\right]_{0}^{\infty}+\int_{0}^{\infty}s e^{-s t} f(t) d t=s\mathcal{L}\{f(t)\}-f(0)$$同理可得$$\mathcal{L}\left\{f^{\prime\prime}(t)\right\}=s \mathcal{L}\{f^{\prime}(t)\}-f^{\prime}(0)=s^2 \mathcal{L}\{f(t)\}-sf(0)-f^{\prime}(0)$$

由$\mathcal{L}\left\{f^{\prime}(t)\right\}=s \mathcal{L}\{f(t)\}-f(0)$和$\mathcal{L}\{\sin (\omega t)\}=\displaystyle\frac{\omega}{s^{2}+\omega^{2}}$，可得$\mathcal{L}\{\cos (\omega t)\}=\displaystyle\frac{s}{s^{2}+\omega^{2}}$
由$\mathcal{L}\{f(t)\}=\displaystyle\frac {1 }{s } (\mathcal{L}\left\{f^{\prime}(t)\right\}+f(0))$和$\mathcal{L}\{1\}=\displaystyle\frac { 1}{ s } $，可得$\mathcal{L}\{t\}=\displaystyle\frac{1}{s^2}$
由$\mathcal{L}\{f(t)\}=\displaystyle\frac {1 }{s } (\mathcal{L}\left\{f^{\prime}(t)\right\}+f(0))$和$\mathcal{L}\{t\}=\displaystyle\frac{1}{s^2}$，可得$\mathcal{L}\{t^2\}=\displaystyle\frac{2}{s^3}$

参考资料：
(1) 拉普拉斯变换—可汗学院
(2) The Laplace Transform-Libretexts

拉普拉斯变换和傅里叶变换

能进行傅里叶变换必须满足狄利克雷条件，说白了就是函数在无穷远处不能下来(不能刹车，信号大小一致变大)，因为傅里叶变换的基函数是等幅振荡的正(余)弦波。傅里叶变换如下$$ F(\omega )=\int_{-\infty}^{+\infty} f(t) e^{-i \omega t} d t $$针对刹不住车的$ f(t)$，我们要想办法将其掰弯，即乘以一个衰减因子$e^{-\sigma t}$，其中$ (\sigma>0)$再进行傅里叶变换，于是有$$F(\omega )=\int_{-\infty}^{+\infty} f(t) e^{-\sigma t} \cdot e^{-i \omega t} \cdot d t$$令$s= \sigma+i\omega $，于是得到$F(\omega )=\displaystyle\int_{-\infty}^{+\infty} f(t) e^{-s t} \cdot d t$，这里实际上是用一系列边振荡边增加幅度的正(余)弦波去表示$f(t)$，也即对于任一固定频率的正(余)弦波，振幅随着时间的增大，只有这样才能跟上$f(t)$在无穷远处的值。

$\sigma=0$，就是不衰减，即对应常规傅里叶变换；
拉普拉斯变换是傅里叶变换的加强版；
拉普拉斯变换的收敛域，即只有当$\sigma>\sigma_0$的时候，才能将$f(t)$掰弯，否则总的效果还是刹不住车；
对于衰减因子$e^{-\sigma t}$其实是有两种理解方式，一是认为直接作用在原始信号$f(t)$上，将函数掰弯；另一种理解是作用在后面的$e^{-i \omega t}$，即基底从之前的$e^{i \omega t}$变为$e^{i \omega t+\sigma t}$。

传递函数

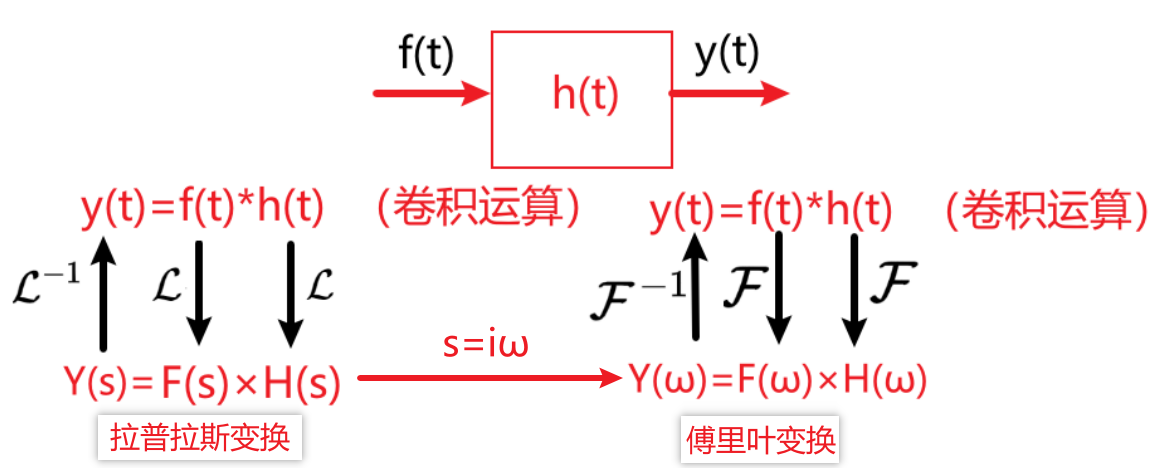
一个系统，有输出函数，有对应的输出函数，而描述输出函数和输入函数之间的关系的是该系统本身的属性，其实就是该系统的传递函数。传递函数其实是系统的单位冲激响应。所谓拉普拉斯变换是将函数从$ t$的域变换到$ s $的域，我们将看到传递函数的拉普拉斯变换，等于输出函数的拉普拉斯变换除以输入函数的拉普拉斯变换。

在信号分析中，经常看到拉普拉斯变换而不是傅里叶变换，是因为拉普拉斯变换对信号的适用范围更广

一阶常微分方程

输入函数$f(t) $的拉普拉斯变换为$F(s) $，而解函数$ y(t) $的拉普拉斯变换为$ Y(s)$，而拉普拉斯变换的定义为$ F(s)=\displaystyle \int_{0}^{\infty} f(t) e^{-s t} d t $，积分之后$ t $消失，而表达式就是$ s $的函数。之前讨论的“好函数”也就是能够在拉普拉斯变换中积分求得解析式的函数。第一个例子为$f(t)=e^{a t} $，因此$ F(s)=\displaystyle\int_{0}^{\infty} e^{a t} e^{-s t} d t=\left.\displaystyle\frac{e^{(a-s) t}}{a-s}\right|_{0} ^{t=\infty}=\displaystyle\frac{1}{s-a} $。注意这里只讨论？？的情况，所以积分上限为$ 0$。注意，该变换的极点(pole)为$ s=a $，此时变换相当于对$ e^{a t} e^{-a t}=1 $进行积分，所得为无限大。
例子1 $$\frac{d y}{d t}-a y=0$$(1) 对$\displaystyle\frac{d y}{d t} $拉普拉斯变换$$\begin{aligned} \int_{0}^{\infty} \frac{d y}{d t} e^{-s t} d t &=-\int_{0}^{\infty} y(t)\left(-s e^{-s t} d t\right)+\left.y e^{-s t}\right|_{0} ^{\infty} \\ &=s Y(s)-y(0) \end{aligned}$$对一个函数$y $求导函数，则其拉氏变换函数$ Y(s) $将乘上一个$ s $，如果求导两次，相当于乘上两次$ s $。
(2) 整个方程的拉普拉斯变换 $$s Y(s)-y(0)-a Y(s)=0$$也就是将一个微分方程转变成了代数方程，解得$ Y(s)=\displaystyle\frac{y(0)}{s-a} $。
(3) 将拉普拉斯变换方程的解$Y(s)=\displaystyle\frac{y(0)}{s-a} $进行反变换求解出$ y(t) $，其中$y(0) $为常数，则所求为$\displaystyle\frac{1}{s-a} $的逆拉普拉斯变换函数，前面已经推导过$ \displaystyle\frac{1}{s-a} $是$ e^{a t} $进行拉普拉斯变换的结果，带入可得$ y(t)=y(0) e^{a t} $。

例子2 $$\frac{d y}{d t}-a y=e^{c t}$$对每一项进行拉普拉斯变换有$ s Y(s)-y(0)-a Y(s)=\displaystyle\frac{1}{s-c} $，解得$$Y(s)=\displaystyle\frac{1}{(s-c)(s-a)}+\displaystyle\frac{y(0)}{s-a}$$第二项就是前面一个例子的情况，也就是零解，而第一项是由input外源引发的，需要分解一下$\displaystyle\frac{1}{(s-c)(s-a)}=\displaystyle\frac{1}{(s-c)(c-a)}+\displaystyle\frac{1}{(a-c)(s-a)} $，其中的$ \displaystyle\frac{1}{c-a}$和$\displaystyle\frac{1}{a-c} $都是常数，因此$\displaystyle\frac{1}{(s-c)(s-a)} \rightarrow \displaystyle\frac{1}{c-a}\left(e^{c t}-e^{a t}\right) $是方程的特解。

总结：拉普拉斯变换的方法，将整个微分方程每一项进行拉普拉斯变换，解出关于$ s $的代数方程，然后进行反变换得到函数$ y(t) $。

二阶常微分方程

例子1 $$g^{\prime \prime}+B g^{\prime}+C g=\delta(t)$$(1) 首先看一下$\delta(t) $函数的拉普拉斯变换$\displaystyle\int_{0}^{\infty} \delta(t) e^{-s t} d t=1 $，脉冲只有在$ t=0$时刻才突然输入一个函数值$1 $，而$e^{-s t} $此时也等于$ 1$，于是整个积分就是$ 1$。
(2) 对微分方程的每一项进行拉普拉斯变换，对于一阶导数就是原函数的拉普拉斯变换乘以$ s$，如果是二阶导那么再乘以一个$ s $，因此原方程变为$$\left(s^{2}+B s+C\right) G(s)=1$$于是$ G(s)=\displaystyle\frac{1}{s^{2}+B s+C}=\displaystyle\frac{1}{\left(s-s_{1}\right)\left(s-s_{2}\right)}=\left(\displaystyle\frac{1}{s-s_{1}}-\displaystyle\frac{1}{s-s_{2}}\right) \displaystyle\frac{1}{s_{1}-s_{2}}$，进行逆变换可以得$ g(t)=\displaystyle\frac{e^{s_{1} t}-e^{s_{2} t}}{s_{1}-s_{2}}$

例子2 $$y^{\prime \prime}+B y^{\prime}+C y=\cos \omega t$$这是典型的弹簧阻尼模型或者RLC电路模型的微分方程。我们前面已经知道$ f(t)=e^{a t} $的拉普拉斯变换$ F(s)=\displaystyle\frac{1}{s-a}$，于是$ e^{i \omega t}$的拉普拉斯变换$ F(s)=\displaystyle\frac{1}{s-i \omega}=\displaystyle\frac{s}{s^{2}+\omega^{2}} + \displaystyle\frac{i\omega}{s^{2}+\omega^{2}} $前面的一项(实数项)对应的其实是$\cos \omega t $的的拉普拉斯变换，而第二项(虚数项)对应的是$\sin \omega t $的拉普拉斯变换。下面对方程的每一项进行拉普拉斯变换，得到$$\left(s^{2}+B s+C\right) Y(s)=\frac{s}{s^{2}+\omega^{2}}$$解得$$Y(s)=\frac{s}{\left(s^{2}+B s+C\right)\left(s^{2}+\omega^{2}\right)}=\frac{A}{s-s_{1}}+\frac{B}{s-s_{2}}+\frac{C s+D}{s^{2}+\omega^{2}}$$前两项包含的$ s_{1}$和$s_{2} $分式其逆变换的结果就是原方程的零解，最后一项的反变换结果就是正余弦函数的线性组合。

拉普拉斯变换的卷积

这里主要引出【卷积】(Convolution)的概念，将其和拉普拉斯变换联系起来。比如微分方程$ y^{\prime \prime}+B y^{\prime}+C y=f(t) $经过拉普拉斯变换得到$ \left(s^{2}+B s+C\right) Y(s)=F(s) $，于是$$Y(s)=G(s) F(s)$$其中$ G(s)=\displaystyle\frac{1}{s^{2}+B s+C} $称为【传递函数】或者说【响应因子】response factor(我们先前提到过)。

对于一个好的输入函数$ f(t) $，我们很容易知道其拉普拉斯变换之后的函数$ F(s)$，对已知的$G(s) $进行逆变换也可以得到$ g(t) $。虽然$Y(s) $是$ G(s) $和$ F(s)$的乘积，但是$ y(t)\not= g(t)f(t) $，而是$$y(t)=g(t) * f(t)=\int_{0}^{t} g(t-T) f(T) d T$$这就是卷积，其实这个表达式在前面出现过(比如储蓄的例子，$ T$时刻新存入的钱在后面的$ t-T $时间段内满足指数增长)，$f(t) $为输入函数，而$g(t-T) $为在时间$T $之后输入函数的增长因子，最后通过积分将所有时刻的输入效果累加在一起。这里其实就是告诉我们如何对两个相乘的函数进行逆拉普拉斯变换。

例子 $\displaystyle\frac{d y}{d t}-a y=e^{c t} $
对每一项进行拉普拉斯变换得到$ s Y(s)-a Y(s)=\displaystyle\frac{1}{s-c}$，解得$Y(s)=\displaystyle\frac{1}{(s-c)(s-a)} $。我们前面是采用partial fraction decomposition的方式求解，找到最基本单元的逆变换；现在我们从卷积的角度有$$y(t)=\int_{0}^{\infty} e^{a(t-T)} e^{c t} d T=\displaystyle\frac{e^{c t}-e^{a t}}{c-a}$$两种方法的得到的结果一致。注意我们这里对$ \displaystyle\frac{d y}{d t}$进行拉普拉斯变换的时候只写成$s Y(s) $，而没有像前面写成$ s Y(s)-y(0) $，那么我么这里最终得到的起始是特解，加上$ -y(0) $，最终得到的才是通解。

s-domain equivalent circuits and impedances

The Laplace transform is often used in circuit analysis, and simple conversions to the $s$-domain of circuit elements can be made. Circuit elements can be transformed into impedances, very similar to phasor impedances.

Here is a summary of equivalents:

参考资料：
(1) Laplace Transform – visualized

Pages: 1 2 3 4 5