激光原理和应用 – 历史的进程

Laser

Laser Diodes

Laser Diodes: The Technology Explained

暂时放这里

激光器构成

谐振腔

激光器有两个反射镜面，它们构成了一个【光学谐振腔】(optical resonant cavity)。激活介质实现了粒子数反转后就能产生光放大；谐振腔的作用是选择频率一定、方向一致的光作最优先的放大，而把其他频率和方向的光加以抑制。如图所示，凡不沿谐振腔轴线运动的光子均很快逸出腔外，与激活介质不再接触。沿轴线运动的光子将在腔内继续前进，并经两反射镜的反射不断往返运行产生振荡，运行时不断与受激粒子相遇而产生受激辐射，沿轴线运行的光子将不断增殖，在腔内形成传播方向一致、频率和相位相同的强光束，这就是激光。为把激光引出腔外，可把一面反射镜做成部分透射的，透射部分成为可利用的激光，反射部分留在腔内继续增殖光子。光学谐振腔的作用有：①提供反馈能量，②选择光波的方向和频率。谐振腔内可能存在的频率和方向称为本征模，按频率区分的称纵模，按方向区分的称横模。两反射镜的曲率半径和间距(腔长)决定了谐振腔对本征模的限制情况。不同类型的谐振腔有不同的模式结构和限模特性。

A【longitudinal mode】(纵模) of a resonant cavity is a particular standing wave pattern formed by waves confined in the cavity. The longitudinal modes correspond to the wavelengths of the wave which are reinforced by constructive interference after many reflections from the cavity's reflecting surfaces. All other wavelengths are suppressed by destructive interference.

A common example of longitudinal modes are the light wavelengths produced by a laser. In the simplest case, the laser's optical cavity is formed by two opposed plane (flat) mirrors surrounding the gain medium (a plane-parallel or Fabry–Pérot cavity). 满足如下条件$$ L=q \frac{\lambda}{2} $$即谐振腔的长度$ L$是介质中的半波长的整数倍，其中$q$称为【mode order】，实际中$q$很大，大约为10⁵ to 10⁶。

参考资料：
(1) 激光器的光学谐振腔是什么？
(2) Longitudinal mode-Wiki

增益介质

【gain medium】(也有叫lasing medium激光介质，或者active laser medium，或者工作介质)，is the source of optical gain within a laser. The gain results from the stimulated emission of photons through electronic or molecular transitions to a lower energy state from a higher energy state previously populated by a pump source.

增益介质的例子：

Certain crystals, typically doped with rare-earth ions (e.g. neodymium, ytterbium, or erbium) or transition metal ions (titanium or chromium); (固体激光)
Glasses, e.g. silicate or phosphate glasses, doped with laser-active ions;
Gases, e.g. mixtures of helium and neon (HeNe), nitrogen, argon, carbon monoxide, carbon dioxide, or metal vapors; (气体激光)
Semiconductors, e.g. gallium arsenide (GaAs), indium gallium arsenide (InGaAs), or gallium nitride (GaN).
Liquids, in the form of dye solutions as used in dye lasers. (染料激光)

固体激光的增益介质是由基质材料+掺杂离子(激活离子)组成，前者决定材料物理性能，后者的能级结构决定了材料的光谱特性。固体激光器对增益介质提出如下要求：

光学和光谱特性：
- 具有三能级或四能级系统，从降低阈值和提高效率的角度来衡量能级结构，四能级优于三能级；
- 具有宽的吸收带、大的吸收系数和吸收截面，以利于储能；
- 掺入的激活离子具有有效的发射光谱和大的发射截面；
- 在泵浦光的光谱区和振荡波长处高度透明；
- 在激光波长范围内的吸收、散射等损耗小，损伤阈值高；
- 激活离子能够实现高浓度掺杂，且荧光寿命长；
- 不因泵浦光激发产生色心而导致对光的有害吸收；
- 足够大的尺寸和良好的光学均匀性。
物化特性：弹性模量大，热导率高，热膨胀系数小；组分、结构及离子价态稳定；对水、溶剂和环境气氛等的化学稳定性好，具有良好的光照稳定性。
热光性：热光稳定性好，热光系数最好接近于零；热光畸变（包括热透镜效应，热应力感生的双轴聚焦，热应力双折射和退偏效应）要小。
机械性能：硬度高，自破坏阈值高，抗破坏强度大，易于加工研磨。

目前，用作激光工作物质的材料主要有晶体、玻璃和陶瓷。激光晶体材料包括氟化物、氧化物、溴化物、硫化物、氧氟化物、氧氯化物和氧硫化物等。激活离子覆盖了镧系、过渡元素和锕系的一些元素。激光玻璃主要有氧化物玻璃系统（硅酸盐、锗酸盐和磷酸盐玻璃等）和非氧化物玻璃系统（卤化物和硫化物玻璃等），迄今为止只有稀土离子在玻璃基质中实现了激光发射。激光陶瓷的研究体系比较少，主要集中在YAG、Y₂O₃、Sc₂O₃、Lu₂O₃和YSAG等立方相体系中，激活离子包括Nd、Yb、Pr、Sm、Cr等稀土离子。

注：【热光系数】(thermo-optic coefficient)又叫折射指数的温度系数，temperature dependence of refractive index。由于材料折射指数会随温度变化，并且通过实验，不同材料的折射指数的温度系数（热光系数）不一样。

参考资料：
(1)固体激光器对激光工作物质有何要求？-李江-2008
(2) 激光晶体材料的发展和思考-徐军-2006

脉冲激光

激光的脉冲宽度：
Image result for laser Pulse-Width 如果激光功率不是恒定的，那么取半高宽作为脉冲宽度

调Q—纳秒级脉冲

Methods of the cavity Q-switching are divided into active and passive groups：

Active methods: use modulation devices that change the cavity losses by a given law or in accordance with an external control signal.
- opto-mechanical
- electro-optical
Passive method: Passive modulating elements are those controlled directly by the radiation field in the laser cavity.

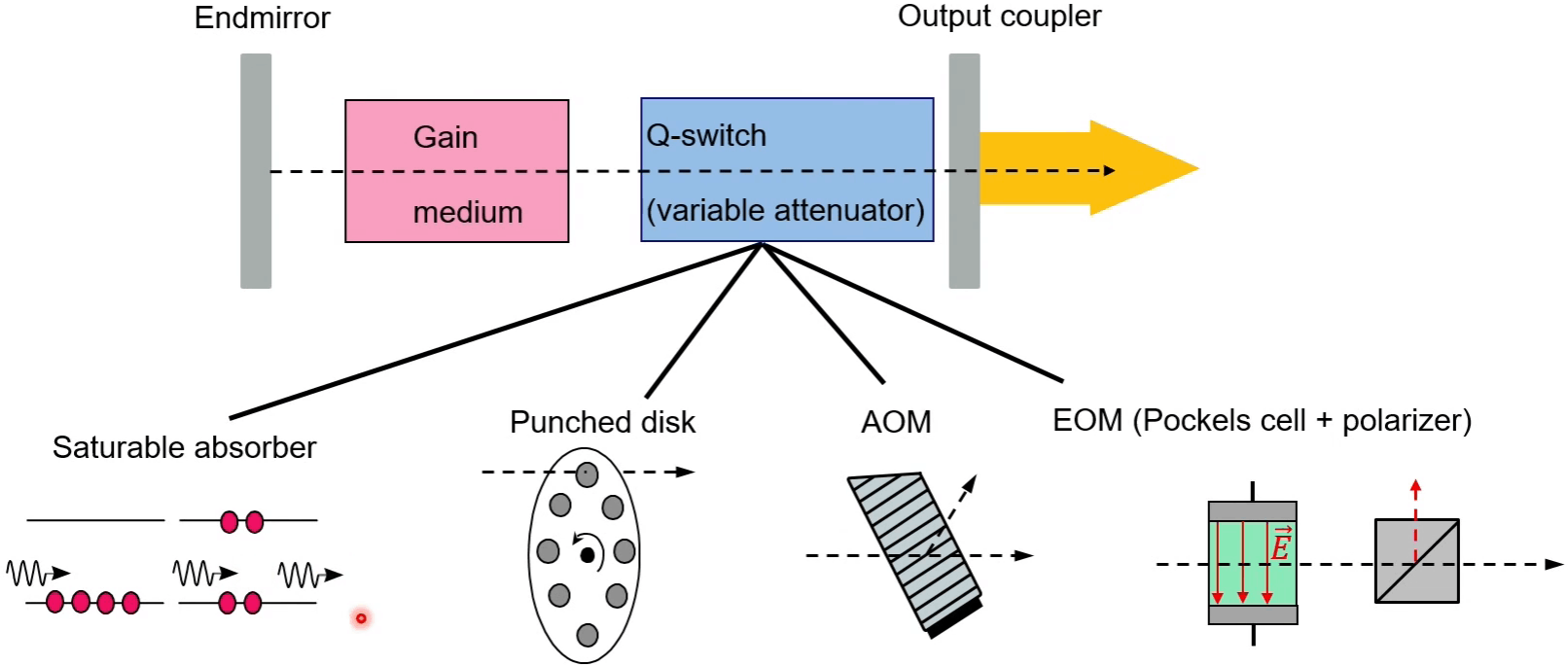
这里的Q指的是Q开关。调Q技术是将一般输出的连续或脉冲的激光能量压缩到宽度极窄的脉冲中发射，从而是光源的峰值功率提高几个数量级的一种技术。调Q技术是高功率脉冲激光器的主要基础技术之一；对常用的脉冲固体激光器来说，采用调Q技术后,输出激光的脉冲时间宽度可压缩到万分之一，峰值功率可提高到千倍以上。

Q值是评定激光器中光学谐振腔质量好坏的指标，一个品质因数。Q值定义=2π×谐振腔内储存的能量/每震荡周期损耗的能量。Q值愈高，所需要的泵浦阈值就越低，亦即激光愈容易起振。在一般的脉冲固体激光器中，若不采用特殊的措施，脉冲激光在腔内的振荡持续时间与光泵脉冲时间(毫秒量级左右)大致相同，因此输出激光的脉冲功率水平亦总是有限的。如果采用一种特殊的技术，使光泵脉冲开始后相当长一段时间，有意降低共振腔的Q值而不产生激光振荡，则工作物质内的粒子数反转程度会不断通过光泵积累而增大，然后在某一特殊选定的时刻，突然快速增大共振腔的Q值，使腔内迅速发生激光振荡，积累到较高程度的反转粒子数能量会集中在很短的时间间隔内快速释放出来，从而可获得很窄脉冲宽度和高峰值功率的激光输出。实现以上目的，最常用的方法是在共振腔内引入一个快速光开关--Q开关，其在光泵脉冲开始后的一段时间内处于“关闭”或“低Q”状态，此时腔内不能形成振荡而粒子数反转不断得到增强。在粒子数反转程度达到最大时，腔内Q开关突然处于“接通”或“高Q”状态，从而在腔内形成瞬时的强激光振荡，并产生所谓的调Q激光脉冲输出到腔外。

Opto-mechanical

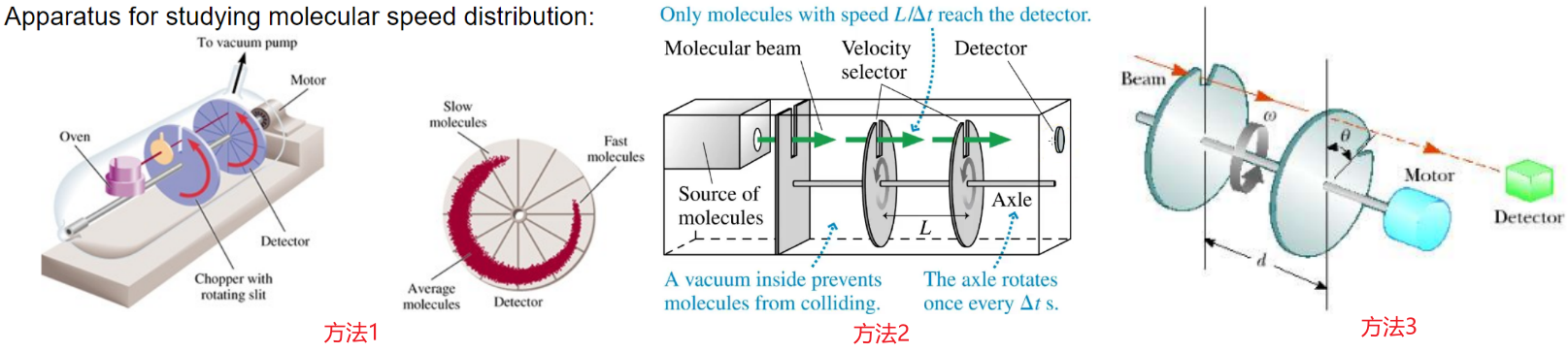
opto-mechanical最简单的调Q的modulator，就是a punched disk of an opaque material。Disk旋转轴的方向平行于谐振腔的axis，the disk blocks and opens the path between the mirrors periodically. The Q-switching time provided by such a device cannot be less than a millisecond. This value is considerable larger than the rise time of a giant pulse, which is the main drawback of a disk modulator. 如果想进一步缩短swictching time，可以同样地沿着垂直于cavity axis的方向旋转另一侧的reflector。这里有点类似测气体分子的速率分布的实验，可以分为下面三种形式(方法-1，2，3)。注意方法3仅考虑分子经过两个disk的间隔时间小于一个旋转周期的情形。

Electro-optical effect

等待补充，参考Fundamentals of Laser Dynamics

参考资料：Pulsed laser radiation I——RWTH

锁模—皮/飞秒级脉冲

锁模是光学里一种用于产生极短时间激光脉冲的技术，脉冲的长度通常在皮秒（10-12秒）甚至飞秒（10-15秒）。该技术的理论基础是在激光共振腔中的不同模式间引入固定的相位关系，这样产生的激光被称为锁相激光或锁模激光。这些模式之间的干涉会使激光产生一系列的脉冲。

Pulsed laser radiation II——RWTH

啁啾放大

啁啾是形容鸟的一种叫声，为什么叫啁啾放大，是因为这个放大技术中间有一个波段，你把它变成声波的话放出来特别特别像一个鸟的叫。

一个飞秒激光器的激光脉冲时间非常短(大约10^-15秒)，那么在这这么短的时间内，你如果想获得可观测的一些光的话你必须功率非常大，因为你能量集中在一个小范围的时间里面了，于是人们希望能量达到$10^15$ W这么大，但是如果我们把能量做到这么高的话激光器就坏掉了，那里边的东西会烧掉。于是人们想到怎么办，我们把激光器放大一点吧，结果这样一来就会造到一个大楼那么大的激光器，所以这个事就很麻烦。那么如果我们放弃这个飞秒激光器，很多物理问题他又研究不了，于是科学家们提出一种方法，说我们能不能把以前雷达波的放大方法也用在这里面。

基本原理：一个激光器发出一束激光，这束激光是一个飞秒激光，时间非常短，但是能量不够大

用途：比如说我们可以给细菌做手术，我们可以在细菌活着的情况下，用一个非常短的大功率的信号在细菌表面打出一个洞来，我们就可以研究细菌的内部结构了。再比如说我们有些同学近视眼要做这个手术，做手术的时候也是用飞秒激光器来做的。

参考资料：
(1)

各种经典激光器

激光的种类
波长分类。

(1)固体激光器

参考这里和这里。

(2)气体激光器

(3)染料激光器

Ti宝石激光器

Ti蓝宝石激光器是最佳的飞秒激光器，它的吸收和发射都是宽带的，也是tunable laser，650—110 nm，也比tunable dye laser更好，因为 it get ultra-short pulses。

基于钕玻璃的激光

参考资料：
(1) 钕玻璃，为何如此“傲娇”？

铥激光器

参考资料：
(1) 掺铥激光——在激光医疗领域大显身手

光纤激光器

参考：特种光纤激光器-杨中民

拉曼激光

分子光力纳米腔：将红外线变成可见光

其他

单频激光器

单频光纤激光器研究进展

3分钟了解单频光纤激光器

掺稀土离子液体激光器的研究进展

激光历史

激光与稀土激光材料是同时诞生的。自从1960年在红宝石中首先实现发射出激光以来，同年就发现CaF₂:Sm²⁺可以输出脉冲激光。1961年，掺钕的硅酸盐玻璃获得脉冲激光。1964年又找出在室温下可以出连续激光的YAG:Nd³⁺。Nd玻璃是目前输出脉冲能量最大、输出功率最高的固体激光材料，它的大型激光器用于热核聚变的研究中。由于玻璃容易制备成大尺寸、容易进行热成形和冷加工 , 故用钕玻璃可制成大型的激光器。随着集成光学和光纤通信的发展，需要有微型的激光器和放大器，于是发展出了稀土类光纤激光材料。Nd的1.33 μm和Er的1.55 μm的激光波长跟光纤通信最佳的窗口匹配，很适合作为低损耗传输的激光光源。

60年代：第一台红宝石晶体(Cr:Al₂O₃)激光器问世，激光诞生；

70年代：掺钕钇铝石榴石(Nd:YAG)，固体激光开始大力发展；

80年代：钛宝石晶体(Ti:Al₂O₃)，超短、超快和超强激光成为可能，飞秒(10^-15s)激光科学技术蓬勃发展，并渗透到各基础学科和应用领域。

90年代：矾酸钇晶体（Nd：YVO₄），固体激光的发展进入新时期——全固态激光技术。

至今，实用化的激光晶体已从最初的几种基质材料发展到数十种，并在各个方面获得了实际应用。但就其应用范围来说，主要有“三大基础激光晶体”，即掺钕钇铝石榴石(Nd:YAG)、掺钕矾酸钇 (Nd:YVO₄)和掺钛蓝宝石(Ti:Al₂O₃)晶体。其中高功率激光应用方面主要是Nd:YAG。

参考：中国牌系列单晶——激光晶体-中科传播

爱因斯坦AB系数

真空电磁场中，能量、动量、波矢以及波速(光速)之间的关系为：$$\begin{array}{l} E=p c \\ \omega=k c \end{array}$$我们求电磁场能态密度的方法其实和量子力学里面求自由粒子能态密度的方法是完全一样的。只不过自由粒子是$E=\displaystyle\frac{p^{2}}{2 m}$。采用周期性边界条件，也就是箱归一化，对于自由粒子，动量为$p$，在$ \varepsilon_{m} \rightarrow \varepsilon_{m}+\mathrm{d} \varepsilon_{m}$内的态密度为$$\mathrm{d} N=\left(\frac{a}{2 \pi \hbar}\right)^{3} m p \mathrm{~d} E \int_{0}^{\pi} \sin \theta \mathrm{d} \theta \int_{0}^{2 \pi} \mathrm{d} \varphi$$于是有$\mathrm{d} N=2 \times\left(\displaystyle\frac{a}{2 \pi \hbar}\right)^{3} p^{2} \mathrm{~d} p \times 4 \pi$，然后换成真空电磁场那一套根据$E=p c$，用$E$替换$ p$，于是有$$\rho(E)=\frac{\mathrm{d} N}{\mathrm{~d} E}=\frac{a^{3}}{\pi^{2} \hbar^{3} c^{3}} E^{2}=\frac{V}{\pi^{2} \hbar^{3} c^{3}} E^{2}$$根据$ E=\hbar \omega$和$ \omega=2 \pi \nu$，很容易知道真空电磁场单位体积的态密度：$$\rho_{v a c}(\nu)=\frac{1}{V} \frac{\mathrm{d} N}{\mathrm{~d} \nu}=\frac{1}{V} \frac{\mathrm{d} N}{\mathrm{~d} E}\frac{\mathrm{d} E}{\mathrm{~d} \nu}=\frac{8 \pi \nu^{2}}{c^{3}}$$根据统计力学知识，取$ \beta=\displaystyle\frac{1}{k T}$，每一状态平均能量为：$$\begin{aligned} \langle\varepsilon\rangle &=\frac{1}{Z} \operatorname{Tr}\left(\hat{H} \mathrm{e}^{-\beta \hat{H}}\right) \\ &=-\frac{\partial}{\partial \beta}\left(\ln \sum_{n=0}^{\infty} \mathrm{e}^{-\beta n h \nu}\right) \\ &=\frac{h \nu}{\mathrm{e}^{\frac{h \nu}{k T}}-1} \end{aligned}$$于是描述黑体辐射的普朗克公式就得到了：$$\rho_{\text {plank}}(\nu)=\rho_{v a c}(\nu)\langle\varepsilon\rangle=\frac{8 \pi \nu^{2}}{c^{3}} \frac{h \nu}{\mathrm{e}^{\frac{h \nu}{k T}}-1}$$
爱因斯坦的辐射理论同时考虑原子的自发辐射、受激辐射和受激跃迁三个过程。

现在我们考虑原子的两个能级，用$ E_1$和$E_2$表示，相应的单位体积内处于两能级的原子数为$n_1$、$n_2$。设自发辐射的概率为$A_{21}$，即单位时间单位体积中$ n_2$个高能态原子自发跃迁的原子数和$n_2$的比值：$$A_{21}=\left(\frac{\mathrm{d} n_{21}}{\mathrm{~d} t}\right)_{s p} \frac{1}{n_{2}}$$自发辐射是一种与辐射场无关的原子本身的物理过程，根据上式很容易得到跃迁概率和原子在$ E_2$能级的自发辐射的平均寿命$\tau_{s2}$的倒数。单位时间内高能级减少的粒子数为：$$\frac{\mathrm{d} n_{2}}{\mathrm{~d} t}=-\left(\frac{\mathrm{d} n_{21}}{\mathrm{~d} t}\right)_{s p}$$由上面两个式子有$$\frac{\mathrm{d} n_{2}}{\mathrm{~d} t}=-A_{21} n_{2}$$在$t=0$时$n_{2}=n_{20} $，则有：$$n_{2}(t)=n_{20} \mathrm{e}^{-A_{21} t}=n_{20} \mathrm{e}^{-\left(\frac{t}{\tau_{s 2}}\right)}$$我们把$$A_{21}=\frac{1}{\tau_{s 2}}$$叫作自发跃迁的爱因斯坦系数$A_{21}$。

如果黑体原子和辐射场相互作用只有上述过程，显然腔内辐射场不稳定，为了维持稳定，爱因斯坦认为必然存在着原子在辐射场作用下受激跃迁的过程。处于$E_1$的原子，在辐射场激励下吸收一个光子向$ E_2$跃迁，这叫受激吸收跃迁，其概率用$W_{12}$表示：$$W_{12}=\left(\frac{\mathrm{d} n_{12}}{\mathrm{~d} t}\right)_{s t} \frac{1}{n_{1}}$$同样，$ \left(\mathrm{d} n_{12}\right)_{s t}$是单位体积内在$ dt$时间元由于受激跃迁引起的由低能级向高能级跃迁的原子数。受激跃迁与辐射场有关，这种关系可以唯象地写为：$$W_{12}=B_{12} \rho_{\nu}$$其中$ B_{12}$就是受激吸收跃迁的爱因斯坦系数，只与原子性质有关。

受激吸收跃迁的逆过程就是受激辐射，在辐射作用下高能级原子也会向低能级跃迁，同理有：$$\begin{array}{l} W_{21}=\left(\displaystyle\frac{\mathrm{d} n_{21}}{\mathrm{~d} t}\right)_{s t} \displaystyle\frac{1}{n_{2}} \\ W_{21}=B_{21} \rho_{\nu}\end{array}$$这里的$B_{21}$是受激辐射跃迁爱因斯坦系数。

空腔黑体处于温度为$ T$的热平衡状态应该是这三种过程的结果，腔内的热平衡黑体辐射由普朗克公式给出，腔内物质原子数按能级分布应该满足热平衡时的玻尔兹曼分布：$$\frac{n_{2}}{n_{1}}=\frac{f_{2}}{f_{1}} \mathrm{e}^{-\frac{\left(E_{2}-E_{1}\right)}{k T}}$$其中$ f_1$、$ f_2$是两个能级各自的统计权重。

热平衡状态下，两个能级原子数保持不变，即：$$\left(\frac{\mathrm{d} n_{21}}{\mathrm{~d} t}\right)_{s p}+\left(\frac{\mathrm{d} n_{21}}{\mathrm{~d} t}\right)_{s t}=\left(\frac{\mathrm{d} n_{12}}{\mathrm{~d} t}\right)_{s t}$$即$$n_{2} A_{21}+n_{2} B_{21} \rho_{\nu}=n_{1} B_{12} \rho_{\nu}$$上式带入普朗克公式有$$\frac{c^{3}}{8 \pi h \nu^{3}}\left(\mathrm{e}^{\frac{h \nu}{k T}}-1\right)=\frac{B_{21}}{A_{21}}\left(\frac{B_{12} f_{1}}{B_{21} f_{2}} \mathrm{e}^{\frac{h \nu}{k T}}-1\right)$$当$T \rightarrow \infty$时，上式仍旧成立，于是有：$$B_{12} f_{1}=B_{21} f_{2}$$将其带回到先前的式子中有$$\frac{A_{21}}{B_{21}}=\frac{8 \pi h \nu^{3}}{c^{3}}$$以上两式就是最后导出的爱因斯坦系数基本关系。当两能级统计权重相等时，还有：$$\begin{array}{l} B_{12}=B_{21} \\ W_{12}=W_{21} \end{array}$$这个爱因斯坦系数关系式虽然在推导的时候利用了热平衡，但是根据量子电动力学的方法仍然可以证明其具有普适性。

参考资料：打开激光之门-爱因斯坦系数及其关系

小知识

【Quantum defect】: In laser science, the term "quantum defect" refers to the fact that the energy of a pump photon is generally higher than that of a signal photon (photon of the output radiation). The energy difference is lost to heat, which may carry away the excess entropy delivered by the multimode incoherent pump. The quantum defect of a laser can be defined as part of the energy of the pumping photon, which is lost (not turned into photons at the lasing wavelength) in the gain medium at the lasing.

ESA

对laser来说，亚稳态必须要有足够长的寿命，但这可能导致ESA，所以必须选用合适E₂能级(发射能级)的离子，即该能级的离子不能吸收pumping光，跃迁到更高能级。YAG:Ce³⁺和MgAl₂O₄:Mn²⁺没有laser action，因为ESA at fluoresence wavelength.这是利用pump-probe测得的CaF₂:Sm²⁺和CaF₂:Eu²⁺的ESA谱，可以看到前者(实线)和Sm²⁺的发光峰没有重叠(有潜力出激光)，但是后者(+表示)有严重重叠(spoiling the potential for a tunable blue laser)。对于CaF₂:Sm²⁺和来说，为了避免ESA效应，激光器中的泵浦光源不能选择宽带的flash-lamp，因为会有500 nm附近的强ESA，可以选择670 nm的diode laser作为泵浦光。另外CaF₂:Sm²⁺激光器的缺点是的工作温度在200 K以下，单独的热电制冷可能可以达到。来自文献[JOSA B-1991]

参考资料：
(1) Excited-state Absorption-RP-photonics

Thin-disk Lasers

The most often used gain medium for thin-disk lasers is Yb:YAG.

参考资料：
(1) Thin-disk Lasers—rp-photonics

激光制冷

参考资料：
(1) 激光制冷- 姬扬- 科学网
(2) 激光制冷液体？还是先去吃根冰棍吧-姬扬- 科学网