静磁现象的基本理论描述

电流（磁的来源、与电荷对比）

电流密度大小\(  j=\frac{\Delta q}{\Delta t \Delta S}\)，而\(j=\frac{\rho \Delta \Omega}{\Delta t \Delta S}=\frac{\rho \Delta S v \Delta t}{\Delta t \Delta S}=\rho v  \)，这就将电流密度和电荷密度联系起来了。

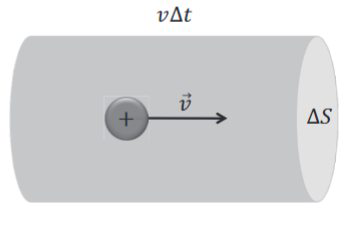
写成矢量\( \vec{j}=\rho(\vec{r}) \vec{v}(\vec{r}) \)电荷密度越大，电流越大，但是电流不动不行，因此速度越大，电流越大。

\(\vec{j}=\rho \cdot \vec{v}(\vec{r}, t)  \)老师上课写的更一般的情况，电流密度和电荷密度联系到一起。

\( I=\int_{S} \vec{j} \cdot d \vec{S} \) 左边是电磁学常用的方法，右边是电动力学常用的表示方法。

电荷守恒：不能凭空消失和产生，只能转移。

\(  \nabla \cdot \vec{j}+\frac{\partial \rho}{\partial t}=0\)(电流密度和电荷密度)这其实是拉普拉斯方程(流守恒定律)，老师形象说，哪里有电流走不动了，哪里就有电荷积累。流和密度是general的，不一定是这里的电流。电磁场-能量密度和能流密度守恒。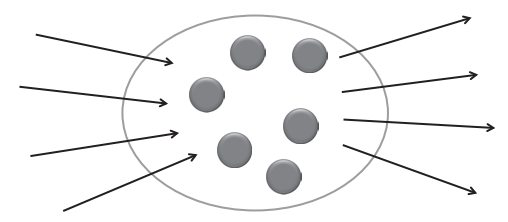$$\frac {\Delta Q  }{ \Delta t } =-\oint_{S} \vec{j} \cdot d \vec{S}$$等式左边表示的是单位时间内某个体积的电荷增量(流入的导致的)，而右侧表示单位时间内由该体积流出的量(流量，不考虑负号)，流入和流出之间差个负号。进一步可以写成$$\oint_{S} \vec{j} \cdot d \vec{S}=-\frac{d}{d t} \int_{V} \rho d \tau$$根据高斯定理$$\oint_{S} \vec{j} \cdot d \vec{S}=\int_{V} \nabla \cdot \vec{j} d \tau$$于是有$$\int_{V}\left(\nabla \cdot \vec{j}+\frac{\partial \rho}{\partial t}\right) d \tau=0$$由于曲面\( S \)是任意选取的，所以被积函数恒为零，即电荷守恒定律的数学表达式(连续性方程)$$\nabla \cdot \vec{j}+\frac{\partial \rho}{\partial t}=0$$上式也可以称为“流守恒定理”，所有的物理量，只要是守恒的，都可以找到类似的流守恒定理。这里有电流密度，常见的还有能流密度、粒子流密度、热流密度等 ，物理意义均为单位时间单位面积通过的粒子数（能量、电荷等） 。所有的“*流密度”的微观形式都是“**密度（乘以）速度”。参考：维基-连续性方程。

注：回忆三维传热方程\( \frac{\partial u}{\partial t}=\alpha\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}+\frac{\partial^{2} u}{\partial z^{2}}\right) \)，温度对位置求梯度，得到温度梯度的矢量场，温度梯度就是温度传导的驱动力，温度梯度相当于上面的\(  \vec{j}\)(热流密度，这里需要用一个系数乘以温度的梯度，因为传热的驱动力大小不仅和温度差有关，和材料本身的性质也有关)，再对热流密度求散度就得到传热方程。注意这里的电荷密度求梯度不是电流密度。

安培定律（与库仑定律对比）

真空中两个电流元\(\vec{j}_{1} d \tau_{1}  \)和\( \vec{j}_{2} d \tau_{2} \)，\( 2 \)对\(  1\)的作用力为$$d \vec{F}_{12}=\frac{\mu_{0}}{4 \pi} \frac{\vec{j}_{1} d \tau_{1} \times\left(\vec{j}_{2} d \tau_{2} \times \vec{R}_{12}\right)}{\vec{R}_{12}^{3}}$$其中\(\vec{R}_{12}=\vec{r}_{1}-\vec{r}_{2}  \)
特点：
(1)  平方反比；
(3)  系数这里写的是\(  \frac{\mu_{0}}{4 \pi}\)，似乎错了，一般写作\( k_{\mathrm{e}}=\frac{1}{4 \pi \varepsilon_{0}}=\frac{c_{0}^{2} \mu_{0}}{4 \pi} \)
(3)  非向心力(与库伦不同)；
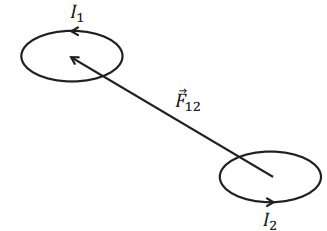
(4  不满足牛顿作用力与反作用力\(  d \vec{F}_{12} \neq d \vec{F}_{21}\)，如下图
注：原因是不可能存在稳定的电流元，实验只能测闭合回路的情况，闭合回路的情况是满足牛顿第三定律的。

磁场

上面的安培定律是一个电流元对另一个电流元产生的“类似库伦作用”的力，库伦作用，我们可以认为是一个电荷处在其他电荷的电场中而感受到的力，而同样地，运动的电流元也可以产生磁场，这个处在这个磁场中的其他电流元也会感受到来自这个磁场的作用。类比电场的定义，可以定义磁场，将作用在电流元\(  \vec{j}_{1} d \tau_{1}\)上的力写为$$d \vec{F}_{1}=\vec{j}_{1} d \tau_{1} \times \vec{B}(\vec{r})$$其中\(\vec{B}(\vec{r})=\frac{\mu_{0}}{4 \pi} \vec{j}_{2} d \tau_{2} \times \frac{\vec{R}_{12}}{R_{12}^{3}}  \)为电流元\(  \vec{j}_{2} d \tau_{2}\)在\(  \vec{r}\)处产生的磁场，由叠加原理，对任意连续的电流分布\(\vec{j}\left(\vec{r}^{\prime}\right)  \)，其在\(\vec{r}  \)处产生的磁场为$$\vec{B}(\vec{r})=\frac{\mu_{0}}{4 \pi} \int \frac{\vec{j}\left(\vec{r}^{\prime}\right) d \tau^{\prime} \times \vec{R}}{R^{3}}$$这就是磁感应强度，等式表示的就是毕奥萨伐尔定律。
注：这里的系数是\( \frac{\mu_{0}}{4 \pi} \)是对的，前面电场的作用也用这个系数其实错了。

不考虑相对论效应，运动电荷产生的电流密度为\(  \vec{j}=q \vec{v} \delta(\vec{r}-v t \hat{x})\)，它在磁场中受到的力为$$\vec{F}=\int_{\tau} q \delta(\vec{r}-v t \hat{x}) d \tau \vec{v} \times \vec{B}=q \vec{v} \times \vec{B}$$若空间中同时存在电场和磁场，那么总的受力为(即为洛伦兹力)$$\vec{F}=q(\vec{E}+\vec{v} \times \vec{B})$$

\(\vec{B}(\vec{r})  \)的散度

研究一个向量场，就必须研究其散度和旋度。
对比电场和磁场：
(1)  电场为径向场，磁场为横向场；
(2)  电场作用力前面的系数为\( \frac{1}{4 \pi \varepsilon_{0}} \)，磁场的为\(  \frac{\mu_{0}}{4 \pi}\)；
(3)  电场可以写成标量势\(\varphi  \)的梯度，磁场可以写成矢量势的散度；
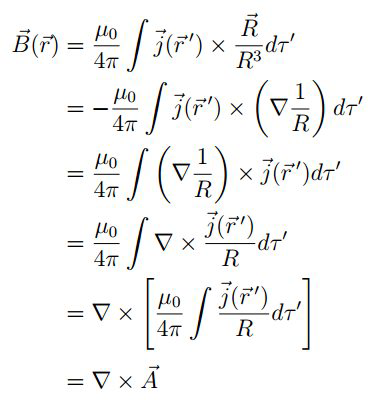其中\( \vec{A}(\vec{r})=\frac{\mu_{0}}{4 \pi} \int \frac{\vec{j}\left(\vec{r}^{\prime}\right)}{R} d \tau^{\prime} \)，定义为矢量势，与电场的标量势对应。因此$$\nabla \cdot \vec{B}(\vec{r})=\nabla \cdot(\nabla \times \vec{A}) \equiv 0$$注：
(1)  \( \nabla \cdot(\nabla \times \vec{A}) \)叉乘要求的方向和梯度要求的方向垂直，所以干脆就躺倒不动了，恒等于零；
(2)  如果积分里面的电流密度\(\vec{j}\left(\vec{r}^{\prime}\right)  \)换成电荷密度\( \rho\left(\vec{r}^{\prime}\right) \)，然后改一下前面的系数，那么的到的就是电场的标量势\(  \varphi \)；
(3)  推导过程，运用了矢量运算公式\( \nabla \times(\vec{a} \psi)=(\nabla \times \vec{a}) \psi+\nabla \psi \times \vec{a} \)这个公式我们可以这样理解，\( \nabla \)即具有矢量性又具有微分性，从微分性角度考虑，我们要分别对\(  \vec{a}\)和\( \psi \)求微分，首先对\(  \vec{a}\)微分(求旋度)，然后\( \psi \)不变，微分后直接相乘，而\( \nabla \)对函数\( \psi \)微分要得到一个矢量，所以必须是求梯度得到一个向量场，但是我们等式左边得到的是一个旋度(向量场)，因此我们必须将前面的梯度结果和\( \vec{a} \)叉乘。注意我们先前给的公式\(  \nabla \times(f A)=f(\nabla \times A)-A \times(\nabla f)\)，叉乘的前后顺序反了的话，就加一个负号。于是利用分步微分\( \nabla \rightarrow \vec{\nabla}_{R}+\vec{\nabla}_{j} \)，$$\nabla \times\left(\frac{\vec{j}\left(\vec{r}^{\prime}\right)}{R}\right)=\left(\nabla_{j} \times \vec{j}\left(\vec{r}^{\prime}\right)\right) / R+\nabla_{R}\left(\frac{1}{R}\right) \times \vec{j}\left(\vec{r}^{\prime}\right)$$对一个纯向量求旋度显然为零，因此等式右边只保留第二项。因此\(\nabla \times\left(\frac{\vec{j}\left(\vec{r}^{\prime}\right)}{R}\right)=\nabla\left(\frac{1}{R}\right) \times \vec{j}\left(\vec{r}^{\prime}\right)  \)

\(\vec{B}(\vec{r})  \)的旋度

$$\nabla \times \vec{B}(\vec{r})=\nabla \times(\nabla \times \vec{A})=\nabla(\nabla \cdot \vec{A})-\nabla^{2} \vec{A}$$注：这个公式可以通过记忆\(  \vec{a} \times(\vec{b} \times \vec{c})=\vec{b}(\vec{a} \cdot \vec{c})-\vec{c}(\vec{a}\vec{b})\)，然后对应起来\(\nabla \leftrightarrow \vec{a}, \nabla \leftrightarrow \vec{b}, \vec{c} \leftrightarrow \vec{A}  \)得到。

第一项$$\nabla \cdot \vec{A}=\nabla \cdot \frac{\mu_{0}}{4 \pi} \int \frac{\vec{j}\left(\vec{r}^{\prime}\right)}{R} d \tau^{\prime}=\frac{\mu_{0}}{4 \pi} \int\left(\nabla \frac{1}{R}\right) \cdot \vec{j}\left(\vec{r}^{\prime}\right) d \tau^{\prime}$$利用恒等式
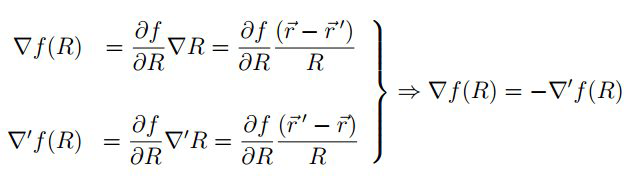注：\( \nabla f(R) \)中\(  R\)为\(\vec{r}-\vec{r}^{\prime}  \)的绝对值，那么\( \nabla f(R) \)是将\( \vec{r}^{\prime} \)看作不变的，\( \nabla^{\prime} f(R) \)是将\( \vec{r} \)看作不变的。前面的式子继续改写$$\begin{aligned} \nabla \cdot \vec{A} &=-\frac{\mu_{0}}{4 \pi} \int\left(\nabla^{\prime} \frac{1}{R}\right) \cdot \vec{j}\left(\vec{r}^{\prime}\right) d \tau^{\prime} \\ &=-\frac{\mu_{0}}{4 \pi} \int\left[\nabla^{\prime} \cdot\left(\frac{\vec{j}\left(\vec{r}^{\prime}\right)}{R}\right)-\frac{1}{R}\left(\nabla^{\prime} \cdot \vec{j}\left(\vec{r}^{\prime}\right)\right)\right] d \tau^{\prime} \end{aligned}$$改写的目的是得到一个散度，有了散度，就可以利用高斯定理来做脉面积分。在稳恒流情况下\( \nabla^{\prime} \cdot \vec{j}\left(\vec{r}^{\prime}\right)=-\dot{\rho}=0 \)，因此$$\nabla \cdot \vec{A}=-\frac{\mu_{0}}{4 \pi} \int \nabla^{\prime} \cdot\left(\frac{\vec{j}\left(\vec{r}^{\prime}\right)}{R}\right) d \tau^{\prime}=-\left.\frac{\mu_{0}}{4 \pi} \oint \frac{\vec{j}\left(\vec{r}^{\prime}\right)}{R} \cdot d \vec{S}^{\prime}\right|_{r^{\prime} \rightarrow \infty}=0$$注：无穷远处，电流密度一定为零。

第二项为$$\nabla^{2} \vec{A}=\frac{\mu_{0}}{4 \pi} \int \nabla^{2} \frac{\vec{j}\left(\vec{r}^{\prime}\right)}{R} d \tau^{\prime}=\frac{\mu_{0}}{4 \pi} \int \vec{j}\left(\vec{r}^{\prime}\right)\left(\nabla^{2} \frac{1}{R}\right) d \tau^{\prime}$$而\( 4 \pi \delta(\vec{R})=\nabla \cdot\left(\frac{\vec{R}}{R^{3}}\right)=-\nabla \cdot\left(\nabla \frac{1}{R}\right)=-\nabla^{2} \frac{1}{R} \)因此$$\nabla^{2} \vec{A}=-\mu_{0} \int \vec{j}\left(\vec{r}^{\prime}\right) \delta(\vec{R}) d \tau^{\prime}=-\mu_{0} \vec{j}(\vec{r})$$两项汇总得到\( \vec{B} \)的旋度为$$\nabla \times \vec{B}=\mu_{0} \vec{j}(\vec{r})$$该微分形式对应的积分形式为$$\oint \vec{B} \cdot d \vec{l}=\mu_{0} I$$一圈积分下来，不为零，说明磁场是有旋场，不是保守场。

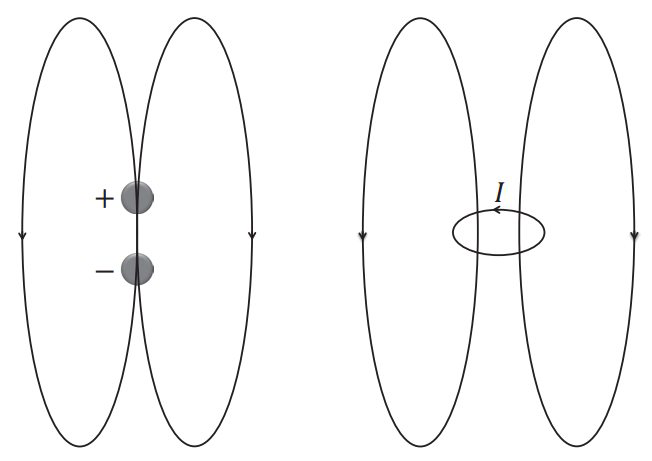
磁偶极子

电偶极子回顾：中性物质，在电场作用下，正负电荷被拉开，描述该物质被拉开的情况是通过被拉开的电荷数多少以及被拉开的距离来描述对电场的响应的。

磁偶极子：中性物质，在无电场的作用下，其中的电荷运动都是随机的，整体不表现出极性，但是当这个物质处在磁场中，那么无规律的电荷运动将会变得有规律，即在洛伦兹力的作用下做回旋运动，形成“分子环流”。因此，一个环形稳恒电流在电磁学中起到与电偶极子在静电场中完全一样的作用，我们把它叫“磁偶极子”，都是物质对外场的基本响应形式。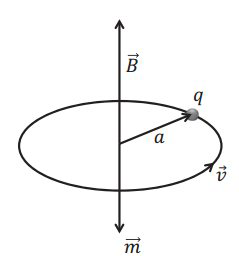

电势(标量)的梯度对应着电场，而磁矢量势的旋度对应的是磁场。对于电偶极子，我们已经研究过其产生的标量势场，这里我们类比求一下磁偶极子的磁矢量势。矢量势为$$\vec{A}(\vec{r})=\frac{\mu_{0}}{4 \pi} \int \frac{\vec{j}\left(\vec{r}^{\prime}\right)}{R} d \tau^{\prime}=\frac{\mu_{0} I}{4 \pi} \int \frac{1}{R} d \vec{l}$$注意\(  \vec{j}\left(\vec{r}^{\prime}\right)\)和横截面积的乘积就是电流，那么\(  d \tau^{\prime}\)的横截面积被搞走了就只剩下\( d \vec{l} \)了。远场条件下\( r \gg r^{\prime} \)泰勒一阶展开(\( \overrightarrow{r^{\prime}} \)看作自变量，从\( \overrightarrow{r^{\prime}}=0 \))处展开$$\frac{1}{R}=\frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|}=\frac{1}{\left(r^{2}-2 \vec{r} \cdot \vec{r}^{\prime}+r^{\prime 2}\right)^{1 / 2}} \approx \frac{1}{r}+\frac{\vec{r} \cdot \vec{r}^{\prime}}{r^{3}}$$由于\(  \frac{1}{r} \oint d \vec{l} \equiv 0\)故$$\vec{A}(\vec{r})=\frac{\mu_{0} I}{4 \pi r^{3}} \int\left(\vec{r} \cdot \vec{r}^{\prime}\right) d \vec{l}$$为了便于计算，考虑如下矩形线圈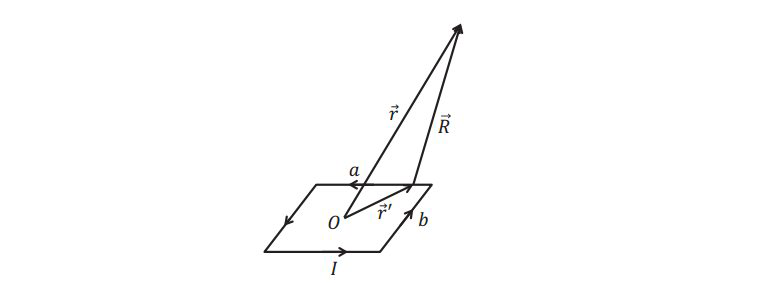计算\( x \)分量得$$\begin{aligned} A_{x}(\vec{r}) &=\frac{\mu_{0}}{4 \pi r^{3}}\left[\int_{-a / 2}^{a / 2}\left(x x^{\prime}-y b / 2\right) d x^{\prime}+\int_{a / 2}^{-a / 2}\left(x x^{\prime}+y b / 2\right) d x^{\prime}\right] \\ &=-\frac{\mu_{0}}{4 \pi r^{3}} y b a \end{aligned}$$注：\(  \vec{r}\)我们可以用\(  (x,y)\)来表示，而下段部分\(  \vec{r}^{\prime}\)可以表示为\( (x^{\prime},-b / 2) \)矢量乘法带进去，然后计算上段部分，汇总即可。用同样的方法可以得到$$A_{y}(\vec{r})=\frac{\mu_{0}}{4 \pi r^{3}} x b a$$综合得到矢量势为$$\vec{A}(\vec{r})=\frac{\mu_{0} I b a}{4 \pi r^{3}}(-y \hat{x}+x \hat{y})$$类比电偶极矩，我们有磁偶极矩$$\vec{m}=I \vec{S}=I a b \hat{z}$$所以磁偶极子的矢量势可以写成更紧凑的形式$$\vec{A}(\vec{r})=\frac{\mu_{0}}{4 \pi} \cdot \frac{\vec{m} \times \vec{r}}{r^{3}}$$注：根据右手螺旋\(\vec{m}  \)的大小就是\( Iab \)，而方向就是\(  \hat{z}\)，而\(  \hat{z} \times  (x\hat{x}+y\hat{y})=-y \hat{x}+x \hat{y}\)，固定\(  r\)的长度，那么围城的就是一个球面，变化\( r \)就得到一个球，从\(z  \)轴俯视，那么所有点的矢量势都投影到\( x-y \)平面(其实矢量势本来就没有\(  z\)轴分量)，那么我们将处于不同位置的\( z \)对应的矢量势都放在\( z=0 \)的平面内可以得到下图的样子。 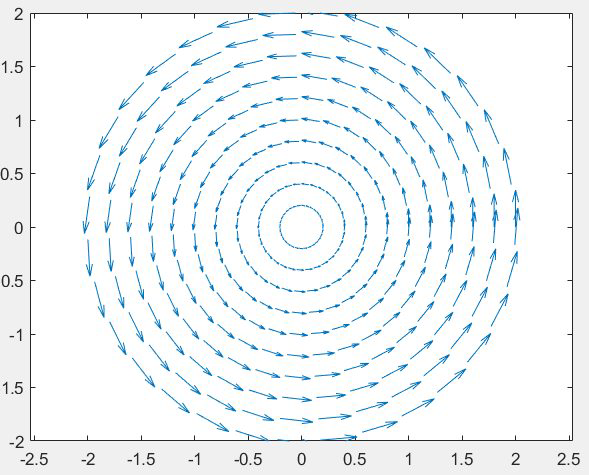代码：
[rou,sita] = meshgrid(0:0.2:2,0:0.2:2*pi);
x=rou.*cos(sita);
y=rou.*sin(sita);
u=-y;
v=x;
quiver(x,y,u,v)
axis([-2,2,-2,2])
axis equal

对矢量势求旋度得到磁场为$$\vec{B}(\vec{r})=\nabla \times \vec{A}=\frac{\mu_{0}}{4 \pi} \nabla \times\left(\vec{m} \times \frac{\vec{r}}{r^{3}}\right)=-\frac{\mu_{0}}{4 \pi}\left[\frac{\vec{m}-3(\vec{m} \cdot \hat{r}) \hat{r}}{r^{3}}\right]$$对比偶极子的电场$$\vec{E}(\vec{r})=-\nabla \varphi=-\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{\nabla(\vec{p} \cdot \vec{r})}{r^{3}}+\vec{p} \cdot \vec{r} \nabla \frac{1}{r^{3}}\right]=-\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{\vec{p}-3(\vec{p} \cdot \hat{r}) \hat{r}}{r^{3}}\right]$$注：无论是电场还是磁场，我们在推导的时候，都是考虑远场，最终得到的形式完全一致！这并不奇怪，在远场看，\(  p\)与\( m \)的场是完全一样的，尽管近场结构很不一样。这事实上蕴含着深刻的物理：在无源区，电场和磁场满足一样的方程。