- S-A距离小于0.8 nm,那么就是exchange interaction
- S-A距离大于0.8 nm,那么就是elecostalic interaction,包F括dipole-dipole,dipole-quadpole,quadpole-quadpole。
荧光粉晶体场理论和Dorenbos model
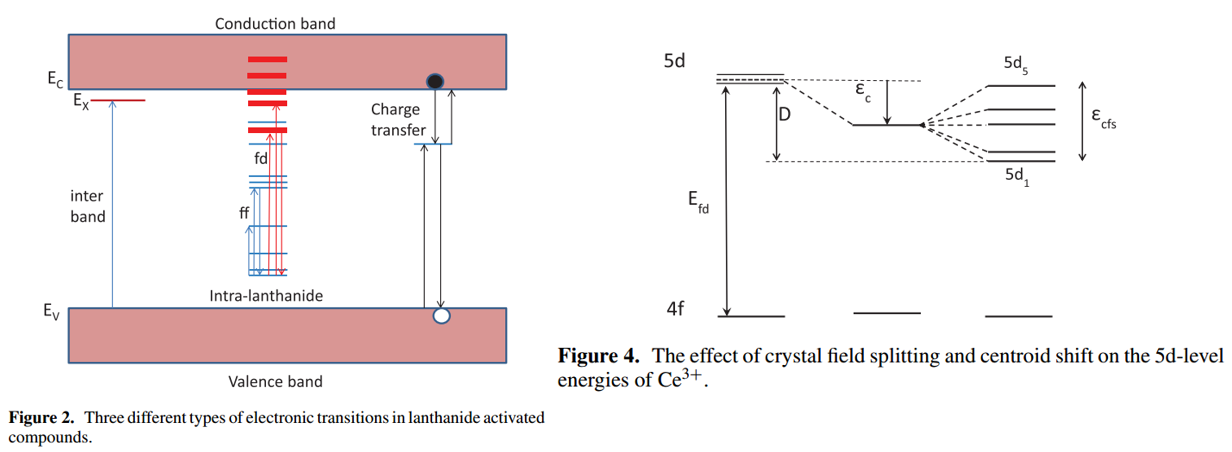
注:
(1) 对于Eu2+也可以画类似的图形。
The effect of the host crystal on this energy difference is expressed by the redshift \( D\) and the Stokes shift \(\Delta S \). The energy of f→d absorption and of the d→f emission can be written respectively, as \(E_{\mathrm{abs}}=E_{\mathrm{free}}-D\) and \(E_{\text {em }}=E_{\text {free }}-D-\Delta S\). \(E_{\text {free }}\)(Eu2+) = 4.19 eV is the energy of the f→d transition for free (gaseous) Eu2+ ions. 参考Luminescent characterization of CaAl2S4:Eu powder-JL-2007(2) Eu2+和Ce3+的CFS差异:[Suppression of Eu2+ Luminescence Loss-AOM-2022] Literally, the CFS energy of 5d state is quantified as the energy difference of 5d1 and 5d5 compo-nents, while because of the heavy overlap between different excitations of Eu2+, this process of evaluation is restricted. In com-parison, Ce3+ owns the explicit distribution of different 4f-5d1-5 transitions in the excitation spectrum
OL6其中O表示中心离子,L表示配体,optical transitions are localized on the central ion O and the surrounding ligands. 对于一个掺杂离子来说,吸收和发射都会受到基质晶格很大的影响,这是因为掺杂离子O的energy level is altered by the ineraction with the neighboring ions L,这种相互作用其实就是nature of the chemcial bonds between O and L:
(1) covalency (共价性)
(2) bond length (键长)
(3) coordination number(配位数)
(4) symmetry (对称性)
例子:gaseous (free) Ce3+的5d and 4f levels能量差在UV区间(约200 nm),但是在crystal里面,该能量差从UV到可见光区都有覆盖。
影响发光性质的两个主要因素
Centroid shift
(determined by the so-called nephelauxetic effect) \(\varepsilon_{c}\)
补充内容参考[T. Jüstel-PPT]
(1) 随着bond的covalency(共价性)的增大而增大,可以解释为键的共价性越强,那么化学键越稳定,5d orbital能量越低。
(2) 配位阴离子的polarizability越大,electronegativity越小,那么bond的covalency越大(解释见块引用)
(3) nephelauxetic effect (电子云扩展效应)的含义:The name ‘nephelauxetic’ originates from the Greek for ‘cloud expanding,’ which refers to increased delocalization (expansion) of the dopant d orbital (‘electron cloud’) as a result of increased covalency.
(4) nephelauxetic series $$F^{-}<O^{2-}<C l^{-}<N^{3-} \approx B r^{-}<I^{-}<S^{2-}<S e^{2-}$$
电负性与共价键
共价键是原子之间通过共用电子对或通过电子云重叠而产生的键合。共价键的特点是具有方向性和饱和性。靠共价键结合的晶体称为共价晶体或原子晶体。书中给出了离子键比例计算的经验公式:\(1-\exp \left[-\frac{1}{4}\left(X_{A}-X_{B}\right)^{2}\right]\),其中\(X_{A}\)和\(X_{B}\)是两个元素的电负性(可以由Pauling电负性数据来计算),反过来其实也是说中心离子和配体原子电负性的差值越小,那么就共价性越强。
极化与共价键
极化会对晶体结构产生显著影响,主要表现为极化会导致离子间距离缩短,离子配位数降低;同时变形的电子云相互重叠,使键性由离子键向共价键过渡,最终使晶体结构类型发生变化。一般来说,正离子半径较小,电价较高,极化力表现明显,不易被极化。负离子则相反,经常表现出被极化的现象,电价小而半径较大的负离子(如I-和Br-)尤为显著。
来源《材料科学基础-张联盟》例子1:3:Eu2+
例子2:氧化物中Mn4+的发光一般在650 nm及之上,但是在氟化物中(K2SiF6:Mn4+),由于F离子的高电负性,低极化率,使得Mn-F键的共价性很弱,因此nephelauxetic effect弱,centroid shift小,即发出的红光能量更高,在波长610 nm附近。
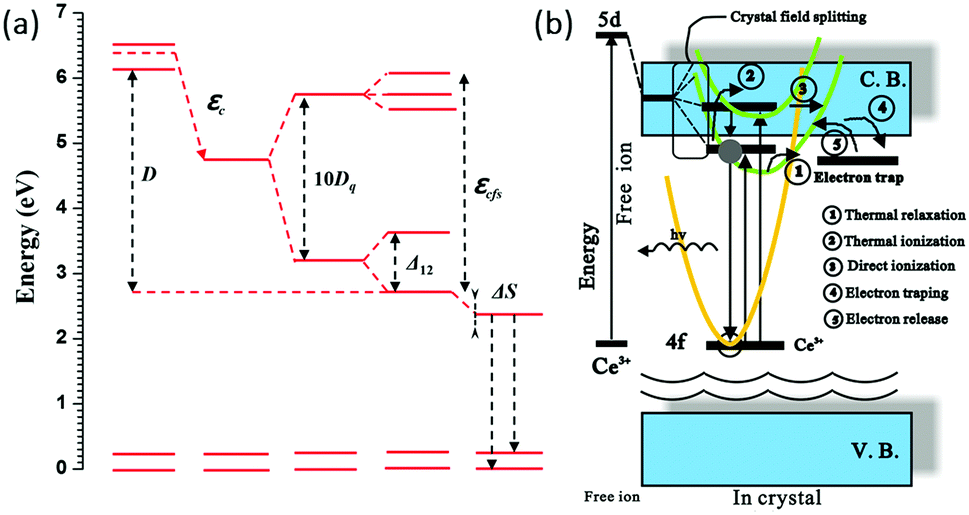
Crystal field splitting of the 5d orbital
(1) 影响CFS的magnitude的因素有:键长,键的共价性,activator site的配位环境、对称性以及distortion
(2) 键长越长,或者配位多面体体积越大,那么CFS就会减小,对于a simple point charge model,the measure of the crystal field strength\( D_{\mathrm{q}}=\displaystyle \frac{z e^{2} r^{4}}{6 R^{5}}\),其中\(R\)是离子距离,\( z\)是配位离子的charge或价态,\(r\)是d 波函数的半径。对于octahedral coordination,CFS是\(10D_{\mathrm{q}}\),也就是劈裂后最高能级到最低能级的能量差。
(3) In cubic symmetry the 5d state splits into two levels (eg and t2g) that will split further for deviations from cubic symmetry. 其中eg劈裂成两个,t2g劈裂成三个。上图中的5d1和5d2的bary center应该就是对应于eg,5d3到5d5的bary center就对应于t2g。对于YAG:Ce3+来说,eg劈裂值\( \Delta_{12}\),也就是5d1和5d2的差值很大(大约一个电子伏特),所以Ce3+的发光波长比较长。
(4) CFS变化趋势,octahedral coordination最大,cubic coordination次之, dodecahedral coordination最小。
(5) 激活离子格位的distortion也会影响CFS,比如在YAG:Ce3+中,影响eg劈裂值\( \Delta_{12}\),从而影响最后的发光峰。
In fact, in the garnet structure the distortion from cubic symmetry is important in explaining the unusually long wavelength for the Ce3+ ion.
(6) bary center
cubic symmetry是什么?YAG
Red shift:(Ce3+/Eu2+)自由气态离子最低激发态到基质晶格环境下的最低激发态之间差值。来源有三个
(1) spin-orbit splitting
(2) centroid shift
(3) crystal field splitting
参考资料:
(1) Ce3+-Doped garnet phosphors: composition modification, luminescence properties and applications
(2) 待整理
(1) Introduction to Crystal Field Theory
(2) 晶体场理论简明读本-Chemistry: the Central Science. 13th Edition, Chapter 23.6
https://www.vedantu.com/question-answer/the-purple-colour-of-kmno4-is-due-to-the-charge-class-12-chemistry-cbse-5f5b05e68f2fe24918ad201b
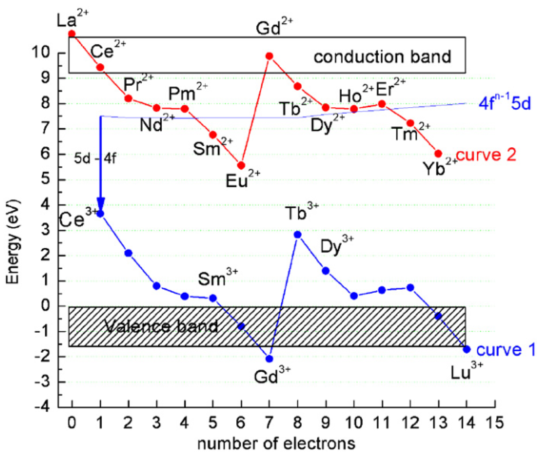
Ziazag的形状:It reflects the strength of electron binding within the 4f shell as described by the Jorgensen's spin pairing theory.
Ziazag的形状-不随基质变化:Curves 1 and 2 show a characteristic pattern which is directly related to the strength of the binding of the 4f electrons. Since the 4f electrons are shielded by the filled 5s2 and 5p6 orbitals this pattern is almost independent of the host material. However, the host material does influence the locations of the (whole) curves 1 and 2 relative to the conduction band and the valence band and relative to each other. [Lanthanide energy levels in YPO4-RM-2008]
相对能级位置参考数据
荧光粉光谱项/耦合/选择定则
谱线的精细结构,塞曼效应,反常塞曼效应,
下图是Dieke diagram

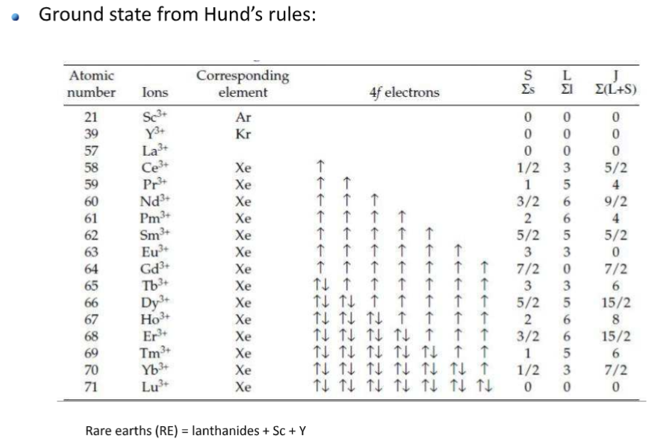
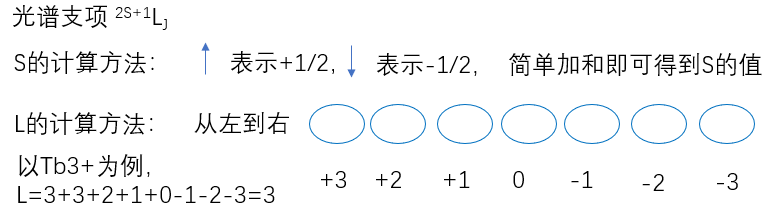
.png) 主量子数,角量子数(轨道量子数),磁量子数,自旋量子数,都服从一下规则:$$n=1,2, \cdots, l<n, m=-l,-l+1, \cdots 0,1, \cdots l, s=\pm 1 / 2$$轨道角动量和角量子数$$\mathbf{L}^{2} \Psi=\hbar^{2} \ell(\ell+1) \Psi$$
主量子数,角量子数(轨道量子数),磁量子数,自旋量子数,都服从一下规则:$$n=1,2, \cdots, l<n, m=-l,-l+1, \cdots 0,1, \cdots l, s=\pm 1 / 2$$轨道角动量和角量子数$$\mathbf{L}^{2} \Psi=\hbar^{2} \ell(\ell+1) \Psi$$
Hund(洪特)规则
洪特规则其实有三条,下面分别讨论。
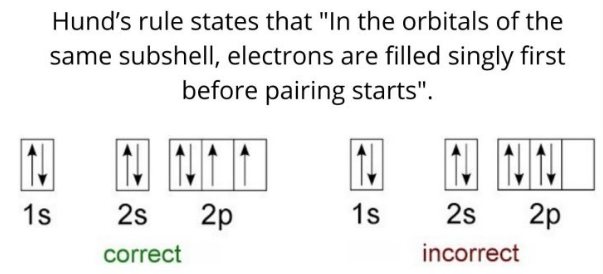 第一规则:洪德最大多重度规则(Hund's rule of maximum multiplicity),因其在原子化学、光谱学、量子化学中的重要性,又常被简称为洪德规则,而忽略洪德的另外两条规则。电子分布到能量简并的原子轨道时,优先以自旋相同的方式分别占据不同的轨道,因为这种排布方式原子的总能量最低。或者描述为“总自旋量子数最大的能量最低”。
第一规则:洪德最大多重度规则(Hund's rule of maximum multiplicity),因其在原子化学、光谱学、量子化学中的重要性,又常被简称为洪德规则,而忽略洪德的另外两条规则。电子分布到能量简并的原子轨道时,优先以自旋相同的方式分别占据不同的轨道,因为这种排布方式原子的总能量最低。或者描述为“总自旋量子数最大的能量最低”。
更专业的说法(wiki):For a given electron configuration, the term with maximum multiplicity has the lowest energy. The multiplicity is equal to \(2 S+1\) , where \(S\) is the total spin angular momentum for all electrons. The multiplicity is also equal to the number of unpaired electrons plus one. Therefore, the term with lowest energy is also the term with maximum \(S\), and maximum number of unpaired electrons.
第二规则:For a given multiplicity, the term with the largest value of the total orbital angular momentum quantum number \(L\), has the lowest energy.
第三规则:For a given term, in an atom with outermost subshell half-filled or less, the level with the lowest value of the total angular momentum quantum number \( J\), (for the operator \(\boldsymbol{J}=\boldsymbol{L}+\boldsymbol{S}\)) lies lowest in energy. If the outermost shell is more than half-filled, the level with the highest value of \( J\), is lowest in energy.
资料:
(1) Chem.libretexts-Hund's Rules
(2) spectroscopic properties and applications of divalent lanthanides apart from Eu2+-JL-2019
等价电子/不等价电子的的光谱项
等价电子,就是说两个电子处在简并的原子轨道(主量子数和角量子数相同),下面先讨论不等价的情况,再讨论等价的情况。
等价电子\(l^{N}\):以p3电子为例,p电子的角量子数\(l=1 \),所以三个轨道角动量耦合之后得到的矢量的大小只可能是0, 1,2这三种情况,同样的三个自旋角动量耦合之后得到的矢量大小只可能是3/2,1/2。
Number of states的计算公式为:\( \displaystyle\frac {[2\times (2l+1)]!}{[2\times (2l+1)- q]!q!} \)
上面的例子,计算得到的结果为20.
角动量耦合/自旋耦合
记住:角动量耦合是矢量耦合,得到的也是一个矢量,\(L\)表示耦合之后矢量的大小,肯定不会是负的。同样地,自旋耦合是矢量耦合,得到的也是一个矢量,\(S\)表示耦合之后矢量的大小,肯定不会是负的。
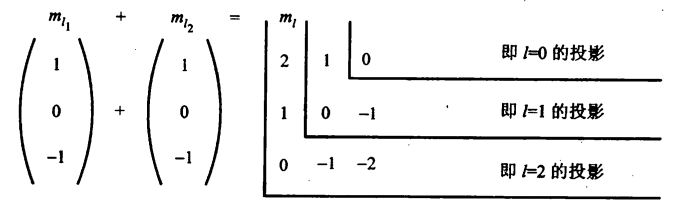
\(L_1\)和\(L_2\)分别表示是以\(l_1\)和\( l_2\)为量子数的角动量,它们的数值分别是:$$\left.\begin{array}{l} L_{1}=\sqrt{l_{1}\left(l_{1}+1\right)} \hbar \\ L_{2}=\sqrt{l_{2}\left(l_{2}+1\right)} \hbar \end{array}\right\}$$把两个角动量加起来:$$L_{1}+L_{2}=L$$显然\(L\)也是角动量,它的数值也满足$$L=\sqrt{l(l+1)} \hbar$$而\(l\)只能有如下取值:$$l=l_{1}+l_{2}, l_{1}+l_{2}-1, \cdots,\left|l_{1}-l_{2}\right|$$为什么\(l\)的取值是这样的?举个例子说明。角动量相加,其实是投影值相加,图中\(m_{l_{1}}\)表示轨道量子数\(l_1=1\)在\(z\)方向的投影取值。
\(LS\)耦合和\(jj\)耦合
 氦原子中两个电子各有其轨道运动和自旋运动,这四种运动都会引起电磁相互作用,代表着四种运动的量子数可以写写\(l_{1} 、 s_{1}、 l_{2} 、 s_{2}\)。是个量子数的组合有六种,即四种运动之间可以有六种相互作用,标记为:$$G_{1}\left(s_{1} s_{2}\right) 、 G_{2}\left(l_{1} l_{2}\right) 、 G_{3}\left(l_{1} s_{1}\right) 、 G_{4}\left(l_{2} s_{2}\right)、 G_{5}\left(l_{1} s_{2}\right) 、 G_{6}\left(l_{2} s_{1}\right)$$这六种相互作用强弱是不同的,而且在不同原子的情况也不一样。一般\(G_5\)和\(G_6\)比较弱,可以忽略。下面讨论两种极端的情形:
氦原子中两个电子各有其轨道运动和自旋运动,这四种运动都会引起电磁相互作用,代表着四种运动的量子数可以写写\(l_{1} 、 s_{1}、 l_{2} 、 s_{2}\)。是个量子数的组合有六种,即四种运动之间可以有六种相互作用,标记为:$$G_{1}\left(s_{1} s_{2}\right) 、 G_{2}\left(l_{1} l_{2}\right) 、 G_{3}\left(l_{1} s_{1}\right) 、 G_{4}\left(l_{2} s_{2}\right)、 G_{5}\left(l_{1} s_{2}\right) 、 G_{6}\left(l_{2} s_{1}\right)$$这六种相互作用强弱是不同的,而且在不同原子的情况也不一样。一般\(G_5\)和\(G_6\)比较弱,可以忽略。下面讨论两种极端的情形:
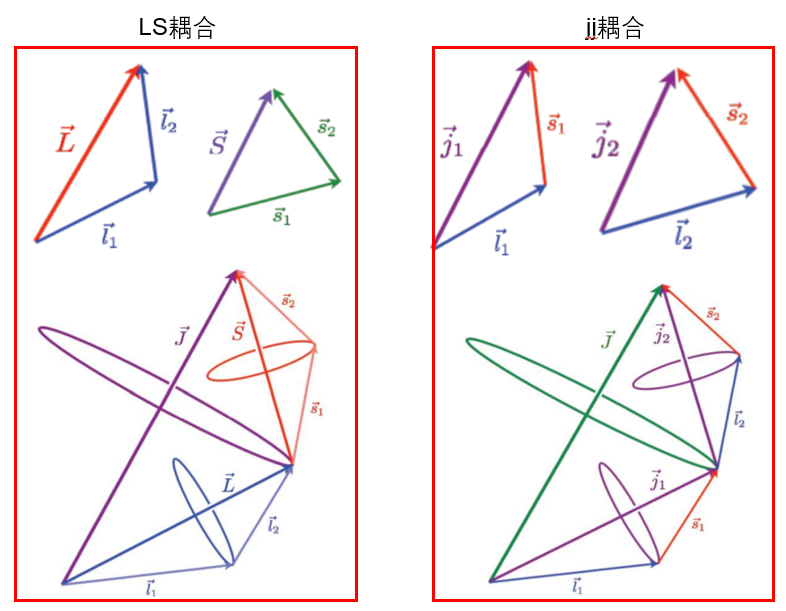
(1) \(G_1\)和\(G_2\)占优(\(LS\)耦合):两个自旋运动合成一个总自旋运动,两个轨道角动量合成一个轨道总角动量,然后轨道总角动量和自旋总角动量合成总角动量。
例子:
(2) \(G_3\)和\(G_4\)占优(\(jj\)耦合):电子的自旋同自己的轨道运动比其余几种要强,这时电子的自旋角动量和轨道角动量要先合成各自的总角动量,然后这两个电子的总角动量又合成原子的总角动量。
弱/中等/强耦合
多电子原子,哈密顿量可以表示为:$$H=-\frac{\hbar^{2}}{2 m} \sum_{i=1}^{N} \Delta_{i}-\sum_{i=1}^{N} \frac{Z^{*} e^{2}}{r_{i}}+\sum_{i=1}^{N} \frac{e^{2}}{r_{i j}}+\sum_{i=1}^{N} \zeta_{r_{i}}\left(r_{i}\right) s_{i} \cdot l_{i}$$等式右边从左到右每一项分别表示电子动能、电子与核的相互作用、电子间的相互作用、自旋轨道耦合。
(1) \(N\)是未满壳层的电子总个数,\( \Delta=\nabla^{2}=\displaystyle\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}}\)
(2) 核电荷因内层电子的屏蔽作用而取\(Z^{*}\)。
(3) 电子间的相互作用\( H_c\)。
(4) 自选轨道耦合\(H_{SO}\),\(\zeta\left(r_{i}\right)\)是耦合系数(决定耦合的强度)。
根据\(H_{c}\)和\(H_{SO}\)的大小关系,有如下三种情形:
(1) \(H_{SO}<<H_{c}\),弱耦合,一般是原子序数小于30的元素,也叫作 Russell-Saunders 耦合,对应于\(LS\)耦合。比如Mn2+的最低激发态是\({ }^{4} G_{11 / 2}\), 实际上,这里\(J \)的值还可以取9/2, 7/2, 5/2。但由于\(H_{SO}\)小,即旋轨耦合弱,不同\(J \)值对 应的能量相差不大,通常只简单写成\( { }^{4} G \),即这个态对\(J \)是简并的。
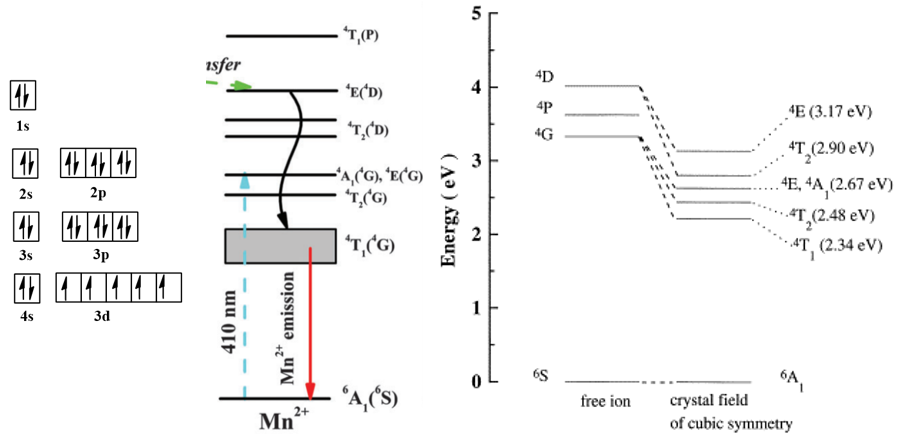 (3) \(H_{SO}>>H_{c}\),强耦合,对应\(j-j\)耦合。
(3) \(H_{SO}>>H_{c}\),强耦合,对应\(j-j\)耦合。
(4) \(H_{SO}\approx H_{c}\),中等耦合。比如稀土离子就是此类,\(J\)值对能量的影响不能忽略。比如Pr3+的\({ }^{3} H_{4}\)和\({ }^{3} H_{5}\)相差2000 cm-1。
上面的稀土能级图,图中的能级符号按理说只适用于弱耦合,在较早的时候,人们认为稀土离子也属于弱耦合,因此和那些较轻的元素一样,仍采用\( L\)、\( S\)、\( J\)这些符号来写光谱项。后来才发现稀土离子的\( LS\)耦合相当强,属于中等耦合。
重原子效应
Heavy Atom Effect (IUPAC):The enhancement of the rate of a spin-forbidden process by the presence of an atom of high atomic number, which is either part of, or external to, the excited molecular entity. Mechanistically, it responds to a spin-orbit coupling enhancement produced by a heavy atom.
按照参考资料4,补充
参考资料:
(1) 《原子物理》杨家福
(2) The Russell Saunders Coupling Scheme-Libretexts
(3) 《固体发光讲义》许少鸿
(4) Heavy Atom Effect of Selenium for Metal-Free Phosphorescent Light-Emitting Diodes-CM-2020
补充:E:\knowledge\科研\荧光粉\基础理论\光谱项+selection_rule+耦合
电偶极跃迁的选择定则:
(1) 自旋禁戒,不同自旋态(\(\Delta S \neq0\))能级之间的电子跃迁是禁戒的。
(2) 宇称禁戒,如\( d\)层、\(f\)层内或\( d\)层和\( s\)层之间。
(3) Ln3+的\(4f\)电子宇称相同,在自由离子时其电偶极跃迁是禁戒的,而另外两种跃迁(磁偶极和电四级)是允许的,但实验中常能观测到\(4f\)的电偶极跃迁,这是晶体场的影响。
J-O强度参数可以由稀土的吸收光谱或透射光谱(材料必须透明)+软件计算得到。(待补充)
强度参数包括:振子强度、辐射跃迁几率、荧光分支比、激发态辐射寿命。

稀土元素的磁性
能量传递
A Tutorial Review on the Nonradiative Energy Transfer Rates between Lanthanide Ions—发光学报-2022
基质晶格激发
激活剂的激发和基质晶格的激发区别:2+掺杂卤磷酸盐,UV光可以直接将GS的Mn2+的电子激发到CB,然后弛豫到Mn2+的激发态,然后发光,这个过程效率很高;如果用阴极射线,直接产生electron-hole pair,最终反而Mn2+
参考资料:
- René M. Williams教授视频
- Főrster, Th. "10th Spiers Memorial Lecture. Transfer mechanisms of electronic excitation." Discussions of the Faraday Society 27 (1959): 7-17.
- Förster resonance energy transfer-Wiki
- Hsu, Chao-Ping. "The electronic couplings in electron transfer and excitation energy transfer." Accounts of Chemical Research 42.4 (2009): 509-518.
- Tanner, Peter A., et al. "Misconceptions in electronic energy transfer: bridging the gap between chemistry and physics." Chemical Society Reviews 47.14 (2018): 5234-5265.
Reabsorption(Radiative ET)
重吸收影响本征寿命:高掺杂浓度下,重吸收明显,重吸收会导致寿命增加,低掺杂浓度下的寿命更能反映本征的寿命。[Andries_CM_2009]
重吸收影响发射峰的位置:重吸收会导致部分短波长发光的部分再次被吸收,从而使得PL光谱出现红移,Ce3+或者Eu2+的掺杂浓度越大,这种效应就越明显。参见下面左侧的图。[Andries_CM_2009]
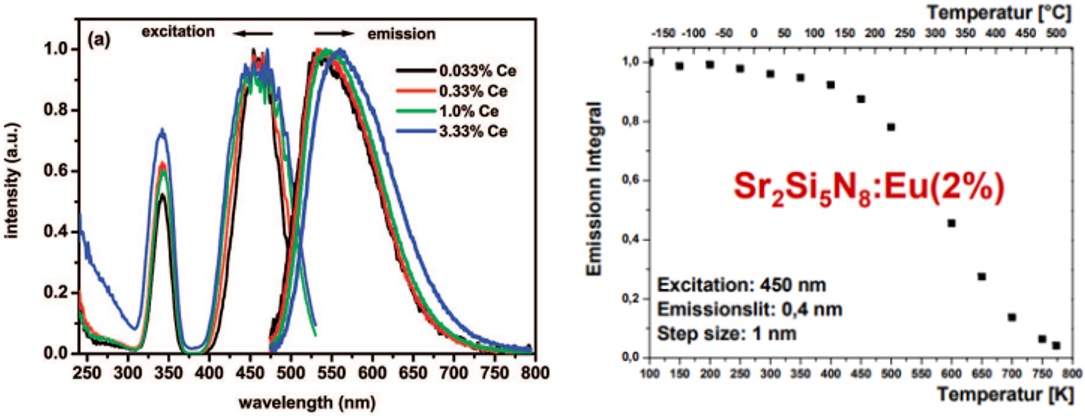
重吸收影响量子效率:上面右侧的图来自[Thomas Jüstel-PPT],他认为100-500 K时是Re-absorption导致了量子效率的下降,继续升高温度,IQE decreases due to IC and/or PI。
重吸收影响太阳能电池的LSC:Reabsorption in luminescent solar concentrators (LSC) is a major factor hindering their commercialisation. This issue is caused by the inherently small Stokes shift of luminophores which creates a large spectral overlap between absorption and emission, leading to reabsorption of waveguided photons. [Journal of Luminescence 236 (2021): 118095.]
拓展:Devices known as luminescent solar concentrators could find use as renewableenergy generators, but have so far been plagued by a major light-reabsorption effect. A new study offers a promising route to tackling this problem.
[Debije, Michael. "Better luminescent solar panels in prospect." Nature 519.7543 (2015): 298-299.]
Non-Radiative ET
- Förster resonance energy transfer (FRET)
-
- Coulomb interaction
- Spectral overlap integral (govern the rate)
- Kappa factor (the orientation of the two transition dipole moments involved in the process)
- Singlet energy transfer (SEnT) (in general)
- the distance between the donor and the acceptor (typically in the range of 1~10 nm)
- 也有人称作fluorescence resonance energy transfer,但是容易误解,因为能量传递不是transferred by fluorescence,所以Förster resonance energy transfer名字更准确。
-
- Dexter energy transfer (DET)
-
- Exchange interaction
- double electron transfer
- electronic coupling (orbital overlap of the of the donor and acceptor)
- triplet energy transfer + short distance SEnT
- short distance的时候可能faster than FRET
-

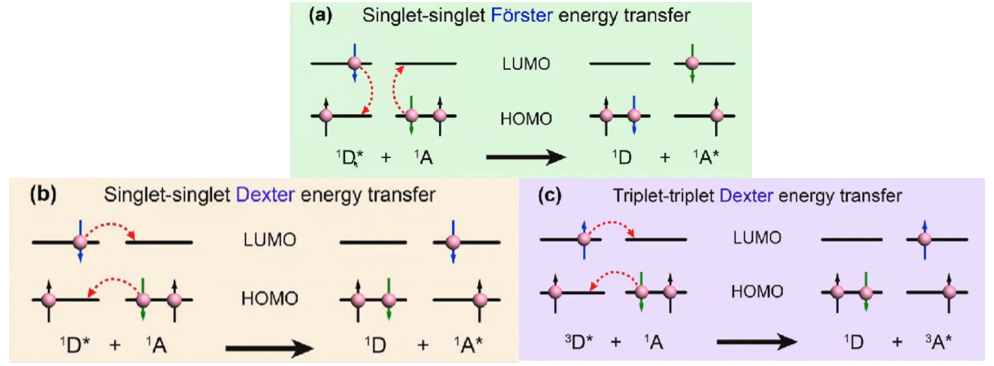
Triplet triplet Förster energy transfer, Can this be possible???
答:No. Molar absorption coefficients of triplet states are so small (spin-forbidden), so that this is basically impossible. Förster mechanism is only for singlets. (apart from some exceptions).
Förster Energy Transfer Efficiency
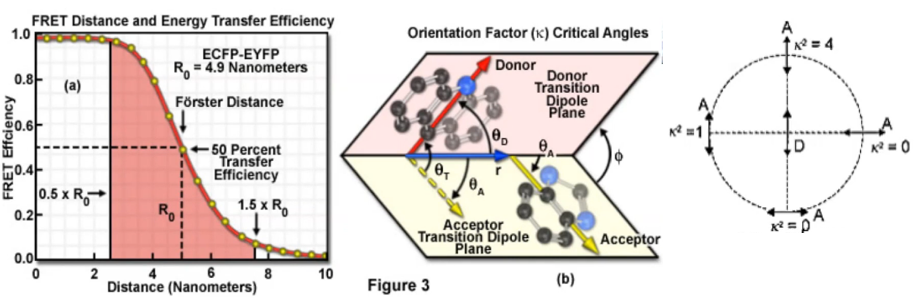
$$\phi_{\mathrm{ET}}=\frac{R_{0}^{6}}{R_{0}{ }^{6}+r_{\mathrm{DA}}{ }^{6}}$$\(R_{0} \equiv\) the Förster distance where \(\phi_{\mathrm{ET}}=0.5\)
\( r_{\mathrm{DA}} \equiv\) the distance between a donor (fluorescent unit) and an acceptor (可以通过modelling或者some other data来估算)
Förster distance $$\mathrm{R}_{0}(\overset\circ{\mathrm{A}})=0.211 \times\left(\kappa^{2} n^{-4} \phi_{\mathrm{D}} J\right)^{1 / 6}$$\( \kappa^{2}\): the orientation factor; (orientation of the two chromophores)
\(n\): the refractive index of the medium;
\(\phi_{\mathrm{D}}\): the fluorescence quantum yield of the donor;
\(J\): the overlap integral.
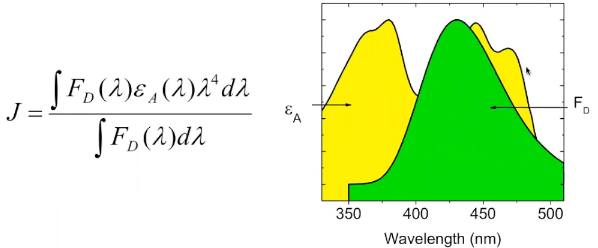
Overlap integral
\(F_{\mathrm{D}}(\lambda)\): the fluorescence intensity of the donor as a function of wavelength.
\(\varepsilon_{\mathrm{A}}(\lambda)\): the molar extinction coefficient of the acceptor at that wavelength;
Orientation factor
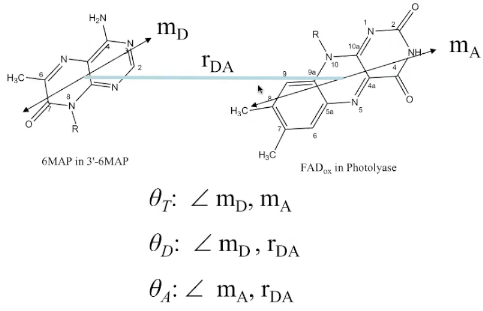 (1) 不知道的情况下用\(\kappa^2 =2/3\) (general accepted value,认为donor和acceptor是isotropically oriented)
(1) 不知道的情况下用\(\kappa^2 =2/3\) (general accepted value,认为donor和acceptor是isotropically oriented)
(2) \( r_{\mathrm{DA}} \)的线connects the centers of the chromophores;
(3) \(\kappa^{2}=\left(\cos \theta_{\mathrm{T}}-3 \cos \theta_{\mathrm{D}} \cos \theta_{\mathrm{A}}\right)^{2}\)
(4) 下图的两个公式是等价的。
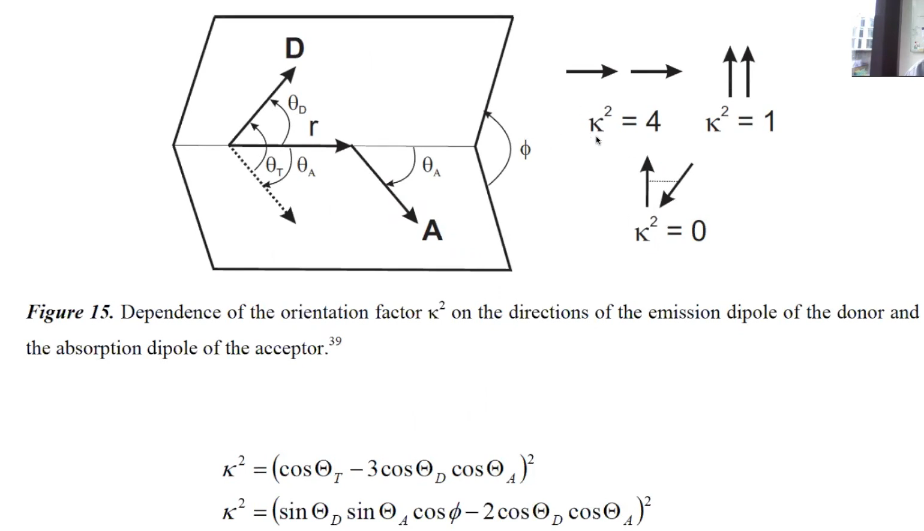 (5)$$\kappa=\hat{\mu}_{\mathrm{A}}\cdot \hat{\mu}_{\mathrm{D}}-3\left(\hat{\mu}_{\mathrm{D}}\cdot \hat{R}\right)\left(\hat{\mu}_{\mathrm{A}} \cdot \hat{R}\right)$$其中\(\hat{\mu}_{i}\) denotes the normalized transition dipole moment of the respective fluorophore, and \(\hat{R}\) denotes the normalized inter-fluorophore displacement.
(5)$$\kappa=\hat{\mu}_{\mathrm{A}}\cdot \hat{\mu}_{\mathrm{D}}-3\left(\hat{\mu}_{\mathrm{D}}\cdot \hat{R}\right)\left(\hat{\mu}_{\mathrm{A}} \cdot \hat{R}\right)$$其中\(\hat{\mu}_{i}\) denotes the normalized transition dipole moment of the respective fluorophore, and \(\hat{R}\) denotes the normalized inter-fluorophore displacement.
 (6) Time-dependent analyses of FRET $$ k_{\mathrm{ET}}=\left(\frac{R_{0}}{r}\right)^{6} \frac{1}{\tau_{\mathrm{D}}} $$其中\(\tau_{D}\) is the donor's fluorescence lifetime in the absence of the acceptor,\(R_{0}\) is the critical distance of Förster radii (\( \phi_{\mathrm{ET}}=0.5\)),\(r\)是D和A之间的距离。
(6) Time-dependent analyses of FRET $$ k_{\mathrm{ET}}=\left(\frac{R_{0}}{r}\right)^{6} \frac{1}{\tau_{\mathrm{D}}} $$其中\(\tau_{D}\) is the donor's fluorescence lifetime in the absence of the acceptor,\(R_{0}\) is the critical distance of Förster radii (\( \phi_{\mathrm{ET}}=0.5\)),\(r\)是D和A之间的距离。
The FRET efficiency relates to the quantum yield and the fluorescence lifetime of the donor molecule as follows: $$\phi_{\mathrm{ET}}=1-\tau_{\mathrm{D}}^{\prime} / \tau_{\mathrm{D}}$$ where \(\tau_{\mathrm{D}}^{\prime}\) and \(\tau_{\mathrm{D}}\) are the donor fluorescence lifetimes in the presence and absence of an acceptor respectively, or as $$\phi_{\mathrm{ET}}=1-F_{\mathrm{D}}^{\prime} / F_{\mathrm{D}}$$ where \(F_{\mathrm{D}}^{\prime}\) and \(F_{\mathrm{D}}\) are the donor fluorescence intensities with and without an acceptor respectively.
应用
(1) 基于FRET,利用technique to analyze molecular interactions (e.g. protein-protein interactions). Different fluorophores are used and tagged to proteins. (参考视频)
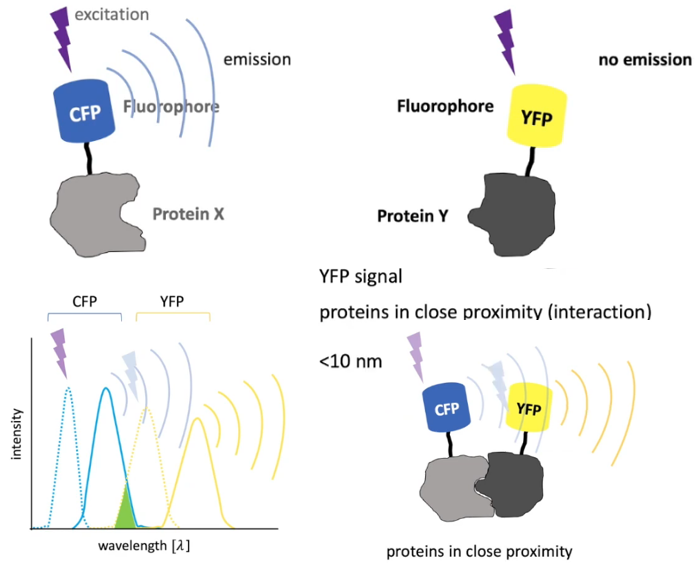
【CFP】: Cyan Fluorescent Protein (青色荧光蛋白)
【GFP】: Green Fluorescent Protein (绿色荧光蛋白)
【YFP】: Yellow Fluorescent Protein (黄色荧光蛋白)
【RFP】: Red Fluorescent Protein (红色荧光蛋白) The original was isolated from Discosoma, and named 【DsRed】.
(2) Single-molecule FRET
参考一文读懂新技术--单分子荧光共振能量转移技术smFRET
实例—Energy transfer and cross relaxation
Energy transfer processes in Sr3Tb0.90Eu0.10(PO4)3
总结
 上图来自[Temporally modulated energy shuffling in highly interconnected nanosystems]
上图来自[Temporally modulated energy shuffling in highly interconnected nanosystems]
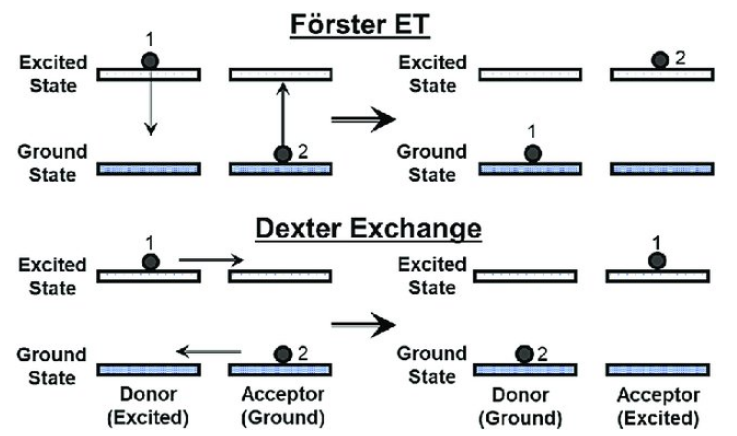
Energy transfer is generally associated with multipolar interactions, radiation reabsorption, or exchange interaction. Among them, Multipolar interactions are usually prevalent which have several types, such as dipole–dipole (d–d), dipole–quadrupole (d–q), and quadrupole–quadrupole (q–q) interactions. Exchange interaction is generally limited to interactions between RE ions in nearest or next nearest neighbor. If migration is rapid compared to direct transfer, quenching tends to be proportional to quenching-ions concentration.
For a better understanding of energy transfer in the host, the relationship of emission intensity and activator concentration is discussed. As the report of Van Uitert and Ozawa, The type of energy transfer can be determined from the change in the emission intensity from the emitting level . The emission intensity per activator ion follows the equation: $$\frac{I}{x}=K\left[1+\beta(x)^{\theta / 3}\right]^{-1}$$where \(x\) is the activator concentration, \( I/x\) is the emission intensity \( (I)\) per activator concentration \( (x)\), and \( K\) and \( \beta\) are constants for the same excitation condition for a given host crystal.
参考[Synthesis and characterization of YNbTiO6:Dy3+ phosphor-JAC-2011]
能量传递:处于激发态的中心,除了通过辐射跃迁和无辐射跃迁回到基态,还可能把能量传给别的中心,这个过程我们称之为能量传递。能量传递过程是发光材料中极其重要的过程,很大程度上影响着发光的效率,甚至决定材料是否发光。
能量传递的基本过程:
(1) S首先被激发进入激发态S*
(2) 随后把能量传递给A,使A进入激发态A*,同时S*回到基态S
(3) 处于激发态的中心A*回到基态有两种可能的方式:
(3-a) 通过辐射跃迁的方式回到基态,这种情况我们把S叫作A的敏化剂;
(3-b) 通过无辐射跃迁的方式回到基态,这种情况我们把A 叫作S的猝灭剂。
不同种类中心之间的能量传递
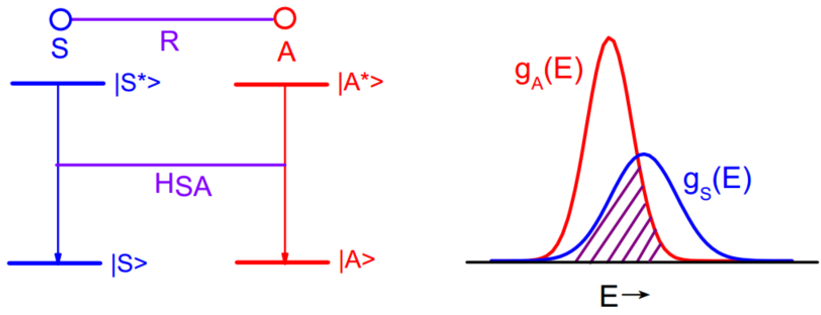 Dexter给出了无辐射ET的几率$$P_{S A}=\left.\frac{2 \pi}{\hbar}\left|<S, A^{*}\right| H_{S A}|S^{*}, A>\right|^{2} \cdot \int g_{s}(E) \cdot g_{A}(E) d E$$其中积分是光谱交叠积分,\(g_S\)是S的发射谱,\(g_A\)是A的吸收谱。矩阵元表示了初态\(\mid S^{*}, A>\)与终态\(\mid S, A^{*}>\)的相互作用贡献,\(H_{SA}\)代表了这种相互作用的哈密顿项。
Dexter给出了无辐射ET的几率$$P_{S A}=\left.\frac{2 \pi}{\hbar}\left|<S, A^{*}\right| H_{S A}|S^{*}, A>\right|^{2} \cdot \int g_{s}(E) \cdot g_{A}(E) d E$$其中积分是光谱交叠积分,\(g_S\)是S的发射谱,\(g_A\)是A的吸收谱。矩阵元表示了初态\(\mid S^{*}, A>\)与终态\(\mid S, A^{*}>\)的相互作用贡献,\(H_{SA}\)代表了这种相互作用的哈密顿项。
要想能量传递几率不等于零,就要求:
(1) \(\left|<S, A^{*}\right| H_{S A}\left|S^{*}, A>\right|^{2} \neq 0\)
(2) \(\int g_{s}(E) \cdot g_{A}(E) d E \neq 0\)
几率大小依赖于:
(1) 共振,即S的发射谱与A的吸收谱有交叠,交叠积分越大则能量传递几率越大;
(2) 相互作用类型
(2-a) 电多极相互作用,满足\(R^{-n}\,(n=6,8...)\)关系,分别对应电偶极-电偶极跃迁,电偶极-电四级相互作用......
(2-b) 交换相互作用,依赖于波函数的交叠,随距离成指数衰减关系。
临界距离\(R_c\):
处于激发态的S*既可以通过自身的辐射跃迁回到基态(几率\( P_S\)),也可以把能量传递给A(几率\(P_{SA}\)),通过A的发射回到基态。当\(P_S=P_{SA}\)时,对应的距离叫作临界距离\(R_c\)。
- 当实际距离\(R\)大于\(R_c\)时,以S的发射为主;
- 当实际距离\(R\)小于\(R_c\)时,以S向A的能量传递为主。
- 通常对于允许的电偶极相互作用,\(R_c\)约为\( 30 \)Å;
- 如果偶极跃迁是禁戒的,则需要交换相互作用,其\(R_c\)约为\(5-8 \)Å。
辐射能量传递:
S*先发光,然后发出的光被A吸收,导致A的激发和发射。这种传递过程与中心间的距离\(R\)无关。
能量传递的实验观察:
(1) A的激发谱包含S的特征激发;
(2) 选择对S有效,但是对A无效的激发波长,最后在S和A共掺杂的样品中还是观察到A的发光。
临界传递几率与临界几率的计算:
假设是电偶极类型,\(P_{SA}=P_S\) $$R_{c}^{6}=3 \times 10^{12} \cdot f_{A} \cdot E^{-4} \cdot S O$$这里\(f_A\)表示A中心吸收跃迁的振子强度,\( \)表示最大光谱交叠能量,\(SO\)表示光谱交叠积分。
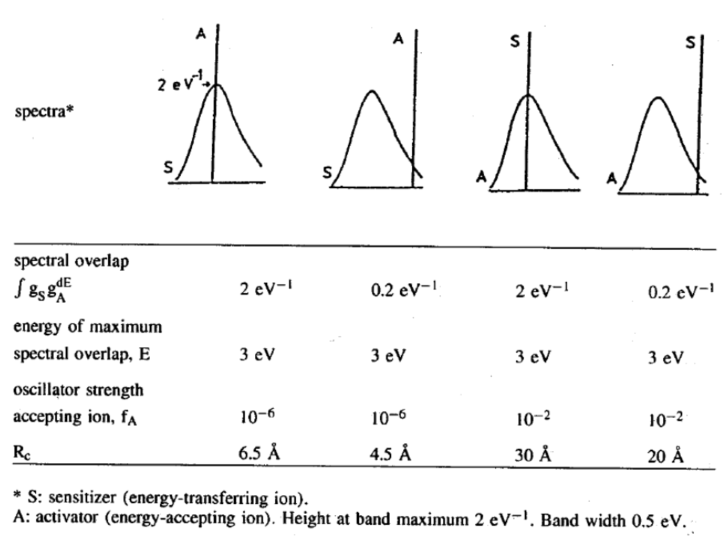
- 带状发射到线谱吸收的\(R_c\)较小,表明ET只能发生在最邻近晶格;
- 线谱发射到带状吸收的\( R_c\)较大,表明ET可以涉及更远的晶格。
例子:
(1) Gd3+的\( { }^{6} \mathrm{P}_{7 / 2}\)可以传递给大多数稀土离子,除了Pr3+和Tm3+,因为没有光谱交叠(Dieke diagram),不满足共振条件。
(2) Ca5(PO4)3F:Sb3+,Mn2+的发光, Sb3+传递能量 给Mn2+, Sb3+的发射谱覆盖了几个Mn2+的吸收 带。由于f值很低(自旋宇称禁戒),能量传递 的相互作用属于交换相互作用\(R_{c} \sim 7\)Å。
(3) Rb2ZnBr4:Eu2+, Eu2+占据Rb+位置,因为Rb+有两个不同格位,因此Eu2+也有两种不同格 位, Eu2+受到晶格场的影响强烈,两个Eu2+具 有不同的能量。 能量传递可以从高能级的Eu2+(415nm)到低 能级的Eu2+(435nm)。 都属于电偶极允许的跃迁, \( R_{c}=\)35 Å。
同种中心之间的能量传递
定义:如果上面讨论的中心A和S是同一种发光中心,并且具有相同的能级系统,就可以产生共振能量传递,称之为同种发光中心之间的能量传递。
注:但是有时对于受到晶格场影响强烈的中心(例如过渡族离子、二价稀土离子), 如果它们占据的格位不同,导致晶格场引起的能级系统有 较大差别时,我们不把它们看做是同种发光中心。
浓度猝灭:( 对于同种发光中心)
(1) 当浓度较大时: 中心间的距离小于临界距离,它们就 会产生级联能量传递,即从一个中心传递到下一个中 心,再到下一个中心。。。。。。(发生能量迁移) 直到最后进入一个猝灭中心,导致发光的猝灭,我们 把这种猝灭叫做浓度猝灭。
(2) 当浓度较小时: 这种级联能量传递过程受到阻碍,可以产生发光。
(3) 实验观察: 实验上如果做出一条发光强度随掺杂浓度变化的曲线,我们会观察到开始随着浓度的增加发光强度逐渐增强,到达某个浓度值以后发光强度开始逐渐下降,这就是浓度猝灭开始产生作用。
半导体中的能量传递
- 半导体的激发涉及到产生自由电子或空穴。或电子-空穴的束缚状态——激子。
- 自由电子和空穴沿着同一方向运动,直到被辐射跃迁中心俘获,产生发光。
- 激子:包括Frenkel和Wannier激子,属于电子空穴的束缚态。它们可以一起移动,产生能量的输运。自由激子可能在某些位置被束缚,形成束缚激子,束缚激子可能产生发光,也可能发生无辐射跃迁。
Inokuti-Hirayama
Photoluminescence properties of Eu2+-activated Sr3SiO5 phosphors
https://www.koushare.com/video/videodetail/9291
稀土掺杂光量子材料
参考资料:
(1) Defect Engineering for Quantum Grade Rare-Earth Nanocrystals-ACS Nano-2020
(2) Philippe Goldner 视频