参考资料： [mathjax]
矢量分析
三重积和矢量变换
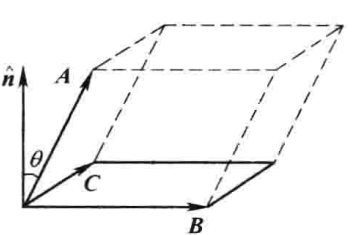
平行六面体的体积可以表示为$$A \cdot(B \times C)=B \cdot(C \times A)=C \cdot(A \times B)$$负号的三重积$$A \cdot(C \times B)=B \cdot(A \times C)=C \cdot(B \times A)$$混合积的行列式计算法$$A \cdot(B \times C)=\left|\begin{array}{lll} A_{x} & A_{y} & A_{z} \\ B_{x} & B_{y} & B_{z} \\ C_{x} & C_{y} & C_{z} \end{array}\right|$$混合积的可交换性$$A \cdot(B \times C)=(A \times B) \cdot C$$矢量三重积(Vector triple product)$$A \times(B \times C)=B(A \cdot C)-C(A \cdot B)\\(A \times B) \times C=-C \times(A \times B)=-A(B \cdot C)+B(A \cdot C)$$注：上面第一个式子的证明有两种方法。一是将所有向量都写成\(\mathbf{i}\)，\(\mathbf{j}\)，\(\mathbf{k}\)的线性组合，那么叉乘就可以用行列式的方法来计算，这种方法繁琐，而且缺乏物理图像。第二种方法：空间中有一个平面由\(B\)和\(C\)张成，那么\(B\)和\(C\)的叉乘得到的新向量必然垂直于这个平面，换句话说任何与该新向量垂直的向量必然落在\(B\)和\(C\)张成的平面内，因此\(A \times(B \times C)\)必然可以写成\(B\)和\(C\)的线性组合，即\(A \times(B \times C)=mB+nC\)。显然根据行列式的性质\(A \cdot[A \times(B \times C)]=0\)，参考之前的混合积的行列式计算法。于是\( m(A\cdot B)+n(A\cdot C) =0\)，那么必然存在一个实数\(p\)使得\(m=p(A\cdot C) \)，\(n=-p(A\cdot B)\)，于是有$$A\times(B\times C) = p[(A\cdot C)B-(A\cdot B)C]$$带入特例，就知道\(p=1\)。另外也可以利用a more familiar mnemonic "BAC − CAB" is obtained, as in “back cab”(后面的出租车).
单位方向矢量$$\hat{r}=\displaystyle{\boldsymbol{r} }/{r}=\displaystyle\frac{x \hat{\boldsymbol{x}}+y \hat{\boldsymbol{y}}+z \hat{\boldsymbol{z}}}{\sqrt{x^{2}+y^{2}+z^{2}}}$$三维向量绕着\( x \)轴旋转的线性变换$$\left(\begin{array}{l} \bar{A}_{y} \\ \bar{A}_{z} \end{array}\right)=\left(\begin{array}{cc} \cos \phi & \sin \phi \\ -\sin \phi & \cos \phi \end{array}\right)\left(\begin{array}{l} A_{y} \\ A_{z} \end{array}\right)$$注：如果将反对角线上两个正弦值前面的正负号变号(其实就是原矩阵的转置矩阵/逆矩阵)，得到的矩阵变换矩阵就是二维平面上向量的旋转矩阵。
绕任意轴旋转的线性变换$$\left(\begin{array}{l} \bar{A}_{x} \\ \bar{A}_{y} \\ \bar{A}_{z} \end{array}\right)=\left(\begin{array}{lll} R_{x x} & R_{x y} & R_{x z} \\ R_{y x} & R_{y y} & R_{y z} \\ R_{z x} & R_{z y} & R_{x z} \end{array}\right)\left(\begin{array}{c} A_{x} \\ A_{y} \\ A_{z} \end{array}\right)$$
梯/散/旋度/Nabla—高斯/斯托克斯定理
梯度
温度\( T(x, y, z) \)的偏导数为$$\mathrm{d} T=\left(\displaystyle\frac{\partial T}{\partial x}\right) \mathrm{d} x+\left(\displaystyle\frac{\partial T}{\partial y}\right) \mathrm{d} y+\left(\displaystyle\frac{\partial T}{\partial z}\right) \mathrm{d} z$$写成点积的形式$$\begin{aligned} \mathrm{d} T &=\left(\displaystyle\frac{\partial T}{\partial x} \hat{x}+\displaystyle\frac{\partial T}{\partial y} \hat{y}+\displaystyle\frac{\partial T}{\partial z} \hat{z}\right) \cdot(\mathrm{d} x \hat{x}+\mathrm{d} y \hat{y}+\mathrm{d} z \hat{z}) \\ &=(\nabla T) \cdot(\mathrm{d} \boldsymbol{l}) \end{aligned}$$其中\(\nabla T=\displaystyle\frac{\partial T}{\partial x} \hat{x}+\displaystyle\frac{\partial T}{\partial y} \hat{y}+\displaystyle\frac{\partial T}{\partial z} \hat{z}\)就是\(T\)的梯度。
梯度具有大小和方向，为了进行几何解释，可以写成$$\mathrm{d} T=\nabla T \cdot \mathrm{d} \boldsymbol{l}=|\nabla T||\mathrm{d}\boldsymbol{l}| \cos \theta$$当\( |\mathrm{d} \boldsymbol{l}| \)固定时，只有当\( \nabla T\)和\( \mathrm{d} \boldsymbol{l}\)方向相同时，\( \mathrm{d} T\)的变化才最大。
- 梯度\(\nabla T \)所指方向是函数\( T \)有最大增加的方向；
- \( |\nabla T| \)给出沿这个最大增加方向的增率(增加速率)；
- 一个点梯度为零的意义：移动一点点，\( dT=0 \)，一阶近似的系数为零。
\(\nabla \)算子$$\nabla= \hat{\boldsymbol{x}} \frac{\partial}{\partial x}+\hat{\boldsymbol{y}} \frac{\partial}{\partial y}+\hat{\boldsymbol{z}} \frac{\partial}{\partial z}$$\(\nabla\)算子求梯度$$ \nabla T=\left(\hat{\boldsymbol{x}} \frac{\partial}{\partial x}+\hat{\boldsymbol{y}} \frac{\partial}{\partial y}+\hat{\boldsymbol{z}} \frac{\partial}{\partial z}\right) T $$\(\nabla\)算子求散度$$\begin{aligned} \nabla \cdot \boldsymbol{v} &=\left(\hat{\boldsymbol{x}} \displaystyle\frac{\partial}{\partial x}+\hat{\boldsymbol{y}} \displaystyle\frac{\partial}{\partial y}+\hat{\boldsymbol{z}} \displaystyle\frac{\partial}{\partial z}\right) \cdot\left(v_{x} \hat{\boldsymbol{x}}+v_{y} \hat{\boldsymbol{y}}+v_{z} \hat{\boldsymbol{z}}\right) \\ &=\displaystyle\frac{\partial v_{x}}{\partial x}+\displaystyle\frac{\partial v_{y}}{\partial y}+\displaystyle\frac{\partial v_{z}}{\partial z} \end{aligned}$$\(\nabla\)算子求旋度$$\begin{aligned} \nabla \times \boldsymbol{v} &=\left|\begin{array}{ccc} \hat{\boldsymbol{x}} & \hat{\boldsymbol{y}} & \hat{\boldsymbol{z}} \\ \partial / \partial x & \partial / \partial y & \partial / \partial z \\ v_{x} & v_{y} & v_{z} \end{array}\right| \\ &=\hat{\boldsymbol{x}}\left(\displaystyle\frac{\partial v_{z}}{\partial y}-\displaystyle\frac{\partial v_{y}}{\partial z}\right)+\hat{\boldsymbol{y}}\left(\displaystyle\frac{\partial v_{x}}{\partial z}-\displaystyle\frac{\partial v_{z}}{\partial x}\right)+\hat{\boldsymbol{z}}\left(\displaystyle\frac{\partial v_{y}}{\partial x}-\displaystyle\frac{\partial v_{x}}{\partial y}\right) \end{aligned}$$
梯度/散度/旋度的积规则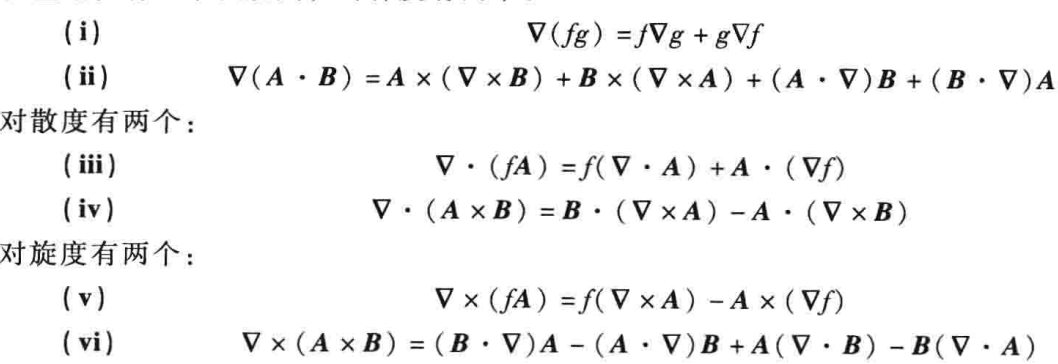
二阶微分
(1) 梯度的散度：\(\nabla \cdot(\nabla T) \)
(2) 梯度的旋度：\( \nabla \times(\nabla T) \)
(3) 散度的梯度：\( \nabla(\nabla \cdot \boldsymbol{v})\)
(4) 旋度的散度：\( \nabla \cdot(\nabla \times \boldsymbol{v})\)
(5) 旋度的旋度：\(\nabla \times(\nabla \times \boldsymbol{v}) \)
讨论：
(1) \(\nabla \cdot(\nabla T) \)简写为\(\nabla^{2} T \)，称为\(T \)的【拉普拉斯】；$$ \nabla^2 T=\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}+\frac{\partial^2 T}{\partial z^2} $$矢量的拉普拉斯\( \nabla^{2} \boldsymbol{v} \)，$$\nabla^{2} \boldsymbol{v} \equiv\left(\nabla^{2} v_{x}\right) \hat{\boldsymbol{x}}+\left(\nabla^{2} v_{y}\right) \hat{\boldsymbol{y}}+\left(\nabla^{2} v_{z}\right) \hat{\boldsymbol{z}}$$(2) 梯度的旋度总是零$$\nabla \times(\nabla T)=0$$对势函数求梯度，然后再求旋度，可以理解为既要沿着一个方向走，又要沿着这个方向的垂直方向走，结果就是动不了了。
注：事实上，该证明的关键是交叉求导的相等性\(\displaystyle\frac{\partial}{\partial x}\left(\frac{\partial T}{\partial y}\right)=\frac{\partial}{\partial y}\left(\frac{\partial T}{\partial x}\right)\)，而二维场的旋度$$ \operatorname{curl} \mathbf{F}=\boldsymbol{\nabla} \times \mathbf{F}(x, y)=\left(\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}\right) \mathbf{k} $$中\(F_x=\displaystyle\frac{\partial T}{\partial x},\quad F_y=\displaystyle\frac{\partial T}{\partial y} \)。显然二者是等价的。
(3) \( \nabla(\nabla \cdot \boldsymbol{v})\)物理上用得很少，注意它不是矢量的拉普拉斯。
(4) \( \nabla \cdot(\nabla \times \boldsymbol{v})=0\)
物理图像：一圈电流环路上套着很多磁场的小环，因为电流产生的磁场是有旋场，而磁场的旋度正好对应电流。如果我们先对磁场作一个旋度，那么得到的就是电流，而这个电流和这里的磁场环一样，都是没有源的，找不到“头”和“尾”，因此再对电流做散度，结果为零。(可能不准确)
证明：
- 方法-1，写出来，硬酸，参考旋度场的散度为零的证明—PengTitus
- 方法-2，根据三重积的性质，有\(\nabla \cdot(\nabla \times \boldsymbol{v})=(\nabla \times \nabla) \cdot \boldsymbol{v}\)，根据下面的式子可知，Nabla算子算子叉乘Nabla算子结果为零。$$ \nabla \times \nabla=\left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \end{array}\right| $$
(5) \( \nabla \times(\nabla \times \boldsymbol{v})=\nabla(\nabla \cdot \boldsymbol{v})-\nabla^{2} \boldsymbol{v} \)
注：这一条结合我们先前\( A \times(B \times C)=B(A \cdot C)-C(A \cdot B) \)这个公式很容易推导出来，注意这个公式是老师要求记住的。
思考：我们上面提到了不仅可以将拉普拉斯算子作用在标量上，也可以将这个算子作用在矢量上。拉普拉斯算子作用在标量上，最终得到的是一个标量；我们可以将原始的标量看作是零阶张量，然后求梯度，相当于升阶到一阶张量(向量)，然后求散度，相当于降阶到零阶张量，即最终结果同样是标量。拉普拉斯算子作用在矢量上，同样地，先是对矢量求梯度，那么升阶到二阶张量，然后求散度，降阶到一阶张量。其实拉普拉斯算子无论是作用在标量还是矢量上，作用过程都是先升阶再降阶，于是最终结果的阶数和原始数据的阶数是一致的。
\( \nabla\)算符同时具有矢量性和微分性
- 微分性：不可以随便移动位置，并且它如果作用在两个量的组合上，那么它就要分别作用到两个量上(类似求导)。
- 矢量性：它是一个矢量，不能像常数那样随意提前提后，要有一定的规律，这个规律包括：
- 点乘叉乘是矢量与矢量之间的运算，而微分算符只能作用到标量上；
- 混合积的轮转公式和三重积公式。
梯度的基本定理$$\displaystyle\int_{a }^{b}(\nabla T) \cdot \mathrm{d} \boldsymbol{l}=T(b)-T(a)$$势函数的梯度的积分和路径无关。
几何解释：假设你想测量埃菲尔铁塔的高度。你可以攀限塔梯，用一把尺子测量每一阶梯的高度，然后把它们加在一起，或者你可以用一个测高仪测量塔顶和塔底的读数，然后把两个读数相减；两种方法的结果应该一样(这就是基本定理)。
散度的基本定理(高斯散度定理，电磁学中的高斯定律)$$\displaystyle\int_{V}(\nabla \cdot \boldsymbol{v}) \mathrm{d} \tau=\displaystyle\oint_{S} \boldsymbol{v} \cdot \mathrm{d} \boldsymbol{a}$$几何解释：如果\( \boldsymbol{v} \)代表一个不可压缩流体的流，那么它的通量就是单位时间内流出表面的总的流量。现在散度是矢量从某点“散出”的量度，即一个具有高散度的地方像一个“水龙头”，向外流出液体。如果在一个体积内存在大量的水龙头，那么这个体积边界流出的总通量就等于这些水龙头流出量的和。实际上，我们有两种方法计算总的流出量：(1) 把所有龙头的流出量加在一起；(2) 在边界的每一点测流量，然后相加。$$ \oint \text { 体积内所有龙头的流量 }=\oint \text { 流出表面的流量 } $$
旋度的基本定理(斯托克斯定理)$$\int_S(\nabla \times \boldsymbol{v}) \cdot \mathrm{d} \boldsymbol{a}=\oint_L \boldsymbol{v} \cdot \mathrm{d} \boldsymbol{l}$$
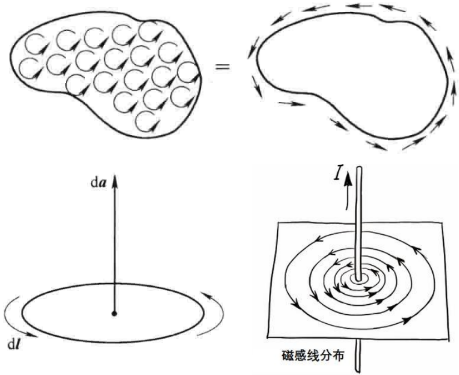一个(向量)函数的旋度对一个面的积分 = 这个函数在面的围线上的环路积分。
几何解释：如果水面上有一个漩涡，如果漩涡越明显的话(环量circulation越大)，那么我们将一个小木轮放在漩涡中心的话，它的旋转就会越快。托克斯定理相当于是说，小木轮的转速是由边缘的切向力(更准确地说是围绕中心的力矩)沿着小木轮外围的路径积分值大小决定的。
推论：
- \(\displaystyle\int_S(\nabla \times \boldsymbol{v}) \cdot \mathrm{d} \boldsymbol{a}\)仅依赖于边界线\(L\)，而与所选取的面\(S\)无关；
- \(\displaystyle\oint_S(\nabla \times \boldsymbol{v}) \cdot \mathrm{d} \boldsymbol{a}=0\)对任何闭合面都成立，因为闭合面的边界像气球的嘴一样，收缩为一个点。
注：
(1) 要对比学习上面三个定理，找到它们的异同点。
(2) George Stokes曾经担任英国皇家学会会长，其在光学(斯托克斯发光)、流体力学(纳维-斯托克斯方程)、数学(斯托克斯定理)。
传统分部积分延伸到矢量微积分
传统的分部积分\( \displaystyle\int_{a}^{b} f\left(\displaystyle\frac{\mathrm{d} g}{\mathrm{d} x}\right) \mathrm{d} x=-\displaystyle\int_{a}^{b} g\left(\displaystyle\frac{\mathrm{d} f}{\mathrm{d} x}\right) \mathrm{d} x+\left.f g\right|_{a} ^{b} \)借助散度定理，对一个体积有$$\nabla \cdot(f \boldsymbol{A})=f(\nabla \cdot \boldsymbol{A})+\boldsymbol{A} \cdot(\nabla f)$$进行积分$$\displaystyle\int \nabla \cdot(f \boldsymbol{A}) \mathrm{d} \boldsymbol{\tau}=\displaystyle\int f(\nabla \cdot \boldsymbol{A}) \mathrm{d} \tau+\displaystyle\int \boldsymbol{A} \cdot(\nabla f) \mathrm{d} \tau=\displaystyle\oint f \boldsymbol{A} \cdot \mathrm{d} \boldsymbol{a}$$即$$\displaystyle\int_{V} f(\nabla \cdot \boldsymbol{A}) \mathrm{d} \tau=-\displaystyle\int_{V} \boldsymbol{A} \cdot(\nabla f) \mathrm{d} \tau+\displaystyle\oint_{S} f \boldsymbol{A} \cdot \mathrm{d} \boldsymbol{a}$$
极/球/柱坐标系
极坐标系
\(\left\{\begin{array}{l} x=r \cos \theta \\ y=r \sin \theta \end{array}\right.\)，坐标为\( (r, \theta) \)的任意点的位置矢量为$$\vec{R}=r \cos \theta \hat{x}+r \sin \theta \hat{y}$$新坐标系的基矢$$ \begin{aligned} &\hat{r}=\frac{\partial \vec{R}}{\partial r}=\cos \theta \hat{x}+\sin \theta \hat{y} \\ &\hat{\theta}=\frac{\partial \vec{R}}{\partial \theta} \frac{1}{r}=-\sin \theta \hat{x}+\cos \theta \hat{y} \end{aligned} $$于是用矩阵的形式表示为$$ \left\{\begin{array}{l} \hat{r}=\cos \theta \hat{x}+\sin \theta \hat{y} \\ \hat{\theta}=-\sin \theta \hat{x}+\cos \theta \hat{y} \end{array} \quad \Rightarrow\left[\begin{array}{l} \hat{r} \\ \hat{\theta} \end{array}\right]=\left[\begin{array}{rr} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{l} \hat{x} \\ \hat{y} \end{array}\right]\right. $$也就是通过矩阵\( A\)作用，将原来的直角坐标的基矢量转变成极坐标系下的基矢量。那么通过矩阵\( A \)的逆矩阵，也可以将极坐标系下的基矢量转换回去，由于\( A \)本身是正交矩阵，所以它的逆矩阵就是它的转置。于是有$$\left[\begin{array}{l} \hat{x} \\ \hat{y} \end{array}\right]=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c} \hat{r} \\ \hat{\theta} \end{array}\right]$$注意，变换前后都是模长为一的基矢量，这种变换矩阵并不反映变换前后实际矢量的大小变化。如果我们将\(\left\{\begin{array}{l} x=r \cos \theta \\ y=r \sin \theta \end{array}\right. \)都写成全微分的形式，然后改写成矩阵的形式有$$ \left\{\begin{array}{l} d x=d(r \cos \theta)=\cos \theta d r+(-r \sin \theta) d \theta \\ d y=d(r \sin \theta)=\sin \theta d r+r \cos \theta d \theta \end{array} \Rightarrow\left[\begin{array}{l} d x \\ d y \end{array}\right]=\left[\begin{array}{cc} \cos \theta & -r \sin \theta \\ \sin \theta & r \cos \theta \end{array}\right]\left[\begin{array}{l} d r \\ d \theta \end{array}\right]\right. $$
球坐标系(参考知乎)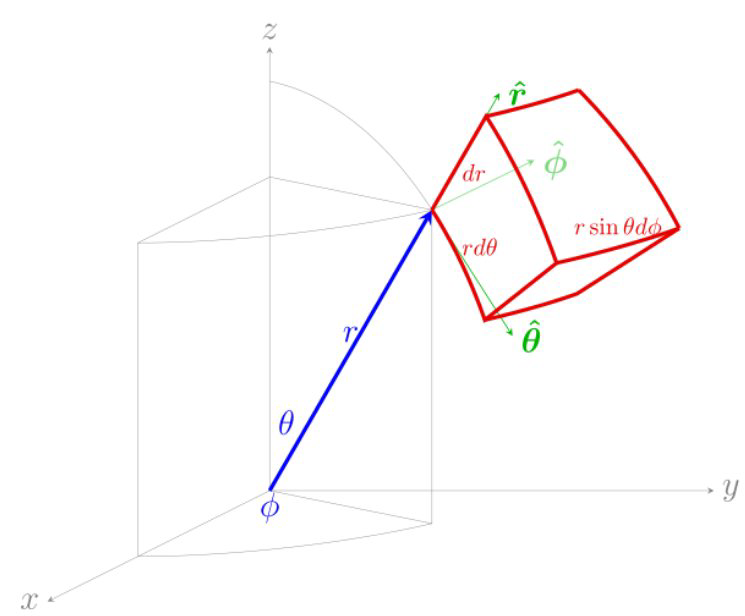
也可以通过类似极坐标的处理方法，我们有\( \left\{\begin{array}{l} x=r \sin \theta \cos \phi \\ y=r \sin \theta \sin \phi \\ z=r \cos \theta \end{array}\right. \)那么坐标为\( (r, \theta, \phi) \)的任意点的位置矢量为\( \vec{R}=r \sin \theta \cos \phi \hat{x}+r \sin \theta \sin \phi \hat{y}+r \cos \theta \hat{z} \)$$\begin{array}{lll} \hat{r}=\displaystyle\frac{\partial \vec{R}}{\partial r}=\sin \theta \cos \phi \hat{x}+\sin \theta \sin \phi \hat{y}+\cos \theta \hat{z} \\ \hat{\theta}=\displaystyle\frac{\partial \vec{R}}{\partial \theta} \displaystyle\frac{1}{r}=\cos \theta \cos \phi \hat{x}+\cos \theta \sin \phi \hat{y}-\sin \theta \hat{z} \\ \hat{\phi}=\displaystyle\frac{\partial \vec{R}}{\partial \phi} \displaystyle\frac{1}{r \sin \theta}=-\sin \phi \hat{x}+\cos \phi \hat{y} \end{array}$$注：上式我们根据图，然后投影，再归一化也能得到一样的结果。
用矩阵表示为$$\left[\begin{array}{c} \hat{r} \\ \hat{\theta} \\ \hat{\phi} \end{array}\right]=\left[\begin{array}{ccc} \sin \theta \cos \phi & \sin \theta \sin \phi & \cos \theta \\ \cos \theta \cos \phi & \cos \theta \sin \phi & -\sin \theta \\ -\sin \phi & \cos \phi & 0 \end{array}\right]\left[\begin{array}{c} \hat{x} \\ \hat{y} \\ \hat{z} \end{array}\right]$$对线性变换矩阵取逆，那么逆变换为$$\left[\begin{array}{l} \hat{x} \\ \hat{y} \\ \hat{z} \end{array}\right]=\left[\begin{array}{ccc} \sin \theta \cos \phi & \cos \theta \cos \phi & -\sin \phi \\ \sin \theta \sin \phi & \cos \theta \sin \phi & \cos \phi \\ \cos \theta & -\sin \theta & 0 \end{array}\right]\left[\begin{array}{c} \hat{r} \\ \hat{\theta} \\ \hat{\phi} \end{array}\right]$$即\( \Rightarrow\left\{\begin{array}{l} \hat{x}=\sin \theta \cos \phi \hat{r}+\cos \theta \cos \phi \hat{\theta}-\sin \phi \hat{\phi} \\ \hat{y}=\sin \theta \sin \phi \hat{r}+\cos \theta \sin \phi \hat{\theta}+\cos \phi \hat{\phi} \\ \hat{z}=\cos \theta \hat{r}-\sin \theta \hat{\theta} \end{array}\right.\)
直角坐标的全微分\(\mathrm{d} \boldsymbol{l}=\mathrm{d} x \hat{\boldsymbol{x}}+\mathrm{d} y \hat{\boldsymbol{y}}+\mathrm{d} z \hat{\boldsymbol{z}} \)换成球坐标，写成$$\mathrm{d} \boldsymbol{l}=\mathrm{d} r \hat{ \boldsymbol{r}}+r \mathrm{d} \theta \hat{\boldsymbol{\theta}}+r \sin \theta \mathrm{d} \phi \hat{\boldsymbol{ \boldsymbol{\phi}}}$$所以微小体积元$$\mathrm{d} \tau=\mathrm{d} l_{r} \mathrm{d} l_{\theta} \mathrm{d} l_{\phi}=r^{2} \sin \theta \mathrm{d} r \mathrm{d} \theta \mathrm{d} \phi$$注：这里表示空间中任意一点，移动\( \mathrm{d} \boldsymbol{l} \)对应的直角坐标系和求坐标系中的体积变化的比例关系。
狄拉克函数
狄拉克\(\delta \)函数的基本性质可以参考我之前的笔记[狄拉克函数的性质—傅里叶变换及其应用]。
具体描述：一个物体，除了某个质点外，密度处处为零，这个质点的密度是无限大，但是对这个物体在密度函数上进行体积分则是有限的，为这个物体的质量。
三维\( \delta \)函数$$\delta(\boldsymbol{r})=\delta(x) \delta(y) \delta(z)$$其中\(\boldsymbol{r}\equiv x \hat{\boldsymbol{x}}+y \hat{\boldsymbol{y}}+z \hat{\boldsymbol{z}}\)$$\displaystyle\int_{\text {整个空间}} \delta(\boldsymbol{r}) \mathrm{d} \tau=\displaystyle\int_{-\infty}^{\infty} \displaystyle\int_{-\infty}^{\infty} \displaystyle\int_{-\infty}^{\infty} \delta(x) \delta(y) \delta(z) \mathrm{d} x \mathrm{d} y \mathrm{d} z=1$$推广$$\displaystyle\int_{\text {整个空间 }} f(\boldsymbol{r}) \delta(\boldsymbol{r}-\boldsymbol{a}) \mathrm{d} \tau=f(\boldsymbol{a})$$注：格里菲斯的书中，\(\delta^3(\boldsymbol{r})=\delta(x) \delta(y) \delta(z)\)。
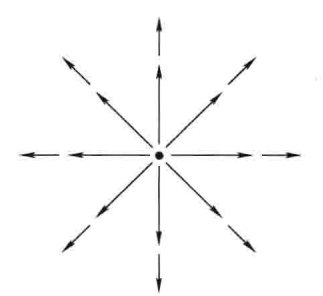矢量函数\( \boldsymbol{v}=\displaystyle\frac{1}{r^{2}} \hat{\boldsymbol{r}} \)，那么对任意距离中心点\(R\)范围内的质点的球体来说，要计算算该矢量势下的通量，根据高斯散度定理，有两种方法：
方法-1：先计算散度，再对散度进行体积分。这里用到了前面提到的球坐标系中的散度公式：$$\nabla \cdot \boldsymbol{v}=\displaystyle\frac{1}{r^{2}} \displaystyle\frac{\partial}{\partial r}\left(r^{2} \displaystyle\frac{1}{r^{2}}\right)=\displaystyle\frac{1}{r^{2}} \displaystyle\frac{\partial}{\partial r}(1)=0$$散度直接为零，都不用下一步进行积分了，于是我们得出通量为零。
方法-2：直接对矢量势进行面积分。$$ \oint \boldsymbol{v} \cdot \mathrm{d} \boldsymbol{a}=\int\left(\frac{1}{R^2} \hat{\boldsymbol{r}}\right) \cdot\left(R^2 \sin \theta \mathrm{d} \theta \mathrm{d} \phi \hat{\boldsymbol{r}}\right)=\left(\int_0^\pi \sin \theta \mathrm{d} \theta\right)\left(\int_0^{2 \pi} \mathrm{d} \boldsymbol{\phi}\right)=4 \pi $$积分结果不为零。
两种方法的结果矛盾，方法-2的结果才是正确的。这是因为所有通量的贡献都来自\(r=0\)的点，该点的散度无穷大。从数学的角度看，\(\delta \)函数不是严格意义上的函数，必须在积分式中才有意义，而方法-1采用的是微分的形式，所以出现了错误的结论。
利用方法-2的结果，以及高斯散度定理，我们有$$\oint \boldsymbol{v} \cdot \mathrm{d} \boldsymbol{a}=\int_{V} \nabla \cdot \boldsymbol{v} \mathrm{d} \tau=4 \pi=\int_{V} \delta(\boldsymbol{r}) 4 \pi \mathrm{d} \tau$$
因此该矢量势函数散度的正确结果为$$\nabla \cdot\left(\displaystyle\frac{\hat{\boldsymbol{r}}}{r^{2}}\right)=4 \pi \delta(\boldsymbol{r})$$方法-3：下面的等式两边消去\(Q / \epsilon_0\)即得。参考[用狄拉克 delta 函数表示点电荷的散度-小时百科]$$ \boldsymbol{\nabla} \cdot \mathbf{E}=\frac{Q}{4 \pi \epsilon_0} \boldsymbol{\nabla} \cdot \frac{\hat{\mathbf{r}}}{r^2}=\frac{Q \delta(\mathbf{r})}{\epsilon_0} $$
矢量场理论
【亥姆霍兹定理】(更准确的说是Helmholtz decomposition)：已知一个矢量场的旋度、散度和边界条件就可以唯一确定一个矢量场。在电动力学中，我们一般要求场在无限远处(远离所有电荷)趋于零，因此一般都可以保证电场或磁场可以由已知的散度和旋度唯一确定。
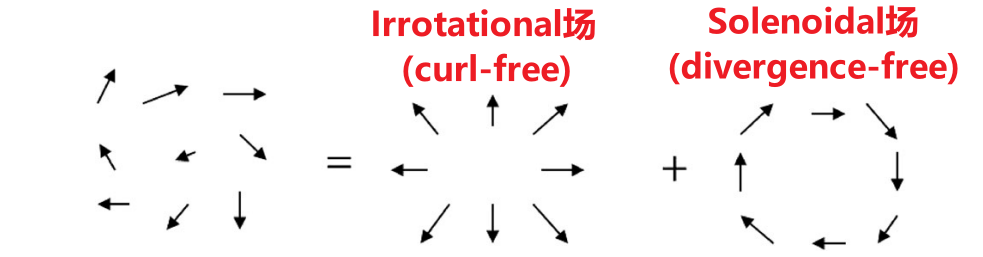Any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational (curl-free) vector field and a solenoidal (divergence-free) vector field. 任意足够光滑、快速衰减的三维向量场(其实就是上面的亥姆霍兹定理)可分解为一个无旋向量场和一个螺线向量场的和，这个过程被称作亥姆霍兹分解。也就是说任意满足条件的矢量场\( \)都可以表示为一个标量(势)的梯度和一个矢量(势)的旋度之和：$$ \boldsymbol{F}=-\nabla V+\nabla \times \boldsymbol{A} $$势函数：可以分为【标量势】(Scalar potential)和【矢量势】(Vector potential)。
Helmholtz decomposition的应用：由Helmholtz分解理论可知，一个矢量场可以被分解成一个无旋的标量场和一个无散的矢量场.而在各向同性介质中，纵波是无旋场，横波是无散场，因此根据Helmholtz分解理论，如果只考虑各向同性的介质，那么对地震波场分别求取散度和旋度，可以提取出纯纵波和纯横波。(参考[基于散度和旋度纵横波分离方法的改进—地球物理学报]。横波无源，纵波无旋，这句话存疑，来自资料1和2)
如果一个矢量场\(\boldsymbol{F}\)的旋度处处为零，那么该矢量场可以表示为一个标量势\(V\)的梯度：$$ \nabla \times \boldsymbol{F}=0 \Leftrightarrow \boldsymbol{F}=-\nabla V $$定理-1：无旋场，下列条件是等价的：
- 对任何一点有\(\nabla \times \boldsymbol{F}=0\)
- 对任何给定的端点，\(\displaystyle\int_a^b \boldsymbol{F} \cdot d \boldsymbol{l}\)是不依赖于路径的
- 对任何闭合路径，\(\displaystyle\oint \boldsymbol{F} \cdot d \boldsymbol{l}=0\)
- \(\boldsymbol{F}\)是一个标势的梯度，\(\boldsymbol{F}=-\nabla V\)
如果一个矢量场\(\boldsymbol{F}\)的散度处处为零，那么该矢量场可以表示为一个矢量势\(\boldsymbol{A}\)的梯度：$$ \nabla \cdot\boldsymbol{F}=0 \Leftrightarrow \boldsymbol{F}=\nabla \times \boldsymbol{A}$$定理-2：无散场，下列条件是等价的：
- 对任何一点有\(\nabla \cdot \boldsymbol{F}=0\)
- 对任何给定边界的面积分\(\displaystyle\int \boldsymbol{F} \cdot d \boldsymbol{a}\)是不依赖于所选面的
- 对任何闭合面，\(\displaystyle\oint \boldsymbol{F} \cdot d \boldsymbol{a}=0\)
- \(\boldsymbol{F}\)是一个矢量的梯度，\(\boldsymbol{F}=\nabla \times \boldsymbol{A}\)
参考资料：
(1) 是否已知一个矢量场的散度和旋度就可以唯一确定一个矢量场?—知乎
(2) 亥姆霍兹定理—知乎 科学巨匠亥姆霍兹—返朴
(3) Helmholtz decomposition—Wiki