课程视频-清华大学
参考笔记
光学基础
光学—北京大学
Fermat's Principle and the Geometric Mechanics of Ray Optics
工程光学笔记—知乎
绪论
课程简介
学习方法：
- 物理性质基本概念
- 实际问题模型化
- 熟能生巧
光的基本属性：
(1) 光是能量的载体；
(2) 光是信息的载体。
光学：研究光的行为和性质以及光和物质相互作用的物理学科。
- 几何光学：光是携带了能量的几何线；
- 波动光学：光是电磁场的传播；
- 几何光学是波动光学在波长趋近于\(0 \)时的一种近似，在光学仪器设计中较为实用。
- 量子光学：光是能量粒子的辐射。
- 物理光学（含量子光学和波动光学）：专门研究光的本质属性、光的传播规律、光与物质相互作用的关系。波动光学和量子光学分别揭示了光的本质属性“波粒二象性”。
激光：方向性好、亮度高、单色性好。
全息显示：利用光的干涉与衍射原理，将激光的干涉条纹记录在材料中，可以真实地显示出物体的三维信息。
预备数学知识
微积分基础
任何标量场梯度的旋度恒为零$$ \nabla \times(\nabla \phi) \equiv 0 $$任何矢量场的旋度的散度恒为零$$ \nabla \cdot(\nabla \times \vec{F}) \equiv 0 $$微分形式的麦克斯韦方程组：
- 高斯定律 \(\nabla \cdot D=\rho_f\)
- 磁通连续定律 \(\nabla \cdot B=0\)
- 法拉第电磁感应定律 \(\nabla \times E=-\displaystyle\frac{\partial B}{\partial t}\)
- 安培全电流定律 \(\nabla \times B=J_f+\displaystyle\frac{\partial D}{\partial t}\)
光学工程中的常用函数：光学系统建模需要这些函数来对这些系统进行描述，比如如何表示一个物体、孔径、双狭缝、点光源等。
光学工程常用函数
一维函数
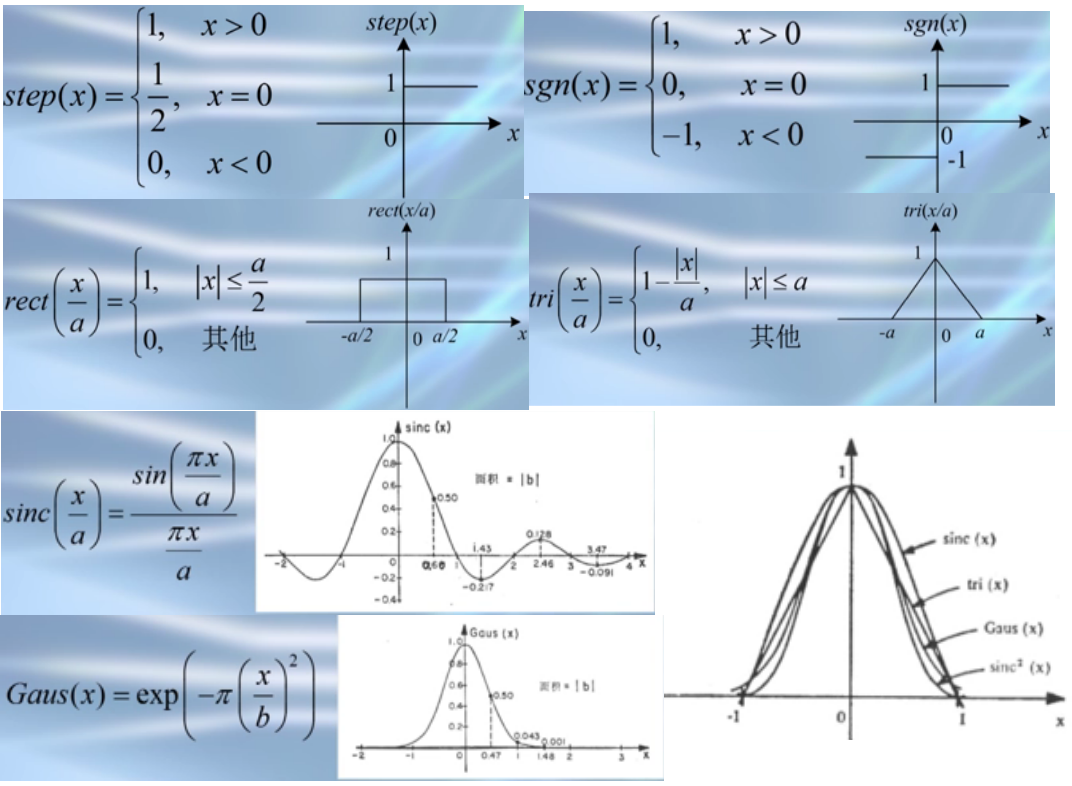
- step函数看起来像一个光学开关；
- sgn函数，函数极性反转，嵌有\(\pi\)位相板可用sgn函数；
- rect函数，表示狭缝或者矩孔的透过率，与其它函数相乘的时候，可以限制自变量的范围，所以又将其称为"门函数"；
- tri函数，表示光瞳为矩形的非相干成像系统的光学传递函数；
- sinc函数，描述狭缝或矩孔的夫琅禾费衍射图样；
- 高斯函数，描述激光器发出的高斯光束。
二维函数
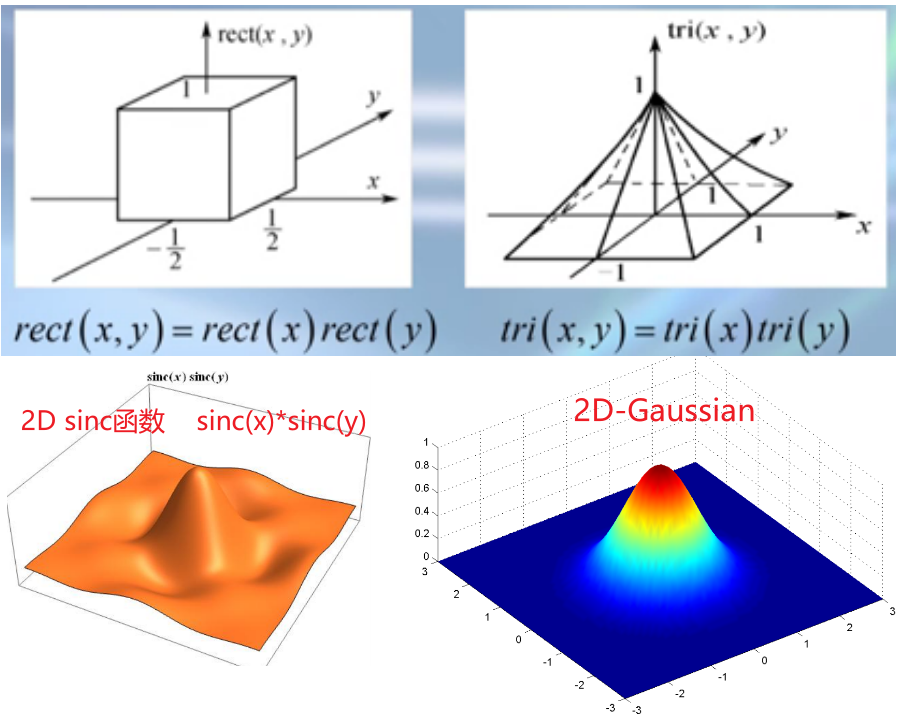
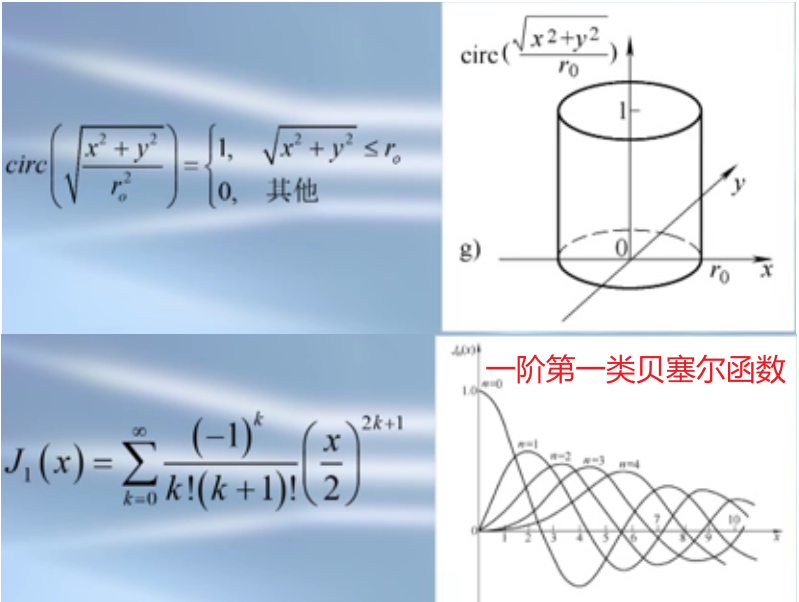
圆域函数/贝塞尔函数：互为傅里叶变换
Delta函数
- 表示点的质量、点电荷、点光源，也就是在某一点高度集中的量，这个点没有大小，所有属性都集中在在该点；
- 还可以表示无限小的孔径；
- 可以看成普通函数构成的序列的极限，比如一维矩形的脉冲，脉冲宽度逐渐变小，幅度逐渐变大，比如rect函数或者高斯函数的极限；
- 广义函数 \(\displaystyle\iint \delta(x, y) \varphi(x, y) d x d y=\varphi(0,0)\)
- 筛选性质 \(\displaystyle\iint \delta\left(x-x_{o}, y-y_{o}\right) \varphi(x, y) d x d y=\varphi\left(x_{o}, y_{o}\right)\)
- 比例变换性质 \(\delta(a x, b y)=\displaystyle\frac{1}{|a b|} \delta(x, y)\)
- 与普通函数的乘积 \(h(x, y) \delta\left(x-x_{o}, y-y_{o}\right)=h\left(x_{o}, y_{o}\right) \delta\left(x-x_{o}, y-y_{o}\right)\)
梳状函数
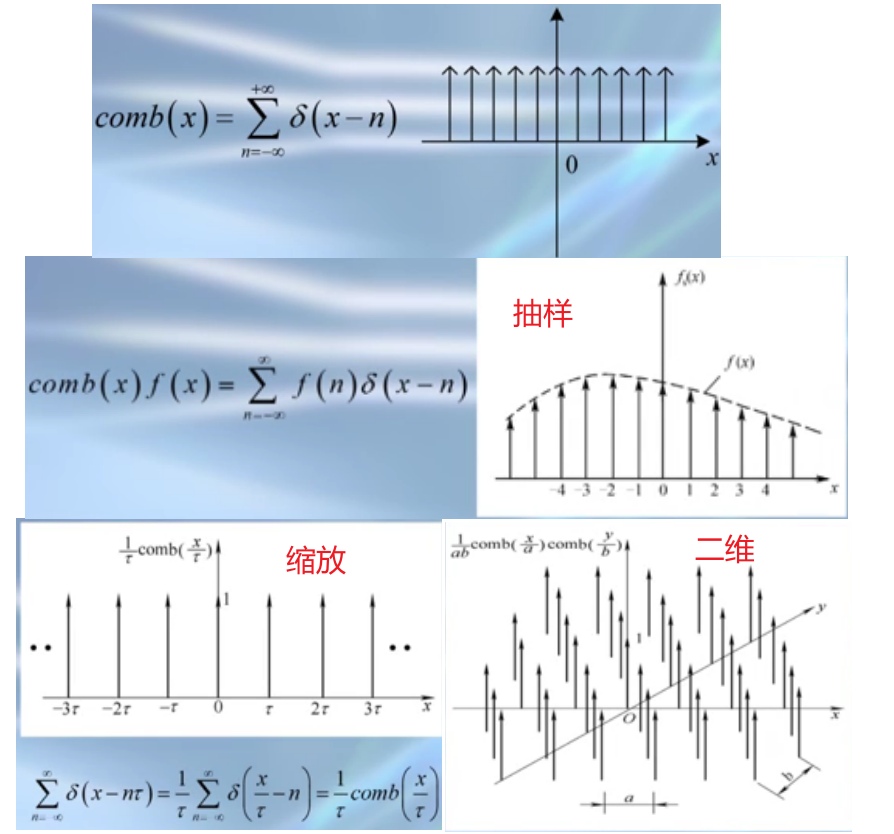
- 多个delta函数的组合构成，沿x轴分布的间隔为1的无穷多个脉冲函数的集合；
- 抽样能力；
- 缩放性质；
- 二维梳状函数，表示点光源阵列、小孔的阵列，在光学系统中经常用到。
常用函数的运算与变换
卷积
卷积的定义：\( *\)表示卷积运算$$ \begin{aligned} g(x, y) &=\iint_{-\infty} f(\xi, \eta) h(x-\xi, y-\eta) d \xi d \eta \\ &=f(x, y) * h(x, y) \end{aligned} $$一维函数的卷积$$ f(x) * h(x)=\int_{-\infty}^{\infty} f(\tau) h(x-\tau) d \tau $$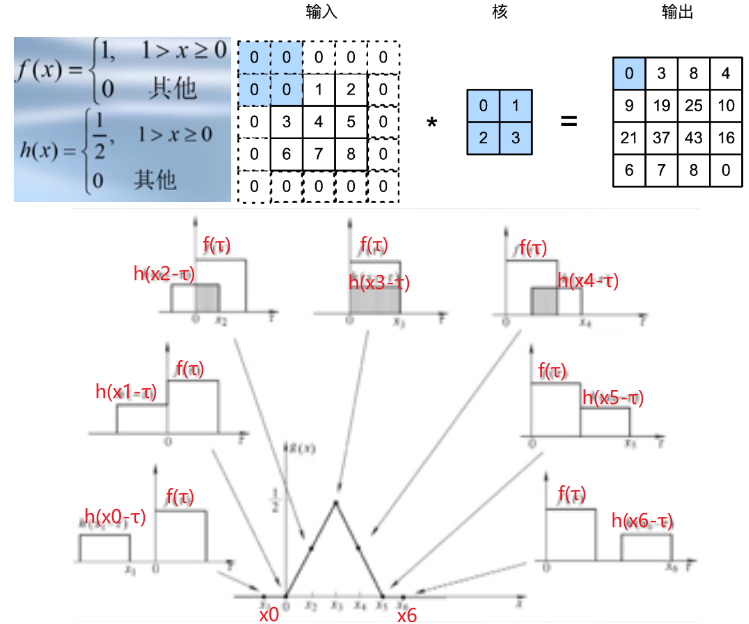
- 按照定义的公式，首先对\( h(\tau)\)进行折叠，也就是取负号，然后进行平移\(x_0\)；
- 两个函数相乘；
- 取积分求面积，面积的值即为在\(x_0\)处卷积的函数值。
- 卷积有展宽的效果，上图中三角形的宽度是两个长方形宽度之和。
- 卷积有平滑的效果。
- 卷积的性质：
- 交换律\(f(x) * h(x)=h(x) * f(x)\)
- 结合律 \([f(x) * g(x)] * h(x)=f(x) *[g(x) * h(x)]\)
- 分配律 \( [a \cdot f(x)+b \cdot g(x)] * h(x) =a \cdot[f(x) * h(x)]+b \cdot[g(x) * h(x)] \)
- 平移不变性 \(g\left(x-x_{0}\right)=f(x) * h\left(x-x_{0}\right)\)
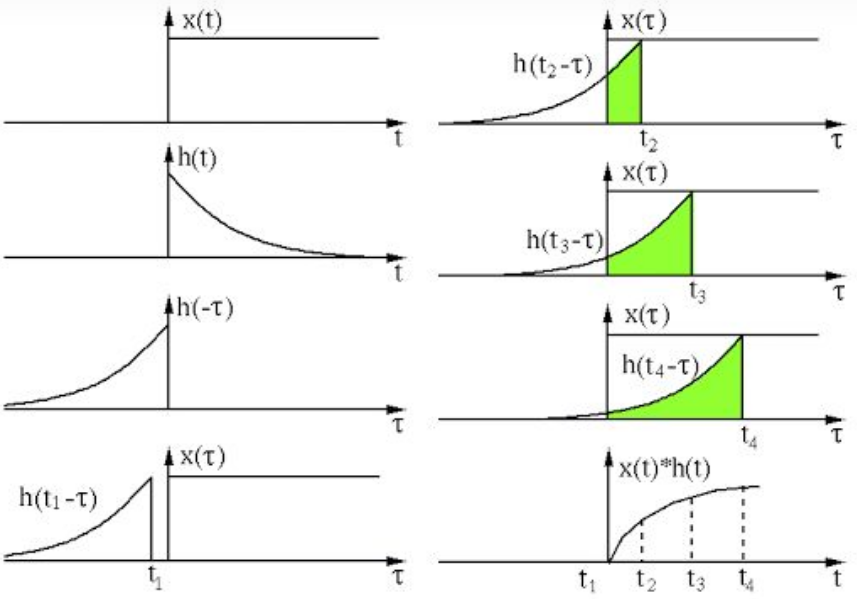
参考资料：
(1) 什么是卷积(convolution)—知乎
相关
相关的定义：\(\star\)表示相关运算，表征的是两个函数的相似程度$$ f(x) \star g(x)=\iint_{-\infty} f(\xi, \eta) g^{*}(\xi-x, \eta-y) d \xi d \eta $$
相关和卷积的对比
空间域的傅里叶变换
光波、光线和成像
基本概念
- 几何光学：
- 定义：撇开光的波动本性，仅以光的直线传播、反射/折射定律为基础，研究光在透明介质中的传播问题。
- 适用范围：
- 光学系统的尺度远大于光波的波长 （n的均匀范围远大波长）；
- 介质是各向同性的 （n是各向同性的）；
- 光强不是很大（n与光强无关）；
- 特点：原理简单、计算复杂，计算软件（追迹）的发展替代了复杂的计算。
- 【光源】从物理学的观点看，任何发光的物体都可以叫作光源。在应用光学中，把凡是发出光线的物体，不论它本身发出光线或是因为被照明而发出光线，都称为光源。
- 【发光点】如果某光源可看成几何学上的点，它只占用空间位置而无体积和线度，则称之为发光点或点光源。
- 【光线】光线是表示光能传播方向的几何线。
- 【光束】有一定关系的一些光线的集合。
- 【光波波面】光是一种电磁波。某一时刻其振动相位相同的点所构成的面称光波波面。在各向同性介质中，光沿光波波面法线方向传播，可以认为光波波面的发现就是应用光学中的光线，与波面对应的法线束就是光束。
- 【光线模型】如果光波波长与光学系统口径相比小到可以忽略，则可以抽象出应用光学中广泛使用的光线模型。
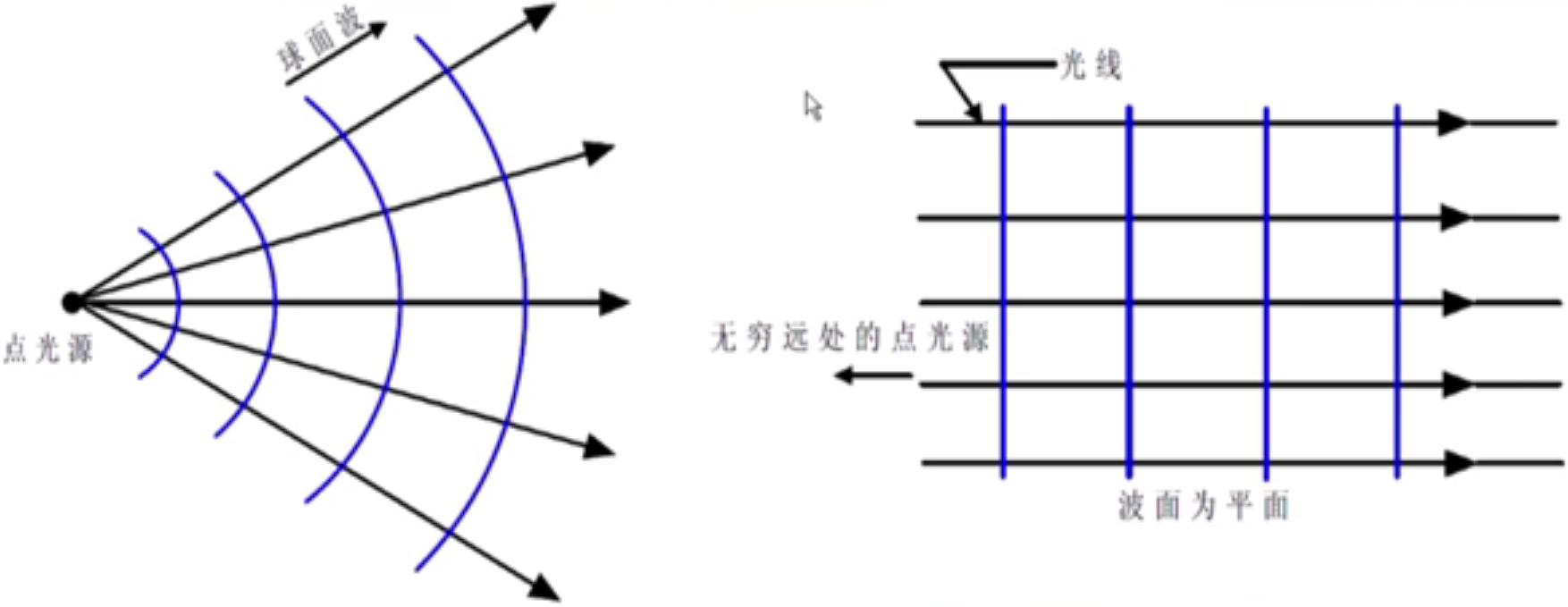
- 【应用光学近似】\(\lambda=0\)，那么在衍射方程\(d \sin \theta=m \lambda\)中，可以推出\(\theta=0\)，即光沿原方向(发生折射或反射的方向)传播。
光线传播基本定律
- 直线传播：光在均匀介质中沿直线传播。
- 独立传播：光线以不同方向通过某点时，彼此互不影响，各光线独立传播。
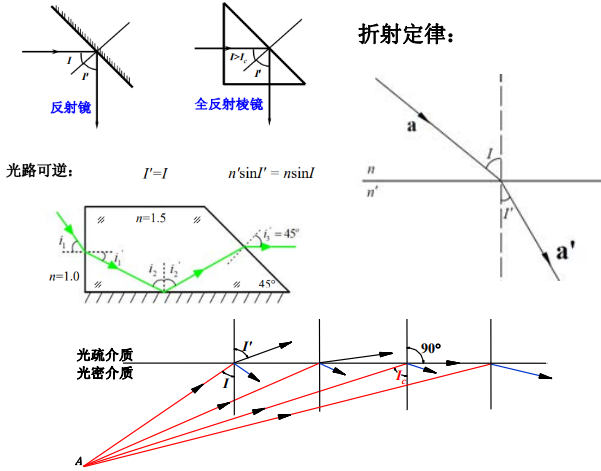
- 反射定律：
- 入射光线、法线和反射光线在同一平面内；
- 入射光线和反射光线在法线的两侧；
- 反射角等于入射角。
- 折射定律：
- 入射光线、法线和折射光线在同一平面内；
- 入射光线和折射光线在法线的两侧；
- 入射角与折射角的正弦之比与入射角无关，是一个与介质以及光的波长有关的常数。
- 全反射：
- 从光密介质入射向光疏介质，且入射角增大到某一程度时，折射角达到90度，折射光线沿界面略射出去，此时的入射角称为临界角；
- 若入射角继续增大到某一程度，入射角大于临界角，则光线不能折射进入第二种介质，而全反射回到第一种介质，即发生了全反射。
- Snell定律：反射定律和折射定律统称为Snell定律，在\(n^{\prime}=-n \)时，折射定律可以推导出反射定律。
思考：在界面上发生折射和反射，入射能量分配到反射光线和折射光线。光路可逆，能量分配如何？体现可逆？
拓展资料：
(1) 麦克斯韦鱼眼透镜的秘密-原理
(2) 龙伯透镜-知乎
费马原理(Fermat's principle)
费马原理最开始描述为"最短时间原理"，即光程最短，光线传播的时间最短，但是人们后来发现费马原理是可以扩充的，大多数时候时间是最短的，但是也有些时候光传播的时间是最长的。因此，现在描述为
(1) 光传播的路径是光程取极值的路径，这个极值可能是最大值、最小值，甚至是函数的拐点；
(2) 光传播的时间是稳定的，附近路径中，光传播的时间可能是最短、也可能最长、也可能不变。
(3) 费马原理更正确的版本应是“平稳时间原理”,光线沿光程为平稳值的路径传播，即\(\displaystyle\int_{Q}^{P} n(\boldsymbol{r}) \mathrm{d} s \)为平稳值。
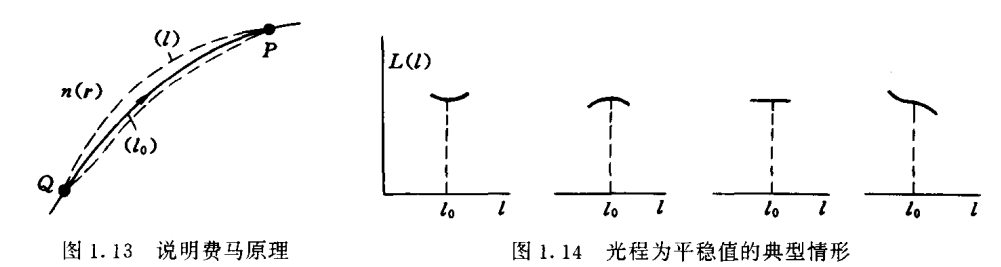
- 如果光在所有路径中，传播时间都相等，就会出现成像，比如椭圆某个焦点发出的光，经过椭圆反射后都会汇聚在另一个焦点，这实际上就是成像，凸透镜成像也是这样的特点；
- 费马原理可以导出几何光学的三个实验定律(直线传播、反射、折射)，是理论上的最高概括；
- 基于三实验定律推演的其他结论，同样可以从费马原理角度出发来研究；
- 最小作用量原理从光学上看就是费马原理；
- 最小作用量原理从电阻串并联的角度看，实际电流分布总是使总功率最小。
费马原理的不同情况
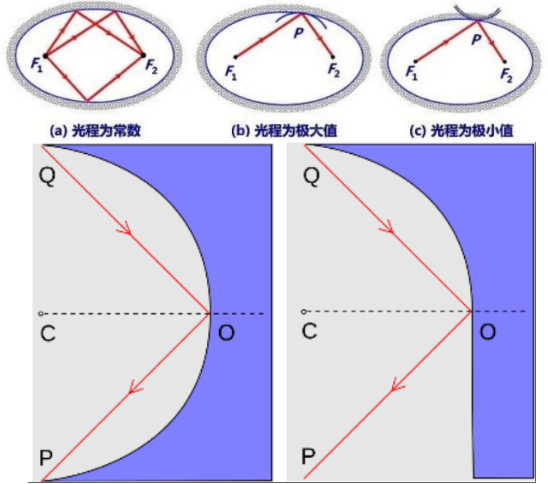
- 平面镜：任意两点的反射路径光程是最小值。
- 椭圆形镜子(内表面反射)：其两个焦点的光线反射路径不是唯一的，光程都一样，是最大值，也是最小值。
- 与椭圆内表面相切的凹面镜反射，自一焦点发出的光—光程取极大值。
- 与椭圆内表面相切的凸面镜反射，自一焦点发出的光—光程取极小值。
- 半圆形镜子：其两个端点Q、P的反射路径光程是最大值。
- 对于由四分之一圆形镜与平面镜组合而成的镜子，同样这两个点Q、P的反射路径的光程是拐值。
- 凸透镜：等光程的。
从 Hamilton's principle的角度看费马原理：\(\displaystyle\int_{Q}^{P} n(\boldsymbol{r}) \mathrm{d} s \)为平稳值的数学表达为$$\delta \int_{Q}^{P} n(\boldsymbol{r}) \mathrm{d} s=0$$其中\(\delta\)为变分算符。\( n(\boldsymbol{r})\)为路径上任意点\((x,y,z)\)的法向折射率(normal refractive index)，其实就是一个简单的标量场(scalar field)，基于此我们可以定义光学拉格朗日量(optical Lagrangian)为$$L(x, y, z, \dot{x}, \dot{y}, \dot{z})=n(x, y, z) \sqrt{\dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2}}$$将路径上的点都写为关于\(z\)的参数方程，于是光学拉格朗日可以改写为$$ L(x(z), y(z), \dot{x}(z), \dot{y}(z), z)=n(x, y, z) \sqrt{1+\dot{x}^{2}+\dot{y}^{2}} $$这样费马原理就变成了$$ \delta S=\delta \int_{A}^{B} L(x(z), y(z), \dot{x}(z), \dot{y}(z), z) d z=0 $$
后面补充
参考资料：
(1) 光为啥沿直线传播？最小作用量又是什么？李永乐老师带你了解“民科王”费马的贡献
(2) 最小作用量原理与物理之美2——费马原理-physixfan
成像
【像】：从物体发出的光线经平面镜、球面镜、透镜、棱镜等反射或折射后所形成的与原物相似的图景。分为实像和虚像。
成像三种说法：波面、光线、等光程。
【光程】：
- 光程就是光在介质中走过一段几何路程所需的时间内光在真空中所走的路程，简言之，光程是等效真空程。
- 点物成点像就是物点与像点之间的光程无论沿哪条实际路径都相等。(由费马原理导出)
- 费马原理：光从空间一点传播到另一点是沿着光程为极值的路径传播的。物点和像点之间连续分布着无穷多条实际的路径。根据费马原理，它们的光程都应取极值，这些连续分布的实际路径的光程都取极大值或极小值是不可能的，唯一的可能是取恒定值，即它们的光程相等。
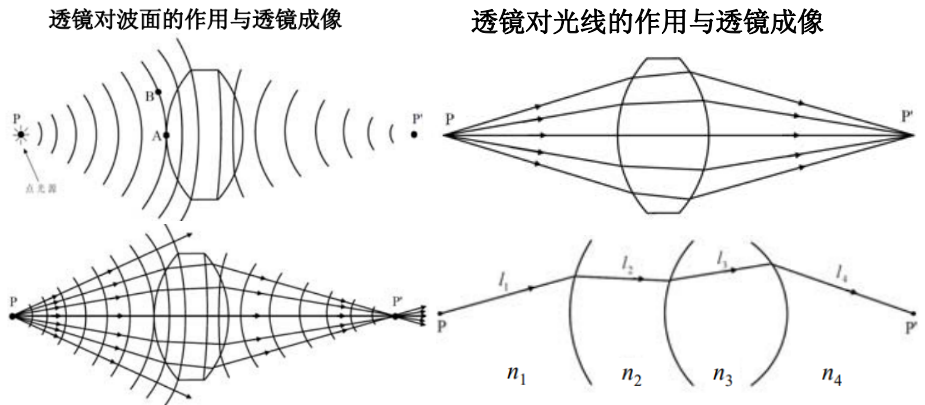从\(P\)到\(P^\prime\)的光程 = 路程*折射率的加和\(\displaystyle\sum_{i=1}^{m} n_{i} l_{i}\)或\(\displaystyle\int_{\mathrm{P}}^{\mathrm{P}^{\prime}} n d l\)，经历的时间(其中\(v_{i}=c / n_{i}\))$$ t=\frac{l_{1}}{\mathrm{v}_{1}}+\frac{l_{2}}{\mathrm{v}_{2}}+\cdots+\frac{l_{m}}{\mathrm{v}_{m}}=\sum_{i=1}^{m} \frac{l_{i}}{\mathrm{v}_{i}} $$
物点和像点之间连续分布着无穷多条实际的光线路径。根据费马原理，它们的光程都应取极值，这些连续分布的实际光线的光程都取极大值或极小值是不可能的，唯一的可能是取恒定值，即它们的光程相等。
【马吕斯定律马吕斯定律】：垂直于波面的光线束（法线集合）经过任意多次反射和折射后，无论折射面和反射面形状如何，出射光束仍垂直于出射波面，保持光线束仍为法线集合的性质。并且入射波面与出射波面对应点之间的光程均为定值。
光线束在各向同性介质的传播过程中，始终保持着与波面的正交性。
光学系统成像
Gaussian optics
1841年，高斯根据近轴近似系统地阐述了几何光学成像理论，其结果就是以其命名的高斯光学(也叫一阶或近轴光学)。高斯光学适用于任何结构的光学系统，但所研究的光线必须满足近轴条件。所谓近轴条件，指的是光线与系统光轴的夹角\(\alpha\)的正弦值可用角值(弧度)代替，即 \(\sin \alpha \approx \tan \alpha \approx \alpha\) ，\( \cos \alpha \approx 1\) 。为便于一般地了解光学系统的成像性质和规律，在研究近轴区成像规律的基础上建立了理想光学系统的光学模型。模型完全撇开具体的光学系统结构，仅以几对基本点的位置及一对基本量的大小来表征。根据基本点的性质能方便地导出成像公式，从而可了解任意位置的物体被此模型成像时，像的位置、大小、正倒和虚实等各种成像特性和规律。反过来也可根据成像要求得出相应的光学模型。任何具体的光学系统都能与一个等效模型相对应，对于不同的系统，模型的差别仅在于基本点位置和焦距大小有所不同而已。高斯光学的理论是进行光学系统的整体分析和计算有关光学参量的必要基础，计算结果(像的大小、成像位置等)接近于实际值。虽然只描述近轴区的成像性质，但在衡量非近轴区的成像状况和质量方面也是必不可少的。特别是在光学系统初步设计阶段，高斯光学的理论和有关计算公式有重要的实用意义。
薄透镜公式的高斯形式
圆锥曲线的光学性质
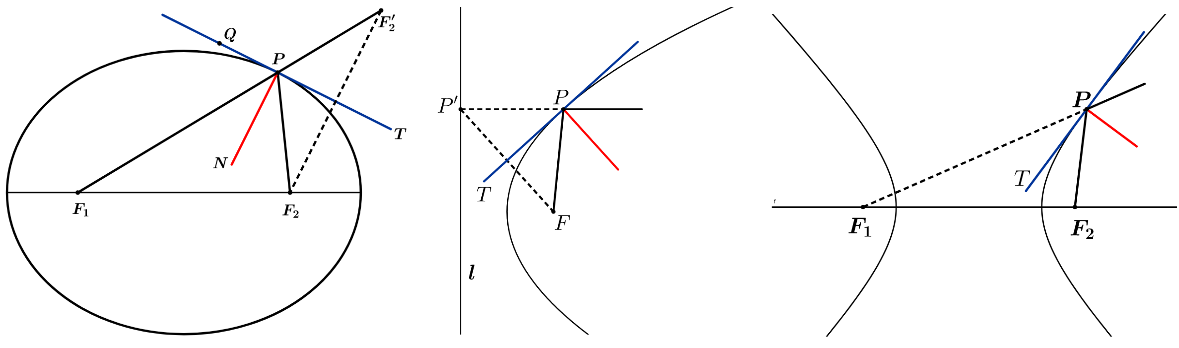
椭圆：\(F_1 ， F_2\)是椭圆的两个焦点，\(P\)是椭圆上任意一点，则\(\angle F_1 P F_2\)的补角平分线\(P T\)是椭圆的切线。
等价命题：真空或同种均匀介质中，从椭圆一个焦点处射出的光线经过在椭圆曲线上的反射后，反射光线都汇聚于另一个焦点。
抛物线：\(F\)是抛物线的焦点，\(l\)是准线，\(P\)是抛物线上的任意一点，作\(P P^{\prime}\perp l\)，垂足为\(P^{\prime}\)，则\(\angle F P P^{\prime}\)的角平分线\(PT\)是抛物线的切线。
等价命题：真空或同种均匀介质中，从抛物线焦点射出的光线，经过抛物线曲线的反射后，反射光线平行于抛物线对称轴。
双曲线：\(F_1 ， F_2\)是双曲线的两个焦点，\(P\)是双曲线上的任意一点，则\(\angle F_1 P F_2\)的角平分线\(P T\)是双曲线的切线。
等价命题：真空或同种均匀介质中，从双曲线一个焦点射出的光线，经过双曲线的反射后，反射光的反向延长线汇聚于另一个焦点。
参考资料：
(1) 透镜成像模型-CSDN
(2) 薄透镜公式应用：从高斯光学到高斯光束
(3) 光学系统像差杂谈（4）：近轴光学
偏振光的分类
线偏振
参考资料：
(1) 偏振—邵晓鹏专栏