钟锡华的《现代光学基础》第二版[mathjax] 参考1 参考2 图床：Optics-img/
费马原理与变折射率光学
惠更斯原理
原理描述和特点：
- 波前上的每一点都是次波源
- 下一时刻的波前是次波是这些大量次波面的公共切面(包络面)
- 次波中心与其次波面上的那个切点的连线方向给出了该处光传播方向
- 适用于一切波场(光波、水波、声波等)
从一个波前到另一个波前，波前上各点消耗的时间是相同的。于是可以导出折射定律$$\frac{\sin i_{1}}{\sin i_{2}}=\frac{v_{1}}{v_{2}}=\mathrm{const}$$牛顿当时认为光是一种粒子，从空气向其他介质传播时，其他介质会对光粒子产生垂直方向的引力，而光水平速度分量不变，于是根据简单的矢量关系可以得到\(\frac{\sin i_{1}}{\sin i_{2}}=\frac{v_{2}}{v_{1}}=\mathrm{const} \)，这个结论和波动说的结论正好倒过来了，1850年实验比较了光在空气和水中的速度，证实了波动说折射公式的正确性。
折射率表达式定义$$\frac{\sin i_{1}}{\sin i_{2}}=n_{12}=\frac{n_{2}}{n_{1}}$$色散：相同介质对不同波长的光的折射率不同，波长越短，折射率越小。色散越强，越容易看到七色光，可用此种方法简单鉴定水晶(色散显著强于玻璃或有机玻璃)。
折射率和传播速度：\( \frac{\sin i_{1}}{\sin i_{2}}=\frac{v_{1}}{v_{2}}, \quad \frac{\sin i_{1}}{\sin i_{2}}=\frac{n_{2}}{n_{1}} \)，折射率为\( n\)的介质的传播速度\(v=\frac{c}{n} \)
注：
1. 光在水中频率不变，波长变短，但是人眼在水中看到的颜色是不变的。
2. 我们说频率不变是针对线性均匀介质，不涉及非线性效应。
光程
定义：光线路径的几何长度所经过的介质折射率的乘积，被定义为光程(optical path). 这一点是我以前不太考虑的。
通用表达式：\( L(Q P)=\int_{Q}^{P} n(\boldsymbol{r}) \mathrm{d} s \).
光程与相位差：\( \varphi(P)-\varphi(Q)=-\frac{2 \pi}{\lambda_{0}} L(Q P) \)，特别注意这个对应关系。
光程与时差：\( t_{P}-t_{Q}=\frac{1}{c} L(Q P) \)，可改写为\( L(Q P)=c\left(t_{P}-t_{Q}\right) \)
反射光束、折射光束的等光程性：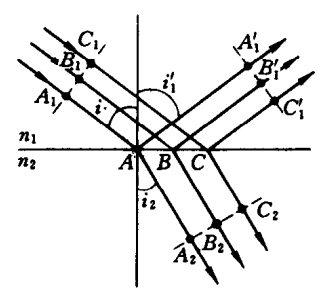
$$L\left(A_{1} A A_{1}^{\prime}\right)=L\left(B_{1} B B_{1}^{\prime}\right)=L\left(C_{1} C C_{1}^{\prime}\right)$$ $$L\left(A_{1} A A_{2}\right)=L\left(B_{1} B B_{2}\right)=L\left(C_{1} C C_{2}\right)$$
费马原理
表述：光线沿光程为平稳值的路径传播，即\( \int_{Q}^{P} n(\boldsymbol{r}) \mathrm{d} s\)为平稳值。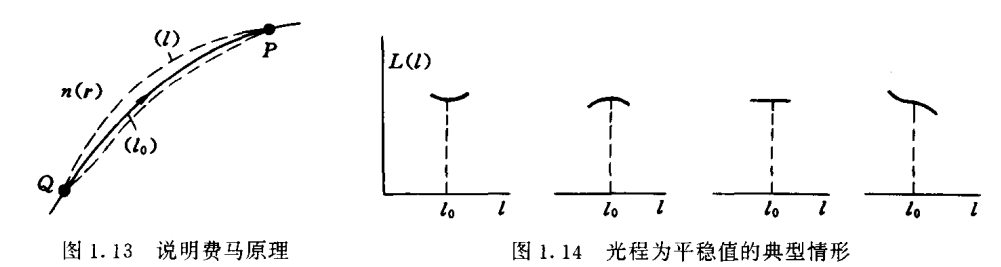
数学表达式：\(\delta \int_{Q}^{P} n(\boldsymbol{r}) \mathrm{d} s=0 \)或\(\delta L(l)=0 \)，其中\( \delta\)为变分算符。
导出反射定律：显然，欧式几何，直线最短，很容易推出。
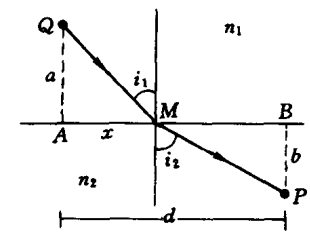
导出折射定律：\( \begin{aligned} L(Q M P) &=n_{1} \overline{Q M}+n_{2} \overline{M P} \\ &=n_{1} \sqrt{a^{2}+x^{2}}+n_{2} \sqrt{b^{2}+(d-x)^{2}}=L(x) \end{aligned}\)，利用其变分为零\(\frac{\mathrm{d} L(x)}{\mathrm{d} x}=0 \)即可导出折射定律。
注：
1. 费马原理可以导出几何光学的三个实验定律(直线传播、反射、折射)，是理论上的最高概括。
2. 基于三实验定律推演的其他结论，同样可以从费马原理角度出发来研究。
费马原理与成像
物像等光程性：有两种证明方法，一是利用反证法，所以所有光线的光程都相等，否则不满足费马原理；另一种是利用两个等相面，然后两个等相面之间的存在光程和相位差之间的对应关系。因此有$$L\left(Q M_{1} N_{1} Q^{\prime}\right)=L\left(Q M_{2} N_{2} Q^{\prime}\right)=\cdots=L\left(Q M_{i} N_{i} Q^{\prime}\right)$$对右图来说，成的是虚像，有$$L\left(Q M_{1} N_{1}\right)-L\left(N_{1} Q^{\prime}\right)=L\left(Q M_{2} N_{2}\right)-L\left(N_{2} Q^{\prime}\right)=\cdots=L\left(Q M_{i} N_{i}\right)-L\left(N_{i} Q^{\prime}\right)$$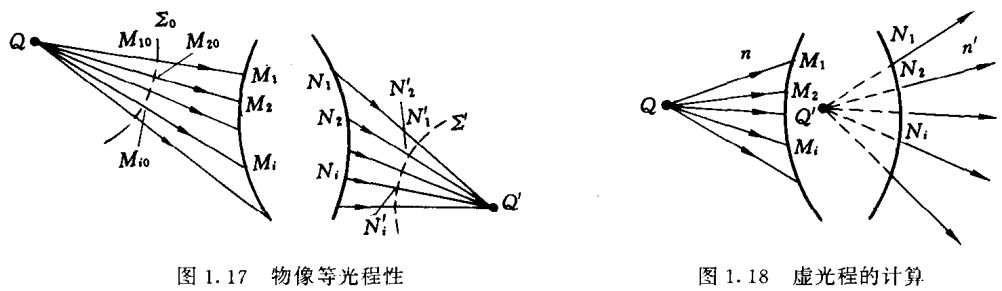
光程和成像：
严格成像 = 严格等光程 近似等光程 = 近似成像 不等光程 = 不成像
注：
1. 理想光学系统—将光学系统在近轴区域成完善像的理论推广到任意大的空间，以任意宽的光束都能成完善像的光学系统称为理想光学系统。
2. 共轭—在理想光学系统中，任何一个物点发出的光纤在系统的作用下所有的出射光线仍然相交于一点。由光路的可逆性和折射、反射定律中光线方向的确定性，可以得出每一个物点对应于唯一的一个像点。通常将这种物像关系叫作“共轭”。
3. 虚光程取负值。
齐明点参考https://blog.csdn.net/liyuanbhu/article/details/78827655
https://zhuanlan.zhihu.com/p/26635624
自然变折射率
人工变折射率 强光变折射率
阶跃型光纤：数值孔径(比\(\theta_{0} \)角度大的光不能全反射)\( \mathrm{N} . \mathrm{A} .=n_{0} \sin \theta_{0}=\sqrt{n_{1}^{2}-n_{2}^{2}}\)
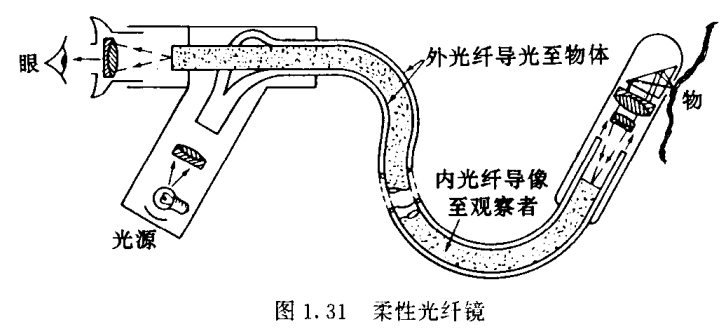
梯度型光纤—聚光纤维：折射率抛物线型函数。微透镜可以组成阵列，用于集成光学。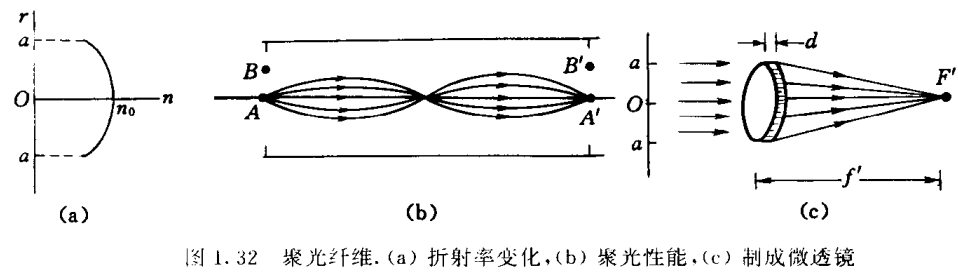
自聚焦与自散焦：超强光在光纤中传播，会有非线性效应，折射率从中间到两侧会发生连续变化。根据介质材料，可分为两类，中间折射率最大或者最小，别人对应自聚焦和自散焦。
光线方程
评述费马原理
波动光学引论
像差
https://www.google.com/search?q=different+aberration&tbm=isch&ved=2ahUKEwjCkoShqbn3AhXrvKQKHSxGALUQ2-cCegQIABAA&oq=different+aberration&gs_lcp=CgNpbWcQAzIGCAAQBxAeMgYIABAIEB4yBggAEAgQHjIGCAAQCBAeOgcIIxDvAxAnOgQIABBDOgUIABCABDoICAAQCBAHEB5QjApYgxlgmRtoAHAAeAGAAXCIAakFkgEDOC4ymAEAoAEBqgELZ3dzLXdpei1pbWfAAQE&sclient=img&ei=neBrYoLQNev5kgWsjIGoCw&bih=722&biw=1536#imgrc=dn4CYSV2aTo5UM
色差(色散)
球差