梯度、散度、旋度、Jacobian、Hessian、Laplacian 的关系图

标量场和矢量场和积分的关系，上面的标量

标量场就是每一点(无论是二维还是三维空间)对应的函数值(比如温度，海拔，湿度)只有大小，没有方向；而矢量场，就是每一点对应的函数(比如温度梯度，湿度梯度，海拔梯度，磁场，电场)既包含数值的大小，又包含方向，当然也是二维/三维均可。对于矢量场，具体来讲，矢量场任意一点的方向，就是对标量场函数值大小变化最快的方向，比如温度梯度变化最快的方向，每一点矢量的模长就是表征标量场函数值变化的速率。 

标量场的梯度就是向量场。标量场比如\(f(x, y)=2 x+3 y^{2}\)，知道\((x, y)\)坐标，就知道每一点对应的函数值(比如海拔)。

矢量场和标量场是互为求偏倒数和积分的关系，上面的标量场求偏导数可以得到矢量场\({ f }_{ x }=2\)，\({ f }_{ y }=6y\)，可以写成$$\operatorname{grad}f(x, y)=\nabla f(x, y)=2 \vec{i}+6 y \vec{j}$$这样矢量场每一点的大小和方向就都知道了。由向量场通过求梯度得到了矢量场，同样地，通常情况下，每个向量场通过积分也可以得到对应的梯度场(必须知道特定点的数值也来确定积分的常数项取值)。

向量微分算子\(\nabla\)

\( \nabla\)叫作Nabla算子/Del算子/向量微分算子。定义为：\(  \nabla=\displaystyle\frac{d}{d r}\)。以三维举例，可以写成$$  \nabla=\frac{\partial}{\partial x} \mathbf{i}+\frac{\partial}{\partial y} \mathbf{j}+\frac{\partial}{\partial z} \mathbf{k}$$

\( \nabla\) 作用于不同类型的量，得到的就是不同类型的新量：

• \( \nabla\) 直接作用于函数\(F(r)\)(不论\(F(r)\)是标量还是向量)，意味着求\(F(r)\)的【梯度】(Gradient)，表示为\(\nabla F(r)\)，(标量函数的梯度为向量，向量的梯度为二阶张量……)
• \( \nabla\)与非标量函数\(  \mathbf{F(r)}\)由点积符号·连接，意味着求\(\mathbf{F(r)}  \)的【散度】(Divergence)，表示为\(\nabla \cdot \mathbf{F(r)}\)
• \( \nabla\)与非标量(三维)函数\(\mathbf{F(r)}\)由叉积符号\(\times\)连接，意味着求\( \mathbf{F(r)} \)的【旋度】(Curl)，表示为\(\nabla \times \mathbf{F(r)}\)

向量算子是指向量分析中使用的微分算子。向量算子使用Nabla算符定义，包括梯度、散度和旋度。$$\begin{aligned} &\text { grad } \equiv \nabla\\ &\text { div } \equiv \nabla \cdot\\ &\text { curl } \equiv \nabla \times \end{aligned}$$

散度—高斯散度定理

对于一个连续可微的三维向量场，可以写成\(\mathbf{F}=F_{x} \mathbf{i}+F_{y} \mathbf{j}+F_{z} \mathbf{k}\)，它的散度可以表示为一个标量函数

$$\operatorname{div} \mathbf{F}=\nabla \cdot \mathbf{F}=\left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right) \cdot\left(F_{x}, F_{y}, F_{z}\right)=\frac{\partial F_{x}}{\partial x}+\frac{\partial F_{y}}{\partial y}+\frac{\partial F_{z}}{\partial z}$$其实按照下面的写法更容易理解，我们按照前面的算符的定义进行计算$$\nabla \cdot \mathbf{F}=\left(\frac{\partial}{\partial x}\mathbf{i}+ \frac{\partial}{\partial y}\mathbf{j}+ \frac{\partial}{\partial z}\mathbf{k}\right) \cdot(F_{x} \mathbf{i}+F_{y} \mathbf{j}+F_{z} \mathbf{k})=\frac{\partial F_{x}}{\partial x}+\frac{\partial F_{y}}{\partial y}+\frac{\partial F_{z}}{\partial z}$$

对于这个向量场来说，空间中每一点的邻域空间上，向量场在这个空间的通量(向量场对曲面积分的值)除以这个邻域空间的体积大小(当这个邻域空间大小收敛到0时)得到的数值就是该处的散度。
$$\left.\operatorname{div} \mathbf{F}\right|_{\mathbf{x}_{0}}=\lim _{V \rightarrow 0} \frac{1}{|V|} {\large\bigcirc}\kern-1.55em\iint_{S(V)} \mathbf{F} \cdot \hat{\mathbf{n}} d S$$其中\(  \hat{\mathbf{n}}\)是微元面积的法线方向。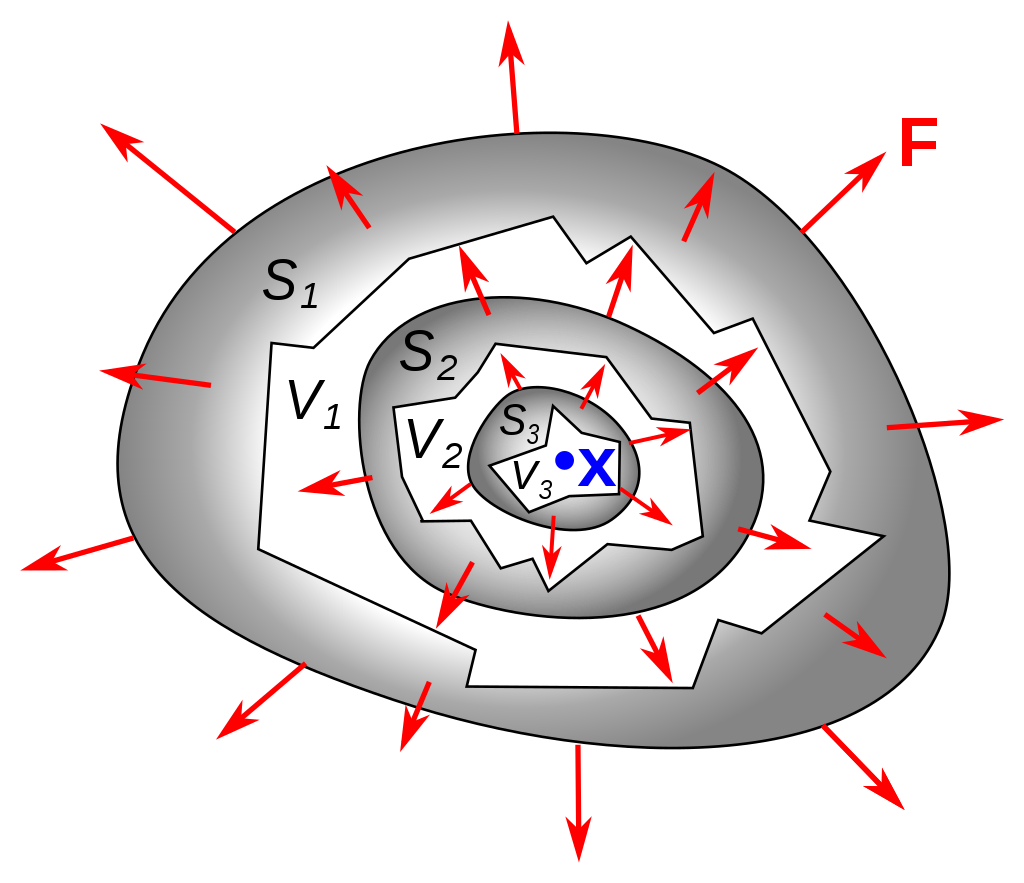

高斯散度定理：$$ \iiint_{\Omega} \nabla \cdot\mathbf{F} d v={\large\bigcirc}\kern-1.55em\iint_{\Sigma} \mathbf{F} \cdot \mathbf{n} d S $$其中\(\Sigma\)是空间闭区域\(\Omega\)的边界曲面，而\(\mathbf{n}\)是曲面\(\Sigma\)上的朝外的单位法向量，\(\mathbf{n} d S=\mathbf{n}d\mathbf{S}\)。

旋度—斯托克斯定理

【环量】(circulation)$$\operatorname{Circ}_{\mathbf{F}}(\Gamma)=\oint_{\Gamma} \mathbf{F} \cdot \mathrm{d} \boldsymbol{l}$$可以看到等式右边的积分项是向量场\( \mathbf{F} \)与环路微元向量\( \boldsymbol{l} \)的内积；对比前面的散度的定义，散度的积分项是向量场\( \mathbf{F} \)与面积微元\( \mathrm{d}S \)(方向由其单位法向量\( \hat{\mathbf{n}} \)体现)的内积。

当环量所对应的环路无穷小时，即可得到$$\operatorname{curl} \mathbf{F}(x) \cdot \mathbf{n}=\lim _{\Delta S_{\mathrm{n}} \rightarrow 0} \frac{1}{\left|\Delta S_{\mathrm{n}}\right|} \oint_{\Gamma_{\mathrm{n}}} \mathbf{F} \cdot \mathrm{d} \boldsymbol{l}$$其中\( \operatorname{curl} \mathbf{F}(x) \)为该点的旋度，而\(  \mathbf{n}\)是\(\Delta S_{n}  \)的单位法向量。

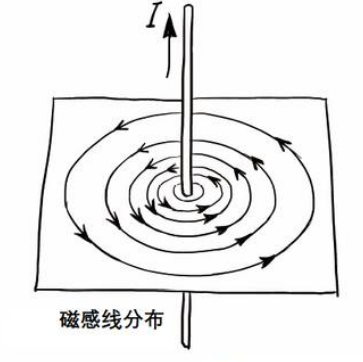旋度与安培环路定律：以稳态的通电长直导线为例，画一个垂直于导线的圆环，而且导线正好过圆环的圆心，而且定义圆环的方向正好为电流产生磁场的方向，如图所示。假设我们选取的圆环的半径大于导线的半径，设半径为\(  R\)，那么圆环上每一个环路微元的方向和磁场的方向正好完全一致。根据毕奥萨伐定律，我们可以知道环路上任意一点的磁场大小为\( B=\displaystyle\frac{\mu_{0} I}{2 \pi R} \)，那么根据安培环路定律\(\displaystyle\oint_{\Gamma}\mathbf{B}\cdot \mathrm{d} \boldsymbol{l}=\displaystyle\frac{\mu_{0} I}{2 \pi R}* 2\pi R=\mu_{0} I\)即为前面提到的“环量”的大小，矢量磁场全部投影到了环路微元方向上。另外，可见环路半径的选取和最终环量的大小无关，实际上都不需要是一个圆环，只要能套住电流，那么按上面的方法计算得到的环量都是\( \mu_{0} I \)。此情形下，环量的方向就是电流方向。点的旋度：当导线无线细，而选取的环路恰好能包住导线，那么这个无穷小的面积微元的点所对应的的\(\mu_{0} I\)就是该点的旋度。对于该通电导线(看截面)，如果圆环半径大于导线半径，那么中间空的那部分面积内所有的面积微元的散度都是零，即没有电流通过，而导线截面上的任意微元都对应一份电流。

旋度的计算：设向量场\(  \mathbf{F}\)为$$\mathbf{F}(x, y, z)=F_{x}(x, y, z) \mathbf{i}+F_{y}(x, y, z) \mathbf{j}+F_{z}(x, y, z) \mathbf{k}$$那么该向量场的旋度为$$\operatorname{curl} \mathbf{F}=\boldsymbol{\nabla} \times \mathbf{F}=\left(\frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z}\right) \mathbf{i}+\left(\frac{\partial F_{x}}{\partial z}-\frac{\partial F_{z}}{\partial x}\right) \mathbf{j}+\left(\frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y}\right) \mathbf{k}$$或者写成$$\operatorname{curl} \mathbf{F}=\left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \displaystyle\frac{\partial}{\partial x} & \displaystyle\frac{\partial}{\partial y} & \displaystyle\frac{\partial}{\partial z} \\ F_{x} & F_{y} & F_{z} \end{array}\right|$$计算方法为$$\nabla \times \mathbf{F}(x, y,z)=\left(\frac{\partial}{\partial x} \mathbf{i}+\frac{\partial}{\partial y} \mathbf{j}+ \frac{\partial}{\partial z} \mathbf{k} \right) \times[F_{x}(x, y, z) \mathbf{i}+F_{y}(x, y, z) \mathbf{j}+F_{z}(x, y, z) \mathbf{k}]$$

我们上面讨论的通电导线的例子，其实是\( \left(\displaystyle\frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z}\right) \mathbf{i}+\left(\displaystyle\frac{\partial F_{x}}{\partial z}-\frac{\partial F_{z}}{\partial x}\right) \mathbf{j} \)为零的特殊情况，因为向量场在\( z \)方向没有分量，而且向量场对\( z \)求导结果也不变，所以也就简化出二维平面\(\mathbf{F}\)力场的旋度计算公式$$\operatorname{curl} \mathbf{F}=\boldsymbol{\nabla} \times \mathbf{F}(x,y)=\left(\frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y}\right) \mathbf{k}$$

斯托克斯定理：(\(\mathbb{R}^3\)空间上，向量场的旋度的曲面积分跟向量场在曲面边界上的线积分之间建立联系)$$ \iint_S \nabla \times \mathbf{F} \cdot d \mathbf{S}=\oint_{\partial S} \mathbf{F} \cdot d \mathbf{r} $$

格林公式—斯托克斯定理二维特例

设闭区域\(D\)由分段光滑的简单曲线\(L\)围成，函数\(P(x,y)\)及\(Q(x,y)\)在\(D\)上有一阶连续偏导数，则有$$\iint_{D}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \mathrm{d} x \mathrm{d} y=\oint_{L^{+}}(P \mathrm{d} x+Q \mathrm{d} y)$$其中\(L^{+}\)是\(D\)取正向边界曲线，也就是说你沿着该边界走，区域\(D\)总是在你的左手边。

理解格林公式最重要的是借用物理图像：力场在面上的旋度的积分 = 力场在边界线上的积分

假设二维平面上的力场\(\mathbf{F} (x,y) =F_x\mathbf{i}+F_y\mathbf{j} = P(x,y)\mathbf{i}+Q(x,y)\mathbf{j} \)

结合上面二维平面\(\mathbf{F}\)力场的旋度，以及斯托克斯定理有$$\iint_{D} \nabla \times \mathbf{F}(x, y) \cdot d \mathbf{s}=\oint_{L^+} \mathbf{F}(x, y) \cdot d \mathbf{r} \Leftrightarrow \iint_{D}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y=\iint_{L^+} P d x+Q d y$$等式左侧是将每一个单位面积微元的旋度加和，因为面积微元的法向量方向和旋度的方向完全一致；格林公式右侧部分用做功的形式来描述(二维力的向量场)。

参考资料：
(1) 如何通俗地理解格林公式?—知乎
(2) 格林公式的意义：边界的做功＝微分矩形做功之和—马同学
(3) 矢量分析—电动力学笔记

拉普拉斯算符，拉普拉斯方程和泊松方程

Laplace拉普拉斯，Poisson泊松。\(\Delta 、\nabla ^{ 2 }、\nabla \cdot \nabla \)都是表示拉普拉斯算符，在笛卡尔坐标系下，二维空间和三维空间分别为$$\Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}\\ \Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}+\frac{\partial^{2} f}{\partial z^{2}}$$拉普拉斯方程，在笛卡尔三维空间下(三个自变量)，可以写成$$\Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}+\frac{\partial^{2} f}{\partial z^{2}}=0$$还可以写成\(\nabla^{2} \varphi=0\)，或者\( div \ grad \varphi=0\)，其中，\(div\)表示矢量场的散度(结果是一个标量场)，\(grad\)表示标量场的梯度(结果是一个矢量场)。具体的应用有待补充和拓展。

拉普拉斯方程\(\nabla^{2} \varphi=0\)具体我们在MIT-微分方程里面也有探讨，等式右边不为零的情况即为泊松方程。

注意算符的运算：$$\nabla ^{ 2 }=\nabla \cdot \nabla=\left(\frac{\partial}{\partial x} \mathbf{i}+\frac{\partial}{\partial y} \mathbf{j}+\frac{\partial}{\partial z} \mathbf{k}\right)\cdot \left(\frac{\partial}{\partial x} \mathbf{i}+\frac{\partial}{\partial y} \mathbf{j}+\frac{\partial}{\partial z} \mathbf{k}\right)=\frac{\partial^{2} }{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2} }{\partial z^{2}}$$