Materials Project
atomly.net
Functional Motif Database

https://new.qq.com/omn/20210203/20210203A0ALMX00.html

https://www.koushare.com/video/videodetail/24306

DFT和第一性原理计算

合金结构稳定性的理论研究：Modeling and Optimization - 杨小宝

高通量：正交试验

狄拉克：人类已经找到了绝大部分物理学和全部化学领域所需要的数学工具，但是很多过于复杂而无法用含有几个摩尔数量级的偏微分方程组得到精确解。这个时候我们要解决实际问题的话，在上个世纪60年代Kohn提出了密度泛函理论，现在发展成我们完全不懂量子力学就可以做输入文件的傻瓜式量子化学计算(计算过程是个黑匣子)。

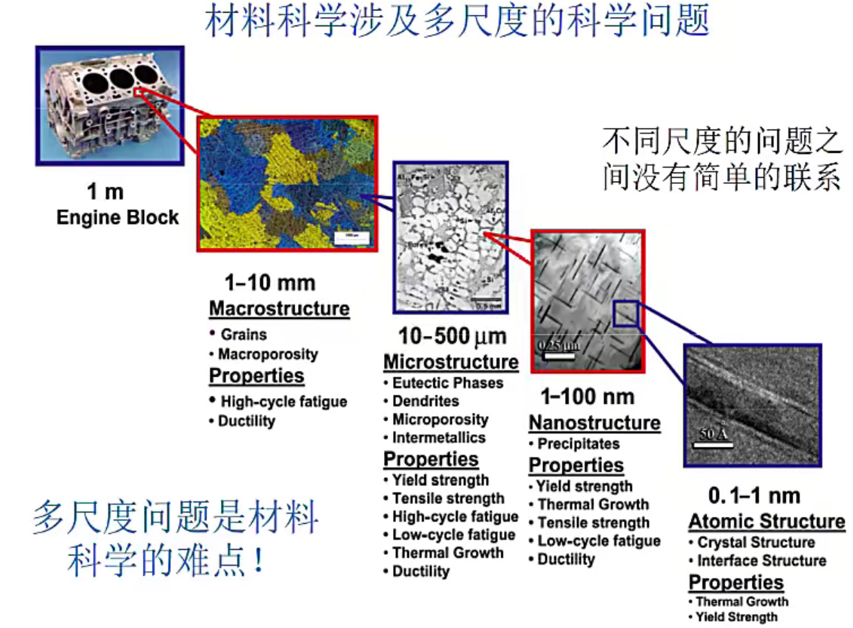
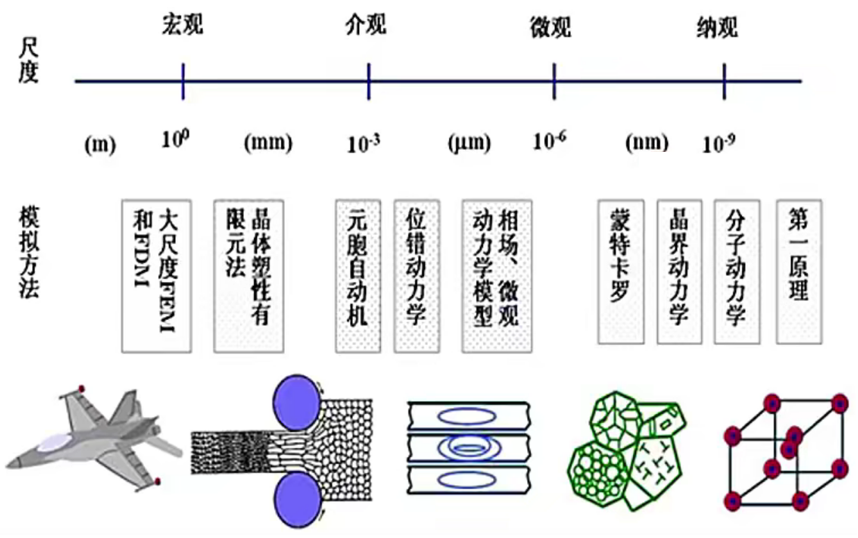
第一性原理计算：所谓第一性原理计算，就是从最基本的量子力学公式出发，不引入或尽量少地引入经验参数，对从原子、分子开始，从头开始计算，所以又称为从头算。通过第一性原理计算，可以较为准确地计算固态、液态、气态等体系中的各种性质，再结合一些实验测量值和理论模拟值，就可以研究关于体系的动力学演化过程。

多体问题：三体也是多体问题，微扰会对系统的平衡和状态产生极大的干扰。多个电子和多个原子的相互作用也是多体问题。CO₂分子中有22个电子，每一个电子由三个坐标决定，所以求解对应的薛定谔方程其实是求解66维的向量，非常复杂。Pt纳米团簇，一个Pt原子包含82个电子，那么100个Pt原子的团簇会有超过8200个电子，乘以三个维度，那么薛定谔方程根本无法求解。

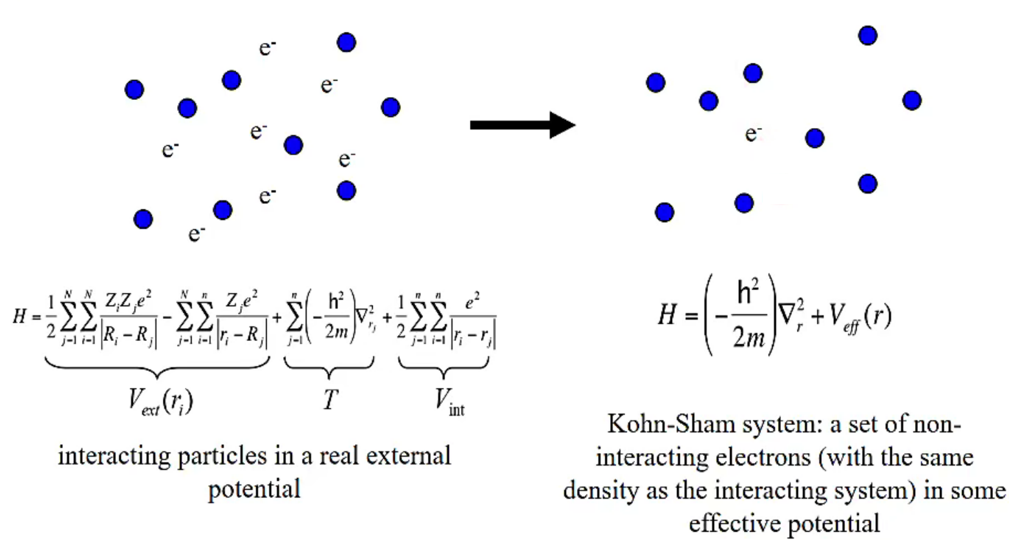
从波函数到电子密度：如果不把电子进行区分，我们得到的实际上是所有参与的电子的分布，这个时候我们可以引入“电子密度”的概念，于是多体的问题变成了一个简单体系的问题，高维求解的方程变成了电子密度在空间分布的问题(三维)，大大降低了维数。在这样的条件下，我们不区分每个电子服从的波函数，而仅仅从参与体系的电子在空间中具有的分布密度函数的求解。

第一性原理的计算，有两种截然不同的发展道路，一个是对每个电子波函数精确求解，即对应的是Hartree-Fock方法，是基于复杂多电子波函数的；另一个道路是密度泛函理论DFT，主要目标是用电子密度取代波函数作为基本的研究量，DFT最普遍的是通过Kohn-Sham方法来实现的。

DFT方法被封装在很多计算软件中，有ABINIT，VASP，CASTEP(Materials Studio里面的一个模块)，Siesta，Quantum Epresso，Wien2K。

DFT第一性原理计算虽然已经降维了，但是考虑到计算精度，体系还是不能过大，另外DFT计算只能模拟O K下的物理性质，但是室温下热起伏对电子密度分布很小，最终物理性质结果影响也很小。如果想研究大尺度或者温度变化的情况，仍然可以用DFT进行第一性原理的计算，因为可以基于第一性原理去开发半经验的势函数，来为更高层级的计算方法，比如分子动力学或者蒙特卡洛方法来开发合理的描述(原子之间相互作用的势能关系式)。

参考资料：
(1) 第一性原理计算在材料科学中的应用
(2) 材料研究中的密度泛函理论和计算方法
(3) 第一性原理计算需要掌握的第一课：DFT的基础理论和发展概述
(4) 材料科学实验人员如何入门第一性原理计算（计算材料学/VASP）
(5) https://www.zybuluo.com/o/note/1127591

材料信息学

AI for Science - 鄂维南

科学研究的基本目的
(1) 寻求基本规律：比如行星运动的三大定律，量子力学的基本方程。
(2) 解决实际问题：比如工程科学、制造行业、材料、航天航空。[mathjax]

研究科学的基本方法——开普勒范式

• 从数据中直接总结出规律并解决实际问题，例如行星运动的第三定律。
• 最成功的的案例：生物信息学(人类基因组工程)。
• 最成功的的工具：统计方法、机器学习、计算方法。

研究科学的基本方法——牛顿范式

• 寻求基本原理并用以解决实际问题。例如行星运动的第三定律可以通过牛顿第二定律以及牛顿的万有引力定律来推导。行星运动规律变成一个数学(微分方程)问题，解微分方程，即可得到新兴运动的第三定律。
• 最成功的的例子：物理学(称为自然科学、工程科学的基础)。
  (1) 牛顿力学(牛顿方程)
  (2) 电力厂理论(麦克斯韦方程组)
  (3) 量子力学(薛定谔方程)
• 把物理问题变成数学问题。
• 最成功的的工具：微分方程。

开普勒模式：高效，但知其然不知其所以然。
牛顿模式：深刻，但难以用来解决实际问题。

量子力学的建立宣告寻求基本原理的任务已经完成

The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble. — Paul Dirac《Quantum mechanics of many-electron systems》

薛定谔方程：\(-\displaystyle\frac{\hbar^{2}}{2 m} \nabla^{2} \psi+V \psi=E \psi\)
(1) 多体(高纬)问题：维数 = 3*粒子的个数；
(2) 对于电子体系，波函数必须是反对称函数。

其他基本原理的例子：

• 空气动力学(欧拉方程)
• 流体力学(纳维-斯托克斯方程)
• 弹性力学(拉梅Lame方程)
• 电磁场问题(麦克斯韦方程)

有效数学方法出现之前，科学家们为解决实际问题，唯一能够做的事情就是简化模型。比方说Thpmas-Fermi密度泛函理论。

第一个时代(50年代到现在)：电子计算机+数值方法

• 差分方法，有限元方法，谱方法等；
• 第一次发规模地实现了直接用基本原理解决实际问题；
• 基本出发点：(分片)多项式可以有效逼近一般函数。

带来的的影响是巨大的

• 结构力学、航空航天、天气预报、石油勘探与开采等等；
• 在工程学科，计算方法已经成为主要工具之一。
• 线代工业和技术赖以生存的基础

新的瓶颈：还有许多问题没有解决

• 材料的性质与设计；
• 分子、药物的性质与设计；
• 基于基本原理的控制论方法；
• 燃烧问题(内燃机的模拟、设计与控制)

造成的问题：理论研究的场景与实际问题的场景差距太远。

共同的根源：维数灾难

• 这些问题的共同特征是依赖的变量(维数)太多；
• 维数灾难：随着维数的增加，计算量变成指数增长；
• 在高纬情形，多项式不是一个有效工具；
• 这正是机器学习(深度学习)能够帮助我们的地方。

深度学习例子——图像识别

维数= 32*32*3 = 3072

深度学习例子——人脸照片生成

深度学习例子——围棋

这些例子的本质都是在解决一个高维数学问题
(1) 图像识别：逼近高维函数；
(2) 人脸照片生成：高维(未知概率密度)取样；
(3) AlphaGo：解高维(超大空间上的)Bellman方程。

其本质原因是深度学习对高维函数提供了有效的逼近方法—深度神经网络(多项式的有效替代品)

函数是最基本的数学工具(之一)！

例子1：高维控制问题

控制论面临的困境：(基于基本原理的)理论研究和实际问题差距太远。
其结果：为解决实际问题，必须做各种近似(放弃基本原理)。

一个重要观察：控制问题和深度学习问题之间有着惊人的相似(Han and E, 2016)
(1) 用深度学习方法解决(高维)控制论问题；
(2) 用控制论方法解决深度学习问题。

Multiple device energy storage problem：这个方法开启了解高维控制问题和高维微分方程的时代。

例子2：分子动力学

关键问题：原子之间相互作用的势能函数。

• 传统方法 : 猜！ - - 有效，但不可靠。
• 第一性原理方法 ( 1985 ) : 通过量子力学模型在线计算原子之 间的相互作用力 - - 可靠，但不有效。
• 机器学习方法 : 量子力学模型提供数据 ; 机器学习方法提供模型。- - 既可靠，有有效。

参考资料：
(1) 鄂维南院士主题演讲【AI for Science】
(2) 机器学习联合研讨计划
(3) 应用数学新时代的曙光
(4) 鄂维南院士：科学与智能——机器学习的新前沿、应用数学时代的曙光
(5) 鄂维南院士：数据科学的基本内容
(6)《笔记——机器学习与物理模型》by鄂维南院士讲座

Materials Project

https://paulingfile.com/

参考资料：
(1) 从非常规复合效应产生新型材料-南策文
(2) 一文读懂材料信息学
(3) 软物质科普：当材料科学遇见机器学习
(4) 两天-张院士带你入门机器学习(材料应用)
(5) 深势科技
(6) 功能基元”开启材料学研究新范式 | NSR综述