注意，电介质和介电质，似乎是同一种东西，英文单词都是Dielectric，实在没有发现二者有啥区别。

每一种介电质可能会涉及到几种不同的电极化机制，每一种电极化机制都有其主要活动频率。都有其特征的截止频率，超过这个频率，对应的机制无法跟着电磁波振动，不再能贡献出电极化。对于每一种介电质，电极化机制的截止频率与电极化程度都不相同。下图是Polarization mechanisms in the dielectric materials.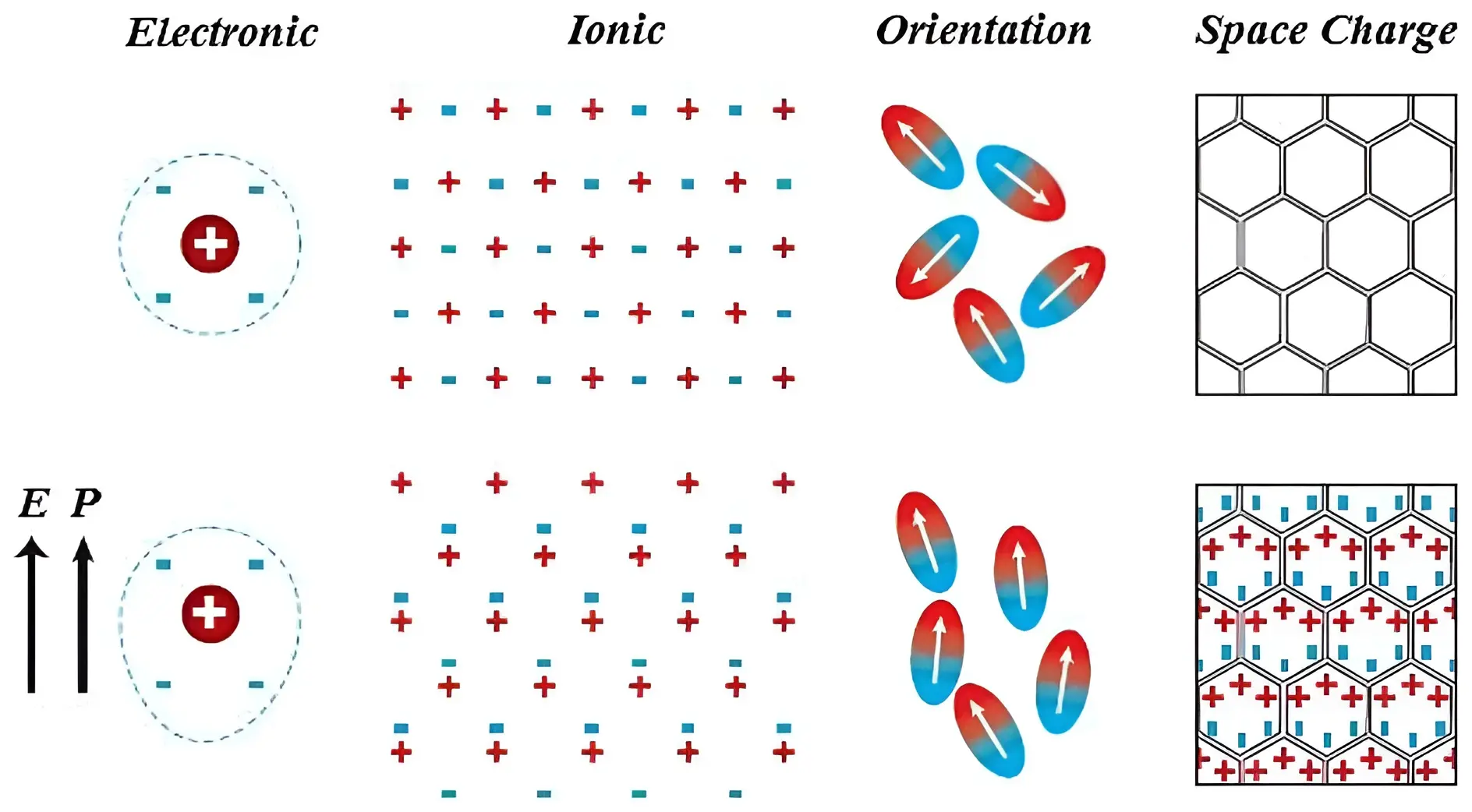

【电子极化】(electronic polarization)：物质内部的每一个原子，都是由带负电荷的电子云和位于电子云中心、带正电荷的原子核所组成。假设将物质置入于外电场，则由于外电场的作用，正电荷会朝着外电场方向迁移位置，而负电荷则会朝着反方向迁移位置。正电荷与负电荷的相对位移会形成电偶极矩。由于外电场与电偶极矩的耦合，从而给出介电质的物理行为。像氦气、氖气等等一类的惰性气体最能展示出电子极化性质。假设将外电场关闭，则原子会回返原来状态。这过程所需要的时间称为弛豫时间。

【离子极化】(ionic polarization)：离子晶体中，阴阳离子按照一定的周期性交替整齐排列，比如NaCl晶体。在正常情况下，假设外电场为零，则巨观电偶极矩为零。但是，假设外电场不为零，则由于正离子会朝着外电场方向迁移位置，而负离子则会朝着反方向迁移位置。正离子与负离子之间的相对位移形成了离子极化。

【取向极化】(orientation polarization)：仅出现在极性分子，又称为dipolar polarization。这种电极化是由永久电偶极子的取向改变而产生。例如，氧原子与氢原子之间的非对称键。虽然在外电场为零的状况，每一个单独永久电偶极子仍具有极性。对于介电质内部任意位置，设定以此位置为中心的尺度够大的区域，将其内部所有电偶极矩的总合除以区域的体积，则可得到在这位置的【巨观电极化强度】。假设施加非零外电场于此介电质，虽然正电荷与负电荷之间的距离，由于跟化学键有关，大致会保持不变，但是，感受到外电场的力矩，电偶极子会旋转，趋向于外电场的方向，从而增加巨观电极化强度。这旋转过程发生的时间尺度与力矩和周围的局域黏滞性有关。这旋转过程不是瞬时的，由于在时间方面的延迟，假设电场的变化频率足够高，介电质会失去响应的能力。另外，电偶极子的旋转运动会造成摩擦和发热。水分子能够微波加热就是应用这效应。

【界面极化】(interfacial polarization)：处于电场的介电质，其内部的电荷载子可能会迁移一段距离，假若这些电荷载子的迁移运动被阻碍，例如在非均质材料的结构界面，由于电荷累积，会发生界面极化现象，对应于上图的space charge。很多种陶瓷材料都会发生界面极化现象，特别是当处于高温状况。

总电极化：上述几种电极化机制并不互相排斥。介电质的总电极化强度是所有可能电极化机制的(矢量)总合

• 非均质介电质，四种都有；
• 均质介电质，除了界面极化，其它三种极化都有；
• 对于像氦气、氖气一类的非极性介电质，由于没有离子键，因此只有电子极化；
• 对于像氯化钠、氯化钾一类的离子晶体，由于在正常状况，取向极化强度为零，所以只有电子极化和离子极化。

电极化与频率的关系：由于含时外电场的作用，介电质内部的带电粒子会迁移位置。但是，这动作需要时间来完成。所以，对于外电场的变化，响应的电极化在时间方面必定会有所推迟。这意味着牵涉到的电极化机制密切地跟外电场的频率有关：

• 由于电荷载子需要时间移动几个原子距离，界面极化是很慢的程序，发生于电功率频率，大约为50-60 Hz；
• 取向极化与分子电偶极子的惯性有关，在较高频率仍旧能产生。可是在微波频域内，频率高达大约10⁸ Hz时，取向极化开始无法跟随含时外电场；
• 离子极化是因离子位移而产生的现象。在红外线或远红外线频域，频率高达大约10¹³ Hz时，离子极化失去响应含时外电场的能力；
• 电子极化涉及到电子的运动，比离子轻很多，可以快捷运动，但在紫外线频域，频率高达大约10¹⁵ Hz时，电子极化不再能够响应含时外电场。

涵盖宽广频域的介电质的电容率频谱。\( \epsilon^{\prime}\)和\(\epsilon^{\prime \prime}\)分别标记电容率的实值部分和虚值部分。图内标示了几种电极化机制：离子导电、取向极化、原子极化、电子极化。

假设缓慢地调高频率，这些极化现象会一个接着一个的消失，电容率的趋势也会越来越低。在频率大于紫外线的频域，电极化率趋向于零，电容率趋向于电常数\(\epsilon _{0}\)。因为电容率表现电极化强度与电场之间的关系，假若电极化的响应能力减弱，则电容率也会随之减小。

复电容率

负折射率

Dispersion and causality：In general, a material cannot polarize instantaneously in response to an applied field, and so the more general formulation as a function of time is$$ \mathbf{P}(t)=\varepsilon_0 \int_{-\infty}^t \chi\left(t-t^{\prime}\right) \mathbf{E}\left(t^{\prime}\right) d t^{\prime} $$It is convenient to take the Fourier transform with respect to time and write this relationship as a function of frequency. Because of the convolution theorem, the integral becomes a simple product$$ \mathbf{P}(\omega)=\varepsilon_0 \chi(\omega) \mathbf{E}(\omega) $$

xx

参考资料：
(1) 电容率—Wiki