MIT-电路和电子学

B站视频   B站视频—edX        官网Lecture Notes-MIT 6.002   (习题)     Circuit sandbox
A Simulation-Based Online Electronic Circuits Laboratory
别人的笔记

  • 什么是engineering：ther purposeful use of science
  • 思想方法：对于复杂事物，进行层层抽象，然后将问题简化后就能进行后续工作了，即构建复杂系统；
  • 工程师不是卖弄数学的人，而是搭建有用的系统的人，并且找到最简单、便利、便宜的方法。工程上的美学就是如何让事情变简单。当问题在数学方面很棘手的时候，我们就应该意识到我们是工程师，让我们找到更简单的方法并运用直觉。
  • 本课程的内容：
    • Gainful employment of Maxwell's equations
    • From electrons to digital gates and op-amps
  • 本课程的学习目标：
    • Analysis—给出具体电路，说出电路特性；
    • Synthesis—给出具体功能，设计电路；
  • 英语单词：takeaway  要点 breeze 轻而易举的事 rinky-dink pull rug out shady

 

Introduction

Lumped Abstraction

  • lump：块，肿块，一小方块。比如 lump of clay / a lump on my shoulder / a lump of sugar
  • 【集总元件】(Lumped element)：
    • 集总元件是指元件大小远小于电路工作频率相对之电磁波波长时，对所有元件之统称，对于信号而言，不论任何时刻，元件特性始终保持固定，与频率无关； 
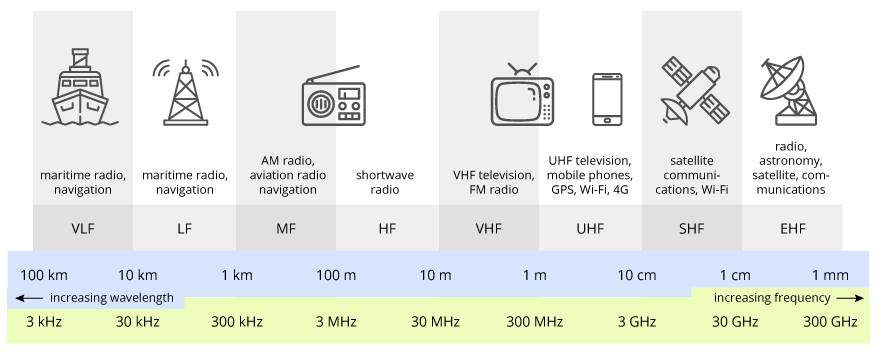
    • 信号波长对于元件大小来说是相当长的，所以当信号通过元件时，信号在元件内部每点之变化相当小，可视为相同，所以元件的特性是一体成，因此集总元件之电流与电压关系可以明确定义；下图是【无线电波】(radio wave)的波长/频率范围，从手机开始，波长可能就比元件短了(【微波】范围：300MHz-300GHz，1 mm ~ 1 m)，元件就不能看作是集总元件了。
    • 集总元件，组成的电路模型称为【Lumped circuit】(集总电路)模型；
    • 集总元件，也是单一特征的元件，比如：
      • 电阻元件集中表征了某一实际部件或某一段实际电路的能量消耗；
      • 电感元件集中反映了磁场的物理现象；
      • 电容元件集中反映了电场的物理现象；
    • outside elements(法拉第定律)   \( \displaystyle\oint E \cdot d l=-\frac{\partial \phi_{B}}{\partial t}=0\)
    • inside elements(连续性要求) \( \displaystyle\oint J \cdot d S=-\frac{\partial q}{\partial t}=0\)
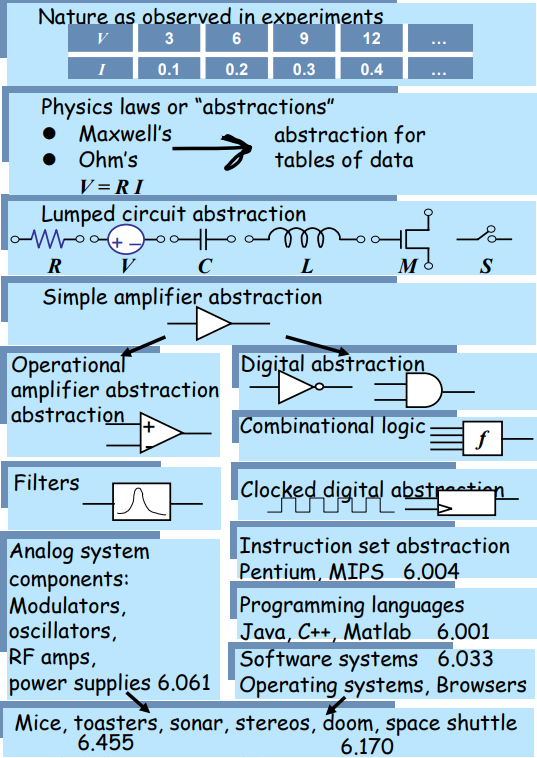
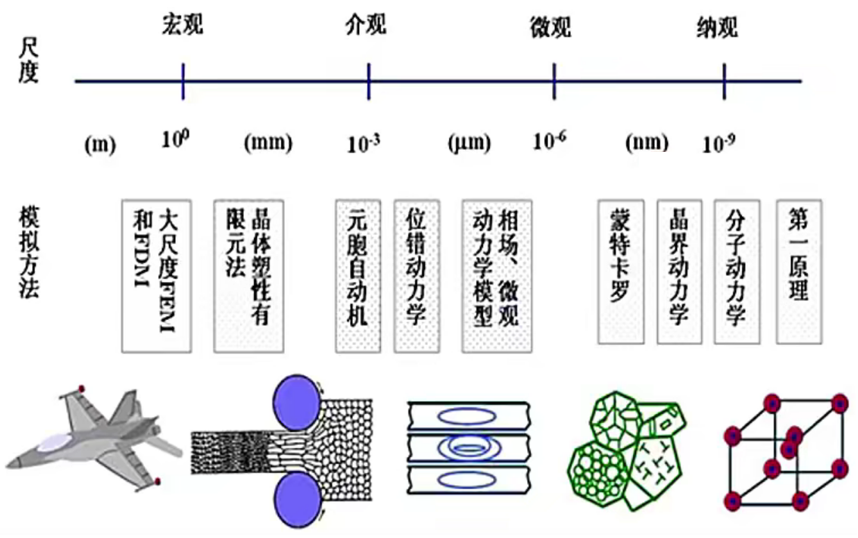
  • 集总元件构建复杂系统：一个系统的基本组成部分的特性越确定，则复用这些基本组成部分、实现一个系统的难度(成本)就越低。(来自博文确定性) 从集总元件出发，就可以通过层层抽象，构建复杂系统。反面例子就是More Is Different (Philip W. Anderson)。反面例子更具体一点，比如材料科学涉及多尺度的科学问题，不同尺度的问题之间没有简单的联系，即不能用抽象某低尺度的模型来得到更高尺度的材料特性。

  • 【分布元件】(Distributed element)：
    • 若元件大小与电路工作频率相对之波长差不多或更大的时候，则当信号通过元件之时，元件本身各点之特性将因信号之变化而有所不同，则此时不能将元件整体视为一特性固定之单一体，而应称为分布元件；
    • 分布元件的例子：在微波电路中，传统导线很可能会成为具有电感及电容串并联特性之复杂组合。

【Lumped-element model】是更广义的概念，比如物理中的质点模型(Point-mass discretization)。更准确的定义如下：The lumped-element model  simplifies the description of the behaviour of spatially distributed physical systems, such as electrical circuits, into a topology consisting of discrete entities that approximate the behaviour of the distributed system under certain assumptions. It is useful in electrical systems (including electronics), mechanical multibody systems, heat transfer, acoustics, etc. This may be contrasted to:
【Distributed parameter system】 in which the behaviour is distributed spatially and cannot be considered as localized into discrete entities. Mathematically speaking, the simplification reduces the state space of the system to a finite dimension, and the partial differential equations (PDEs) of the continuous (infinite-dimensional) time and space model of the physical system into ordinary differential equations (ODEs) with a finite number of parameters.

用Anant Agarwal的话来说，对于电路，从distributed parameter system变为Lumped-element model，意味着Replace the differential equations with simple algebra using 【lumped circuit abstraction】 (LCA). 即Maxwel's equations simplify to algebraic KVL and KCL under LMD (Lumped Matter Discipline).

参考资料：
(1) 集总电路—知乎
(2) Lumped-element model—Wiki

 

不懂：inverter和operational amplifier，just like the different way looking at the same device.

 

Basic circuit analysis method

Method 1 — Basic KVL, KCL method of Circuit analysis

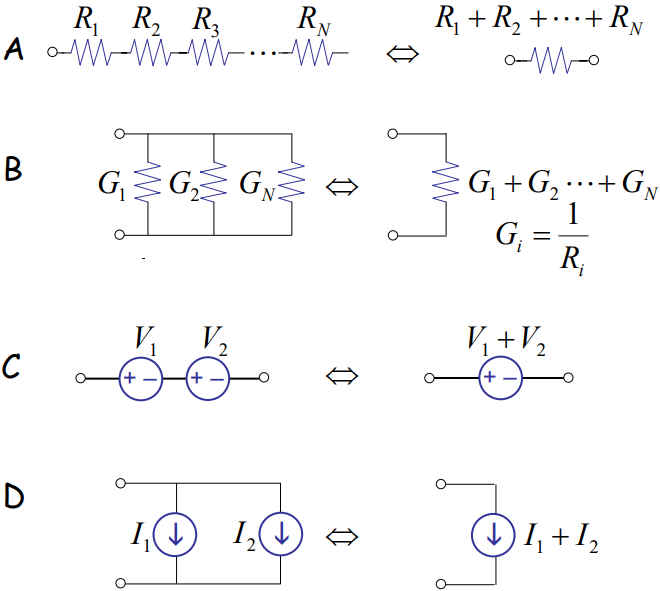
Method 2 — Apply element combination rules

Method 3 — Node analysis (Particular application of KVL, KCL method)
(1) Select reference node (ground) from which voltages are measured.
(2) Label voltages of remaining nodes with respect to ground. These are the primary unknowns.
(3) Write KCL for all but the ground node, substituting device laws and KVL.
(4) Solve for node voltages.
(5) Back solve for branch voltages and currents (i.e., the secondary unknowns)

 

Superposition

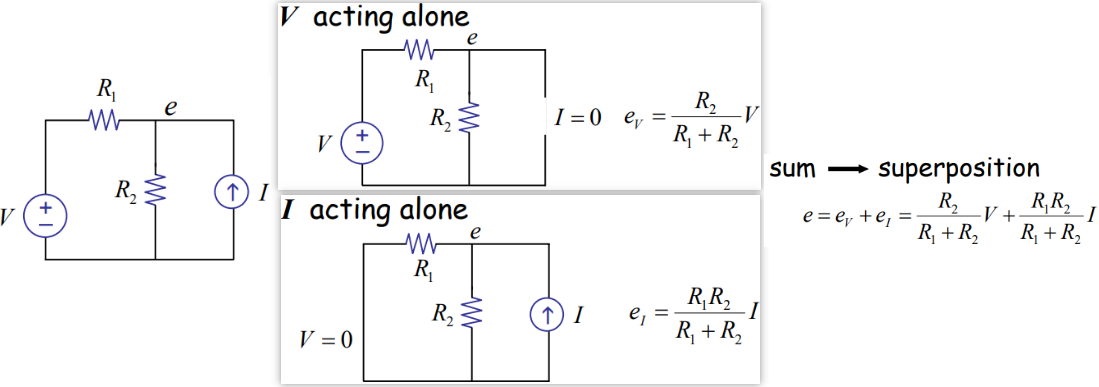
Method 4 — Superposition method: The output of a circuit is determined by summing the responses to each source acting alone.

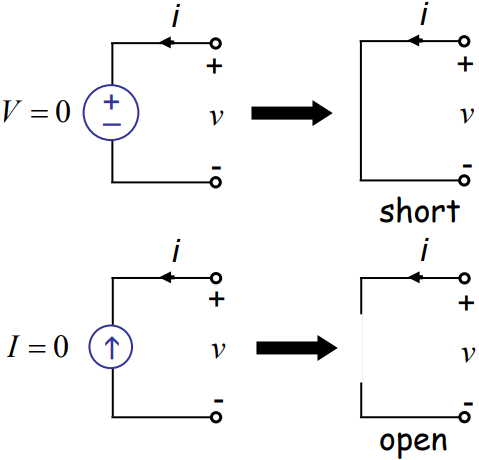其实就是线性叠加原理，在研究某一结点的电压，电路中存在一个恒流电源，一个恒压电源。我们在观察恒流电源对结点电压的影响的时候，无视恒压电源(将其短路)；在观察恒压电源对结点电压的影响的时候，无视恒流电源(将其开路，记成开溜(流)，或者IO)。当然了，我们的研究对象也可以是某一段导线的电流，处理方法还是一致的。

换成更容易理解的说法，研究电路对电流源的响应的时候，让电压源为零，电压源为零显然就成了单纯的导线(short状态)；研究电路对电压源的响应的时候，让电流源为零，说明该线路上电流必须为零，即处于开路open的状态。

具体实现过程，见下面的例子，分治法的思想。

 

Thévenin and Norton

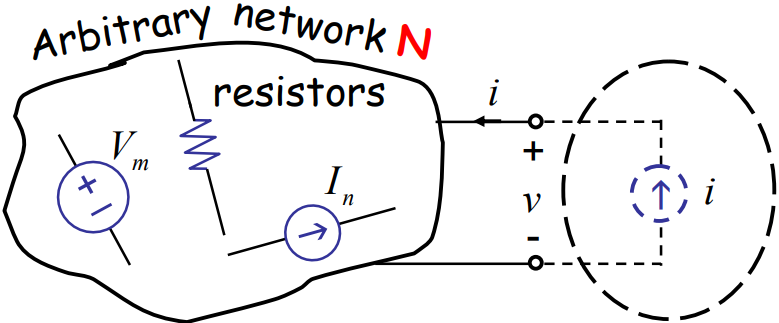
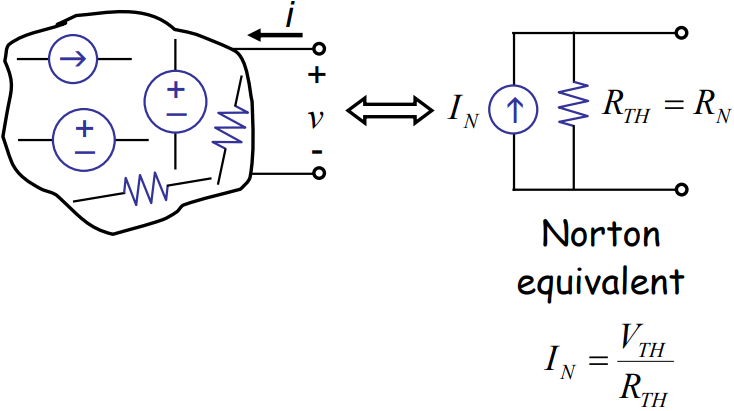
假设上图左侧部分是一个线性网络，里面有各种电阻、电压源、电流源等等元件以某种连线形式接起来，我们只关心网络中的两个结点，我要算的是，假如结点接上右侧的小电流源(电流为\(i\))，那么回路中的结点两端的电压\(v\)是多少。通过前面的叠加法，我们知道电路的总的响应，等于各个分响应之和，每个分量是一个源单独作用的响应，如果我们能算出每个源单独作用的响应，就能求出总的响应。$$ v=\sum_m \alpha_m V_m+\sum_n \beta_n I_n+R i $$即所求结点之间的电压\(v\)等于下面三者的线性组合：

    • \(m\)个左侧系统内电压源；
    • \( n\)个左侧系统内的电流源；
    • 右侧外接(系统外)电流源；

系数的讨论：

    • \(\alpha_m\)、\(\beta_n\)和\(R\)其实就是响应系数，响应系数是系统的内在特征，只和电路中的电阻及接线方式有关，和电流源、电压源的大小无关；
    • 为了求解每一项的系数，我们让该项以外其他源为零，就可以利用单一元件的V-I特性即可迅速求解出系数，比如为了求解\(R\)，只需要\(\forall_n I_n=0 \quad \forall_m V_m=0\)，然后测量结点的电压，就可以知道左侧图的等效电阻；
    • \(\alpha_m\)没有单位(dimensionless quantity)，\(\beta_n\)和\(R\)的单位都是resistance units；

线性系统：正如我们前面所说的，这些是一个线性系统，那么就可以和我们之前学的数学或者物理中涉及的其他的表现形式联系起来，比如这里的系数求解和我们量子力学波函数的系数求解很类似，只是量子力学是用一个正交向量和波函数相乘，摘出目标分量的系数，应该也和线性代数的特征值相对应。

线性系统各部分的独立性：对于上图的左侧图，里面的电压源与电流源大小给定的情况下，\(\sum_m \alpha_m V_m+\sum_n \beta_n I_n\)作为一个整体，是不受右侧图外接电流源的影响，用老师的话说independent of external excitation and behaves like a voltage "\(v_{T H}\)"。另外\(R i\)中的\(R\)同样不受外接电流源的影响，independent of external excitement & behaves like a resistor。因此，上面的式子可以简化为(下标TH表示Thévenin)$$ v=\sum_m \alpha_m V_m+\sum_n \beta_n I_n+R i=v_{T H}+R_{T H} i $$"Arbitrary network N" is indistinguishable from: (a.k.a = also known as)

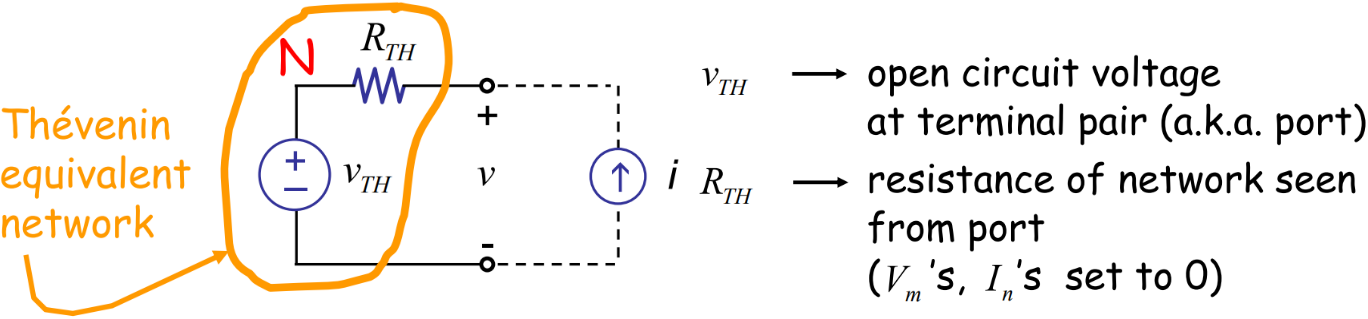
这就引出了下面的【戴维南方法】(Thévenin Method)

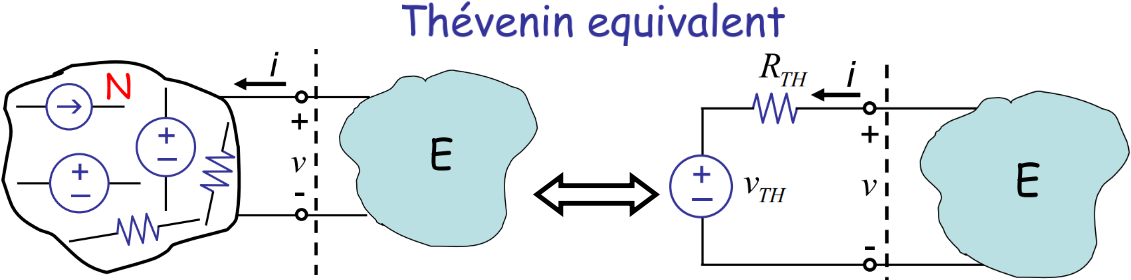
下面举例学习一下

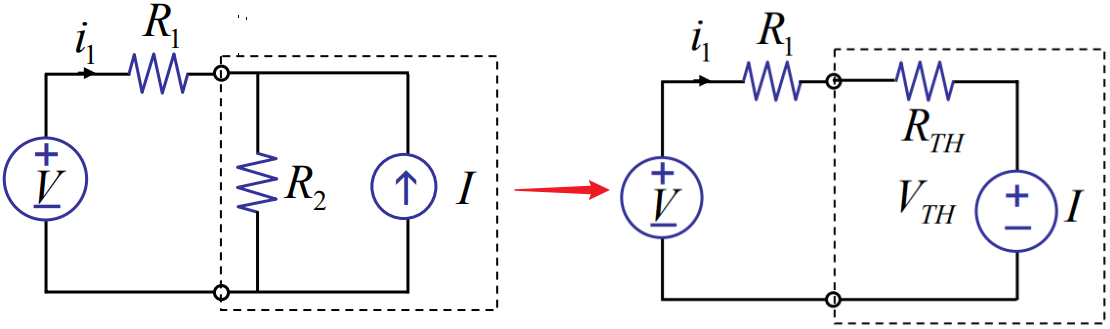
左图是原始的电路，现在我们想求解\(i_1\)，根据戴维南方法，我们可以将左图虚线框中的内容等效为一个电压源\(V_{T H}\)和一个电阻\(R_{T H}\)，如果知道这两个等效值，就能立马通过\(i_1=\displaystyle\frac{V-V_{T H}}{R_1+R_{T H}}\)求出\(i_1\)。

按照前面方法，我们先把两个结点给摘出来，只关注左图虚线框的部分，显然\(v=v_{T H}+R_{T H} i\)中的外接\( i\)为零，而虚线框里面只有一个电流源，老老实实让其工作，直接测结点两端的电压即有\(V_{T H}=I R_2\)。求\(R_{T H}\)，即让\( v_{T H}\)系统里面的电压源和电流源都为零，当然了此处我们只有电流源，电流源为零其实就等于开路，于是可以知道\(R_{T H}=R_2\)。

注：有的资料会说戴维南方法的关键是"电压源要短路，电流源要开路"，电压源短路，实际上等效于上面说的电压源输出电压为零，电流源开路，实际上等效于上面说的电流源的输出电流为零。

例子：利用戴维南方法分析下面的电路

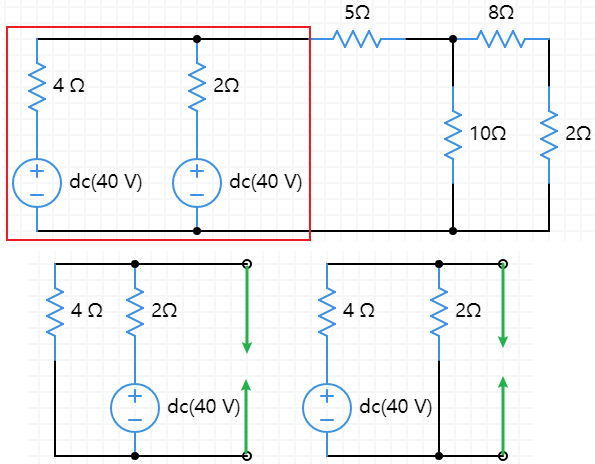
将上述电路分为两部分，主要研究红色框中的戴维南等效。先将红色框中一个电压源的电压变为零，计算端口的分压；选择另外一个电压源进行同样的操作。将两次计算的分压加在一起就是等效电路电压源的电压。另外，将红色框中两个电压源的电压同时设定为零，那么即可计算出戴维南的等效电阻。(参考 电路基本原理那些事儿之 戴维南定理)

【诺顿定理】 (Norton's theorem)：由线性时不变电阻，电压源和电流源组成的网络，在网络的一对端子处，可以用一个电流源和一个并联的单个电阻代替它。要计算等效电路：
(1) 负载电阻为零，计算输出电流，即为\( I_N\)
(2) 负载电阻或者阻抗无穷大，计算输出电压，输出电压除以(1)中的输出电流得到等效电阻\( R_{TH}\)

 

 

The Digital Abstraction

模拟信号的缺点：因为在实际传输过程中，会有外界环境等各种因素影响，使得我们实际传输过程中的模拟信号与理想状态有偏差，比如我想传输\(3.1 \mathrm{~V}\)的电压，但是噪音可能是\(0.1 \mathrm{~V}\)，即实际传输的电压是在\(3.0 \mathrm{~V}\)到\(3.2 \mathrm{~V}\)之间。那么对接收端来说，它是无法准确判断自己感知到的\(3.2 \mathrm{~V}\)对应的实际sender想传输的电压是多少。

数字信号的特点：

  • 数字信号采用discrete value(也即\( 0\)和\( 1\))进行传输，即"低电平"和“高电平”两种状态；
  • 判断是高电平还是低电平，是看电压是否落在对应某一个较大的区间。如果最理想的高电平是\(5 \mathrm{~V}\)，低电平是\(0 \mathrm{~V}\)，那么只要在\(2.5 \sim 5 \mathrm{~V}\)范围我们都可以认为是高电平，\(0 \sim 2.5 \mathrm{~V}\)范围我们都可以认为是低电平，即noise margin都是\(2.5 \mathrm{~V}\)；
  • numbers larger than \( 1\) can be represented using multiple binary digits and coding, much like using multiple decimal digits (多重十进制数字) to represent numbers greater than \( 9\), the binary number \(101\) has decimal value \(5\).
  • better noise immunity; lots of noise margin；

 

新一步提升信号传输的稳定性：这里的关键是sender和receiver限定在一个活动范围，并在这里定义规则，如果电压在这个范围内，就可以应用之前定义的规则，这称之为discipline，你规定自己要呆在这里，这毫无逻辑可言，这只是一个规定，你只要这样做就行了。实际电路中，如果有东西跑到禁区，那么就需要进一步讨论了。


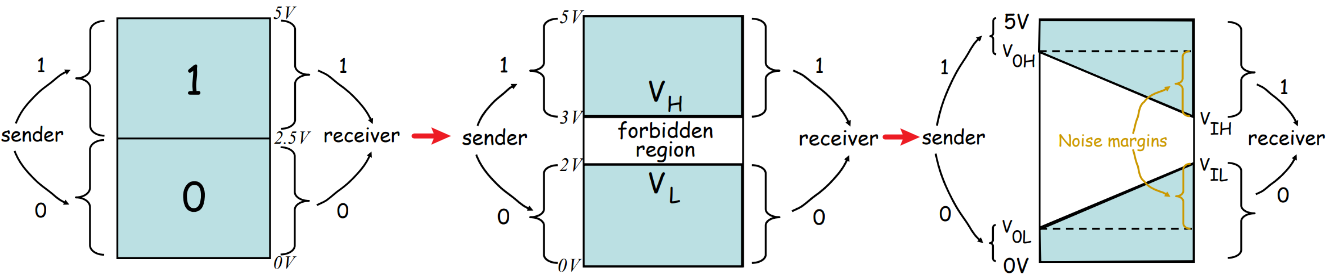
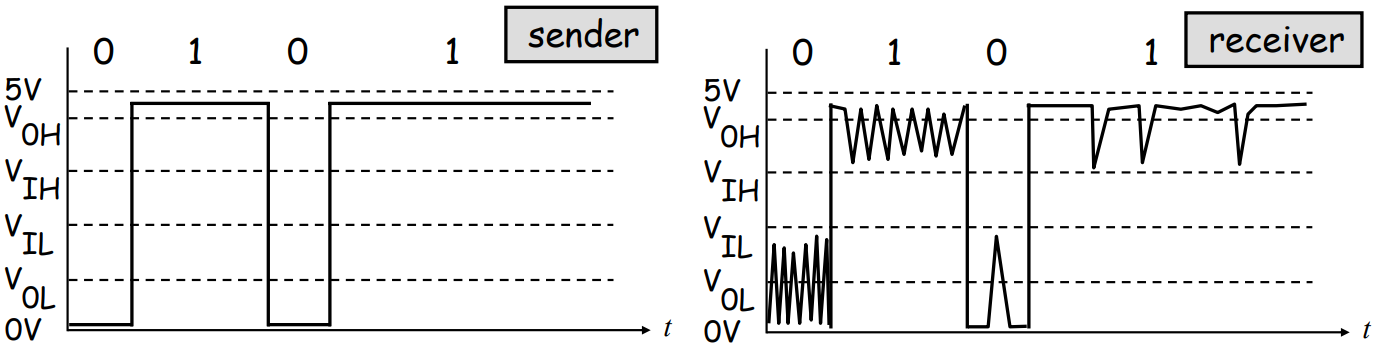
  • 左侧是sender，即输出了信号，而右侧是receiver，其收到的信号作为input，注意别搞反了，这也是为什么上图中sender对应的电压下标首字母为O(output)，receiver对应的电压下标首字母为I(input)；
  • 实际应用中，VOH都比VIH大不少，而且严格要求sender的范围，这样即使有很大的噪音，但是由于noise margin很大，所以仍然能够保证接收端提取出正确的信息。
  • Digital systems follow【static discipline】(静态规则): if inputs to the digital system meet valid input thresholds, then the system guarantees its outputs will meet valid output thresholds；
  • static discipline实际就规定了VOH，VOL，VIH，VIL这四个阈值，所有数字系统都必须遵守，使得彼此之间能够相互通信，比如intel和摩托罗拉想兼容彼此的器件，那么就都要遵守这个静态规则；
  • 对消费电子来说，noise margin相对比较小，因为消费者能容忍更多的故障，但是对于医疗领域，或者太空设备，就需要遵守严格得多的标准，这些设备可使用的sender的带宽就很窄，也就有了更大的noise margin。
  • 串口通信的TTL高低电平可能会被其他外界电场干扰，进一步提升数字信号传输的稳定性，工业控制中经常使用RS232/RS485总线，参考labview笔记；

进一步说明为什么用数字电路  （来自确定性）

要高效地解决工程问题，就要尽量消除元件之间的相互影响。相互影响的因素越少，实现某个工程目标的方法就越简单，系统就越容易设计。(其实社交生活也是一样的，大家都希望自己的各种社会关系、活动之间不要相互影响，以便活得轻松些)

因为我们要求电阻必须遵守欧姆定律，所以电阻厂家就专门生产严格符合欧姆定律的电阻；我们要求环路之间不能相互影响，所以我们经常在电路设计中增加屏蔽和缓冲。总而言之，电路和电路元件的特性越确定，工程师的工作就越轻松。

如果要再进一步提高确定性呢？于是人们定义了一类比较特殊的电路，这些电路几乎总是工作在饱和状态，用高低电平表示和传递信息，称为数字逻辑电路。它们的行为几乎完全不受环境干扰，而它们的工作规律也从基尔霍夫电路定律(信号可以顺路径来回传递；信号可以取实数值)简化到了逻辑运算(信号只能朝某个方向传递；信号只能取逻辑值)。

提高确定性当然有很多好处。在线性(模拟)电路中，我们虽然强行规定环路之间不会相互影响，但这种影响肯定是存在的，区别只是程度高低而已；而元件本身的特性也总是很难完美。到了数字逻辑电路中，这种影响就几乎可以忽略不计了，元件特性也非常容易保证完美，这就是为什么数字逻辑电路的规模可以比模拟电路的规模大成千上万倍。

正是因为元件确定性高，互相影响小，我们总是可以把一个大的设计拆分成许多小的设计，其中每个小设计的特性都是确定且无须怀疑的。在模拟设计中，要保证1000个电阻的误差在0.01%以内是一件非常奢侈、只有高端设计才会考虑的事情；而在数字设计中，由1,000,000个逻辑门组成的、连续工作10年不出错的芯片，比快递费还要便宜得多。

 

 

 

Inside the Digital Gate

四种简单的gate：

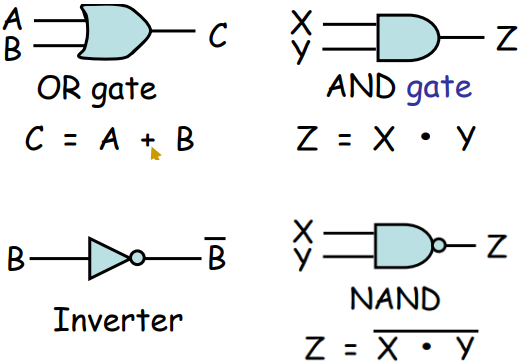
Digital Circuits的例子(多个简单gate的组合)

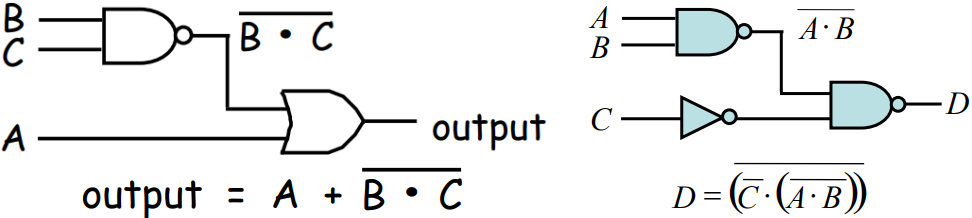
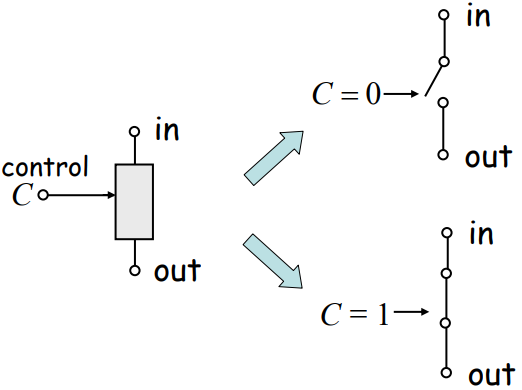
Switch的Electrical Analogy：对于传统开关，控制信号来自机械压力。

下图进一步描述了如何在实际电路中得到inverter、NAND、NOR以及compound gate。

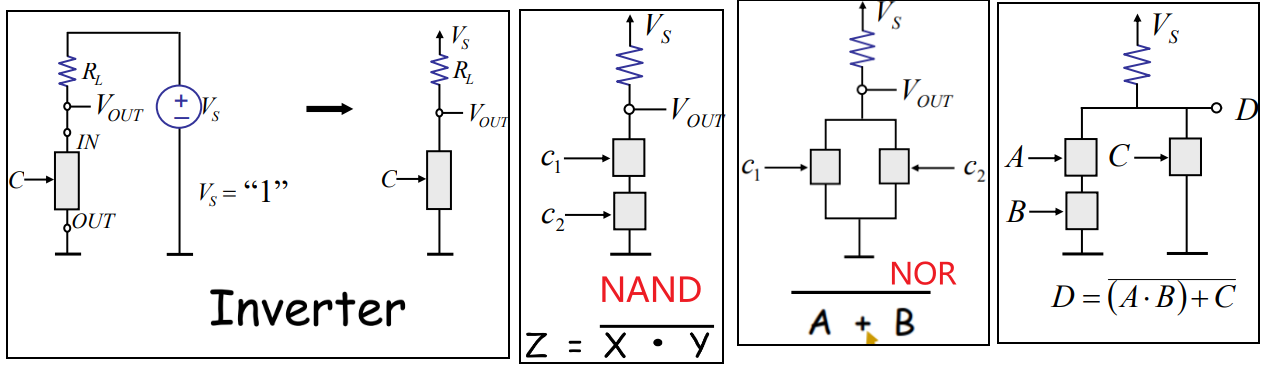
因为VOUT的探测点接地点之间只有开关，所以总会有一个反相的作用，这也是为什么NOR和NAND是电路中最初始的元件，而不是AND和OR GATE。如果要得到AND，就要在下图NAND的VOUT的探测点再接出一个反相器，然后再探测反相器另一端的电压，同理也可以在NOR的基础上加上反相器得到OR。

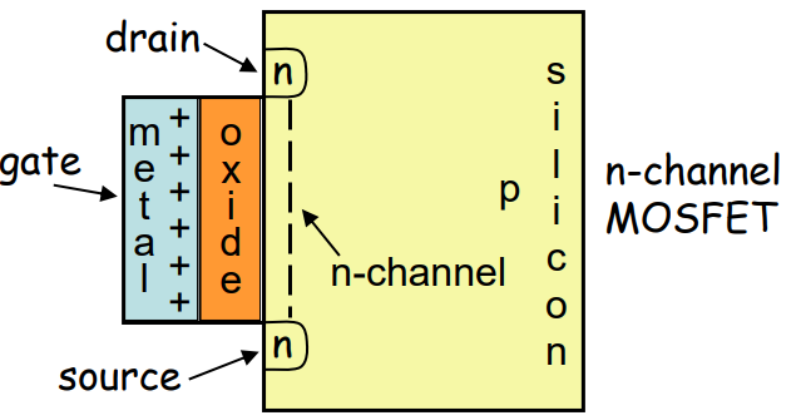
【MOSFET】(Metal-Oxide Semiconductor Field-Effect Transistor): Understand its operation by viewing it as a two-port element. 也叫MOS管。(下图是NMOS的结构)

【Switch model】S model of the MOSFET，忽略了DS之间的电阻。

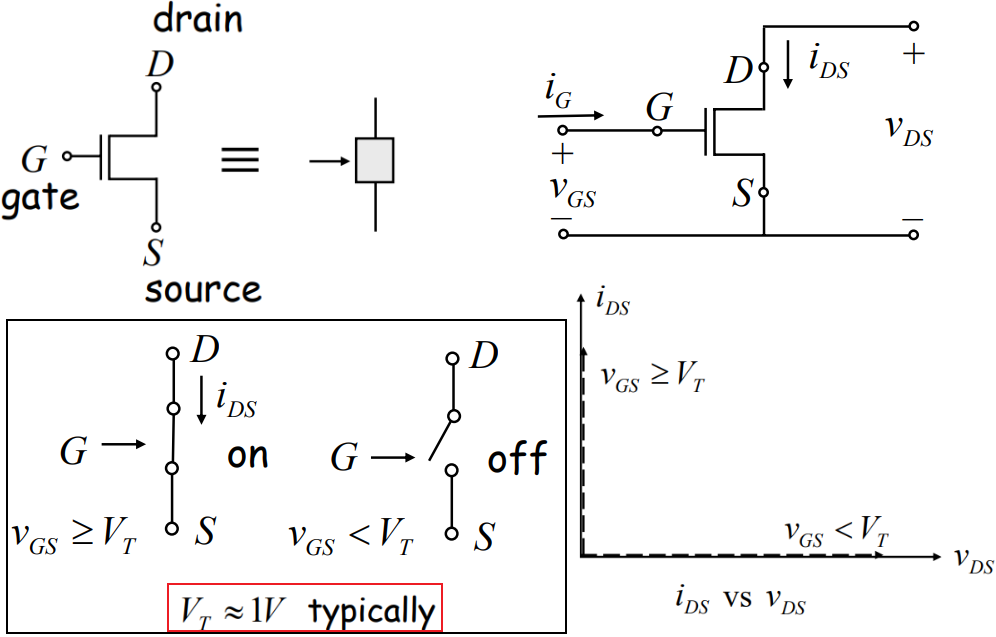
【MOSFET Inverter】：The abstract inverter gate representation hides the internal details such as power supply connections, RL, GND, etc.

下面的左图就是一个MOSEFTE Inverter的Vin-Vout。构建输入和输出之间映射关系的东西就是transfer function(传递函数)。传递函数是用来拟合或描述黑箱模型（系统）的输入与输出之间关系的数学表示。传递函数通常用于分析诸如单输入、单输出的滤波器系统中，主要用在信号处理、通信理论、控制理论。更准确的传递函数的说法为：For continuous-time input signal \(x(t)\) and output \(y(t)\), the transfer function \(H(s)\) is the linear mapping of the Laplace transform of the input, \(X(s)=\mathcal{L}\{x(t)\}\), to the Laplace transform of the output \(Y(s)=\mathcal{L}\{y(t)\}\) : $$ Y(s)=H(s) X(s) $$

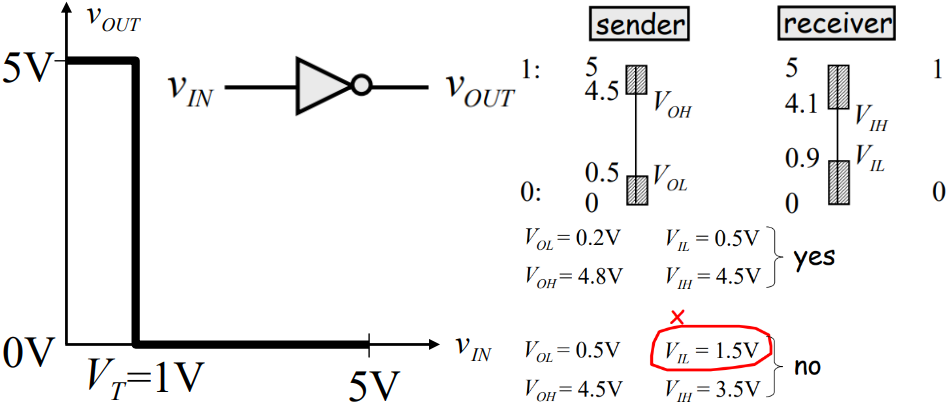
对于反相器，我们经常关心的一个问题是检查这个反相器的Vin-Vout是否满足了某个电压阈值(Does our inverter satisfy the static discipline for these thresholds)，比如是否满足上图右上角sender和receiver标注的电压阈值：(注意反相)

  • Vout是表示低电平的时候，输出要小于0.5 V(图中是0 V)，满足；
  • Vout是表示高电平的时候，输出要大于4.5 V(图中是5 V)，满足；
  • 有没有将所有低于VIL的视为低电平，是的(看横轴，低于0.9 V的对应的都是5 V低电平，反相之后即对应低电平)；
  • 有没有将所有高于VIH的视为高电平，是的(看横轴，高于4.1 V的对应的都是0 V低电平，反相之后即对应高电平)；

其他类型的反相器：参考Inverter (logic gate)—Wiki

 

 

 

【Switch resistor model】SR model of the MOSFET，考虑了DS之间的电阻。

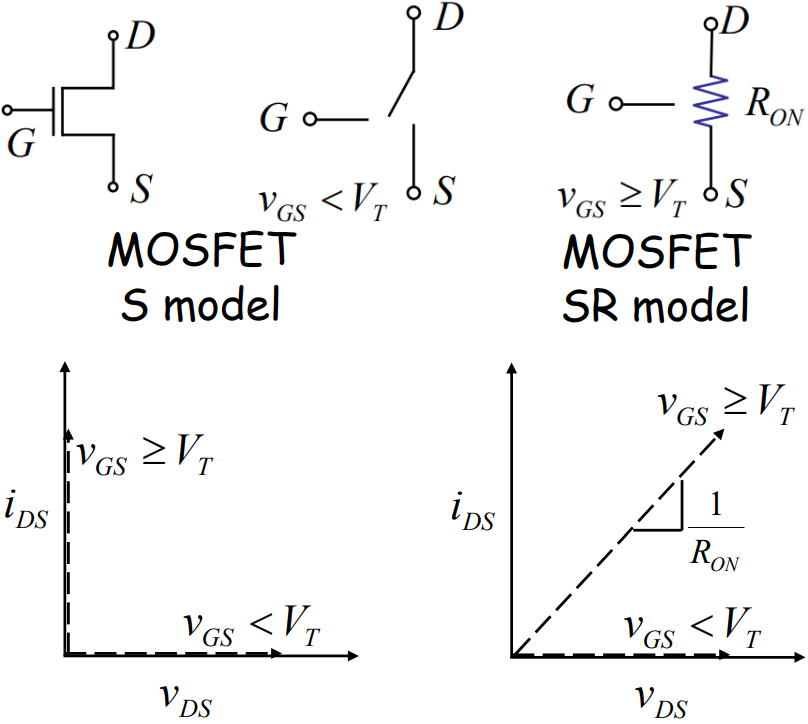
SR model下之前研究的inverter的电路响应，如果要得到正确的输出，要满足什么条件？(下面左图的\(C=1\))

参考资料：
(1) MOSFET Physics
(2) 三极管、场效应管、IGBT管的作用及区别

 

 

 

Nonlinear analysis

数字电路天生具有非线性，不过一旦所有数字开关的\(0\)和\(1\)都确定之后，就可以用使用线性的方法去分析。非线性电路同样属于集总这个"大操场"，非线性电路同样是集总电路，也要遵守集总问题的规定，而且也可以用KVL、KCL或者结点法来分析。郑益慧：非线性电路用图解法来分析。

How do we analyze nonlinear circuits, for example: 

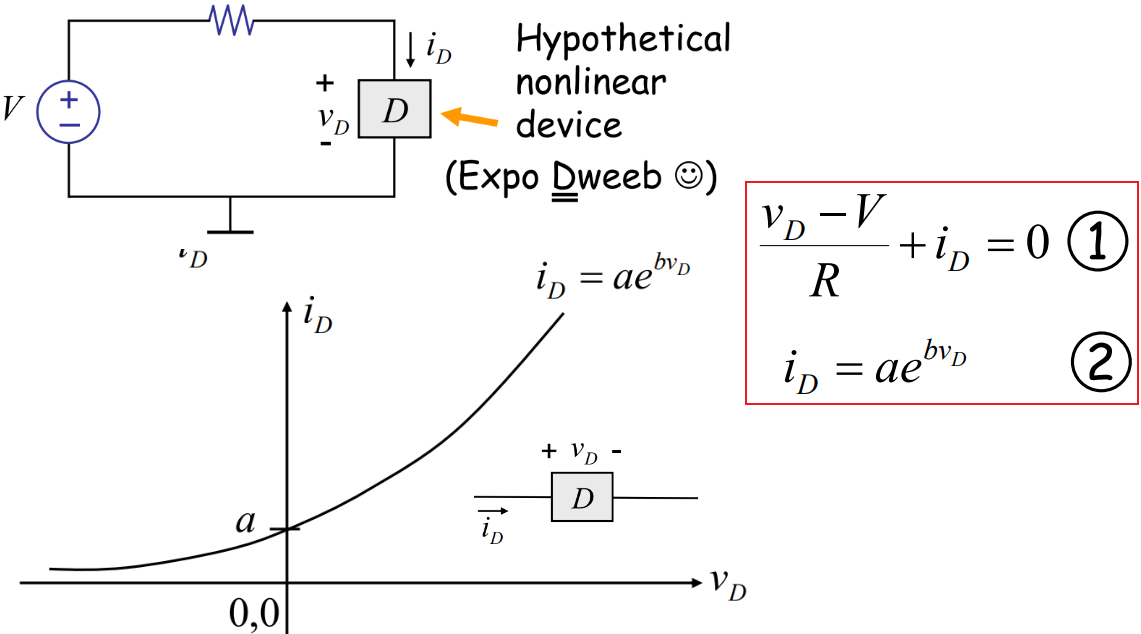
有趣的地方在于它是一个【有源器件】(Active Devices)，当\(v_D\)大于零的时候，电压和电流都是正的，说明这个器件是消耗能量的；当\(v_D\)小于零的时候，电压降方向和电流方向相反，这必然暗示了这个器件是产生能量的。但是我们并不需要担心这个，因为我们只需要从数学上分析并找出其特征。只要是一个复杂的线性电路连着某个有趣的器件，如果你只关心分析这个器件特性的话，你完全可以把它用戴维南/诺顿方法进行等效简化处理。通过上面红色框，两个方程两个未知数，就可以解出结果。求解既可以用Numerical Methods，也可以用Graphical Method，下图是图解法的例子，下面两个图叠在一起，曲线和直线相交得到的交点即为解。

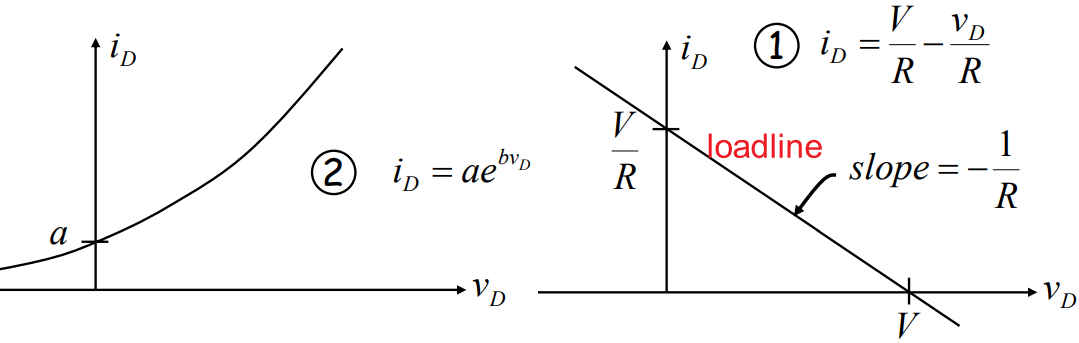
图解法：我们通过观察图像化的事物，常常可以更好地洞察电路的特性，基于此你可以做很酷的响应图像演示，演示输入输出之间的关系，获得这样的直观感受是很有趣的。

piecewise linear method看课本4.4节。

无源器件 versus 有源器件：简单地讲就是需要能(电)源的器件叫有源器件，无需能(电)源的器件就是无源器件。

Passive Devices——Components incapable of controlling current by means of another electrical signal are called passive devices. Resistors, capacitors, inductors, transformers, and even diodes are all considered passive devices.

Active Devices——An active device is any type of circuit component with the ability to electrically control electric charge flow (electricity controlling electricity). In order for a circuit to be properly called electronic, it must contain at least one active device. Active devices include, but are not limited to, vacuum tubes, transistors, silicon-controlled rectifiers (SCRs), and TRIACs.

参考：
(1) all about circuits
(2) 无源与有源器件的这些区别你都知道吗？——面包板社区

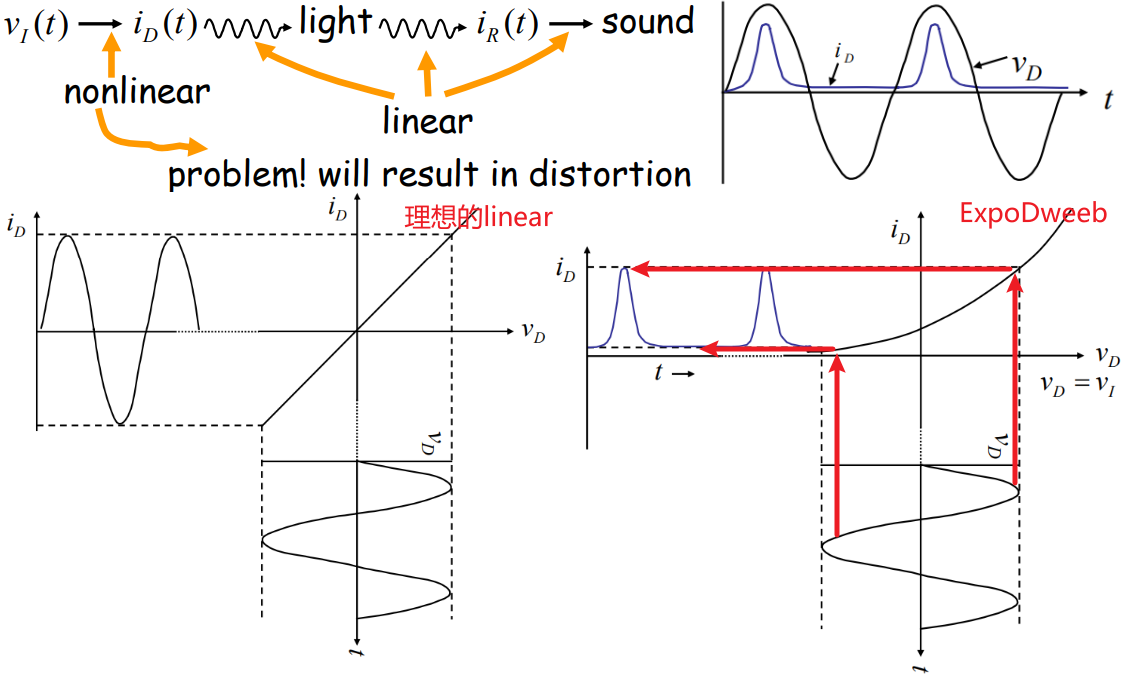
【Incremental Analysis】(也叫small signal method)

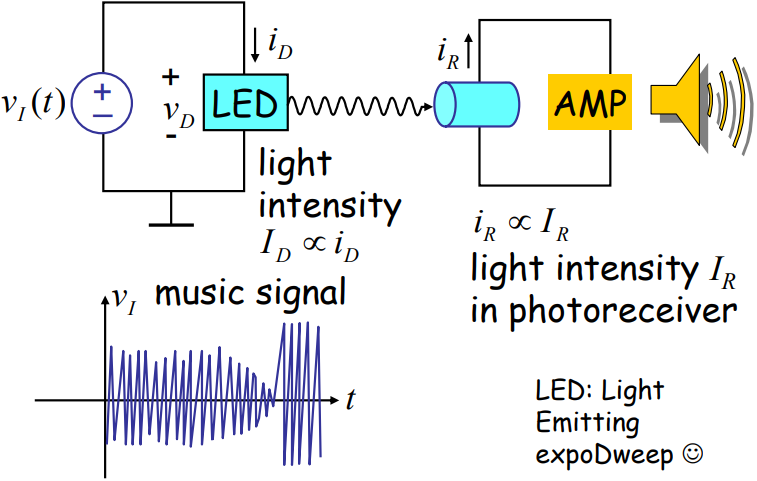
假设这里的LED = Expo Dweeb，LED的发光强度和和流过的电流成正比。在接收端，电流大小和接收到的光强成正比。通过调整电源两端的输出，使得LED两端的电压\(v_D\)是一个正弦函数的输入，如果LED也是一个线性元件的话，那么这个原始信号的正弦特征会毫无保留地传递出去，即表现为正弦变化为光强。但是实际上LED是个Expo Dweeb，如果输入电压\(v_D\)为负，那么根据Expo Dweeb的VI特性曲线，会得到一个较低的正值，即表现为似乎是一段较为平滑的水平线。

Pages: 1 2 3

Leave a Reply