单缝衍射/双缝干涉和干涉仪
这里先讲一下用于一维简谐振动的合成的【旋转矢量法】，后面再光栅强度计算中可以用到。(参考上海交通大学普通物理学web，另外也可以参考Single Slit Amplitude Construction—hyperphysics)
\(N\)个同方向、同频率的简谐振动，它们的振幅相同，初相位分别为\( 0\)，\( \alpha \)，\(2\alpha \)……，依次差一个常量\(\alpha \)，振动表达式可以写为$$ \begin{aligned} &x_1=a \cos \omega t \\ &x_2=a \cos (\omega t+\alpha) \\ &x_3=a \cos (\omega t+2 \alpha) \\ &x_N=a \cos [\omega t+(N-1) \alpha] \end{aligned} $$
对这种情况，采用旋转矢量法，可以避免繁杂的三角函数运算，有很大的优越性。将每一个简谐振动在\(t=0\)时刻的振幅矢量首尾相连，而相邻矢量的夹角均为\(\alpha \)。它们构成正多边形的一部分。可见合振动的振幅矢量\(\vec{A}\)等于各分振动振幅矢量的矢量和。在图中作\(\vec{a}_1\)和\(\vec{a}_2\)的中垂线，交于\(C\)点，根据几何个关系，很容易知道合振幅矢量\(\vec{A}\)的大小为$$ A=2 R \sin \frac{N \alpha}{2} $$在\(\triangle O C P\)中，\(\alpha=2 R \sin \frac{\alpha}{2}\)，两个式子相除可以得到$$ A=a \frac{\sin \frac{N \alpha}{2}}{\sin \frac{\alpha}{2}} $$又因为$$ \angle C O M=\frac{1}{2}(\pi-N \alpha) \quad \quad \angle C O P=\frac{1}{2}(\pi-\alpha) $$所以合振幅矢量\(\vec{A}\)与\(x\)轴的夹角，也就是合振动的初相位为$$ \varphi=\angle C O P-\angle C O M=\frac{N-1}{2} \alpha $$最后求得合振动的表达式为：$$ x=A \cos (\omega t+\varphi)=a \frac{\sin \frac{N \alpha}{2}}{\sin \frac{\alpha}{2}} \cos \left(\alpha t+\frac{N-1}{2} \alpha\right) $$如果各分振动的初相相同，即\(\alpha = 0\)，于是有(这时合振幅为最大值。)$$A=\lim _{\alpha \rightarrow 0} a \frac{\sin \frac{N \alpha}{2}}{\sin \frac{\alpha}{2}}=N \alpha \quad \quad\varphi=0$$
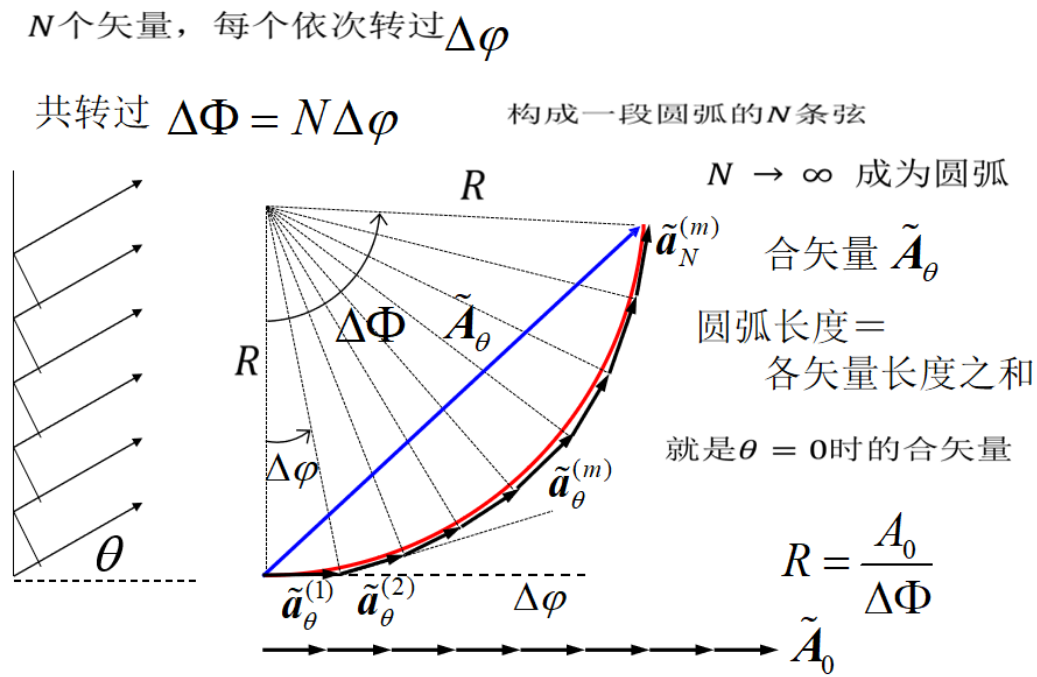旋转矢量法/振幅矢量法，不仅可以用于单缝衍射强度的计算，也可以用于双缝干涉(理想状况，不考虑狭缝宽度)的强度计算，二者的乘积就是实际光栅强度分布，即理想双缝干涉的结果被单缝衍射的envelope modulated。包络线(envelope)是很常见，无论是量子力学中波包(群速度/相速度)还是【拍频】(beat frequency)，或者信号调制(高频信号加载到一个低频信号上)都有出现。
【光的波粒二象性】(Wave–particle duality)：牛顿和惠更斯关于光的本质的争论，到了1801年托马斯杨用实验证实了光是一种波，似乎证实了惠更斯(荷兰人)是对的，牛顿是错的。20世纪初，光的粒子特征再次出现，直到后面量子力学的发展将光的波动性和粒子性融合在一起，也就是光具有波粒二象性。
【衍射】(Diffraction)又称绕射，是指波遇到障碍物时偏离原来直线传播的物理现象。其实物理原理和干涉一样，只是换了个名字。在经典物理学中，波在穿过狭缝、小孔或圆盘之类的障碍物后会发生不同程度的弯散传播。假设将一个障碍物置放在光源和观察屏之间，则会有光亮区域与阴暗区域出现于观察屏，而且这些区域的边界并不锐利，是一种明暗相间的复杂图样。
【夫琅禾费衍射】(Fraunhofer diffraction) deals with the limiting cases where the source of light and the screen on which the pattern is observed are effectively at infinite distances from the aperture causing the diffraction.
【菲涅尔衍射】(Fresnel diffraction) refers to the general case where those restrictions are relaxed. This makes it much more complex mathematically. Some cases can be treated in a reasonable empirical and graphical manner to explain some observed phenomena.
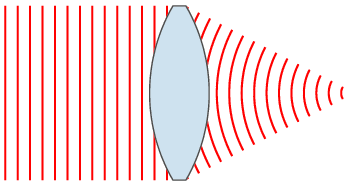Focal plane of a positive lens as the far field plane
观察夫琅和费衍射，要满足远场条件，即屏幕离aperture很远，不利于直接实验观察，所以加一个凸透镜，将无限远的衍射图像拉近到焦平面；另外，如果实验用的光源不是平行光，那么同样需要在光源和aperture之间放一个凸透镜。(右图为Plane wave focused by a lens) 在干涉、衍射装置中经常要用到透镜，光线经过透镜后并不附加【光程差】(Optical path length)。物点到象点（亮点）各光线之间的光程差为零。光程差\(\Delta=n s\)，即折射率和几何路径长度的乘积。光程的重要性在于确定光的相位，相位决定光的干涉和衍射行为。
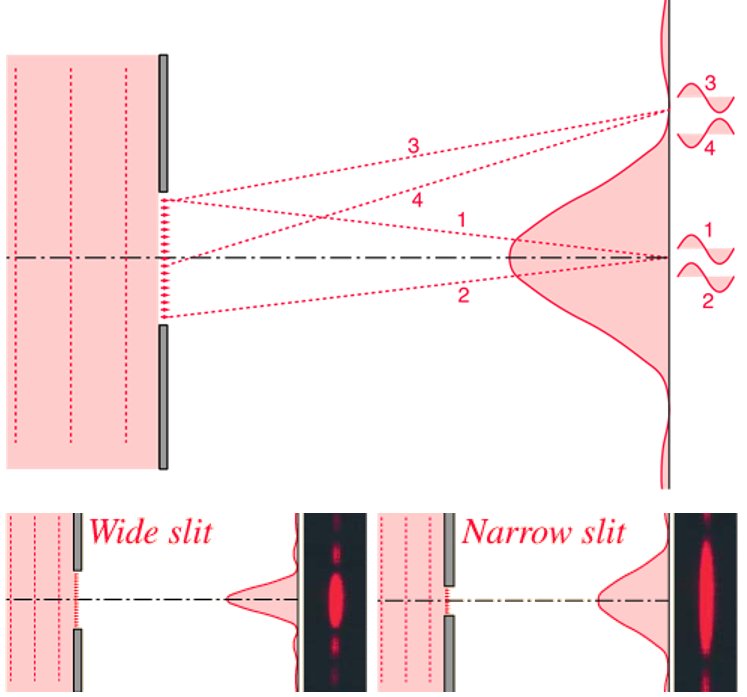narrower slit—wider diffraction pattern
One of the characteristics of single slit diffraction is that a narrower slit will give a wider diffraction pattern as illustrated below, which seems somewhat counter-intuitive. One way to visualize it is to consider that rays 3 and 4 must reach one half wavelength difference in light pathlength, and if the slit is narrower, it will take a greater angle of the rays to achieve that difference. 另外也可以定性分析波长的影响，
【半波带法】
半波带法全程其实是菲涅尔半波带法，可以用来处理上面的单封夫琅禾费衍射问题，还可以处理菲涅尔衍射(圆孔)问题，后者比较复杂，所以在这里没有展开讲。
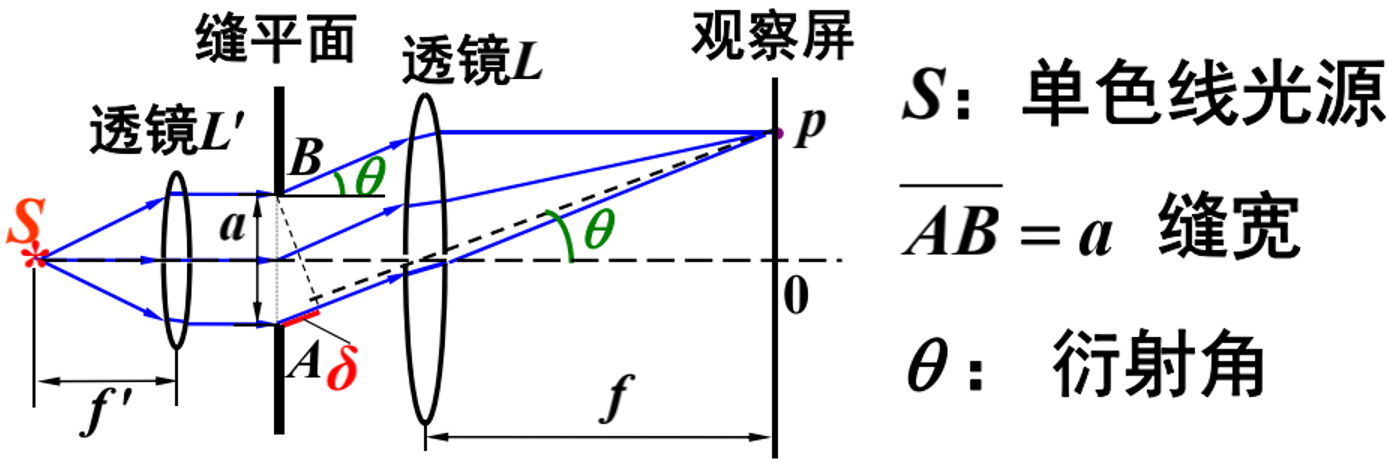
缝的两个顶点A和B到P点的光程差为\(\delta=a \sin \theta\)。
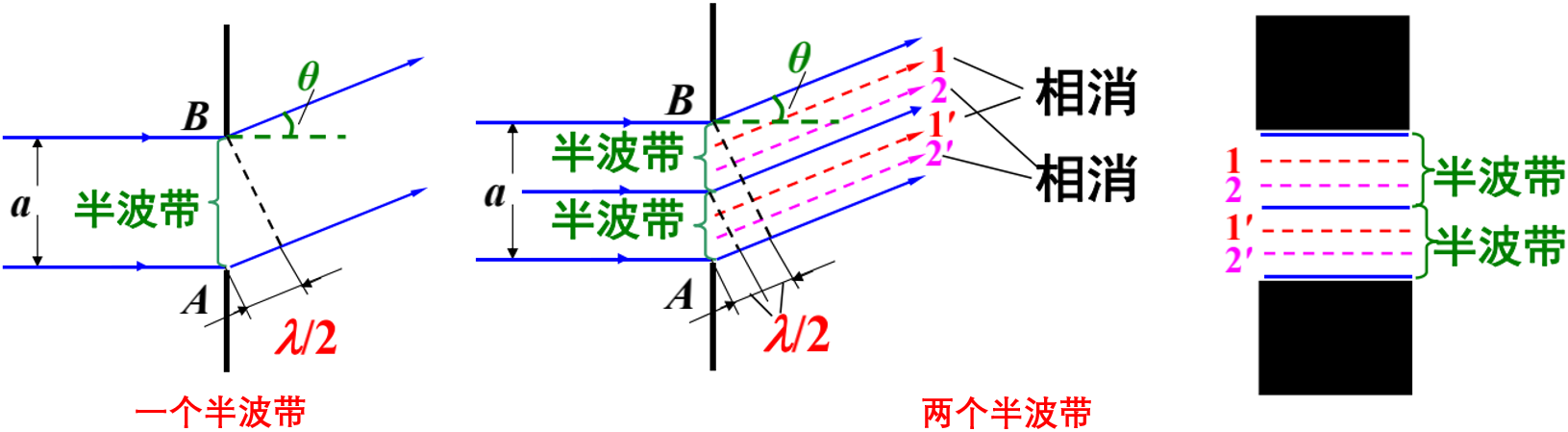
- 当\(a \sin \theta=\lambda / 2\)，可将缝看成一个半波带，此时是一个特殊情形(处在中央明纹中)，见下面讨论；
- 当\(a \sin \theta=\lambda\)，可将缝看成两个半波带，P点干涉相消，暗条纹；
- 当\(a \sin \theta=\displaystyle\frac{3}{2} \lambda\)，可将缝看成三个半波带，其中两个干涉相消，余下一个半波带不被抵消，P点形成明条纹(中心)；
- 为什么在夫琅禾费单缝衍射实验中，高中课本上不放凸透镜，而大学课本上放?—知乎
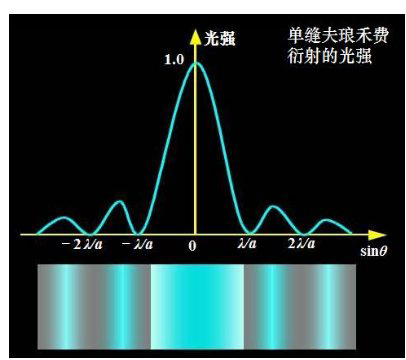次级明纹的强度只有中央明纹强度的4.5 %。如果我们将aperture改为圆孔(circular opening)，得到的就是将下面的图沿着光强轴旋转，屏幕上看到的就是中间一个亮的圆斑，周围一圈一圈明暗交替的圆圈，而且即使是亮的圆圈，亮度也很弱。在实际实验演示中，如果\( a\)比较大，那么\(\lambda/a\)很小，相邻明纹中间的暗纹宽度就不那么明显；如果\( a\)比较小，那么\(\lambda/a\)很大，不仅明纹宽度变宽，暗纹宽度也会变宽，此时我们就可以很容易观察到暗纹了。(这部分在之前的narrower slit—wider diffraction pattern也有讨论)
半波带法得到的一般结果：
- \(\delta=a \sin \theta=0\)——中央明纹中心(准确)
- \(a \sin \theta=\pm k \lambda, k=1,2,3, \cdots\)——暗纹(准确)
- \(a \sin \theta=\pm\left(2 k^{\prime}+1\right) \displaystyle\frac{\lambda}{2}, k^{\prime}=1,2,3, \cdots\)——次级明纹中心(近似)
- 中央明纹中心、暗纹位置准确，其他明纹中心的位置是近似的，与准确值稍有偏差；
- 其它各级明条纹的宽度为中央明条纹宽度的一半；
- 当半波带的数目正好是\(1\)，显然不满足暗纹公式，但是也不是次级明纹中心，而是处在中央明纹范围内。
采用振幅矢量法分析求解单缝衍射的结果，参考hyperphysics
拓展资料：
(1) 重温光学衍射，详解菲涅尔与夫琅禾费衍射
(2) 波动光学—PPT
(3) Single Slit Diffraction Intensity—hyperphysics
衍射和干涉的区别
费曼指出，没有人能够令人满意地定义干涉和衍射的区别，这只是术语用途的问题，其实二者在物理上并没有什么特别的、重要的区别。他还提到，如果只有少数的波源（例如两个的时候），我们称这现象为干涉，例如我们称杨氏双缝实验实验中双缝所产生的两束光源产生了干涉现象。而当大量波源存在时，对应的过程被称作是衍射。在实际情况中，衍射和干涉往往是同时出现的。
- 干涉是有限多个波束"相加"的结果，而衍射则是无限多个波束"积分"的结果；
- 干涉和衍射都是波的相干叠加，但干涉是有限多个分立光束的相干叠加，衍射是波阵面上无限多个子波的相干叠加，二者又常出现在同一现象中。
双缝干涉
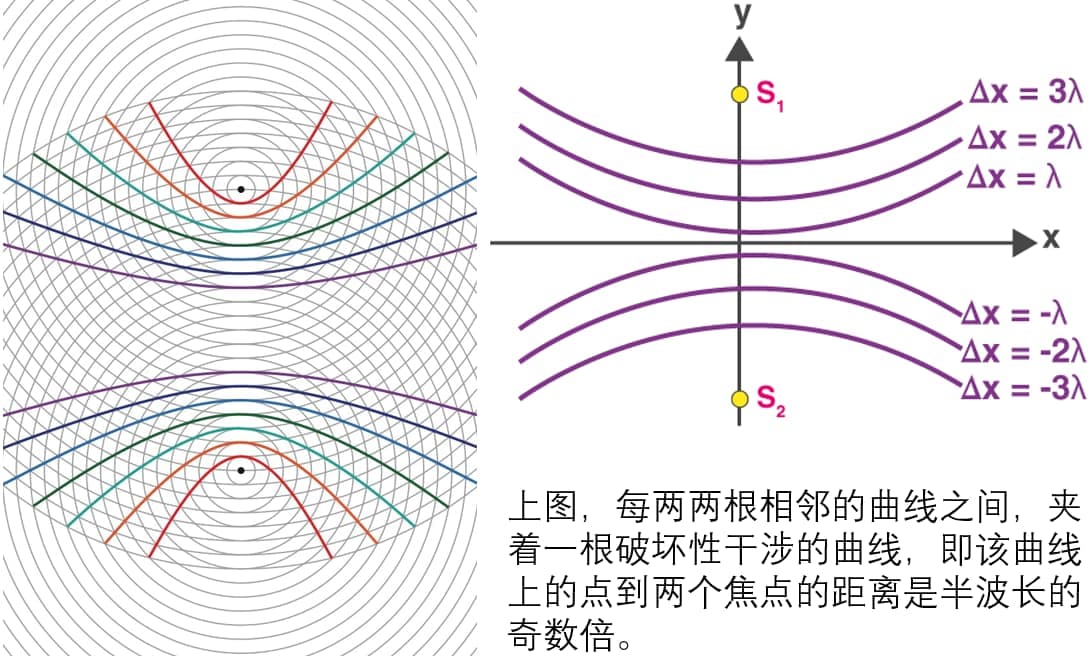
两个光源，完全相同(频率，相位，振幅)。对于【相长干涉】(建设性干涉，constructive interference)来说，点到振动源\(1\)和\(2\)的距离差是波长的整数倍，如果波是在二维平面传播，那么这些相干增强的点都在特定的双曲线上。当然，如果该点到\(1\)和\(2\)的距离相等，那么形成的集合就不是双曲线，而是点\(1\)和\(2\)连接的中垂线。【相消干涉】(摧毁性干涉，destructive interference)的分析方法和上面的一致。
分析：
- 如果是三维传播的球面波，其振幅按照\( 1/r \)衰减；如果是二维传播的波，比如水面中心振动导致的一圈一圈的水波，其振幅必须按照根号\( \sqrt{1/r} \)下降。
- 如果两个振动源都是向三维空间传播，那么只需要将前面的双曲线(或者中垂线)围绕着\(12\)连线轴旋转一周即可。
- 考虑P点离两个光源很远的情况，那么\(r_1\)和\(r_2\)都将远大于两个光源之间的距离，那么从P点看，两个光源是紧紧挨在一起，于是我们可以忽略这一事实：即光源\(2\)传播到P点的振幅，稍微小于光源\(1\)传播到P点的振幅。
双曲线与干涉
对于两个光源连线上的点，相邻振幅最大的点之间的距离是\( \displaystyle\frac {\lambda }{ 2 } \)，振幅最大处的数目和振幅最小处的数目都约为\( \displaystyle\frac {2d}{\lambda } \)。
杨氏双缝干涉
- 从双曲线的角度看，两个狭缝对应两个焦点，而\(D\)很大，所以\(P\)和中心点的连线可以看作是双曲线的一条【渐近线】(asymptote)，从\(P\)的观察视角看，实际的\( \theta \)叫很小；
- \(r_1\)和\(r_2\)的光程差两种理解方式：
- 从上焦点往\(r_2\)做垂线，得到一个顶角非常小，两个底角中，一个维90度，另一个非常接近90度，这样我们就可将其近似看作是【等腰三角形】(Isosceles triangle)，于是光程差为图中\(\delta \)；
- 由于屏幕很远，所以从屏幕去观察两个焦点的角度非常接近，想象一下自己站在一个半径很大的圆的圆心去观察圆周上两个靠得很近的点，观察角度变化非常小，所以我们直接将\(r_1\)和\(r_2\)化成两条平行线，类似于之前的单个半波带的画法，认为两条平行线在无穷远处相交与\(P\)点。
- 近似处理：\(\delta=r_2-r_1 \approx d \sin \theta \approx d \tan \theta=d \displaystyle\frac{x}{D}\)
- 明纹中心的计算：\(d \sin \theta_n=n \lambda\)，其中\(n=0,1,2, \cdots\)
- 暗纹中心的计算：\(d \sin \theta_n=(2 n+1) \displaystyle\frac{\lambda}{2}\)，其中\(n=0,1,2, \cdots\)
激光双缝干涉实验—实际结果
laser beam的宽度(直径3 mm )远大于双缝宽度(0.088 mm)。两个开口就是两个惠更斯源，理论上亮纹区域的亮度应该不会差很多，但实际并不是。这是因为我们的狭缝是有宽度的，如果狭缝非常非常窄，那么不同亮纹区的强度就会比较接近，但是这会导致只有很少亮的光通过狭缝，使得我们看到的干涉条纹强度很弱。因此需要有一个平衡点trade-off。总之这里的现象表明反相位光与光叠加之后肯能变为没有光，表明了光的波动性。
注：在我们Edinburgh光谱仪测试中，其中也有同样的问题，对diffraction grating来说，如果想分光很准确(即能分出单色性很好的光)，那么狭缝要开得很小，但是这个时候的强度必然很小，也要有一个trade-off。
激光双缝干涉实验—理想理论结果
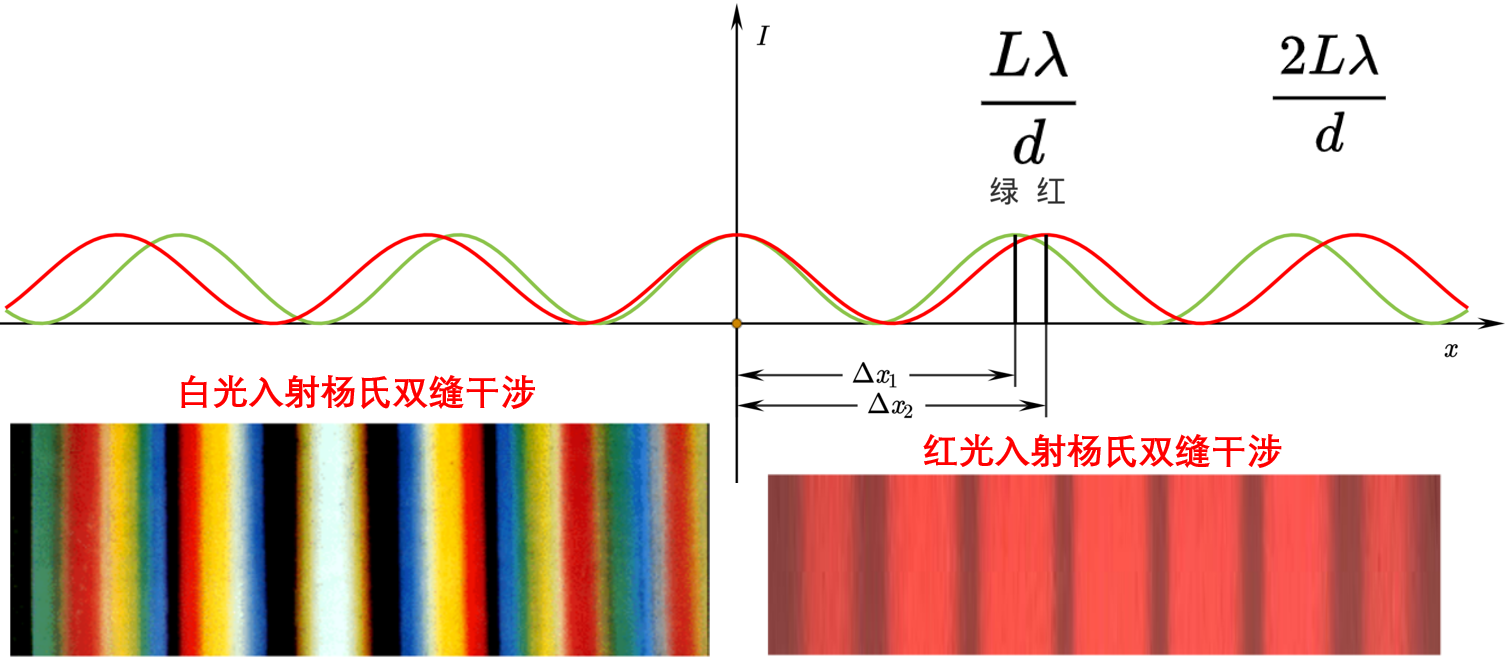
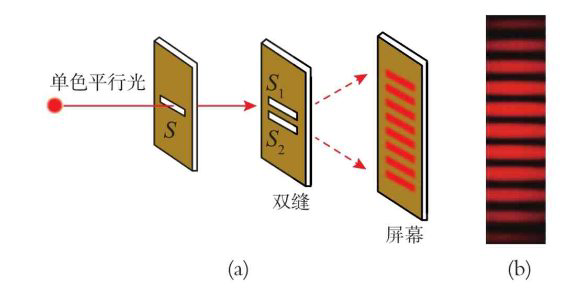单色/双色/多色光的杨氏双缝干涉结果
教授的雷达实验，用1000Hz的音频信号来调制这个10GHz信号，这句话如何理解？调幅(amplititude modulation)
扬声器实验
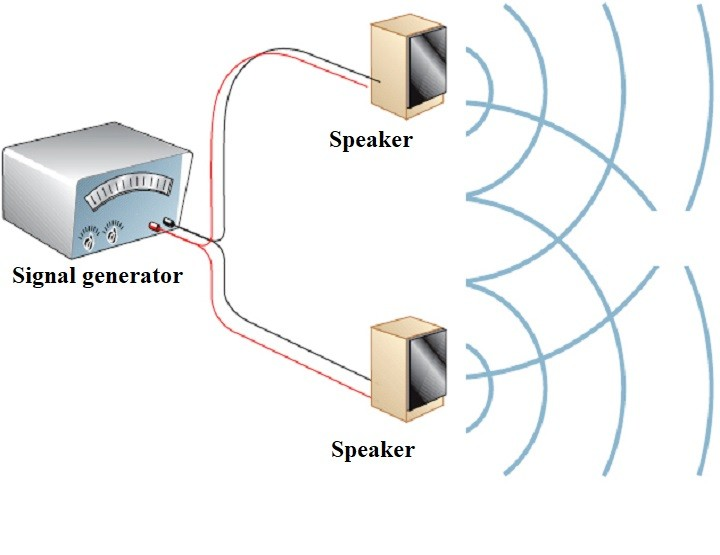教授用两个扬声器模拟光源，两个扬声器靠的很近，在教室的不同位置听到的声音强度不同。听的时候必须捂住一个耳朵，可能移动一点点就可以，感受到声音强度的剧烈变化(从干涉增强点到干涉相消点)。
法布里－佩罗干涉仪
待补充
光栅和分辨率
【光栅】(grating)是由大量的等宽等间距的平行狭缝构成的光学元件。广义上来讲，任何具有空间周期性的衍射屏都可叫作光栅。
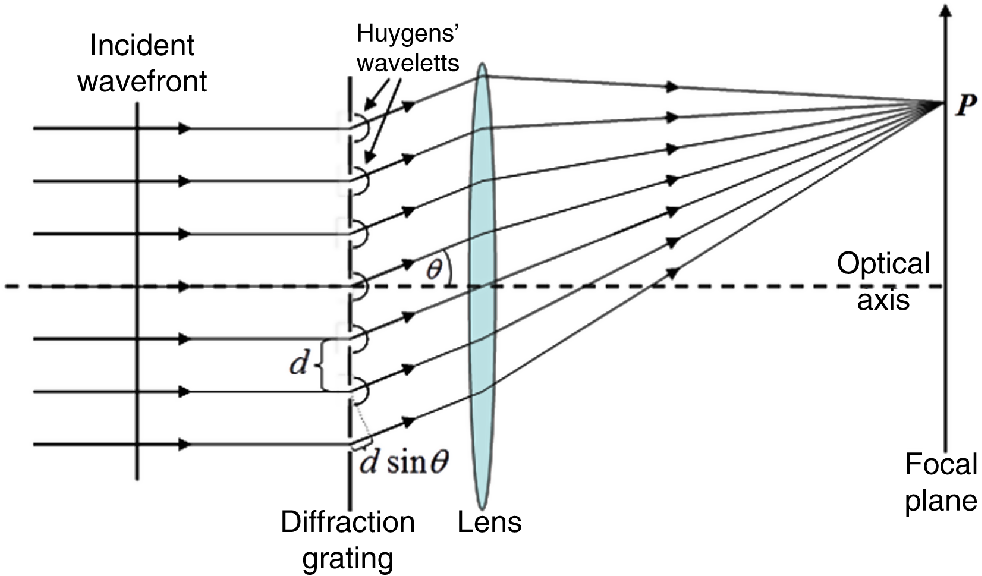
光栅常数\(d=a+b\)，其中\(a\)为透光部分的宽度，\(b\)为不透光部分的宽度。普通光栅刻线为数十条/mm到数千条/mm；用电子束刻制可达数万条/mm。
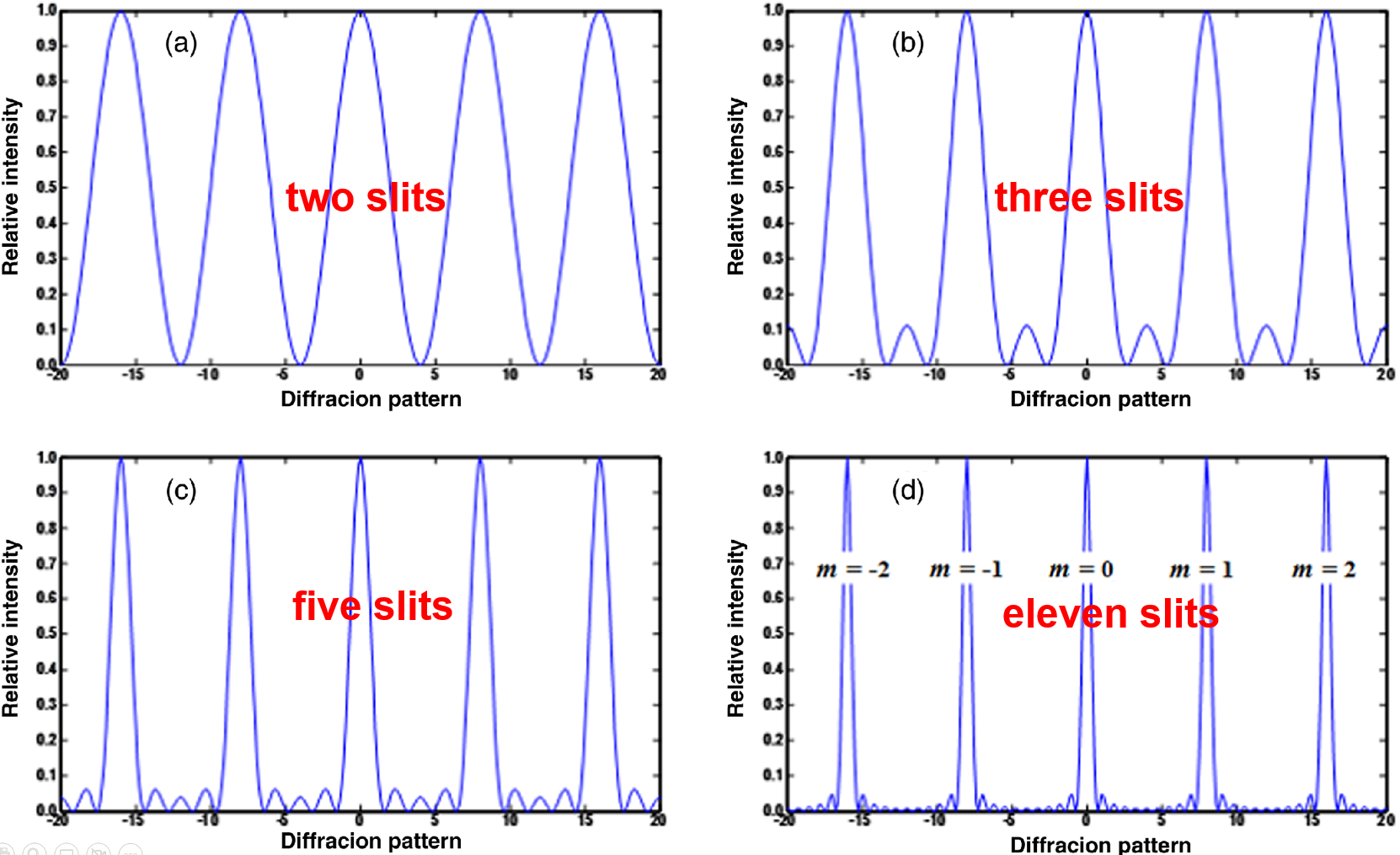
The Fraunhofer diffraction pattern of an array of equally spaced narrow slits is illustrated above as the number of slits is increased. 在间距\(d\)(光纤常数)不变的情况下，设slit的个数为\(N\)个，那么：
- 变化\(N\)并不改变明纹中心的位置，即位置和我们之前讨论的杨氏双缝干涉的结果是一样的，明纹中心的计算结果如下：$$\begin{gathered} \sin \theta_n=\frac{n \lambda}{d} \approx \theta_n \\ \theta_n \approx \frac{n\lambda}{d} \quad x_n \approx \frac{L n \lambda}{d} \end{gathered}$$
- 变化\(N\)，虽然每个明纹的强度都会变化，但是各个明纹的强度是相同的(在不考虑狭缝宽度的影响下是成立的)；
- \(N\)越大，那么这些线(干涉增强的spike)会变的极窄，这就是多缝干涉和双缝干涉的重大区别；
- \(N\)越大，那么通过所有狭缝的总的光强也越大；
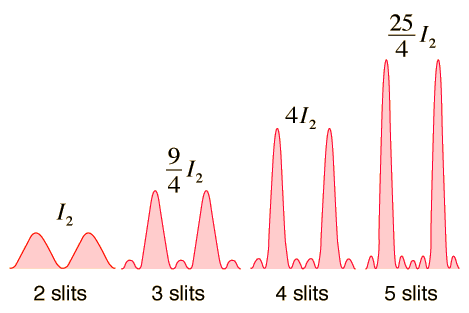
- 同时考虑上面两个因素，那么spike对应的max的光强度\(\propto N^2\)，以此保证了能量守恒，如上图；
- 从上图也可以看出，\(N\)个slits的结果，相邻max之间的min的个数为\(N-1\)个；
- 从上图也可以看出，相邻max和min的radians宽度为\(\displaystyle\frac {\lambda}{dN} \)，一个周期要跨过\(N\)个这样的radians宽度；
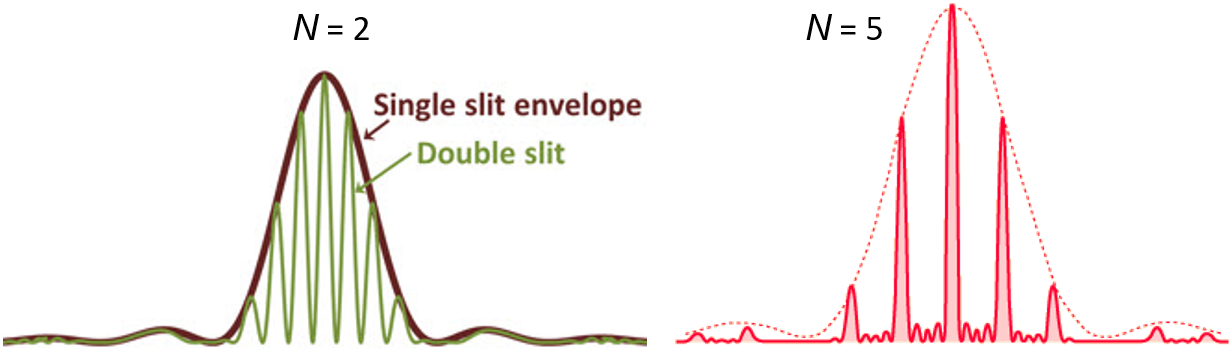
实际的光栅，狭缝的宽度不是无限小的，所以要考虑狭缝宽度造成的影响(即每个狭缝都有自己的单封夫琅禾费衍射)，那么得到的会是上面强度分布modulated by the single slit diffraction envelope for the slits which make up the grating。不同\(N\)下的结果可以参考hyperphysics，可以选择Diffraction and interference和Interference only两种模式去观察强度分布。上图给出了同时考虑Diffraction and interference下的杨氏双缝干涉的结果，以及\(N=5\)个slits的结果。以\(N=5\)个slits为例，首先利用旋转矢量法求解出了interference intensity expression：(其中\(\delta=\displaystyle\frac{2 \pi}{\lambda} d \sin \theta\)，\( d\)为光栅常数)$$ I=I_0 \frac{\sin ^2\left[N \frac{\delta}{2}\right]}{\sin ^2\left[\frac{\delta}{2}\right]} $$然后再次利用此方法得到envelope的强度$$ I=I_0 \frac{\sin ^2\left[\frac{\delta}{2}\right]}{\left[\frac{\delta}{2}\right]^2} $$Their product gives the total intensity expression:$$ I=I_0 \frac{\sin ^2\left[\frac{\delta}{2}\right] \sin ^2\left[N \frac{\delta}{2}\right]}{\left[\frac{\delta}{2}\right]^2 \sin ^2\left[\frac{\delta}{2}\right]} $$- 如果用白光进行光栅实验，由于每种光的波长不同，在中间的条纹为白色，其余的为彩色。
光栅小实验
光栅的应用
- 鉴定元素，课堂上老师用的是氖灯放在光栅前面；
- XRD
- 等待补充。
参考资料：
(1) All About Diffraction Gratings—Edmund
(2) Understanding diffraction grating behavior: including conical diffraction and Rayleigh anomalies from transmission gratings-SPIE
(3) Grating concepts—hyperphysics
【瑞利分辨率准则】(Rayleigh criterion of resolution)参考这里，有待补充扩展
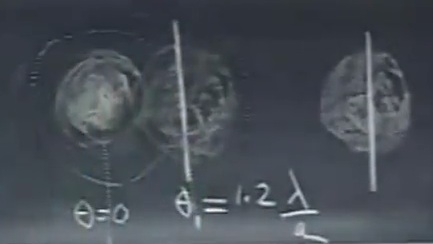定义角分辨率的标准。两个光源的距离为第二个光源中心落在第一个光源的暗带上。大于这个角度是两个光源，小于即是一个光源。
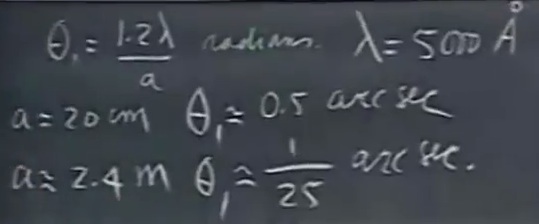
望远镜越大，得到的角分辨率越高，分辨两个亮度一样的星星的能力越强。
多普勒效应和宇宙大爆炸