材料磁性
电场可以在物体中感应出电偶极子,当分子和原子自身是永久电偶极子时,外部电场会试图让它们有序排列,这在之前的电介质中有详细讨论过。电偶极子排列的有序程度完全取决于外部电场的强度和温度。如果温度很低,热扰动会很小,这样偶极子定向排列更容易一些,磁场也有类似情况。
如果我有一个外磁场,它可以在物质中感应出磁偶极子(在原子尺度上)。如果原子或分子自身拥有永久磁偶极矩,那么外磁场会试图排列这些偶极子,排列的有序程度取决于外磁场的强度和温度,温度越低越容易排列它们。所以把物质放入到真空磁场中,场会发生变化,即内部磁场和外部磁场(真空磁场)是不同的。
【磁偶极矩】(Magnetic moment) 一个回路电流,磁偶极矩\(\vec{\mu}\)就是电流\(I\)乘以面积\(\vec{A}\)。根据右手螺旋定则定义,向量\(\vec{A}\)方向垂直向上。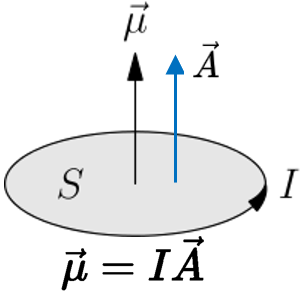
【顺磁性】(paramagnetism)和【抗磁性】(diamagnetism)的产生都可以对应到电流,在外磁场下,对顺磁性物质来说,电流的磁场进一步增强原来的磁场,对抗磁性物质来说,电流的磁场削弱原来的外磁场,两种物质的“电流”方向是不同的。注意这里讨论的情况是外磁场固定,所以抗磁性物质的抗磁性来源并不是楞次定律或者涡电流。
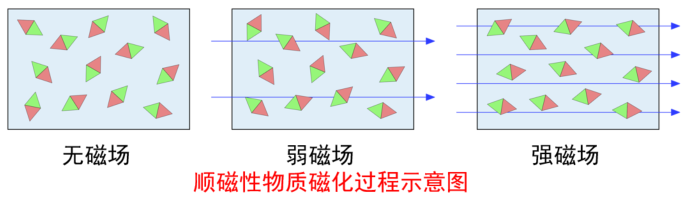
顺磁性物质被磁铁吸引的本质原因是磁场的非均匀性。将顺磁性物质放在非均匀磁场中,该物质会被拉向磁场最强的地方。顺磁性物质,在没有外界磁场下,每一个微元“磁矩”都是随机排列的,宏观上表现出没有方向性,随着外界磁场越来越强,宏观表现出的方向性越来越强,也就是说,单个“磁矩”来看,它们产生的磁场方向似乎是随机的(热运动导致的),但是宏观统计上表现出一定的方向性。外界磁场移去后,立马不存在宏观上的方向性,恢复到初始的杂乱无章的状态。顺磁性材料产生的力通常只有自身重量的百分之几,所以铝放在磁铁下端会掉。
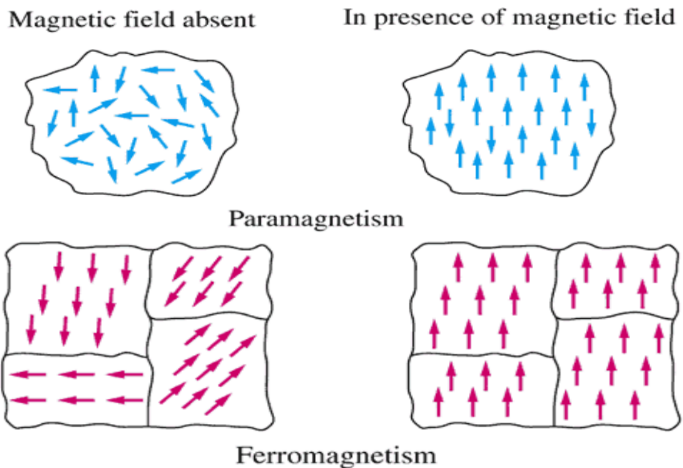
【铁磁性】(ferromagnetism)物质(最典型的就是铁),存在很多磁畴(尺度在~0.1 mm量级),每个磁畴内包含方向相同的多个磁矩,不同磁畴之间的磁矩不一样,所以这样看,宏观上也没有方向性(净磁矩),因为“磁畴”是没有方向性的。在外界磁场(不需要很大)作用下,这些磁畴立马都朝同一个方向,大大增强了原有的磁场(三个数量级以上)。移开外界磁场,会有少量磁畴的方向又恢复到杂乱无章的状态,但是总的趋向还是没有变化,也就是说得到“永久磁性”,如果不断提高温度,那么磁畴的取向混乱度增加,直到宏观上不表现任何方向性,也就是恢复到初始的杂乱无章的状态,另一种undo磁性的方法就是用锤子敲(bang on it with a hammer)。对于铁磁性物质,内部的磁场可能比外界的真空磁场强几千倍。关于铁磁性的理论可以看这里。
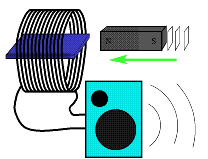 【巴克豪森效应】:When an external magnetizing field through a piece of ferromagnetic material is changed, for example by moving a magnet toward or away from an iron bar, the magnetization of the material changes in a series of discontinuous changes, causing "jumps" in the magnetic flux through the iron. These can be detected by winding a coil of wire around the bar, attached to an amplifier and loudspeaker. The sudden transitions in the magnetization of the material produce current pulses in the coil, which when amplified produce a sound in the loudspeaker.
【巴克豪森效应】:When an external magnetizing field through a piece of ferromagnetic material is changed, for example by moving a magnet toward or away from an iron bar, the magnetization of the material changes in a series of discontinuous changes, causing "jumps" in the magnetic flux through the iron. These can be detected by winding a coil of wire around the bar, attached to an amplifier and loudspeaker. The sudden transitions in the magnetization of the material produce current pulses in the coil, which when amplified produce a sound in the loudspeaker.
巴克豪森效应是指将铁磁材料从退磁状态加磁场磁化到饱和,在中间阶段,铁磁材料是以磁畴突然长大,不可逆和不连续位移过程实现磁化的。巴克豪森效应用来看磁畴的变化,磁畴的跳跃变化。巴克豪森效应说明两点:在磁化的中间阶段,铁磁材料以磁畴完成磁化;而不是以单个原子完成磁化。参考动画网站 和康奈尔大学网站,注意存在两种情况,coil里面不放iron core和放iron core:
coil里面不放iron core——那么非常快速移动磁铁会使得线圈磁通量发生变化,于是产生EMF,喇叭会出现低沉的声音。如果磁铁的移动速度很慢,你什么也听不到,因为磁通量变化率太小了。
coil里面放iron core——非常慢速移动磁铁(从远处靠近coil),可以听到噼啪声,即磁畴发生变化,于是铁磁性材料内部有一个磁通量的变化,线圈感知到它,你就听到那个电流。
在很多情况下,材料内部的磁场强度和外界的磁场强度成正比(这个比值就叫做相对磁导率),但是很多都不成正比。顺磁性和铁磁性的特性都和温度相关,温度越低(thermal agitation小),越容易实现磁偶极子的alignment;抗磁性物质的特性和温度没有关系。
\(\mathbf{B}\)和\(\mathbf{H}\)的区别
(1) 矢量场\(\mathbf{B}\):常叫作“磁通量密度”(magnetic flux density)、“磁感应强度”(magnetic induction)、“B场”,多数物理学家公认B场为更基本的物理量,因此他们称呼B场为“磁场”。
(2) 矢量场\(\mathbf{H}\):常称为“磁场强度”(magnetic field intensity或magnetic field strength)或“附属磁场”(auxiliary magnetic field)或干脆“H场”。
(3) Andrea Lommen: So what I’m about to call \(\mathbf{H}\) is really the field NOWHERE. It’s not a physical quantity. It’s just way more useful for doing problems than calculating bound currents.
(4) 二者的关系:\(\mathbf{H} \stackrel{\text { def }}{=} \displaystyle\frac{\mathbf{B}}{\mu_{0}}-\mathbf{M}\),将\(\mathbf{B}\)写在右边是因为其实更基本的物理量。
磁导率和磁化率
(1) 【磁导率】(Permeability): 由\( \mathbf{B}=\mu \mathbf{H}\),磁导率\(\mu\)在各向同性介质中为一个标量,在各向异性的介质中为张量。
(2) 【相对磁导率】(Relative permeability):是特殊介质的磁导率和真空磁导率\(\mu_0\)的比值\( \displaystyle \mu_{r}=\frac{\mu}{\mu_{0}} \)
(3) 【磁化率】(magnetic susceptibility):\( \chi_{m}=\mu_{r}-1\),一个无量纲的量,有时候被称为体积磁化率,以区别于\(\chi_{P}\)(质量磁化率)和\(\chi_{M}\)(摩尔或摩尔质量磁化率)。其实这里的磁化率类似电介质产生的内建电场,但是总的叠加的电场效果是由最终的介电系数决定的,介电系数就对应于这里的相对磁导率。类比这里的磁场,电介质的“磁化率”(电极化率)都是负的,因为其方向和外加电场的方向相反。

- \(\mathbf{D}\)和\(\mathbf{H}\)只是辅助矢量,它们的引入使方程组只出现自由电荷和自由电流,仅仅是为了讨论方便,它们本身不是真实的场,它们不会对身处其中的电荷/电流产生作用力。
- 顺磁性和铁磁性的特性取决于温度,但是反磁铁特性不取决于温度;
- 反磁性材料的磁导率,为负数;
- 顺磁性材料的磁导率,为正,但是也很小;
- 铁磁性材料的磁导率,为正,数量级很大。
Gd钆是一种很特殊的材料,在16℃以下是铁磁性的,在此温度之上是顺磁性的。
【居里温度】:如果加热铁磁性材料,加热到一个特定的温度,那么它可以完全丧失铁磁特性,这是因为此时磁畴解体消失了。这个过程发生在一个非常精确的温度即居里温度,要理解这一现象需要量子力学。对于铁来说是770度,加热到此温度铁从铁磁性变为顺磁性。也就是说如果铁磁性材料挂在一块磁铁上,你把它加热到居里温度以上,它就会掉下来,因为顺磁性物质通常不会挂在磁铁上(产生的力太小)。
电流可以分为自由电流和束缚电流,而束缚电流又可以分为磁化电流和电极化电流。写成公式,总的电流密度$$\mathbf{J}=\mathbf{J}_{\mathbf{f}}+\mathbf{J}_{\mathbf{M}}+\mathbf{J}_{\mathbf{P}}$$ 【自有电流】就是我们教科书通常默认的“电流”,也就是自由载流子的定向移动。例如通过一个导线或者一个电池的电流。自有电流与束缚电流的区别是,后者出现于可以被磁化或者电极化的宏观物质里(每一种物质都会或多或少地被电极化或磁化)。
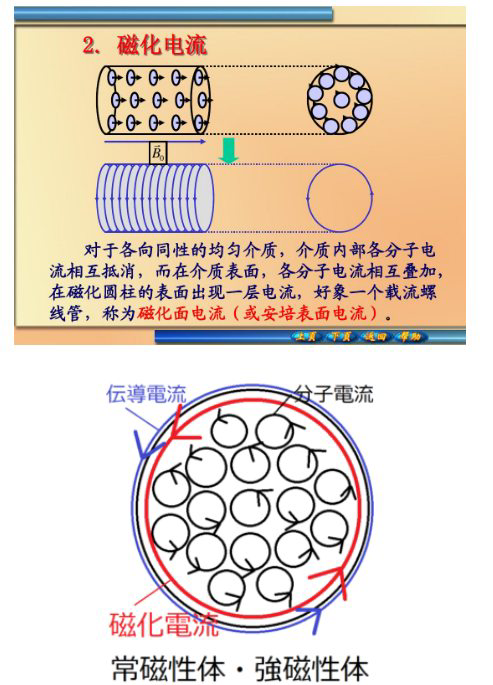
【磁化电流】当一个物质被磁化的时候(例如将此物质置于外磁场),电子仍旧束缚于它们所属的原子。但是,它们的物理行为有所改变(会与感受到的磁场耦合),产生微观电流。将这些电流总和在一起,就会有如同宏观电流一般的效应,环绕于磁化物体的内部或表面,称为磁化电流。\(\mathbf{J}_{M} \stackrel{\text {def}}{=} \nabla \times \mathbf{M}\),其中\(\mathbf{M}\)是磁化强度(电位体积的磁偶极矩)。
【电极化电流】可电极化物质内的正束缚电荷和负束缚电荷会以原子的距离相互分立。假设电场随着时间而变化,束缚电荷也会随着时间而移动,因而产生“电极化电流”。电流密度\(\mathbf{J}_{P} \stackrel{\text {def}}{=} \displaystyle\frac{\partial \mathbf{P}}{\partial t}\),其中\(\mathbf{P}\)是电极化强度。
磁滞和麦克斯韦方程组
波尔氢原子轨道理论的三个假设:
(1) 电子在原子中,可以在一些特定的圆轨道上运动而不辐射电磁波,这时原子处于稳定的状态(简称稳态),并具有一定的能量;
(2) 电子以速度\( v\)在半径为\( r\)的圆周轨道上绕核运动,只有当电子的角动量\( L\)为\( \displaystyle\frac{h}{2 \pi}\)的整数倍时的轨道才是稳定的,即\(mvr=n \displaystyle\frac{h}{2 \pi} \),因此量子化的角动量\( L=n \hbar\)。其实这和电子形成驻波的条件是一致的,通过\( n\lambda=2 \pi r \)和\( p=h / \lambda \)我们同样可以得到上述角动量的量子化结果。
(3) 当原子从高能量的定态跃迁到低能量的定态时,要发射光子。
上述理论不足之处:
(1) 波尔假设的量子化条件是为了凑结果而做的,实际上的轨道角动量的量子化结果是\( L=\sqrt{l(l+1)} \hbar\)(\( l\)从零开始的整数),而不是\( n \hbar \)(\( n \)从\( 1\)开始的整数)。在量子力学中,可以将\( L\)写作角动量的算子,然后作用在波函数上,得到的特征值集合就是其角动量的集合。参考:资料 李威仪固体物理
(2) 波尔所谓的角动量量子化,最终其实得到的是主量子\( n\),而量子力学中决定角动量的是角量子数\( l\),量子化是指角动量\( \sqrt{l(l+1) \hbar} \)在外磁场下,其\( z \)轴分量的角动量是量子化的。总而言之,波尔其实是为了凑结果,和量子力学出入很大。
(3) 经典力学中,做加速运动的电子会辐射出电磁波,致使能量不断损失,而玻尔模型无法解释为什么处于定态中的电子不发出电磁辐射。
【波尔半径】(Bohr radius):
(1) 直观来说,波尔半径就是氢原子核到核外第一层(最近一层,满足驻波条件的最小半径)的距离。
(2) 根据库仑力等于向心力,以及驻波条件\(mvr=n \displaystyle\frac{h}{2 \pi} \)求出\( r=\displaystyle\frac{4 \pi \varepsilon_{0} \hbar^{2}}{m_{e} e^{2}} n^{2}\),\( n=1\)时的半径即为波尔半径,一般用\(a_0\)表示,大约为\(0.53 \overset{\circ}{\mathrm{A}}\)。
【玻尔磁子】(Bohr magneton)
玻尔磁子\( \mu_{B}\)是与电子相关的磁矩基本单位,是一项常数,是轨道磁矩/自旋磁矩的基本单元,而\(\hbar\)是电子角动量改变间隔的基本单位。
氢原子,核外电子围绕着带一个正电的原子做圆周运动,圆周半径(也就是波尔半径)已知,向心力也很容易知道,于是就可以算出电子的速度(就知道运动周期),也就知道环绕质子的电流大小(电子所带电荷除以周期,结果约为1 mA)。利用\(\boldsymbol{\mu}=I \mathbf{a}\)就可以求得磁矩大小。量子力学表明,轨道上所有电子的磁矩大小都只能是这个波尔磁子产生的磁矩大小的整数倍(量子化,最小是0)。磁矩就是磁偶极矩。
令\( m v r=n \displaystyle\frac{h}{2 \pi} \)中的\( n=1 \)或者更严谨的话,令\(m v r=\sqrt{l(l+1)} \displaystyle\frac{h}{2 \pi} \)中的\( l=0\) (H原子的\(1 s \)轨道),但是不改变结果。于是就可以得到\( vr=\displaystyle\frac { \hbar }{ 2m } \),于是磁偶极矩,或者说玻尔磁子的大小计算方法如下:(大约为\(9.27 \times 10^{-24} \mathrm{A} \cdot \mathrm{m}^{2} \))$$ \mu_B=I \mathrm{a}=\frac{e}{T} \pi r^2=\frac{e v}{2 \pi r} \pi r^2=\frac{e v r}{2}=\frac{e \hbar}{2 m} $$Total magnetic moment = Intrinsic spin magnetic moment + Orbital magnetic moment
电子【自旋磁矩】在外场方向上的投影等于玻尔磁子$$\mu_{S z}=\pm \mu_{B}=\gamma_{s} m_{s} \hbar$$其中\(\gamma_{s}=-\displaystyle\frac{e}{m}\)为【电子自旋旋磁比】,\( m_{s}=\pm \displaystyle\frac{1}{2} \)为【自旋量子数】。注意旋磁比是磁矩比上角动量,电子自旋在磁场方向的角动量大小为\( \displaystyle\frac{1}{2} \hbar\),所以旋磁比为\( \gamma \approx \displaystyle\frac{\mu_{B}}{\frac{1}{2} \hbar}=\displaystyle\frac{2 \mu_{B}}{\hbar}\),更精确的结果是\( \displaystyle\frac{g_{\mathrm{e}} \mu_{B}}{\hbar}\),其中\(g_{\mathrm{e}}\)是电子的朗德\(g\)因子。
经典体系的磁旋比(For a classical rotating body)为\(\gamma=\displaystyle\frac{q}{2 m}\),计算如下:$$ \mu=I A=\displaystyle\frac{q v}{2 \pi r} \times \pi r^{2}=\frac{q}{2 m} \times m v r=\frac{q}{2 m} L$$ 电子【轨道磁矩】:\(\vec{\mu}_L=-\displaystyle\frac{e}{2 m} \vec{L}\)其中\(-\displaystyle\frac{e}{2 m}\)为【电子轨道磁旋比】,等于电子自旋磁旋比的一半。轨道磁矩的方向和电子角动量的方向正好相反,而\(L=\hbar \sqrt{l(l+1)}\),因此电子的轨道磁矩可以写成$$ \mu_L=\mu_B \sqrt{l(l+1)} $$
电子【轨道磁矩】:\(\vec{\mu}_L=-\displaystyle\frac{e}{2 m} \vec{L}\)其中\(-\displaystyle\frac{e}{2 m}\)为【电子轨道磁旋比】,等于电子自旋磁旋比的一半。轨道磁矩的方向和电子角动量的方向正好相反,而\(L=\hbar \sqrt{l(l+1)}\),因此电子的轨道磁矩可以写成$$ \mu_L=\mu_B \sqrt{l(l+1)} $$
拓展资料:
1. 参考资料:固体的磁性(百度文库)2. 自旋角动量没有经典对应,是纯粹的量子效应,在宏观世界没有类比,所以不要深究这个概念。当然了也不要深究自旋的概念。我们计算经典的经典体系的旋磁比,似乎和量子力学的轨道旋磁比结果一致,但是不要简单类比,以为轨道角动量是电子在围绕原子核打圈圈,但是事实上不是的!按照经典的角动量概念,角动量是矢量,有方向。那我现在给你一个原子,比如碳原子吧,它的电子轨道角动量在哪个方向?谁知道?没人知道,因为它不是我们经典的角动量!量子力学里的角动量只是描述空间旋转不变性的一个物理量而已!
3. 自旋角动量与轨道角动量的物理意义?(知乎)
常见的净磁矩大小是一个或者两个波尔磁子
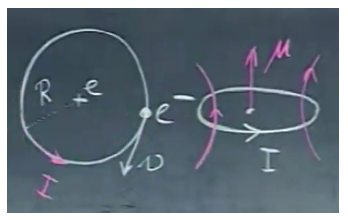
材料内部总的磁场
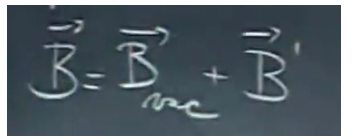
如果由磁偶极子产生的磁场强度正比于外界的真空磁场大小,那么材料内部总的磁场大小正比于外界磁场大小(对于顺磁性物质,这是成立的)。
铁磁性物质中磁场强度的计算
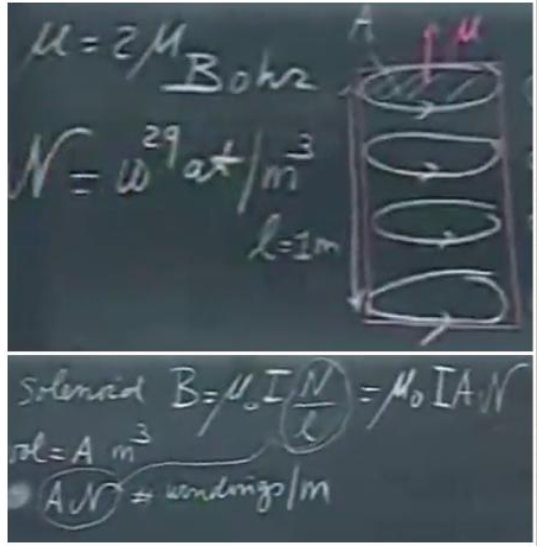
假设所有偶极子偏转的情况。带入数值,得到2.3T。
铁磁性材料内部磁场
 开始的时候线性增加,然后增加的速度原来越慢,到后面几乎饱和了,也就是说磁偶极子产生的磁场保持不变,增加的只是外界磁场的部分,这边一部分变化很小,所以后面接近水平线。如果温度越低(磁偶极子更容易定向排列),那么开始的斜率就更大,在更低的外界磁场强度下,就达到了饱和状态。
开始的时候线性增加,然后增加的速度原来越慢,到后面几乎饱和了,也就是说磁偶极子产生的磁场保持不变,增加的只是外界磁场的部分,这边一部分变化很小,所以后面接近水平线。如果温度越低(磁偶极子更容易定向排列),那么开始的斜率就更大,在更低的外界磁场强度下,就达到了饱和状态。
磁滞回线(hysteresis loop)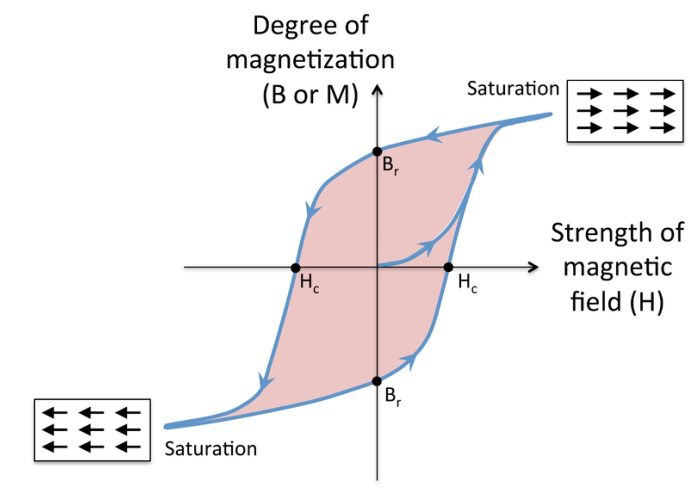
- 外界磁场强度(真空磁场强度)是由线圈的电流控制的,电流越大,真空磁场强度(磁感应强度)越大;
- 在相同的电流下,铁磁性物质内部的总磁场大小有两种可能(作y轴的平行线),也就是说和这个材料的历史有关;
- 注意在这个包裹的区域内的那条蓝色的线是处子线(virginal curve),也就是说一旦启动就回不去了。
退磁的方法
铁磁性材料带磁后,因为磁滞回线,不会自行回到初始状态,需要退磁,有三种方法:
1,加热到居里点(居里温度)以上,再冷却;
2,用锤子砸,迫使磁畴重新排列;
3,使用交变磁场磁场,但是磁场幅度逐渐减小。
注:退了磁之后,还可以通过外界磁场再次给铁磁性物质充磁。
铁磁性材料会显著改变外磁场的分布(原有磁铁的磁力线),吸引外磁场(磁力线)进入铁磁性材料,从而减少在别处的分布。
拓展:铁磁性物质控制电饭煲温度
其实原理很简单。在锅底中心,有一种特殊的材料:感温铁氧体。感温铁氧体是用氧化锰、氧化锌、氧化铁粉沫混合烧结而成,常温下是铁磁性的,也就是说磁性比较强。但是温度上升到约103度时就会变为顺磁性,此时的磁性就很弱了。这种磁性转变的温度称为“居里点”。注意由于水烧不到103度,所以用电饭煲烧水不会自动断电。参考李永乐视频
麦克斯韦方程组总结$$\begin{aligned}
&\oint \vec{E} \cdot d \vec{A}=\frac{Q_{f e e e}}{\kappa \varepsilon_{0}}\\
&\oint \vec{B} \cdot d \vec{A}=0\\
&\oint \vec{E} \cdot d \vec{l}=-\frac{d \Phi_{B}}{d t}\\
&\oint \vec{B} \cdot d \vec{l}=\kappa_{m} \mu_{0}\left(I_{e n c}+\varepsilon_{0} \kappa \frac{d \Phi_{E}}{d t}\right)
\end{aligned}$$
第一个公式是高斯定律,封闭面的电通量和里面包含的电荷成正比;
第二个公式描述的是磁场的无源性,也就是不存在磁单极子,封闭曲面的磁通量为0,有多少进,就有多少出;
第三个公式描述的是感生电动势和磁通量的变化率有关,左边电场强度的路径积分是电动势;
第四个公式是麦克斯韦修正的安培定律,左边是对close loop的积分,右边是穿过open surface的真实电流+位移电流。
参考资料:
(1) 如何深入浅出地讲解麦克斯韦方程组?—知乎
(2) 为什么我在学习完麦克斯韦方程组后并没有感觉很惊讶?—知乎
(3) 麦克斯韦方程组与波动方程—知乎
(4) 麦克斯韦方程组在数学和物理上揭示了什么联系?为什么它也不是完全对称的?—知乎
变压器、RC电路
RC电路
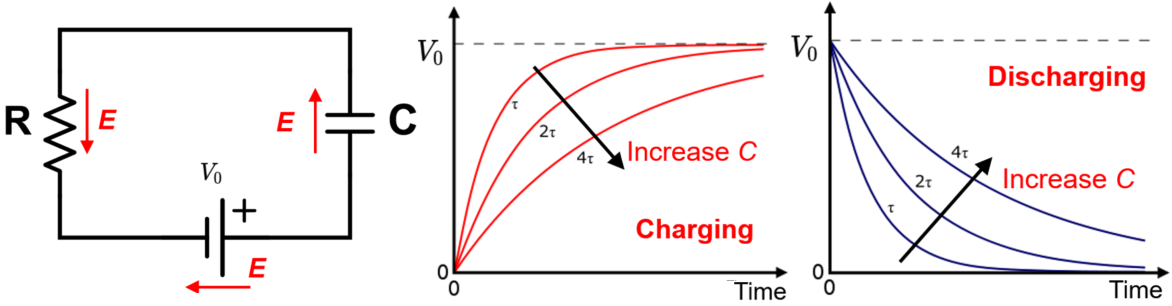 $$\begin{aligned} &\oint \vec{E} \cdot d \vec{l}=0 \Longrightarrow+V_C+I R-V_0=0 \\ &\frac{Q}{C}+R \frac{d Q}{d t}-V_0=0 \\ &Q=V_0 C\left(1-e^{-t / R C}\right) \Longrightarrow I=\frac{V_0}{R} e^{-t / R C} \\ &V_C=V_0\left(1-e^{-t / R C}\right) \end{aligned}$$基尔霍夫和法拉第都很高兴,这里处理的是保守场,没有磁通量的变化。当时间为无穷大的时候,没有电流的流动,电源的电压都加载电容两端。我们看电流随时间的表达式,和我们发光的衰减很类似,我们发光寿命(单指数)的定义是发光强度变为初始强度的\(1/e=0.368\),这里的电流类似,电路接通的瞬间,电流最大,然后逐渐衰减,类比发光寿命的衰减,这里的“寿命”可以认为是RC。
$$\begin{aligned} &\oint \vec{E} \cdot d \vec{l}=0 \Longrightarrow+V_C+I R-V_0=0 \\ &\frac{Q}{C}+R \frac{d Q}{d t}-V_0=0 \\ &Q=V_0 C\left(1-e^{-t / R C}\right) \Longrightarrow I=\frac{V_0}{R} e^{-t / R C} \\ &V_C=V_0\left(1-e^{-t / R C}\right) \end{aligned}$$基尔霍夫和法拉第都很高兴,这里处理的是保守场,没有磁通量的变化。当时间为无穷大的时候,没有电流的流动,电源的电压都加载电容两端。我们看电流随时间的表达式,和我们发光的衰减很类似,我们发光寿命(单指数)的定义是发光强度变为初始强度的\(1/e=0.368\),这里的电流类似,电路接通的瞬间,电流最大,然后逐渐衰减,类比发光寿命的衰减,这里的“寿命”可以认为是RC。
变压器
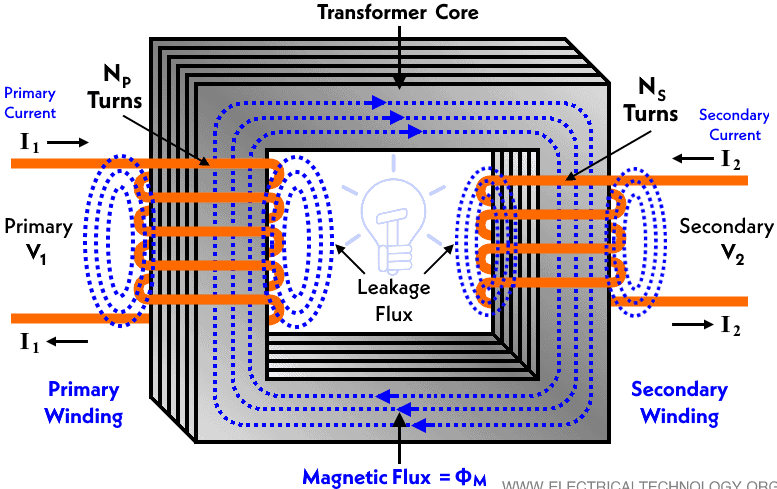 利用法拉第电磁感应定律,很容易求得$$\frac{V_2}{V_1}=\frac{N_2}{N_1}$$变压器输入端必须是交流电,不然产生的磁通量变化不正确。
利用法拉第电磁感应定律,很容易求得$$\frac{V_2}{V_1}=\frac{N_2}{N_1}$$变压器输入端必须是交流电,不然产生的磁通量变化不正确。
完美耦合需要满足两个条件:
- R<<wL (R是次级电路的电阻)。
- 没有涡流损耗(通常两个线圈用一个铁芯耦合,铁芯中会有涡流,所以有能量损耗)。
- 理想的磁通耦合(通过初级线圈的磁通量和通过次级线圈的磁通量相等)。
RLC电路和谐振
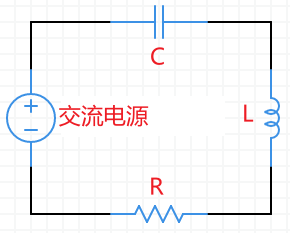
沿回路的电场闭合积分不为\( 0 \),电感中电场总是为\( 0 \),因为没有电阻,也就没有电势差(电压降)。
RLC电路微分方程$$ \begin{aligned} & V=V_0 \cos (\omega t) \\ & V_c+0+I R-V_0 \cos \omega t=-L \frac{d I}{d t} \\ & L \frac{d^2 Q}{d t}+R \frac{d Q}{d t}+\frac{Q}{C}=V_0 \cos \omega t \end{aligned} $$方程的稳态解$$I=\frac{V_{0}}{\sqrt{R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}}} \cos (\omega t-\phi)$$ $$\tan \phi=\frac{\omega L-\frac{1}{\omega C}}{R}, X=\omega L-\frac{1}{\omega C}$$ $$Z=\sqrt{R^{2}+X^{2}}$$\( X \)称为电路的电抗,\( Z\)称为电路的阻抗。对于上面电流的结果,我们可以去直观地感受。如果\( \omega \)很小很小,那么可以看作是直流电,稳态时候的电流当然就非常小(\( Z\)很大)。如果\( \omega \)很大很大,那么相当于交流电的频率变化很快,那么自感将会提供巨大的阻抗,最终稳态的结果依旧是电流很小很小(这里同样是\( Z\)很大)。
- \( \phi \)为正时,电流落后于电压,电感起主要作用;
- \( \phi \)为负时,电流超前于电压,电容起主要作用。
谐振频率
$$\begin{array}{lll} \omega L=\displaystyle\frac{1}{\omega C},\omega_{0}=\displaystyle\frac{1}{\sqrt{L C}}\\ \phi=0, Z=R,I_{\text{max}}=\displaystyle\frac { V_0 }{ R } \end{array}$$\( \omega_0 \)使电路电流最大,此时\( X=0\)。
电流频率曲线
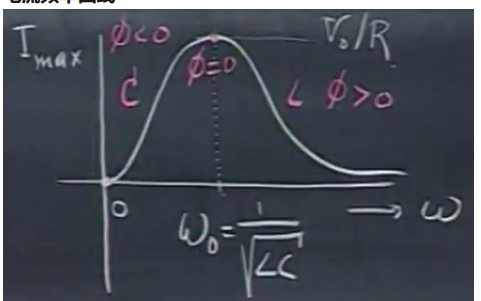
【品质因数】

在\(0.7I \)的地方,截面曲线的宽度,\( \Delta \omega=R / L\)。\(R \)越大,宽度越大。\( Q \)为谐振的品质因数。品质因数越大,图像越窄,系统越灵敏;品质因数越小,图像越扁。之所以用\(0.7I \)的地方,是因为功率与\(I \)的平方成正比(其实就是功率为最大值一半的地方)。
谐振由\( \omega \)、\( C \)、\( L \)共同决定,只要修改一个使整个电路达到谐振即可。我们收音机/电视机(比较老的,接楼顶天线的),就是通过调整电容大小,使得电路的谐振频率,在那个谐振频率下,系统会非常灵敏,产生很强的电流,就会选出那个频率的特定的电台。
金属探测器

两个RLC电路,同时二者之间存在互感,各自产生的磁场通量都部分穿过对方。
所以对于左边的系统,我们可以列一个微分方程,除了上面写的参数之外,还要考虑互感这一部分的影响;同理,对右边的体系,也要考虑互感,才能列出完整的微分方程。所以这是两个相互耦合的微分方程,不好解,但是数学家有办法。两个线圈,两个谐振频率,而且其中至少有一个和互感系数密切相关,系统调谐至其中的一个谐振频率。拿来金属,金属中产生涡流,涡流会改变两个线圈之间的磁耦合系数。系统的\( Q \)值很高,也就是很灵敏,谐振曲线非常窄,互感变化导致微小偏离谐振,电流剧烈减小,于是系统报警。 可以把两个线圈放在门的两侧来探测金属,手持式的金属探测器则是如下样子(感觉像扫雷用的)。