课程视频-B站     网友笔记—1，网友笔记—2    
其他相关课程资料：
(1) Haverford-Advanced Electromagnetism
(2) 赵凯华-电磁学讲义
(3) TED-电学词汇历史
(4) 电和磁—hyperphysics      Light and Vision—hyperphysics 
(5) Physics 12th Std
(6) 思维与实验并重,深度认知光学物理图像
(7) 物理光学—云端小站
(8) 光学课件—USTC

动画交互：

• Ripple Tank (2-D Waves) A​​pplet
• 2-D Waves Applet
• 几何光学模拟

学到的单词：approach it in a very cold-blooded way 用非常冷酷的方式推导  mica [ˈmaɪkə] 云母 mind-boggling [ˈmaɪnd bɑːɡlɪŋ] 令人难以置信的 stroboscope ['strəʊbəskəʊp] 频闪仪 artery [ˈɑːtəri] 动脉 ventricle [ˈventrɪkl] 心室 atrium [ˈeɪtriəm] 心房 aurora borealis 北极光 aurora [ɔː'rɔːrə] 极光 magnetic suspension 磁悬浮 magnetic levitation 磁悬浮 in unison 同时; 一起; 和谐地; 一致地; kosher [ˈkəʊʃə(r)] 合适的; 正确的 tuning fork 音叉 eardrum [ˈɪədrʌm] 耳膜 string instruments 弦乐器 wind instrument 管乐器，吹奏乐器 refracted ray 折射光[rɪˈfræktɪd] are in phase with each other  相位相同 constructive interference 建设性干涉 destructive interference 相消干涉 loudspeaker 扬声器 nail in the coffin 钉在棺材里 razor 剃须刀 handcuff 手铐 picky 挑剔的; 难伺候的

是什么将世界连在一起

In ancient times, amber was noticed to attract light bits of matter. 比如摩擦琥珀(amber)可以吸引树叶。希腊语的琥珀就是elektron。

富兰克林定义：
丝绸摩擦玻璃棒，玻璃棒带正电；
毛皮摩擦橡胶棒，橡胶棒带负电。

【摩擦起电】(Triboelectric-/traɪboʊɪˈlektrɪk/ Effect)：是通过摩擦的方式使得物体带上电荷，或使物体之间的价电子转移。摩擦起电的第一步即是将两种不同的物体相互摩擦，使它们最外层的电子得到足够的能量，摆脱原子核的束缚，在两个物体之间转移。价电子转移的原因是因为不同原子核对电子的吸引力会有差别。摩擦起电后两个物体必带等量异性电荷。

材料的绝缘性越好，越容易产生静电。在冬天用手摸金属门把手容易产生高压放电现象，因为冷空气不能容纳与热空气一样多的水分，当天气温暖时，空气中的水分使空气更容易导电。因此在潮湿的日子里，人积累的任何电荷在接触金属之前就会泄漏到潮湿的空气中。棉衣服相比人工合成的化纤面料不容易产生静电，也是因为棉更好的吸湿性，产生景点后，传到导分散空间，不会有电荷积累。

日常生活中防静电：
(1) 出门前去洗个手，或者先把手放墙上抹一下去除静电，还有尽量不穿化纤的衣服。
(2) 小金属器件（如钥匙）、棉抹布等先触碰大门、门把、水龙头、椅背、床栏等消除静电，此过程即使有放电，手也不会感到疼痛，因为放电的接触点不是手上皮肤的某个点。
(3) 穿全棉的内衣。
(4) 冬天在暖气下放置一盆水，用一条旧毛巾(或吸水好的布)，一头放在水里，一头搭在暖气上，这样一昼夜可以向屋里蒸发大约三升水。

静电感应气球试验：带电棒(假设带正电)去靠近不带电的气球分两种情况
(1) 如果气球导电，很显然，存在电荷移动，靠近带电棒的一侧带负电，远离的一侧带正电，气球被吸引；
(2) 如果气球不导电，虽然电子不能自由移动，但是仍存在极化作用，也就是说靠近带电棒的一侧的气球的原子层，它们的电子都围绕各自的原子核运动，但是现在电子在靠近带电棒的一侧出现的概率更大，换句话说电子云发生了形变，趋向于靠近带正电的棒子，故同样出现气球靠近带电棒的情况。
(3) 导电的气球，如果接地，很容易把自身带的电放走；不导电的气球接地，很难完全放电完全。

让我们这个世界保持在一起(hold our world together)的力：
在原子核的尺度是【核力】；在原子尺度到几千米，是【电磁力】；更大的尺度(宇宙来看)，是【引力】在起作用。考虑两个质子的相互作用的话，静电力是其万有引力的十的36次方倍；但是我们在考虑天体之间的相互作用的时候，可以把天体看做是中性不带电的物体，因为天体的质量很大，引力很大，但是基本不带电，所以万有引力其主要作用。

【核力】：核力是使核子组成原子核的作用力，属于强相互作用力的一类。原子核中有中子、质子，质子是带正电的，所以质子之间会互相排斥。是非常强大的核力将它们吸引在一起，使它们在非常小的区域形成原子核。核力是短程力，只有在原子核尺度上才显现出来。核力有如下基本性质：短程性、饱和性、电荷无关性、交换性、非中心力。

【四种基本力】：自然界中只存在四种基本的力(或称相互作用)其他的力都是这四种力的不同表现。这四种力是：引力、电磁相互作用力、弱相互作用力、强相互作用力。四种力中，除了引力都可以用【杨-米尔斯规范场理论】来描述。

【验电器】(electroscope)：The electroscope is an early scientific instrument used to detect the presence of electric charge on a body. It detects charge by the movement of a test object due to the Coulomb electrostatic force on it. The amount of charge on an object is proportional to its voltage.

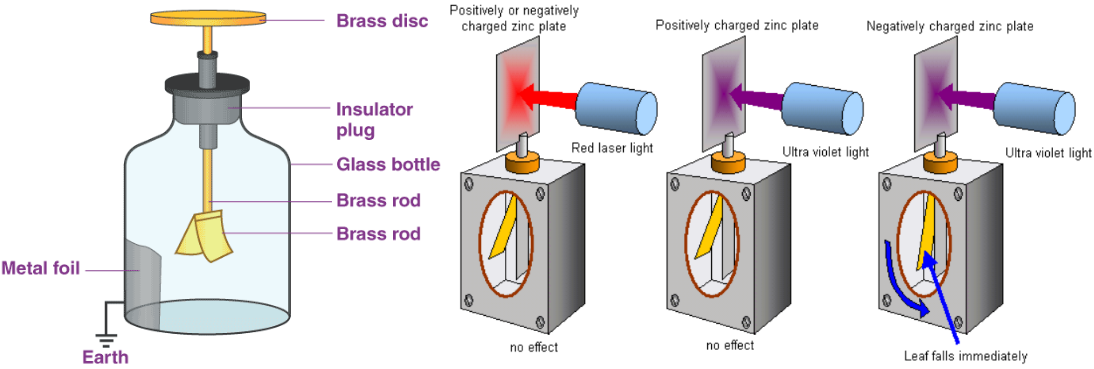
上图也展示了光电效应的现象(四个重要事实)：

• no electrons were emitted from the plate if it was positive
• the number of electrons emitted per second depended on the intensity of the incident radiation
• the energy of the electrons depended on the frequency of the incident radiation
• there was a minimum frequency below which no electrons were emitted no matter how long radiation fell on the surface

 

电场和偶极子

正电想像成hair dryer吹风机，负电想像成vacuum cleaner吸尘器。
电场线越密集的地方，电场强度越大，也是【平方反比定律】(inverse R square)导致的。我们可以用"力线"绘出电场的图，其中力线与空间每一点场的方向相切，线的密度与场成正比。更精确的说，电场是"线通量"，即穿过垂直于场方向单位面积的力线的数目。

库仑力和万有引力都有平方反比定律，差异在于：
(1) 库仑力比引力大多了，大\(10^{35}\)个数量级；
(2) 电荷有正负之分，同性相斥，异性相吸，两个相反的电荷相遇会彼此中和。

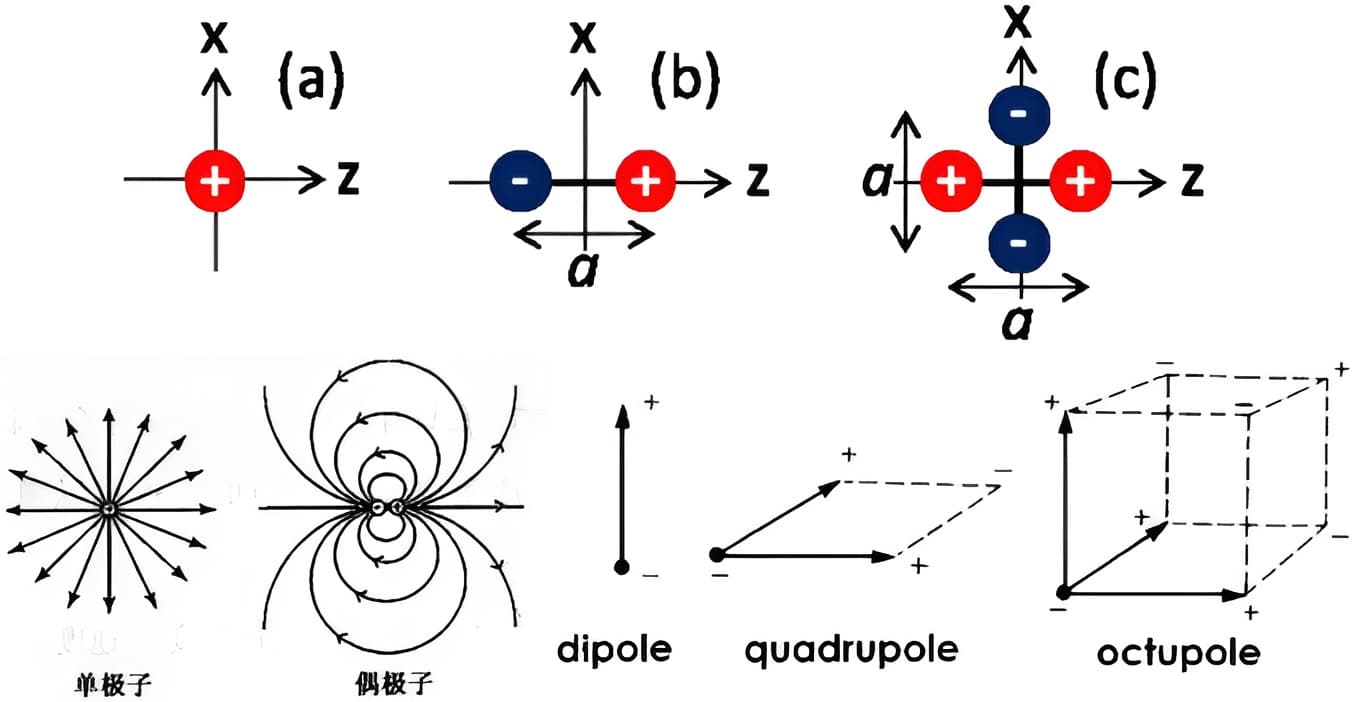
【多极子】(multipoles)：既然电荷可以分正负，我们就可以为元电荷不同的组合构建一个被称为多极子的系统。

• 单个电荷\(q\)是电单极子(electric monopole)，它的电场随\(r^{-2}\)减小；
• 两个电量相等、符号相反的电荷形成一个偶极子(dipole)，不存在电场为零的点，远距离处电场随\(r^{-3}\)减小；
• 两个相等、相反的偶极子组成一个四极子(quadrupole)，在远距离处电场随\(r^{-4}\)减小；
• 两个近邻的电荷，一个带\(+3\)的电，一个带\(-1\)的电，那么很远离这两个电荷的地方，受到的电场力可以将两个电荷等效为带\(+2\)的电荷，电场强度随距离的衰减仍然满足平方反比定律；另外也存在电场为\(0\)的特殊点。
• 还可以继续构建更多的多极子。如果你把这些不同的极子混合起来放进一个“黑盒子”里，在盒子外面可以产生任何类型的电场，如果不打开盒子就不可能知道盒子里面到底装的是什么。

【电偶极子】

• 举例：比如一个原子，没有电场作用下，(电介质，或者说绝缘体)正负电荷的中心是重叠的，但是在电场中，电子会更倾向于处在电场线的上游，原子核更倾向于处在电场线下游的方向，因此就会出现正负电荷中心不重合的情况，那么就形成了偶极子。另外，当一段金属线(无线电发射天线)里电子做周期性运动，使得金属线的两端交替地带正、负电荷，形成振荡偶极子。
• 电偶极子的场强与距离的三次方\(r^3\)成反比，比点电荷随距离的衰减速度快得多。
• 通过简单计算(计算细节见《电磁学—赵凯华》，电偶极子的场强公式
  两个电荷延长线上\(E \approx \displaystyle\frac{1}{4 \pi \varepsilon_{0}} \frac{2 p}{r^{3}}\)，中垂面上\(E \approx \displaystyle\frac{1}{4 \pi \varepsilon_{0}} \frac{p}{r^{3}}\)。
• 电偶极子在均匀电场中所受的力矩：\(\boldsymbol{L}=q \boldsymbol{l} \times \boldsymbol{E}\)，【电偶极矩】\(p=q \boldsymbol{l}\)，从负电荷指向正电荷。
• 演示实验：
  • 两个分别带\(+\)电和\(-\)电的金属球用绝缘棒连接，就可以形成一个偶极子的演示实验，将这个偶极子放在一个电场中(范式起电机)，绝缘棒中间位置用个绳子吊着，可以发现由于带正电的小球和带负电的小球的受力方向相反，所以偶极子会来回摆动，然后由于阻尼(damping)作用，摆动幅度越来越小。
    
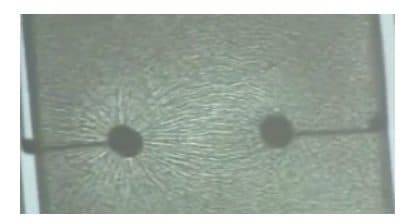  • 右图是演示偶极子在电场中的状态。左右两边分别是带正负电荷的电极，然后整个是在油里面，油里面分布有很多草种子，这些种子在电场作用下，会类似磁铁砂在磁场中的分布一样，呈现一定方向的排列，展示出电场的形状，锥形草种子稳定的时候，电场线下游的一端带正电，另一端带负电，锥形草的方向就是电场线的方向。

电/磁力，究竟是怎么传递的？围绕这个问题，在历史上曾经有过长期的争论，一种观点认为这类力不需要任何介质，也不需要时间，就能够由一个物体立即作用到相隔一定距离的另一个物体上，这就是【超距作用】的观点；另一种观点认为这类力也是近距作用，电力和磁力是通过一种充满在空间的弹性介质"以太"来传递的。

当然我们知道以太不存在，但是超距作用的观点也是错误的，因为电力和磁力的传递虽然速度很快(光速)，但是并非不需要时间。

 

电通量和高斯定律

电通量(electric flux)$$\Phi_{E}=\mathbf{E} \cdot \mathbf{S}=E S \cos \theta$$面积矢量的方向就是法线(normal)方向。对于封闭的曲面，我们默认向外为正，向内为负，高斯定律

$$\Phi_{E}={\large\bigcirc}\kern-1.55em\iint  \mathbf{E} \cdot d \mathbf{S}=\frac { Q }{ \varepsilon _{ 0 } } $$微分形式$$\nabla \cdot \mathbf{E}=\frac{\rho}{\epsilon_{0}}$$

1. \( \rho\)是体电荷密度。对于积分形式等式右边我们取特殊情况，也就是正电荷\(Q\)处在球中心来计算，球面每点的场强都相等，都和对应的微元面积垂直，所以电场强度乘以球表面的面积即可得到等式右边。
2.散度\(\operatorname{div} \mathbf{F}=\nabla \cdot \mathbf{F}=\left(\displaystyle\frac{\partial}{\partial x}, \displaystyle\frac{\partial}{\partial y}, \displaystyle\frac{\partial}{\partial z}\right) \cdot\left(F_{x}, F_{y}, F_{z}\right)=\displaystyle\frac{\partial F_{x}}{\partial x}+\displaystyle\frac{\partial F_{y}}{\partial y}+\displaystyle\frac{\partial F_{z}}{\partial z} \)
3. 库伦常数和真空介电常数之间的关系\(k_{e}=\displaystyle\frac{1}{4 \pi \varepsilon_{0}}\)
4.\(E=\displaystyle\frac{Q}{4 \pi r^{2} \varepsilon_{0}}\)，如果是介质中的点电荷，那么这里的真空介电常数将会由更大的介电常数(相对介电常数乘以真空介电常数\(\varepsilon_0\))替代，相同距离的地方的电场强度显然更小。
5.\(E=\displaystyle\frac{Q}{4 \pi r^{2} \varepsilon_{0}}\)单位面积包裹(这里是直观的球体，对于平板电容器\( \displaystyle\frac{Q}{A}=\varepsilon_{0} E\))的电荷数和产生的电场之间的比例常数(必须是任意位置电场线和面积微元垂直)是\(\varepsilon_0\)。

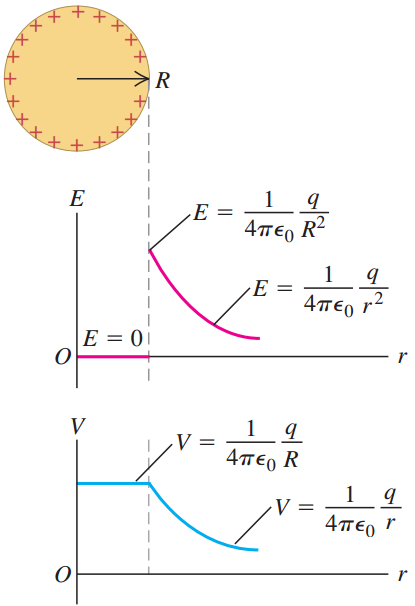(外表面)均匀带电的空金属球(如右图)内部，电场强度都为\(0\)，因为取球内任意一点作等圆心的球面，球面包含的电荷为\(0\)，故每处的电场强度都是\(0\)。同理，球外任意一点的场强也可以通过作高斯面的方法求得，影响场强大小的因素是里面包含的电荷量，而与电荷到底是怎样的空间分布无关。注意，事实上带电金属球的电荷只能分布在表面，可以用反证法说明。

能计算电场强度的几种电荷分别情况：

• 球形对称；
• 柱对称；
• 无线平面分布。

hollow行星，或者说在一个质量均匀分布的球体里面，按照相同的球心位置挖出一个球，那么中空的部分重力场为\(0\)。牛顿还研究了这样一个问题，假设地球是质量均匀分布的完美球体，那么地球外任意一点(即使离地球不远)的引力场(地球造成的)很容易计算，因为引力也是平方反比，也可以用高斯定律处理，也就是说，可以把地球看成一个质点，所有的质量都集中在地球的球心。

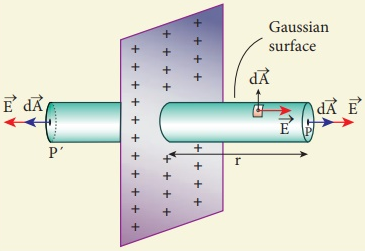
柱对称电场强度：即均匀带电圆柱体的电场分布。注意这里的电荷是均匀分布在圆柱体中，表面有，内部也有。如果这个圆柱体是导体的话，净电荷只分布在表面，所以显然这里的情况不是导体。求解电场分为两种情况，圆柱外的电场，以及圆柱内的电场。取高斯面的时候，相当于围绕轴取一个圆柱体，由于对称性使得圆柱体的上下表面的电通量为零，所以只需要考虑该圆柱体的测面通量，利用高斯定理即可求解。

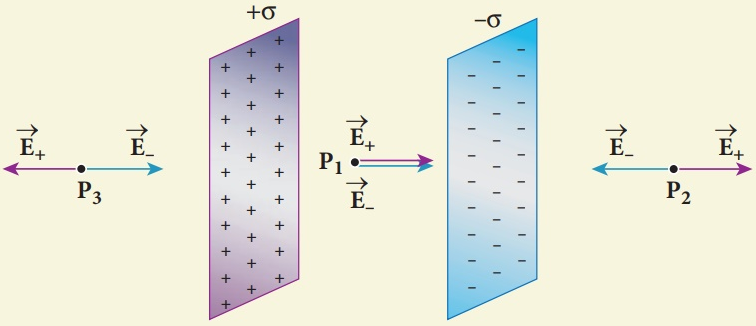
带电无线平面(charged infinite planar sheet)，假设单位面积的带电量为\(σ=Q/A\)，那么任意一点的场强为$$ E=\frac { \sigma }{ 2{ \varepsilon }_{ 0 } } $$与该点到带电平面的距离无关，关键在于高斯面的选取。图中只有两侧圆形有电通量。计算方法如下：$$ 2 E \int_P d A=\frac{\sigma A}{\varepsilon_0} $$

两块带电平行板(Electric field due to two parallel charged infinite sheets)周围的电场分布(假设平行板无限大，实际上不可能)

注：上面讨论的都是无限大的平板，实际上的平板不可能是无限大，于是在板子的边缘处的电场强度就不是我们上面考虑的简单情形，需要利用麦克斯韦方程组求解。

 

静电势能和电势

对于一个正电荷产生的电势，我们规定无穷远处为\(0\)，其他地方电势都为正；对于一个负电荷产生的电势，我们同样规定无穷远处为\(0\)，但是其他地方都为负。点电荷\(Q\)产生的电势为$$V=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{r}$$等势面和电场线垂直；等势面不会相交。金属都是等势体，因为金属内部存在自由电子，如果不是等势体，内部存在电势差，则内部会存在电场，电子会因为电场力自动向电势高的地方移动(电子为负)，从而达到整个金属电势相等(内部电场为\(0\))。金属是等势体的前提是金属内没有电流流动。

计算闭合曲面的电场：$${\large\bigcirc}\kern-1.55em\iint \overrightarrow{E} \cdot \mathrm{d}\overrightarrow{\mathrm{A}}=\frac{1}{\varepsilon_{0}} \sum Q_{\text {内 }}$$计算\(\mathrm{P}\)点的电势：$$V_{\mathrm{P}}=\int_{\mathrm{P}}^{\infty} \overrightarrow{E} \cdot \mathrm{d}\overrightarrow{l}$$计算\(\mathrm{AB}\)间电势差：$$V_{\mathrm{B}}-V_{\mathrm{A}}=-\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{E} \cdot \mathrm{d}\overrightarrow{l}$$对标量电势求梯度取负号即为矢量电场：$$ \vec{E}=-\nabla V=-\left(\frac{\partial V}{\partial x} \hat{x}+\frac{\partial V}{\partial y} \hat{y}+\frac{\partial V}{\partial z} \hat{z}\right) $$稳定状态的实心导体内部电场强度处处为零；带电实心导体，净电荷只能分布在导体的外表面。
对于实心导体来说，当外界电场不变时，导体内部就是等电势的，在导体内部任意取一个点，会发现沿着坐标轴三个垂直方向移动微小距离，电势都没有发生变化，也说明三个方向的电场强度分量都是零，即总的电场强度为零。于是得出稳定状态的实心导体内部电场强度处处为零。然后根据高斯定律，可以知道内部不存在净电荷，所以对带电实心导体来说，净电荷只能分布在导体的外表面。另一方面理解，如果导体内部存在净电荷，那么同样根据高斯定律，对于包围这个净电荷的区域来说，就会存在电场。不同位置的净电荷都处在别的净电荷的电场中，这会导致电荷进一步移动，知道达到平衡状态，也即导体内部不存在净电荷。总之就是，内部有净电荷，那么内部有电场，那么净电荷就会移动，这个电场就会迅速变化(净电荷移动)，直到净电荷都在表面，内部没有净电荷(电场)。
【范氏起电机】(Van de Graaff generator)会产生很大的电场，沿着径向方向放置荧光灯管，可以看到灯亮了，这是因为灯管两端的电势不同，存在很大的电势差(电压)，于是产生放电现象，激发Hg蒸汽，使得Hg释放出紫外光打在荧光粉内壁上，释放出可见光(混合产生的白光)。

 

静电屏蔽

带电中空球电荷分布
在导体内部画一个包围中空体积的高斯面，可以知道这个高斯面都是存在导体实心部分，所以电场都为零，根据高斯定律，那么图包围的电荷也是零，所以内表面不可能存在净电荷，净电荷依然分布在外表面。

任何稳定带电导体内部的静电场都是零
先前的内容提到必须满足球形对称导体内部的静电场才是零，但是实际上任何形状都可以的。

大自然的神奇之处：将一个不带电的封闭的铁盒子放在一个电场中，盒子马上由于电场的左右产生极化，一侧带正电，另一侧带负电，而且电荷的分布会使得盒子内部的电场强度处处为零，盒子外部所有的电场线都是垂直于盒子表面(保证盒子是个等势体)。这种电荷的重新分布是在一瞬间完成的，而且遵循所有的物理定律。

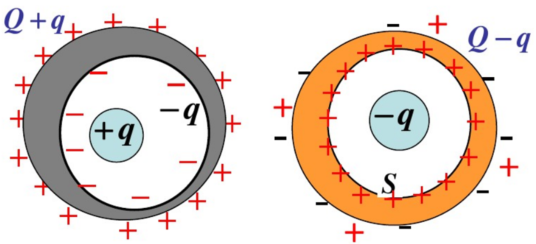腔体内部有电荷
内部有其它带电体的空腔导体，其内外表面都有净电荷，且内表面的电量与空腔内的电荷量等值异号。

 

【Faraday Cage】(法拉第笼)教授做实验，可以屏蔽收音机(电磁波)，但是不能屏蔽扩音器(声波)。

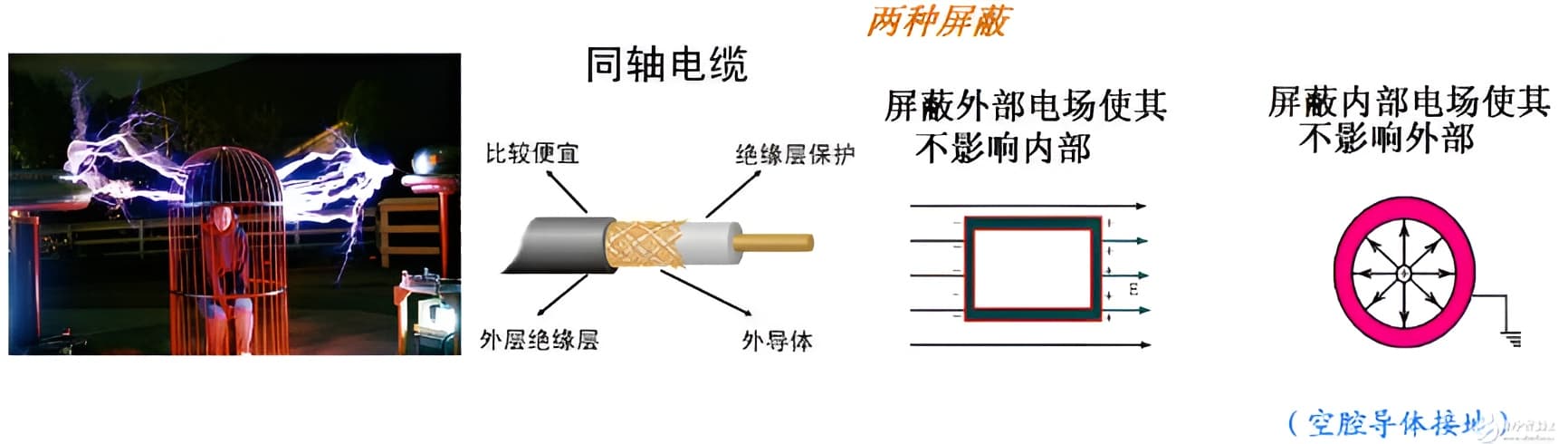
(1)  同轴电缆就是利用了法拉第笼的静电屏蔽效应;
(2)  汽车、飞机等交通工具中的人是不会被雷击的;
(3)  如果电梯内没有中继器的话，那么当电梯关上的时候，里面任何电子讯号也收不到。
(4)  为防止干扰，一些精密仪器需放在笼内才可进行运作或量测。

 

 

高压击穿和闪电

Dependence of Charge Density on Surface Curvature of an Isolated Conductor 对于孤立导体：表面上的电荷密度的大小与该处表面的曲率有关。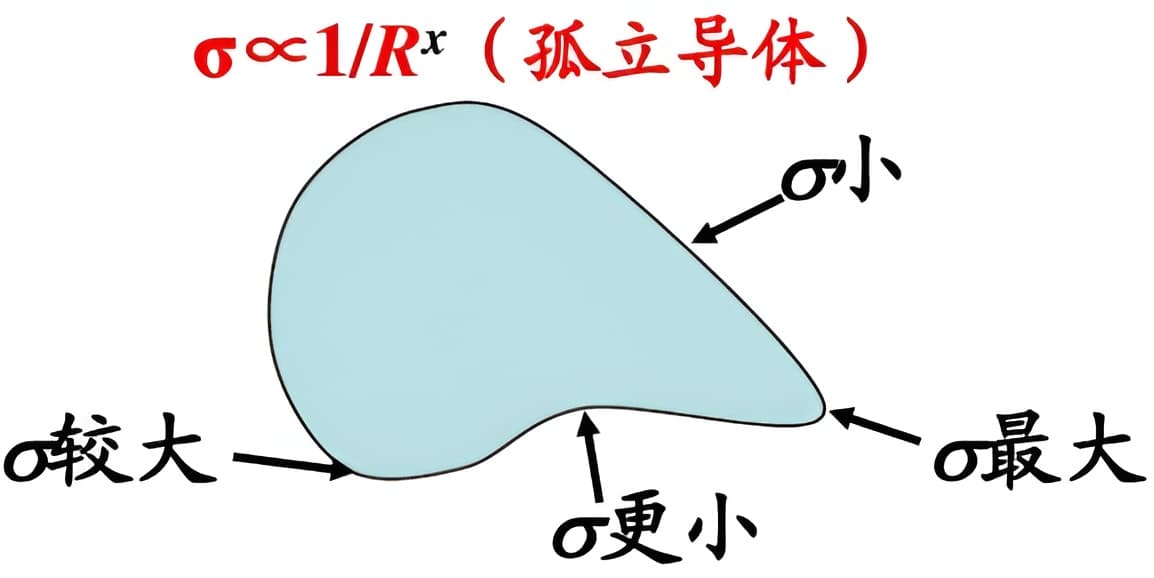

• 曲率较大，表面尖而凸出部分，电荷面密度较大；
• 曲率较小，表面比较平坦部分，电荷面密度较小；
• 曲率为负，表面凹进去的部分，电荷面密度最小。

Electrically connected charged balls
两个分别带电的实心小铁球，用导线相连，那么两个球就是等势体，而且根据高斯定律，可以吧两个球所带的电荷都等效到球心处，那么可以很容易求出A的电势(表面和内部都一样)，同理求出B的电势，那么可以知道A和B半径的比(假设为\( 5:1 \))，就是对应的带电量的比值，但是表面积确是按照半径平方变化的，所以球的半径越大，反而表面的电荷面密度越小。表面电荷越密集的地方，显然周围电场强度越大。$$ \begin{gathered} V_A=\frac{Q_A}{4 \pi \varepsilon_0 r_A}=V_B=\frac{Q_B}{4 \pi \varepsilon_0 r_B} \quad \Longrightarrow \frac{Q_A}{r_A}=\frac{Q_B}{r_B} \\ \because \sigma=\frac{Q}{4 \pi r^2} \therefore \sigma_B=\frac{1}{5} \sigma_A \end{gathered} $$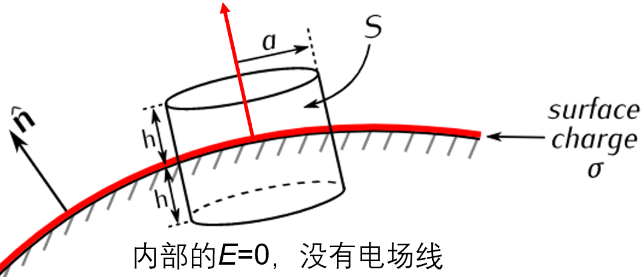对于任何一个导体，如果内部电场强度为零，那么找表面上一个地方，画个无限小的高斯pillobx，其上下表面平行于导体表面，根据高斯公式有$$ A E=\frac{\sigma A}{\varepsilon_0} \quad \Longrightarrow \quad E=\frac{\sigma}{\varepsilon_0} $$所以当你有一个导体，如果你知道局部电荷密度，那么你就知道局部的电场。曲率半径大的地方，电荷密度最大，所以电场强度也最大。

【Townsend avalanche】(雪崩avalanche [ˈævəlɑːnʃ] )就是一次电击穿(electric breakdown)，你就可以看到电火花(spark)。The Townsend discharge or Townsend avalanche is a gas ionisation process where free electrons are accelerated by an electric field, collide (/ kəˈlaɪd /) with gas molecules, and consequently free additional electrons. Those electrons are in turn accelerated and free additional electrons. The result is an avalanche multiplication that permits electrical conduction through the gas. The discharge requires a source of free electrons and a significant electric field; without both, the phenomenon does not occur.

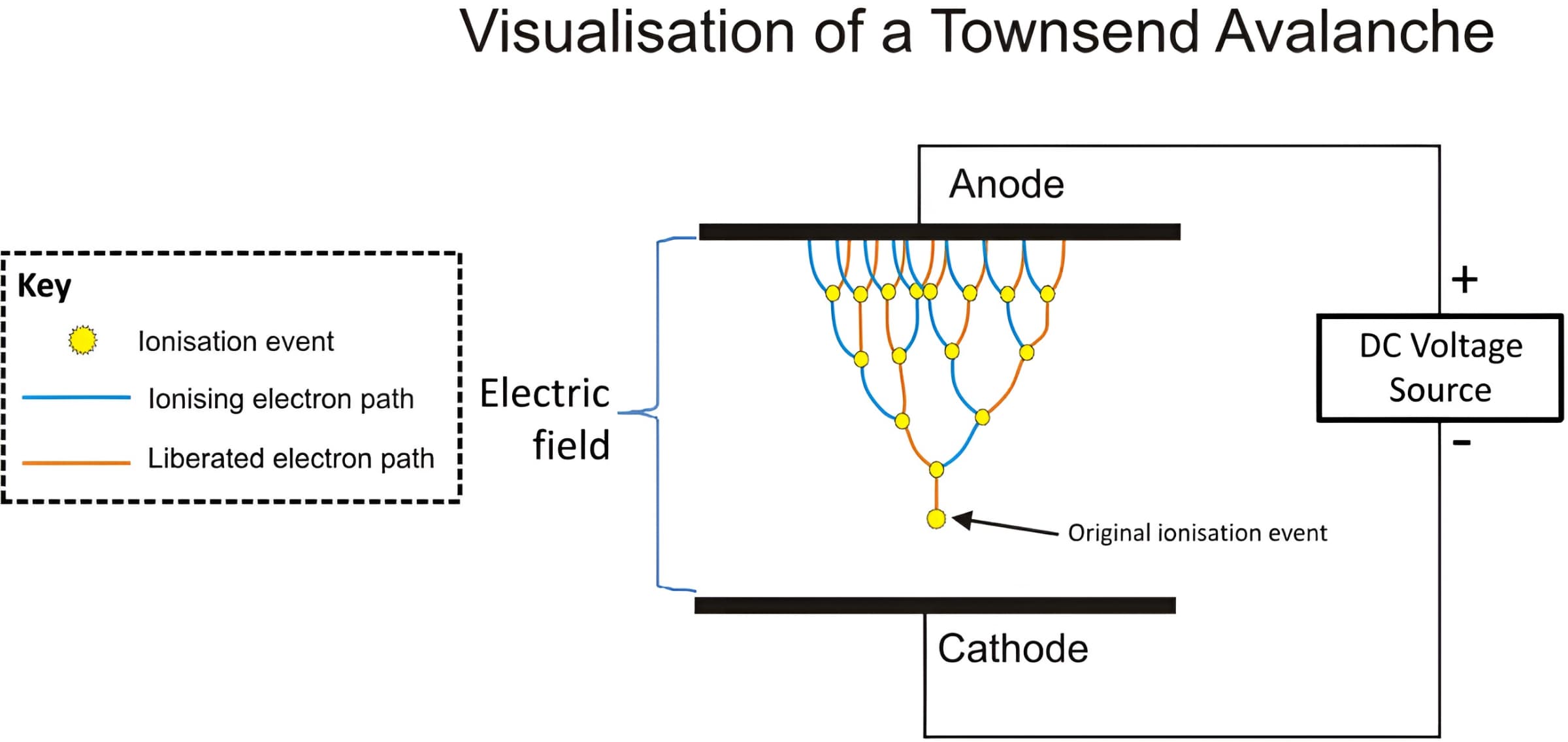
在电场中的电子，如果经电场加速动能足够大，电子和空气中氮气、氧气分子碰撞时，会使分子电离，这样一个电子就变成了两个电子，两个电子继续加速，就会继续电离，产生雪崩，这个雪崩就是一次电击穿，当这些离子变回中性的时候，在空气中产生火花，这个过程会加热空气，形成空气的压力波，于是你也可以听到声音。火花通常发生在尖锐的点上，因为那里的曲率非常大(半径很小)，电场强度很高。

击穿电场的单位是伏特每米，\({\rm V}/{\rm m}\)，空气中，一个大气压下击穿大概需要300万\({\rm V}/{\rm m}\)。因此，距离很小时(两个物体最靠近的地方，电场强度最大)，可以很容易达到这个击穿电压。在干燥时候，我们接触铁质门把手就常常“触电”。在距离门把手3mm地方，电势差大约3万V。高压并不是致死的主要因素，主要是通过你的电流。这一集有点复杂，需要详细补充，还有各种放电现象，是不是自持，和电压的关系，温度的关系等等，很复杂，因为这个教授讲述的闪电过程比较复杂，李永乐也有视频讲闪电以及避雷针，但没那么复杂。

 

电容和场能

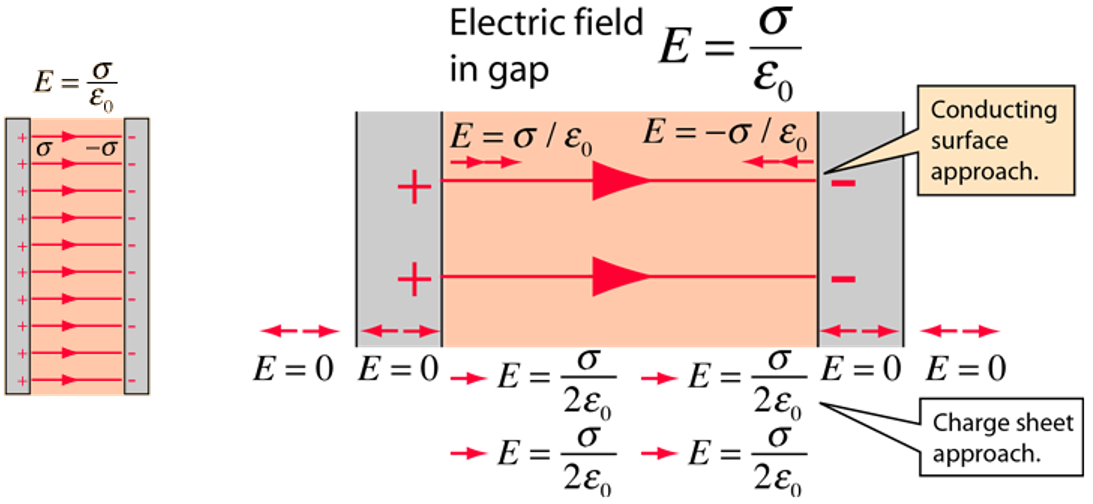
我们先前已经知道，对于单个无限大均匀带电的平板，周围的电场强度\(  \frac { \sigma }{ 2{ \varepsilon }_{ 0 } }\)和距离无关。图中是两个分别带等量正电荷负电的平板，显然平板之外的电场强度为零，平板中间的电场强度是左右板引发的电场强度的叠加，也就是\(\displaystyle E=\frac { \sigma }{ { \varepsilon }_{ 0 } }\)。注意移动左板时，我们只考虑右板产生的电场，这一部分的强度是\( \displaystyle\frac { E }{ 2 } =\displaystyle\frac { \sigma }{ 2{ \varepsilon }_{ 0 } } \)，也就是平行板内部电场强度的一半，然后乘以带电量以及移动的距离即可得到做功的大小。注意下面的式子中分子分母同时乘以\(\epsilon_0\)，于是可以用\(E\)去替代\(\displaystyle\frac{\sigma}{\varepsilon_0}\)。$$W = Fx =\frac {QEx}{ 2 } =\frac {\sigma A Ex\epsilon_0 }{ 2\epsilon_0 } =\frac {1}{ 2} \epsilon_0 E^2Ax$$其中\(Ax\)是新创造的电场的体积，于是单位体积做的功(因为这个功创造了电场，所以我们把她叫做【场能密度】)$$ W_{s}=\frac{\epsilon_{0} E^{2}}{2}$$一般电场能密度都可以这样表示，这个公式不是针对特定的电荷分布，是通用的。对任何的电场分布都有效。 现在我们有了一个新的视角来看待把电荷组装起来所需要的能量。早先我们是通过从无穷远搬运到各自位置所做的功，现在我们有了一个计算静电势能更方便的式子：把电场能密度在整个空间内积分(当然可以积分到无穷远的地方)。$$\begin{aligned} &Q=A \sigma, V=E h\\ &U=\int \frac{1}{2} \varepsilon_{0} E^{2} d V=\frac{1}{2} \varepsilon_{0}\left(\frac{\sigma}{\varepsilon_{0}}\right)^{2} A h=\frac{1}{2} Q V \end{aligned}$$带电金属小球的电容
对于平行板电容器来说这个电势就是两个板子之间的电势差，对于带电金属小球，电荷是分布在外表面，我们可以将电荷等效于在球心，然后计算出外表面的电势为\( \displaystyle\frac{Q}{4 \pi \varepsilon_{0} r} \)。根据电容的第一种定义：\(C=\displaystyle\frac{Q}{V}\)带电量除以电势得到$$C=4 \pi \varepsilon_{0} r$$也就是说金属球半径越大，电容也就越大，也就是能存储的电荷越多。正如我们先前讨论的，将两个带电金属球互连成等势体，那么大球上的电荷更多，但是电荷密度更小，电场强度更小。

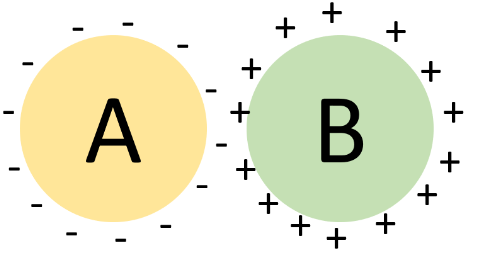电势的定义是，单位电荷到指定位置所做的功，于是对于独立的B来说\(C_B=\displaystyle\frac{Q_B}{V_B}\)。如果将A放在B旁边，由于A的存在，单位电荷达到B所做的功会减小，所以B的电势\(V_B\)会变小，则B的电容\(C_B\)就变大了。注意此时我们把\(C_B\)叫作B的电容是不准确的，我们把它看作是A存在的情况下B的电容，而不是单独考虑B。

电容的第二种定义：两个导体带有等量的电荷，但是电荷的极性不同，这样两个导体组合起来的电容是其中一个上面的电荷电量与两者电势差的比值\(C=\displaystyle\frac{Q}{V_{\text {diff }}}\)。电容通常处理的是两个物体，也就是电容第二种定义的情形。

解释平板电容与面积成正比与距离成反比：

• 与面积成正比比较好理解，面积越大所能携带电荷越多；
• 与距离成反比，距离越近，负电荷板把正电荷板的电势降低越多(因靠的越近，单位电荷从无限远处移动到正电荷板所需的功越小)，根据电容是电荷量与电势的比值，电势越小，电容就会越大。或者这样想，因为带电量固定后，电容中的电场强度就固定了，因此距离越小，两个板之间电势差就越小，不变的电量除以变小的电势差，于是电容就变大了。

平行板电容器的电势差、电容以及存储的能量计算如下$$ \begin{aligned} & V=E d=\frac{\sigma d}{\varepsilon}=\frac{Q d}{\varepsilon A} \\ & C=\frac{Q}{V}=\frac{\varepsilon A}{d} \\ & U=\frac{1}{2} Q V=\frac{1}{2} C V^2 \end{aligned} $$一块平行板电容器，充电之后，断开电源，然后增大两个板之间的距离，相当于做功，会使得电容器的电压差增大。另外，利用高斯定律，也可以判断出平行板电容器，电荷只分布在内侧两个相对的表面。

电容器的应用：

• 闪光灯
  • 飞机/机场灯塔的警示信号
  • 相机闪光灯，高速摄影闪光灯
  • 测量电机转速
• 电蚊拍
• AED(除颤器)
• 频闪观测仪

我们日常的闪光灯就是利用电容器的原理制作的，给一个电容充电，然后在一个灯泡上放电。因电容不变，充电电压越高，电容上储存的电能越多，通过灯泡释放时，能量的多少决定了亮度的高低；充电电压太高，放电的时候灯泡可能被烧坏。常见的电容类型：

• MLCC (Multi layer Ceramic Capacitors)，多层陶瓷电容，也叫独石电容，用于小功率的滤波，旁路，耦合；
• 瓷片电容；
• 铝电解电容：贴片和插件两种形式，内部电介质为铝电解液，区分正负极，用于低频直流电场合，最主要的作用是给电源滤波；
• 钽电容：耐压不行，价格高，钽电容对高低频信号的响应都较好，频率适用范围宽，等效串联电阻小；
• 薄膜电容；

 

电介质及极化

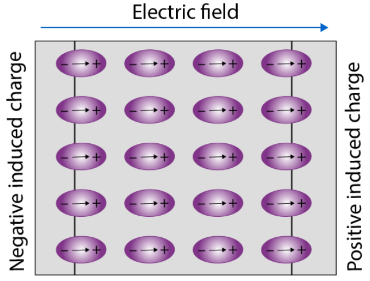电介质的极化，对于绝缘体来说，在外界电场作用下，虽然没有自由电子的移动，但是原子的电子云会被一定程度上拉长变形，于是正负电荷中心不重叠，形成了偶极子，在绝缘体的上下表面就会分别聚集电性相反的电荷，形成内部的一个感应电场。在电容的中间插入电介质，电容上的电荷称作自由电荷，电介质上的电荷称作【感应电荷】(induced charges，对应的有感应电场)。

\begin{aligned}
&E_{\text {free}}=\frac{\sigma_{\text {free}}}{\varepsilon_{0}}, E_{\text {indu}}=\frac{\sigma_{\text {indu}}}{\varepsilon_{0}}\\
&\vec{E}_{\text {net}}=\vec{E}_{\text {free}}+\vec{E}_{\text {indu}}=E_{\text {free}}-E_{\text {indu}}\\
&\sigma_{\text {indu}}=b \sigma_{\text {free}},(b<1)\Rightarrow E_{\text {indu}}=b E_{\text {free}}\\
&E_{\text {net}}=(1-b) E_{\text {free}}\end{aligned}\( (1-b) \)我们叫做\({  1}/{ \varepsilon_r}\)，\(  \varepsilon_r\)称作【相对介电常数】(relative permittivity，或者dielectric constant)。没有量纲的数值。解释一下就是：电容充电后，和电源断开，然后插入电介质，由于电介质产生感应电场，电容内部的电场强度会被削弱，不插入电介质时候的电场强度和插入电介质后的电场强度(net)之比就是相对介电常数，另外很容易知道插入电介质，电容两端的电势差会降低。\(\varepsilon=\varepsilon_0 \varepsilon_r\)为【电容率】(absolute permittivity，或者直接简写为permittivity)。

真空的相对介电常数是\( 1 \)，日常环境的相对介电常数比\(  1\)大一点点，可以认为也是\( 1\)，塑料为\(3\)，很好的绝缘体玻璃的相对介电常数是\(5\)。天然的偶极子分子(极性分子)具有很高的相对介电常数，比如水(相对介电常数\(80\))，水分子本身正负电荷中心就不重合，是极性分子，在温度的热作用下，水分子随机排列，但是一旦外界存在电场，那么水分子就倾向于按一定方向排列。热运动导致的随机排列和电场导致的定向排列是两个相互竞争的过程，所以高温介电材料也是大家的研究热点之一。

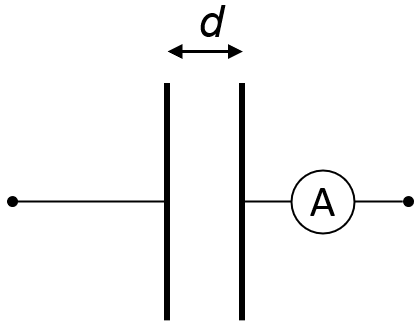平行板电容器充电后断电，再插入电介质：
(1) 电流表不动，表明两极板各自所带电荷\(Q\)没变—极板没有放电也没有充电；
(2) \(V=Ed \)，\(d\)不变，\(E\)变小了，所以两极板间电压变小；
(3) \(Q = VC\)，\(Q\)没变，\(V\)变小，所以两极板的电容变大了。

平板电容新公式：$$\uparrow C=\frac{Q_{\text {free }}}{V \downarrow}, C=\frac{A \varepsilon_{0}}{d} \varepsilon_r$$插入电介质，电容会变为原来的\(\varepsilon_r\)倍。$$E=\frac{\sigma_{\text {free }}}{\varepsilon_0 \varepsilon_r} \quad\quad V=E d \quad\quad C=\frac{Q_{\text {free }}}{V}=\frac{A \varepsilon_0}{d} \varepsilon_r$$如果电容两端始终和电源相连，那么插入电介质之后，电容所存储的电荷就变成原来的\(\varepsilon_r\)倍(电介质上的感应电荷也是通电源情况下的\( \varepsilon_r\)倍)。电容不接电源，那么电荷不变，电容本身产生的电场不变；电容接电源，那么电势差不变，电容本身带的电荷会变。关键问题是把握什么在变，什么不变。始终接电源，开始的时候，电容两侧有电荷，然后插入电介质，电介质感应出电荷，使得净电场强度下降，那么两极板之间的电压就下降了，为了使极板间的电压和电源保持一致，那么电源必须给电容充电，以保持净电场的强度不变。

电介质的选择
一个电容器，想要存储更多的电荷(更大的电容)，那么尽可能减小电容器的厚度，但是在电压一定的情况下，电容器越薄，里面的电场强度越大，不同的电介质击穿电场不一样。虽然水的介电系数比较大(相对介电常数\(80\)，水是极性分子)，但是击穿电场很小(因为水电离出正负离子)，所以不适合用作电介质。好的电介质，应该是介电系数很大，击穿电场强度很大；这样的话，可以存储更多的电荷，但是电容里面的净电场强度又不是很大。空气中，击穿电场(breakdown electric field)是300万伏特每米；聚乙烯的介电常数为3，击穿场强为1800万伏特每米，可以作为电容的电介质，有很多电容就是利用这种材料——薄膜电容中一种。电容的特点是隔直流，通交流。

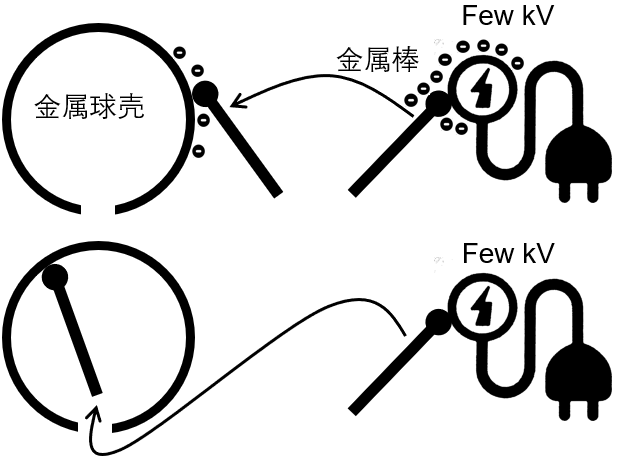
几千伏的电源产生\(30\)万伏的电压(空气击穿)
(1) 如果每次用金属棒接触电源(成为一个等势体)，然后再将金属棒贴在金属球壳的外表面，由于金属棒的电势比金属球壳高，所以电子会从金属棒流向金属球壳，然后再将金属棒接触电源，不断重复这个过程，于是金属球壳上的电子越来越多，直到金属球壳的电势和电源的电势相等，我们就无法再往球壳上转移电子了。
(2) MIT教授Van de Graaff发现，在(1)的终态的基础上，可以将接触了电源的金属棒移动到金属球壳的内部，这个过程其实是对电子做功，使得金属棒的电势比金属球壳的内表面高，如果金属棒接触金属球壳内表面，那么电子就会从金属棒转移到金属球壳内表面，然后快速转移到外表面。不断重复这个过程，就可以使金属球壳产生\(30\)万伏的电压。这就是【范氏起电机】(Van de Graaff generator)的原理。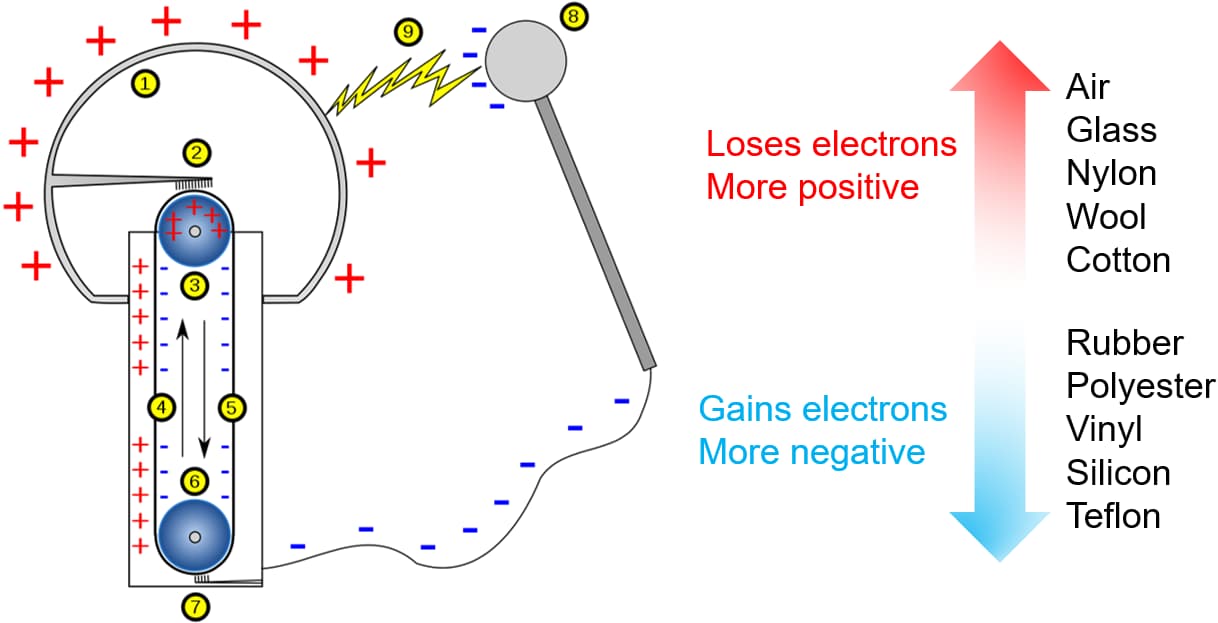

传送带：用棉花制作，等待补充

参考资料：
(1) How Van De Graaff Generators Work—油管

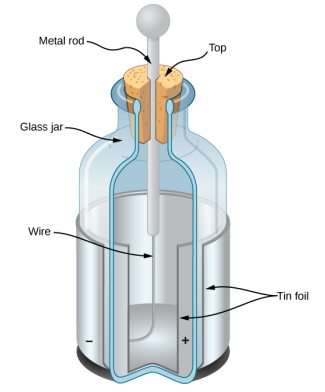【莱顿瓶】(Leyden jar )，是一种用以储存静电的装置。作为原始形式的电容器，莱顿瓶曾被用来作为电学实验的供电来源，也是电学研究的重大基础。莱顿瓶的发明，标志着对电的本质和特性进行研究的开始。至今，莱顿瓶任然在演示静电学原理时被使用。利用了莱顿瓶把天上的闪电引入到莱顿瓶中，证实了闪电和日常生活中的摩擦起电实质上是同一类东西，相当于把二者统一起来，牛顿也是把天体之间的引力和苹果落到地上的重力统一为万有引力。

 

 

电流、电阻率和欧姆定律

当在导体两端施加电势差的时候，它会在导体内部创造一个电场，那么导体中有自由电子，它们可以运动，但是离子不能运动因为被锁在固定的位置。所以当导体中有电流时，通常都是由电子产生的。电子感受到电场，它会向消灭电场的趋势运动，但是不会成功，因为我们保持两端有一定的电势差。通常电流和电势差之间有一个线性关系，也就是我们说的欧姆定律。

先谈谈铜导体，作为导体里面的自由电子无时无刻都在做热运动，这种热运动方向是随机的，我们不考虑自由电子之间的相互作用，那么自由电子不可能一直朝着一个方向运动，隔一段时间就会和原子碰撞，那么就会存在【平均碰撞时间】\(\tau\)。在外电场作用下，在两次碰撞之间，就会存在电场对该自由电子的加速作用，通过简单计算，我们可以发现，通过电场加速得到的【定向漂移速度】要远远小于它【随机运动的速率】，差不多就是乌龟的速度。也就是说在外电场下，观察单个电子似乎依然无规则运动，但是统计大量自由电子的运动状况，是有着定向移动的表现。

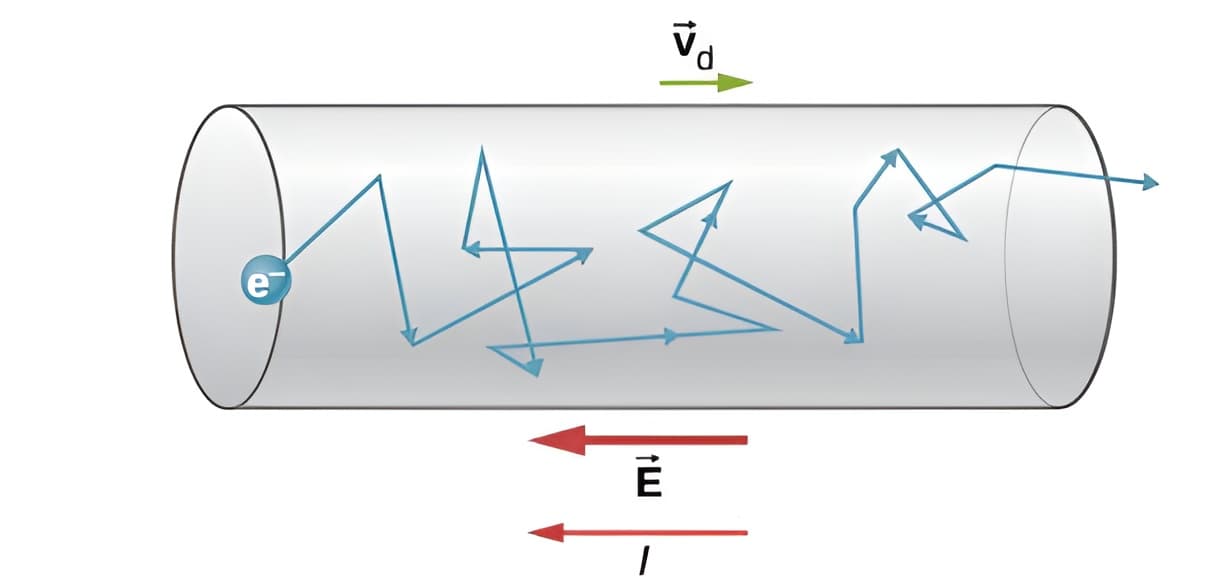
drift velocity漂移速度 \(v_d=a \tau=\displaystyle\frac{e E}{m_e} \tau\)。电场加强时，漂移速度会增加；间隔增大，加速时间变长，漂移速度也会增大。可以由此推出欧姆定律(其中\(R =l/ \sigma A \)，\(n\)为体电荷密度)$$I=v_dAne =\displaystyle\frac{e^2n\tau}{m_e} AE= \sigma AE=\frac {\sigma AV }{l}= \frac {V}{R}$$

温度越高，导体导电性越差
自由电子的热运动越剧烈，那么更容易和原子碰撞，也就是平均碰撞时间变小，每次在电场下加速得到的定向漂移速度就会减小，也就导致了电导率下降；简而言之就是，温度升高，离子实的振动加剧，阻碍了载流子的运动。钨灯丝刚点亮的时候，温度低，电阻小，慢慢加热之后，温度高，电阻大，电阻是温度的函数。

冷、干燥、一个大气压下，空气的电导率很低，但是一旦加热，就会得到更多的自由氧离子和氮离子以及电子，使得空气的导电性明显增大。验电器上的电荷，一般来说可以待很久，是因为空气的电导率很低，但是把点燃的蜡烛放在附近，空气被加热，电导率显著增大，那么验电器上的电荷就很容易被导出。闪电，先导闪电击中地面，形成充满离子和电子的通道，电阻率很低，电导率很高。另外，即使是完全中性的水，也存在可以导电的离子，这会使得潮湿空气相对于干燥空气的电导率显著增大。

 

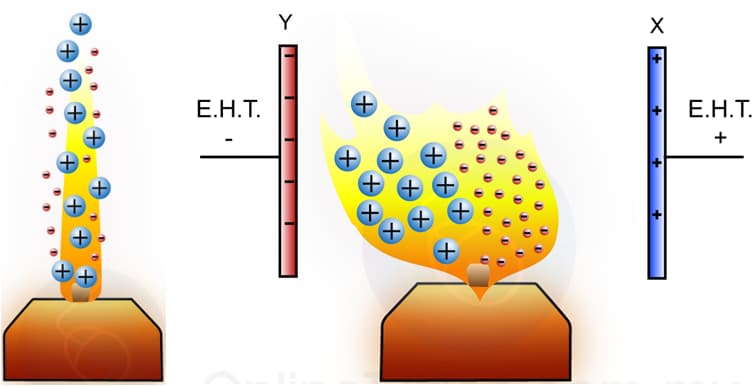
The heat of the candle flame removes electrons from the air molecules around it, and therefore ionised the molecule. 如果在蜡烛两侧的金属板上连接Extra High Tension (E.H.T.) power supply，那么会出现如图所示的形状。The spreading of the flame is not symmetry. This is because the positive ions are much bigger than the negative ions; it will collide with the other air molecule and bring more air molecule towards the negative plate. 火焰至少部分有处在等离子体状态。

 

电池和电动势

将一个电压源连接一个电阻，发现在电源内电流与电场方向相反。所以存在类似一种像泵的装置强迫电流在电源中，沿电场的反方向运动。就像水往低处流，必须有外力才能让其抬高。范式起电机中，我们把电荷放在传送带上，然后转动带子，传送带强制把电荷送到球内部，我们必须克服球面上电荷的斥力，所以必须做功。对于范式起电机，显然是电机驱动带子运动做功，韦氏感应起电机是转动盘子做功。对于通常使用的电池，是化学能做功，铜锌原电池为例如图：Zn板和Cu板之间会产生电势差(通常在1V左右)，要解释它必须用到量子力学。另外再引申一下，不一定是在溶液中，这两个金属板(或者两个不同的导体)直接接触，也会产生电势差。

The electrochemical reaction is$$ \mathrm{Zn}(\mathrm{s})+\mathrm{Cu}^{2+}(\mathrm{aq}) \longrightarrow \mathrm{Zn}^{2+}(\mathrm{aq})+\mathrm{Cu}(\mathrm{s}) $$当右边铜溶液浓度变淡(镀铜)，或者说锌溶液变浓(锌溶解)到一定程度，电池就停止工作。我们可以利用外接电源提供一个反方向的电流，使整个化学反应逆转。汽车蓄电池的原理和这个实验完全一样，只是用铅和氧化铅替代锌和铜，也是用到硫酸。常见的镍镉电池也一样，他们可以充电。

【电动势】(electromotive force) \(\mathcal{E}\)：is the measure of energy that it gives to each coulomb of charge. 电动势的大小等于非静电力把单位正电荷从电源的负极，经过电源内部移到电源正极所作的功。这个做功的物理过程是产生电源电动势的本质。非静电力所做的功，反映了其他形式的能量有多少变成了电能。因此在电源内部，非静电力做功的过程是能量相互转化的过程。电池的电动势为12V，这意味着电池为每库仑电荷提供12焦耳的能量。注意：电势差（我们常说的电压）是一库仑电荷从一点移动到另一点所消耗的能量，这个能量由电源提供，电动势是对电源这种能力的度量。电动势在整个电路中传递能量。【电位差】(Potential Difference)是电路上任意两点之间能量的度量。即使电流不在电路中流动，电路中也存在电动势，而当电流的大小保持为零时，电路中不存在电位差。电动势是电路所能达到的最大电压（开路）。两个是完全不同的概念，只是电动势的单位也是伏特，常常混淆，参考Difference Between Electromotive Force & Potential Difference。

short out a battery可以得到最大电流\(I_{\max }=\displaystyle\frac{E M F}{r_i}\)，其中\(r_i\)为电源内阻。

人的发热功率100瓦，但是散热面积很大，所以温度不会升高。

【基尔霍夫电路定律(KCL和KVL)】
第一定律：所有进入某节点的电流的总和等于所有离开这节点的电流的总和\(\displaystyle\sum_{k=1}^n I_k=0\)。
第二定律：沿着闭合回路所有元件两端的电势差(电压)的代数和等于零\(\displaystyle\sum_{k=1}^n V_k=0\)。

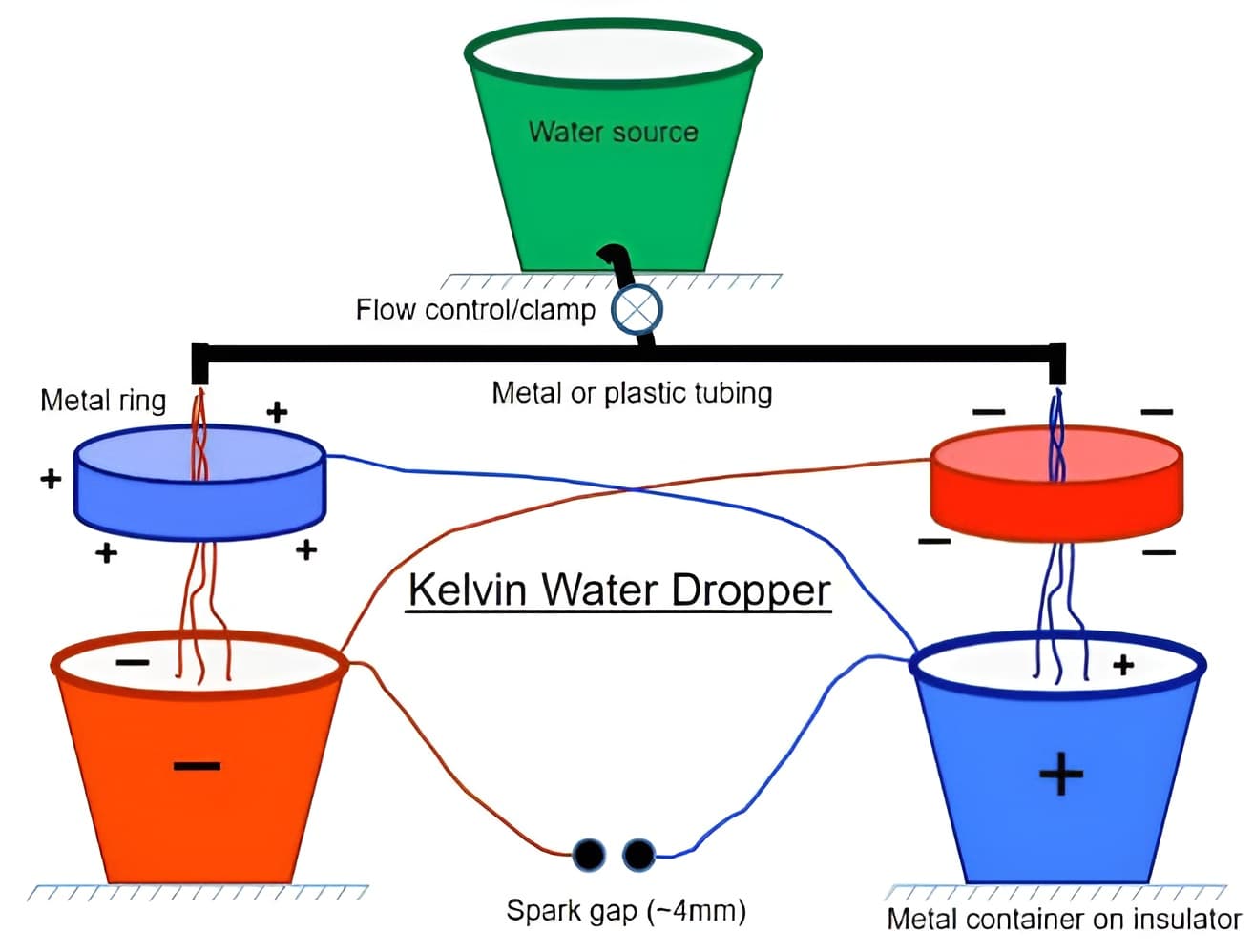
【开尔文滴水起电机】(Kelvin water dropper )
开尔文滴水器是个正反馈的过程，一点点电荷被慢慢放大直至放电中和，有点儿类似蝴蝶效应。水柱散开是由于导电环上面电场已经足够强，而水是极性分子，会收到电场的吸引力。正电荷吸引氧离子端，负电荷吸引氢离子端，电场强度越大发散越厉害，最大到放电级别的场强，然后开始下一轮循环。