双粒子体系[mathjax]
我们讨论的体系不是真的只存在两个粒子,如果真只有两个粒子,那么其实类似双星问题,我们可以将两个点到参考点的矢径差这个向量作为研究对象,其实就是转化成了研究单粒子体系的问题(比如氢原子体系)。这里我们说的双粒子体系,比如氦原子,存在原子核已经核外的两个电子,我们说的双粒子就是指核外的这两个电子。氢原子可以得到解析解,但是对于双粒子体系或者更加复杂的来说,无法得出解析解,只能用计算机算。
单粒子体系是坐标和时间的函数,那么双粒子体系我们可以表示为\( \Psi\left(\mathbf{r}_{1}, \mathbf{r}_{2}, t\right) \),它随时间演化由薛定谔方程来决定\( i \hbar \displaystyle\frac{\partial \Psi}{\partial t}=H \Psi\),整个系统的哈密顿量\( H=-\displaystyle\frac{\hbar^{2}}{2 m_{1}} \nabla_{1}^{2}-\frac{\hbar^{2}}{2 m_{2}} \nabla_{2}^{2}+V\left(\mathbf{r}_{1}, \mathbf{r}_{2}, t\right)\)。归一化条件有\( \displaystyle\int\left|\Psi\left(\mathbf{r}_{1}, \mathbf{r}_{2}, t\right)\right|^{2} d^{3} \mathbf{r}_{1} d^{3} \mathbf{r}_{2}=1 \),即两次积分之后同时覆盖了两个粒子所有出现“位置组合”的可能。如果势能项不随时间变化,那么可以将波函数写成分离变量的形式\( \Psi\left(\mathbf{r}_{1}, \mathbf{r}_{2}, t\right)=\psi\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right) e^{-i E t / \hbar} \),所以空间的不含时的波函数方程如下:(其中\( E \)是系统总能量)$$-\frac{\hbar^{2}}{2 m_{1}} \nabla_{1}^{2} \psi-\frac{\hbar^{2}}{2 m_{2}} \nabla_{2}^{2} \psi+V \psi=E \psi$$假设粒子\( 1\)处在\( \psi_{a}(\mathbf{r})\),粒子\( 2 \)处在\(\psi_{b}(\mathbf{r}) \),\( a\)和\( b \)我们可以简单想象成不能能级(或者电子轨道),那么(两个粒子可分辨)$$\psi\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)=\psi_{a}\left(\mathbf{r}_{1}\right) \psi_{b}\left(\mathbf{r}_{2}\right)$$
电子是基本粒子,任意两个电子长得一模一样。所以当我们在\( \psi_{a}\)和\( \psi_{b}\)波函数的重叠的地方发现了一个电子,其实我们是无法tell out这个电子到底是属于波函数\(\psi_{a} \)还是属于波函数\( \psi_{b}\)。
\( \psi\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right) \)不具有交换对称性exchange symmetry。我们定义一个exchange operator \( P \),具有如下效果$$P f\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)=f\left(\mathbf{r}_{2}, \mathbf{r}_{1}\right)$$那么再作用一次$$P^2 f\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)=f\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)$$即\( P^2 \)算符的对应于本征态\( \left(\mathbf{r}_{1}, \mathbf{r}_{2}\right) \)的特征值为\( 1\),所以\( P \)算符的对应于本征态\( \left(\mathbf{r}_{1}, \mathbf{r}_{2}\right) \)的特征值为\( 1\)或者\( -1\),即有$$P f\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)=\pm f\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)$$写成空间波函数的形式即(存在两种可能性)$$\psi\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)=\pm \psi\left(\mathbf{r}_{2}, \mathbf{r}_{1}\right)$$事实上,所有的基本粒子都满足上面的等式,当等式右边取正号(特征值为\( 1\))的时候,对应的是玻色子(比如准粒子,声子),取负号(特征值为\( -1\))对应的是费米子。相对论量子力学发现,所有的玻色子,自旋都是整数;对费米子来说,自旋都是半整数。
下面讨论自旋的影响。前面我们只讨论了波函数的部分,并没有涉及自旋,现在我们同时考虑波函数和自旋,于是\( f\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right) \)变为\(f\left(\mathbf{r}_{1}, \mathbf{s}_{1}; \mathbf{r}_{2}, \mathbf{s}_{2} \right) \),交换两个粒子的时候,不仅是交换波函数,自旋也会交换。对于只考虑波函数的双粒子(全同)波函数,由于我们不能确定到底是\( 1 \)粒子处于\( a\)态,同时\( 2\)粒子处于\( b\)态还是说\( 1 \)粒子处于\( b\)态,同时\( 2\)粒子处于\( a\)态;我们只能知道粒子\( 1\)和粒子\( 2\)其中一个处于\( a\)态,另一个处于\( b\)态,所以我们只能将双粒子系统的波函数状态写成两者情况的线性组合,即有:$$\begin{array}{l} \psi_{symmetry}\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)=\displaystyle\frac { 1 }{ \sqrt{2}} \left[\psi_{a}\left(\mathbf{r}_{1}\right) \psi_{b}\left(\mathbf{r}_{2}\right) + \psi_{b}\left(\mathbf{r}_{1}\right) \psi_{a}\left(\mathbf{r}_{2}\right)\right]\\ \psi_{anti-symmetry}\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)=\displaystyle\frac { 1 }{ \sqrt{2}} \left[\psi_{a}\left(\mathbf{r}_{1}\right) \psi_{b}\left(\mathbf{r}_{2}\right) - \psi_{b}\left(\mathbf{r}_{1}\right) \psi_{a}\left(\mathbf{r}_{2}\right)\right] \end{array}$$这个和表示两个电子一个自旋向上一个自旋向下的方式是一样的。
考虑波函数和自旋,那么有\( |f\rangle=\psi(\mathbf{r}) \chi(\mathbf{s})\),对双玻色子来说,为了满足其对交换算符的特征值为\( 1\)(即交换对称),那么有两种情况,即\( \psi(\mathbf{r}_{1}, \mathbf{r}_{2}) \)和\( \chi(\mathbf{s}_{1}, \mathbf{s}_{2})\)同时是交换对称或同时是非交换对称。对于双费米子来说,\( \psi(\mathbf{r}_{1}, \mathbf{r}_{2}) \)和\( \chi(\mathbf{s}_{1}, \mathbf{s}_{2})\)必须其中一个是满足交换对称,另一个交换反对称,这样才能保证最终的其对交换算符的特征值为\( -1\)。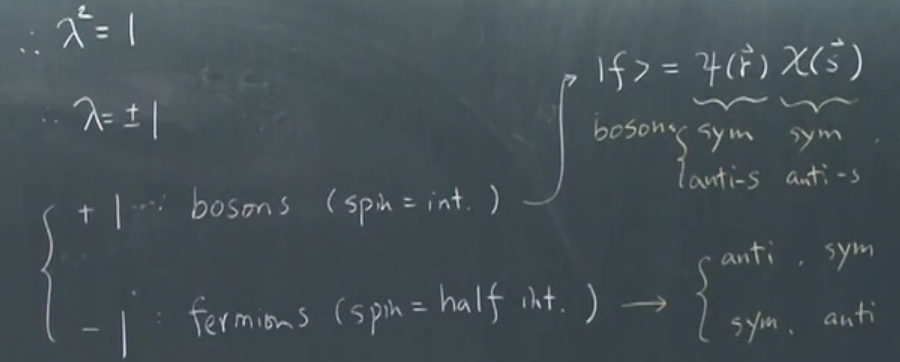
我们以电子作为例子,由于电子是费米子,其交换算符的特征值为\( -1\)(anti-symmetry)。如果双电子的波函数选择\( \psi_{\text {anti-symmetry}}\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)\),那么双电子自旋的spin state一定就是三重态(交换对称);如果波函数选择\( \psi_{\text {symmetry}}\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)\),那么双电子自旋的spin state一定就是单态(交换不对称)。
对于氦原子来说,假设两个电子都在基态\( 1s\)轨道上,那么\( a=b\),按前面的描述,波函数有两种选择的方式,但是现在如果选择\( \psi_{\text {anti-symmetry}}\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right)\),你会发现它始终等于零,因此只有\( \psi_{\text {symmetry}}\left(\mathbf{r}_{1}, \mathbf{r}_{2}\right) \)是满足条件的,那么自旋的话只能选择单态(\( |00\rangle=\displaystyle\frac{1}{\sqrt{2}}(\uparrow \downarrow-\downarrow \uparrow) \))。如果先考虑自旋,那么如果两个电子自旋相同\( |11\rangle=\uparrow \uparrow \)或\( |1-1\rangle=\downarrow \downarrow\),那么必然是交换对称的,那么波函数只能选选择\( \psi_{\text {anti-symmetry}} \),两个电子的自旋和轨道都一样,那么必然波函数等于零,矛盾。这其实就是泡利不相容原理,当然我们化学里面学的泡利不相容是说的电子,实际上是针对所有的费米子,即所有的费米子都满足泡利不相容原理,它是由exchange symmetry requirement来的。我们说的\( 1s\)轨道的两个电子,一个自旋上一个自旋下,但是由于我们无法区分这两个电子,所以实际上的情况是处于\( |00\rangle=\displaystyle\frac{1}{\sqrt{2}}(\uparrow \downarrow-\downarrow \uparrow)\)的叠加态。