卷积与中心极限定理
中心极限定理(Central Limit Theorem)
中心极限定理,简称CLT。一句话说清楚就是:独立同分布的随机变量之和服从正态分布。大多数概率事件,当有足够多的取样时,都服从高斯分布。(Most probabilities – some kind of average – are calculated or approximated as if they are determined by a Gaussian.)我在概率统计资料中也讲到了中心极限定理,举例掷骰子,比如连续掷骰子\( 30 \)次,然后将结果加和,重复\( 10000 \)次这个“掷骰子\( 30\)次的动作”,那么加和的结果分布是高斯分布。
我们先前已经知道,一个不怎么平滑的函数,卷积之后也会变平滑,似乎卷积是一种平滑操作。Let's begin with some graphical examples.
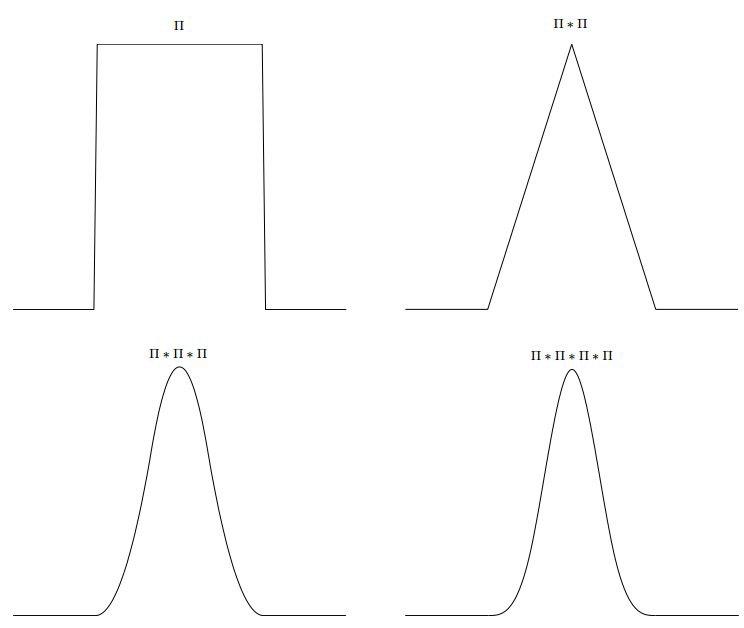
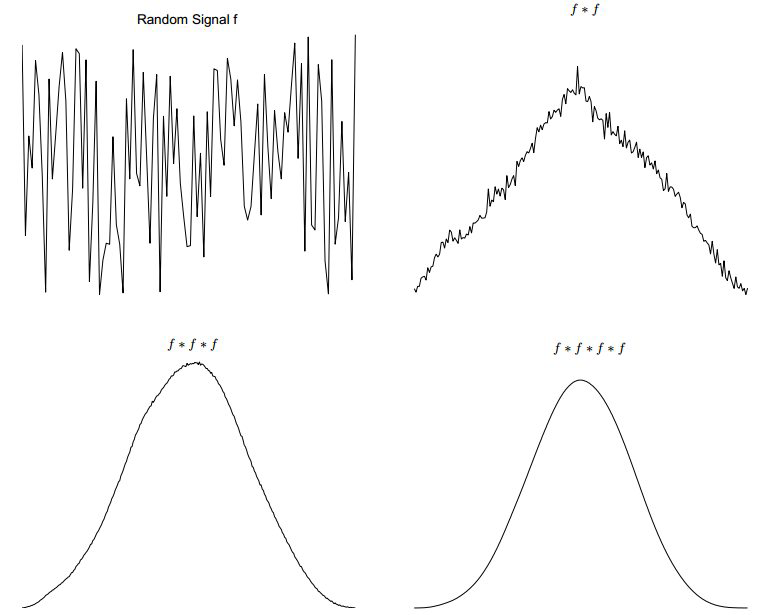
标准正态(高斯)分布
在傅里叶变换中,我们用\( f=e^{-\pi t^{2}} \)作为高斯函数傅里叶变换的例子,因为它的正逆傅里叶变换都是\( f=e^{-\pi t^{2}}\)。其实这个高斯函数是非常特殊的,对于一般性的高斯函数(概率密度分布的那种,当然前面的例子也是其中的特例),傅里叶变换后的函数也是高斯函数,只是幅度和方差发生了变化。对中心极限定理来说,标准正态分布的密度函数(probability density function)是$$p(x)=\frac{1}{\sqrt{2 \pi}} e^{\frac{-x^{2}}{2}}$$采用这个式子作为标准正态分布的原因是它的均值(期望值)是\( 0 \),它的标准差与方差为\( 1 \)。那么,连续随机变量\( X\)出现在\(a \)和\( b \)之间的概率为$$\operatorname{Prob}(a \leqslant X \leqslant b)=\int_{a}^{b} p(x) d x=\frac{1}{\sqrt{2 \pi}} \int_{a}^{b} e^{-\frac{x^{2}}{2}} d x=F(b)-F(a)$$其中\( F(x)=P(X \leq x)\)为概率分布函数,其导数即为概率密度函数。
分布与卷积的关系
假设独立随机变量\( X_1\)和\( X_2 \),它们的和\( X_1+X_2\)的概率密度分布\( p(x_1+p_2)\)和它们独立的概率密度分布\( p_{1}\left(x_{1}\right)\)、\( p_{2}\left(x_{2}\right)\)有什么关系?
求解过程如下:.png)
坐标落在阴影部分的概率$$\operatorname{Prob}\left(X_{1}+X_{2} \leqslant t\right)=\iint_{x_{1}+x_{2} \leq t} p_{1}\left(x_{1}\right) p_{2}\left(x_{2}\right) d x_{1} d x_{2}$$变量代换$$\left\{\begin{aligned} x_{1} &=u \\ x_{2} &=v-u \\ t &=v \end{aligned}\right.$$新平面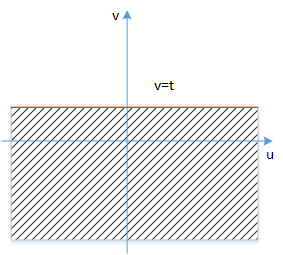
$$\begin{aligned} \operatorname{Prob}\left(X_{1}+X_{2} \leqslant t\right) &=\int_{-\infty}^{\infty} \int_{-\infty}^{t} p_{1}(u) p_{2}(v-u) d u d v \\ &=\int_{-\infty}^{t}\left(\int_{-\infty}^{\infty} p_{1}(u) p_{2}(v-u) d u\right) d v \\ &=\int_{-\infty}^{t}\left(p_{1} * p_{2}\right) d v \end{aligned}$$ \( \displaystyle\int_{-\infty}^{t}\left(p_{1} * p_{2}\right) d v \)对\( t\)求导得到\( p_{1} * p_{2}\),即自由随机变量\(X_1+X_2 \)的概率密度分布\(p_{1} * p_{2} (t) \)。
如果\( X_{1}, X_{2}, \ldots, X_{n}\)都是独立随机变量,且对应的概率密度函数分别为\( p_{1}, p_{2}, \ldots, p_{n}\),那么\( X_{1}+X_{2}+\cdots+X_{n} \)的概率密度函数为\( p_{1} * p_{2} * \cdots * p_{n}\)。
特别地,当\( X_{1}, X_{2}, \ldots, X_{n}\)属于相同分布的时候,即独立同分布时,我们可以将\( X_{1}+X_{2}+\cdots+X_{n} \)的概率密度函数写成:$$p^{* n}(x)=(p * p * \cdots * p)(x)=p\left(x_{1}+x_{2}+\ldots+x_{n}\right)$$
结论:
1. 独立随机变量的和的密度函数为他们各自密度函数的卷积
2. 任意连续概率密度函数或者离散概率密度函数,每卷积一次,就变得更平滑,更接近高斯分布,一般四五次之后就非常像高斯分布的形状了(任意频域(和上面的密度函数无关)卷积多次都成了高斯)。
中心极限定理推导过程
设\( n \)个独立随机变量\(X_{1}, X_{2}, \ldots, X_{n} \)它们的概率分布函数都相同,其中任意一个变量\( X_i \)的期望值是\(\mu \),标准差是\(\sigma \)。设\( S_{n} \)有\( S_{n}=X_{1}+X_{2}+\ldots+X_{n}\),随着\( n \)的增大,\(S_{n} \)越来越像一个高斯函数,那么它的期望值(均值)和标准差是如何随着\( n\)而变化的呢?(可以从期望和标准差的定义(见注释)中感受出下面的结果,严格证明见教材3.9 Appendix: The Mean and Standard Deviation for the Sum of Random Variables)$$\begin{array}{l} \mu\left(S_{n}\right)=n \mu \\ \sigma\left(S_{n}\right)=\sqrt{n} \sigma \end{array}$$接下来我们将\( S_{n} \)标准化为标准正态分布函数:$$\frac{S_{n}-n \mu}{\sqrt{n} \sigma}$$当\( n \rightarrow \infty \)时,中心极限定理定理的一种形式如下:$$\lim _{n \rightarrow \infty} \operatorname{Prob}\left(a<\frac{S_{n}-n \mu}{\sqrt{n} \sigma}<b\right)=\frac{1}{\sqrt{2 \pi}} \int_{a}^{b} e^{-x^{2} / 2} d x$$其中的\( (1 / \sqrt{2 \pi}) e^{-x^{2} / 2}\)就是标准正态分布的密度函数。
现在我们假设\( X_i \)都满足期望\( \mu=0 \),标准差\(\sigma=1 \),这意味着$$\int_{-\infty}^{\infty} x p(x) d x=0 \quad \text { and } \quad \int_{-\infty}^{\infty} x^{2} p(x) d x=1\quad \text { and } \int_{-\infty}^{\infty} p(x) d x=1$$那么现在\( S_n \)的期望值显然也是\( 0\),标准差为\(\sqrt{n} \)。为了往我们想要的标准正态分的密度函数上靠,必须用\( S_{n} / \sqrt{n}\)替代\( S_n\),这样才能满足期望\( 0\),标准差为\( 1 \),这种替代可以从附录中的标准差计算公式看出来。根据前面的知识,我们已经知道独立同分布下\( p^{* n}(x)=(p * p * \cdots * p)(x)\),那么\( S_{n} / \sqrt{n}\)的概率密度函数为$$p_{n}(x)=\sqrt{n} p^{* n}(\sqrt{n} x)$$ 中心极限定理的描述:Central limit Theorem Let \( X_{1}, X_{2}, \ldots, X_{n} \) be independent, identically distributed random variables with mean 0 and standard deviation 1. Let \( p_{n}(x) \) be the probability density function for \( S_{n} / \sqrt{n}=\left(X_{1}+X_{2}+\cdots+X_{n}\right) / \sqrt{n} \). Then$$ p_{n}(x) \rightarrow \frac{1}{\sqrt{2 \pi}} e^{-x^{2} / 2} \quad \text { as } n \rightarrow \infty $$
下面我们来证明:
我们用大写字母来表示概率密度的傅里叶变换:\( P(s)=\mathcal{F} p(s)\),那么前面我们得到的\( p_{n}(x)=\sqrt{n} p^{* n}(\sqrt{n} x) \)的傅里叶变换为$$P^{n}\left(\frac{s}{\sqrt{n}}\right) \quad(\text { ordinary } n \text { th power here })$$\( P\left(\frac{s}{\sqrt{n}}\right) \)可以通过傅里叶变换(卷积运算转换为乘法运算)以及指数函数的泰勒展开得到$$\begin{aligned} P\left(\frac{s}{\sqrt{n}}\right) &=\int_{-\infty}^{\infty} e^{-2 \pi i s x / \sqrt{n}} p(x) d x \\ &=\int_{-\infty}^{\infty}\left(1-\frac{2 \pi i s x}{\sqrt{n}}+\frac{1}{2}\left(\frac{2 \pi i s x}{\sqrt{n}}\right)^{2}+\text { small }\right) p(x) d x \\ &=\int_{-\infty}^{\infty}\left(1-\frac{2 \pi i s x}{\sqrt{n}}-\frac{2 \pi^{2} s^{2} x^{2}}{n}+\operatorname{sinall}\right) p(x) d x \\ &=\int_{-\infty}^{\infty} p(x) d x-\frac{2 \pi i s}{\sqrt{n}} \int_{-\infty}^{\infty} x p(x) d x-\frac{2 \pi^{2} s^{2}}{n} \int_{-\infty}^{\infty} x^{2} p(x) d x+\int_{-\infty}^{\infty}(\text { small }) p(x) d x \\ &=1-\frac{2 \pi^{2} s^{2}}{n}+\text { small } \end{aligned}$$其中small的term在\( n \rightarrow \infty \)时,比\(1 / n \)更快地趋近于\( 0 \)。借助于\( (1+x / n)^{n} \rightarrow e^{x} \),在\( n \)很大的情况下有:$$P^{n}\left(\frac{s}{\sqrt{n}}\right) \approx\left(1-\frac{2 \pi^{2} s^{2}}{n}\right)^{n} \approx e^{-2 \pi^{2} s^{2}}$$用傅里叶逆变换求出(当\( n \rightarrow \infty\)):$$p_{\text {normal }}=p_{n}(x)=\mathcal{F}^{-1}\left(e^{-2 \pi^{2} s^{2}}\right)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^{2}}{2}}$$其中\( n\)可以理解为某个独立随机变量连续测量的次数,当测量次数足够多时,其概率的密度函数会符合正态分布。这也就是我们所称的中心极限定理。
注:
1. 标准差的计算公式:
离散型随机变量的公式为 \( S D=\displaystyle\sqrt{\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2}} \)
连续型随机变量的公式为\( \sigma=\sqrt{\displaystyle\int(x-\mu)^{2} f(x) d x} \)。
2. \( p^{* n}(\sqrt{n} x)\)等价于\( (p * p * \cdots * p)(\sqrt{n} x) \),不等于\( p(\sqrt{n} x) * p(\sqrt{n} x) * \cdots p(\sqrt{n} x)\)。
3. 可以参考我学仿照的笔记这部分的内容,以及对应书本的补充材料。
4. 参考知乎:【AP统计】期望E(X)与方差Var(X)
(1)期望运算性质:
\( E(c X)=c E(X) \)
\( E(X+Y)=E(X)+E(Y)\)
\( E(X-Y)=E(X)-E(Y)\)
\( E(X Y)=E(X) E(Y) \)两个独立随机变量
(2)方差运算性质:
\( D(c X)=c^{2} D(X) \)
\( D(X+a)=D(X) \)
\( D(c X+a)=c^{2} D(X)\)
\( D(X \pm Y)=D(X)+D(Y)\)两个独立随机变量
(3)期望和方差的关系:\( D(X)=E\left(X^{2}\right)-[E(X)]^{2} \)
二项分布是正态分布的一个特殊情况,正态分布的随机变量是连续的,而二项分布的变量取值只有两项,是离散的。二项分布在我们的日常生活中比较常见。用游戏抽卡来举个例子,取值只有出货或者没出货两个。设\( n\)是某一个人抽卡的次数,如果\( n \rightarrow \infty\),那么这个人抽卡出货的情况,呈二项分布。简而言之,假设有非常多的人(比如\( 1000\)人)在玩某个抽卡游戏,并且每个人的抽卡次数都比较多(\( 30\)次足够),那么这些人抽卡的出货量会分布符合高斯分布。