傅里叶正(反)变换复习

傅里叶变换没有统一的定义

傅里叶变换的符号在不同的书籍可能有不同的写法：
如正变换的符号：\(  \mathcal{F} f(s), \hat{f}(s), F(s)\)
如反变换的符号：\(  \mathcal{F}^{-1} f(t), \quad \check{f}(t), \quad f(t)\)

傅里叶变换的公式也没有统一的写法：
本课程(光学都用这种，老师也认为这种用的多)$$\mathcal{F} f(s)=\int_{-\infty}^{\infty} e^{-2 \pi i s t} f(t) d t$$另外有些书本的写法是：$$\mathcal{F} f(\omega)=\int_{-\infty}^{\infty} e^{-i \omega t} f(t) d t$$注：其实前者频谱的横坐标是频率，而后者频谱的横坐标其实是\(  \omega \)角频率。\(  2 \pi i\)的写法光学中用更常见。

高斯函数的傅里叶变换

首先我们复习一下正态分布的概率密度函数\( f(x)=\displaystyle\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} \)；高斯函数的一般形式为\( f(x)=a e^{-(x-b)^{2} / 2 c^{2}} \)。我们选择归一化之后的一个选定的正态分布函数$$f(t)=e^{-\pi t^{2}}$$通过极坐标积分我们知道该函数的在整个范围内的积分结果为\(  1\)，即$$\int_{-\infty}^{\infty} e^{-\pi t^{2}} d t=\sqrt{1}=1$$对高斯函数进行傅里叶变换$$F(s)=\mathcal{F} f(s)=\int_{-\infty}^{\infty} e^{-2 \pi i s t} e^{-\pi t^{2}} d t$$不好积，我们采用迂回微分的方式$$\begin{aligned} F^{\prime}(s)=\mathcal{F} f^{\prime}(s) &=\int_{-\infty}^{\infty} \frac{d\left(e^{-2 \pi i s t}\right)}{d s} e^{-\pi t^{2}} d t \\ &=\int_{-\infty}^{\infty}-2 \pi i t e^{-2 \pi i s t} e^{-\pi t^{2}} d t \\ &=i \int_{-\infty}^{\infty} e^{-2 \pi i s t}\left(-2 \pi t e^{-\pi t^{2}}\right) d t \\ &=i\left(\left.e^{-2 \pi i s t} e^{-\pi t^{2}}\right|_{-\infty} ^{\infty}-\int_{-\infty}^{\infty} e^{-\pi t^{2}}\left(-2 \pi i s e^{-2 \pi i s t}\right) d t\right) \\ &=-2 \pi s \int_{-\infty}^{\infty} e^{-2 \pi i s t} e^{-\pi t^{2}} d t \quad \text { eliminate }\left.e^{-2 \pi i s t} e^{-\pi t^{2}}\right|_{-\infty} ^{\infty} b e c a u s e\left|e^{-2 \pi i s t}\right|=1, \lim _{t \rightarrow \infty} e^{-\pi t^{2}}=0 \\ &=-2 \pi s F(s) \end{aligned}$$求偏微分方程得$$F(s)=F(0) e^{-\pi s^{2}}=\int_{-\infty}^{\infty} e^{-\pi t^{2}} d t \times e^{-\pi s^{2}}=e^{-\pi s^{2}}$$也就是说归一化为1的高斯函数的傅里叶变换还是归一化为1的高斯函数。

反转信号(reverse signal)

这是一个新的定义，目的是为了方便式子的表达，定义如下$$f^{-}(t)=f(-t)$$ \(  f^{-}(t)\)即为\(  f(t)\)的反转。

傅里叶变换的对偶性(Fourier Transform Duality)

回顾一下傅里叶变换：$$F(s)=\mathcal{F} f(s)=\int_{-\infty}^{\infty} e^{-2 \pi i s t} f(t) d t$$当取值为\(  -s\)时，$$F(-s)=\mathcal{F} f(-s)=\int_{-\infty}^{\infty} e^{2 \pi i s t} f(t) d t=\mathcal{F}^{-1} f(s)$$\(  f(t)\)傅里叶变换得到\(  F(s)\)，\(  F(s)\)通过逆变换得到\( f(t) \)；而上面的式子是对\(  f(t)\)进行傅里叶逆变换，在这里我们并不需要分析这个等式所表示的含义，而是把傅里叶变换当工具来使用。

对偶性的来源：傅里叶变换和逆变换公式上的相似性。

对偶定理1

把反转信号引入傅里叶变换的对偶性中，得$$\mathcal{F} f(-s)=(\mathcal{F} f)^{-}(s)$$而\(  \mathcal{F} f(-s)=\mathcal{F}^{-1} f(s)\)，即有$$\begin{aligned}
(\mathcal{F} f)^{-}(s) &=\mathcal{F}^{-1} f(s) \\
(\mathcal{F} f)^{-} &=\mathcal{F}^{-} f
\end{aligned}$$函数的傅里叶变换的反转等于对该函数进行傅里叶逆变换。

对偶定理2

如果对\(  f^{-}(t)\)进行傅里叶变换会得到什么结果呢？$$\begin{aligned}
\mathcal{F}\left(f^{-}(s)\right) &=\int_{-\infty}^{\infty} e^{-2 \pi i s t} f(-t) d t \\
&=\int_{+\infty}^{\infty} e^{-2 \pi i s(-u)} f(u) d(-u) \quad \text { let } u=-t \\
&=\int_{-\infty}^{\infty} e^{2 \pi i s u} f(u) d u \\
&=\mathcal{F}^{-1} f(s)
\end{aligned}$$即$$\mathcal{F}\left(f^{-}\right)=\mathcal{F}^{-} f$$函数的反转的傅里叶变换等于对该函数进行傅里叶逆变换。

对偶定理3

把对偶定理1与对偶定理2结合起来，得$$(\mathcal{F} f)^{-}=\mathcal{F}\left(f^{-}\right)$$函数的傅里叶变换的反转等于对该函数反转的傅里叶变换。

注：前面三个对偶定理，其实本质上就是对\(  (\mathcal{F} f)^{-}\)，这个负号既可以单独转移到\( \mathcal{F} \)上，也可以单独转移到\( f \)上；放在\( \mathcal{F} \)负号就是表示傅里叶逆变换，放在\(  f\)上表示信号的翻转。

对偶定理4

对函数进行两次傅里叶变换等于该函数的反转。$$\mathcal{F} \mathcal{F} f=\mathcal{F}(\mathcal{F} f)=\mathcal{F}\left(\mathcal{F}^{-}\left(f^{-}\right)\right)=f^{-}$$

对偶定理的应用

对偶定理的目的是为了方便计算，如：求\(  \operatorname{sinc}\)函数的傅里叶变换$$\mathcal{F} \operatorname{sinc}=\mathcal{F} \mathcal{F} \pi=\pi^{-}=\pi$$

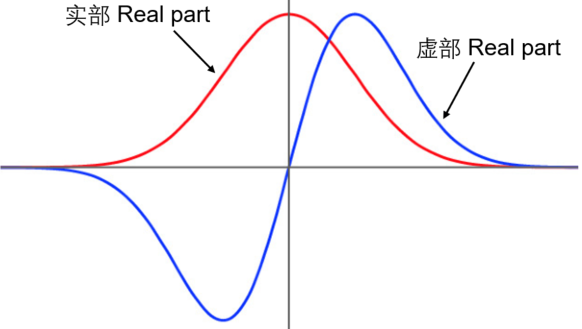【埃尔米特函数】(Hermitian function)：在数学分析领域中，埃尔米特函数是当一个函数的共轭复数与将原函数的自变量变号后的值相等的复变函数。对于所有在\(f\)定义域内的所有\(x\)满足：(其中上横线表示复共轭)$$f(-x)=\overline{f(x)}$$这个定义也可以拓展到两个或多个变量的函数，比如\(f\left(-x_1,-x_2\right)=\overline{f\left(x_1, x_2\right)}\)。根据这个定义，可以得出一个很显然的推论：当且仅当\(f\)的实部为偶函数，且虚部为奇函数时，\(f\)是埃尔米特函数。

埃尔米特函数经常出现在数学、物理和信号处理中。根据傅里叶变换的性质，可以得出以下几条叙述：
(1) 实函数的傅里叶变换为埃尔米特函数；
由于实信号的傅里叶变换可以保证是埃尔米特函数，因而可以将埃尔米特奇/偶对称性用于压缩。这使得经过离散傅里叶变换的信号(为一般复数)可以存储在与原实数信号相同的空间中。此处可以参考我的FFT笔记。
(2) 埃尔米特函数的傅里叶变换为实函数；
(3) 若\(f\)为埃尔米特函数，则\(f \star g=f * g\)
(4) 若\(f\)与\(g\)都为埃尔米特函数，则\(f \star g=g \star f\)
注：\(\star\)是互相关，\(*\)是卷积。