静电现象的基本理论描述

库仑定律/叠加原理

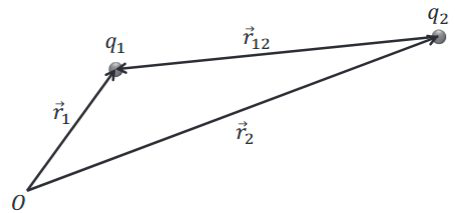点电荷库仑定律(向心力)$$\vec{F}_{12}=\displaystyle\frac{1}{4 \pi \varepsilon_{0}} \displaystyle\frac{q_{1} q_{2}}{r_{12}^{3}} \vec{r}_{12}$$

 

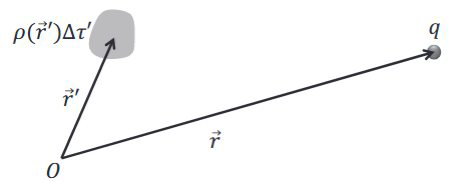叠加原理(离散/连续积分描述)$$ \begin{aligned} &\vec{F}_i=\frac{1}{4 \pi \varepsilon_0} \sum_{i \neq j}^N \frac{q_i q_j}{r_{i j}^3} \vec{r}_{i j} \\ &\vec{F}=\frac{1}{4 \pi \varepsilon_0} \int \frac{q \rho\left(\vec{r}^{\prime}\right) d \tau^{\prime}}{R^3} \vec{R} \end{aligned} $$对于两个带电体，1受到2总的静电作用力$$\vec{F}_{12}=\displaystyle\frac{1}{4 \pi \varepsilon_{0}} \displaystyle\int \displaystyle\frac{\rho_{1}(\vec{r}) \rho_{2}\left(\vec{r}^{\prime}\right) d \tau d \tau^{\prime}}{R^{3}} \vec{R}$$电场：与放入的检验电荷无关。$$\vec{E}(\vec{r})=\vec{F}(\vec{r}) / q$$电场引入的作用：
(1)  计算静电力；
(2)  静电相互作用的新图像
旧：电荷 \(q_1 \stackrel{\text { 超距 }}{\Longleftrightarrow}\)电荷 \(q_2\)
新：电荷 \(q_1 \Longleftrightarrow\) 电场 \(\Longleftrightarrow\) 电荷 \(q_2\)

当所有物理量随时间变化，可以看到第二种物理图像是正确的，而先前的是错误的，四大基本作用都不是超距相互作用。电场是一种客观存在的物理，具有能量、动量等。连续带电体产生的电场：$$\vec{E}(\vec{r})=\displaystyle\frac{1}{4 \pi \varepsilon_{0}} \displaystyle\int \displaystyle\frac{\rho\left(\vec{r}^{\prime}\right) d \tau}{R^{3}} \vec{R}$$注：
(1) \( \rho\left(\vec{r}^{\prime}\right) \)表示的是单位体积所带的电荷量；
(2) 习惯将右上角有一撇的作为“源”，作用点不用撇；
(3) 这里的\(d \tau\)严格来说并不严谨，用\(d \tau^{\prime}\)表示更严谨，即对应场源的微体积，\(d \tau^{\prime}=d^3{r^{\prime}}\)，因为我们只讨论源的体积，所以这种表达也不会引发歧义；
(4) \(\vec{R}= \overrightarrow{r}-\overrightarrow{r}^{\prime}\)，即表示\(\vec{r}^{\prime}\)的端点到\(\vec{r}\)的端点的矢量，也表示从原点出发的观察点的位置；
(5) 上面如果积分里面分子是\(R^{3}\)，如果改成平方，那么分母的\( \vec{R} \)要改为单位方向向量。

 

电场的散度性质-高斯定理

闭合曲面包围电荷\(q\)(不要求是球)$$\begin{aligned} \vec{E} \cdot \Delta \vec{S} &=\displaystyle\frac{1}{4 \pi \varepsilon_{0}} \displaystyle\frac{q}{r^{2}} \cdot \Delta S \\ &=\displaystyle\frac{1}{4 \pi \varepsilon_{0}} \displaystyle\frac{q}{r^{2}} \cdot r^{2} \cdot \Delta \Omega \\ &=\displaystyle\frac{q}{4 \pi \varepsilon_{0}} \Delta \Omega \end{aligned}$$其中\(  \Delta \Omega\)为立体角，上面的表达式消去了\( r \)，只保留了体积微元和立体角微元，那么对体积积分$$\displaystyle\oint \vec{E} \cdot d \vec{S}=\displaystyle\int \displaystyle\frac{q}{4 \pi \varepsilon_{0}} d \Omega=\displaystyle\frac{q}{4 \pi \varepsilon_{0}} \displaystyle\int d \Omega=\displaystyle\frac{q}{\varepsilon_{0}}$$高斯定理：对包裹一坨电荷密度为\(\rho(\vec{r})\)的闭合曲面积分$$\displaystyle\oint \vec{E} \cdot d \vec{S}=\displaystyle\int[\nabla \cdot \vec{E}(\vec{r})] d \tau=\displaystyle\int \rho(\vec{r}) \cdot d \tau / \varepsilon_{0}$$曲面积分变成体积分，向量场的散度$$\nabla \cdot \vec{E}(\vec{r})=\rho(\vec{r}) / \varepsilon_{0}$$连续的电场线的散度为零，因为没有电场线的汇聚和发散，这有点类似平面横波，也是无散的；一旦空间有一个电荷，那么原有的电场线的连续性就会被打破，有正电荷电场线会发散，有负电荷电场线会汇聚。

散度的理解：
(1)  一个场到底有没有汇聚和发散的地方；
(2)  散度为零，场线在此处连续；
(3)  散度不为零，空间中出现奇点(导致场线汇聚/发散)
(4)  自己的形象理解，把电荷看成泵，这个泵在不断地抽电场线，往外延伸，电荷越多，泵的功率越大，电场线越密集。

注：
(1)  如果\(\vec{r}=(x,y,z) \)，那么模长\(r=\sqrt{x^{2}+y^{2}+z^{2}}  \)，对\( \vec{r} \)求梯度，我们当然可以用三个坐标轴的向量场来表示，但是还可以用更简洁的方式来描述$$ \nabla r=\frac{\vec{r}}{r}=\hat{\boldsymbol{r}} $$(2)  直接对\( \vec{E}(\vec{r})=\displaystyle\frac{1}{4 \pi \varepsilon_{0}} \displaystyle\int_{\tau} \displaystyle\frac{\rho\left(\vec{r}^{\prime}\right) d \tau}{R^{3}} \vec{R} \)等式两边求散度有$$\nabla \cdot \vec{E}(\vec{r}^{\prime})=\displaystyle\frac{1}{4 \pi \varepsilon_{0}} \displaystyle\int \rho\left(\vec{r}^{\prime}\right) d \tau\left(\nabla \cdot \displaystyle\frac{\vec{R}}{R^{3}}\right)$$而\( \nabla \cdot \vec{E}(\vec{r})=\rho(\vec{r}) / \varepsilon_{0} \)，两个公式结合起来可以推出$$\nabla \cdot\left(\displaystyle\frac{\vec{R}}{R^{3}}\right)=4 \pi \delta(\vec{R})$$注：在矢量分析那一章节，我们已经说明了\(  \nabla \cdot\left(\displaystyle\frac{\hat{\boldsymbol{r}}}{r^{2}}\right)=4 \pi \delta(\boldsymbol{r})\)，而\(\displaystyle\frac{\hat{\boldsymbol{r}}}{r^2}=\frac{\boldsymbol{r}}{r^3}\)。

 

静电场的旋度–安培环路定理

先了解两个公式：$$\begin{array}{c} \nabla r=\vec{r} / r \rightarrow \nabla R=\vec{R} / R \\ \nabla\left(\displaystyle\frac{1}{R}\right)=-\displaystyle\frac{\nabla R}{R^{2}}=-\displaystyle\frac{1}{R^{2}} \displaystyle\frac{\vec{R}}{R}=-\displaystyle\frac{\vec{R}}{R^{3}} \end{array}$$注：分部微分\(  \nabla f(r)=\displaystyle\frac{\partial f}{\partial r} \nabla r\)，\( \nabla \)算符同时具有矢量性和微分性。

静电场可以改写为(标量势的梯度运算)$$ \begin{aligned} \vec{E}(\vec{r}) &=\frac{1}{4 \pi \varepsilon_0} \int \frac{\rho\left(\vec{r}^{\prime}\right) d \tau}{R^3} \vec{R}=-\frac{1}{4 \pi \varepsilon_0} \int \rho\left(\vec{r}^{\prime}\right) d \tau \cdot \nabla\left(\frac{1}{R}\right) \\ &=-\nabla\left[\frac{1}{4 \pi \varepsilon_0} \int \frac{\rho\left(\vec{r}^{\prime}\right)}{R} d \tau\right] \\ &=-\nabla \varphi(\vec{r}) \end{aligned} $$其中标量势$$\varphi(\vec{r})=\displaystyle\frac{1}{4 \pi \varepsilon_{0}} \displaystyle\int \displaystyle\frac{\rho\left(\vec{r}^{\prime}\right)}{R} d \tau$$静电场的环路积分$$\displaystyle\oint \vec{E} \cdot d \vec{l}=-\displaystyle\oint \nabla \varphi(\vec{r}) \cdot d \vec{l}=-\displaystyle\oint(\partial \varphi / \partial l) \cdot d l \equiv 0$$写成微分的形式$$\nabla \times \vec{E}(\vec{r})=-\nabla \times \nabla \varphi(\vec{r}) \equiv 0$$

无旋场 = 保守场 = 可以定义标量势(势函数的梯度形成的场) = 积分与路径无关

电场：无旋，有源，从正电荷出来(有源)，跑到负电荷，中间不打转(打转就有旋)。

注：
(1)  想一想为什么里面的梯度可以提到外面?
(2)  电势梯度的方向是从小的势指向大的势的地方，而电场线的方向是从大的势指向小的势，所以二者的方向差了一个负号。
(3)  \( \partial \varphi / \partial l \)表示沿着环路的切线方向求偏导数;
(4)  电场的环路积分，根据斯托克斯公式，其实是对旋度场的曲面积分，结果为零的话，用微分表达就是旋度场为零，即电势梯度场的负号的旋度场为零。

 

电偶极子

物质对外电场最简单的响应就是形成电偶极子，所以说电偶极子是最基础且重要的研究对象。

一点点地拆分靠近观察：
人-点电荷的性质-----衰减慢，电势按\(r\)的一次方decay  (粗糙)；
女-电偶极子的性质---衰减较快，电势按\(r\)的二次方decay  (细节)；
30岁-电四极子的性质---衰减快，电势按\(r\)的三次方decay   (更细节)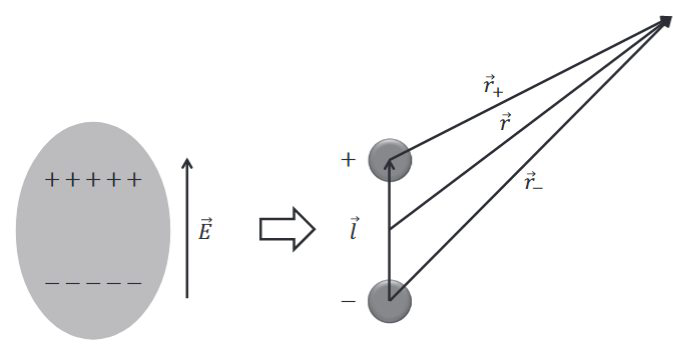；如果分别求解正电荷和负电荷形成的电场，然后按照叠加原理，算出最终的电场分布，这种做法很复杂。下面采用的是计算电势的方法$$\begin{aligned} \varphi(\vec{r}) &=\displaystyle\frac{q}{4 \pi \varepsilon_{0}}\left(\displaystyle\frac{1}{r_{+}}-\displaystyle\frac{1}{r_{-}}\right) \\ & \approx \displaystyle\frac{q}{4 \pi \varepsilon_{0}} \displaystyle\frac{r_{-}-r_{+}}{r^{2}} \\ & \approx \displaystyle\frac{q}{4 \pi \varepsilon_{0}} \displaystyle\frac{l \cos \theta}{r^{2}} \\ &=\displaystyle\frac{p \cos \theta}{4 \pi \varepsilon_{0} r^{2}} \\ &=\displaystyle\frac{\vec{p} \cdot \vec{r}}{4 \pi \varepsilon_{0} r^{3}} \end{aligned}$$对电势求梯度得到电场(分部运算，类似分部求导)$$\begin{aligned} \vec{E}(\vec{r}) &=-\nabla \varphi \\ &=-\displaystyle\frac{1}{4 \pi \varepsilon_{0}}\left[\displaystyle\frac{\nabla(\vec{p} \cdot \vec{r})}{r^{3}}+\vec{p} \cdot \vec{r} \nabla \displaystyle\frac{1}{r^{3}}\right] \\ &=-\displaystyle\frac{1}{4 \pi \varepsilon_{0}}\left[\displaystyle\frac{\vec{p}-3(\vec{p} \cdot \hat{r}) \hat{r}}{r^{3}}\right] \end{aligned}$$设\(\hat{p} \| \hat{z}  \)，那么在球坐标系的三个分量(不太友好的表达方式)$$ \begin{array}{lll} E_r=\displaystyle\frac{p \cos \theta}{2 \pi \varepsilon_0 r^3} \quad E_\theta=\displaystyle\frac{p \sin \theta}{4 \pi \varepsilon_0 r^3} \quad E_\phi=0 \end{array} $$

注：
(1)   电偶极子的方向为什么是负电荷指向正电荷?
(2)  对电场的响应体现在两个方面：拉开多少电量和拉开多远距离。这就是电偶极子公式所描述的，物质的响应；
(3)  \( \nabla(\vec{p} \cdot \vec{r})=\vec{p} \)，\( \nabla\left(r^{n}\right)=n r^{n-1} \hat{r} \)，\(  \nabla r=\vec{r} / r\)，\( \nabla^{2}(1 / r)=-4 \pi \delta(\vec{r}) \)常见的记住。