插值法-以及拉格朗日乘数法

Post author:zhejie
Post published:2020年4月13日
Post category:微积分 / 数学
Post comments:0 Comments

我们在matlab-ODE23中提到里面涉及三次Hermite插值，所以这篇文章我具体讲一下什么是插值法。拉格朗日乘数法先前碰到过几次，这里也顺便总结一下

拉格朗日乘数法

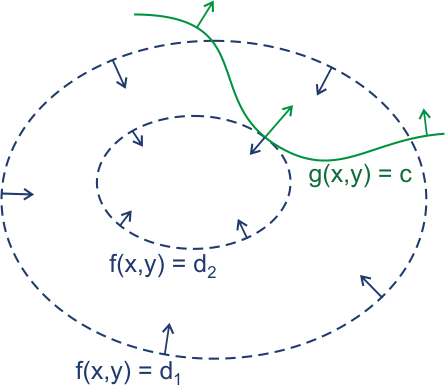
要求解函数$f(x,y) $在约束$ g(x,y)=c $的情况下的极值点。方法是不断变化$ f(x,y)=d $中的$ d$值，从而绘制出一系列等高线，图中是椭圆，实际上也可能为不规则的图形或者最简单的一圈一圈的圆。当$d=d_{1} $的时候等高线正好和约束曲线相切，那么相切的点就是我们要求的极值点，切点所对应的的切线同时是$ f(x,y)=d_{1} $和$ g(x,y)=c $的切线。

我们也可以把这里的等高线想象成物理中电场的“等势线”，那么图中的切点所对应的的切线就是等势线的方向，而与之垂直的就是电场线的方向 (电势变化最快的电场方向)。对约束条件$ g(x,y)=c $来说，前面过切点的电场线方向也是函数$g $的梯度方向，也就是说如果画出$ g(x,y)=c +\Delta d $那么对该切点来说，梯度方向变化的距离是最短的(这其实和前面提到的电场线一样，沿着电场线方向电势下降最快)。

我们也可以把这里的等势场，想成“等温线”，那么梯度的方向就是温度变化最快的方向。总而言之，在切点处(对应极值点)，目标函数和约束函数的梯度向量的方向在同一条直线上(大小可能不同)。

例子1：求解$f(x,y)= x^{2}+y^{2} $在$ x^{2}y=3 $条件下的极值点，这个例子来自马同学

求解方法是$$\left\{\begin{array}{l} \nabla f=\lambda \nabla g \\ x^{2} y=3 \end{array}\right.$$ 其中$ \nabla f $和$ \nabla g $都是在描述梯度场(向量场)$$\nabla f=\left(\begin{array}{l} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{array}\right)=\left(\begin{array}{l} 2 x \\ 2 y \end{array}\right)\quad \quad \nabla g=\left(\begin{array}{l} \frac{\partial g}{\partial x} \\ \frac{\partial g}{\partial y} \end{array}\right)=\left(\begin{array}{c} 2 x y \\ x^{2} \end{array}\right)$$最终求得$ \left\{\begin{array}{l} x \approx \pm 1.61 \\ y \approx 1.1 \\ \lambda \approx 0.87 \end{array}\right. $

用matlab我们自己可以画一下向量向量场

%%  vector field of f
[x,y] = meshgrid(-2:0.2:2,-2:0.2:2);
u=2*x;
v=2*y;
quiver(x,y,u,v,'r')

%%  vector field of g
[x,y] = meshgrid(-2:0.2:2,-2:0.2:2);
u=2*x.*y;
v=x.*x;
quiver(x,y,u,v)

函数$ f(x,y) $的向量场
函数$ g(x,y) $的向量场

变形形式：求解$F=f+\lambda g $函数的极值点，同样的有三个偏导数都为零$$\left(\begin{array}{c} \frac{F}{\partial x} \\ \frac{F}{\partial y} \\ \frac{F}{\partial \lambda} \end{array}\right)=\left(\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right)$$其实和前面表示方法是一样的，前面的一种方法更侧重函数图像上的具象性，这一种方法更侧重数学公式上的抽象性。(注意这里的$ g $其实是前面的$ g(x,y)-c$)

线性插值

两个点直线相连，那么就可以推断出中间其他点的位置。

传统多项式差值(Polynomial interpolation )

我们知道四个点的坐标值，就可以用$ f(x)=a+b x+c x^{2}+d x^{3} $列出四个方程，通过求解4阶线性方程组就可以确定四个系数。假设插值多项式为$$p(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{2} x^{2}+a_{1} x+a_{0}$$令$ p\left(x_{i}\right)=y_{i} $，则有$$\left[\begin{array}{cccccc} x_{0}^{n} & x_{0}^{n-1} & x_{0}^{n-2} & \ldots & x_{0} & 1 \\ x_{1}^{n} & x_{1}^{n-1} & x_{1}^{n-2} & \ldots & x_{1} & 1 \\ \vdots & \vdots & \vdots & & \vdots & \vdots \\ x_{n}^{n} & x_{n}^{n-1} & x_{n}^{n-2} & \ldots & x_{n} & 1 \end{array}\right]\left[\begin{array}{c} a_{n} \\ a_{n-1} \\ \vdots \\ a_{0} \end{array}\right]=\left[\begin{array}{c} y_{0} \\ y_{1} \\ \vdots \\ y_{n} \end{array}\right]$$上面的系数矩阵(范德蒙矩阵)的行列式不为零，所以列向量之间线性无关，它们的线性组合可以张满整个$\mathbf{R}^{\mathrm{n}} $空间，所以方程组一定有唯一解。

缺点：
(a) 计算量大
(b) 新增一个数据点的话，需要将前面的计算结果推到，然后全部重新计算。

参考资料：
(1) 寻找“最好”（3）——函数和泛函的拉格朗日乘数法
(2) 马同学—从牛顿插值法到泰勒公式
(3) 牛顿插值的几何解释是怎么样的？
(4) 如何直观地理解拉格朗日插值法？