资料:
- MIT-ODE-matlab笔记
- RES.18-009课程视频-MIT
- 18.03课程视频-MIT 官网
- Math 4B - Summer 2018
- 中文笔记参考-知乎
- 思维导图
- 《微分方程、动力系统与混沌导论》书籍,参考笔记
- Differential Equations for Engineers-Libretexts
微分方程概述
基本概念
微积分的基本定理(Fundamental theorem of calculus) :
- \( \displaystyle\frac{d f(g(x))}{d x}=\displaystyle\frac{d f}{d g} \frac{d g}{d x} \)
- \(\displaystyle\frac{d}{d x} \int_{0}^{x} y(t) d t=y(x)\)
一阶线性齐次常微分方程:
- 一阶:有一阶导数项,也是最高阶导数项。
- 线性:含有\( y\)或者\(y \)导数的项都是满足线性关系的,也就是指数为\(1 \)。如果等式右侧含有\( y^{2},\sin{y}, e^{y}\)等函数,就是非线性的。
- 常微分:这里的“常”(ordinary differential equation,ODE)是为了体现和偏微分方程( partial differential equation,PDE)的区别。
一阶线性常微分方程例子:\( \displaystyle\frac{d y}{d t}=a y+q(t)\),函数\( y\)随时间的变化率既和自身大小有关,也和输入项\( q(t)\)有关,而且这个输入项有自身随时间变化的规律。
微分方程有很多具体应用,例如函数\( y\)可以是是银行中的存款,随着时间增长、衰减或者振荡,\( y\)也可以是弹簧的长度,描述一个物理模型。
【齐次】(Homogeneous):
- 对于一阶而言,齐次体现在方程能写成\( \displaystyle\frac{d y}{d x}=F\left(\displaystyle\frac{y}{x}\right)\)这种形式,可以用分离变量法求解
- 如果它的一个解乘以任意常数后,仍是它的解,\(f(\lambda x, \lambda y)=\lambda^{k} f(x, y)\)
- 不存在不含未知函数及其导数的项,也就是\(q(t) =0\)
二阶线性常微分方程:二阶导数为加速项,告诉我们曲线的弯曲状态信息(思考一下二阶导数大,曲线的特点)。
例子:\( \displaystyle\frac{d^{2} y}{d t^{2}}=-k y \),可以描述物体光滑平面上连接有弹簧的物理的加速度和位移的关系。更一般的形式是:\( m y^{\prime \prime}+b y^{\prime}+k y=f(t) \),这是常出现在物理模型中的表达式,其中第一项是质量和加速度乘积,第二项是阻尼项(某种摩擦力的大小和速度正比),第三项可以看作是“和位移成正比”(弹簧力的作用),等式右侧的\( f(t)\)可以是外力作用。
分类:
- \(f(t) \)是线性函数,与\( y\)及其变换率有关的项前面的系数都是常数。则很好解和处理。
- \(f(t) \)是好函数,比如指数函数,那么解函数的形式也比较简单。
注:后面我们将会知道好函数是能在拉普拉斯变换中积分求得解析式的函数。 - \(f(t) \)是非线性函数,通常只能用数值方法进行处理。
偏微分方程( partial differential equation)
本课程最后会触及到偏微分方程,例如
(1) 热传导方程:$$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}} $$涉及到时间和空间坐标两个自变量
(2) 波动方程:$$\frac{\partial^{2} u}{\partial t^{2}}=\frac{\partial^{2} u}{\partial x^{2}} $$
(3) 拉普拉斯方程:$$\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}=0$$
数值解法
微分方程的两个解法,一个是求出解析式,对于不好求出解析式的我们可以采用数值解法。这一系列视频里面有专门介绍数值解法的视频,采用函数ODE45,它是最常用的求解常微分方程数值解的函数命令,4和5意味着该算法有很高的精度,它采用4阶方法提供候选解,5阶方法控制误差。最开始对微分方程进行数值求解的是大数学家欧拉,见欧拉方法,现在不怎么用了。
函数的切线
\( f(t+\Delta t) \approx f(t)+\Delta t \displaystyle\frac{d f(t)}{d t}\,\Rightarrow \,\displaystyle\frac{\Delta f}{\Delta t} \approx \displaystyle\frac{d f}{d t} \)一阶导数作为斜率值带入得到切线,但是切线只能“模拟出”非常靠近切点的值,如果想提高模拟的精度,而且提高能模拟的范围,那就需要引入“二阶近似”、“三阶近似”,直到无穷阶近似(和原方程相等,能在所有区间模拟出原函数的所有精确值);随着阶数的提高,拟合的函数在图像上从切点周围看,越来越贴合实际的函数曲线。对于高阶近似来说,可以用“见微知著”来形容,知道一个点的函数值以及各阶导数值,就可以知道所有点的函数值。
二阶近似:物理中在平衡点附近展开,经常用到二阶近似$$f(t+\Delta t) \approx f(t)+\Delta t \frac{d f}{d t}+\frac{1}{2}(\Delta t)^{2} \frac{d^{2} f}{d t^{2}}$$无穷阶表示$$f(t+\Delta t)=f(t)+\Delta t \frac{d f}{d t}+\frac{1}{2}(\Delta t)^{2} \frac{d^{2} f}{d t^{2}}+\cdots+\frac{1}{n !}(\Delta t)^{n} \frac{d^{(n)} f}{d t^{n}}+\cdots$$ 对于高阶函数,只有少数比较好求解,比如\( e^{x}\)、\(\sin{x} \)等。
常微分方程ODE,质点动力学。物理学中真正有用的是一阶和二阶,更高阶的只有数学上的意义。二阶线性常系数常微分方程最重要,最简单的就是一维简谐振子。会有线性独立解的概念,因为我们可以把函数看作是向量,那么向量的线性独立的概念同样也可以用在函数上。还涉及到算符、线性算符;本征值、本征函数(是否正交),可以定义函数和函数的内积。施图姆-刘维尔问题,引出特殊函数(勒让德函数、贝塞尔函数、伽马函数),以及傅里叶级数/分析。傅里叶变换、拉普拉斯变换是求解ODE和PDE的重要工具。
偏微分方程PDE,场动力学,物理量在时间和空间的分布。比如温度场,压力场,密度场,力场,电场,磁场,当然这里面既有标量场,又有矢量场。三维空间的话,自变量是四个。特例:均匀场,静场(静电学、静磁学)。
有耗散的波动方程,如果电磁波在真空中传播则没有耗散,如果是有介质的(可导电),那么就存在耗散项。
线性微分方程,无论是常微分还是偏微分都很好解,它们的解具有线性叠加性,这点很重要,对于我们求解很关键。数学家利用线性叠加的性质,发展出求解线性常/偏微分方程的方法,比如傅里叶级数、傅里叶变换、拉普拉斯变换、格林函数的方法以及猜的方法(有经验的话,物理/数学感觉)。
齐次/非齐次是针对线性方程而言的,如果微分方程都不线性,那么就无所谓齐次/非齐次。
典型微分方程举例
线性微分方程\( y^{\prime}=a y+q(t)\)是一个重要的方程,导数中包含增长率\( ay\)和外源\( q(t)\)。给出\( a=1, y(0)=0\)时的解:$$\frac{d y}{d t}=y+q(t) \Rightarrow y(t)=\int_{0}^{t} e^{t-s} q(s) d s$$不放心的可以验算一下$$\frac{d y}{d t}=\left(\frac{d e^{t}}{d t}\right) \int_{0}^{t} e^{-s} q(s) d s+e^{t} \frac{d}{d t}\left(\int_{0}^{t} e^{-s} q(s) d s\right)$$注意这里的解没有考虑初始条件
微分方程组(线性代数的关系)
与线性代数中的求解线性方程组\( A\mathbf{x}=\mathbf{b}\)一样,分别求出方程的特解和零空间解。于是:通解 = 特解 + 零空间解
看了GS老师这个视频进一步理解
一阶微分方程组
系统包括多个弹簧或者阻尼器的情况。以一阶举例$$\frac{d \mathbf{y}}{d t}=\boldsymbol{A} \mathbf{y}$$这个的解法我们在线性代数中讲过,直接解的难点在于未知数之间是相互耦合的,我们必须通过对角化(引入特征值和特征向量)的方式将方程解耦,转化成一个个独立的线性方程,分别求解。
二阶微分方程
对于微分方程\( \displaystyle\frac{d^{2} y}{d x^{2}}+y=0\),求解该方程可以视为求解它的列空间。我们可以得到的特征解为:\( y=\cos x, y=\sin x\)或者等价地描述为\( y=e^{i x}, y=e^{-i x} \),指数项上的\( i\)和\( -i \)其实就是矩阵的两个特征值。以前者为例,通解写成\(y=c_{1} \cos x+c_{2} \sin x \),其中\( c\)可以为任意复数。也将解的线性组合构成的空间称为解空间,其维数为\( 2\)。\(\cos x \)和\(\sin x \)可以成为解空间的一组基。这些不是向量,而是函数,但是同样可以对其进行线性运算,在线性代数的讨论范围之类。
更一般的情况\(y^{\prime \prime}+b y^{\prime}+k y=0\),令\( \mathbf{y}=\left[\begin{array}{l} y^{\prime} \\ y \end{array}\right]\),则\(\mathbf{y}^{\prime}=\left[\begin{array}{l}y^{\prime \prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{cc}-b & -k \\ 1 & 0\end{array}\right]\left[\begin{array}{l}y^{\prime} \\ y\end{array}\right]\),于是可以按照一阶微分方程组的方式求解。具体参见“线性代数中的微分方程”章节。
一阶微分方程
不变利率不同输入函数
对于微分方程\( \displaystyle\frac{d y}{d t}=a y+q(t) \),可以写成$$y^{\prime}-a y=q(t)$$等式右侧的函数\(q(t) \)可以称之为“输入”函数或者【激励】,而解函数\(y \)通常称之为“输出”或者【响应】。
- \(q(t) \)为正号时,称之为【源】
- \(q(t) \)为负号时,称之为【漏】
- \(q(t) \)是外部环境对函数增量的影响。换句话说函数的增长速度一方面和自身有关,另一方面也和外部环境变化有关(内外因哲学)。
- 如果没有外界的影响,也即增长率只和自己有关\( q(t)=0\),这个时候就成了“齐次微分方程”
GS老师用信号系统或者电子电路的角度去解释微分方程,比抽象的纯数学语言更直观,反过来也有助于加深我们对物理过程的理解。
指数输入的响应
对于方程$$\frac{d y}{d t}=a y+e^{s t} $$如果以储蓄为例子,初值\( y(0)\)可以视为第一次存进去的钱,\( ay\)可以视为利息,“输入”为指数函数\( e^{s t}\),可以视为每个时间段内新存入的储蓄,而解函数可以称为“指数响应”,反映的是存款总额随时间的变化。
方法—1
(1) 方程的特解(particular solution)
具有这样的结构\( y_{p}=Y e^{s t} \),求解方法是回代进方程求出其具体的表达式。$$Y s e^{s t}=a Y e^{s t}+e^{s t} \Rightarrow Y=\frac{1}{s-a}$$这里的\(Y \)是一个【传递函数】(transfer function)(也是相对于input输入\( e^{s t}\)的response factor),任何常系数线性方程都有一个传递函数,而且很容易找到。当\( s\)接近\( a\),将会得到一个很大的“响应”,因此称为【共振】。
(2) 方程的零解(null solution)
零解即\(\displaystyle\frac{d y}{d t}=a y \)的解,求得\( y_{n}=C e^{a t} \)
(3) 方程的通解
注意特解与初始条件\( t=0, y=y(0)\)并不匹配。最终的通解为特解和通解的加和,然后用初始条件确定相关系数。$$y(t)=y_{p}+y_{n}=\frac{e^{s t}}{s-a}+C e^{a t}$$带入初始条件可得$$y=\frac{e^{s t}}{s-a}+\left[y(0)-\frac{1}{s-a}\right] e^{a t}$$还可以写成一个非常特殊解\(y_{vp} \)和零解\(y_{n} \)之和(分成含有\( s\)的项,和不含有\( s\)的项)$$y(t)=\frac{e^{s t}-e^{a t}}{s-a}+y(0) e^{a t}$$其中的\(y_{vp} \)很特殊因为是从\( y_{vp} =0\)开始积累的;这里的零解是为了保证满足初始条件。如何从存钱的角度理解这个式子?
【共振】:当\( s=a\)时,\(y_{vp} \)的分子分母都等于零,这个时候要用洛必达法则来处理,最终得到的结果为$$y(t)=y_{p}+y_{n}=t e^{a t}+y(0) e^{a t}$$其最重要的特点是,观察第一项,可以发现随着时间的增长,函数值越来越大,而且增速越来越快,最后直接blow up,类似共振使得桥梁坍塌。
方法—2
我们首先回忆一下如何求解线性方程组\( A\mathbf{x}=\mathbf{b}\),一阶线性常微分方程中的“线性”和前面的线性方程组的“线性”是一回事。比如对于\( \displaystyle\frac{d y}{d t}=a y+1 \),我们这里的\(1\)就是\( A\mathbf{x}=\mathbf{b}\)中的\( \mathbf{b}\)。
(1) 对线性方程组来说,求零空间解,就是令\( \mathbf{b}=0\),然后求解;同样地,对于线性微分方程来说,GS使用“零解(null solution)”来表示“齐次”或者说\( q(t)=0\)的情况,或者说Input/Source为零的情况。$$ \frac{d y_{n}}{d t}=a y_{n}\,\Rightarrow \, y_{n}=Ce^{a t}$$(2) 特解的话,随便哪种特殊情况下的解都行,也是和线性方程组类似(自由变量按一定规则任取),比如我们令等式左边的\( \displaystyle\frac{d y_{p}}{d t}=0 \)可以求得$$\frac{d y_{p}}{d t}=a y_{p}+1\,\Rightarrow \, y_{p}=-{ 1 }/{ a }$$组合在一起\( \displaystyle\frac{d(y_{n}+y_{p})}{d t}=a(y_{n}+y_{p})+1 \)
复指数函数的响应
对于微分方程$$\frac{d y_{c}}{d t}=a y_{c}+\cos \omega t+i \sin \omega t$$我们根据欧拉公式,可以写成$$\frac{d y}{d t}=a y+e^{i \omega t}$$在之前我们已经讨论了指数响应的情况,于是我们可以尝试特解\( y_{c}(t)=Y e^{i \omega t} \)这里的下标\( c \)表示复数。回代得到$$\begin{array}{l} \displaystyle\frac{d y_{c}}{d t}=a y_{c}+e^{i \omega t} \Rightarrow i \omega Y e^{i \omega t}=a Y e^{i \omega t}+e^{i \omega t} \\ \Rightarrow Y=\displaystyle\frac{1}{i \omega-a} \end{array}$$将参数\( Y \)化为极坐标的形式\( i \omega-a=r e^{i \alpha}=\sqrt{a^{2}+\omega^{2}} e^{i \alpha}\)于是$$y_{c}(t)=Y e^{i \omega t}=\frac{1}{i \omega-a} e^{i \omega t}=\frac{1}{\sqrt{a^{2}+\omega^{2}}} e^{-i \alpha} e^{i \omega t}=\frac{1}{\sqrt{a^{2}+\omega^{2}}} e^{i(\omega t-\alpha)}$$解函数的实部\(\operatorname{Re}\left(y_{c}(t)\right)=\displaystyle\frac{1}{\sqrt{a^{2}+\omega^{2}}} \cos (\omega t-\alpha)=G \cos (\omega t-\alpha) \)就是我们之前在输入简谐振荡函数时计算得到的响应函数,这里的\( G \)就是gain。同理可以从虚部得到输入为正弦函数(虚部)时的响应函数,都是一一对应关系。欧拉公式和复指数参见这里。
极坐标(polar coordinates)表示:
\( a \cos (\omega t)+b \sin (\omega t)=A \cos (\omega t-\phi) \)其中\(A=\sqrt{a^{2}+b^{2}}, \quad \phi=\tan ^{-1} \displaystyle\frac{b}{a} \)。于是前面的特解可以表示为$$y_{p}(t)=G(\cos \omega t-\alpha)$$参数\( G \)和\( \alpha\)可以看作是极坐标系下的幅长和相位角。如果两个角度相同的正弦和余弦相加得到的叫作“sinusoidal identity”。GS说这个的G表示的是gain或者magnitude,和radio的调谐有关(后面再理解)。
结果总共有三种表示方法,除了三角函数表示,极坐标表示,还有复指数表示(后面讲解),可以参考这个资料。
简谐振荡的输入响应
将\( \displaystyle\frac{d y}{d t}=a y+q(t)\)中的输入变成\( q(t)=\cos \omega t \),于是$$\frac{d y}{d t}=a y+\cos \omega t$$这里的输入是一个余弦函数,它会发生振荡,而不是随着时间增长或者衰减(指数函数形式)。在信号、电子电路、交流电等应用领域会遇到这类问题。
下面开始求解:
(1) 特解:观察容易发现,函数中一定含有\( \sin \)项目,这样求导才能有余弦项目,同样地由于求导有一部分是自身的倍数,所以也一定含有余弦项。尝试\(y_{p}(t)=M \cos \omega t+N \sin \omega t \),带入原方程可以求得系数\(M \)和\(N \),通过两个系数方程,得到$$M=\frac{-a}{\omega^{2}+a^{2}}, \quad N=\frac{\omega}{\omega^{2}+a^{2}}$$(2) 零解:即\(\displaystyle\frac{d y}{d t}=a y \)的解。
零解同时也称为暂态响应或者“瞬态响应”,而特解则称为“稳态响应”。瞬态响应是当时间足够大时趋近于\( 0\)的部分,而稳态响应则是最后保留下来的相应分量。(先抄下来,不是很理解)
何时该带入初始条件
在上一问中我们对于任意input的微分方程\( \displaystyle\frac{d y}{d t}=a y+q(t) \)是先求出其满足初始条件的零解,然后加上一个特解,就是通解。在更前面的问答中,对于微分方程\( \displaystyle\frac{d y}{d t}=a y+1 \)和\( \displaystyle\frac{d y}{d t}=a y+e^{s t} \),我们采用的方法是先确定零解和特解,组合成通解之后再带入初始条件,求得零解前面的系数。
这两种方法其实是相通的,问题的关键在于采用何种函数表达式去try特解。比如我们对于\(\displaystyle\frac{d y}{d t}=a y+e^{s t} \),容易猜到的特解形式是\(y_{p}=Y e^{s t} \),但是这个特解对应的零解就不是\(y=y(0) e^{a t} \),前面的系数不再是满足初始条件的\( y(0) \)。要注意,如果我们开始try的特解形式是\( y_{p}=Y({e^{s t}-e^{a t}}) \),那么我们的零解前面的系数正好是\( y(0) \),这也是我们前面求解之后可以化简得到的通解形式,所以GS老师说这个特解是very particular solution,好虽然好,但是不容易猜到。
任意输入函数的响应(储蓄模型)
微分方程\(\displaystyle\frac{d y}{d t}=a y+q(t) \)在初始条件\( t=0, y=y(0) \)下的解,先前讨论的都是input或者说\(q(t) \)是一些简单形式(常数/指数函数/正余弦函数)的解,那么对于任意的input函数,方程的解又是什么样的呢?
储蓄过程
我们首先去理解储蓄这个过程,假设存一笔钱,年利率为\(r \),那么我在一年内,不断地把本金+利息取出来,然后作为新的本金存进去,也就是不断地进行“复利”操作,于是$$\lim _{n \rightarrow \infty}(1+\frac {r }{ n } )^{\frac { n }{r }*r }=e^{r}$$如果在一年取存操作无穷多次,那么最终得到的一年利率是\( e^{r}\),比如如果原来是\( 100 \% \)年利率,那么按照上面的操作,最终的一年理论可以高达\( e \)。
我们同样从储蓄的角度去理解写个微分方程,现在有一个running clock用\( s\)来表示时间,在\( s=0 \)的时候,我们存入第一笔钱\( y(0) \),在不考虑input的情况下(为零),我们存入的第一笔钱不断地按照指数增长,于是我们很容易求得“零解”为\( y=y(0) e^{a t} \)(考虑了初始条件)。现在考虑input,也就是说每时每刻都有新的钱存入,这一时刻新存入的钱从下一个时刻开始也按照指数规律变化,当\( s=t \)的时候在\( s=0 \)这一时刻给的input值\( q(0) \)钱已经经历了这一段\( t \)时间的指数增长;换句话说,对于固定的\( t\)来说,任意\( s\)时刻存入的钱,都将经历\( t-s \)时间范围的指数增长。因此解函数的完全表达式为$$y(t)=y(0)e^{a t} +\int_{s=0}^{s=t} e^{a(t-s)} q(s) d s$$ 对于任意的输入函数,\( e^{a t}\)都是其增长或者衰减因子。如果输入\( y(0)\),则输出是\( e^{a t} y(0) \),即“零解”或称“瞬态响应”。如果在\( s \)时刻输入\( q(s) \),则在\( t \)时刻这一输入对于输出函数的贡献为\( e^{a(t-s)} q(s) \),这代表着输出的增长或者衰减只发生在剩余的\( t-s \)时间段内。将所有的输入在\( t\)时刻造成的输出结果全部累加起来就是完全解的表达式:$$y(t)=y(0)e^{a t} +e^{a t} \int_{s=0}^{s=t} e^{-a s} q(s) d s$$我们先前讨论的输入\( q(t)=e^{st} \),注意我们这里的\( s \)是个常系数,而\( t \)是变量;因此如果我们先借用刚才推导出来的公式直接算通解的话,\(q(s)=e^{ms} \),\( m \)是个常系数,而\( s \)是变量,积分完之后再将\( m\)换成\( s \),就会得到与先前计算同样的结果\( y(t)=\displaystyle\frac{e^{s t}-e^{a t}}{s-a}+y(0) e^{a t}\)。
目前我们讨论的都是利率不变的情况,后面我们将学习利率随时间变化的情况,以及非线性方程。
科学和工程问题,常见的input:(GS老师眼中的nice functions,解出来的结果都很simple,direct和interesting)
(1) 常数\( q(t)=q\)
(2) 时间幂次\( q(t)=t^{n} \)
(3) 指数函数\( q(t)=e^{a t}\)
(4) 简谐振荡\( q(t)=\cos \omega t\)或\( R e^{i \omega t} \)
(5) 在\( T \)时刻出现阶跃函数\( q(t)=H(t-T) \)
(6) 在\( T \)时刻出现狄拉克函数\( q(t)=\delta(t-T) \)
移位冲激函数的响应
这里必须提到阶跃函数的发明人Oliver Heaviside,他是一个自学成才的电子工程师,他创立了矢量分析分析方法,而且很多电磁学的术语都是他提出来的,比如阻抗、电感、介电常数。是他首先提出了阶跃函数,所以用其姓氏首字母表示【阶跃函数】\(H(x) \)。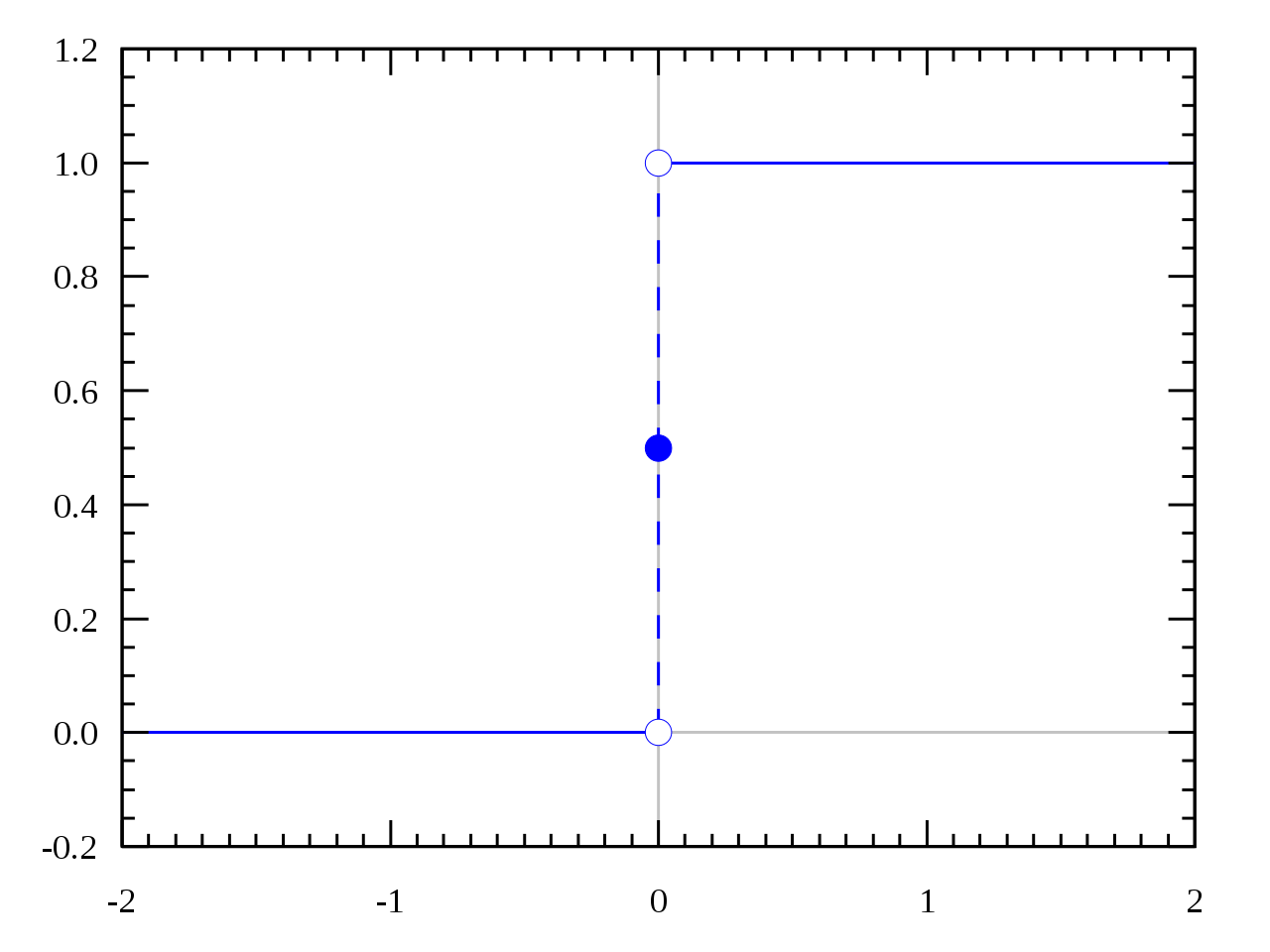 (1) 阶跃函数\( H(t) \)在\( t=0\)时刻从\(0 \)跃迁至\( 1\)
(1) 阶跃函数\( H(t) \)在\( t=0\)时刻从\(0 \)跃迁至\( 1\)
(2) 移位的阶跃函数\( H(t-T)\)在\( t=T \)时刻从\(0 \)跃迁至\( 1\)
(3) 对\( H(t) \)来说,\( t<0\)的时间段内函数值都是常数,同样地,在\( t>0\)时间段内,函数值也是常数。这两段常数范围的导函数都是零,所有的变化都发生在\(0 \)时刻,因此它的导函数就【冲激函数】—\( \delta \)函数
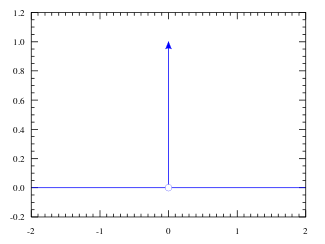 上图就是\( \delta \)函数,注意中间这一条线表示的面积是\( 1\);注意这不同于连续随机分布中选出某一个特定值出现的概率,虽然整个图的积分面积是\( 1\),但是从中画一条竖线,对应的数值出现的概率一定是\(0 \),这条线对应的面积也是\( 0\)。我们只关心\( \delta \)函数本身的性质以及其积分函数的性质,至于其导函数我们不需要了解。这个函数的特点$$\int_{-\infty}^{\infty} \delta(t) f(t) d t=f(0) \quad \quad \delta(t)=\left\{\begin{array}{cl} +\infty & (t=0) \\ 0 & (t \neq 0) \end{array}\right.$$比如\( \displaystyle\int_{-\infty}^{\infty} \delta(t) \sin t d t=\sin 0=0\),还有\(\displaystyle\int_{-\infty}^{\infty} \delta(t) e^{t} d t=e^{0}=1\)。
上图就是\( \delta \)函数,注意中间这一条线表示的面积是\( 1\);注意这不同于连续随机分布中选出某一个特定值出现的概率,虽然整个图的积分面积是\( 1\),但是从中画一条竖线,对应的数值出现的概率一定是\(0 \),这条线对应的面积也是\( 0\)。我们只关心\( \delta \)函数本身的性质以及其积分函数的性质,至于其导函数我们不需要了解。这个函数的特点$$\int_{-\infty}^{\infty} \delta(t) f(t) d t=f(0) \quad \quad \delta(t)=\left\{\begin{array}{cl} +\infty & (t=0) \\ 0 & (t \neq 0) \end{array}\right.$$比如\( \displaystyle\int_{-\infty}^{\infty} \delta(t) \sin t d t=\sin 0=0\),还有\(\displaystyle\int_{-\infty}^{\infty} \delta(t) e^{t} d t=e^{0}=1\)。
【移位冲激函数】$$\int_{-\infty}^{\infty} \delta(t-T) e^{t} d t=e^{T}$$如果将移位冲激函数作为我们前面讨论的微分方程的input$$\frac{d y}{d t}=a y+\delta(t-T)$$其中\( t=0, y(0)=0\)。这相当于没有预先的存款,因此初值为\( 0 \),从\( t=0 \)开始一直没有钱在户头,直到\(t=T \)时刻突然瞬间存进去\( 1 \)块钱,之后就按照利率\( a\)增长或者衰减。因此解函数为$$y(t)=\left\{\begin{array}{cc} 0 & t<T \\ e^{a(t-T)} & t \geq T \end{array}\right.$$这个解函数称作“冲激响应”,也就是输入冲激函数信号产生的响应。
在很多模型中,冲激函数都是描述运动或者状态所必需的的函数,比如高尔夫球击球或者敲锣的瞬间,我们可以近似看作是时间接近于\(0 \),可以用\( \delta \)函数来描述。
变利率条件下的积分因子
Integrating Factor for a Varying Rate \( a(t)\)
现在对于微分方程$$\frac{d y}{d t}=a(t) y+q(t)$$其中的利率不再是一个定值,而是一个随着时间变化而变化的量,下面我们用积分因子法解决。
首先我们很直观的感受是,这里的利率是个变量,使得事情复杂了,但是无论利率是常数还是变量,这一项对应的都是零解(input为零的时候的解),最终的通解还是零解加上特解。于是我们可以构造出一个函数\(M \)(积分因子),这个函数的初始条件和\( y\)一样,不同的是:
(1) \( M \)的微分方程中没有input
(2) \( M \)的变化率和\(y \)的零解随着时间的变化率互为相反数,换句话说,\( t=0\)存入一比钱后,对\( M(t)\)来说,钱不断减少,对\(y_{n}(t) \)来说不断增加,但是始终有\( M(t) y_{n}(t)=1\),等于说\( M(t)\)一直压制着二者乘积的变化。那么\( M(t) y_{n}(t)\)的导数始终就是零。这个时候我们可以构造一个新的函数\( My \),零解部分的变化率相互抵消变成零了,那么对变化率起作用的只有新的input,也就是\( Mq(t) \),由于\( M \)和\( My \)都好求解,于是就可以得到\( y\)。$$\frac{d M}{d t}=-a(t) M\,\Rightarrow \,M=e^{-\int_{0}^{t} a(T) d T}$$压制零解部分变化$$\frac{d(M y)}{d t}=\frac{d y}{d t} M-a(t) M y=(a(t) y+q(t)) M-a(t) M y=M q(t)$$两边积分$$\int_{0}^{t} \frac{d}{d t}(M y)=M(t) y(t)-M(0) y(0)=\int_{s=0}^{s=t} M(s) q(s) d s$$由于\(M(0)=1 \),因此$$\begin{aligned}
\Rightarrow y(t) &=e^{\int_{0}^{t} a(T) d T} y(0)+e^{\int_{0}^{t} a(T) d T} \int_{0}^{t} e^{-\int_{0}^{s} a(T) d T} q(s) d s \\
&=e^{\int_{0}^{t} a(T) d T} y(0)+\int_{0}^{t} e^{\int_{s}^{t} a(T) d T} q(s) d s
\end{aligned}$$
例子
\(a(t)=2 t \),于是\( M=e^{-t^{2}},\, e^{\int_{s}^{t} a(T) d T}=e^{t^{2}-s^{2}}\),\( y(0) \)的增长因子为\(e^{\displaystyle\int_{0}^{t} a(T) d T}=e^{t^{2}} \),解得$$y(t)=e^{t^{2}} y(0)+\int_{0}^{t} e^{t^{2}-s^{2}} q(s) d s$$对比一下我们之前讨论的恒定利率下的结果$$y(t)=y(0)e^{a t} +\int_{s=0}^{s=t} e^{a(t-s)} q(s) d s$$ 从解函数的表达式我们可以看到,在恒定利率下求得的初值\( y(0) \)的增长因子\( e^{at}\)变成了现在的\(e^{t^2} \)。同样地,输入函数\( q(t)\)的增长因子也变成了\( e^{t^{2}-s^{2}}\)。
Logistic 方程
 典型例子$$\frac{d y}{d t}=a y-b y^{2}$$初值条件为\(t=0, y=y(0) \)。这个方程称为“Logistic方程”,它可以粗略描述人口增长。\( a y \)表示人口增长的速度和现存人口的数量存在一个正比关系,而\(-b y^{2} \)表示人与人之间的竞争关系导致了人口的负增长。
典型例子$$\frac{d y}{d t}=a y-b y^{2}$$初值条件为\(t=0, y=y(0) \)。这个方程称为“Logistic方程”,它可以粗略描述人口增长。\( a y \)表示人口增长的速度和现存人口的数量存在一个正比关系,而\(-b y^{2} \)表示人与人之间的竞争关系导致了人口的负增长。
马尔萨斯在《人口论》中提出三条假设:(1) 如果不加以限制,人口的增长呈现指数趋势;(2) 食物的供应是线性趋势;(3) 食物是人类赖以生存的必要条件之一。那么长时间之后,食物必将供应不足,导致人类大面积饿死,疾病蔓延,战争爆发,这就是马尔萨斯灾难。如果想要避免马尔萨斯灾难,就必须控制人口生育。其对应的数列递推公式为\(N_{n+1}-N_{n}=r N_{n}\),生老病死、自然灾害等的因素考虑在了系数\(r \)里面,所以只要\(r\)大于零就是指数增长。1838年比利时数学家Pierre François Verhulst给出了另外一个模型,他认为死亡率不是和人口数量相关的,而是和人口数量的平方相关的,所以死亡项要单独计算。于是他给出新的数列递推公式\(N_{n+1}-N_{n}=r N_{n}-\displaystyle\frac{r}{K} N_{n}^{2}\),这就是Logistic map(逻辑斯谛映射)。写成微分方程的的话如下$$ \frac{d N}{d t}=r N\left(1-\frac{N}{K}\right) $$这其实就是生态学中的\(r/K\)选择理论,其中的\(r\)就是人口增长率,\(K\)就是生态学中的环境承载能力(不同场景,定义不一样),即当前环境能够承载的最大人数
这个方程的“非线性”体现在\( y^{2} \)项,很容易看出可以通过移项然后等式两边积分的方式求解,这一部分GS老师在后面要讲的。这里GS老师采用的是变量代换的方式,其实是个小技巧,令\( z=1 / y \),则可以将非线性的微分方程转化为线性的来求解:$$\frac{d z}{d t}=-\frac{1}{y^{2}} \frac{d y}{d t}=-\frac{1}{y^{2}}\left(a y-b y^{2}\right)=-a z+b$$求得$$ y(t)=\displaystyle\frac{a}{d e^{-a t}+b}$$其中\( d=\displaystyle\frac{a}{y_{0}}-b\)。
我们来看一下\( y \)的函数图像,\( t=0 \)时,函数处在初值\( y(0) \),随着\( t\)的增长,函数不断增长,但是到后面增长速度越来越缓慢,最终逼近极限\(y=a / b \)但是始终触碰不到。这主要因为当\( t\)很小的时候\( ay\)起主要作用,而当\( t \)很大的时候,\( -by^2\)起主要作用(压制增长速度)。其实这是比较典型的图像,教授称之为“S-curve”(Logistic曲线),其实如果\( y(0) \)取值大于\( a / b \),那么曲线就不太一样了,但是如果我们只观察\(t \geq0 \),函数还是随着时间的增长逐渐逼近\( y=a / b \)。
例子1(分别逼近\( y(t) \rightarrow a / b \)和\(y(t) \rightarrow 0 \))
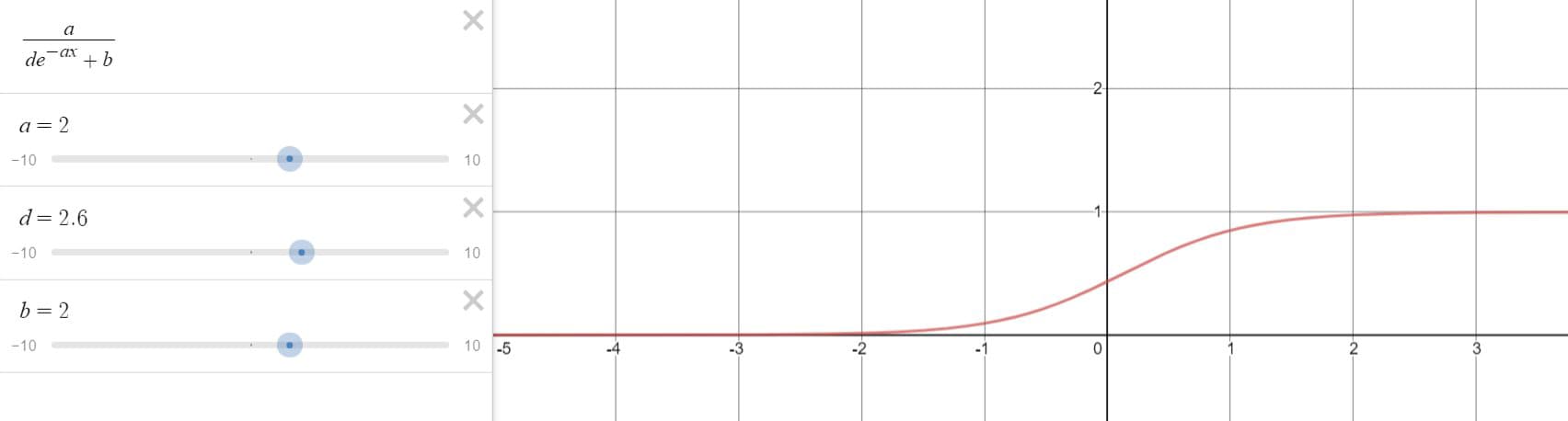
例子2

例子1中的图是我们主要的研究对象,两个极限值被称之为“稳态”。稳态就是导数为零的位置。设稳态为\( y=Y\),那么\(a Y-b Y^{2}=0 \)得到稳态\(Y=0, Y=a / b \)
(1) 不稳定的稳态(\( Y=0 \))
在考虑\( t\)可以为任意正负值的情况,假设初始值\(y=0 \)(函数图像左侧无穷远),那么我随便给他一点点点点“阳光”,虽然这点阳光很少,但是接下来有点“链式反应”或者说“铝热反应”(不是很高温度的镁条引燃产生两千多度的高温),不稳定的稳态,也可以类比tipping point。
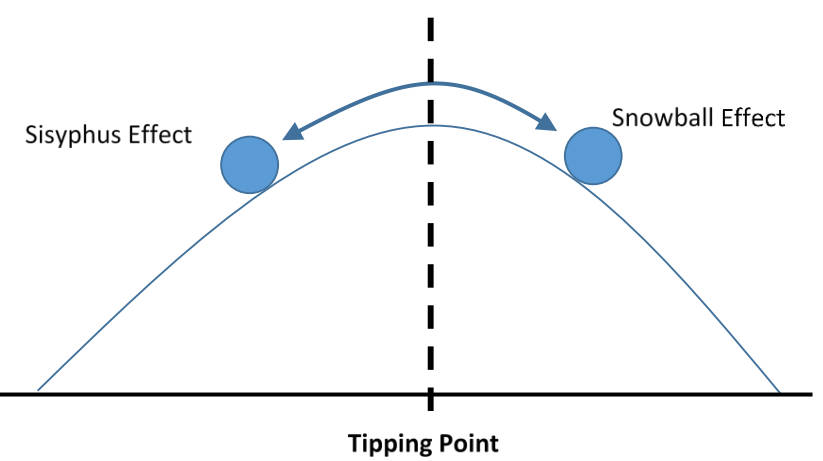 随着\( t\)的流逝,\(y \)值一直在增大,而且反馈到导函数进一步增大了增长速率,当接近“上逼近值”,更具体地说,是当\( y \)越过\( a(\displaystyle\frac { a }{2b } ) -b(\displaystyle\frac { a }{2b })^2\)之后
随着\( t\)的流逝,\(y \)值一直在增大,而且反馈到导函数进一步增大了增长速率,当接近“上逼近值”,更具体地说,是当\( y \)越过\( a(\displaystyle\frac { a }{2b } ) -b(\displaystyle\frac { a }{2b })^2\)之后
增长速率变得越来越慢。 想想下面的函数图像\( y^\prime=y-y^2 \)我们讨论的都是\(y \)在\( [0,\,1] \)范围的情况,此函数\( \displaystyle\frac { a }{ b} =1 \)。(下图就是增长速率(和y有关)和y值之间的关系)
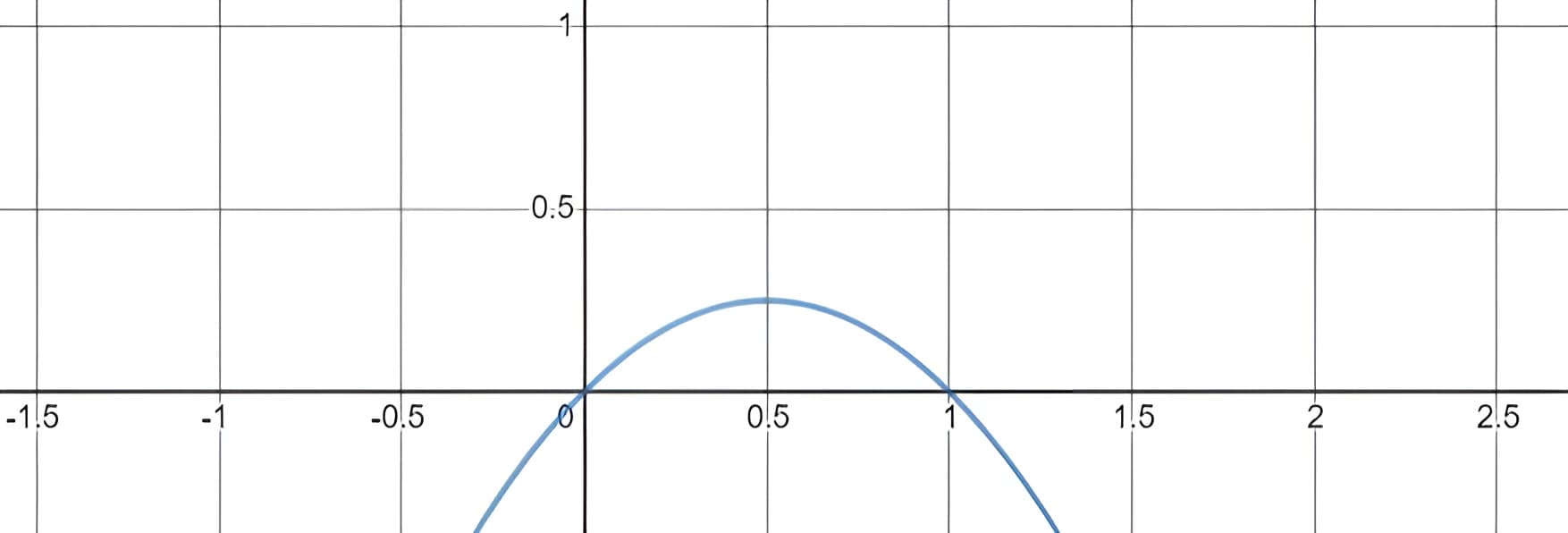
(2) 稳定的稳态(\( Y=\displaystyle\frac {a }{ b} \))
函数值处在\(\displaystyle\frac { a }{ b } \)附近时,随着时间的变化都会越来越接近\( Y=\displaystyle\frac { a}{ b} \),对应于上面的图,就是\( y=1\)两侧值都有往\( 1\)不断靠近的趋势,但是一直“可望不可及”。
对于一个非常复杂的非线性微分方程\(\displaystyle\frac{d y}{d t}=f(y) \),我们可以通过\( f(y)=0\)求解出其稳态,下面具体讨论如何区分不稳定和稳定的稳态。
两种稳态的判定\(\displaystyle\frac{d y}{d t}=f(y)\)
对于讨论微分方程\( \displaystyle\frac{d y}{d t}=f(y) \)的稳态来说,线性或者非线性都不影响,判定方法都是统一的。
【稳定稳态】:逼近值附近变化都会被“拉回”到逼近值。
【不稳定的稳态】:逼近值附近变化都会“跑的远远的”。
这里的逼近值就是满足\(f(Y)=0 \)的\( y=Y \)。当其导数\( \displaystyle\frac{d f(Y)}{d y}\)小于零时,则稳态为稳定的,否则为不稳定的稳态。下图是三个例子:
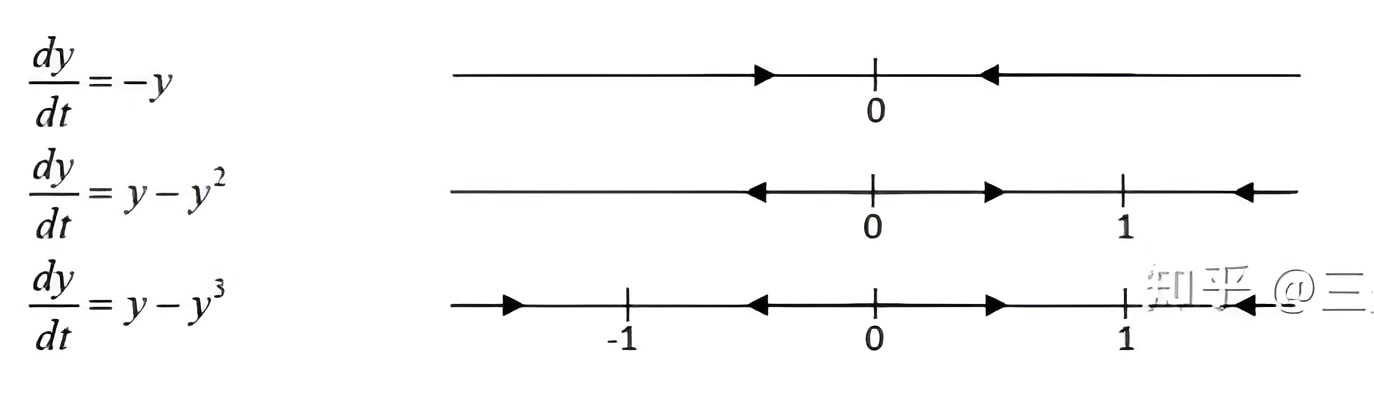 下面讨论一下判定方法的由来,实际上表征函数\( y\)是否远离或者逼近稳态值\( Y\)的参数是\(\displaystyle\frac{d}{d t}(y-Y) \),而$$\frac{d}{d t}(y-Y)=f(y)-f(Y) \approx\left(\frac{d f}{d y}\right)(y-Y)$$这一部分可以称为“线性化”,在\( Y \)附近我们可以忽略\( (y-Y) \)的高次方项所以约等于可以定性分析。因此当该导数小于零时,\( y \)的值逼近于\( Y \),所以该稳态值稳定。
下面讨论一下判定方法的由来,实际上表征函数\( y\)是否远离或者逼近稳态值\( Y\)的参数是\(\displaystyle\frac{d}{d t}(y-Y) \),而$$\frac{d}{d t}(y-Y)=f(y)-f(Y) \approx\left(\frac{d f}{d y}\right)(y-Y)$$这一部分可以称为“线性化”,在\( Y \)附近我们可以忽略\( (y-Y) \)的高次方项所以约等于可以定性分析。因此当该导数小于零时,\( y \)的值逼近于\( Y \),所以该稳态值稳定。
事实上,对于第三个例子\( \displaystyle\frac{d y}{d t}=y-y^{3} \)我们得不到函数的解析式,但是还是能够分析它的稳态的稳定性。关于稳定性的实际应用的例子,即所谓的翻滚实验,从不同方向翻滚课本,可以明显观察到其中一个方向的旋转是不稳定的,其他的稳定,关于这部分后面会有详细讨论。
可分离变量的微分方程
对于形如\( \displaystyle\frac{d y}{d t}=\displaystyle\frac{g(t)}{f(y)}\)的微分方程,可以左右移项\(f(y) d y=g(t) d t \)然后各自积分,该方程可以是非线性的,因为结构特殊,是最容易处理的一类微分方程。费话不多少,举两个例子。
例子1 \(\displaystyle\frac{d y}{d t}=\displaystyle\frac{t}{y} \) $$\begin{aligned}
&\Rightarrow y d y=t d t\\
&\Rightarrow \int_{y(0)}^{y(t)} y d y=\int_{0}^{t} t d t\\
&\Rightarrow \frac{1}{2} y(t)^{2}-\frac{1}{2} y(0)^{2}=\frac{1}{2} t^{2}
\end{aligned}$$整理得\( y(t)=\sqrt{y(0)^{2}+t^{2}} \)
例子2 \( \displaystyle\frac{d y}{d t}=y-y^{2}\) $$\begin{aligned}
&\Rightarrow \frac{1}{y-y^{2}} d y=d t\\
&\Rightarrow \int \frac{1}{y-y^{2}} d y=\int_{0}^{t} d t=t
\end{aligned}$$ 等式左边进行分母的因式分解\(\displaystyle\frac{1}{y-y^{2}}=\displaystyle\frac{A}{y}+\displaystyle\frac{B}{1-y} \)确定相应参数之后再各自积分加和。最后得到的是\( t=f(y) \),还需要处理一下,变成\(y=g(t) \)。其实这个例子是Logistic方程,我们先前已经采用变量代换\(z=1 / y \)进行了求解,比这里的分离变量的方法更简单。