反馈互动:
- 每个交易者都试图在遵守某些规则的同时最大化利润,做出有助于总体结果的决策——比如股票价格的变动——而这反过来影响了交易员的后续决策。
- 麦克斯韦方程组
- PID?
管理原则:让部下知道干什么,也知道为什么干。而不是"民可使,而不可知"。
管理科学=系统工程=系统分析+决策分析+运筹学+控制论+数理统计+计算机算法(优化算法+搜索算法+网络算法),系统分析=做事情的框架和流程
数学
数学会培养人两种思维方式:同构映射和分析还原。简单说就是映射+极限(所以搞清楚这两个名词的含义十分有价值),稍微复杂一点说就是化繁为简+分而治之,最准确说就是同构映射+分析还原。
【同构映射】是指面对一个复杂问题或复杂系统,先把其本质结构抽象出来,映射到一个同构或同态的我们了解的结构上去,通过这个我们了解结构的性质和变化规律,反过来了解复杂问题或结构的性质和变化规律。这个思维方式是抽象代数,微分几何和拓扑典型的方式,最早是伽罗华在研究一元N次方程代数解的过程中发现的,通过讨论解结构同构的交换群的对称性质,得到了5次以上方程不可能代数解这种超出常识和直觉的结论。其实现在这种思维方法已经非常普及,我们在处理政治,军事,经济问题时,经常采用同构映射方法,把问题化繁为简,把复杂问题变成一个我们了解的结构上的问题。这个以前举过很多例子,不再重复。
【分析还原】是数学分析的典型方法,简单说就是分而治之,把一个复杂系统或复杂问题分解成一堆模块,而这些被分解的模块,往往是已经了解或者利用现有知识和技术容易搞清楚的,然后搞清楚这些模块,再组合还原到原始系统或原始问题,根据研究模块得到的判断,来对整体问题或系统进行判断。例如魏尔斯特拉斯定理:任意一个连续函数可以用多项式级数逼近就是这种思想,把连续函数展开成多项式(泰勒级数和傅利叶级数是其具体表达形式之一),通过研究容易得多的多项式性质(例如微分,积分,连续),然后通过收敛性判断还原到原来函数性质。分而治之在国家管理、巨型项目管理和巨型企业管理中是常用方法,那就是任务分解,当然这个管理方法的核心是分解后的还原和分解后模块处理过程的控制协调。
这套思维方法,能够让我们准确,迅速,简单明了抓住问题重点,了解核心问题,听懂别人云山雾罩后面的想法和本质。思维方式是人类知识的结构,没有结构的知识,就是一堆散件,也就相当于散装水泥,乱堆的砖头,一团乱麻的钢材和满地的玻璃碎片。有结构的知识,可以成为一幢摩天大厦。所以:知识不是力量,思维方式才是力量。成功不靠知识多少,而是靠运用知识的能力----你的思维方式是否强大。知识不能改变命运,改变命运靠你的知识组成的大厦的高度。
有人会问,我为什么要用数学来做介绍的载体?我想有两个原因,第一个原因是数学可能是唯一一个老师一开课,就会说:本课程的基本目的就是为了培养你们什么什么思维方式的学科,其他学科估计都没有这么威武霸气;第二个原因是数学有若干人类耀眼的天才留下的巨大思维财富,人类到目前为止,可能主要天才的大多数不是物理就是数学。这里稍微要说几句杨振宁,杨振宁创立的规范场论,在现代物理学中地位非常重要,与量子力学和相对论可以相提并论,1994 年,美国富兰克林学会颁发鲍尔奖给杨振宁时,对他的评价是极高的:“他提出了一个广义的场论,这个理论综合了有关自然界的物理规律,为我们对宇宙中基本的力提供了一种理解。作为20世纪观念上的杰作,它解释了原子内部粒子的相互作用,他的理论很大程度上重构了近40年来的物理学和现代几何学”。
当然,判断一个学科是否伟大,不仅仅是看其诞生了多少天才,更需要看其发现或证明了多少超出直觉和常识的伟大定理,例如数学中就有:
- 哥德尔不完全性定理(公理系统存在不可证伪,也不可证真的命题);
- Brouwer 不动点定理(连续映射存在不动点\(x_0=f(x_0)\));
- 诺特定理(系统每一个对称性对应一个物理守恒定律);
- 康托连续统的不可数性定理;
- 科恩对ZF公理系统连续统假设的不可判定性定理;
- 伽罗华定理(5次以上方程无根式解);
- 魏尔斯特拉斯连续函数逼近定理(包括泰勒定理和傅里叶级数收敛定理);
- 牛顿--莱布尼兹分微积分基本定理(积分是微分的逆运算);
- 中心极限定理(多因素干扰下的随机系统收敛于正态分布)。
当然不仅仅是数学有伟大定理,在经济学中,也有一些超出人类直觉和常识的伟大定理,例如:
- 科斯定理(交易成本为零时,产权与效率无关);
- 阿罗均衡存在定理(供需一定有平衡点);
- 阿罗不可能定理(不存在绝对公平);
- 萨缪尔森大道定理(经济增长一定存在最优路径);
- 资源优化存在定理(凸约束下,非劣解一定存在);
- 网络分工优化存在定理(分工网络存在最优解)。
不过人类发现的超出常识和直觉最伟大的定理还是物理学的,例如牛顿力学方程,开启了蒸汽机时代,引导了工业革命;麦克斯韦方程,开启了电气化时代,目前一切与电有关的行业,电子,电气,电工,电力,电机等等都是他的结果;薛定谔方程,开启了信息化时代,没量子力学,就没有现在的微电子,计算机;爱因斯坦方程,开启了原子能时代等等。
当然,不仅仅数学在训练人的思维方式,其他学科也在,只是不这么理直气壮而已。例如经济学就强调实证(为类比提供对象)和归纳(类比)的思维方式,而管理学强调仿真建模(本质是搭建信息流,物流和资金流的逻辑结构和反馈通道,构建计划、组织、指挥、控制和协调平台)和流程(本质是建立一直算法,对数学来讲,任何步骤,次序,流程都是算法)。但是从思维培训的效率来讲,远远不如数学,一般情况下,一个具有成熟经济学思维方式的人,至少需要20年时间才能形成,管理学也需要十年,而数学培养出熟悉化繁为简+分而治之的思维方式,一般情况5年就能成功。
群体智能
群体智能简介
【群体智能】(Swarm intelligence):是指一些简单的具有信息处理能力的单元结构(个体)在交互作用的过程中表现出的具有解决问题的一种能力。Swarm intelligence is the property of a system whereby the collective behaviours of (unsophisticated) agents interacting locally with their environment cause coherent functional global patterns to emerge.
- 由单个复杂个体完成的任务通常都可以由大量简单的个体组成的群体合作完成,而后者往往更具有健壮性、灵活性和经济性;
- 通常是无中心控制的、具有自我组织能力和自适应能力的自然/人工的系统所表现出来的能够完成特定任务的某种区别于个体行为的群体行为;
- 是对生物群体的一种仿生,模仿生物群体的群体 (涌现) 行为。
【涌现】: 简单规则导致群体行为的叠加,导致出现复杂系统状态突变。个体只遵守筒单的规则,在无中心接制下而表现出的的复杂群体行为。
例子:鸟群、蚂蚁、蜜蜂、昆虫群体等等。更具体的比如蚂蚁搬运食物到巢穴的最短路径,鸟群觅食,蜂群筑巢,无人机群控制,城市交通流,股票定价。
群体智能优化方法
定义:通过模拟生物种群或自然现象行为,由一群简单个体遵循特定的交互机制完成给定复杂优化任务的算法。
Motivation:
- 生物群体(PSO,ACO)
- 社会效应(Seeker)
- 其他自然现象(SA,FWA,WD,BSO)
分类:
- 生物群体智能算法:通常研究的是生物界的种群,比如鸟群鱼群、蝙蝠、布谷鸟、磷虾群、细菌等种群的行为。
- 人工群体智能算法:通过从日常的自然现象抽象出来的一些物理模型,由多个个体组成一个群体,利用该群体模型进行优化计算。
典型的群体智能优化算法:
- Particle Swarm Optimization (PSO) 鸟群觅食的模拟
- Ant Colony Optimization (ACO) 蚂蚁搬运食物到巢穴的最短路径的模拟
- Differential Evolution (DE)
- Bee Colony Optimization (BCO)
- Bacterial Foraging Optimization (BFO)
- Fish School Search (FSS)
- Seeker Optimization Algorithm (SOA)
- Fireworks Algorithm (FWA) 观察烟花的爆炸行为
主要是用来求解复杂优化问题—智能优化搜索方法,是通用的。Complexities的困难在于:
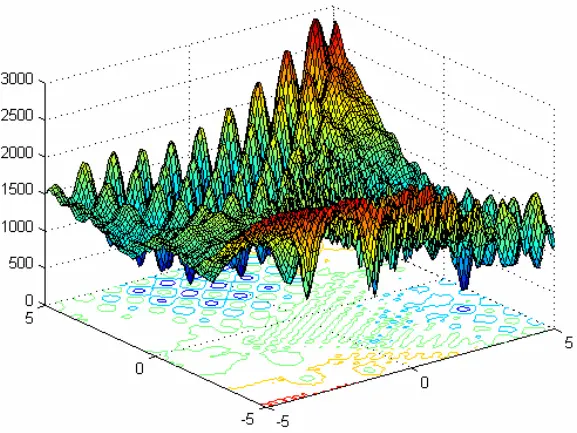
- Irregular
- Multiple local optima
- Non-separable
- Asymmetrical
Typical SI algorithms
Particle Swarm Optimization (PSO). Inspired by the search food of flocks. Flying principle of each bird in a swarm如图。
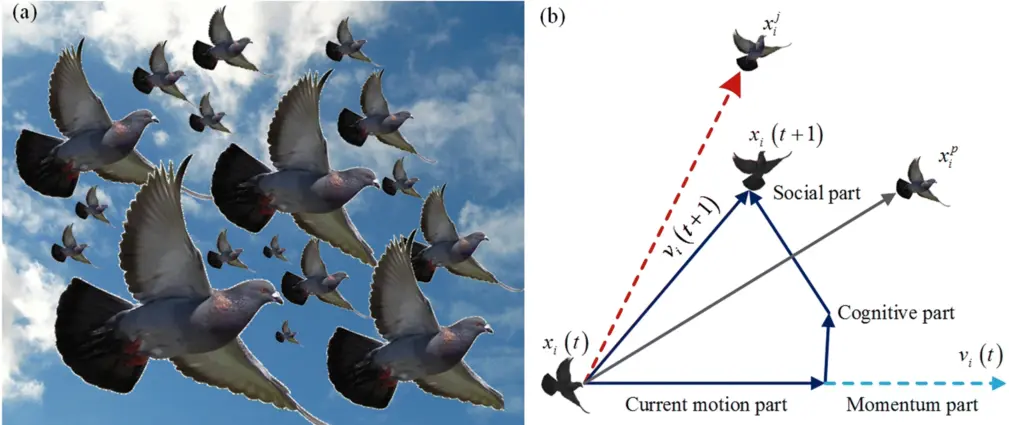
忙总说有四条规则:
- 凝聚规则:每只鸟都往其最近的鸟靠拢;
- 追随规则:每只鸟都要把自己位置对齐在其最近的鸟的平均方向上,也即追随最近的鸟的飞行方向;
- 避开规则:每只鸟要避免撞上其临近的鸟;
- 躲避规则:当靠近障碍物时,个体都能主动避开障碍物。
用上述四条简单规则建立的模型(具体算法程序网上一大堆,自己可以搜索),计算发现很神奇的结果,如果展示成动画,那就是:一开始高度分散,到处乱飞的鸟,会很快形成群体,并开始统一向一个方向飞行,途中如果遇到障碍,鸟群会立即分散,从障碍两边越过,越过后,鸟群又会立即形成一个统一群体,继续向某一方向飞行。
Ant Colony Optimization (ACO) Ant system searches Food from Nest.
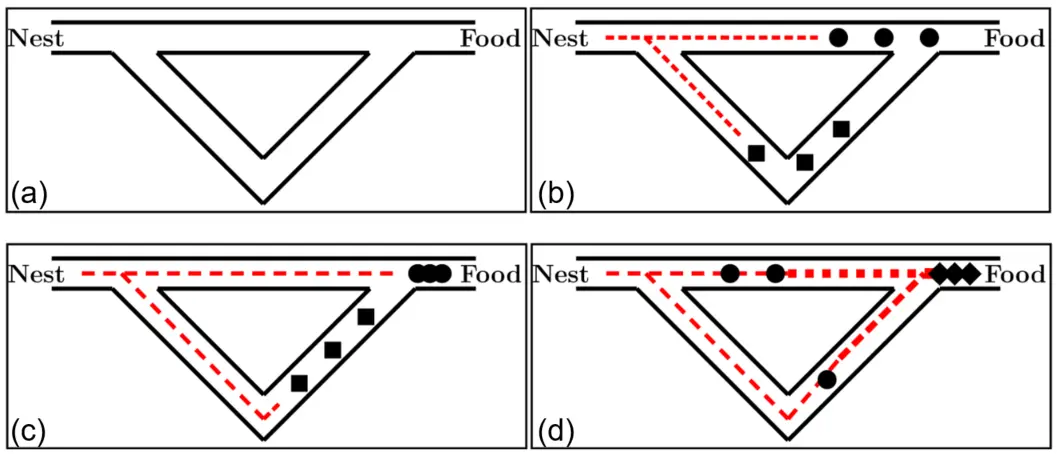
上图是An experimental setting that demonstrates the shortest path finding capability of ant colonies. Between the ants' nest and the only food source exist two paths of different lengths. In the four graphics, the pheromone trails are shown as dashed lines whose thickness indicates the trails' strength. 最终的结果是Auto-catalytic (positive feedback) process。四张图分别表示的过程为:
- All ants are in the nest. There is no pheromone in the environment.
- The foraging starts. In probability, \(50 \%\) of the ants take the short path (symbolized by circles), and \(50 \%\) take the long path to the food source (symbolized by rhombs).
- The ants that have taken the short path have arrived earlier at the food source. Therefore, when returning, the probability to take again the short path is higher.
- The pheromone trail on the short path receives, in probability, a stronger reinforcement, and the probability to take this path grows. Finally, due to the evaporation of the pheromone on the long path, the whole colony will, in probability, use the short path.
也许有人会问蚂蚁群体行为是局部最短路径还是全局最短路径,实际上蚂蚁群体是逐渐接近全局最短路径的。因为源于蚂蚁会犯错误,也就是它会按照一定的概率不往信息素高的地方走而另辟蹊径,这可以理解为一种创新,这种创新如果能缩短路途,那么根据刚才叙述的原理,更多的蚂蚁会被吸引过来。
现代复杂系统理论不断得到超出我们直觉和常识的结论,上面的蚂蚁的行为就是一个很好的例子,蚂蚁之所以具有智能行为,完全归功于它的简单行为规则,而这些规则综合起来具有以下两个方面的特点:
(1) 多样性,即保证了蚂蚁在觅食的时候不至于走进死胡同而无线循环;
(2) 正反馈,正反馈机制保证了相对优良的信息能够被保存下来。
我们可以把多样性看成是一种创造能力,而正反馈是一种学习强化能力。正反馈的力量也可以比喻成权威的意见,而多样性是打破权威体现的创造性,证实这两点结合才使得蚂蚁的智能行为涌现出来。
注:【Pheromones】(/ˈferəməʊn/,信息素) are substances which are secreted to the outside by an individual and received by a second individual of the same species. Many examples exist in animals but their role in humans remains uncertain since adults have no functioning vomeronasal organ(犁鼻器), which processes pheromone signals in animals.
烟花算法:不太懂。
群体机器人
【群体机器人】(Swarm robotics):将群体智能引入机器人学。Swarm robotics is an approach to the coordination of multiple robots as a system which consist of large numbers of mostly simple physical robots. In a robot swarm, the collective behavior of the robots results from local interactions between the robots and between the robots and the environment in which they act. It is supposed that a desired collective behavior emerges from the interactions between the robots and interactions of robots with the environment. This approach emerged on the field of artificial swarm intelligence, as well as the biological studies of insects, ants and other fields in nature, where swarm behaviour occurs.
启发自社会性生物群体:
- 鸟类迁徙、蚂蚁觅食;
- 个体较弱;
- 群体行为复杂;
群体机器人:
- 大量、简单的实物智能体;
- 集体行为从局部交互涌现。
特点:
- 成本低;
- 覆盖范围更广;
- 冗余容量大(如果其中一个机器人由于故障,堵塞等原因而失败,则另一个机器人可以采取措施在其任务中进行故障排除或更换);
- 覆盖大面积的能力。
相较于传统的单机器人系统,具有以下三个属性:
- 鲁棒性,这意味着尽管某些个体的失败和/或环境中可能发生的变化,群体仍然能够继续运作;
- 灵活性,这意味着能够提出适合于要执行的任务的解决方案;
- 可伸缩性,,这意味着无论其大小(从某个最小大小),群都必须起作用。
应用场景:
- 区域覆盖与搜索:大空间、非结构性;
- 危险任务:灾后救援;
- 有冗余性要求的任务:战场通信;
- 无法或难以预先确定所需资源:环境改变迅速。
实际应用:
- 吸油装置:美国麻省理工学院的研究人员开发出了一种名为"海洋峰群(SeaSwarm)"的吸油装置,它由一组小型机器人组成,这些机器人可以评估海洋浮油的状况,并立刻展开清理工作,比起大型石油回收船等设备,其成本更低、效率更高。
- 药物治疗:在磁场的作用下,可以控制微型机器人群体,使其自由运动;不感染其他的微型机器人活动;探测病灶,将药物精确释放到肿瘤部位。
- 游戏AI:星际争霸等。
参考资料:
(1) 群体智能及其应用研究进展-谭营—B站
(2) 以蚂蚁算法为例说明简单规则在复杂系统里的力量—忙总—豆瓣
(2) Ant colony optimization: Introduction and recent trends—Physics of Life Reviews—2005
(3) 群体智能新论:个体过于聪明会导致群体死板—集智俱乐部
(4) 一文读懂复杂网络与群体智慧—集智俱乐部