图床 semiconductor-img/      Electronics Desk
Principles of Semiconductor Devices     半导体物理-北大
Semiconductor Technology from A to Z
半导体奇妙旅程：从原子结构的量子探索到人工智能

词汇：[mathjax]
intimate contact （缺润滑油）直接接触;
rectifying contact 整流接触  (rectify vt. 改正；精馏；整流)
ohmic contact 欧姆接触
blende [blend] [矿物] 闪锌矿；褐色闪光矿物
zinc blende [矿物] 闪锌矿
arsenide [ˈɑːsəˌnaɪd] [无化] 砷化物
chronological order （事情发生或发展的）时间次序 [ˌkrɑːnəˈlɑːdʒɪkl]
minute 极小的; 微小的; 细微的; 细致入微的; 详细的;
supplant vt. 代替；排挤掉
a threedimensional periodic fashion  样式
stray 偏离  ([streɪ])
theorem for equipartition of energy  能量均分定理  [ˌekwɪpɑːˈtɪʃən ]
nonvolatility 非易失性 ['nɔn,vɔlə'tiliti]
annihilated 湮灭的 [ə'naɪəleɪtɪd]
proportionality constant  比例常数
infinitesimal [ˌɪnfɪnɪˈtesɪml] 无穷小的；无限小的；极小的
algebraic sum 代数和
fictitious [fɪkˈtɪʃəs] 虚假的; 虚幻的，虚构的(This fictitious particle is called a hole. )
on the order of 属于…同类的；与…相似的；近似
quotient [ˈkwəʊʃnt] 商(除法所得的结果)
dangling bonds 悬空键 [ˈdæŋɡlɪŋ]
dissimilar [dɪˈsɪmɪlə(r)]不一样的; 不同的; 不相似的
planar technology 平面工艺 [ˈpleɪnə(r)]
metallurgical junction( The "metallurgical junction" is the transition location from the p-doped region to the n-doped region of a semiconductor.)
metallurgical [ˌmetəˈlɜːdʒɪkl] 冶金的；冶金学的
avalanche [ˈævəlɑːnʃ] 雪崩; 山崩;

基本概念：

• 半导体的平衡态，指的是没有外界刺激injection，而且自身达到热平衡的状态。其他的状态都是非平衡态，即使在稳定injection下维持的平衡。
• thermal equilibrium: \(p n=n_{i}^{2}\)   nonequilibrium:  \(p n>n_{i}^{2}\)
• nonequilibrium是存在外界excitation，nonequilibrium也可以有steady state.

Introduction

Main topics:

• 4 building blocks of semiconductor devices.
• 18 important semiconductor devices and their roles in electronic applications.
• 23 important semiconductor technologies and their roles in device processing.
• Technology trends toward high-density, high-speed, low-power consumption, and nonvolatility

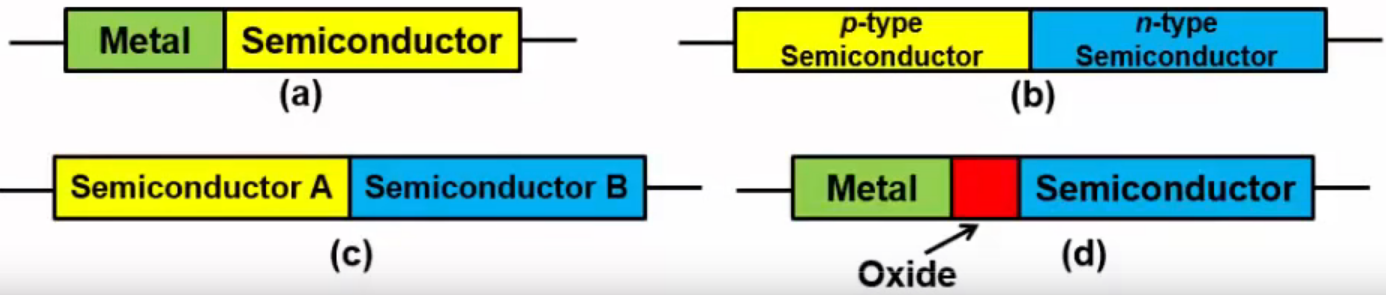
(a) Metal-Semiconductor contact: the first semiconductor device ever studied (1874).  it can be used as 【rectifying contact】(one current direction) or 【ohmic contact】( pass current in either direction).
注：【MESFET 】(metal-semiconductor field-effect transistor)，using one rectifying contact as gate, two ohmic contacts as the source and drain.
(b) p-n junction: it's a key building block for most semiconductor devices advanced types. 【p–n–p  bipolar transistor】(BJT三极管，1980年中期开始逐渐被MOSFET取代),   【p–n–p–n thyristor 】( 晶闸管).
(c) formed by dissimilar semiconductors, like  GaAs + AlAs. key components for high-speed and photonic devices.
(d) 【MOS】, one MOS as the gate, 2 p-n junctions as the source and drain, forming 【MOSFET 】(the most important in integrated circuits IC).

MOSFET is the most important device for logic circuits, and【NVSM】is the most important device for long-term information storage. There is synergy between MOSFET and NVSM. 

(1) Difference between JFET MOSFET and MESFET
(2) 碳化硅二极管

Energy Bands and Carrier Concentration in Thermal Equilibrium

Conductivity of a semiconductor is generally affected by:
(1) temperature
(2) illumination
(3) magnetic field
(4) minute amounts of impurity atoms (typically, \( 10^{-9} \) to \( 10^{-3} \) in terms of atoms)

Element Semiconductors: Ge(since 1950s) and Si(since 1950s).
The main reasons we now use Si (\(>97 \%\) of all semiconductor devices，室温下禁带宽度 1.12 eV) are that:
(1)  silicon devices exhibit better properties at room temperature (small bandgap change within the operating temperature range)
(2)  high-quality silicon dioxide can be grown thermally
(3)  economic considerations,  in terms of abundance in crust.
注：Why Silicon is preferred over Germanium ?

Compound Semiconductors:

More complex preparation processes than element semiconductors. They especially GaAs, are used mainly for high-speed electronic and photonic applications.

•  \( \text { III-V }\) compounds (\(\sim 2 \%\))
  • Binary: GaAs(1.42), InP(1.35), GaN(3.44)
  • Ternary:  Al_xGa_1-xAs(1.42-2.51)
  • quaternary- Ga_xIn_1-xAs_yP_1-y(0.36-2.2)
• \(\text { II-VI }\) compounds (\( 0.1 \%\))
  CdSe(1.7), ZnS(3.66), ZnO, CdTe, ZnTe

注：红外线发射管(IR LED）也称红外线发射二极管，属于二极管类。它是可以将电能直接转换成近红外光（不可见光）并能辐射出去的发光器件，主要应用于各种光电开关、触摸屏及遥控发射电路中。红外线发射管的结构、原理与普通发光二极管相近，只是使用的半导体材料不同。红外发光二极管通常使用GaAs、GaAlAs等材料，采用全透明或浅蓝色、黑色的树脂封装。

Basic Crystal Structures
The atoms are arranged in a three-dimensional periodic fashion. For a given semiconductor, there is a 【unit cell】 that is representative of the entire lattice; by repeating the unitl cell throughout the crystal, one can generate the entire lattice.

Every equivalent lattice point in the three-dimensional crystal can be found using the set $$\boldsymbol{R}=m \boldsymbol{a}+n \boldsymbol{b}+p \boldsymbol{c}$$It should be mentioned that the end point of the vector stands for the 【basic block】 rather than specific atom. There are seven different crystal systems, for example cubic crystal system, which has three differen subtypes(primitive cubic, body-centered cubic, face-centered cubic).

Diamond Structure

For Si/Ge element semiconductors, they belong to the diamond structure, or more specifically fcc crytstal family and can be seen as two interpenetrating fcc sublattices with one sublattice displaced from the other by a specific angle and distance. Most of the III-V compound semiconductors (e.g., GaAs) have a zincblende lattice,  which is identical to a diamond lattice except that one fcc sublattice has Column III atoms (Ga) and the other has Column V atoms (As).

Silicon has a diamond lattice structure, its surface and orientation are defined by Miller indices (the most important one is [1 0 0]).

Valence Bonds and Energy Bonds

Covalent bonding occurs between atoms of the same element or between atoms of different elements that have similar outer-shell electron configurations, for example, Si. While for GaAs,  gallium arsenide has a small ionic contribution that is an electrostatic attractive force between gallium ions and arsenide ions.

At low temperatures, the electrons are bound in ion pairs. Consequently, they are not available for conduction. At higher temperatures, thermal vibrations may break the covalent bonds (ionize one electron from the bond). When a bond is broken, a free electron results and can participate in current conduction. Actually, the electron deficiency(hole) can also shift to a neighboring electon position. The concept of a hole is analogous to that of a bubble in a liquid.

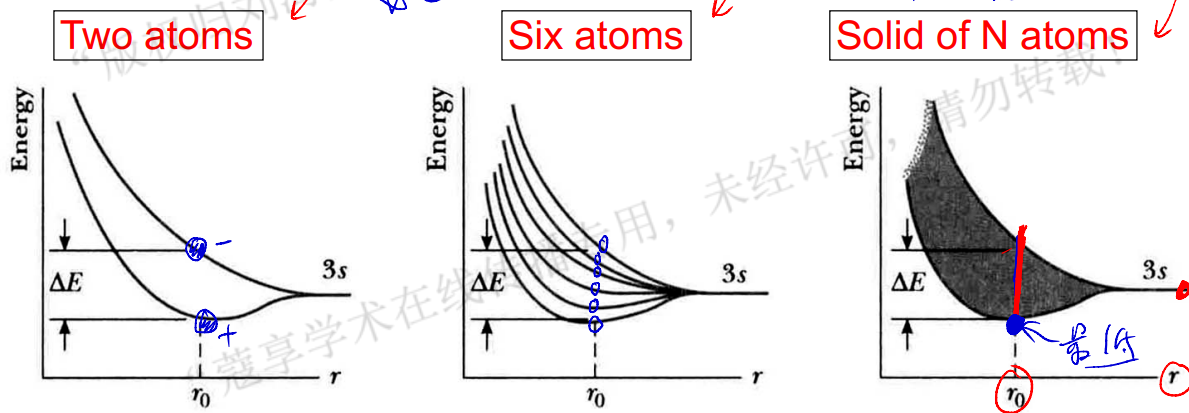
(1) As the interatomic distance decreases, the 3s and 3p subshell of the N silicon atoms will interact and overlap to form bands. As the 3s and 3p bands grow, they merge into a single band containing 8N states. At the equilibrium interatomic distance determined by the condition of minimum total energy, the bands will again split, with 4N states in the lower band and 4N states in the upper band.
(2) At a temperature of absolute zero, electrons occupy the lowest energy states, so that all states in the lower band (the valence band) will be full and all states in the upper band (the conduction band) will be empty.
(3) Physically, bandgap is the energy required to break a bond in the semiconductor to free an electron to the conduction band and leave a hole in the valence band.
The Energy-Momentum Diagram
The energy of a free electron is given by \(E =\displaystyle\frac{p^{2}}{2 m_{0}}  \). In a semiconductor crytstal, an electron in the CB band is simliar to a free electron in being relatively free to move about in the crystal. However, this equation is no longer valid. We replace the free-electron mass by an effective mass. $$E =\frac{p^{2}}{2 m_{n}}\quad\quad m_{n} \equiv\left(\frac{d^{2} E}{d p^{2}}\right)^{-1}$$The  【effective-mass】concept is very useful because it enables us to treat electrons and holes essentially as classical charged particles.

有效质量：是用来方便引入经典力学的解决方法牛顿第二定律的一种近似。它近似认为电子受到原子核的周期性势场(这个势场和晶格周期相同)以及其他电子势场综合作用的结果。在数学处理上采用在能带极值点处用泰勒展开，这样略去二阶以上项，就可以很好刻画。At the highest energies of the valence band in many semiconductors (Ge, Si, GaAs, ...), and the lowest energies of the conduction band in some semiconductors (GaAs, ...), the band structure E(k) can be locally approximated as \( E(\mathbf{k})=E_{0}+\displaystyle\frac{\hbar^{2} \mathbf{k}^{2}}{2 m^{*}}\)注意this parabolic form is not valid for describing most materials，参看wiki。

For Si, \(m_{n}=0.26m_{0}\), \(  m_{p}=0.55m_{0}\). For GaAs, \(m_{n}=0.063m_{0}\), \(  m_{p}=0.55m_{0}\).

Feartures for actual energy-momentum relationships (also called energy-band diagram) :
(1)  The narrower the parabolic curve is, the smaller the effective mass is.
(2)  Visualized in three dimensions, the relationship between \(  E\) and \( p \) is a complex surface. Since the periodicity of most lattice is different in various directions, the energy-momentum diagram is also different for different directions. 
(3) If the minimum of the conduction band occurs at \( p=0 \), this means the effective mass of the electrons in every direction in the crystal is the same. It also indicates that the electron motion is independent of crystal direction.
(4) If \(p \neq 0  \) for min of CB,  this means that the electron behavior in every direction is not the same in the crystal.
(5) In general, the minimum of conduction band of polar (with partly ionic binding) semiconductors tends to be at \( p=0 \), which is related to the lattice structure and the fraction of ionicity in the bond.

(1) The valence bands are simpler than the conduction bands. They are qualitatively similar for most semiconductors because the environments for holes moving in the covalent bonds are similar due to the similar structures in diamond and zincblende.
(2) Near the min of CB and the max of VB, the E-p curves are essentially parabolic.
(3) For silicon, the max of VB  occurs at \( p=0 \), while the min of CB occurs along the [1 0 0] direction at \( p=p_{c} \).
(4) For GaAs, no momentum change is required for the electron transition.

Conduction in Metals, Semiconductors, and Insulators

Metal
Two different cases, a CB that either is partially filled (as in Cu) or overlaps the VB (as in Zn or Pb) so that there is no bandgap. From an applied electric field, the free electrons gain kinetic energy and can move to the next higher available energy levels, even with only a small applied field because therea are many unoccupied states close to the occupied energy states.

Insulators
In an insulator such as silicon dioxide (SiO₂), the valence electrons form strong bonds between neighboring atoms. Since these bonds are difficult to break, there are no free electrons to participate in current conduction at or near room temperature. This can also be explained by the big bandgap as is shown above.

Semiconductor
Compared with insulator, it has a much smaller energy gap, on the order of \( 1 \mathrm{eV} \). At \( T=0 \mathrm{~K} \), no electrons in CB. While at RT and under normal atmospheres, the bandgap for Si and GaAs are \( 1.12 \mathrm{eV} \) and \(1.42 \mathrm{eV}  \), respectively. For these senarios, the thermal energy \( kT \) is a good fraction of \( E_g \), and appreciate numbers of electrons are thermally excited to CB. Also, since many empty energy states exist in CB, a small applied potential can easily move these electrons, resulting in a moderate current. 99 %的半导体，温度升高，禁带宽度减小。

Intrinsic Carrier Concentration

An intrinsic semiconductor is one that contains relatively small amount of impurities compared with thermally generated electrons and holes. For an intrinsic semiconductor in the thermal equilibrium state, the electron density(i.e. the number of electrons per unit volume) in the CB is given as follows (\( E_c \) initially taken to be \( E=0 \) for simplicity)$$n =\int_{0}^{E_{t o p}} n(E) \mathrm{d} E =\int_{0}^{E_{t o p}} N(E) F(E) \mathrm{d} E$$Fermi distribution function: $$F(E)= \frac{1}{1+\mathrm{e}^{\left(E -E_{F}\right) / k T}}$$Note that \( F(E) \) is symmetrical around the Fermi level \( E_F \), which is effective even beyond the bangap (exceed several \(  kT\)). 对称性可以从如下式子看出来：$$\frac { 1 }{1+e^x } +\frac { 1 }{ 1+e^{-x}} =\frac {1 }{ 1+e^0 } *2=1$$

For energies that are \(  3kT\) above or below the Fermi energy, the exponential term  becomes larger than \(  20\) or smaller than \( 0.05 \), respectively. The Fermi distribution function can thus be approximated by simpler expressions (Boltzmann distribution function): $$\begin{array}{l} F(E) \cong e^{-(E -E_{F}) / k T} \quad \quad \,\,\,\, \text { for }(E-E_{F})>3 k T \\ F(E) \cong 1-e^{(E -E_{F}) / k T} \quad \quad \text { for }(E-E_{F})<-3 k T\end{array}$$For these two expressions, \(  (1-F(E))\) can be regarded as the occupation probability of hole. Note that these two expressions also imply the symmetrical property.

(1) The figure of \(  N(E)\) (density of energy states) shows it varies as \(\sqrt{E}  \) for a given electron effective mass, the Fermi distribution function, and the carrier concentrations for an intrinsic semiconductor. Note that here \( E \) is the difference between energy levle (in CB) and \( E_c \) or energy levle (in VB) and \( E_g \).

(2) According to 固体物理-车静光&李威仪 or appendix H of this book, we know (\(N(E)\propto \sqrt{E}  \)) $$N(E)=4 \pi\left(\frac{2 m_{n}}{h^{2}}\right)^{3/2} E^{1/2}$$Derivation of the density of states

(3) The electron density can be written as : $$n =\frac{2}{\sqrt{\pi}} N_{C}(k T)^{-3 / 2} \int_{E_C}^{\infty} (E-E_C)^{1 / 2} \exp[-(E - E_{F}) / k T ] \mathrm{d} E $$where \(  N_{C} =2\left(\displaystyle\frac {2 \pi m_{n} k T    }{ h^{2} } \right)^{3 / 2}\). If we let \( x \equiv (E-E_C) / k T \), then we have $$n =\frac{2}{\sqrt{\pi}} N_{C} \exp \left(-\frac { E_C-E_F }{ kT } \right) \int_{0}^{\infty} x^{1 / 2} e^{-x} \mathrm{~d} x$$ The intergral term equals \( \sqrt{\pi} / 2 \), therefore we get$$n=N_{C} \exp \left(-\frac{E_{C}-E_{F}}{k T}\right)$$where \(  N_C\) is  effective density of states in the conduction band, which is propotional to \( T^{3/2} \) (和\(E\)无关). If there is only one energy state \( E_C\) in CB, then \(N_C  \) is the corresponding energy states density. 

By the same method, we can obtain hole density in VB $$p=N_{V} \exp \left(-\frac{E_{F}-E_{V}}{k T}\right)$$where \(  N_{V} \equiv 2\left(2 \pi m_{p} k T / h^{2}\right)^{3 / 2}\) is  effective density of states in the VB.

(4) For an intrinsic semiconductor, we have $$n=p=n_{i}$$where \(n_{i}  \) is the  intrinsic carrier density. Above figure(d), note that the shaded area in the conduction band is the same as that in the valence band.

(5) By equating \( n \) and \(p  \), we get the Fermi level for an intrinsic semiconductor: $$E_{F}=E_{i}=\frac {E_{C}+E_{V}}{2 } + \frac {kT}{2} \ln \frac {N_{V}}{N_{C}}=\frac{E_{C}+E_{V}}{2}+\frac{3k T}{4} \ln \left(\frac{m_{p}}{m_{n}}\right) $$At room temperature, the second term is much smaller than the bandgap. Hence, the intrinsic Fermi level \( E_i \) of an intrinsic semiconductor generally lies very close to the middle of the bandgap. Then, it's easy to get $$\begin{array}{l} n p=n_{i}^{2} \\ n_{i}^{2} = N_{C} N_{V} \exp \left(\frac {-E_{g}  }{k T }\right) \\ n_{i}=\sqrt{N_{C} N_{V}} \exp \left(\frac {-E_{g}  }{2 k T } \right) \end{array}$$where \(  E_{g} \equiv E_{C}-E_{V}\).

Donor and Acceptor

Actually, in last section, we use Boltzmann distribution function to calculate the electron density, which is on the premise of \( \left(E_C-E_{F}\right)>3 k T \). In this case, the final electron density is much lower than the effective density of states since \(\exp \left(-\frac{E_{C}-E_{F}}{k T}\right)  \) is a very small term, and the similar senario occur for hole concentration. In other words, the Fermi level \(  E_F\) is at least \(  3kT\) above \( E_V \) or \( 3kT \) below \( E_C \). In these cases, the semiconductor is referred to as a "nondegenerate" semiconductor. (注：半导体中价带简并是什么意思？)

Complete Ionization
For shallow donors(roughly \(0.025 \, \mathrm{eV}\),the energy of \( kT\) at RT) in n-type Si or GaAs, at RT, thermal energy is enough for all impurities to ionize, resulting the same number of electrons in the CB as that of donors/impurities. This condition is called "complete ionization". $$n=N_{D}$$where \( N_{D} \) is the donor concentration.

Note that we usually use \(\text { atoms } / \mathrm{cm}^{3}\) as the unit of doping concentration.

Then with \(  n=N_{C} \exp \left(-\displaystyle\frac{E_{C}-E_{F}}{k T}\right)\), we have $$E_{C}-E_{F}=k T \ln \left(N_{\mathrm{C}} / N_{D}\right)$$

From above equation, we can see that the higher the donor concentration, the smaller energy difference \(  (E_C-E_F)\); that is, the Fermi level will move closer to the bottom of the CB. Similarly, for higher acceptor concentration, the Fermi level will move closer to the top of the valence band.
It's useful to express electron and hole densities in terms of the intrinsic carrier concentration \(n_i  \) and the intrinsic Fermi level \( E_i \) since \(E_F \) is frequently used as a reference level when discussing extrinsic semiconductors. $$n=N_{C} \exp (-\frac{E_{C}-E_{F}}{k T})=N_{C} \exp (-\frac{E_{C}-E_{i}}{k T}) \exp (\frac{E_{F}-E_{i}}{k T})= n_i \exp (\frac{E_{F}-E_{i}}{k T})$$where constant \(n_i=N_{C} \exp (-\frac{E_{C}-E_{i}}{k T})\) (see section "Intrinsic Carrier Concentration") and similarly, $$p=n_i \exp (\frac{E_{i}-E_{F}}{k T})$$Note that $$np=n_{i} \exp \left(\frac{E_{F}-E_{i}}{k T}\right)n_{i} \exp \left(\frac{E_{i}-E_{F}}{k T}\right)=n_{i}^2$$This result is identical to that for the intrinsic case, which can be called  the Law of mass action, and is valid for both intrinsic and extrinsic semiconductors under thermal equilibrium conduction at given temperature. In other words, the above equation holds true even for lightly doped extrinsic semiconductors as the product \( np \) is independent of doping concentration (nondegenerate case，此处特别注意).

video here. Constant K is the reaction quotient (反应系数) at the equilibrium state, and is only the function of temperature. At any given point, the reaction direction is determined by whether Q is smaller or larger than K. 
For electronics, \( n_{i}^2 \) is the K(the reaction is one electron plus one hole into “1”), and it only depends on temperature for intrinsic and lightly doped extrinsic semiconductors.

If both donor and acceptor impurities are present simultaneously, the impurity that is present in a greater concentration determines the type of conductivity. The Fermi level must adjust iteself to perserve charge neturality.
                       electrons + ionized acceptors = holes + ionized donors

Under complete ionization condition, we have $$n+N_{\mathrm{A}}=p+N_{\mathrm{D}}$$Sloving the above equation and \( n p=n_{i}^{2} \)  yields the equilibrium electron and hole concentrations in an n-type semiconductor:
注：这就是用已知的\(N_{\mathrm{D}} \)、\(N_{\mathrm{A}}\)和\(n_i\)来表示未知的\(  n_{\mathrm{n}}\)和\(n_{\mathrm{p}} \) 
$$\begin{array}{l} n_{\mathrm{n}}=\displaystyle\frac{1}{2}\left(N_{\mathrm{D}}-N_{\mathrm{A}}+\sqrt{\left(N_{\mathrm{D}}-N_{\mathrm{A}}\right)^{2}+4 n_{\mathrm{i}}^{2}}\right) \\ p_{\mathrm{n}}={n_{\mathrm{i}}^{2}}/{n_{\mathrm{n}}} \end{array}$$The subscript \(  n\) refers to the n-type semiconductor. Because the electron is the dominant carrier, it is called the "majority carrier". The hole in the n-type is called the "minority carrier". Similarly, we obtain the concentration of holes and electrons in p-type semiconductor as: $$\begin{array}{l} p_{\mathrm{p}}=\displaystyle\frac{1}{2}\left[N_{\mathrm{A}}-N_{\mathrm{D}}+\sqrt{\left(N_{\mathrm{A}}-N_{\mathrm{D}}\right)^{2}+4 n_{\mathrm{i}}^{2}}\right] \\ n_{\mathrm{p}}={n_{\mathrm{i}}^{2}}/{p_{\mathrm{p}}} \end{array}$$Generally, the magnitude of the net impuritiy concentration \(N_{\mathrm{D}}-N_{\mathrm{A}}\) is greater than (for n-type) the intrinsic carrier concentration \(n_i  \); therefore, the above relationship can be simplified to $$\begin{array}{ll} n_{\mathrm{n}} \approx N_{\mathrm{D}}-N_{\mathrm{A}}, & N_{\mathrm{D}}>N_{\mathrm{A}} \\ p_{\mathrm{p}} \approx N_{\mathrm{A}}-N_{\mathrm{D}}, & N_{\mathrm{A}}>N_{\mathrm{D}} \end{array}$$
Information:
(1) Higher temperature, closer the distance between the Fermi level and the intrinsic Fermi level. That is, the semiconductor becomes intrinsic.
(2) Higher temperature, smaller bandgap. (从图中可以看出来)
注：实际上，除了PbTe和HgTe等少数几种半导体的禁带宽度具有正的温度系数之外，其余的如Si,Ge,GaAS等半导体的禁带宽度的温度系数都是负的。参考禁带宽度与温度的关系？-知乎
(3) Higher concentration of impurities, larger the distance between the Fermi level and the intrinsic Fermi level.
(4) For the right figure, there exists three different regins: freeze-out region/ extrinsic region/ intrinsic region. The turning point between extrinsic region and intrinsic region is when \( n_{i} \) equals to the impurities concentration \(N_{\mathrm{D}}\).
注：\(n_{i}=\sqrt{N_{C} N_{V}} \exp \left(\frac{-E_{g}}{2 k T}\right) \)，其中的根号项和温度的\(3/2\)次方成正比，对后面的指数项来说，温度越高数值也越大，所以两方面作用，到达一定温度后，本征载流子的数量会急剧增加。

Degenerate Semiconductor
When the  doping concentration is comparable to the corresponding effective density of states, we can no longer use Boltzmann distribution as the approxiamted one for Fermi distribution. For very heavily doped n-type or p-type semiconductor, \(E_F  \) will be above \( E_C \) or below \(E_V  \). The semiconductor is referred to as a "degenerate semiconductor".

An important aspect of high doping is the "bandgap-narrowing effect"; that is, high impurity concentration causes a reduction of the bandgap. The bandgap reduction \( \Delta E_{g} \) for silicon at room temperature is given by$$\Delta E_{g}=22\left(\frac{N}{10^{18}}\right)^{1 / 2} \mathrm{meV}$$