书籍和工具：
- 在线绘制交换图
- Seven Sketches in Compositionality: An Invitation to Applied Category Theory
- Conceptual Mathematics: A First Introduction to Categories
- category theory—nLab
- 应用范畴论的网站
- Category Theory: The Beginner's Introduction 2
- MIT— 18.S097: Programming with Categories
范畴和态射
【范畴】是由一些对象及其间的箭头(称为态射，或者关系)组成的结构，通常用来描述某一类数学对象及其间的映射全体。范畴为数学提供了一个模板，将不同内容输入模板，就能重建一个数学领域。例子如下：
- 集合范畴由所有集合和它们之间的映射(关系)组成；
- 向量空间范畴由所有向量空间和它们之间的线性映射组成；
- 群范畴由群和它们之间的关系(群同态)组成；
- 拓扑空间范畴由拓扑空间和它们之间的关系(连续映射)组成；
范畴论的特点：
- 范畴论是一门关于箭头(态射)的科学，箭头是用来连接两个点(对象)的。
- 范畴论是一门元关系(meta-relation)学科。
- 不同领域的问题，如果具有相似的关系，在范畴论便可以统领(套路)。
- 借助范畴论的各种套路，可以把某个领域的问题转化为其它领域的问题(函子)。
范畴的定义：
函子：
参考香蕉空间
【态射】(Morphism)在数学中是指两个数学结构之间保持结构的一种映射(抽象过程)。
态射的分类
- 单态射，
- 满态射，
- 同构，
- 自同构，
- 自同态
函子
我们将范畴与范畴之间的映射称之为【函子】()。映射是一种特殊的态射，所以函子也是一种态射。我们可以利用范畴和函子构建一种新的范畴。而函子本身也可以看成一种对象，所以函子之间也会存在态射。这种函子之间的态射我们称之为“自然变换”。
- 【马丁·库佩的数学地图】范畴论高高悬挂在天空，提供了整个地图的缩略图。它让我们能够看到在地面看不到的各个领域之间的关系，证明看似不相关的数学领域并不是完全不同。当你想解决某个领域(比如说拓扑)中的问题，但没有合适的工具可以使用时，这就变得非常有用。通过将问题转移到不同领域(比如群论)，就能让你换个角度看问题，说不定还能发现新的工具，让问题变得更容易解决。事实上，范畴论就是这样产生的。它诞生于20世纪40年代，背景是人们试图用更简单的代数方法来解决一个困难的拓扑问题。参考Mathematics: Measuring x laziness²(视频)
- 范畴论的一个主要特点是它剥离了很多细节：它并不具体关心集合中的某个元素，或者某个群是否可解，或者某个拓扑空间是否有可列基。剥离细节的一个好处是，我们的注意力从单个对象上转移开，转向它们之间存在的关系——态射，关系就是一切。
- 一个数学对象完全由它与所有其他对象的关系决定。换句话说，当且仅当两个对象以同样方式与范畴中的每个对象相关时，两个对象本质上是不可区分的。
参考资料：
(1) Category Theory—EuclideanSpace
(2) 范畴论入门视频—Geek学院
(3) 范畴论视频—Maki's Lab
(4) 范畴论：数学的数学 | 众妙之门—返朴 英文原文
(5) 集合论 vs 范畴论 = 汇编语言 vs C++？｜范畴论哲学 I—返朴
(6) 范畴论入门宣讲课—集智学园
交换图
看香蕉
旧笔记
函数的复合(Compositions of functions)可以表示为如下的流程图(flowcharts)
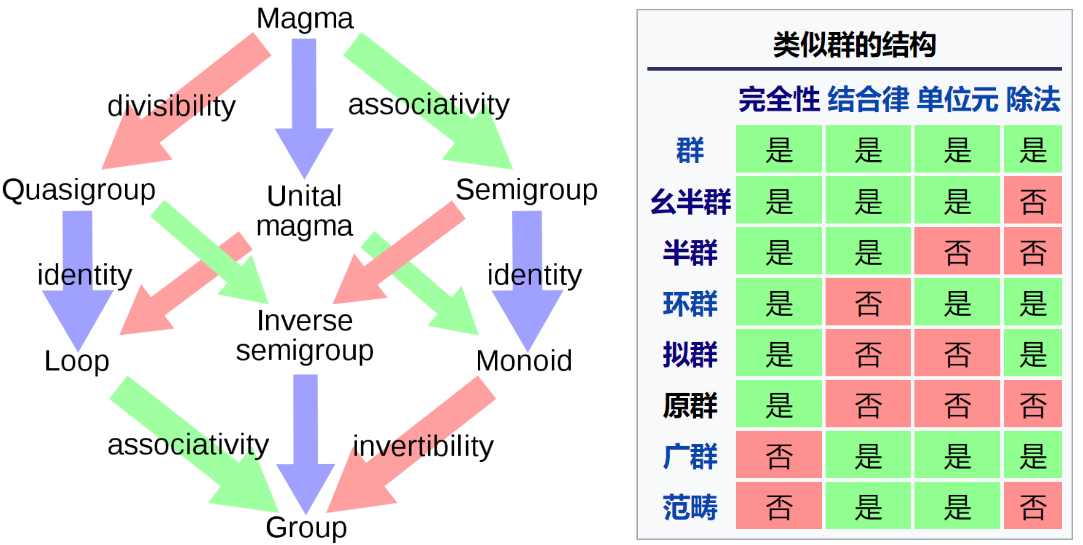
我们可以将一个函数表示为\(f: X \rightarrow Y\)，类似一个黑盒子，丢进去一个东西，吐出来一个东西，丢进去的可以是数、向量、函数等等，吐出来的东西也可以是各种类型的东西，用下面的两个图可以看更容易理解：
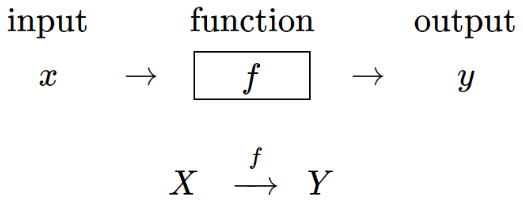
如果对输入值先后作用函数\( f \)和\( g\)，那么这个过程可以有下面四种表示方式：
上面右下侧的两种表示方式，给出了新的函数\(gf\)，completes the diagram。从\(X\)到\(Z\)，两条路线都是殊途同归的，即\(g(f(x))=(g f)(x)\)。
下面再给出其他的几个例子，帮助熟悉交换图：
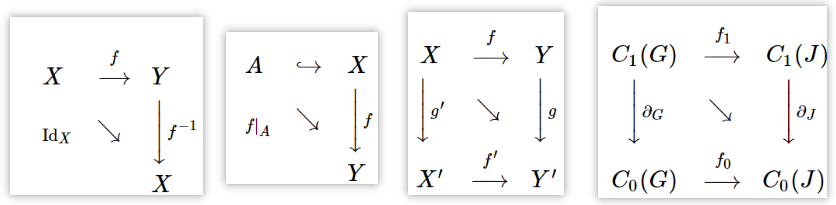
- 用到了函数\(f\)的逆运算\(f^{-1}\)；
- \(A\)是\(X\)的子集\(A \subset X\)，交换图中\( \displaystyle\hookrightarrow\)表示，最常见的子集，比如\(A=\operatorname{ker} f\)；
- square shape的交换图，\(g f=f^{\prime} g^{\prime}\)，也就是说，先垂直往下走，再往右走，等价于先往右走，再往下走，也等价于直积走对角线。Both give you the diagonal function! This identity is the reason why it makes sense to call such a diagram "commutative".感觉在织布！
- Algebraic continuity condition，表示为\(\partial_J f_1(e)=f_0\left(\partial_G e\right)\)。
上面内容，参考Maps of graphs
【线性映射的复合】：A composition of linear maps is represented by the matrix product of the representatives.
比如用矩阵\({\mathrm{H}}\)表示映射\(h: V \rightarrow W\)，用矩阵\(G\)表示\(\mathrm{g}: \mathrm{W} \rightarrow \mathrm{X}\)，对应的基\(\mathrm{B} \subset \mathrm{V}\)，\(\mathrm{C} \subset \mathrm{W}\)，\(\mathrm{D} \subset \mathrm{X}\)，于是可以用下面的交换图表示映射的复合：
上图中的wrt表示with respect to，\(V_{\text {wrt } \mathrm{B}}\)表示将\(V\)空间写成以\( \mathrm{B}\)为基底的形式。或者等价地表示为$$ \vec{v} \stackrel{g \circ h}{\longmapsto} g(h(\vec{v})) \quad \vec{v} \stackrel{h}{\longmapsto} h(\vec{v}) \stackrel{g}{\longmapsto} g(h(\vec{v})) $$注意：映射和基的选取无关，但是表示映射的矩阵和基的选取有关，即描述同一件事可以用不同的表达方式，但是殊途同归。
特别地，如果\(g\)和\( h\)互为逆映射，或者说\(h\)是单射且满射，那么有如下交换图：
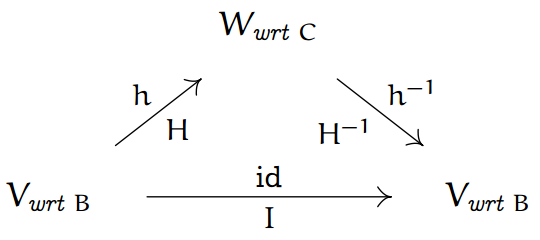
向量的表示变换(Changing Representations of Vectors)：In converting \(\operatorname{Rep}_{\mathrm{B}}(\vec{v})\) to \(\operatorname{Rep}_{\mathrm{D}}(\vec{v})\) the underlying vector \(\vec{v}\) doesn't change. 也就是说我们进行的是【恒等映射】(identity map) on the space，domain space vectors用基\(B\)来表示，codomain space vectors的基用\(D\)来表示。
注：
- 小写字母表示映射，大写字母表示在domain space的基确定的情况下，该映射的矩阵表示；
- \(\operatorname{Rep}_{\mathrm{B}}(\vec{v})\)为向量\(\vec{v}\)在基\(\mathrm{B}\)下的坐标表示，或者说该向量在该基下各基向量方向的投影大小组成的一组数；
- \(\operatorname{Rep}_{\mathrm{B}, \mathrm{D}}(h)\)，即存在一个映射\(h\)，domain space的基为\(\mathrm{B}\)，codomain space的基为\(\mathrm{D}\)，至于两个space是不是同一个space或者说维度上有什么关系，我们并不关心。\(\mathrm{D}\cdot\operatorname{Rep}_{\mathrm{B}, \mathrm{D}}(h)\)表示的codomain space的基(列向量)组成的矩阵\(\mathrm{D}\)乘以\(\operatorname{Rep}_{\mathrm{B}, \mathrm{D}}(h)\)，即为domain space的基通过映射\(h\)作用后得到的codomain space中的向量组(绝对结果，和基无关)，这个可以看作是自然基状态下的表示(更容易理解)，因为映射就是映射，和基的选取无关。