薛定谔方程

分离变量法和stationary state

假设：势函数\(V(x, t)  \)和时间无关，只是位置的函数，在绝大多数量子力学及其应用的理论计算中，势函数都是不随时间变化的。势函数不随时间变化就可以采用分离变量法，得到定态解，定态解就是不含时间指数项的解，因为和时间有关的那一项很容易求解，所以我们要重点求解的是定态解，最后乘以时间有关的指数项就是含时的最终解。

【分离变量法】对于薛定谔方程$$i \hbar \frac{\partial \Psi}{\partial t}=-\frac{\hbar^{2}}{2 m} \frac{\partial^{2} \Psi}{\partial x^{2}}+V \Psi$$将波函数进行改写$$\Psi(x, t)=\psi(x) \varphi(t)$$于是$$\frac{\partial \Psi}{\partial t}=\psi \frac{d \varphi}{d t}, \quad \frac{\partial^{2} \Psi}{\partial x^{2}}=\frac{d^{2} \psi}{d x^{2}} \varphi$$代回到薛定谔方程(偏微分方程变成了微分方程)$$i \hbar \psi \frac{d \varphi}{d t}=-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}} \varphi+V \psi \varphi$$两边同时除以\( \psi \varphi \)得到$$i \hbar \frac{1}{\varphi} \frac{d \varphi}{d t}=-\frac{\hbar^{2}}{2 m} \frac{1}{\psi} \frac{d^{2} \psi}{d x^{2}}+V=E$$等式左边仅仅是时间\(  t\)的函数，而等式右边仅仅是位置\(  x\)的函数，因此等式要在任意时刻任意位置都成立的话，必然有等式两边都等于一个常数\(E  \)。将等式两边乘以\(\psi  \)于是有【定态(time-independent)薛定谔方程】(这里不含虚数项) $$-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}+V \psi=E \psi$$我们只有在给定势函数\(V(x)  \)的情况下才能求解。另一半方程中$$i \hbar \frac{1}{\varphi} \frac{d \varphi}{d t}=E$$上面这个式子是一个非常简单的微分方程，容易求得解函数为\(  C \exp (-i E t / \hbar)\)，这里我们直接将这部分的结果归一化即取\(C=1  \)。那么下一步就是求解\(  \psi(x)\)中，并将其前面的系数也归一化，那么最终得到的\( \Psi(x, t)=\psi(x) \varphi(t) \)一定也是归一化的。$$\varphi(t)=e^{-i E t / \hbar}$$

上面通过分离变量法得到的\( \Psi(x, t)=\psi(x) \varphi(t) \)被称作【stationary state】，对其性质的讨论如下：

• \(\rho(x)\) has no time dependence. (概率分布和时间无关)
• \(\langle\ldots\rangle\) has no time dependence. (期望和时间无关)
• Energy is exactly specified, no uncertainty.
• 其线性组合(薛定谔方程的一般解)不满足上述性质。

(1)   几率密度上的定态性
波函数\(\Psi(x, t)=\psi(x) e^{-i E t / \hbar}\)虽然是时间的函数，但是在任意时刻，波函数的几率密度分布都一样(这里讨论的其实是stationary/eigen state，而不是general state，下面的计算结果也表明\(|\Psi(x, t)|^{2}\)和\(t\)无关)$$|\Psi_n(x, t)|^{2}=\Psi_n^{*} \Psi_n=\psi_n^{*} e^{+i E t / \hbar} \psi_n e^{-i E t / \hbar}=|\psi_n(x)|^{2}$$对于stationary/eigen state的任意【动力学变量】(坐标、动量、动能等等，时间不是动力学变量)的期望值，我们先前写到$$\langle Q(x, p)\rangle=\int \Psi^{*} Q\left(x, \frac{\hbar}{i} \frac{\partial}{\partial x}\right) \Psi d x$$我们用分离变量的方法改写\(\Psi^{*}  \)和\(\Psi  \)，得到和时间无关的公式$$\langle Q(x, p)\rangle=\int \psi^{*} Q\left(x, \frac{\hbar}{i} \frac{d}{d x}\right) \psi d x$$波函数的几率密度分布以及任意动力学变量的期望值(速度、动量、总能量等)都可以写成和时间无关的形式，这也体现着“定态”的特征。似乎我们可以直接将\(\psi(x)  \)表示波函数，但这样做是草率而危险的。关于几率密度的定态性，特别地，当\(\psi(x)=0  \)，那么\(\langle p\rangle=m \displaystyle\frac{d\langle x\rangle}{d t}=0  \)。Nothing ever happens in a stationary state.

(2)    能这样分解的波函数具有确定总能量的状态。对于经典力学来说，哈密顿量$$H(x, p)=\frac{p^{2}}{2 m}+V(x)$$我们先前已经提到\( (\hbar / i)(\partial / \partial x) \)表示动量算符，于是上式可以改写为$$\hat{H}=-\frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}+V(x)$$其中的\(\hat{H}  \)是一个总能量算符，以示和\( H \)的区别。$$\hat{H} \psi_n=E_n \psi_n$$借用此公式，又可以得到能量的期望值$$\langle H\rangle=\int \psi^{*}_n \hat{H} \psi_n d x=E_n \int|\psi_n|^{2} d x=E_n$$(注意：我们前面已经证实了\( |\Psi(x, t)|^{2}=|\psi(x)_n|^{2} \)，所以\(\displaystyle \int|\psi_n|^{2} d x=1  \))

我们把\( \psi_n \)想成特征向量，能量\(E_n  \)想成特征值，那么显然有$$\hat{H}^{2} \psi_n=E^{2}_n \psi_n$$因此其平方的期望$$ \left\langle H^{2}\right\rangle=\int \psi_n^{*} \hat{H}^{2} \psi_n d x=E_n^{2} \int|\psi_n|^{2} d x=E^{2}_n$$那么根据我们前面对于期望的计算方法，可知方差$$\sigma_{H}^{2}=\left\langle H^{2}\right\rangle-\langle H\rangle^{2}=E_n^{2}-E_n^{2}=0  $$所以必然有对于任意时刻而言，波函数的能量都为\(E_n  \)，即在特征状态\(  \psi_n\)下(stationary/eigen state)，不管什么时候去量它，它的能量都是\(  E_n\)。

(3)   数学意义上，一般解是分离变量解的线性叠加。前面的定态薛定谔方程\( \hat{H} \psi=E \psi  \)我们能求出一堆(无限多个)特征向量\( \psi_{1}(x), \psi_{2}(x), \psi_{3}(x), \cdots \)，每一个特征向量对应一个特征值(能量常数)，于是每一个允许能量有不同的波函数：$$\Psi_{1}(x, t)=\psi_{1}(x) e^{-i E_{1} t / \hbar}, \quad \Psi_{2}(x, t)=\psi_{2}(x) e^{-i E_{2} t / \hbar , \cdots}$$对于薛定谔方程(含时的，最原始的那个方程)，满足线性叠加原理，即解的线性组合仍是方程的解。于是对于我们前面研究的定态的情况，一般解可以写成$$\Psi(x, t)=\sum_{n=1}^{\infty} c_{n} \psi_{n}(x) e^{-i E_{n} t / \hbar}$$剩下的问题就是求解满足初始条件\(  \Psi(x, 0)\)的系数向量。

总结：知道\(  V(x)\)(定态)和初始波函数\( \Psi(x, 0) \)；求解任何时刻的波函数\(\Psi(x, t)  \)

方法：
(1)   采用分离变量法，将一个复杂的偏微分方程变成两个简单的微分方程；
(2)   利用\( \hat{H} \psi=E \psi \)求解特征值与特征向量；
(3)   特征向量的线性组合满足初始波函数条件，确定各项系数(取\( t=0 \))$$\Psi(x, 0)=\sum_{n=1}^{\infty} c_{n} \Psi_{n}(x)=\sum_{n=1}^{\infty} c_{n} \psi_{n}(x) e^{-i E_{n} t / \hbar}=\sum_{n=1}^{\infty} c_{n} \psi_{n}(x)$$(4)   每一项乘以时间因子，得到波函数的一般解(general solution)为$$\Psi(x, t)=\sum_{n=1}^{\infty} c_{n} \psi_{n}(x) e^{-i E_{n} t / \hbar}=\sum_{n=1}^{\infty} c_{n} \Psi_{n}(x, t)$$

注：对含时方程，同样有\(\Psi(x, t)=\displaystyle\sum_{n=1}^{\infty} c_{n} \Psi_{n}(x, t)  \)，但是由于\( \Psi_{n}(x, t) \)不能将时间因子分离出来，因此在求解几率密度分布或者期望的时候，时间因子不能相互抵消，所以这些值都依赖于时间而变化，这是与定态方程的区别之处。特征状态(\(  \psi_{n}\))单独来说都是stationary state(位置/动量的的期望都是零，而且粒子在某处出现的几率和时间无关)，但是它们的线性组合(一般解)不是stationary state(粒子在某处出现的几率和时间有关)。

 

波函数形状和连续性讨论

我们讨论的是time-independent的部分\( \psi(x)\)，\(-\displaystyle\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}+V \psi=E \psi\)可以改写为$$ \frac{\partial^{2} \psi}{\partial x^{2}}=\frac{2 m}{\hbar^{2}}(V(x)-E) \psi $$显然\(\psi\)的二阶导数的正负号由\((V(x)-E)\)和\(\psi\)共同决定，下面分两种情况讨论：

• \(V(x)>E\)，那么\(\psi\) curves away from axis.
• \(V(x)<E\)，那么\(\psi\) curves towards from axis.
  

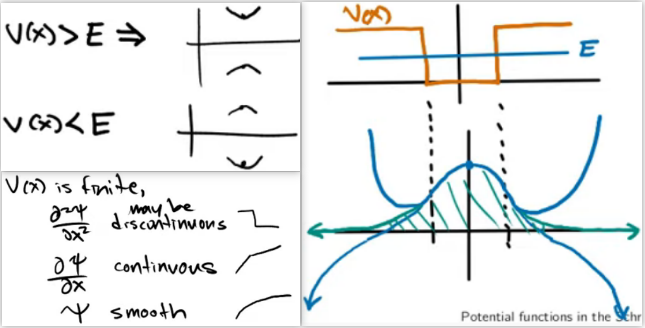
如果\(V(x)\) is finite，那么\(\displaystyle\frac{\partial ^{2}\psi }{\partial x^{2}}\) 可能discontinuous，但是\(\displaystyle\frac{\partial \psi}{\partial x}\) continuous，这意味着\(\psi\) is effectively smooth(也就是没有corner)。

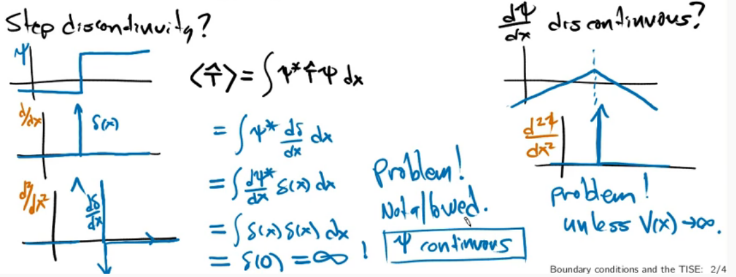
下面讨论allowed behavior of \(\psi\)：
(1) 问题1：是否允许\(\psi\)存在step discontinuity？
如果存在，那么其一阶导数就是\(\delta\)函数，其二阶导数就是\(\delta\)的一阶导数。我们知道波函数的动量对应于\(\psi\)的二阶导数，求动能的期望，得到最终的结果为无穷大，出现probelm！
因此不允许\(\psi\)存在step discontinuity。
(2) 问题2：是否允许\(\displaystyle\frac{d \psi}{d x}\)不连续？
如果一阶导数不连续，那么其二阶导数就会出现\(\delta\)函数，但是 this is not necessarily a problem，因为可以用\(V(x)\)去balance。
因此只有在\(V(x)\)无穷大的时候，才允许\(\displaystyle\frac{d \psi}{d x}\)不连续。

 

一维无限深方势阱

关于这个例子的特点，不多赘述。提一点，当粒子运到到两侧的边界的时候，由于边界势垒无穷大(换句话说，存在无穷大的反向斥力)，所以刚接近边界的时候，就会被“推开”，于是波函数在边界分布的概率为零。这里可以举个例子，化学中的链多烯(从拓扑角度，可以想象成直线)，π电子大共轭，电子可以在整个体系上自由运动(势能为零)，但是电子要想出来，就必须克服很高的能量(这里我们简单设为无穷大)。

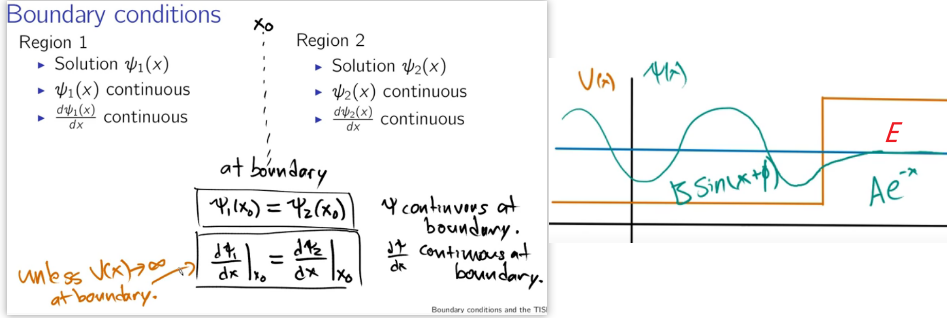
特征向量和特征值方程为(在势阱内部\(V =0\))$$-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}=E \psi$$如果取\(k \equiv \displaystyle\frac{\sqrt{2 m E}}{\hbar}  \)，方程可以简化为$$\frac{d^{2} \psi}{d x^{2}}=-k^{2} \psi$$这就是经典的弹簧振荡(简谐子)方程，根据我在MIT微分方程课程中学习的内容，可以得到方程的解为$$\psi(x)=A \sin k x+B \cos k x$$当然我们也可以写成复指数的形式，这里不赘述。根据连续性和边界条件要求有$$\psi(0)=\psi(a)=0$$

注：从哈密顿算符或者动量算符的角度考虑，\(\psi(x)\)必须是continuous，否则不连续的地方would do very strange things to any sort of operator that you could think of，以动量算符\(\displaystyle\frac{\hbar}{i} \frac{\partial}{\partial x}\)为例，在不连续点该动量算符对应的偏导数会直接爆掉(blow up)，不符合条件。

(1)   由\(  \psi(0)=A \sin 0+B \cos 0=B\)推出\( B=0 \)，即\( \psi(x)=A \sin k x \)；
(2)   根据\(\psi(a)=A \sin k a=0  \)，有一下两种情形:
(2-a)   \( A=0 \)，那么\( \psi(x)=0 \)，每点波函数均为零，不可归一化，没意义
(2-b)   \( \sin k a=0 \)，即\(k a=0, \pm \pi, \pm 2 \pi, \pm 3 \pi, \cdots  \)，如果\(ka  \)取零，同样成了(a)中的情况，没意义，不考虑；由于正弦函数是奇函数，所以\( ka \)等于负数的情况等价于将系数\( A \)取负号，所以只需要考虑(不限定\(  A\)正负)$$k_{n}=\frac{n \pi}{a}, \quad n=1,2,3, \dots$$所以我们得到了分立的所有可能的能量值(边界条件决定了quantize的状态)$$E_{n}=\frac{\hbar^{2} k_{n}^{2}}{2 m}=\frac{n^{2} \pi^{2} \hbar^{2}}{2 m a^{2}}$$下图可以看成是一系列“驻波”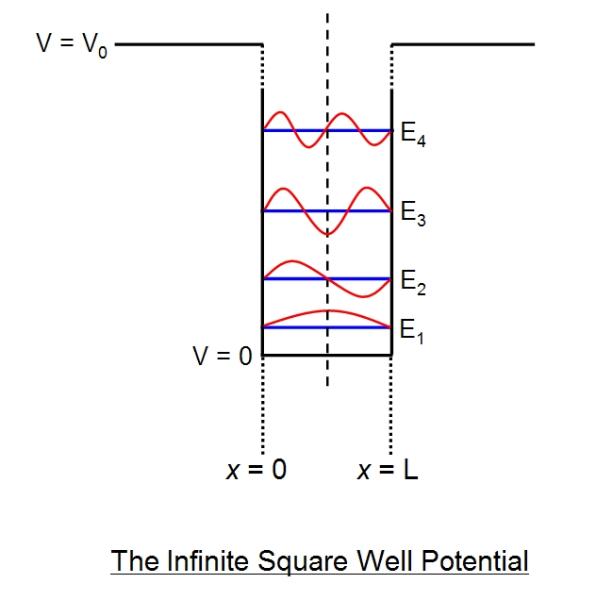归一化\(  \psi\)，有$$\int_{0}^{a}|A|^{2} \sin ^{2}(k x) d x=|A|^{2} \frac{a}{2}=1$$取正根(按道理应该可以取负值，对应前面的\(  k a\)为负数的情况)，得到\(  A=\sqrt{2 / a}\)，因此体系的解为$$\psi_{n}(x)=\sqrt{\frac{2}{a}} \sin \left(\frac{n \pi}{a} x\right)$$ \(\psi_{1}  \)具有最低的能量，称为“基态”，其他态为“激发态”，能量正比于\( n^{2} \)，即\( 1:4:9:16 :25\cdots\cdots \)。

\(\psi_{n}(x)  \)的特点：
(1)   从中垂线看，函数是奇函数和偶函数交替;
(2)   不考虑边界，驻波波节(node)的个数分别是\( 0,\,1,\,2,\,3,\,4 \cdots \cdots \);
(3)   任意两个不同的波函数相互正交 (orthogonal)$$\int \psi_{m}^{*}(x) \psi_{n}(x) d x=\delta_{m n}$$

证明\(\psi_{n}(x)  \)的特点(3):
首先我们回顾一下定积分的变量代换，对于定积分\(\displaystyle\int _{ b}^{ a }{ f(x)dx }   \)，如果\(  x=\varphi(t)\)，那么原来的定积分可以改写为\( \displaystyle\int_{\alpha}^{\beta} f(\varphi(t)) \varphi^{\prime}(t) d t \)。那么对于我们两个不同的波函数解(不考虑时间项)的乘积在\( 0 \)到\( a \)内的积分为$$\int \psi_{\mathrm{m}}^{*}(x) \psi_{\mathrm{n}}(x) d x=\frac{2}{a} \int_{0}^{a} \sin \left(\frac{m \pi}{a} x\right) \sin \left(\frac{\mathrm{n} \pi}{a} x\right) d x$$注意，实数的共轭就是其本身，所以取星号没有影响。我们在傅里叶变换及其应用中知道，对于周期为\(2\pi  \)的函数来说，从\(-\pi  \)到\( \pi \)内，\(\sin m x  \)和\(\sin n x  \)是相互正交的，但是不带相位的两个正弦函数的乘积必是偶函数，所以必有在\(0 \)到\( \pi \)内也是正交的。对我们这里来说，用\(x=\displaystyle\frac { at }{ \pi } \)代入\(  \displaystyle\int_{0}^{a} \sin \left(\frac{m \pi}{a} x\right) \sin \left(\frac{\mathrm{n} \pi}{a} x\right) d x\)中就可以证实两个函数解的正交性。当然也可以通过积化和差的方式求解积分值，但是我们这里通过将其与傅里叶级数联系起来，说明其正交性。

(4)   解组合是完备的 (complete basis)
对于任意一个两端为\(0  \)和\(a  \)的驻波函数\(f(x)  \)，我们都可以表示为上面解函数的线性叠加。在我们这里$$f(x)=\psi_(x)=\sum_{n=1}^{\infty} c_{n} \psi_{n}(x)=\sqrt{\frac{2}{a}} \sum_{n=1}^{\infty} c_{n} \sin \left(\frac{n \pi}{a} x\right)$$其实就是傅里叶展开，然后由于驻波的特殊性，只保留正弦项。

一维无线深方势阱的定态为$$\Psi_{n}(x, t)=\sqrt{\frac{2}{a}} \sin \left(\frac{\mathrm{n} \pi}{a} x\right) e^{-i\left(n^{2} \pi^{2} \hbar / 2 m a^{2}\right) t}$$含时薛定谔方程的一般解是定态解的线性叠加$$\Psi(x, t)=\sum_{n=1}^{\infty} c_{n} \sqrt{\frac{2}{a}} \sin \left(\frac{n \pi}{a} x\right) e^{-i\left(n^{2} \pi^{2} \hbar / 2 m a^{2}\right) t}$$

【傅立叶技巧】（Fourier's trick）$$c_{n}=\int \psi_{\mathrm{n}}^{*}({x}) \psi_(x)d x$$根据初始波函数有$$\Psi(x, 0)=\psi_(x)=\sum_{n=1}^{\infty} c_{n} \psi_{n}(x)$$傅里叶技巧的系数推导$$\int \psi_{n}^{*}(x) \psi_(x)d x =\int \psi_{n}^{*}(x)\sum_{m=1}^{\infty} c_{m} \psi_{m}(x)d x=\sum_{m=1}^{\infty}c_n\delta_{mn}=c_m=c_n$$于是系数$$c_{n}=\sqrt{\frac{2}{a}} \int_{0}^{a} \sin \left(\frac{n \pi}{a} x\right) \Psi(x, 0) d x$$我们现在讲述的是一维无线深势阱的情况，如果是其他的势函数类型，而且已知初始的\( \Psi(x, 0) \)，我们均能通过相同的方法求解出波函数\(  \Psi(x, t)\)。

线性代数思考：将向量的第三个元素摘出来$$\left[\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{array}\right]^{T} \times\left[\begin{array}{c} 34 \\ 57 \\ 65 \\ 85 \\ 78 \\ 79 \end{array}\right]$$将\(  1\)换成正弦函数，就成了所谓的“基”，只是函数\(f(x) \)每一个基是无限长的(每一个向量内包含无限个元素，分别对应不同的正弦基函数)。

傅里叶级数的指数回顾：对于周期为\( 2\pi\)的函数\( f(t)\)有$$f(t)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos (n \omega t)+b_{n} \sin (n \omega t)\right]$$其中$$\begin{aligned} &a_{n}=\frac{2}{T} \int_{t_{0}}^{t_{0}+T} f(t) \cos (n \omega t) d t \\ &b_{n}=\frac{2}{T} \int_{t_{0}}^{t_{0}+T} f(t) \sin (n \omega t) d t \end{aligned}$$

\(|c_{n}|^{2}  \)的含义
\(|c_{n}|^{2}  \)告诉你的是对能量的一个测量得到的结果是对应的\(E_{n}  \)的几率。所有的几率只和为\(  1\)，即$$\sum_{n=1}^{\infty}|c_{n}|^{2}=1$$ 证明：(只简单说一下\(t=0\)的情况，即\(\Psi(x, 0)  \)) $$\begin{aligned} 1 &=\int|\Psi(x, 0)|^{2} d x=\int\left(\sum_{m=1}^{\infty} c_{m} \psi_{m}(x)\right)^{*}\left(\sum_{n=1}^{\infty} c_{n} \psi_{n}(x)\right) d x \\ &=\sum_{m=1}^{\infty} \sum_{n=1}^{\infty} c_{m}^{*} c_{n} \int \psi_{m}^{*}(x) \psi_{n}(x) d x \\ &=\sum_{m=1}^{\infty} \sum_{n=1}^{\infty} c_{m}^{*} c_{n} \delta_{m n}=\sum_{n=1}^{\infty}\left|c_{n}\right|^{2} \end{aligned}$$系统总的能量的期望值$$\langle H\rangle=\sum_{n=1}^{\infty}\left|c_{n}\right|^{2} E_{n}$$证明(用\( t=0 \)的特例证明)：$$\begin{array}{c} \langle H\rangle=\displaystyle\int \psi^{*} H \psi d x=\displaystyle\int\left(\sum c_{m} \psi_{m}\right)^{*} H\left(\sum c_{n} \psi_{n}\right) d x \\ =\displaystyle\sum \sum c_{m}^{*} c_{n} E_{n} \displaystyle\int \psi_{m}^{*} \psi_{n} d x=\sum\left|c_{n}\right|^{2} E_{n} \end{array}$$注意得到的每个特征能量对应的几率是不依赖时间的，这样一来， \( H \)的期望值也是不依赖时间的。这就是能量守恒在量子力学中的体现。\( c_{n} \)越大(更准确地说是\( \left|c_{n}\right|^{2} \)越大)，那么越像那个state，就越待在那个state。\( \left|c_{n}\right|^{2} \)表出现在\( E_{n} \)能量状态的概率。

例题：在一维无线深方势阱中运动的粒子，其初始状态波函数是$$\Psi(x, 0)=A x(a-x), \quad(0 \leq x \leq a)$$其中\(A  \)为常数，当然在阱外\(  \Psi=0\)。求\(\Psi(x, t)  \)。
解：首先归一化出是波函数，求解系数\(A  \)$$1=\int_{0}^{a}|\Psi(x, 0)|^{2} d x=|A|^{2} \int_{0}^{a} x^{2}(a-x)^{2} d x=|A|^{2} \frac{a^{5}}{30}$$所以$$A=\sqrt{\frac{30}{a^{5}}}$$把各项系数用傅里叶技巧摘出来$$c_{n}=\sqrt{\frac{2}{a}} \int_{0}^{a} \sin \left(\frac{n \pi}{a} \mathrm{x}\right) \sqrt{\frac{30}{a^{5}}} x(a-x) d x==\left\{\begin{array}{l} 0, \quad even \\ 8 \sqrt{15} /(n \pi)^{3}\quad odd \end{array}\right.$$因此$$\Psi(x, t)=\sqrt{\frac{30}{a}}\left(\frac{2}{\pi}\right)^{3} \sum_{n=1,3,5, \ldots } \frac{1}{n^3} \sin \left(\frac{n \pi}{a} x\right) e^{-i n^{2} \pi^{2} \hbar t / 2 m a^{2}}$$思考：\( n=\text{even} \)对应其实是奇函数(相对于中间轴\(\displaystyle\frac {a  }{  2}   \))，而初始波函数是偶函数，所以\( n=\text{even} \)的分量为零；另外由于本身\( n=1 \)的波函数和初始条件就很像，但是不是完全一致的，这种差异性需要不断用其\(n=\text{odd} \)的波函数去修正，我们可以进行一个频谱分析，\( n=1 \)的分量占比是非常大的，也就是说其他修正项(激发态项)的比例很低很低，从\(c_{n}  \)结果知呈现三次方反比的衰减。

顺便，我们也得到了$$\sum_{n=1}^{\infty}\left|c_{n}\right|^{2}=\left(\frac{8 \sqrt{15}}{\pi^{3}}\right)^{2} \sum_{n=1,3,5, \ldots}^{\infty} \frac{1}{n^{6}}=1$$即有级数$$\frac{1}{1^{6}}+\frac{1}{3^{6}}+\frac{1}{5^{6}}+\cdots=\frac{\pi^{6}}{960}$$

 

谐振子-阶梯算符法

这里给出的是利用ladder operator的方法来求解，另外也可以用power series来求解，可以参考Brant Carlson油管视频，这里不详述。

弹簧振子模型

$$F=-k x=m  \frac{d^{2} x}{d t^{2}}$$在忽略摩擦力(阻尼)的情况下，它的解为$$x(t)=A \sin (\omega t)+B \cos (\omega t)$$其中\( \omega \equiv \sqrt{\displaystyle \frac{k}{m}} \)，而两个系数\( A \)和\( B \)需要根据初始条件(物体的初始位置和速度)来确定。

任何势能在其极小值(平衡点\(x_{0}  \)，一阶导数为零)附近二阶展开，一阶导数项为零，同时我们将\(x_{0}  \)点作为基准，于是极小值点邻近区域的是能变化为\(  \displaystyle\frac{1}{2} V^{\prime \prime}\left(x_{0}\right)\left(x-x_{0}\right)^{2}\)，其中有效弹性常数\(k=V^{\prime \prime}\left(x_{0}\right)  \)，忽略【非简谐效应】的项(比如固体热胀冷缩的非简谐项很小)。如果离平衡点很远了，那么就必须考虑非简谐项，类似晶体加热加热，突然融化了。

量子力学的问题是要解势能为$$V(x)=\frac{1}{2} m\omega^{2} x^{2}$$时的薛定谔方程。无限远的地方势能是无限大(类似无线深势阱)，所以粒子不会跑到无限远处。

弹簧常数与分子振动光谱：分子振动是指分子内原子间进行的周期性来回运动，而不包含分子的移动和转动。这种周期性的运动频率称为振动频率。在光谱学上常用红外吸收光谱法与拉曼光谱学来测量分子的振动频率，并用来分析分子结构。不同分子键的“弹簧常数”不一样，通过测量弹簧常数，判定分子种类。

构建阶梯算符

对于定态方程$$-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}+V \psi=E \psi$$将\(V(x)=\displaystyle\frac{1}{2} m\omega^{2} x^{2}  \)代入，另外代入动量算符\(p=(\hbar / i)(d / d x) \)得到$$\frac{1}{2 m}\left[p^{2}+(m \omega x)^{2}\right] \psi=E \psi$$对于哈密顿算符有\(\hat{H}=\displaystyle\frac{1}{2 m}\left(\hat{p}^{2}+(m \omega \hat{x})^{2}\right)\)是两个平方项的加和，我们可以联想到因式分解，即两个共轭的复数相乘得到的是两个数平方的加和，但是这里有算符运算，两个算符不互易，因此我们可以将哈密顿量写成两个算符的乘积，然后再添加一个是由于算符不对易造成的附加项即可。

定义\(  a_{\pm}\)为“阶梯算符”，\( a_{+} \)是升阶算符，\( a_{-} \)是降阶算符。$$a_{\pm} \equiv \frac{1}{\sqrt{2 \hbar m \omega}}(\mp i p+m \omega x)$$这是一种特殊的解法，只是针对谐振子的情况，下面的这种定义方法将会使我们引出新的物理量更容易，那么$$\begin{aligned} a_{-} a_{+} &=\frac{1}{2 \hbar m \omega}(i p+m \omega x)(-i p+m \omega x) \\ &=\frac{1}{2 \hbar m \omega}\left[p^{2}+(m \omega x)^{2}-i m \omega(x p-p x)\right] \end{aligned}$$式子中包含\(  x\)和\( p \)的对易子\((x p-p x)  \)，两个算符交换次序结果往往会发生变化。算符\( A \)和\( B \)的【对易子】(commutator)表示为$$[A, B]=A B-B A$$代入有$$a_{-} a_{+}=\frac{1}{2 \hbar m \omega}\left[p^{2}+(m \omega x)^{2}\right]-\frac{i}{2 \hbar}[x, p]$$

用上面的对易子\([x, p]\)(本质是算符)作用在(任意)测试函数\(  f(x)\)上，看看效果$$[x, p] f(x)=\left[x \frac{\hbar}{i} \frac{d}{d x}(f)-\frac{\hbar}{i} \frac{d}{d x}(x f)\right]=\frac{\hbar}{i}\left(x \frac{d f}{d x}-x \frac{d f}{d x}-f\right)=i \hbar f(x)$$去掉测试函数有正则对易关系$$[x, p]=i \hbar$$

注意：
(1) 两个算符交换顺序，两个复数分别对应两个算符，调换顺序分别做内积，那么就得到两个互为共轭的复数。
(2) 对易子和【泊松括号】：在数学及经典力学中，泊松括号是哈密顿力学中重要的运算，在哈密顿表述的动力系统中时间演化的定义起着中心角色。在正则坐标\((q_{i}, p_{j})\)表示中，相空间内两个函数\(f(\mathbf{q}, \mathbf{p}), g(\mathbf{q}, \mathbf{p})\)的泊松括号具有如下形式：$$\{f, g\}=\sum_{i=1}^{N}\left[\frac{\partial f}{\partial q_{i}} \frac{\partial g}{\partial p_{i}}-\frac{\partial f}{\partial p_{i}} \frac{\partial g}{\partial q_{i}}\right]$$(3) \(\hbar\)的量纲其实就是角动量的量纲，\(p\)的量纲就是动量的量纲，根据普通物理中的\(\mathbf{L}=\mathbf{r} \times \mathbf{p}\)，显然动量量纲乘以一个长度量纲即得到角动量的量纲。
(4) 阶梯算符的量纲是没有任何单位的。

于是前面的关于\( a_{-} a_{+} \)的式子可以写为$$a_{-} a_{+}=\frac{1}{\hbar \omega} H+\frac{1}{2}$$其中哈密顿算符$$H=\frac{1}{2 m}\left[p^{2}+(m \omega x)^{2}\right]$$同样地，我们可以将哈密顿算符改写为$$H=\hbar \omega\left(a_{-} a_{+}-\frac{1}{2}\right)$$用同样的方法可以得到$$H=\hbar \omega\left(a_{+} a_{-}+\frac{1}{2}\right)$$利用\(a_{\pm}  \)，谐振子薛定谔方程可以写为$$\hbar \omega\left(a_{\pm} a_{\mp} \pm \frac{1}{2}\right) \psi=E \psi$$

证明能量阶梯：如果\(H \psi=E \psi \)，那么\(H\left(a_{+} \psi\right)=(E+\hbar \omega)\left(a_{+} \psi\right)  \)

上面的证明用线性代数的说法是，如果薛定谔方程\(H \psi=E \psi  \)成立，即有特征值\(  E\)和对应的特征向量\( \psi   \)，那么\((E+\hbar \omega)  \)也是该方程的特征值，且对应的特征向量为\(  \left(a_{+} \psi\right)\)。证明方法如下：$$\begin{aligned} H\left(a_{+} \psi\right) &=\hbar \omega\left(a_{+} a_{-}+\frac{1}{2}\right)\left(a_{+} \psi\right)=\hbar \omega\left(a_{+} a_{-} a_{+}+\frac{1}{2} a_{+}\right) \psi \\ &=\hbar \omega a_{+}\left(a_{-} a_{+}+\frac{1}{2}\right) \psi=a_{+}\left[\hbar \omega\left(a_{+} a_{-}+1+\frac{1}{2}\right) \psi\right] \\ &=a_{+}(H+\hbar \omega) \psi=a_{+}(E+\hbar \omega) \psi=(E+\hbar \omega)\left(a_{+} \psi\right) \end{aligned}$$上面的第二行我们用了\( \left[a_{-}, a_{+}\right]=1 \)关系。同样的方法我们也可以证明$$H\left(a_{-} \psi\right)=(E-\hbar \omega)\left(a_{-} \psi\right)$$

下面讨论两个问题：
(1) 由一个满足归一化条件的解\(\psi  \)推导出下一个阶梯解\( a_{-} \psi \)，那么\( a_{-} \psi \)是否满足归一化条件呢？
(2) 不断进行升阶计算，当然所有的能量状态都是满足要求的，但是如果不断向下进行阶梯运算，如果不加以限制，必然存在能量\(  E\)或者说特征值为负数的情况，这是没有物理意义的，不符合条件。所以，必然有一个能量下限值。

第一个问题，每一个新得到的\( \psi \)，其表达式前面必然有一个系数\( A_{n} \)，通过归一化操作，即\(  1=\displaystyle \int_{-\infty}^{+\infty} \psi^{*}\psi d x \)确定系数。类比线性代数，如果我们知道了一个矩阵的特征向量\( \mathbf{x} \)，那么\(  n\)倍的\( \mathbf{x} \)，即\( n\mathbf{x} \)必然也是特征向量，但是这里的波函数是有归一化的限定条件的，所以我们这里的\(  n\)值必然是唯一的，不能随便取的。

第二个问题，如果\(  \psi_{0}\)是最下面的一级梯子，那么如果再往下\( a_{-} \psi_{0}=0 \)，也就是说直接到地面了，继续再用\(  a_{-} \)作用，那么还是地面。类比线性代数的投影矩阵\( P \)，用\( P \)作用\(  \psi_{0}\)，那么向量就被投影到特定的平面上了，如果继续作用的话，也就是\(  P^{2}\psi_{0}\)，得到的结果不变(在我们的情况中是继续为零)。

最低阶梯子\( \psi_{0}(x) \)及对应能量\( E_{0} \)

由前面提到的\(a_{-} \psi_{0}=0  \)(降阶到了地面)，有$$\frac{1}{\sqrt{2 \hbar m \omega}}\left(\hbar \frac{d}{d x}+m \omega x\right) \psi_{0}=0$$等式左边括号外的常数项不可能为零，所以只可能有$$\frac{d \psi_{0}}{d x}=-\frac{m \omega}{\hbar} x \psi_{0}$$很容易解得$$\psi_{0}(x)=A e^{-\frac{m \omega}{2 \hbar} x^{2}}$$现在进行归一化操作确定常数项$$1=|A|^{2} \int_{-\infty}^{\infty} e^{-m \omega x^{2} / \hbar} d x=|A|^{2} \sqrt{\frac{\pi \hbar}{m \omega}}$$ \(A  \)取正值得到最终的解函数为(高斯函数)$$\psi_{0}(x)=\left(\frac{m \omega}{\pi \hbar}\right)^{1 / 4} e^{-\frac{m \omega}{2 \hbar} x^{2}}$$利用\( a_{-} \psi_{0}=0 \)代入\( \hbar \omega\left(a_{+} a_{-}+1 / 2\right) \psi_{0}=E_{0} \psi_{0} \)很容易得到基态的能量为$$E_{0}=\frac{1}{2} \hbar \omega$$

推广：每一阶梯子的表达式和对应能量
(The classical limits of the oscillator’s motion are indicated by vertical lines, corresponding to the classical turning points at \( x=\pm A \) of a classical particle with the same energy as the energy of a quantum oscillator in the state indicated in the figure.  波函数的纵坐标是标度不同\( n\)的取值对应的唯一系统总能量\( E\)，多色曲线的波动是为了描述波的形状，而不是同一曲线不同的能量取值。借助升阶算符，我们可以得到本征态和本征值的表达式$$\psi_{n}(x)=A_{n}\left(a_{+}\right)^{n} \psi_{0}(x), \quad E_{n}=\left(n+\frac{1}{2}\right) \hbar \omega$$其中的\(  A_{n}\)为归一化参数，利用归一化的特性可以确定其数值。

类比线性代数

归一化常数\(  A_{n}\)

两种方法，一是“笨办法”，求出非常数项，然后按照归一化条件计算，确定\( A_{n}  \)。
方法二：
在讲述这个方法之前，我们先回忆一下线性代数的一个知识点$$(ABC)^{-1}=C^{-1}B^{-1}A^{-1},\quad (ABC)^{\mathrm{T}}=C^{\mathrm{T}}B^{\mathrm{T}}A^{\mathrm{T}}$$根据前面的结论，我们知道对于任意归一化后的\( \psi_{n-1}、\psi_{n}、\psi_{n+1}\)有$$a_{+} \psi_{n}=c_{n} \psi_{n+1}, \quad a_{-} \psi_{n}=d_{n} \psi_{n-1}$$下面我们引出一个结论：对于任意可积函数\(  f(x)\)和\(  g(x)\)有$$\int_{-\infty}^{\infty} f^{*}\left(a_{\pm} g\right) d x=\int_{-\infty}^{\infty}\left(a_{\mp} f\right)^{*} g d x$$证明：$$\int_{-\infty}^{\infty} f^{*}\left(a_{\pm} g\right) d x=\frac{1}{\sqrt{2 \hbar m \omega}} \int_{-\infty}^{\infty} f^{*}\left(\mp \hbar \frac{d}{d x}+m \omega x\right) g d x$$分部积分使\( \int f^{*}(d g / d x) d x \)变为\( -\int(d f / d x)^{*} g d x \)所以$$\int_{-\infty}^{\infty} f^{*}\left(a_{\pm} g\right) d x=\frac{1}{\sqrt{2 \hbar m \omega}} \int_{-\infty}^{\infty}\left[\left(\pm \hbar \frac{d}{d x}+m \omega x\right) f\right]^{*} g d x=\int_{-\infty}^{\infty}\left(a_{\mp} f\right)^{*} g d x$$注意：平方可积函数，的boundary term的一定是零。

前面我们知道\( \hbar \omega\left(a_{\pm} a_{\mp} \pm \displaystyle\frac{1}{2}\right) \psi_{n}=E _{n}\psi_{n} \)，而\(E_{n}=\left(n+\displaystyle\frac{1}{2}\right) \hbar \omega  \)，所以$$\begin{array}{c} a_{+} a_{-} \psi_{n}=n \psi_{n} \\ a_{-} a_{+} \psi_{n}=(n+1) \psi_{n} \end{array}$$我们有时吧\(  a_{+} a_{-} \)称为【number operator】\(  \hat{n}\)，作用在哪个\(  \psi_{n}\)上面，就立马可以知道\(  \psi_{n}\)对应的\(n \)是多少。所以：$$\begin{array}{l} \displaystyle\int_{-\infty}^{\infty}\left(a_{+} \psi_{n}\right)^{*}\left(a_{+} \psi_{n}\right) d x=\left|c_{n}\right|^{2} \displaystyle\int_{-\infty}^{\infty}\left|\psi_{n+1}\right|^{2} d x=(n+1) \displaystyle\int_{-\infty}^{\infty}\left|\psi_{n}\right|^{2} d x \\ \displaystyle\int_{-\infty}^{\infty}\left(a_{-} \psi_{n}\right)^{*}\left(a_{-} \psi_{n}\right) d x=\left|d_{n}\right|^{2} \displaystyle\int_{-\infty}^{\infty}\left|\psi_{n-1}\right|^{2} d x=n \displaystyle\int_{-\infty}^{\infty}\left|\psi_{n}\right|^{2} d x \end{array}$$我们前面已经提到这里的\( \psi \)都是归一化了的，所以必有$$\left|c_{n}\right|^{2}=n+1, \quad\left|d_{n}\right|^{2}=n$$因此$$a_{+} \psi_{n}=\sqrt{n+1} \psi_{n+1}, \quad a_{-} \psi_{n}=\sqrt{n} \psi_{n-1}$$显然有$$\psi_{n}=\frac{1}{\sqrt{n !}}\left(a_{+}\right)^{n} \psi_{0}$$即对\( \psi_{n}(x)=A_{n}\left(a_{+}\right)^{n} \psi_{0}(x) \)来说，归一化因子：\(A_{n}=1 / \sqrt{n !}  \)。所以整个的解我们重新写为$$\left\{\begin{array}{l} \psi_{n}(x)=\displaystyle\frac{1}{\sqrt{n !}}\left(a_{+}\right)^{n} \psi_{0}(x) \\ E_{n}=\left(n+\displaystyle\frac{1}{2}\right) \hbar \omega \end{array}\right.$$

\( a_{+} \)和\(  a_{-}\)来计算物理量的期望值(先前用的是积分法)

前置知识：正交性证明\(\displaystyle\int \psi_{m}^{*}(x) \psi_{n}(x) d x=\delta_{m n}  ==\left\{\begin{array}{ll} 0, & \text { 如果 } m \neq n \\ 1, & \text { 如果 } m=n \end{array}\right.\)(正交性)

因为前面\( m=n \)的情况，已经归一化过了，必然满足条件，所以下面只说一下\(  m \neq n\)的情况。$$\begin{aligned} \int_{-\infty}^{\infty} \psi_{m}^{*}\left(a_{+} a_{-}\right) \psi_{n} d x &=n \int_{-\infty}^{\infty} \psi_{m}^{*} \psi_{n} d x \\ &=\int_{-\infty}^{\infty}\left(a_{-} \psi_{m}\right)^{*}\left(a_{-} \psi_{n}\right) d x=\int_{-\infty}^{\infty}\left(a_{+} a_{-} \psi_{m}\right)^{*} \psi_{n} d x \\ &=m \int_{-\infty}^{\infty} \psi_{m}^{*} \psi_{n} d x \end{aligned}$$即\((m-n) \displaystyle\int_{-\infty}^{\infty} \psi_{m}^{*} \psi_{n} d x=0\)，因此除非\(m=n  \)，否则\( \displaystyle\int_{-\infty}^{\infty} \psi_{m}^{*} \psi_{n} d x \)必须为零。

\(\delta_{m n}  \)是【克罗内克\(\delta  \)函数】，不是狄拉克\(\delta  \)函数，是对应于狄拉克\(\delta  \)函数的离散函数。

(1)  证明：\(  \langle x\rangle=0\)  (从波函数的对称性也能看出来)
从升阶和降阶算符的表达式可以推出\(x=\sqrt{\displaystyle\frac{\hbar}{2 m \omega}}\left(a_{+}+a_{-}\right)  \)，于是第\(  n\)个state位置的期望值为：$$\langle x\rangle=\int_{-\infty}^{+ \infty} \psi_{n}^{*}\left(\sqrt{\frac{\hbar}{2 m w}}\left(a_{+}+a_{-}\right)\right) \psi_{n} d x$$分析一下：\( a_{+} \)作用在\(\psi_{n}  \)上，相当于提出一个常系数得到\(\psi_{n+1}  \)，同样地，\( a_{-} \)作用在\(\psi_{n}  \)上，相当于提出一个常系数得到\(\psi_{n-1}  \)，根据前面正交性的证明，我们知道必然这两项积分都等于零，即\(\langle x\rangle=0\)
(2)  证明：\(  \langle x^2\rangle=\displaystyle\frac{\hbar}{2 m \omega }(2 n+1)\)
首先注意\(x  \)是一个位置的operator，不是数，因此要乖乖展开，即有$$x^{2}=\frac{\hbar}{2 m w}\left(a_{+}+a_{-}\right)\left(a_{+}+a_{-}\right)=\frac{\hbar}{2 h w}\left(a_{+}^{2}+a_{+} a_{-}+a_{-} a_{+}+a_{-}^{2})\right.$$所以$$\left\langle x^{2}\right\rangle=\frac{\hbar}{2 m w} \int_{-\infty}^{+\infty} \psi_{n}^{*}\left(a_{+}^{2}+a_{+} a_{-}+a_{-} a_{+}+a_{-}^{2}\right) \psi_{n} d x$$很容易知道里面的平方项都等于零，因为改变了梯子的阶数，也就是改变了\(  n\)，根据正交性就为零。非平方项，根据\(  a_{+} \psi_{n}=\sqrt{n+1} \psi_{n+1}, \quad a_{-} \psi_{n}=\sqrt{n} \psi_{n-1}\)很容易化简得到要证明的结论。
(3) 证明：\( \langle V\rangle=\displaystyle\frac{1}{2} E_{n} \)
$$\langle V\rangle=\left\langle\frac{1}{2} m \omega ^{2} x^{2}\right\rangle=\frac{1}{2} m \omega ^{2}\langle x^{2}\rangle=\frac{1}{2} m \omega ^{2}\frac{\hbar}{2 m \omega }(2 n+1)=\frac{1}{2} E_{n}$$即时间平均上，总能量\(E_n  \)(任意eigen state的总能量/特征值)的一半就是势能，显然另一半是动能。这就是古典学的，简谐运动，势能平均值(时间上)是动能的一半。

 

总结

(1)  量子效应什么时候明显：

• 对于一维无线深势阱来说(上左图)，要想区分出不同的能量状态，那么必须\(m  \)和\(a  \)都很小很小，但是实际上不可能那么小，也就是说相邻能量状态之间的能量差异非常非常小，已经小于我们的测试或者仪器能够分辨的最小极限，也就是说，从经典的角度来看，这些能量都是连续的。另外图中下面的线段是经典的能量最低点，而\( E_{1} \)这个线段表示的是量子力学角度的能量最低点；室温下，由于热的关系(\(kT\)大约26 meV，远红外区)，无法区分这两个状态。
• 对谐振子来说(上右图)，要想能级之间的差距变大，必须让\( \omega  \)很大，而\(  w=\sqrt{\displaystyle\frac{k}{m}}\)，所以必须很大的“弹簧常数”(键力常数)，很小很小的质量，所以只能是原子分子尺度上能有比较大的能级差。要想排除室温热扰动的影响，那么\( \omega  \)必须在\( 10^{16} \)数量级，宏观上的物体不可能有这么高的振动频率。分子键是可以看到的，分子质量很小，振动频率很高，所以可以观测到。

(2)  形象理解“谐振子”的quantization

• 这里的\( A \)必须是特定的分立值，而不能是随意连续值；
• 在\( A \)点放手，物体有几率(虽然几率很小很小)跑到\( A \)点右侧的位置，这个时候，动能就是“负值”(对微观粒子来说，它在运动中有可能进入势能大于其总能量的区域，这在经典理论看来是不可能的)，类似“隧穿效应”；
  注：这里动能为"负值"是经典的思维，实际上这种情况是不确定性关系(测不准原理)导致的。位置和动量不可能同时具有确定的值，而位置直接决定了势能大小，动量决定了动能大小，于是势能和动能不可能同时具有具体的确定值，这个时候我们说粒子的总能量等于动能和势能之和是没有意义的，我们只能说，在这一个量子态中平均总能量等于平均势能和平均动能之和。
• 最小振幅不能是零，真空里面无论什么情况都会有电磁场(温度绝对零度)，因为电磁波本身也是谐振子，能量不可能为零，叫作“真空电磁场”，spontaneous emission和这个有关。任何原子，即使在绝对零度的时候，也会振动(真空也有量子场，也必然存在最小的不为零的振动能量)，总能量为\( H=\displaystyle\frac{p^{2}}{2 m}+\displaystyle\frac{1}{2} m \omega^2 x^{2} \)。

(3)  位于谐振子势阱中的质点：

• 量子力学的结果认为：当\( n=0 \)时，在\( x=0 \)处粒子出现的几率最大。
• 经典力学则认为：当\( n=0 \)时，在\( x=0 \)处粒子出现的几率最小。
• 当量子数n很大时与经典力学的结果趋于一致！也就是“对应原理”。
  

(4)  固态物理的角度，声子是一种【准粒子】，相邻能级的跳跃，其实是吸收或者释放声子。\( a_{+} \)叫作【creation operator】，\( a_{-} \)叫作【annihilation operator】，阶梯往上走就是创造一个粒子，往下走就是湮灭一个粒子。

(5) 【Normal mode(简正模式)】的"collective behavior"
首先解释一下collective bahvior，形象描述就是，划龙灯，一群人站成一条线，每个人都举着龙的一部分，那么每个人其实是都在观察他前后的人在干什么，划到什么位置，然后根据相邻位置的运动，判断自己该怎么运动，从而使整个龙灯的运动协调起来，而不是每个人都在自己的位置上瞎动。

1-D linear atomic chain
总的哈密顿量$$H=\sum_{n=1}^{N} \frac{p_{n}^{2}}{2 m}+\sum_{n} \frac{1}{2} k\left(x_{n+1}-x_{n}\right)^{2}$$那么每个点的振动位置可以写成复指数的形式(注意是正比于实数部分)$$x_{n}(t) \sim e^{i(k n a-\omega t)}$$我们讨论\( t=0 \)的情形，复指数按欧拉公式展开，那么实部对应的是真正的位置，虚部其实类似“相位”，不直接反应在图像上。如果我们取\( k a=\pi \)，那么\( x_{n}(0)=\cos (k n a)=\cos ( n \pi) \)，也就是图中的红色圆点；如果我们让\(  k\)更小，即让“波矢”更小，那么波长就更大(\(k=\displaystyle\frac{2 \pi}{\lambda}  \))，也就是图中黄色点的振动情况。这些点(原子)的振动都表现出刚才说的collective behavior。实际上存在无穷多个normal mode，我们按照离散傅里叶变换有(将坐标和动量都用\(  k\)来表示)$$\begin{aligned} &x_{k} \equiv \frac{1}{\sqrt{N}} \sum_{n} x_{n} e^{i k n a}\\ &P_{k} \equiv \frac{1}{\sqrt{N}} \sum_{n} P_{n} e^{-i k n a}\\ &H=\sum_{k}\left(\frac{\left|P_{k}\right|^{2}}{2 m}+\frac{1}{2} m \omega_{k}^{2}\left|x_{k}\right|^{2}\right) \end{aligned}$$(注意最后的表达式和前面的“形象理解“谐振子”的quantization”很像)也就是说在实际振动中，存在很多很多不同波长或者更准确地说不同弹簧常数(\( k \))的simple harmonic oscillator，对应于不同的的normal mode。我们把每一种的能量都算出来，然后加和在一起，就是整个系统的哈密顿量。对每一种normal mode都去定义\(  a_{+}\)和\(a_{-}  \)。每一种mode相邻能级的能量差不一样，越来越大。系统由\(  n\)个原子，那么理论上就有\( n \)种normal mode，或者是simple harmonic oscillator。
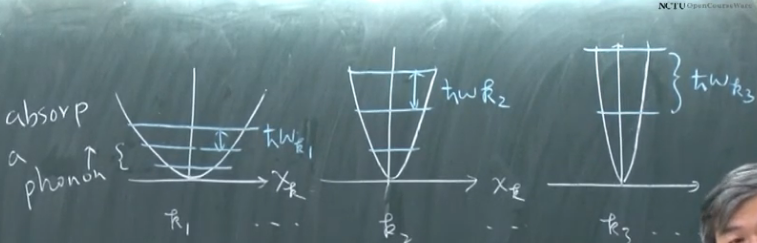phonon 是 classical normal mode 的quantization。从GS态到ES就是吸收(或generate)了声子，从ES到GS就是让声子湮灭了。根据麦克斯韦-玻尔兹曼分布，在任何温度下，上面的各种各样的能量的声子都是存在的，只是产生的概率不同。在低温下，显然\( \hbar \omega_{1} \)这种低能量的声子容易产生；随着温度的升高，高能量声子产生的概率也越来越大，而且前面的低能声子会处在更高的ES。

(1) 一个系统一般的运动可以写成其简正模的叠加。之所以简正模被称作“简正的(normal)”，是因为它们可以独立运动，即给物体施加一种模的激发，永远不会导致物体以另一个模运动。In mathematical terms, normal modes are orthogonal to each other.
(2) 固体物理中由简正坐标所代表的振动模怎么理解？
(3) 多自由度小振动系统初步(1)-绪论

(6)  电磁波(也有simple harmonic quantization，即大众熟悉的光量子)，能量也可以写成类似形式，\(a_{+}  \)这个算符的意思就是吸收了一个光子， \(a_{-}  \)表示释放一个光子。真空电磁场能量(也可以用\(  a_{+} \)和\(a_{-}   \)改写)$$u(\vec{r}, t)=\frac{1}{2}\left(\varepsilon_{0} E^{2}+\frac{1}{\mu_{0}} B^{2}\right)$$

(7)  LC电路的量子计算\(E=\displaystyle\frac{Q^{2}}{2 C}+\displaystyle\frac{1}{2} L \Phi^{2}  \)
将系统温度降低到接近绝对零度，那么就可以看到quantized effect(simple harmonic quantization)，或者说最小基态能量，以及相邻能级之间的差别，这里也是按照\(E_{n}=\left(n+\displaystyle\frac{1}{2}\right) \hbar \omega\)分布能级。

(1) LC振荡电路及其量子化-知乎专栏
(2) 超导量子计算简介

上述的都可以称为【正则变换】(canonical transformation)，即一个谐振子系统的能量可以用类似的方式来描述(一个物理量的平方+另一个物理量的平方)，但是可以有不同的物理表现形式。比如力学用\(x  \)和\(  p\)，电磁学是\( E \)和\(  B\)，LC电路是\(  Q\)和\( \Phi \)。