向量空间和子空间

几种空间简介

【向量空间】(Vector Space)
向量空间对线性运算具有封闭性。即一个数域和一个集合，具有加法和数乘两种二元运算且封闭，并且满足线性空间的八条公理。空间\(\mathbf{R}^{2} \)就是\(x-y\)的整个二维平面。\( \mathbf{R}^{n}\)是向量空间，它是具有\( n\)个实数分量的所有向量的集合，说它是\( n\)维空间并不准确。
反例：\(\mathbf{R}^{2} \)中的第一象限不是向量空间。

【子空间】(Linear subspace)
包含于一个向量空间之内的一个向量空间是一个子空间。更学术的说法是，如果向量空间\(V\)的子集\(U\)(采用与\(V\)相同的加法和标量乘法)也是向量空间，则称\(U\)是\(V\)的子空间。子空间一定是子集，但是子集不一定是子空间，只有满足线性运算封闭的子集才可以叫做子空间。

举例，空间\(\mathbf{R}^{2} \)内任取一个向量\( v\)(不为0)，那么\( cv\)(其中系数\(c \)，可变)就是一个子空间，图像上描述就是过原点的一条直线，它同样对于线性运算封闭。

• 子空间必须穿过原点，否则线性组合系数取零不封闭。
• \( \mathbf{R}^{3}\)的子空间比\( \mathbf{R}^{2}\)多一个过原点的平面
• \( \mathbf{R}^{2}\)的子空间包括
  • 其本身；
  • 过原点的直线(并不是\( \mathbf{R}^{1}\)空间)；
  • 原点。

【列空间】(Column space)
矩阵\(\boldsymbol{A}\)的列空间\(\mathrm{C}(\boldsymbol{A}) \)是其列向量线性组合所构成的空间。

例如，如果\( \boldsymbol{A}=\left[\begin{array}{ll} 1 & 3 \\ 2 & 3 \\ 4 & 1 \end{array}\right]\)，则其列空间是\( \mathbf{R}^{3}\)空间中包含向量\(\left[\begin{array}{l} 1 \\ 2 \\ 4 \end{array}\right] \)和\( \left[\begin{array}{l} 3 \\ 3 \\ 1 \end{array}\right]\)并且穿过原点的平面，这两个向量的线性组合张成了这个平面。

现在我们来思考一个问题，方程\(\boldsymbol{A} \mathbf{x}=\mathbf{b} \)，对于给定的矩阵\(\boldsymbol{A} \)，对于任意\(\mathbf{b} \)方程都有解吗？换句话说，矩阵\(\boldsymbol{A} \)列向量(每个由\(n \)个实数构成)的线性组合能否铺满整个\( \mathbf{R}^{n}\)空间？如果\(\boldsymbol{A}=\left[\begin{array}{lll} 1 & 1 & 2 \\ 2 & 1 & 3 \\ 3 & 1 & 4 \\ 4 & 1 & 5 \end{array}\right]\)显然答案是否定的，不可能用三个基向量表示(充满)一个\( \mathbf{R}^{4}\)空间，必定存在子空间属于\( \mathbf{R}^{4}\)，但是不属于\(\mathrm{C}(\boldsymbol{A}) \)，这个时候方程无解；只有当\(\mathbf{b} \)属于\(\mathrm{C}(\boldsymbol{A}) \)这个列空间时，方程才有解。另外这个三个列向量不是线性无关，所以实质上的列空间是由两个列向量张成的空间。我们说矩阵\(\boldsymbol{A} \)的列空间为\( \mathbf{R}^{4}\)内的一个二维子空间。

【零空间】(null space/Kernel)
矩阵\(\boldsymbol{A} \)(和上一问相同)的零空间\(N(\boldsymbol{A}) \)是指满足\( \boldsymbol{A} \mathbf{x}=\mathbf{0}\)所有解的集合。这里的矩阵\(\boldsymbol{A} \)只有三个列向量，所有线性组合的系数只有三个，故\( \mathbf{x}\)是含有3个分量的向量，那么矩阵\(\boldsymbol{A} \)的零空间是\( \mathbf{R}^{3}\)的子空间。很容易看出，该零空间\(N(\boldsymbol{A}) \)是包含\(\left[\begin{array}{ccc} 1 \\ 1 \\ -1 \end{array}\right] \)任何倍数(包括零倍)的子空间。此零空间为\( \mathbf{R}^{3}\)中的一条直线。

方程的解与\( \mathbf{R}^{3}\)的子空间
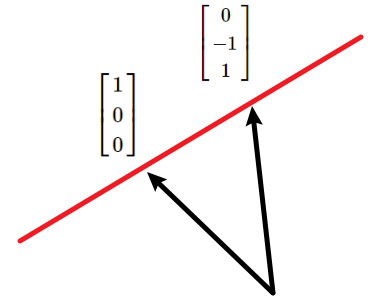子空间一条重要的性质就是必须包含零向量。若方程为$$\left[\begin{array}{lll} 1 & 1 & 2 \\ 2 & 1 & 3 \\ 3 & 1 & 4 \\ 4 & 1 & 5 \end{array}\right]\left[\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}\right]=\left[\begin{array}{l} 1 \\ 2 \\ 3 \\ 4 \end{array}\right]$$显然其解集是空间\( \mathbf{R}^{3}\)内过\(\left[\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right] \)和\( \left[\begin{array}{c} 0 \\ -1 \\ 1 \end{array}\right]\)的一条直线，但是不过原点，所以不是\( \mathbf{R}^{3}\)的子空间。

通过\(\boldsymbol{A} \mathbf{x}=\mathbf{b} \)构造子空间方法
(1) 矩阵\(\boldsymbol{A} \)的列向量张成的空间构成一个子空间，显然包含零向量。
(2) 令\(\mathbf{b}=\mathbf{0} \)，那么方程\(\boldsymbol{A} \mathbf{x}=\mathbf{0} \)的解集构成的空间是一个子空间。

注意：
(1) 一个是矩阵向量张成的空间，一个是解集张成的空间；
(2) 如果矩阵\(\boldsymbol{A} \)不是方阵的话，上面构造的两种子空间并不同属于一个\( \mathbf{R}^{n}\)空间。

 

 

计算零空间(简化行阶梯形)

对于方程\( \boldsymbol{A} \mathbf{x}=\mathbf{0}\)，我们取\(\boldsymbol{A}=\left[\begin{array}{llll} 1 & 2 & 2 & 2 \\ 2 & 4 & 6 & 8 \\ 3 & 6 & 8 & 10 \end{array}\right]\)注意几个列向量并不是线性无关的。我们先采用消元法处理，注意消元的时候并不改变零空间，或者说方程的解，但是列空间改变了。
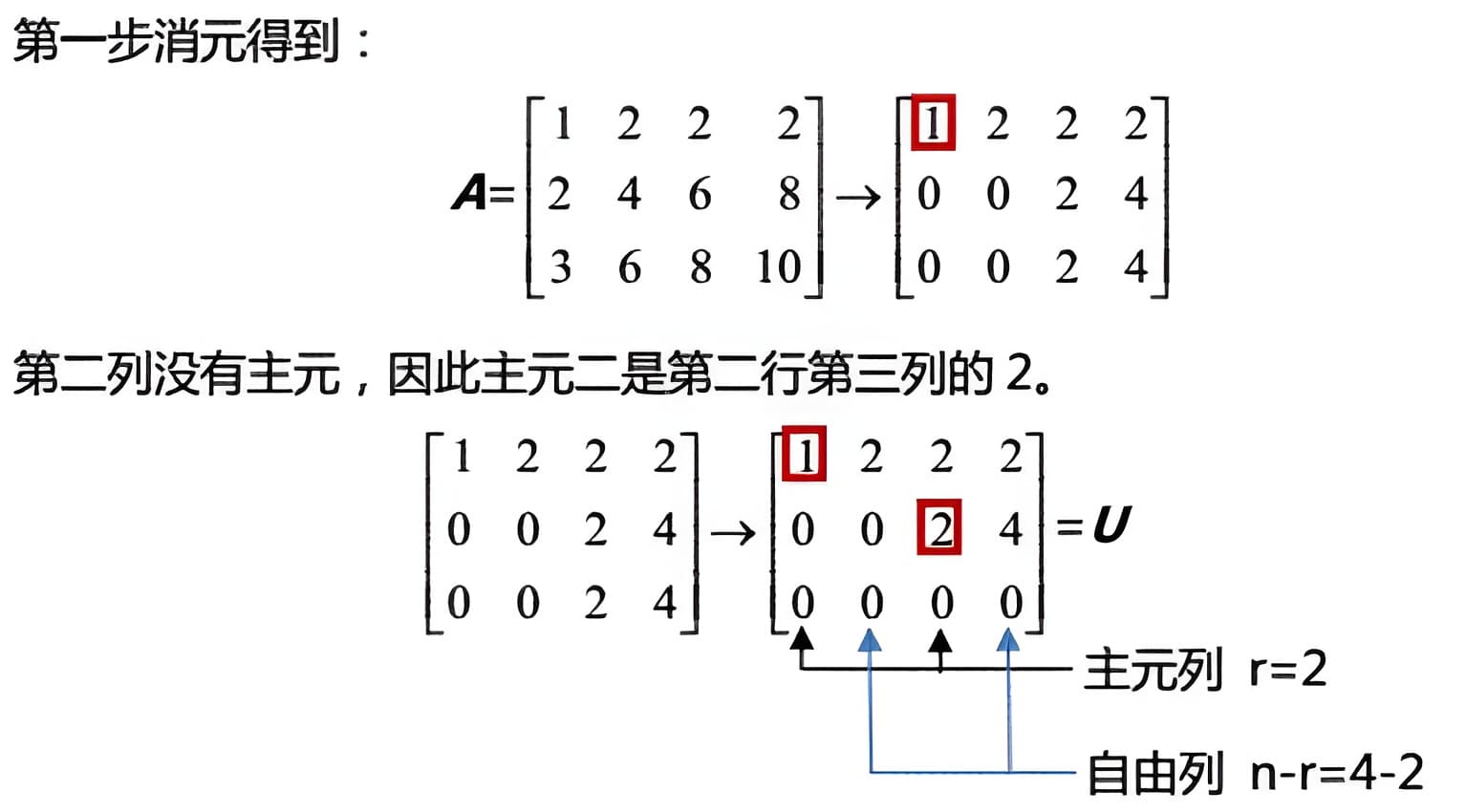注意这里红色框起来的就是pivot主元，主元所在的列就是【主元列(pivot column)】，其他的就是【自由列(free column)】。主元列和自由列的一个重要区别是，自由列可以表示为其左侧所有主元列的线性组合，而主元列则不可以，主元列是线性无关的。第三行是前面两行的线性组合，所以消元之后，所有的元素都为\(0\)。这里的矩阵\(\boldsymbol{U} \)叫作【行阶梯型】(row echelon form)矩阵。消元后，主元的个数\(r\)就是【矩阵的秩(rank)】。由于\( \boldsymbol{A} \mathbf{x}=\mathbf{0}\)等式的右侧是零，所以该方程的解等价于\( \boldsymbol{U} \mathbf{x}=\mathbf{0}\)的解；或者说矩阵\(\boldsymbol{A} \)的零空间就是矩阵\(\boldsymbol{U} \)的零空间。而这里的\(\boldsymbol{U} \)是上三角矩阵，那么求解就容易多了。

自由列对应的\(x \)就是【自由变量(free variable)】，比如前面说的第二列和第四列对应的\( x_{2}\)和\( x_{4}\)都是自由变量。我们首先对其进行赋值，如令\( x_{2}=1\)，\( x_{4}=0\)，于是有$$\begin{array}{c} 2 x_{3}+4 x_{4}=0 \Rightarrow x_{3}=0 \\ x_{1}+2 x_{2}+2 x_{3}+2 x_{4}=0 \Rightarrow x_{1}=-2 \end{array}$$得到【特解(special solution)】\( \mathbf{x}=\left[\begin{array}{c} -2 \\ 1 \\ 0 \\ 0 \end{array}\right]\)，这个向量的任意倍数(想象成直线)均在矩阵\(U \)的零空间。同理再次赋值(\( x_{2}=0\)，\( x_{4}=1\))，得到另一个特解\(\mathbf{x}=\left[\begin{array}{c} 2 \\ 0 \\ -2 \\ 1 \end{array}\right] \)。

• 矩阵\( \boldsymbol{A} \)(或者说\( \boldsymbol{U} \))的零空间就是这些“特解”的线性组合。
• 自由列的数目 = 零空间的“维数” = 零空间基元的数目 = \( n-r\)
• 主元列和自由列的一个重要区别就是，自由列可以由其左侧的所有主元列线性组合而成，反过来则不行。

【简化行阶梯形】(Reduced row echelon form，简写rref)，matlab的reff(\(\boldsymbol{A}\))的命令实现过程如下

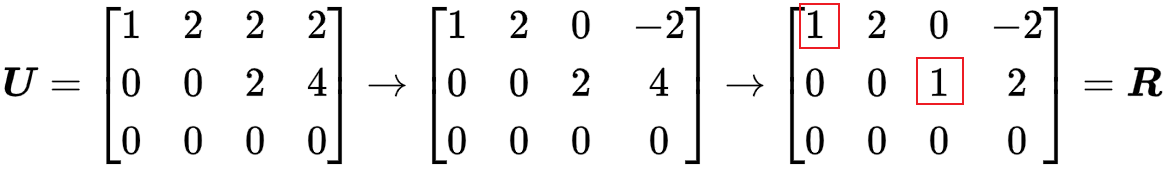
• 非零行首非零元为\(1\)；
• 这些首非零元所在的列的其他元素全为零；
• 再次强调，\(\boldsymbol{A}\)、\(\boldsymbol{U}\)、\(\boldsymbol{R}\)的零空间相同；

下面对矩阵\(\boldsymbol{R}\)进行移列和分块计算。简化行阶梯形矩阵\(\boldsymbol{R}\)的主元列都移到左边，即第二列和第三列互换，然后将矩阵进行如下的分块

根据分块后的矩阵特点，显然可以猜出其null space matrix的解即\(\left[\begin{array}{c}-\mathrm{F} \\ \mathrm{I}\end{array}\right]\)，于是移列后的\(\boldsymbol{R}\)的零空间就是该null space matrix的列的线性组合。这个null space matrix的\(\mathrm{I}\)就相当于对自由变量轮换取\(1\)。在这个null space matrix的基础上，进行移行操作(消除之前\(\boldsymbol{R}\)移列操作对零空间的影响)，即得到\(\boldsymbol{R}\)的零空间，列向量的线性组合就是零空间。

 

 

求解\(\boldsymbol{A} \mathbf{x}=\mathbf{b}\)

步骤
(1) 判断是否有解；
(2) 如果有解，先求解\(\boldsymbol{A} \mathbf{x}=\mathbf{0}\)，即零空间向量；
(3) 找到一个特解；
(4) 通解 = 特解+零空间列向量

\(\boldsymbol{A} \mathbf{x}=\mathbf{b}\)可解条件

先前我们讨论的是等式右边为零的情况，这里我们开始讨论更一般的不全为0的情况，同样以前面的系数矩阵\(A \)作为例子进行分析。$$\left[\begin{array}{lllr} 1 & 2 & 2 & 2 \\ 2 & 4 & 6 & 8 \\ 3 & 6 & 8 & 10 \end{array}\right]\left[\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array}\right]=\left[\begin{array}{l} b_{1} \\ b_{2} \\ b_{3} \end{array}\right]$$对增广矩阵进行消元操作，得到行阶梯型$$\left[\begin{array}{lllrl} 1 & 2 & 2 & 2 & b_{1} \\ 2 & 4 & 6 & 8 & b_{2} \\ 3 & 6 & 8 & 10 & b_{3} \end{array}\right] \rightarrow \ldots \rightarrow\left[\begin{array}{lllll} 1 & 2 & 2 & 2 & b_{1} \\ 0 & 0 & 2 & 4 & b_{2}-2 b_{1} \\ 0 & 0 & 0 & 0 & b_{3}-b_{2}-b_{1} \end{array}\right]$$这里就是如果对系数矩阵\( A\)进行行向量的线性组合得到零向量，那么对应的\(b \)经过此操作，也应该为\( 0\)，即此处必有\(b_3-b_2-b_1=0\)。

先前我们讨论说对于方程组\( \boldsymbol{A} \mathbf{x}=\mathbf{b}\)，只有当b可以用\(\boldsymbol{A} \)列向量的线性组合得到时，或者说只有当\(b \)处于矩阵\( A\)的列空间\(C(A) \)的情况下，方程才有解。总而言之，这说的是列向量的线性操作。

从行向量的线性组合、从列向量的线性组合的角度都可以分析出\(\boldsymbol{A} \mathbf{x}=\mathbf{b}\)有解的限制条件，但是这二者实质上是等价的。

 

\(\boldsymbol{A} \mathbf{x}=\mathbf{b}\)特解

阶梯型矩阵以及零空间我们之前都已经知道了，现在求特解。
令所有的自由变量都为\(0 \)，得到的就是特解。这里我们令\( \mathbf{b}=\left[\begin{array}{l} 1 \\ 5 \\ 6 \end{array}\right]\)，而自由变量\( x_{2}=x_{4}=0\)，于是$$\begin{aligned} x_{1}+2 x_{3} &=1 \\ 2 x_{3} &=3 \end{aligned}$$得到特解\(\mathbf{x}_{\mathrm{p}}=\left[\begin{array}{c} -2 \\ 0 \\ 3 / 2 \\ 0 \end{array}\right] \)。自由变量取\(0 \)是为了消除自由列的影响。

\(\boldsymbol{A} \mathbf{x}=\mathbf{b}\)通解

\( \boldsymbol{A} \mathbf{x}=\mathbf{b}\)的通解为\(\mathbf{x}_{\text {complete }}=\mathbf{x}_{p}+\mathbf{x}_{n} \)，其中\( \mathbf{x}_{n}\)为矩阵零空间中的一般向量。将\( A \mathbf{x}_{\mathrm{p}}=\mathbf{b}\)和\(A \mathbf{x}_{n}=\mathbf{0} \)相加得到\(A\left(\mathbf{x}_{p}+\mathbf{x}_{n}\right)=b \)。零空间\( \mathrm{N}(\boldsymbol{A})\)的解我们前面已经求出来了，而\(\boldsymbol{A} \mathbf{x}=\mathbf{b} \)的特解求出来了，于是方程\(\boldsymbol{A} \mathbf{x}=\mathbf{b} \)的通解为：$$\mathbf{x}_{\text {complete }}=\left[\begin{array}{c} -2 \\ 0 \\ 3 / 2 \\ 0 \end{array}\right]+\mathrm{c}_{1}\left[\begin{array}{c} -2 \\ 1 \\ 0 \\ 0 \end{array}\right]+\mathrm{c}_{2}\left[\begin{array}{c} 2 \\ 0 \\ -2 \\ 1 \end{array}\right]$$

注意，这里的零空间\( \mathrm{N}(\boldsymbol{A})\)是\( \mathrm{R}^{4}\)的二维子空间(二维体现在有两个基向量)，但是方程\( \boldsymbol{A} \mathbf{x}=\mathbf{b}\)的解构成了穿过特解\( \mathbf{x}_{p}\)点并且和零空间\( \mathrm{N}(\boldsymbol{A})\)平行的“平面”，但是该“平面”不是\( \mathrm{R}^{4}\)的子空间。总之，将零空间\( \mathrm{N}(\boldsymbol{A})\)平移\( \mathbf{x}_{p}\)得到通解空间。如果在求解\( \boldsymbol{A} \mathbf{x}=\mathbf{b}\)不令自由变量全为\(0 \)，那么得到的特解实际上就是通解中系数\( c_{1}\)和\( c_{2}\)不全为\( 0\)的情况。

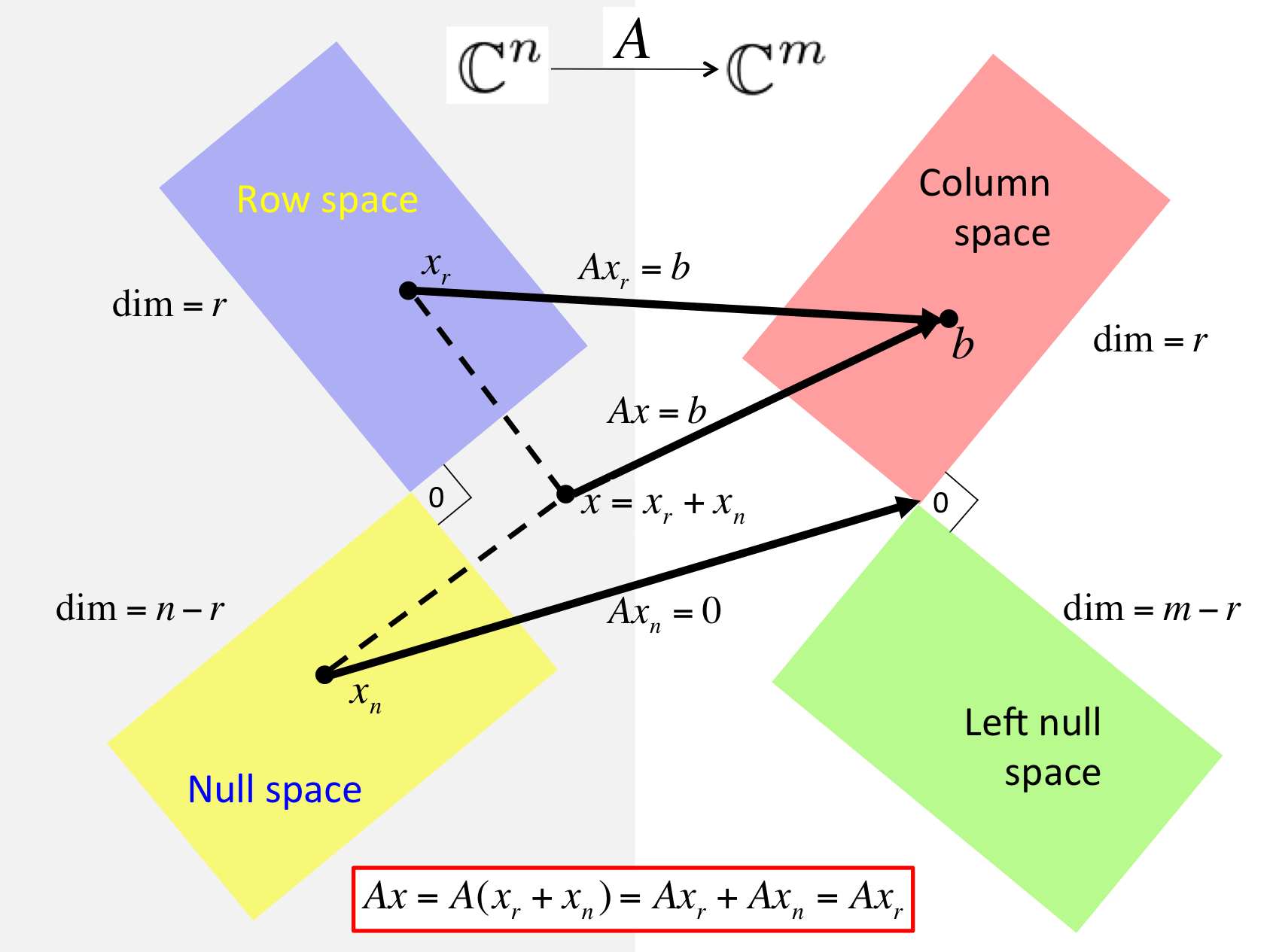
根据上面的图，可以知道，对于如果矩阵\(A\)为满秩方阵，那么就不存在下面两个零空间和左零空间，即线性变换对应于一个空间到其自身的双射(单射且满射)，所以存在逆映射，也即存在矩阵\( A\)的逆矩阵。

\(\boldsymbol{A} \mathbf{x}=\mathbf{b}\)解的个数

矩阵的秩就是主元的数目(消元化为行阶梯型就可以看出来)。如果\( m \times n\)的秩为\(r \)，显然\(r \leq m \)且\( r \leq n\)，下面分类讨论满秩(full rank)的情况：

(1) 列满秩——\( r=n\)，那么\( x\)中所有的元素都是主变量，自由变量数目\(n-r=n-n=0 \)。换句话说所有列向量都线性无关，那么要使得\(\boldsymbol{A} \mathbf{x}=\mathbf{0}\)，必有\(\mathbf{x}=\mathbf{0}\)，即矩阵\(\boldsymbol{A}\)的零空间只有零向量。另一方面，等式右边的列向量\( \mathbf{b}\)不一定在矩阵\( \mathbf{A}\)的列空间之内，如果在的话，那么就有唯一特解(也是唯一解，\(\mathbf{R}^{n} \)空间的一个列向量和\( I\)中列向量线性组合的系数是一一对应的)，不在的话，就没有解。

我们可以想象零空间是一个零向量，就是零点，那么方程的解就是从零点移动\( \mathbf{x}_{p}\)得到的新的点，\( \mathbf{x}_{p}\)不存在的话就不能在空间中找到这一点。例子：$$A=\left[\begin{array}{ll} 1 & 3 \\ 2 & 1 \\ 6 & 1 \\ 5 & 1 \end{array}\right] \rightarrow\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \\ 0 & 0 \\ 0 & 0 \end{array}\right]=R$$

(2) 行满秩——\( r=m\)，每一行都有主元，无论\(\mathbf{b}\)取何值，方程都有解，主变量为\( r\)个，自由变量\( n-r\)个。例子$$A=\left[\begin{array}{llll} 1 & 2 & 6 & 5 \\ 3 & 1 & 1 & 1 \end{array}\right] \rightarrow\left[\begin{array}{cccc} 1 & 0 & * & * \\ 0 & 1 & * & * \end{array}\right]=R$$上面的矩阵\(R\)如果从\(x_{3} \)开始的元素都为\(0 \)，即右侧分块矩阵\(F\)的列向量分量为零，那么左侧分块矩阵(二阶单位阵)的列向量的线性组合可以表示\(\mathbf{R}^{2} \)空间任何向量。

(3) 行列满秩——\( r=m=n\)，那么矩阵可逆(或者说nonsingular，非奇异)。零空间只有零向量，无论\(b \)取何值，方程都有解。我们可以想像成情形(1)和(2)的并集。例子$$A=\left[\begin{array}{ll} 1 & 2 \\ 3 & 1 \end{array}\right] \rightarrow\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]=R$$总结(\(  R\)为简化行阶梯形)

• \(r=m=n\)，\( R=I\)，有唯一解；
• \(r=n<m\)，\(R=\left[\begin{array}{l} I \\ 0 \end{array}\right]\)，无解或唯一解；
• \(r=m<n\)，\(R=\left[\begin{array}{ll}I & F\end{array}\right]\)，无穷多解；
• \(r<n\)，\(r<m\)，\(R=\left[\begin{array}{ll}I & F \\ 0 & 0\end{array}\right]\)，无解或无穷多解。
  

秩决定了方程解的数目。\( m \times n\)给出了矩阵的尺寸，但是秩给出的是矩阵的实际“大小”，后面会有详细讨论。

 

 

 

线性无关/基/维数/坐标

【线性相关】(linearly dependent)：对于\( m \times n\)的矩阵\(A \)来说，如果\( m<n\) (\( A \mathbf{x}=\mathbf{b}\)中未知数的数目大于方程的个数)。那么通过消元法，我们肯定可以得到一些自由列，于是方程\( A \mathbf{x}=0\)一定有非零解，也就是说\(A \)的列向量的(系数非全为零的)线性组合可以得到零向量，所以列向量组矩阵\(A \)是线性相关的。

【线性无关】(linearly independent)
若\(c_{1} \mathbf{x}_{1}+c_{2} \mathbf{x}_{2}+\ldots \ldots+c_{n} \mathbf{x}_{n}=\mathbf{0} \)仅在\( c_{1}=c_{2}=\ldots \ldots=c_{n}=0\)时才成立，则称这\(n \)个向量是线性无关的。

【最大无关组】(Maximal Linearly Independent subset)：设有向量组\(\mathcal{A}_0\)，如果在\(\mathcal{A}_0\)中选出\(r\)个向量\(\boldsymbol{a}_1, \boldsymbol{a}_2, \ldots, \boldsymbol{a}_r\)满足：
(1) 向量组\(\mathcal{A}_0=\left\{\boldsymbol{a}_1, \boldsymbol{a}_2, \ldots, \boldsymbol{a}_r\right\}\)线性无关；
(2) 向量组\(\mathcal{A}\)中任意\(r+1\)个向量(如果\(\mathcal{A}\)中有\(r+1\)个向量的话)都线性相关；
那么称向量组\(\mathcal{A}_0\)是向量组\(\mathcal{A}\)的一个"最大线性无关组"，简称"最大无关组"。

• 最大无关组的选取并不唯一，比如三原色的选取，我们用RGB可以，也可以用"R黄B"，都可以用来描述人眼能看到的颜色空间；
• 只包含零向量的向量组，比如\(\mathcal{A}=\left\{\left(\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right)\right\}\)，因为只包含零向量，所以必然线性相关，因此该向量组没有最大无关组。

线性无关的等价描述：

(1) 延续线性无关的定义，这些线性无关的列向量构成的矩阵\( A\)，那么方程\(\boldsymbol{A} \mathbf{x}=\mathbf{0}\)只有零解，或者说矩阵\(A \)的零空间只有零向量。

以\(\mathbf{R}^{2} \)为例，两个向量只要不在一条直线上就是线性无关的；同样地，对于\(\mathbf{R}^{3} \)，三个向量线性无关的条件是它们不在一个平面上。如果在\(\mathbf{R}^{2} \)空间选定三个向量，那么它们必然是线性相关的(未知数个数大于方程个数)。比如\(\boldsymbol{A}=\left[\begin{array}{ccc}2 & 1 & 2.5 \\ 1 & 2 & -1\end{array}\right]\)的三个列向量是线性相关的，也就是方程\(\boldsymbol{A} \mathbf{x}=\mathbf{0} \)有非零解。

(2) 如果矩阵\(\boldsymbol{A} \)的列向量为线性无关，则\(\boldsymbol{A}\)所有的列均为主元列，不存在自由列，矩阵的秩为\(n \)。如果\(\boldsymbol{A} \)的列向量线性相关，那么一定有矩阵的秩小于\(n \)，并且存在自由列。

【张成空间】(spanning a space)
向量\(\mathbf{v}_{1}, \mathbf{v}_{2} \ldots \ldots \mathbf{v}_{k} \)所有的线性组合构成的空间就是这些向量张成的空间。例如矩阵的列向量张成了该矩阵的列空间。如果向量\(\mathbf{v}_{1}, \mathbf{v}_{2} \ldots \ldots \mathbf{v}_{k} \)张成空间\(\mathbf{S}\)，那么该空间是包含这些向量的最小空间。

 

【基】(basis)
向量空间的基是具有如下两种性质的一组向量\(\mathbf{v}_{1}, \mathbf{v}_{2} \ldots \ldots \mathbf{v}_{\mathrm{d}} \)：
(1) \(\mathbf{v}_{1}, \mathbf{v}_{2} \ldots \ldots \mathbf{v}_{\mathrm{d}} \)线性无关；
(2) \(\mathbf{v}_{1}, \mathbf{v}_{2} \ldots \ldots \mathbf{v}_{\mathrm{d}} \)张成该空间。
空间的基告诉了我们空间的一切信息。

例子：如果\( \mathbf{R}^{n}\)空间的\(n \)个向量构成的矩阵为可逆矩阵(自由列为零个，矩阵的零空间只有零向量)，则这些向量可以构成\( \mathbf{R}^{n}\)空间的一组基。

【自然基】(标准基，Standard basis)：In mathematics, the standard basis (also called natural basis or canonical basis) of a coordinate vector space (such as  \(  \mathbb {R} ^{n}\) or \( \mathbb {C} ^{n}\)) is the set of vectors, each of whose components are all zero, except one that equals \(1\).

对应于直角坐标系的基，如下图二维实平面的情况。

对于\( \mathbf{R}^{n}\)，都有自然基\(\mathcal{E}: \boldsymbol{e}_1=\left(\begin{array}{c}1 \\ 0 \\ \vdots \\ 0\end{array}\right), \quad \boldsymbol{e}_2=\left(\begin{array}{c}0 \\ 1 \\ \vdots \\ 0\end{array}\right), \quad \cdots, \quad \boldsymbol{e}_n=\left(\begin{array}{c}0 \\ 0 \\ \vdots \\ 1\end{array}\right)\)

列空间和零空间的基 (Basis of a column space and nullspace)
$$A=\left[\begin{array}{llll} 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 1 \\ 1 & 2 & 3 & 1 \end{array}\right]$$讨论列空间：很显然，前两列为主元列，构成了列空间\( C(\boldsymbol{A})\)的一组基，矩阵的秩为\( 2\)。

上面的例子中，矩阵的列向量不是线性无关的，所以其零空间必然包含非零的向量。很容易看出零空间的两个解\( \left[\begin{array}{c} -1 \\ -1 \\ 1 \\ 0 \end{array}\right]\)和\(\left[\begin{array}{l} 1 \\ 0 \\ 0 \\ 1 \end{array}\right] \)，那么零空间是否是由这两个特解张成的呢？由于矩阵的秩是\( 2\)，所以自由列(自由变量)的数目就是\( 4-2=2\)，所以零空间的维数就是\(2 \)，而我们得到的两个解是线性无关的，所以我们就可以说，这两个解向量可以构成矩阵\( A\)的零空间。

                                                零空间的维数 = 自由列的数目 = \(n-r \)

【维数】(dimension)
假设向量空间\( V\)的基为\(A=\left\{\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_r\right\}\)，则\(A\)的秩\(r\)称为该向量空间的维数，或者称\(V\)为\(r\)维向量空间。

• 比如色彩空间的基RGB或者CMY的维数为\(3\)，注此处忽略CMYK (cyan, magenta, yellow, and key (black))中的黑色K；
• 只包含零向量的空间，没有基，所以其维数为\(0\)；
• \( \mathbf{R}^{2}\)空间的基\(\boldsymbol{e}_1,\boldsymbol{e}_2\)，于是其空间维数为\(2\)；
• 空间的每一组基都含有相同的向量数，这个数就是空间的维数；
• \(m \)个线性无关的向量通过线性组合得到的空间维数就是\(m \)；
• \( \mathbf{R}^{n}\)空间的每一组基都包含\( n\)个向量。
• 秩是相对于矩阵而言的，维数是相对于空间而言的；
• 矩阵的秩\( r\) = 矩阵的主元数目 = 列空间的维数；
• 向量\( \left[\begin{array}{l} 1 \\ 1 \\ 2 \end{array}\right]\)和\(\left[\begin{array}{l} 2 \\ 2 \\ 5 \end{array}\right] \)可以张成\( \mathbf{R}^{3}\)的一个平面，但是无法成为\( \mathbf{R}^{3}\)空间的基，该平面空间的维数是\( 2\)。
• 在\( \mathbf{R}^{4}\)空间中，所有满足分量之和\(v_1+v_2+v_3+v_4=0\)的向量\(\mathbf{v}=\left[\begin{array}{l}v_1 \\ v_2 \\ v_3 \\ v_4\end{array}\right]\)构成了一个子空间\(\mathbf{S}\)，包含零向量并对线性运算封闭。它是矩阵\(\boldsymbol{A}=\left[\begin{array}{llll}1 & 1 & 1 & 1\end{array}\right]\)的零空间，因为矩阵\(\boldsymbol{A}\)的秩为\( 1\)，因此其零空间的秩为\( n-r=3 \)。零空间的基就是\(\boldsymbol{A} \mathbf{x}=\mathbf{0}\)的特解，\(\left[\begin{array}{c}-1 \\ 1 \\ 0 \\ 0\end{array}\right],\left[\begin{array}{c}-1 \\ 0 \\ 1 \\ 0\end{array}\right],\left[\begin{array}{c}-1 \\ 0 \\ 0 \\ 1\end{array}\right]\)。这个例子的意义就是寻找空间维数的逆向思路，可以考虑它是不是某个方程的解空间，在这里它是\(\boldsymbol{A}=\left[\begin{array}{llll}1 & 1 & 1 & 1\end{array}\right]\)的零空间，我们可以从矩阵推出这个空间的维数。

 

【坐标】：假设\(\mathcal{A}=\left\{\boldsymbol{a}_1, \boldsymbol{a}_2, \ldots, \boldsymbol{a}_n\right\}\)是向量空间\(V\)的一个基，则\(V\)中的每个向量\(\boldsymbol{x}\)都可以唯一地表示为：$$ \boldsymbol{x}=k_1 \boldsymbol{a}_1+k_2 \boldsymbol{a}_2+\cdots+k_n \boldsymbol{a}_{\boldsymbol{n}} $$上式的系数可以组成向量：\([\boldsymbol{x}]_{\mathcal{A}}=\left(\begin{array}{c} k_1 \\ k_2 \\ \vdots \\ k_n \end{array}\right) \)我们将其称为\(\boldsymbol{x}\)在基\(\mathcal{A}\)下的【坐标向量】(coordinate vector)，或者简称为\(\boldsymbol{x}\)在基\(\mathcal{A}\)下的坐标。

选择一个基后，就可以给出向量空间中某个向量的坐标，不同的基下坐标会不同，下面给一些例子：

• “粉暖”是色彩空间中的一个向量，其在RGB基下坐标为\(\left(\begin{array}{l}212 \\ 125 \\ 124\end{array}\right)\)，在CMY基下坐标为\(\left(\begin{array}{c}0 \\ 63 \\ 38\end{array}\right)\)；
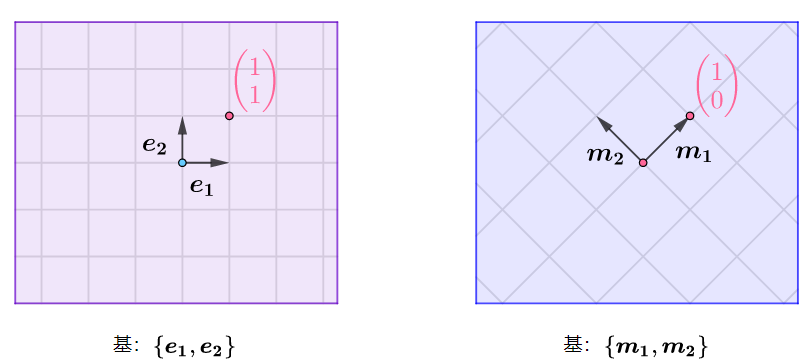• 二维实数平面中，对于同一个向量\(\boldsymbol{x}=\left(\begin{array}{l}1 \\ 1\end{array}\right)\)，在两组不同基下的坐标如下：$$ \begin{aligned} &\mathcal{E}: \boldsymbol{e}_1=\left(\begin{array}{l} 1 \\ 0 \end{array}\right), \quad \boldsymbol{e}_2=\left(\begin{array}{c} 0 \\ 1 \end{array}\right) \\ &\mathcal{M}: \boldsymbol{m}_1=\left(\begin{array}{l} 1 \\ 1 \end{array}\right), \quad \boldsymbol{m}_2=\left(\begin{array}{c} -1 \\ 1 \end{array}\right) \\ &{[\boldsymbol{x}]_{\mathcal{E}}=\left(\begin{array}{l} 1 \\ 1 \end{array}\right), \quad[\boldsymbol{x}]_{\mathcal{M}}=\left(\begin{array}{c} 1 \\ 0 \end{array}\right)} \end{aligned} $$

 

 

 

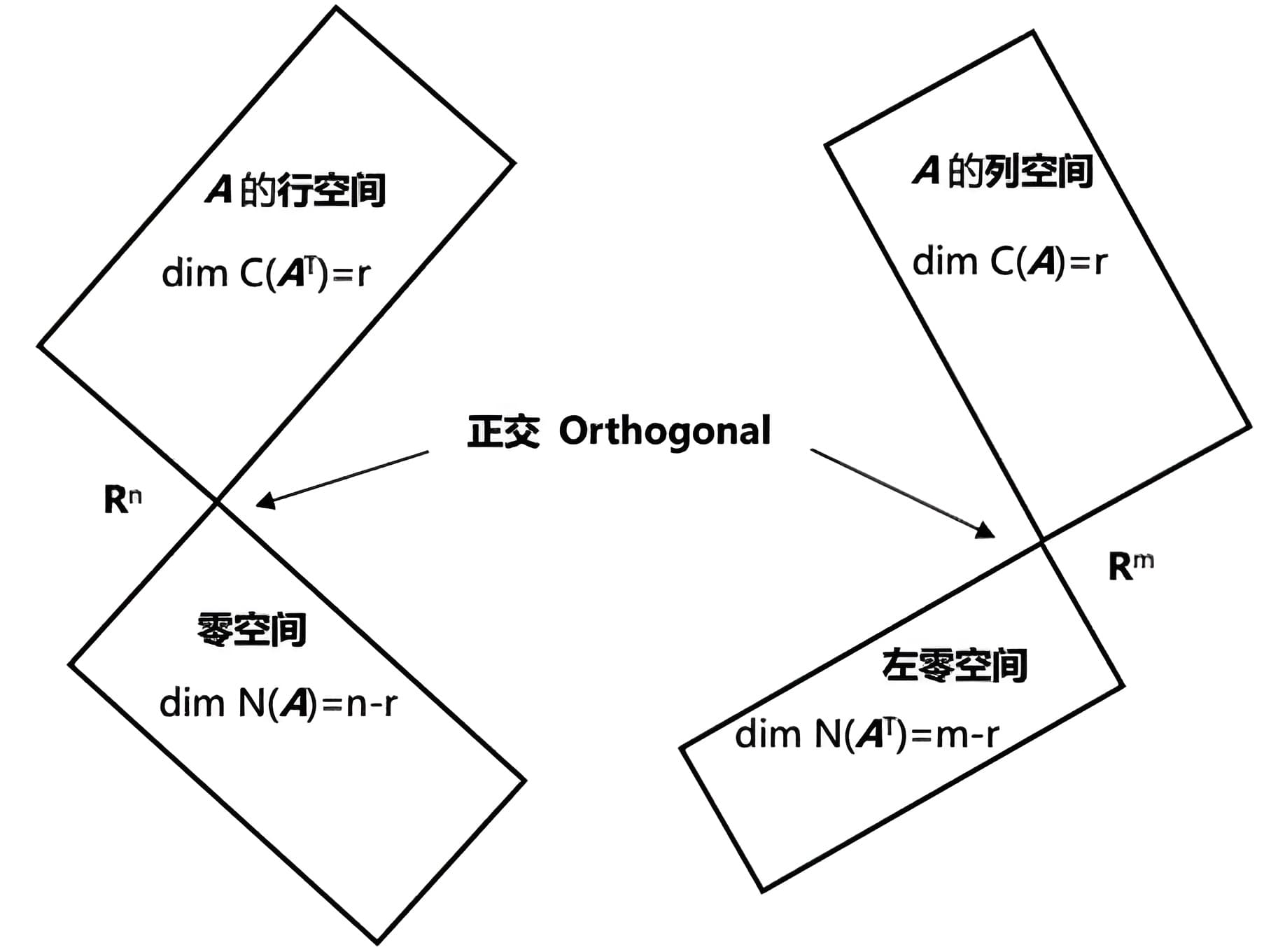
四个基本子空间/Kernel

四个基本子空间(four fundamental subspaces)及其基和维数
任意\( m \times n\)矩阵\( A\)都定义了四个子空间。

(1) 列空间\(C(A)\)
矩阵\(A \)的列空间是\(A \)的列向量的线性组合在\( \mathbf{R}^{m}\)空间中构成的子空间。(\( m\)是方程的个数，也是列向量中元素的个数)

矩阵中有\(r \)个主元列构成了列空间的一组基，所以\(\operatorname{dim} C(A)=r \)。

(2) 零空间\(N(A) \)
矩阵\( A\)的零空间是\(\boldsymbol{A} \mathbf{x}=\mathbf{0} \)的所有解\(x \)在\( \mathbf{R}^{n}\)空间。(\( n\)是未知数的个数)

矩阵中有\(n-r \)个自由列，也就是说\(A \mathbf{x}=\mathbf{0} \)每一个特解(\( x_{free}\)依次取\(1\)，其他取\(0\))对应一个自由列，这些自由列构成了零空间的一组基，\(\operatorname{dim} N(A)=n-r \)。

(3) 行空间\(C(A^\mathrm{T}) \)
显然，每一行包含的元素个数是\( n\)，也就是未知数的个数，所以\(C\left(A^\mathrm{T}\right) \)是\(A\)的行向量的线性组合在\( \mathbf{R}^{n}\)空间构成的子空间，也就是矩阵\( A^\mathrm{T}\)的列空间。

我们将矩阵\(A \)化为行最简形矩阵\(R \)$$A=\left[\begin{array}{llll} 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 1 \\ 1 & 2 & 3 & 1 \end{array}\right] \rightarrow \ldots \rightarrow\left[\begin{array}{llll} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right]=\left[\begin{array}{ll} I & F \\ 0 & 0 \end{array}\right]=R$$特别注意，化简之后，可以用含有主元的所有行(前\( r\)行)的线性组合表示原矩阵\( A\)的任一行，但是不能用含有主元的所有列(这里是前两列)来表示原矩阵\( A\)的任一列。也就是说，矩阵\( A\)和\(R \)的列空间不同，但是行空间是相同的(消元是行变换的线性操作，是可逆的)，所有\( A\)行向量可以表示为\( R\)行向量的线性组合。

\(R \)的前\(r \)行最简形“行向量”就是矩阵\( A\)行空间的一组基，\(\operatorname{dim} C\left(A^\mathrm{T}\right)=r \)。

(4) 左零空间\(N\left(A^\mathrm{T}\right) \)
矩阵\(A^\mathrm{T}\)的零空间，是\( \mathbf{R}^{m}\)空间的子空间。

 

【秩-零化度定理】(rank–nullity theorem)：is a theorem in linear algebra, which asserts that the dimension of the domain of a linear map is the sum of its rank (the dimension of its image) and its nullity (the dimension of its kernel). 

Let \(T: V \rightarrow W\) be a linear transformation between two vector spaces where \(T\)'s domain \(V\) is finite dimensional. Then$$ \operatorname{Rank}(T)+\operatorname{Nullity}(T)=\operatorname{dim} V $$其中\(\operatorname{Rank}(T):=\operatorname{dim}(\operatorname{Image}(T))\)，\(\operatorname{Nullity}(T):=\operatorname{dim}(\operatorname{Ker}(T))\)。换句话说$$ \operatorname{dim}(\operatorname{im} T)+\operatorname{dim}(\operatorname{ker} T)=\operatorname{dim}(\operatorname{domain} T) $$从矩阵的角度看，该定理给出了一个矩阵的秩和它的零化度之间的关系。对一个元素在域\(F\)中的\(m \cdot n\)矩阵\(A\)，该定理说明它的秩和零化度之和等于\(n\)，即$$\text{rank}A+\text{nullity} A=n$$

【Kernel】对线性映射(linear map)来说，Kernel核就是零空间(null space)。Given a linear map \(L: V \rightarrow W\) between two vector spaces \(V\) and \(W\), the kernel of \(L\) is the vector space of all elements \(\mathbf{v}\) of \(V\) such that \(L(\mathbf{v})=\mathbf{0}\), where \(\mathbf{0}\) denotes the zero vector in \(W\). More symbolically: \(\operatorname{ker}(L)=\{\mathbf{v} \in V \mid L(\mathbf{v})=\mathbf{0}\}\)
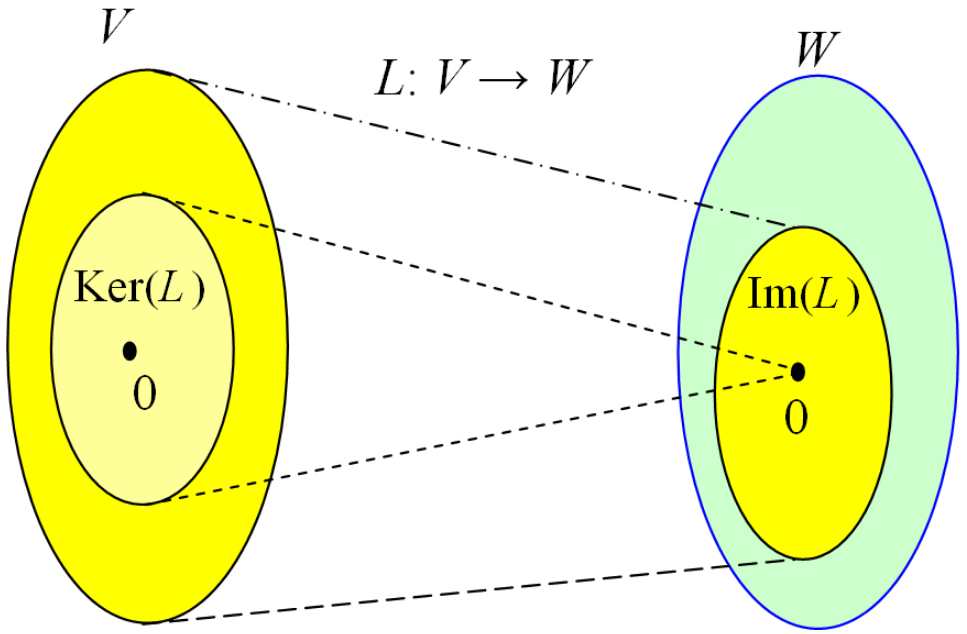Kernel的例子：

• \(A\)是一个矩阵，\(\mathrm{N}(A)=\operatorname{Null}(A)=\operatorname{ker}(A)=\left\{\mathbf{x} \in K^{n} \mid A \mathbf{x}=\mathbf{0}\right\}\)
  The kernel of A is the same as the solution set to the above homogeneous equations.
• If \(L: \mathbf{R}^{m} \rightarrow \mathbf{R}^{n}\), \(L\left(x_{1}, x_{2}, x_{3}\right)=\left(2 x_{1}+3 x_{2}+5 x_{3},-4 x_{1}+2 x_{2}+3 x_{3}\right)\). Then the kernel of \(L\) is the set of solutions to the equations$$ \begin{array}{r} 2 x_{1}+3 x_{2}+5 x_{3}=0 \\ -4 x_{1}+2 x_{2}+3 x_{3}=0 \end{array} $$
• \(C[0,1]\)表示的是the vector space of all continuous real-valued functions on the interval \([0,1]\)。定义\(L: C[0,1] \rightarrow \mathbf{R}\) by the rule \(L(f)=f(0.3)\). Then the kernel of \(L\) consists of all functions \(f \in C[0,1]\) for which \(f(0.3)=0\).
  注：\(L\)作用在函数上，那么吐出来的就是该函数在\(0.3\)处的值。
• Let \(C^{\infty}(\mathbf{R})\) be the vector space of all infinitely differentiable functions \(\mathbf{R} \rightarrow \mathbf{R}\) and let \(D: C^{\infty}(\mathbf{R}) \rightarrow C^{\infty}(\mathbf{R})\) be the differentiation operator: \(D(f)=\displaystyle\frac{d f}{d x}\). Then the kernel of \(D\) consists of all functions in \(C^{\infty}(\mathbf{R})\) whose derivatives are zero, i.e. the set of all constant functions.
• Let \(\mathbf{R}^{\infty}\) be the direct product of infinitely many copies of \(\mathbf{R}\), and let \(s: \mathbf{R}^{\infty} \rightarrow \mathbf{R}^{\infty}\) be the shift operator $$ s\left(x_{1}, x_{2}, x_{3}, x_{4}, \ldots\right)=\left(x_{2}, x_{3}, x_{4}, \ldots\right) $$Then the kernel of \(s\) is the one-dimensional subspace consisting of all vectors \(\left(x_{1}, 0,0,0, \ldots\right)\).
  注：对于实数集合\(\mathbf{R}\)，直积\(\mathbf{R} \times \mathbf{R}\)完全就是笛卡尔积\(\{(x, y) \mid x, y \in \mathbf{R}\}\)
• If \(V\) is an inner product space and \(W\) is a subspace, the kernel of the orthogonal projection \(V \rightarrow W\) is the orthogonal complement to \(W\) in \(V\)

 

 

 

 

新向量空间、秩1矩阵

矩阵空间

矩阵空间可以看作是新的向量空间 (New vector space)
以所有3*3矩阵构成的空间\( \mathbf{M}\)为例，该空间内的矩阵符合对于线性运算的封闭性。它含有一些有意思的子空间，包括：
(1)所有上三角阵，记为\( \mathbf{U}\)—Upper Matrix
(2)所有对称阵，记为\( \mathbf{S}\)—Symmetric Matrix
(3)所有对角阵，记为\( \mathbf{D}\)—Diagonal Matrix，它是前面两个子空间的交集

空间\( \mathbf{M}\)的维数为\(9 \)，与\( \mathbf{R}^{9}\)空间很类似，可以选定其一组基：$$\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right], \ldots \ldots\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right]$$

上三角阵构成的子空间\( \mathbf{U}\)的维数为\(6\)，它的一组基为：$$\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right]$$

对称阵构成的子空间\( \mathbf{S}\)的维数为6(知道对角线之上的三个，就知道对角线之下的三个，所以\(9-3=6\)，它的一组基为：$$\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right]$$

对角阵构成的子空间\( \mathbf{D}\)的维数为\( 3\)，可以选定\( \mathbf{U}\)和\( \mathbf{S}\)的基的交集(intersection)作为\( \mathbf{D}\)的基：$$\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right]$$这里我们是把整个矩阵看做一个基，多个矩阵的线性组合(加法和数乘)依旧在这个新空间之中，这个新空间可以看作是\(\mathbf{R}^{n \times n}\)

\( \mathbf{U}\)和\( \mathbf{S}\)空间的交集是\( \mathbf{M}\)的子空间，那么二者的并集是否也是\( \mathbf{M}\)的子空间呢？
不是，\( \mathbf{U}\)空间和\( \mathbf{S}\)空间可以看作是\( \mathbf{M}\)空间中两个不同朝向的子空间(heading for different directions)，或者举个例子形象理解，就像在\( \mathbf{R}^{2}\)空间有两条线分别过零向量的直线(两个子空间)，但是这两条线构成的空间是\( \mathbf{R}^{2}\)的子空间吗？显然不是。

如果我们将\( \mathbf{U}\)空间和\( \mathbf{S}\)空间的所有可能的元素加和，那么可以构成一个新的集合，可以成为和集\( \mathbf{U} + \mathbf{S}\)，它是\( \mathbf{M}\)的一个子空间，其实就是\( \mathbf{M}\)空间本身，其维数为\( 9\)。总结一下就是$$6+6=\operatorname{dim} \mathrm{S}+\operatorname{dim} \mathrm{U}=\operatorname{dim} (\mathrm{S} \cap \mathrm{U})+\operatorname{dim} (\mathrm{S}+\mathrm{U})=3+6$$

微分方程解空间

上面的例子是矩阵空间作为向量空间，下面介绍微分方程的解空间作为向量空间的例子：对于给定微分方程\(\displaystyle\frac{d^2 y}{d x^2}+y=0\)，求解该方程可以视为求解零空间。很容易得到一组解的两个基\(y=\cos x\)和\(y=\sin x\)，即通解为\(y=c_1 \cos x+c_2 \sin x\)。当然解的基不唯一，另一组为\(y=e^{i x}\)和\(y=e^{-i x}\)。\(\operatorname{dim} \text{(solution space)} = 3\)，因为方程是二阶的。这个例子的要点在于这些基不像向量，而是函数，但是我们还是可以称之为向量(更广义的定义)，因为满足线性运算的要求，因此可以在线性代数的范畴内讨论。

 

秩为1的矩阵

矩阵\( \boldsymbol{A}=\left[\begin{array}{lll} 1 & 4 & 5 \\ 2 & 8 & 10 \end{array}\right]=\left[\begin{array}{l} 1 \\ 2 \end{array}\right]\left[\begin{array}{lll} 1 & 4 & 5 \end{array}\right]\)，秩为\( 1\)，同样其转置的秩也是\( 1\)。对于所有秩为\(1 \)的矩阵我们都可以分解为：$$\boldsymbol{A}=U V^\mathrm{T}$$其中\(U \)和\(T \)都是列向量，我们可以将其看做构建其他矩阵的“积木”(building blocks)。

对于任意一个\(5 \times 17 \)并且秩为\(4 \)的矩阵，我们一定可以通过四个秩为\( 1\)的矩阵搭建而成。

所有满足\(5 \times 17 \)并且秩为\(4 \)的矩阵是否构成一个子空间？
不是的，即使加入零矩阵也不行，主要是这个集合不具有封闭性。两个矩阵之和的秩一定小于两个秩的加和，同样也一定小于行数和列数的最小值，但是不一定是\(4\)。

 

 

 

图、网络和关联矩阵

【图和网络】(graphs and networks)
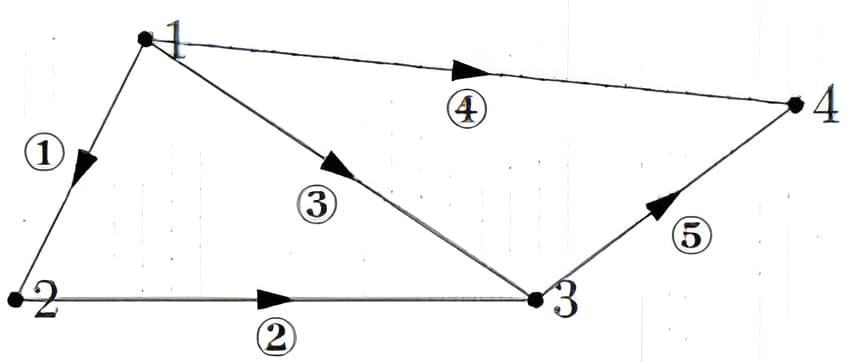
"图"就是“结点”和“边”的一个集合\(\mathrm{G}=\{\) nodes， edges \(\}\)。边线上的箭头表示结点流出的正方向。下面的图包含\(4\)个结点和\(5\)条边，我们可以利用一个\(5 \times 4\)的矩阵完全描述它。

我们可以用图来描述一个实际问题，如果每个人是一个结点，两个人互相认识为一个边，那么整个美国可以以此构成一张大图。我们可以通过这张图来确认两个人之间的最短距离是多少，即两个人需要通过最少几个朋友才能建立联系。G.Strang本人和克林顿之间的距离为2，他的一个朋友是参议员，他认识这个参议员朋友，那个人认识克林顿。班里的学生跟克林顿的距离因此不会大于3。还可以继续算希拉里和莱温斯基…… 所谓【六度分割理论】(six degrees of separation)猜想一个人和陌生人之间间隔的点不会超过六个。因此当陌生的两人聊起这种联系都会感叹：“世界真小啊！”这也是【小世界图/小世界网络】(Small-world network)这个名字的由来。

【关联矩阵】(incidence matrices)
构造一个矩阵来表示图的内在含义，此矩阵称为关联矩阵，图中每个结点代表一列，每个边代表一行。于是上面的图可以表示为\( 5 \times 4\)的矩阵，反过来，从这个矩阵出发我们也能画出图，矩阵和图是一一对应的。

\( 1\)表示流入，\( -1\)表示流出。边123构成一个封闭的回路(loop)。反映在矩阵上式三个行向量线性相关。如果我们研究一个很大的图，则会构建一个很大的矩阵，但是这个矩阵会是稀疏矩阵。

(1) 矩阵\( A\)的零空间
令$$A \mathbf{x}=\left[\begin{array}{l} x_{2}-x_{1} \\ x_{3}-x_{2} \\ x_{3}-x_{1} \\ x_{4}-x_{1} \\ x_{4}-x_{3} \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array}\right]$$如果\( x_{i}\)表示的是结点\( i\)的电势，那么\(\boldsymbol{A} \mathbf{x} \)表示的是每个边上的电势差。很容易知道矩阵\( A\)的秩是\( 3\)，所以零空间的维数\(n-r=4-3=1 \)，也即\(\operatorname{dim} \mathrm{N}(\boldsymbol{A})=1 \)，基向量为\(\left[\begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \end{array}\right] \)，解集为\( \mathbf{x}=\mathrm{c}\left[\begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \end{array}\right]\)，表示的是各个结点的电势大小。等式\( \boldsymbol{A} \mathbf{x}=\mathbf{0}\)就表示，在通解的集合(零空间)内，由于各点是等电势，所以不会有电流，对应于等式右侧的\( 0\)。常数\( c\)的确定需要边界条件，比如我们将结点\( 4\)接地，则\(x_{4}=0 \)。

        如果是求解\(\boldsymbol{A} \mathbf{x}=\mathbf{b}\)，相当于在给定了这五条边上的电势差，让你求每一个结点的电势大小。当然如果\(b \)选取不恰当的话，方程是无解的，比如如果回路\(123 \)的电压降加和不是\( 0\)，方程肯定无解，因为不符合实际。在考虑有解的情况，由于零空间的存在，使得最终的通解是一个向量空间，只有当零空间的系数\( c\)确定，我们才能得到每个结点电势的准确值。这类似于求积分要加上常函数，常函数的值由边界条件来确定，我们这里的边界条件就是让某个结点接地。

(2) 矩阵\( A\)的列空间
边\( 123\)构成了一个封闭回路，边\( 345\)构成了一个封闭回路。于是只有当\( b\)满足\(b_{1}-b_{2}+b_{3}=0 \)和\(b_{3}-b_{4}+b_{5}=0 \)的时候，方程\(\boldsymbol{A} \mathbf{x}=\mathbf{b} \)才有解。另外也存在一个更大的闭合回路\(1245 \)，于是又可以得到一个与\( b\)有关的等式，但是是前面两个的等式的组合，也就是说三个环路，只有两个是线性无关的。这些等式，从物理的角度看，就是KVL(基尔霍夫电压定律)，即环路电势差之和为\(0 \)。

(3) 矩阵\( A\)的左零空间(无源场)
左零空间就是满足\( \boldsymbol{A}^{\mathrm{T}} \mathbf{y}=\mathbf{0}\)的向量\( \mathbf{y} \)的集合。矩阵\(\boldsymbol{A}^{\mathrm{T}} \)有\(5\)列(未知数个数为\( 5\))，而秩为\( 3\)，于是左零空间的维数为\(2 \)(自由变量的个数\( 5-3=2\))。这反映了行向量的线性关系，整个图中，环数为\( 2\)。$$A^\mathrm{T} \mathbf{y}=\left[\begin{array}{rrrrr} -1 & 0 & -1 & -1 & 0 \\ 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 1 & 1 \end{array}\right]\left[\begin{array}{l} y_{1} \\ y_{2} \\ y_{3} \\ y_{4} \\ y_{5} \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \end{array}\right]$$\( \mathbf{y} \)分量的值为“边”上的电流。在电势差和电流之间建立联系的就是欧姆定律。前面我们通过\(A \mathbf{x} \)得到了相邻结点之间的电势差，这里我们又得到了每一对相邻结点的边上的电流大小，于是我们就很容易求出每个边的电阻大小。

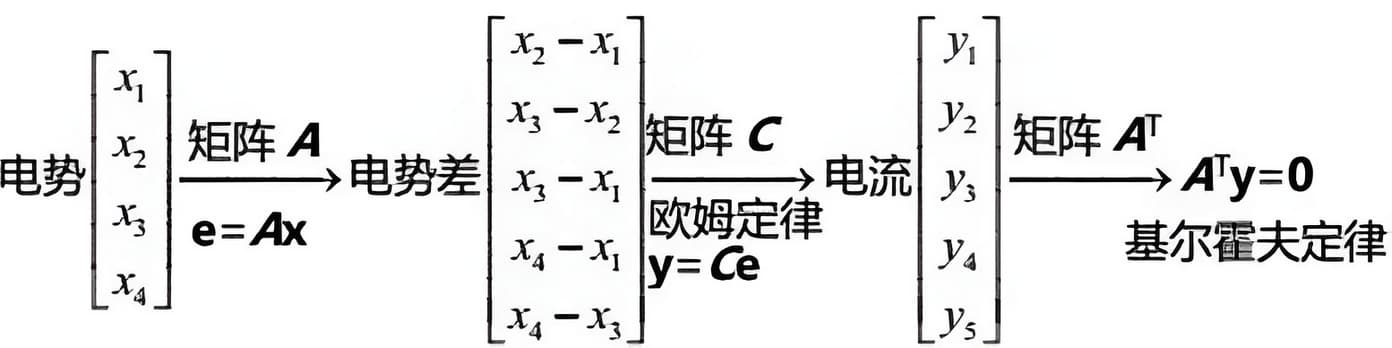
求解\( \boldsymbol{A}^{\mathrm{T}} \mathbf{y}=\mathbf{0}\)实际是在构建\( 5\)个结点的基尔霍夫电流定律KCL方程。
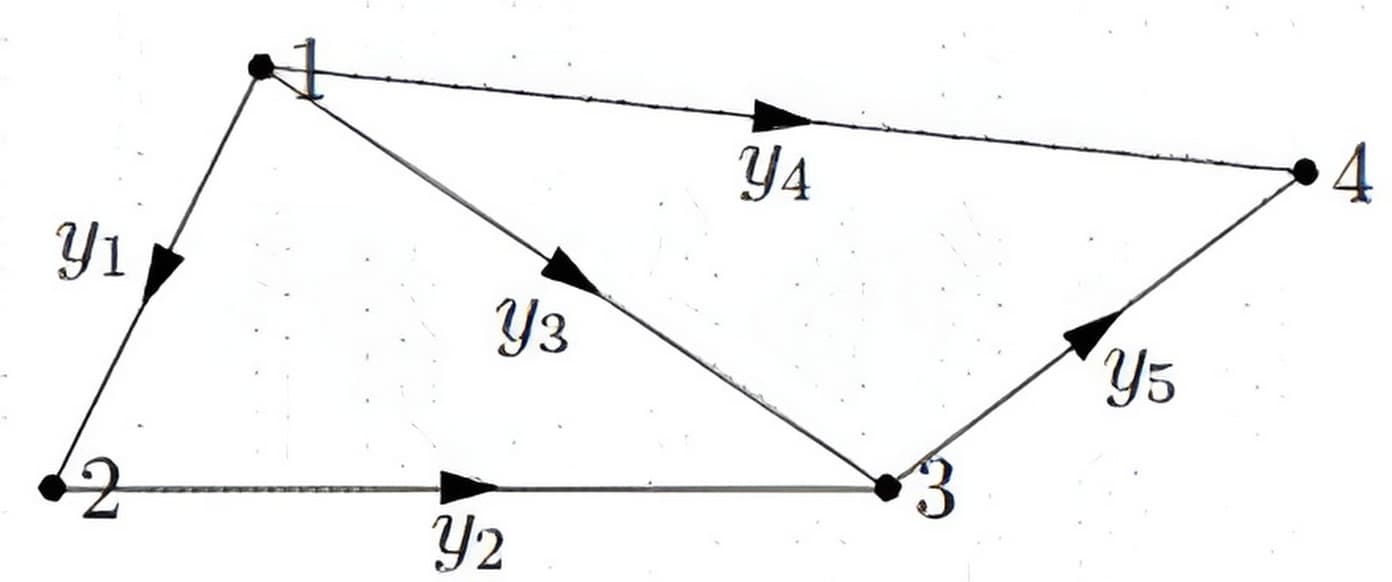每一个结点，电流的净流量为零(流入和等于流出和)。方程的形式如下$$\begin{aligned} -y_{1}-y_{3}-y_{4} &=0 \\ y_{1}-y_{2} &=0 \\ y_{2}+y_{3}-y_{5} &=0 \\ y_{4}+y_{5} &=0 \end{aligned}$$先前我们已经知道了方程零空间的维数是2，那么我们这里只需要求解出两个不相关的基即可张成零解的空间。当然我们可以将矩阵化成行最简形，然后让两个自由变量依次取1，对应的另一个取0，可以得到零解的两个基。这里我们直接采用观察的办法，先让\(y_{1}=1 \)，那么对于结点2，流入必须等于流出，所以\(y_{2}=1 \)，另外我们可以考虑最特殊的情况，即\(y_{4}=0 \)和\(y_{5}=0 \)，那么对于环123，没有电荷积累，那么必有\(y_{3}=-1 \)，这里的负号其实表示真正的电流方向和图中的箭头方向相反，总之最终的特解一为\(\mathbf{y}=\left[\begin{array}{r} 1 \\ 1 \\ -1 \\ 0 \\ 0 \end{array}\right] \)。同样的方法，我们让\(y_{1}=0 \)和\(y_{2}=0 \)，然后给环路345赋上合理的值，得到特解二\( \mathbf{y}=\left[\begin{array}{r} 0 \\ 0 \\ 1 \\ -1 \\ 1 \end{array}\right]\)。这两个特解的线性组合构成了矩阵\(  A\)的左零空间。当然我们也可以让\(y_{3}=0 \)，从而给环路1254的电流赋上合理的值，但是得到的结果和前面的两个特解是线性相关的，即只可能有两个基。

(4) 矩阵\( A\)的行空间
因为矩阵\( A\)的秩为\( 3\)，所以存在三个线性无关的向量。第一行、第二行和第四行线性无关。在图中表现的就是这三条边不构成一个回路。一组向量线性相关的问题就变成了是否能够形成闭合回路的问题，相关性来源于回路。很显然，边\( 124\)不构成闭合回路，但是其他的所有的边都可以由这三个边组合而成，而且多加其他任何一个边，都会形成闭合回路，使得这组行向量线性相关。线性无关的边\(124 \)包含\(4 \)个结点，\(3 \)条边。没有回路的图称为【树】。

维数公式在“图”中的意义
左零空间的维数\(\operatorname{dim} \mathrm{N}\left(\boldsymbol{A}^\mathrm{T}\right)=\mathrm{m}-\mathrm{r} \)；
等价于“环”的数量=“边”的数量-(“结点”数量-1)；
即【欧拉公式】：“结点”-“边”+“环”=1对所有图都成立。
2022补充理解：环的数量，对应于独立KVL的数量，节点数量-1代表的是独立结点的个数，因为我么只要知道(节点数量-1)个结点的信息，那么最后一个结点的信息也可以推出来。上面的式子可以进结点数量和环的数量位置互换，那么等式左侧即结点的数量，那么对应于独立KCL的数量。

上面的“环”的数量严格来讲是网洞的数量，或者说不囊括(包围)任何边的的环路的数量。“边”的数量就对应于矩阵的行数，“结点”的数量就是列的数量\( n\)，由于我们先前得到矩阵\(A \)的零空间是一维的，也就是说只有一个自由变量(自由列)，于是秩(主元列)就是\(n-1 \)(即结点数量-1)。这里的秩也可以看做是线性无关边的数目，也就是“树”中的边数。

对于一个球面同胚的多面体，其欧拉公式为\(V-E+F=2 \)，这里的\(2 \)是【欧拉示性数】，对应的是一个【拓扑不变量】。我们前面讨论的平面情况，其欧拉示性数为\(1 \)。我们这里讲的每一个“环”其实是空间中多面体的每一个“面”。如果将上图中的点\( 24\)相连，然后拉成一个多面体，那么“环”(面)会加\( 2\)，边会加\(1 \)，于是得到的欧拉示性数加一变成\( 2\)。

参考资料：
(1) Euler's polyhedron formula-Wiki
(2) 欧拉公式—数学乐

 

有源场
之前讨论的都是无源场，有源场的情况分为电流源和电压源。对于电流源(接在特定的节点上)，我们需要修改等式\( \boldsymbol{A}^{\mathrm{T}} \mathbf{y}=\mathbf{0}\)右边，变成\( \boldsymbol{f}\)(表示外部流入的电流)。对于电压源，我们需要修改\(e=\boldsymbol{A} \mathbf{x} \)。注意我们这里都是平衡态的电路，和时间是无关的(不考虑电感)。

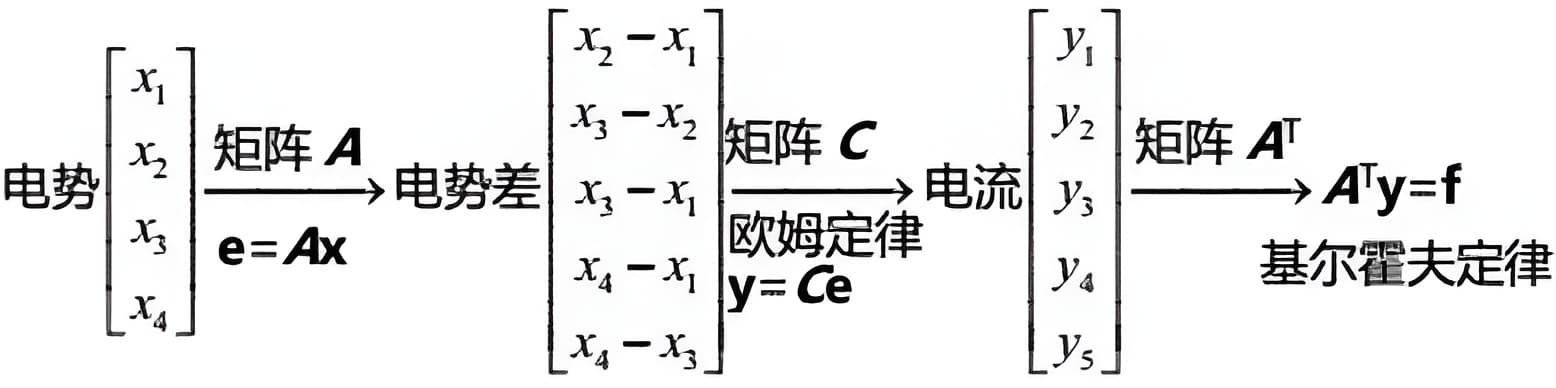将\(\mathbf{e}=A \mathbf{x}, \mathbf{y}=C e, A^\mathrm{T} \mathbf{y}=\mathbf{f} \)三个等式结合得到应用数学中的基本方程\(\mathbf{A}^\mathrm{T} C \mathbf{A} \mathbf{x}=\mathbf{f} \)。\(\mathbf{A} \)转置和自身相乘得到的是对称阵，教授特别提到，另外有网友提到“结点导纳矩阵”，有时间可以看一下。具体例子可以看MIT-电路和电子的笔记，如下图：图中的conductivity matrix对应的就是导纳矩阵，因为这里没有虚部的电抗，所以阻抗就是电阻，导纳就是电阻的导数，该矩阵其实就是\(\mathbf{A}^\mathrm{T} C \mathbf{A}\)。参考资料：电路分析的计算机方法初步

 

 

复习1

Q-1. \(\mathbf{R}^{7} \)空间中的三个非零向量，它们张成了\(\mathbf{R}^{7} \)空间中的子空间，那么这个子空间可能的维数是多少？
答：1、2、3，空间的基的个数不超过三个。

Q-2. 给定矩阵\(\mathbf{U}\)为\( 5 \times 3 \)阶梯型矩阵(这里其实是行最简形)，其秩为\(3 \)。
(1) 求解\( \mathbf{U}\)的零空间\( N(\mathbf{U}) \)
答：列向量线性无关，所以没有自由变量，于是\(\mathrm{N}(\mathcal{\mathbf{U}})=\{0\}=\left\{\left[\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right]\right\} \)
(2)令\( B=\left[\begin{array}{c} U \\ 2 U \end{array}\right]\)，求其行最简形和秩？
答：行最简形为\( \left[\begin{array}{l} U \\ 0 \end{array}\right]\)，秩为\(3 \)。
(3)求\(C=\left[\begin{array}{ll} U & U \\ U & 0 \end{array}\right] \)的行最简形以及它的秩？
答：消元操作$$\left[\begin{array}{ll} U & U \\ U & 0 \end{array}\right] \rightarrow\left[\begin{array}{cc} U & U \\ 0 & -U \end{array}\right] \rightarrow\left[\begin{array}{cc} U & 0 \\ 0 & -U \end{array}\right] \rightarrow\left[\begin{array}{ll} U & 0 \\ 0 & U \end{array}\right]$$当然要得到行最简形，需要把上面那个\( U\)最下面的零行移到整体的大矩阵的最下面。秩为\(6 \)。
(4)求\(C \)的左零空间\( \operatorname{dim} \mathrm{N}\left(\boldsymbol{C}^\mathrm{T}\right)\)的维数？
答：\( \operatorname{dim} \mathrm{N}\left(\boldsymbol{C}^\mathrm{T}\right)=m-r=10-6=4\)

Q-3. \(A \mathbf{x}=\left[\begin{array}{l} 2 \\ 4 \\ 2 \end{array}\right] \)其中\(\mathbf{x}=\left[\begin{array}{l} 2 \\ 0 \\ 0 \end{array}\right]+c\left[\begin{array}{l} 1 \\ 1 \\ 0 \end{array}\right]+d\left[\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right] \)为通解。
(1)矩阵\(A \)的形状？
答：很容易知道行数为\(3 \)，列数的话，我们看通解，从通解的形式看，我们知道主元只有一个，自由变量有两个，说明矩阵的列数为\( 3\)，所以是\(3 \times 3 \)矩阵。
(2)矩阵\( A\)的行空间的维数？
答：根据前面那四个子空间的图，现在我们知道零空间的维数是\( 2\)，那么行空间的维数就是\( 3-2=1\)。
(3)求解矩阵\( A\)？
答：第一步，仅考虑特解，不考虑零空间的解，于是得到第一列的元素为1、2、1；第二步，根据\(A\left[\begin{array}{l} 1 \\ 1 \\ 0 \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right] \)，我们知道每一行的前两个元素的加和为零，于是得到第二列的二元素为-1、-2、1；第三步，采用第二步的方法作用于第三列和另外一个零空间的基向量，得到第三列的元素为0、0、0。于是$$A=\left[\begin{array}{lll} 1 & -1 & 0 \\ 2 & -2 & 0 \\ 1 & -1 & 0 \end{array}\right]$$(4)什么样的向量\( b\)使得\( \boldsymbol{A} \mathbf{x}=\mathbf{b}\)有解？
答：要想方程有解，那么向量\( b\)必须处在\(A \)的列向量张成的空间中，很容易知道，这个空间的维数是\(1 \)，于是\(b \)必须是\(\left[\begin{array}{l} 1 \\ 2 \\ 1 \end{array}\right] \)的倍数方程才有解。

Q-4. 矩阵\( B=C D=\left[\begin{array}{lll} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array}\right]\left[\begin{array}{llrr} 1 & 0 & -1 & 2 \\ 0 & 1 & 1 & -1 \\ 0 & 0 & 0 & 0 \end{array}\right]\)
(1) 给出矩阵\(B \)零空间的一组基？
答：左乘以一个可逆矩阵，相当远对行向量进行可逆的线性变换，既不改变行空间，也不改变零空间。上面已经是行最简形，所以我们让非主元列对应的\( x\)依次取\(1 \)，很容易得到，零空间的一组基为\(\left[\begin{array}{r} 1 \\ -1 \\ 1 \\ 0 \end{array}\right] \)和\(\left[\begin{array}{r} -2 \\ 1 \\ 0 \\ 1 \end{array}\right] \)。

(2)求解\(B \mathbf{x}=\left[\begin{array}{l} 1 \\ 0 \\ 1 \end{array}\right] \)的通解？
答：通解为\(\mathbf{x}=\left[\begin{array}{l} 1 \\ 0 \\ 0 \\ 0 \end{array}\right]+c\left[\begin{array}{r} 1 \\ -1 \\ 1 \\ 0 \end{array}\right]+d\left[\begin{array}{r} -2 \\ 1 \\ 0 \\ 1 \end{array}\right] \)。很容易看出特解(观察第一列)，接着利用利用两个自由变量求出零空间。

 

真假判断

Q-1. 一个矩阵是方阵，其零空间只有零向量，那么它转置的零空间是否也是只有零向量？
答：是的，其转置的零空间只有零向量。

Q-2. 所有五阶可逆矩阵，是否构成五阶可逆矩阵空间的子空间？
答：否，首先不包含零矩阵，所以不是子空间。顺便说一下，奇异矩阵(非可逆矩阵)也不是一个子空间。

Q-3. 如果有\( B^{2}=0\)，是否一定有\( B=0\)？
答：不一定，反例\(B=\left[\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right] \)。

Q-4. \(A\)是方阵，那么列空间和行空间相同？
答：显然错误，因为方阵能够保证行空间和列空间的维数相同(主元数和自由变量的数目都一样)，但是二者的空间不一定相同，比如\(B=\left[\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right] \)。

Q-5. 矩阵\(A \)和\(-A \)的四个子空间是否相同？
答：相同。

Q-6. 如果\(A \)和\( B\)的四个子空间相同，那么\(A \)一定是\(B \)的倍数？
答：不一定，比如二者是同阶可逆矩阵。

Q-7. 如果对矩阵\( A\)进行行交换，四个子空间都不变？
答：错误，只有零空间和行空间。

Q-8. 向量\( \mathbf{v}=\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]\)既在矩阵\(A \)的零空间中，又是\(A \)的一个行向量，可能吗？
答：不可能，如果都满足的话，自己给自己做内积结果应该是\(0 \)，实际上不是零，矛盾。

 

 

 

正交向量和正交子空间

【正交向量】(Orthogonal vectors)
正交是垂直的另一种说法。两个向量正交，那么\(\mathbf{x}^{\mathrm{T}}\mathbf{y}=\mathbf{y}^{\mathrm{T}} \mathbf{x}=0 \)，按照勾股定理有$$|| x||^{2}+|| y||^{2}=|| x+y||^{2}$$其中\( \|\mathbf{x}\|^{2}=\mathbf{x}^{\mathrm{T}} \mathbf{x}\)。

根据勾股定理展开有\( \mathbf{x}^\mathrm{T} \mathbf{x}+\mathbf{y}^\mathrm{T} \mathbf{y}=(\mathbf{x}+\mathbf{y})^\mathrm{T}(\mathbf{x}+\mathbf{y})=\mathbf{x}^\mathrm{T} \mathbf{x}+\mathbf{y}^\mathrm{T} \mathbf{y}+\mathbf{x}^\mathrm{T} \mathbf{y}+\mathbf{y}^\mathrm{T} \mathbf{x}\)，于是\(2 \mathbf{x}^\mathrm{T} \mathbf{y}=0\)零向量与所有向量都正交。

【正交子空间】(Orthogonal subspaces)

在\(\mathbf{R}^{n} \)空间中的向量会向两个子空间投影，并向\(\mathbf{R}^{m} \)空间形成映射，反之亦然。

两个子空间正交，那么各自从中任选一个向量，都正交。黑板平面和地板平面垂直，但是这两个子空间不正交，而且交线不可能垂直于自己。

零空间和行空间，左零空间和列空间
矩阵\(A \)的行空间和它的零空间正交。$$\left[\begin{array}{c} r o w_{1} \\ r o w_{2} \\ \vdots \\ r o w_{m} \end{array}\right][\mathbf{x}]=\left[\begin{array}{c} r o w_{1} \cdot \mathbf{x} \\ r o w_{2} \cdot \mathbf{x} \\ \vdots \\ r o w_{m} \cdot \mathbf{x} \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \\ \vdots \\ 0 \end{array}\right]$$同理可以知道列空间和左零空间正交。

行空间和零空间实际上是\(\mathbf{R}^{n} \)空间分割成的两个子空间，二者相互正交，而且二者的维数和就是\(n \)，我们称二者为\(\mathbf{R}^{n} \)空间的正交补。比如对于矩阵$$A=\left[\begin{array}{lll} 1 & 2 & 5 \\ 2 & 4 & 10 \end{array}\right]$$对于其行空间来说，只有一个基向量\( \left[\begin{array}{l} 1 \\ 2 \\ 5 \end{array}\right]\)，而其零空间正好是垂直于这个向量并且穿过原点的二维平面。

【\(A^\mathrm{T} \boldsymbol{A} \)】
我们在求解方程组\(A \mathbf{x}=\mathbf{b} \)时，方程不一定是有解的，特别是当方程的个数很多，但是未知数的个数很少时，很大概率出现无解的情况。实际应用中，我们对天上的卫星位置进行测试，可能得到上千个方程，但是定位卫星位置的参数也就几个。每一组数据，或者说每一个方程都是有实际意义的，只是说“噪音”的存在(或者突然混入“坏”的数据)，以及数据本身的精度问题都会导致方程无解。我们如果强行减少方程的个数，让方程的个数等于未知数的个数，那么方程就有解，但是这个情况下，我们其实是牺牲了很多有用的数据的，反而使得最终算出的结果不够准确。

线性代数要做的就是在这种条件下求一个方程的“最优解”。矩阵\(A^\mathrm{T} \boldsymbol{A} \)会发挥重要作用，这是一个\( n\)阶对称方阵。下面讨论的核心问题就是当\(A \mathbf{x}=\mathbf{b} \)无解的时候，求解\( A^\mathrm{T} A \hat { x } =A^\mathrm{T} b\)得到最优解。

例子1：\( A=\left[\begin{array}{ll} 1 & 1 \\ 1 & 2 \\ 1 & 5 \end{array}\right]\)，则\(A^\mathrm{T} A=\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 2 & 5 \end{array}\right]\left[\begin{array}{ll} 1 & 1 \\ 1 & 2 \\ 1 & 5 \end{array}\right]=\left[\begin{array}{ll} 3 & 8 \\ 8 & 30 \end{array}\right] \)是可逆矩阵。

例子2：\(A=\left[\begin{array}{ll} 1 & 3 \\ 1 & 3 \\ 1 & 3 \end{array}\right] \)，则\(A^\mathrm{T} A=\left[\begin{array}{lll} 1 & 1 & 1 \\ 3 & 3 & 3 \end{array}\right]\left[\begin{array}{ll} 1 & 3 \\ 1 & 3 \\ 1 & 3 \end{array}\right]=\left[\begin{array}{ll} 3 & 9 \\ 9 & 27 \end{array}\right] \)是不可逆矩阵。

实际上，二者的零空间相同\(\mathrm{N}\left(\boldsymbol{A}^\mathrm{T} \boldsymbol{A}\right)=\mathrm{N}(\boldsymbol{A}) \)，并且二者的秩相同。因此矩阵\(A^\mathrm{T} \boldsymbol{A} \)可逆要求\(A \)的零空间只有零向量，也就是\(A \)的列向量线性无关。

 

子空间投影

【投影(projections)】
投影问题的几何解释就是：如果在向量\( \mathbf{a}\)的方向上寻找向量\( \mathbf{b}\)距离最近的一点。如果我们将向量\(\mathbf{p} \)视为\(\mathbf{b} \)的一种近似，则长度\(\mathbf{e}=\mathbf{b}-\mathbf{p} \)就是这一近似的误差。

因为\( \mathbf{p}\)在向量\( \mathbf{a}\)的方向上，因此可以令\( \mathbf{p}=x \mathbf{a}\)，而因为它和\( \mathbf{e}\)正交，我们可以得到方程\( \mathbf{a}^\mathrm{T}(\mathbf{b}-x \mathbf{a})=0\)。解得：$$x=\frac{\mathbf{a}^\mathrm{T} \mathbf{b}}{\mathbf{a}^\mathrm{T} \mathbf{a}}, \mathbf{p}= \mathbf{a} x=\mathbf{a} \frac{ \mathbf{a}^\mathrm{T} \mathbf{b}}{ \mathbf{a}^\mathrm{T} \mathbf{a}}$$【投影矩阵(projections matrix)】
我们将投影问题用投影矩阵的方式来描述，即\(\mathbf{p}=P \mathbf{b} \)，其中\(P \)为投影矩阵，\(P=\displaystyle\frac{a a^\mathrm{T}}{a^\mathrm{T} a}\)，其中分子是一个矩阵，分母是一个数。继续观察这个投影矩阵，我们会发现其列空间就是向量\(\mathbf{a} \)所在的直线，因此秩为\(1 \)。右边再乘以一个列向量\(\mathbf{b} \)，显然得到的结果仍处在列向量\(\mathbf{a} \)张成的空间。如果再用投影矩阵作用，得到的结果不变，\(P^{2} \mathbf{b}=P \mathbf{b} \)，第二次投影还在原来的位置。因此矩阵\( P \)具有如下的性质：$$P^\mathrm{T}=P, P^{2}=P$$

投影的好处：
方程组\(A \mathbf{x}=\mathbf{b} \)可能无解，我们需要得到方程的“最优解”。这里的问题在于\(A \mathbf{x} \)一定在\(A \)的列空间之内，但是\( \mathbf{b}\)不一定，因此我们希望将\( \mathbf{b}\)投影到\(A \)的列空间得到\( \mathbf{p}\)，于是将问题转化为求解\(A \hat { x } = \mathbf{p} \)。

【高纬投影(projection in higher dimensions)】
在\(\mathbf{R}^{3} \)空间内，如何将向量\( \mathbf{b}\)投影到它距离平面最近的一点\(\mathbf{p} \)？

注：在证明投影矩阵是对称矩阵的时候，其实用到了矩阵转置和求逆的可交换性\( \left(A^{T}\right)^{-1}=\left(A^{-1}\right)^{T}\)，可以看知乎进一步理解。

【误差向量\( \mathbf{e}\)】和投影平面垂直，位于矩阵\(A \)的左零空间，这两点在和GS的经典四个子空间图对应；左零空间的任何向量一定垂直于列空间(前面提到的投影平面)的任何向量。$$\begin{array}{l} e \text { in } N\left(A^\mathrm{T}\right) \\ e \perp C(A) \end{array}$$对比方程\( \mathbf{a}^\mathrm{T}(\mathbf{b}-x \mathbf{a})=0\)和\( A^\mathrm{T}(b-A \hat{x})=0\)。

【最小二乘法(least squares)】

应用投影矩阵求方程组最优解(前面我们提到的\( \hat { x }\))的方法，最常用于“最小二乘法”的拟合曲线。三个点代表三个方程$$\begin{aligned} &C+D=1\\ &C+2 D=2\\ &C+3 D=2 \end{aligned}$$写成矩阵的形式$$\left[\begin{array}{ll} 1 & 1 \\ 1 & 2 \\ 1 & 3 \end{array}\right]\left[\begin{array}{l} C \\ D \end{array}\right]=\left[\begin{array}{l} 1 \\ 2 \\ 2 \end{array}\right]$$这个方程\( \boldsymbol{A} \mathbf{x}=\mathbf{b}\)是无解的，解决办法就是求最优解，即求\(\boldsymbol{A}^\mathrm{T} \boldsymbol{A} \hat{\mathbf{x}}=\boldsymbol{A}^\mathrm{T} \mathbf{b} \)的解。

再谈投影(projection)
在高维投影的问题中，我们谈到了投影矩阵\(P=A\left(A^\mathrm{T} A\right)^{-1} A^\mathrm{T} \)，当它作用于向量\( \mathbf{b} \)，相当于把\( \mathbf{b} \)投影到矩阵\(A \)的列空间。
(1)如果向量\( \mathbf{b} \)本身就在\(A \)的列空间(也就是存在\( \mathbf{x} \)使得\(A\mathbf{x}=\mathbf{b} \)，则有：$$\begin{aligned} \boldsymbol{P} \mathbf{b} &=\boldsymbol{A}\left(\boldsymbol{A}^\mathrm{T} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^\mathrm{T} \mathbf{b} \\ &=\boldsymbol{A}\left(\boldsymbol{A}^\mathrm{T} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^\mathrm{T} \boldsymbol{A} \mathbf{x} \\ &=\boldsymbol{A}\left(\left(\boldsymbol{A}^\mathrm{T} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^\mathrm{T} \boldsymbol{A}\right) \mathbf{x} \\ &=\boldsymbol{A} \mathbf{x}=\mathbf{b} \end{aligned}$$
(2)如果向量\( \mathbf{b} \)与\(A \)列空间正交，也就是在矩阵\( A\)的左零空间，则有：$$P \mathbf{b}=A\left(A^\mathrm{T} A\right)^{-1} \boldsymbol{A}^\mathrm{T} \mathbf{b}=\boldsymbol{A}\left(\boldsymbol{A}^\mathrm{T} \boldsymbol{A}\right)^{-1}\left(\boldsymbol{A}^\mathrm{T} \mathbf{b}\right)=\boldsymbol{A}\left(\boldsymbol{A}^\mathrm{T} \boldsymbol{A}\right)^{-1} \mathbf{0}=\mathbf{0}$$

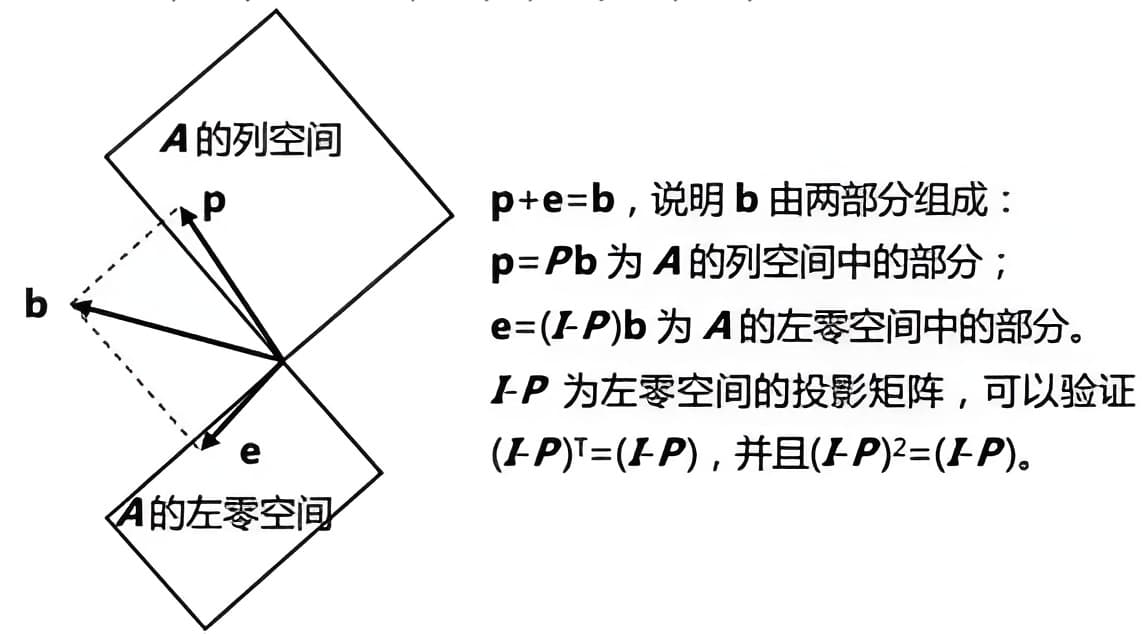
仔细品味左零空间的投影矩阵。

再谈最小二乘法

要求拟合的直线尽量接近这三个点。根据点坐标有方程：$$\begin{matrix} & C+D=1 \\ & C+2D=2 \\ & C+3D=2 \end{matrix}\left[ \begin{array}{ll} 1 & 1 \\ 1 & 2 \\ 1 & 3 \end{array} \right] \quad \Rightarrow \quad \left[ \begin{array}{l} C \\ D \end{array} \right] =\left[ \begin{array}{l} 1 \\ 2 \\ 2 \end{array} \right] $$方程是无解的，现在要做的是求“最优解”，也就是让误差平方和最小，也就是让\(||\mathbf{e}||^{2}=||\boldsymbol{A} \mathbf{x}-\mathbf{b}||^{2} \)最小。注意这里其实每个点代表一个维度，在三个维度上误差平方和就是“总的误差向量”的模长平方。\(||\mathbf{e}||^{2}=||\boldsymbol{A} \mathbf{x}-\mathbf{b}||^{2}=e_{1}^{2}+e_{2}^{2}+e_{3}^{2} \)这就叫做“线性回归”，在没有离群值(outlier)的情况下这种方法比较有效。接下来用两种方法求解最优解：
(1)方法一(向量空间角度)：我们知道向量\(\mathbf{b} \)在左零空间的投影就是误差向量\(\mathbf{e} \)，投影到\( \mathbf{A} \)的列空间得到的是向量\(\mathbf{p} \)。根据误差向量属于左零空间，我们有\(A^\mathrm{T}(\mathbf{b}-A \hat{\mathbf{x}})=0 \)，其中\( \mathbf{b}-A \hat{\mathbf{x}}=\mathbf{b}-\mathbf{p}=\mathbf{e}\)。我们想一下，\( A^\mathrm{T}\)每一行就是\(A \)的列向量，我们知道\(A \)的列空间和误差向量\(\mathbf{e} \)正交，于是有\( A^\mathrm{T}\)每一行和\(\mathbf{e} \)的每一列内积都是零。$$A^\mathrm{T}(\mathbf{b}-A \hat{\mathbf{x}})=0 \quad \Rightarrow \quad A^\mathrm{T} A \hat{\mathbf{x}}=A^\mathrm{T} \mathbf{b}$$其实我们把\(A^{\mathrm{T}} A  \)移到等式右边，然后两边同时乘以矩阵\(  A\)即“投影矩阵”的形式$$A \hat{x}=\boldsymbol{P} \mathbf{b}$$其中\(\boldsymbol{P}   \)为投影矩阵。带入数据到\( A^{\mathrm{T}} A \hat{\mathbf{x}}=A^{\mathrm{T}} \mathbf{b} \)我们得到$$\left[\begin{array}{cc} 3 & 6 \\ 6 & 14 \end{array}\right]\left[\begin{array}{l} \hat{C} \\ \hat{D} \end{array}\right]=\left[\begin{array}{c} 5 \\ 11 \end{array}\right]$$于是解得\( \hat { { \mathbf{x} } } =\left[ \begin{array}{l} \hat { C } \\ \hat { D } \end{array} \right] =\left[\begin{array}{l} 3 / 2 \\ 1 / 2 \end{array}\right]\)

注意：我们不能写成\((\mathbf{b}-A \hat{\mathbf{x}})A^{\mathrm{T}}=0  \)的形式，因为这样写会让\(A^{\mathrm{T}} A  \)不是一个整体，而是分开了，后面就不能变换了。另外\(A^{\mathrm{T}} A \hat{\mathbf{x}}=A^{\mathrm{T}} \mathbf{b}  \)不能直接把等式左边的\(  A^{\mathrm{T}}\)移到右边，因为\(  A^{\mathrm{T}}\)不是方阵，不存在逆矩阵，能移动的是\( A^{\mathrm{T}} A \)，此矩阵比为方阵，存在逆矩阵。

(2)方法二(误差最小角度)：$$e_{1}^{2}+e_{2}^{2}+e_{3}^{2}=(C+D-1)^{2}+(C+2 D-2)^{2}+(C+3 D-2)^{2}$$求解偏导数为零的点，同样可以得到相同的结果。

我们求得最优解直线的表达式之后，就可以得到向量\(\mathbf{p} \)和向量\(\mathbf{e} \)的具体值，二者求内积为零。

如何证明矩阵\( A\)的列向量线性无关时，\( A^\mathrm{T} A\)为可逆矩阵？
假设不是可逆矩阵，那么存在不等于零的\(x \)使得\( A^\mathrm{T} Ax=0\)，于是\(\mathbf{x}^\mathrm{T} \boldsymbol{A}^\mathrm{T} \boldsymbol{A} \mathbf{x}=\mathbf{0}=(\boldsymbol{A} \mathbf{x})^\mathrm{T}(\boldsymbol{A} \mathbf{x}) \)，接下来就很容易证明了。