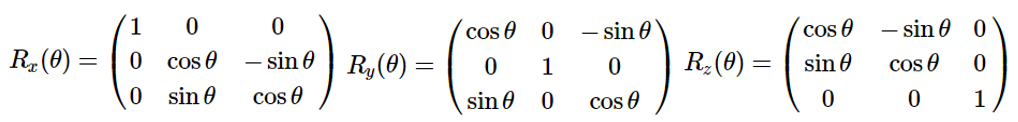参考资料:
姐妹课程笔记:群论及其在物理学中的应用导论
国科大群论笔记
Chem.Libretexts — Symmetry
ChemTube3D-symmetry图片
Advanced Inorganic Chemistry
Character table-查询
山西师范大学
群的数学&对称操作/元素
- 封闭性(closure):任何两个元素的乘积仍然属于;
- ,它与中任何元素\(g_i\)的乘积仍等于\(g_i\),即\(g_i \times E = E\times g_i=g_i\);
- 结合律(associate law):对任何三个元素必有\(g_j\times (g_k \times g_l)=(g_j\times g_k) \times g_l\)
群。注意这里所谓的“乘积”,并不等同于两个数在算术意义上的相乘,而是一种二元运算方式,可以自己定义。
群中任意两个元素(操作)\(g_i g_k=g_k g_i\)则对应Abelian群。
群的例子: 定义群的乘法为数的加法,则全体整数构成一个群,\(0\)是其中的单位元素,\(n\)与\(-n\)互逆。同理,全体实数也在这个乘法规则下构成一个群,全体复数也是。但如果我们把乘法定义为数乘,那么它们就不再是群了,因为这种情况下 单位元素只能是\(1\),而\(0\)是没有逆的。
【阶】可以分为两种:下文中采用第一种定义
- 一个群的阶是指其势,即其元素的个数;
- 对任意一个有限群\(G\),从中取一个元素\(a\),从\(a\)出发作幂操作,总是可以构成\(G\)的一个循环子群\(Z_k\)的,这个\(Z_k\)等于\(\{a, a^{2}, \cdots, a^{k-1}, a^{k}=e\}\),这时称\(k\)(满足这个性质的最小的\( k\))为群元素\(a\)的阶。
对称操作(symmetry operation) & 对称元素 (symmetry element): Molecular symmetry will dictate chemical bonding, consequently it also dictates the spectroscopic properties that molecules possess and their reactivity. A point group is a set of symmetry operations that obey the laws of groups, all of which will leave one point in an object unchanged.
Some applications of group theory that will be covered in this course include:
- Predicting whether a given molecule will be chiral ([ˈkaɪrəl] 手性的), or polar.
- Examining chemical bonding and visualising molecular orbitals.
- Predicting whether a molecule may absorb light of a given polarization, and which spectroscopic transitions may be excited if it does.
- Investigating the vibrational motions of the molecule.
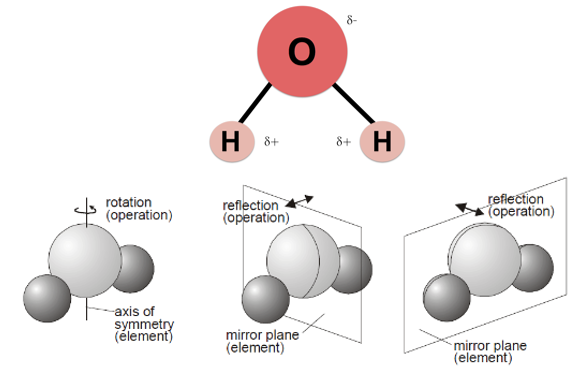 Symmetry Example: H2O,是轴对称(Axial symmetry),即沿着对称轴(a symmetry axis)旋转180度和原来的状态重合,另外有两个对称面(a plane of symmetry),而且都之前的对称轴都在对称面上。
Symmetry Example: H2O,是轴对称(Axial symmetry),即沿着对称轴(a symmetry axis)旋转180度和原来的状态重合,另外有两个对称面(a plane of symmetry),而且都之前的对称轴都在对称面上。
Symmetry Elements:
- \(E\) —— the identity.
- \(C_n\) —— an \(n\)-fold axis of rotation. 水分子有\( C_2\) axis. 一些molecules有more than one \( C_n\)轴,其中with the highest value of \(n\) is called the principal axis(主轴). 习惯逆时针旋转。
- \( \sigma\) —— a plane of symmetry. In a molecule that also has an axis of symmetry,
- \( \sigma_{v}\) —— a mirror plane that includes the axis is called a vertical mirror plane
- \(\sigma_{h}\) —— a mirror plane that perpendicular to the axis is called a horizontal mirror plane
- \(\sigma_{d}\) —— a mirror plane that bisects the angle between two \(C_2\) axes is called a dihedral mirror plane
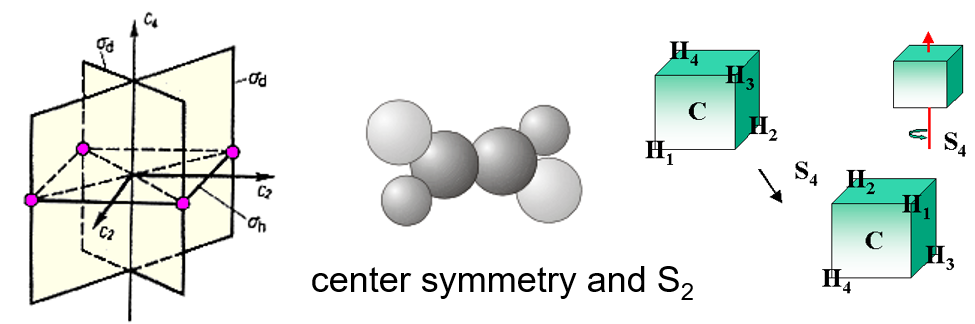
- \(i\) —— 中心对称
- \(S_n\) —— \(S_n\) = rotation of 360°/\(n\) + perpendicular mirror reflection = \(C_n\) + \( \sigma_{h}\) 中文叫作【瑕旋转】(improper rotation axis)或旋转反射(rotary-reflection)
- \(S_1\) = \( \sigma\)
- \(S_2\) = \(i\),上图中间的分子有两个\(S_2\) axes
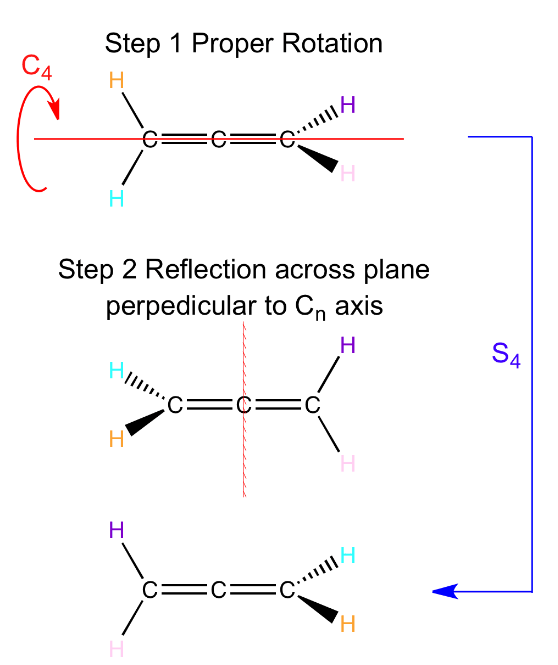
- 丙二烯的\(S_4\)对称元素,注意丙二烯不是\(S_4\)的point group
- \(C_2= S_4^2\); \(E= S_4^4\)
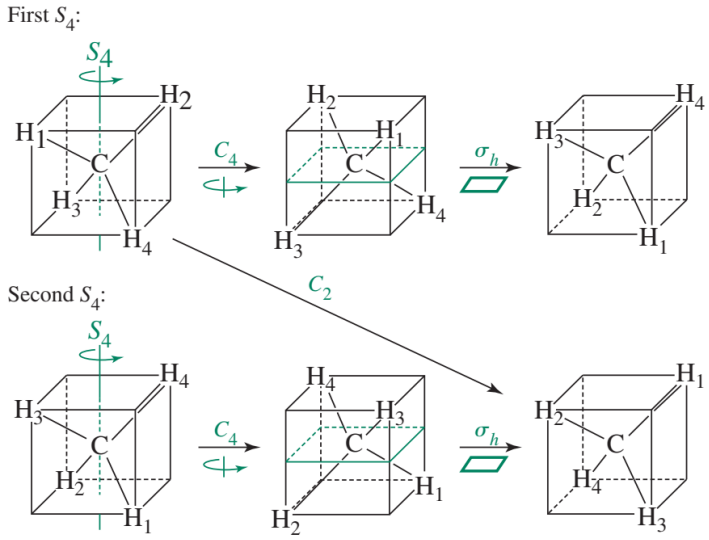
数学上,将unchanged point放在三维坐标原点,那么沿着\(Z\)轴旋转\(\varphi\),然后做\(x-y\)面的反射,这样的旋转反射可以表示为矩阵$$ A=\left(\begin{array}{ccc} \cos \varphi & -\sin \varphi & 0 \\ \sin \varphi & \cos \varphi & 0 \\ 0 & 0 & -1 \end{array}\right) $$实际上就是一个行列式值为\(-1\)的正交矩阵;纯旋转的矩阵是行列式值为\(+1\)的正交矩阵。参考线性代数-2笔记。
Proper Symmetry Operations: \(E\) and rotations \( C_n\) are symmetry operations that could actually be carried out on a molecule. For this reason they are called proper symmetry operations.
Improper Symmetry Operations: Reflections, inversions and improper rotations can only be imagined (it is not actually possible to turn a molecule into its mirror image or to invert it without some fairly drastic rearrangement of chemical bonds) and as such, are termed improper symmetry operations.
对称的分类-分子点群
Grouping together molecules that possess the same symmetry elements and classify molecules according to their symmetry. These groups of symmetry elements are called point groups (due to the fact that there is at least one point in space that remains unchanged no matter which symmetry operation from the group is applied). 化学中的研究的群是Point Group点群。7大晶系,14种点阵,32种点群,230种空间群。下面的学习用的point groups表示方法是【Schoenflies notation】(熊夫利记号),用来描述individual molecules的对称性。【Hermann–Mauguin notation】(赫尔曼–莫甘记号)相比熊夫利记号,在晶体学中更加常用,其原因在于赫尔曼–莫甘记号更易于包含平移对称的元素,且指定了对称轴的方向。
注意,有的point group的名字和某个对称操作的名字一样,不要搞混了,要根据上下文判断。比如丙二烯具有\(S_4\)对称元素,但是不是\(S_4\)点群。
点群的阶数:The total number of operations is called the order \((h)\) of a point group. The order is always an integer multiple of \(n\) of the principal axis. For staggered ethane, \(h=4 n(4 \times 3=12)\).
Nonaxial Point Groups
也是Low-Symmetry Point Groups:含有1-2个symmetry elements
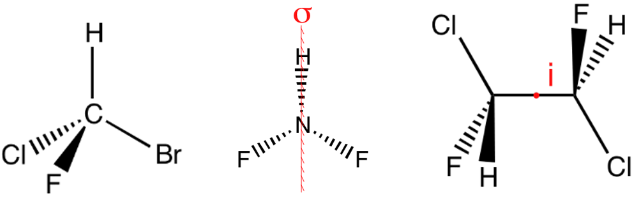
(1) \(C_1\) —— CHBrClF, contains only the identity
(2) \(C_S\) —— NHF2, contains the identity \( E\) and a plane of reflection \( \sigma\)
(3) \(C_i\) —— contains the identity \(E\) and a center of inversion \( i\)
Single-axis Rotation Point Groups
C Groups
These groups have a principal axis \(\left(C_n\right)\) but no \(\perp C_2\) axes.
(4) \(C_n\) —— H2O2 (C2) contains the identity and an \(n\)-fold axis of rotation.
对称元素\(\left\{E,(n-1) C_n\right\}\)
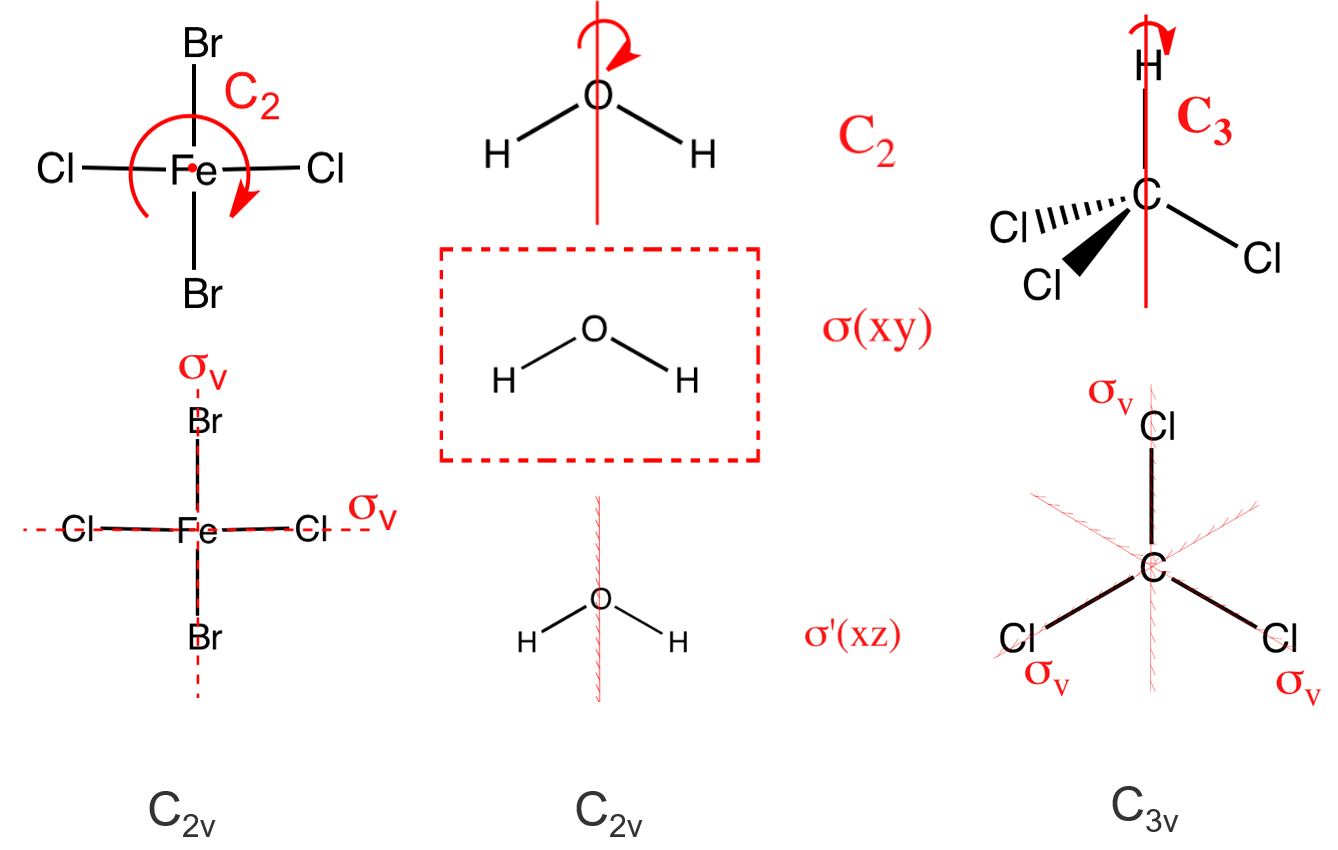
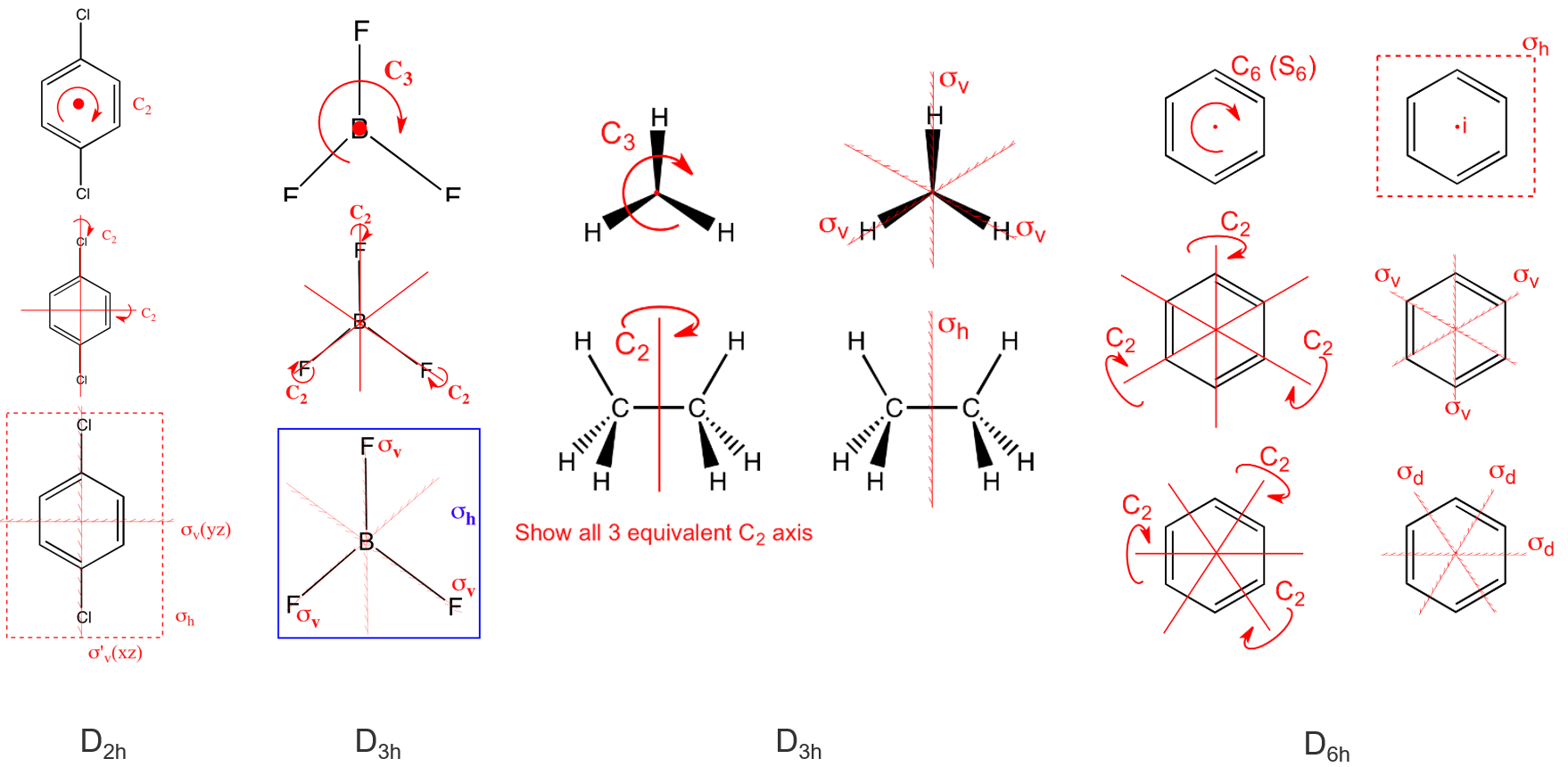
(5) \(C_{nv}\) ——H2O, NH3, CHCl3, contains the identity, an \(n\)-fold axis of rotation, and \(n\) vertical mirror planes \(\sigma_v\).
对称元素\(\left\{E,(n-1) C_n, n \sigma_v\right\}\)
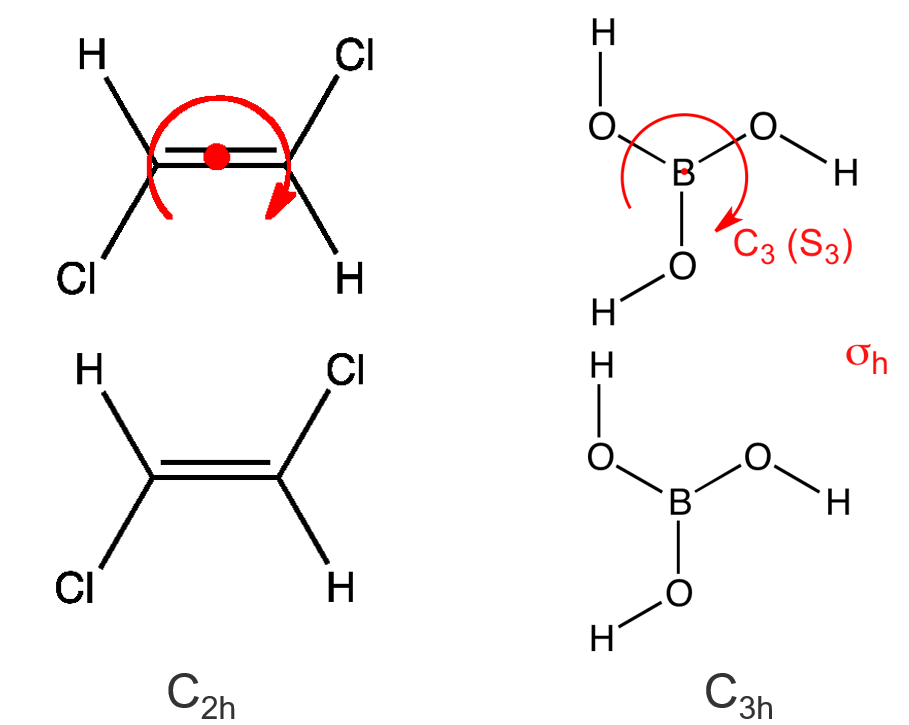
(6) \(C_{nh}\) —— H3BO3 (C3h), contains the identity, an \(n\)-fold axis of rotation, and a horizontal reflection plane \(\sigma_{h}\) (note that in \(C_{2 h}\) this combination of symmetry elements automatically implies a center of inversion)
对称元素{depends on \(n\), with \(h=2 n\)}
(7) \( C_{\infty v} \) —— HBr, HCN, linear molecule with an infinite number of rotation axes and vertical mirror planes \(\sigma_v\).
S Groups
(8) \(S_{2n}\) —— 12-Crown-4 (\(S_{4}\),冠醚的一种),只有 \(S_{2n}\)一种子类,where \(n\) refers to the principal axis of rotation. The \(S\) set of groups is characterized by the absence of \(nC_2\) axes perpendicular to the principal \(C_n\) axis, as well as the absence of horizontal and vertical/dihedral mirror planes. However, there is an improper rotation (or a rotation-reflection) axis collinear with the principal \(C_n\) axis.
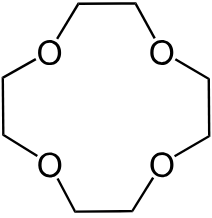
Note: molecules only belong to \(S_{2n}\) if they have not already been classified in terms of one of the preceding point groups (e.g. \( S_{2}\) is the same as \(C_{i}\), and a molecule with this symmetry would already have been classified).
Dihedral Point Groups
These point groups have \(n C_2\) axes perpendicular to a principal axis \(C_n\)
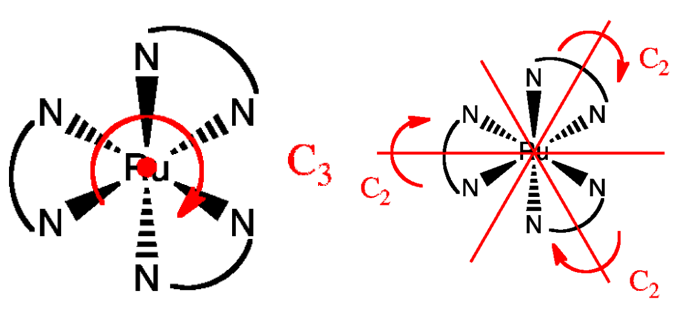
(9) \(D_n\) —— \(\left\{E,(n-1) C_{\mathrm{n}}, n \perp C_2\right\}\) = "contains the identity, an \(n\)-fold axis of rotation, and \(n\) 2-fold rotations about axes perpendicular to the principal axis (\(C_n\))" 下图是\(D_3\)
(10) \(D_{n d}\) —— contains the same symmetry elements as \(D_{n}\) with the addition of \(n\) dihedral mirror planes. 对称元素的个数\(h\)等于\(n\)的四倍。 注意下面\(D_{3 d}\)所对应的的环己烷的碳元素不在同一个平面上。
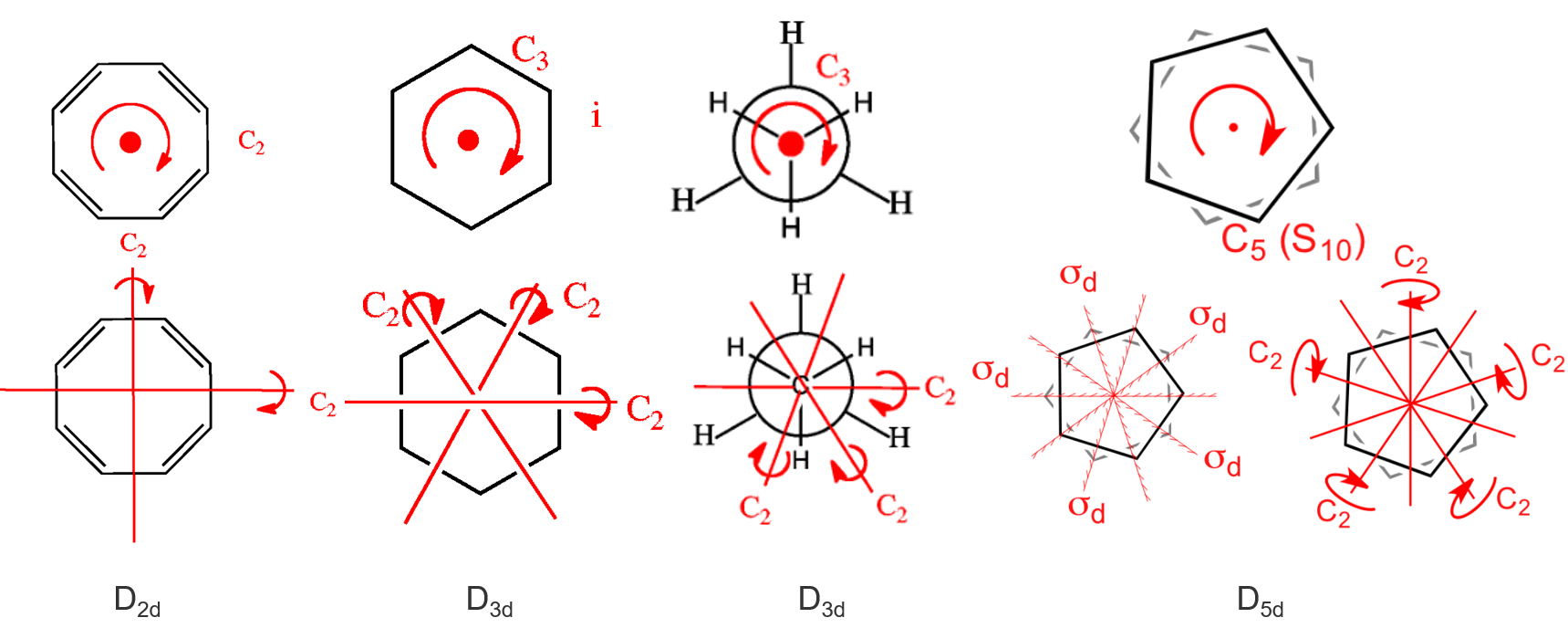
另外的一个例子就是我们之前谈到过的丙二烯 \(D_{2d} = \left\{ E, 2 S_4, C_2, 2 C_2^{\prime}, 2 \sigma_d \right\}\)
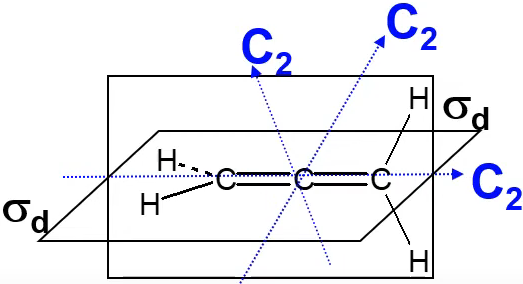
(11) \(D_{nh}\) —— 乙烯(\(D_{2h}\) ) / XeF4 (\(D_{4h}\)) / BF3 (\(D_{3h}\)) /苯环 (\(D_{6h}\)), contains the same symmetry elements as \(D_n\) with the addition of a horizontal mirror plane.对称元素的个数\(h\)等于\(n\)的四倍,比如 \(D_{3 h} = \left\{E, 2 C_3, 3 C_2, \sigma_h, 2 S_3, 3 \sigma_v\right\}\)
(12) \(D_{\infty h}\) ——H2 / CO2, Same as \(D_{n h}\), except the principal rotational axis is an infinite-fold \(C_{\infty}\). This is the point group for all linear centrosymmetric molecules.
Cubic Point Groups
- The cubic groups are the groups of symmetries of the platonic solids:
- tetrahedral groups: \(T_{d}\), \(T_{h}\) and \(T\)
- octahedral groups: \(O_h\) and \(O\)
- icosahedral group: \(I_h\) and \(I\)
- Containing more than one principal axis.
Five regular Platonic solids: the tetrahedron \(\left(T_d\right)\), cube \(\left(O_h\right)\), octahedron \(\left(O_h\right)\), dodecahedron \(\left(I_h\right)\), and icosahedron \(\left(I_h\right)\).
-
- \(T\) = tetrahedral = \(4C_3\) axes
- \(O\) = octahedral = \(3C_4\) axes
- \(I\) = icosahedral = \(6C_5\) axes
【Platonic Solid】(柏拉图立体):在几何学中,凸正多面体,又称为柏拉图立体,是指各面都是全等的正多边形且每一个顶点所接的面数都是一样的凸多面体,是一种三维的正几何形状,符合这种特性的立体总共只有5种,分别是正四、正六、正八、正十二、正十二。李永乐老师讲柏拉图立体





【Archimedean solid】(阿基米德立体): 是一种高度对称的半正多面体,且使用两种或以上的正多边形为面的凸多面体,并且都是可以从正多面体经过截角、截半、截边等操作构造。阿基米德立体的每个顶点的情况相同,共有13种。其中最具代表性的是截角二十面体,即足球的形状,也是C60的形状,包含正五边形*12 + 正六边形*20。李永乐老师讲正多面体, 富勒烯、多面体和中国守门狮
(13) \(T_d\) —— CH4 / P4(白磷),其实就是正四面体(regular tetrahedron)所对应的的point group。
对称元素集合 \(= \left\{E, 8 C_3, 3 C_2, 6 S_4, 6 \sigma_d\right\}=24 \)
包含单位元、\(4C_3\) axes (每个轴对应两个 \(C_3\))、\(3C_2\) axes (每个轴对应一个\(C_2\))、6 dihedral mirror planes (对应\(6 \sigma_d\))、 \(3S_4\) axes (每个对应两个\(S_4\),因为分别是旋转90°和270°)
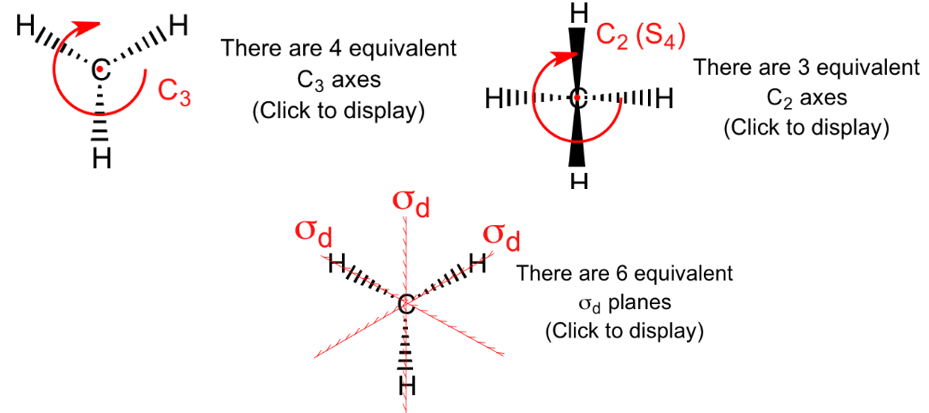
补充C2
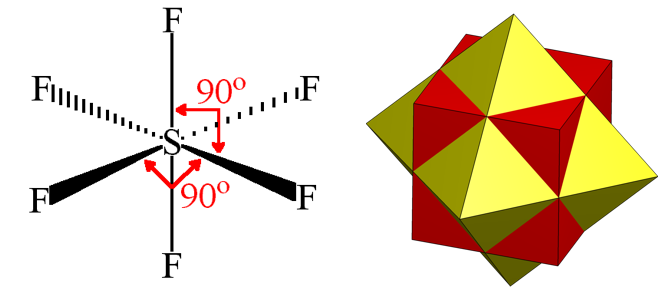
(14) \(O_h\) —— SF6,其实就是正八面体(regular octahedron)所对应的的point group。
(15) \(I_h\) —— [B12H12]2− and C60 (富勒烯,巴基球,Buckyball)
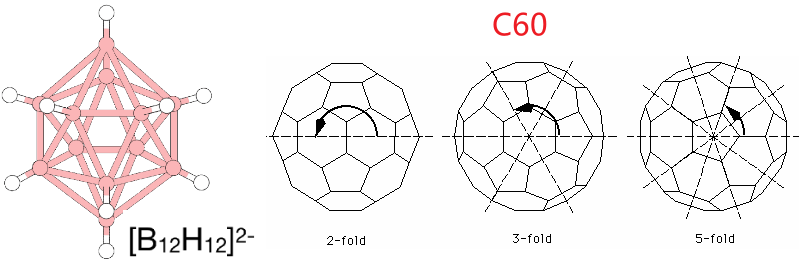
其不太常见的:In addition to \(T_d\), \(O_h\), and \(I_h\), there are corresponding point groups that lack the mirror planes (\(T\), \(O\) and \(I\)). Adding an inversion center to the \(T\) point group gives the \(T_h\) point group. 没有下标的就是表示没有对称面。
Once you become more familiar with the symmetry elements and point groups described above, you will find it quite straightforward to classify a molecule in terms of its point group. In the meantime, the flowchart shown below provides a step-by-step approach to the problem.

Hermann-Mauguin system: Though the Hermann-Mauguin system can be used to label point groups, it is usually used in the discussion of crystal symmetry. In crystals, in addition to the symmetry elements described above, translational symmetry elements (平移对称性) are very important.
Space groups versus Point group: Translational symmetry operations leave no point unchanged, with the consequence that crystal symmetry is described in terms of space groups rather than point groups.参考资料:
(1) 示意图-chemtube3d
(2) Point Group-Kai Landskron
(3) slideplayer
(4) Wiki-Molecular_symmetry
(5) [化學鍵] 第八講、Symmetry and Point Group
(6) 晶体几何系列之一:晶体的点群与空间群-曹则贤
(7) What is the Difference Between Point Group and Space Group?
Symmetry and Physical Properties
Carrying out a symmetry operation on a molecule must not change any of its physical properties.
Polarity
- For a molecule to have a permanent dipole moment, it must have an asymmetric charge distribution. The point group of the molecule not only determines whether the molecule may have a dipole moment, but also in which direction(s) it may point.
- If a molecule has a \(C_{n} \) axis with \(n>1\) , it cannot have a dipole moment perpendicular to the axis of rotation. Any dipole must lie parallel to a \(C_{n} \) axis.
- The only groups compatible with a dipole moment are \(C_{n} \) , \(C_{nv} \) and \(C_{S} \) . In molecules belonging to \(C_{n} \) or \(C_{nv} \) the dipole must lie along the axis of rotation.
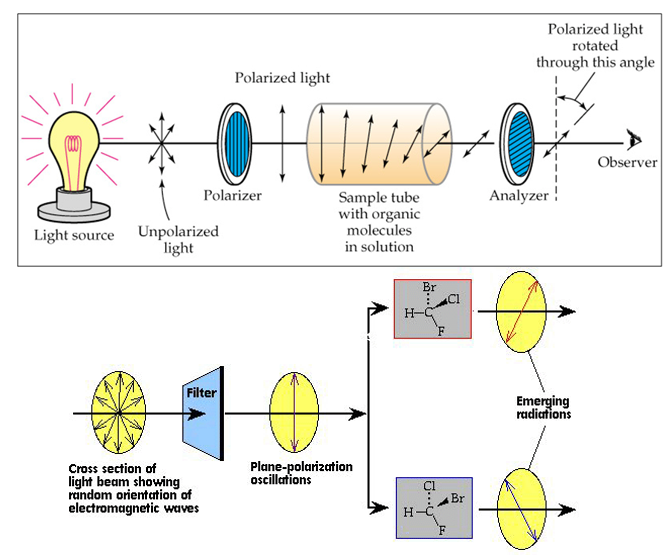
Chirality
- Enantiomers (手性异构体): non-superimposable mirror images of each other, and one consequence of this symmetrical relationship is that they rotate the plane of polarized light passing through them in opposite directions.
- Chiral: cannot be superimposed on their mirror image. No symmetry elementa rotation-reflection axis \( S_{n}\).
- 其他对称元素可能就包含了\( S_{n}\),比如含有\(C_n\) and \(\sigma_h\)对称元素的点群也会有\( S_{n}\)对称元素,a center of inversion is equivalent to \( S_{2}\)。
- 经验判据(As a rule of thumb):a molecule definitely cannot have be chiral if it has a center of inversion or a mirror plane of any type (\(\sigma_h\) , \(\sigma_v\) or \(\sigma_d\) ), but if these symmetry elements are absent the molecule should be checked carefully for an \( S_{n}\) axis before it is assumed to be chiral.
参考资料:
(1) 手性
Combining Symmetry Operations - ‘Group Multiplication’
下面我们来研究apply two symmetry operations in sequence的情况,以NH3分子作为例子,它属于\( C_{3v}\) point group。
按照\(\sigma_{v} C_{3} \)来操作,得到如下结果(会发现\( \sigma_{v} C_{3}= \sigma_{v}^{\prime \prime}\))

按照\( C_{3}\sigma_{v} \)来操作,得到如下结果(会发现\( C_{3}\sigma_{v} = \sigma_{v}^{\prime }\))

There are two important points that are illustrated by this example:
(1) Order Matters,就像量子力学中的算符一样。如果对两个对称操作来说作用顺序没影响的话,那么它们就属于同一个阿贝尔群。 In some groups the symmetry elements do commute; such groups are said to be Abelian.
(2) 两次的对称操作都属于同一个point group,那么最后的结果必然等价于该point group中的另一个操作(元素)。Symmetry operations that are related to each other by other symmetry operations of the group are said to belong to the same class. 对NH3分子来说,the three mirror planes (见上图) belong to the same class (related to each other through a \(C_3\) rotation), as do the rotations \(C_{3}^{+}\) and \(C_{3}^{-}\) (anticlockwise and clockwise rotations about the principal axis, related to each other by a vertical mirror plane.
The effects of applying two symmetry operations in sequence within a given point group are summarized in group multiplication tables. 下图是, the complete group multiplication table for \(C_{3v}\). The operations written along the first row of the table are carried out first, followed by those written in the first column, 注意结果会有些许改变如果我们choose \(\sigma_{v}\)、\(\sigma_{v}^{\prime}\)和\(\sigma_{v}^{\prime \prime}\) in some different order。
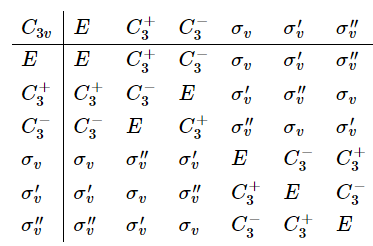
Constructing higher groups from simpler groups
A group that contains a large number of symmetry elements may often be constructed from simpler groups. This is probably best illustrated using an example. Consider the point groups \( C_2\) and \(C_S\). \( C_2\) contains the elements \( E\) and \( C_2\), and has order 2, while \(C_S\) contains \( E\) and \(\sigma\) and also has order 2 . We can use these two groups to construct the group \( C_{2v}\) by applying the symmetry operations of \( C_2\) and \(C_S\) in sequence.
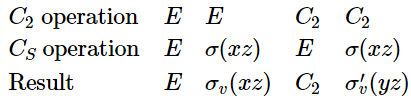 Notice that \(C_{2v}\) has order 4 , which is the product of the orders of the two lower-order groups. \(C_{2v}\) may be described as a direct product group of \( C_2\) and \(C_S\). The origin of this name should become obvious when we review the properties of matrices.
Notice that \(C_{2v}\) has order 4 , which is the product of the orders of the two lower-order groups. \(C_{2v}\) may be described as a direct product group of \( C_2\) and \(C_S\). The origin of this name should become obvious when we review the properties of matrices.
注:有限群元素的数目叫作该群的阶(order)。
Review of Matrices
Matrix multiplication: Matrix multiplication is not generally commutative, a property that mirrors the behavior found earlier for symmetry operations within a point group.
Direct Products: The direct product of two matrices (given the symbol ⊗ ) is a special type of matrix product that generates a matrix of higher dimensionality if both matrices have dimension greater than one. The easiest way to demonstrate how to construct a direct product of two matrices \(A\) and \(B\) is by an example:
 Though this may seem like a somewhat strange operation to carry out, direct products crop up a great deal in group theory.
Though this may seem like a somewhat strange operation to carry out, direct products crop up a great deal in group theory.
Transformation matrices
Matrices can be used to map one set of coordinates or functions onto another set. Matrices used for this purpose are called transformation matrices. In group theory, we can use transformation matrices to carry out the various symmetry operations considered at the beginning of the course. As a simple example, we will investigate the matrices we would use to carry out some of these symmetry operations on a vector \((x, y)\).
The identity Operation: leaves the vector unchanged, and as you may already suspect, the appropriate matrix is the identity matrix. $$(x, y)\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right)=(x, y)$$
Reflection in a plane: The simplest example of a reflection matrix corresponds to reflecting the vector \((x,y)\) in either the x or y axes. Reflection in the \(x\) axis maps y to \(-y\) , while reflection in the y axis maps x to \(-x\) . The appropriate matrix is very like the identity matrix but with a change in sign for the appropriate element. 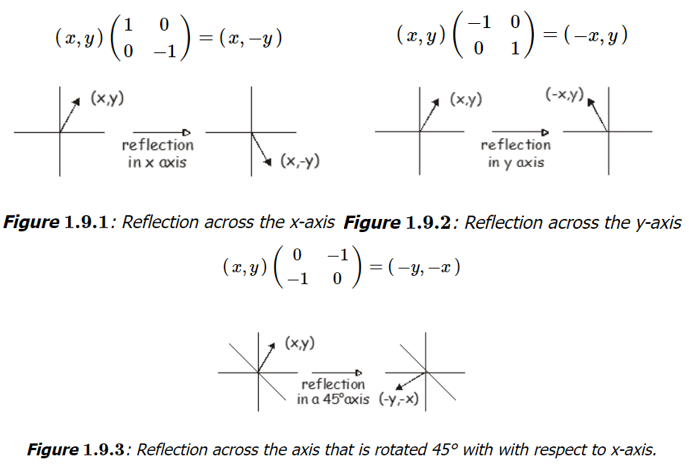 Rotation about an Axis:
Rotation about an Axis:
In two dimensions, the appropriate matrix to represent rotation by an angle \( \theta\) about the origin is
 In three dimensions, rotations about the \( x\), \( y\) and \(z\) axes acting on a vector \( (x, y, z)\)) are represented by the following matrices.
In three dimensions, rotations about the \( x\), \( y\) and \(z\) axes acting on a vector \( (x, y, z)\)) are represented by the following matrices.