https://pubs.acs.org/doi/abs/10.1021/jacs.8b09059
Introduction to Electron Transfer: Theoretical Foundations and Pedagogical Examples
继续看https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Time_Dependent_Quantum_Mechanics_and_Spectroscopy_(Tokmakoff)/15%3A_Energy_and_Charge_Transfer/15.05%3A_Marcus_Theory_for_Electron_Transfer
和
Marcus电荷转移理论
加州理工的马库斯Marcus凭借电子转移反应理论研究中的杰出贡献而获得了1992年诺贝尔化学奖。
颁奖词:马库斯发现了用简单的数学公式表示分子体系的能量如何受反应分子和最邻近分子结构的变化的影响。借助这些数学表达式,他计算并解释了所测得的电子转移反应中迅速变化的速度,马库斯的理论使得理论量和实践量通过数学方式联系起来,使得实验化学家获得了一种有用的工具。在解释许多化学现象方面都证明是有用的。
电荷转移(氧化还原反应)的重要性
(1) Life is nothing but an electron looking for a place to rest. —Albert Szent-Györgyi (Nobel Prize, Physiology or Medicine, 1937)
(2) Life is all about redox reaction.
(3) Looking from the perspective of charge transfer may be one of the most universal and fundamental approaches to study biology, chemistry, and materials science. (Redox biology on the rise)
两种转移机理
Electron transfer reactions occur by one of two fundamental mechanisms. (There are two mechanisms by which inorganic complexes transfer electrons. ,只是针对无机配合物?)

Outer sphere mechanism
- Simpler process when compared with the other one.
- Marcus theory最早的发展是基于Outter sphere electron transfer的,不过最后它也扩展涵盖了Inner sphere electron transfer。
- Very common in biological systems.
- Reaction occurs between redox centers that remain separate and intact before, during, and after the ET event.
Inner sphere mechanism
- Electron transfer occurs between complexes via a bridging ligand.
- Inner sphere electron transfer is very sensitive to bridging ligand.
- Bonds are broken and formed.
- Relatively rare in biological systems since large molecules often shield redox sites, preventing the formation of the bridge.
理论简介
这里主要参考知乎的帖子,然后再拓展。这里我们来考虑一下最简单的反应,电子受体A和电子给体D发生outer sphere单电子转移:(注意下图中的A和D只是表示位置)$$A+D \rightarrow[A-D] \rightarrow\left[A^{\bullet-}-D^{\bullet+}\right] \rightarrow A^{\bullet-}+D^{\bullet+}$$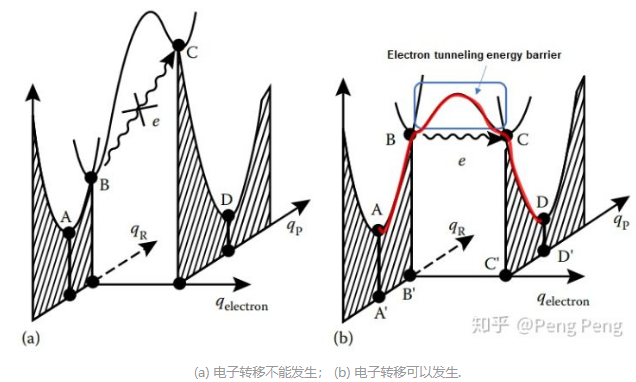
- Parabolas, because nuclear vibrations are harmonic oscillators, and obey Hooke's Law.
- \(q_{\mathrm{R}}\)表示核坐标(nuclear coordinate),可以理解为分子中各原子的相对位置。当原料\( [A-D]\)发生分子振动或旋转,键长键角改变时候,会改变核坐标,因此改变电子的能量(比如从A点升高到B点)。图b中右半边是产物\(\left[A^{\bullet-}-D^{\bullet+}\right]\)的电子势能面。当处于\(C\)点的时候(对原料来说是\(B\)点),产物和原料的核坐标相同,也就是说这个时候产物和原料的原子在空间位置重合(长得一模一样);
- Frank-Condon原理,我们知道原子和电子的质量差距很大,所以原子运动比电子转移(in a vibrational frequency)慢很多,因此电子转移发生的时候,原子基本上是静止的 ,所以核坐标应该没有改变。换句话说,电子转移只有在原料\( [A-D]\)和产物\(\left[A^{\bullet-}-D^{\bullet+}\right]\)核坐标相同时才能发生;
- 左图电子转移不能发生,因为虽然满足原料和产物核坐标相同,但是前者电子能量\( B\)小于产物中电子能量\( C\),当然了,继续增大原料复合物中电子的能量(同时也改变了核坐标),肯定也会到达两个抛物线的线的相交处(从侧边观察,位置、能量都相同)。
- 右图电子转移能发生,\( B\)点和\( C\)点不仅核坐标相同,电子能量也相同,电子的空间坐标从\(B^\prime\)变化到\(C^\prime\),\(q_{\mathrm{electron}}\)是电子坐标。
- 重点总结:电子转移只有在原料和产物的核坐标相同, 且原料和产物中电子能量一致的时候才能发生。
- 电子隧穿(electron tunneling),从\( B\)点跑到\( C\)点的过程中是电子隧穿,但还要克服一个小小的能垒(图中蓝色圈处)。
- 能垒,这个能垒的高度和分子\(A\)分子\(D\)之间轨道的重叠程度相关,重叠程度越高,能垒越低。如果轨道重合时的stabilization energy大于1 kcal/mol, 那么能垒就相当低,electron tunneling发生的概率是100%, 我们把这种电子转移称为绝热过程(adiabatic electron transfer)。对于大部分的有机反应而言,电子转移都是绝热过程。
拓展:
Jonas-JPCL中采用的是diabatic approximation(非绝热近似),也就是上面左侧的图。根据这里的资料:
Diabatic — electron transfer is a quantum jump from one curve to the other (curves cross).
Adiabatic — involving neither loss nor acquisition of heat. 进一步地我们体会一下在不同语境下adiabatic(绝热)的含义。
(1) In thermodynamics, an adiabatic process is one in which no exchange of heat with the environment occurs.
(2) In the Carnot cycle of an ideal gas engine, the steps in which expansion or contraction occur without exchange of heat are adiabatic.
(3) In the electron transfer context, an adiabatic process is one in which no quantum jump occurs, - the electron lingers at the barrier, and the curves representing the two states smooth to form a continuum, with a quasi-state at the top of the activation barrier.
(4) DeVault从量子力学的角度给出了更多的说明,这里不再赘言,有兴趣再看前提到的资料链接。
现在我们把电子转移的过程在平面上画出来就得到了我们平时常常看到的反应势能图。在Marcus电荷转移理论中,人们下图的横轴为Nuclear Configuration,纵轴为Gibbs Free Energy。
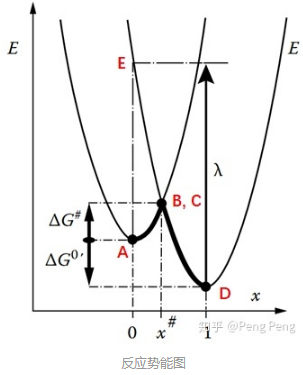
- 反应活化能\( \Delta G^{\ddagger}\),对应于从A点到B点的能垒(在上图中为正值) ;
- Gibbs自由能变化\(\Delta G^{0^{\prime}}\),对应于A点和D点之间的能量差(在上图中为负值);
- 重组能(reoorganization energy)\(\lambda \),它的值通常在0.5 ~ 1 eV之间。
- 重组能—理解1(IUPAC):Reorganization energy: Gibbs energy dissipated when a system that has undergone 'vertical' electron transfer (i.e., electron transfer obeying the Franck–Condon principle) relaxes to the equilibrium state for its new charge distribution.简单理解就是,体系从初始态\( A\)点经过电子垂直跃迁(比如辐射激发跃迁)到高能态\( E\)点后,体系会经过重组(比如分子会改变键长键角,溶剂分子取向改变等)释放能量达到平衡态\( D\)。这个过程释放的能量就是重组能。
- 重组能—理解2:the energy necessary to transform the nuclear configurations in the reactant and the solvent to those of the product state.
- 重组能—大小:上面两种理解其实在数学表达上是等价的,大小都是\(\lambda=\displaystyle\frac{1}{2} k\left(q_{D}-q_{A}\right)^{2}\),其中\(q_{A}\)和\(q_{D}\)分别是原料和产物的核坐标。
- 重组能的拆分:\(\lambda=\lambda_{i}+\lambda_{o}\),\(\lambda_{i} \)为 inner shell reorganization energy,而\(\lambda_{o}\)是outer shell reorganization energy。\(\lambda_{i} \)体现了A-D分子自身重组的能量变化,\(\lambda_{o}\)体现了环境重组(溶剂分子取向改变)的能量变化。\(\lambda_{i} \)可以通过X射线光谱,IR或者理论计算得到。不过对于大部分的有机反应,由于电子转移通常在离域化分子(delocalized molecule)之间发生,所以\(\lambda_{i} \)远小于\(\lambda_{o}\),因此大家都把重心放在\(\lambda_{o}\)上。
- \(\lambda_{o}\)详解:
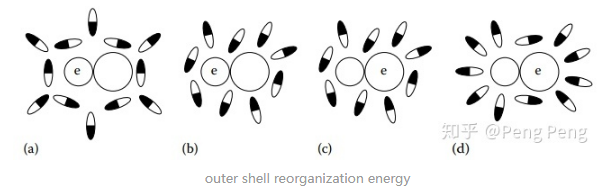 和溶剂相关。由上图可知,当电子从左边物质转移到右边物质后,周围溶剂分子会受到极化,且其分子取向会改变。这种改变带来的能量差就叫outer shell reorganization energy。对于单电子转移,其大小可由下面公式可得:$$\lambda_{\mathrm{o}}=\left[\displaystyle\frac{N_{\mathrm{A}} \mathrm{e}^{2}}{8 \pi}\left(\displaystyle\frac{1}{\varepsilon_{\mathrm{op}}}-\displaystyle\frac{1}{\varepsilon_{\mathrm{s}}}\right)\right]\left(\displaystyle\frac{1}{a_{\mathrm{A}}}+\displaystyle\frac{1}{a_{\mathrm{D}}}-\frac{2}{r}\right)$$\( \varepsilon_{o p}\) = the optical dielectric constant of solvent
和溶剂相关。由上图可知,当电子从左边物质转移到右边物质后,周围溶剂分子会受到极化,且其分子取向会改变。这种改变带来的能量差就叫outer shell reorganization energy。对于单电子转移,其大小可由下面公式可得:$$\lambda_{\mathrm{o}}=\left[\displaystyle\frac{N_{\mathrm{A}} \mathrm{e}^{2}}{8 \pi}\left(\displaystyle\frac{1}{\varepsilon_{\mathrm{op}}}-\displaystyle\frac{1}{\varepsilon_{\mathrm{s}}}\right)\right]\left(\displaystyle\frac{1}{a_{\mathrm{A}}}+\displaystyle\frac{1}{a_{\mathrm{D}}}-\frac{2}{r}\right)$$\( \varepsilon_{o p}\) = the optical dielectric constant of solvent
\( \varepsilon_{s}\) = the static dielectric constant of solvent
\(a_{A} \) = 分子A直径
\(a_{D} \) = 分子D直径
\( r=\displaystyle\frac{a_{A}+a_{D}}{2}\),是分子A中心与分子D中心的距离
如果是\(n\)电子转移反应,上式中\(e^{2}\)要改成\((n e)^{2}\)。这个公式很重要,首先它解释了溶剂效应。而且我们可以通过一些易得的基本常数(比如分子大小,介电系数)的得到电子转移反应的溶剂重组能。另外,我们发现如果是\( n\)电子转移反应,溶剂重组能会以\(n^2\)的倍数迅速增大。这也是为什么几乎所有的多电子反应都是连续的单电子反应组成,而不是一步到位。比如CO2还原成CO需要经过两步单电子还原反应,而不是一次性得到两个电子。看来大自然也是想教育我们要脚踏实地,一步一个脚印,不要老想着一步登天。 - 反应活化能\( \Delta G^{\ddagger}\)、Gibbs自由能变化\(\Delta G^{0^{\prime}}\)、 重组能(reoorganization energy)\(\lambda \)的关系(Marcus equation):$$\Delta G^{\ddagger}=\frac{1}{4\lambda}\left(\lambda+\Delta G^{0^{\prime}}\right)^{2}$$
Marcus方程的推导非常非常简单,可以说是大道至简。 它把分子键当做弹簧处理,根据harmonic oscillator approximation,可以知道分别写出原料和产物其势能和核坐标的一元二次方程关系式。然后用初中学过的一元二次方程求解就够了。难以想象这么牛逼的理论竟然只用用初中知识来推导。大家有兴趣可以去网上看看它的推导过程。Allen Bard的书118-120页有推导过程。
活化能:
https://blog.sciencenet.cn/blog-3474471-1289913.html
https://baike.baidu.com/item/%E5%8F%8D%E5%BA%94%E6%B4%BB%E5%8C%96%E8%83%BD/22124300
https://www.google.com/search?q=%E5%8F%8D%E5%BA%94%E6%B4%BB%E5%8C%96%E8%83%BD&sourceid=chrome&ie=UTF-8
量子力学的处理,参考Andrei Tokmakoff-MIT的资料,
xxx
一般性的应用
我们来看看Marcus equation告诉我们什么信息。它有什么指导意义。
- 当\(\Delta G^{0^{\prime}}=0\)时,反应仍然存在一个活化能,它的值是\(\lambda / 4\) , 这个叫做intrinsic activation energy barrier。可以看做反应的内在能垒。
- 当\(\Delta G^{0^{\prime}}=-\lambda\)时,活化能\(\Delta G^{\ddagger}=0\),也就是说这时候反应速率达到极值。如果Gibbs自由能差进一步变负,反应速率反而会变慢。这违背我们以前的认知。因为我们都认为Gibbs自由能差越负,反应驱动力越强,反应速率应该越快才对。这就是Marcus理论厉害的地方,它预测了Marcus inverted region的存在, 也就是\(\Delta G^{\ddagger}=0\)越负,反应速率反而越慢。这个预测一直到28年之后才被实验证明。
- Marcus理论很好的解释了溶剂效应,位阻效应,离域化作用等等。
- 最重要的是我们通过反应重组能和Gibbs自由能变化可以预测反应速率。它把热力学和动力学很好的联系到一起。 反应重组能和Gibbs自由能变化都是很容易获得的热力学参数。(顺便说一句,用通过cross-relationship,还能用已指反应的反应重组能算出未知反应的反应重组能。Gibbs自由能变化的计算也很容易。

Marcus theory在电化学中的应用
(1) 对于电极反应而言,电极充当了电子给体\(D\)或者电子受体\(A\)。Gibbs自由能差\(\Delta G^{0^{\prime}}\)可通过电极电势改变。所以Marcu equation可以改写成下面的形式$$\Delta G^{\ddagger}=\frac{1}{4\lambda}\left(\lambda+{F\left(E-E^{0}\right)}\right)^{2}$$利用Marcus theory可以预测不同电压下,电极反应的活化能和反应速率如何随之改变,我们就能得到电流和电压的关系式。和传统的Butle Volmer电极反应动力学相比,从Marcus theory角度出发能更微观的理解电荷转移。比如,电压等于\(E^{0}\)时,活化能为\(\displaystyle\frac{\lambda}{4} \),这时\(k_{f}=k_{b}=k_{0}\) 。如果重组能越小,那么反应速率就会越大。这说明,如果分子得失电子时结构变化越小,反应速率就会越快。另外对于大分子和高度离域化分子而言,其得失电子时溶剂化能较小,反应速率就会较快。所以,我们可以推测有机相溶液中\(\mathrm{O}_{2}+e \rightarrow \mathrm{O}_{2}^{\bullet-}\)的\(k_{0}\) 会比 \( A r+e \rightarrow A r^{\bullet-}\)慢很多。
(2) 此外,用Marcu theory有助于我们更深刻理解转移常数\(\alpha\)。从下面公式中$$\alpha=\frac{1}{F} \frac{\partial G_{\mathrm{f}}^{\ddagger}}{\partial E}=\frac{1}{2}+\frac{F\left(E-E^{0}\right)}{2 \lambda}$$我们可以看出B-V方程里的转移常数其实和电压及重组能有关。而且在电压不是很大/很小的时候,后面一项可以忽略。这也是为什么\(\alpha \approx 0.5\)。
(3) 值得一提的是,电极反应不存在Inverted region,主要是因为金属电极中电子能级排布和有机 物中不同。对于有机物而言,其电子能级分布是不连续的,氧化还原集中在狭窄的HOMO和LUMO轨道。而金属电极或者半导体,其电子分布以Fermi Level为界。Fermi Level以上无电子,以下充满电子。发生氧化还原时,电子转移不一定就发生在Fermi level上,从而避免Inverted region。我说的很简陋,具体可以看看Marcus-Gerischer theory。
(4) 虽然Marcus theory 一开始是为了解释电子转移而发展的理论,但是现在它已经被扩展到proton transfer, proton coupled electron transfer 以及 hydride transfer。 而且这些反应都存在Marcus inverted theory。真的很神。
参考资料:
(1) Electron Transfer Reactions in Chemistry: Theory and Experiment (Nobel Lecture)
(2) Difference Between Inner Sphere and Outer Sphere Mechanism
(3) What is the inner sphere and outer sphere electron exchange, and how do they differ?-Quora
(4) Outer sphere and Inner Sphere Electron Transfer
(5) Electron Transfer Reactions-PPT
(6) 电子是怎么转移的?Marcus theory(知乎)
(7) Marcus 电荷转移理论(李永乐-知乎)
(8) 光致电子转移(PPT-百度文库)
(9) Marcus Theory for Electron Transfe-chem.libretexts
(10) René M. Williams 视频
稀土发光中的应用(Semi-classical thermodynamic approach)
下面是参考文献(1)的内容,作者也将内容发表在[ECS Transactions-2009]
对于localized donors和acceptors来说,ET(electron transfer)的速率随着D-A距离而呈现指数下降:$$k_{\mathrm{ET}}=k_{0} \exp \left[-\beta\left(R-R_{0}\right)\right]$$\(k_{0}\) — ET rate at the shortest possible DA distance;
\(\beta\) — a constant related to a tunneling energy barrier;
\(R \) — the centerto-center distance;
\(R_0\) — the closest possible DA distance; $$\mathrm{Ce}^{3+}\left(5 \mathrm{~d}^{1}\right)+\mathrm{RE}^{3+}\rightarrow \mathrm{Ce}^{4+}+\mathrm{RE}^{2+}$$上式的ET过程可以通过quantitatively analyzed(基于前面的公式),因为这里 the donors and acceptors are well-defined, localized ions. 但是大多数的研究都是定性分析 localized RE3+在晶体或多晶hosts中的ET,比如:
(1) 前面的公式被用于estimate the critical distance for Ce3+ luminescence quenching by Eu3+ with a \(\beta\) value taken from molecular ET experiments.
(2) qualitatively correlated the strength of ET quenching versus RE3+ acceptor composition to the change in the free energy, ∆G, of the ET reaction.
从quantitative analysis for these reactions来说,上面的公式essentially describes the distance dependence for \( H_{\mathrm{AB}}\), the electronic matrix coupling element between the ET reactants and products. 除了距离依赖参数\( H_{\mathrm{AB}}\)之外,我们还要考虑两个能量参数:
\(\Delta G^{0} \) — the change in the free energy for the ET reaction;
\(\lambda\) — the reorganizational energy;
在位型坐标图中,\(\Delta G^{0} \) is represented by the energy difference between the zero-phonon lines for each CC parabola, whereas \(\lambda\) describes the offset between the two CC parabolas due to relaxation after ET.
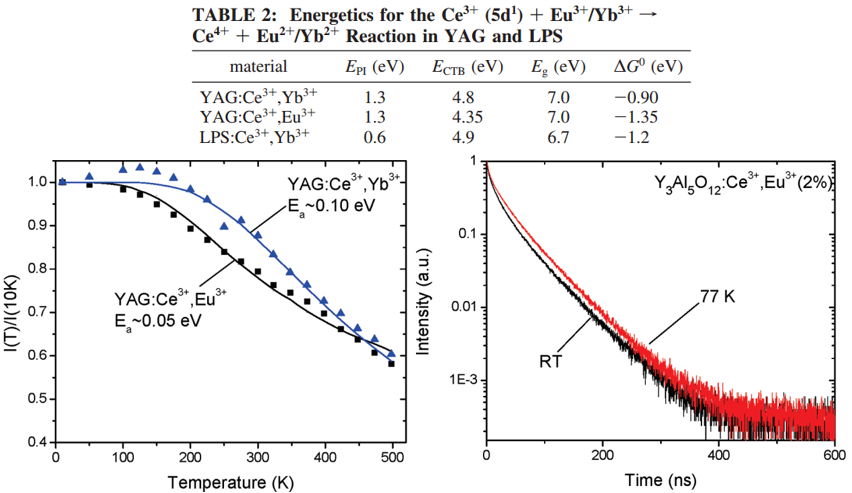
作者选择的基质: Y3Al5O12 (YAG) and Lu2Si2O7 (LPS)
MMCT的反应:
\(\mathrm{Ce}^{3+}\left(5 \mathrm{~d}^{1}\right)+\mathrm{Eu}^{3+} / \mathrm{Yb}^{3+} \rightarrow \mathrm{Ce}^{4+}+\mathrm{Eu}^{2+} / \mathrm{Yb}^{2+}\)
制备条件:固相法,还原气氛,但是要控制Yb3+/Eu3+不被还原为Yb2+/Eu2+(通过反射光谱测试确认)
Ce3+掺杂浓度: 0.1%, minimize energy transfer and migration between Ce3+ ions.
实验结果分析:
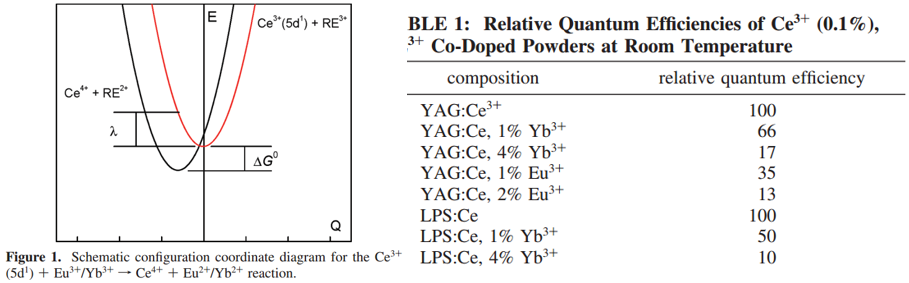
- 共掺杂Eu3+/Yb3+导致Ce3+发光的strongly quenching;
- Multiexponential decay profile indicates that this quenching does occur beyond nearest neighbor sites;
- 作者将观察到的Ce3+发光的quenching归结于ET reactions for several reasons
(1) Ce3+的发光和Yb3+的吸收没有光谱重叠,eliminating nonradiative energy transfer as a quenching path.
(2) 虽然Ce3+的发光和Eu3+的一些吸收跃迁有重叠,但是这些跃迁是parity forbidden,振子强度很弱,所以偶极-偶极跃迁不太可能发生;另外(super)exchange 也不可能,因为根本没有观察到Eu3+的发光(460 nm激发Ce3+);Our analysis of ET rates (vide infra) indicate that nearest-neighbor ET is >4 orders of magnitude larger than typical nearest-neighbor energy transfer rates by (super)exchange (∼107-108 s-1).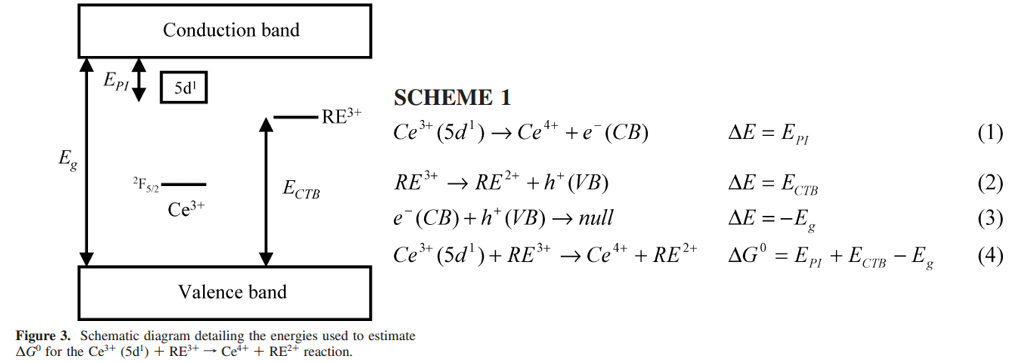
- \( E_{\mathrm{PI}}\)是Ce3+(5d1) photoionization threshold,对于YAG该值is taken as the onset for excited-state absorption from the lowest Ce3+ 5d1 level to the host conduction band,对于LPS该值为thermal activation energy;
- \(E_{\mathrm{CTB}}\left(\mathrm{Yb}^{3+}\right) \) uses the midpoint between the excitation and emission maxima for Yb3+-O2- charge transfer luminescence;
- \(E_{\mathrm{CTB}}\left(\mathrm{Eu}^{3+}\right) \) is estimated using the difference between the position of the Yb3+-O2- and Eu3+-O2- CTBs (∼0.45 eV);
- \(E_g\) is estimated using the maximum in the excitation spectra after the host lattice absorption edge.
下面是提到Marcus电荷转移理论的其他有关荧光粉的文章:
(1) Intervalence charge transfer (IVCT, electron transfer ffering only in oxidation state) in lanthanide-containing materials has received very little attention compared with the vast amount of work focused on transition-metal compounds. [Jonas-JPCL-2019]也引用了Marcus电荷转移理论的文章。
(2) [Intervalence charge transfer luminescence: The anomalous luminescence
of cerium-doped Cs2LiLuCl6 elpasolite - JCP - 2014]
The basic theory for electron transfer was formulated by Marcus and the systematic study of intervalence compounds has played a key role in elucidating electron transfer reactions.
The Marcus theory of electron transfer was complemented by Hush with a theory of heteronuclear MMCT and homonuclear IVCT considering a two-state problem.
(2) Kinetics of Photoinduced Electron Transfer in Alternately Stacked Eu3+:LaNb2O7– and W2O72– Nanosheets As Demonstrated by f–f Radiative Transition of Doped Eu3+ 待定
(3) Synthesis of Compositionally Defined Single-Crystalline Eu3+-
Activated Molybdate−Tungstate Solid-Solution Composite
Nanowires and Observation of Charge Transfer in a Novel Class of 1D
CaMoO4−CaWO4:Eu3+−0D CdS/CdSe QD Nanoscale Heterostructures 待定
(4)
参考文献:
(1) Quantitative Analysis of Electron Transfer-JPCC-2010-Anant Setlur
(2)
Taube Isopic experiment
ss
Taube Isopic(亨利·陶布)由于对Inner sphere electron transfer的贡献获得1983年诺贝尔奖,对特别是金属配合物中电子转移反应机理的研究。