姐妹课程笔记：对称性在化学中的应用
国科大群论笔记
李新征(北京大学)-群论视频及其配套讲义
妈咪说MommyTalk—科普视频(五次方程)
李新征-《分子及凝聚态系统物性的计算模拟：从电子结构到分子动力学》
群论学习资料备忘录(凝聚态物理专业)- 视频
奇妙的旋转-张天蓉
宇宙的基础是对称：群论在物理的应用
Glimpses of Symmetry
抽象代数—万门大学笔记
图床：Group-Theory-img/
参考资料：
1. M. S. Dresselhaus, G. Dresselhaus, A. Jorio, 《Group Theory: Applications to the Physics of Condensed Matter》 . Springer(强烈推荐)
2. Anthony Zee, 《Group Theory in a Nutshell for Physicists》 , Princeton University Press. (徐一鸿，科普读物中经常称为阿热，题目大意为：物理学家眼 中的群论简言， in a nutshell 本意是：一言以蔽之，简约的)
3. F. Albert Cotton, 《Chemical Applications of Group Theory》 , John Willey & Sons. Inc(化学家写的群论中的经典， 对读者很友善)
名言/感悟：
(1) Starting from a few innocuous (无害的；无伤大雅的) sounding axioms (公理；公设；原理) defining what a group is, an elegant mathematical structure emerges, with many unexpected theorems (定理；原理). —阿热
(2) Algebra is generous; she often gives more than is asked of her. —达朗贝尔
(3) 定义群的概念，然后我们就可以创造出各种群的例子；计算编程中我们也是先定义什么是“类”，然后根据此定义创造出各种属于类的对象。向量空间，比如矢量加法的情况下，群具有的性质，它都有，那么我们说它是群的一个子类。群中推出的定理，子类可以直接继承。鸭子类型，各种表现都像鸭子，那我们就认为它是鸭子，实际可能是鹅，我们不管，我们只关心它有鸭子的性质。ZFC集合论，并没有说集合是什么，只是在描述其特点。
课程导言
在我们的兄弟学科化学上，在量子力学建立后，敏锐的化学家们，以鲍林为代表已经认识到化学分子的存在形式及其化学反应的发生本质上是由量子力学与统计物理基本原理支配的。既然对称性在量子力学中具备上述重要性，与之响应，在描述由量子力学等基本原理所决定的反应物、过渡态、生成物特性(比如电子能级、振动谱)描述中，对称性原理的数学语言(即群论)必然也会发挥重要的作用。因此，在近代化学，特别是物理化学的研究中，人们也认识到由对称性决定的内在规律对人们理解这些物性与过程的本质至关重要。换句话，要想真正地在分子设计层面理解化学，对称性的知识同样必不可少。化学的本质是分子设计-北大化学与分子工程学院(唐有琪-鲍林的学生)
注：鲍林是第一个将量子力学基本原理、分子轨道、分子设计这些概念引入到化学研究中的人，也是我们现在公认的量子化学、分子生物学的开创人。物理和化学两个大的学科的交融，才使得两者都发展到了目前的这个相当成熟的状态， 而最早去推动这种交融的人，鲍林就是代表。
微分散射截面是唯一可观测量。
碳纳米管-Dresselhaus-拉曼+群论
各章节概述：
1. 群的基础知识： 集合总体的结构特征及其规律；
2. 群表示理论： 对这些规律进行数学描述要用到的数学语言(基础是线性代数)；
3. 点群、空间群： 人们面对分子、晶体系统的时候，系统具有的对称性操作的集合。它们是我们在掌握前两章(群论的理论基础)后面对的第一类具体的群；
4. 群论和量子力学： 群论在近代的物理、化学等学科研究中的应用；
5. 转动群： 是中心力场系统的对称群(物理体系中的一类对称群)；
6. 置换群： 是全同粒子系统的对称群(物理体系中的一类对称群)。
群论的理解：群论从本质上而言是研究数的结构及其生成规律的，是数学，不是物理。群论这门学科发展的初期，是人们对一些“理”的认识，这些“理”是“数理”，不是“物理”。人们基于对这些“数理”的认识，建立起了一套理论。后来人们又逐渐意识到它在物理、化学上有很 大的用途，才开始要求物理、化学这些专业背景的人来学习，以期对本学科中的问题有更深入的认识。
人们在求解一元高次方程根式解的时候，引入了置换群的概念，进而建立起了群论这个理论体系。
在数学家建立了《群论》的概念体系之后，物理学家做的三个重要工作：
(1) 几何晶体学的发展，晶体点阵、点群、空间群这些概念的诞生以及他们 在晶体学中的应用。
(2) 对称性与守恒量之间的关系，诺特定理的基本内容是“any differentiable symmetry of the action of a physical system has a corresponding conservation law”，也可以说是任何一个保持拉格朗日量不变的微分算符，都对应一个守恒的物理量。比如空间平移对称性对应动量守恒、时间平移对称性对应能量守恒、旋 转对称性对应角动量守恒，等等。(待补充)
资料：
对称破缺——美妙思想来自凝聚态物理 | 量子群英传
爱因斯坦告诉你：谁是最伟大的女数学家？
(3) 对称性在量子力学中的应用，这个代表人物是维格纳。
群的基本概念
群、子群和陪集
- 封闭性(closure)：任何两个元素的乘积仍然属于；
- ，它与中任何元素\(g_i\)的乘积仍等于\(g_i\)，即\(g_i \times E = E\times g_i=g_i\)；
- 结合律(associate law)：对任何三个元素必有\(g_j\times (g_k \times g_l)=(g_j\times g_k) \times g_l\)
群。注意这里所谓的“乘积”，并不等同于两个数在算术意义上的相乘，而是一种二元运算方式，可以自己定义。
群的例子： 定义群的乘法为数的加法，则全体整数构成一个群，\(0\)是其中的单位元素，\(n\)与\(-n\)互逆。同理，全体实数也在这个乘法规则下构成一个群，全体复数也是。但如果我们把乘法定义为数乘，那么它们就不再是群了，因为这种情况下 单位元素只能是\(1\)，而\(0\)是没有逆的。
\(n\)阶置换群：这样一系列操作的集合，它们中每一个操作，都把\( 1, 2, 3..., n\)这\(n\)个数，一对一的对应到\( 1, 2, 3..., n\)这\(n\)个数上。 比如$$P=\left(\begin{array}{cccc} 1 & 2 & \ldots \ldots & n \\ {m}_{1} &{~m}_{2} & \ldots \ldots & m_{n} \end{array}\right)$$ 很容易验证这些操作的集合也构成一个群，我们称为\(n\)阶置换群，它的群元的个数是\(n!\)。在物理上，处理全同粒子体系的时候，会经常用到这一类群，我们后面会专门介绍。
注：固体发光讲义-许少鸿
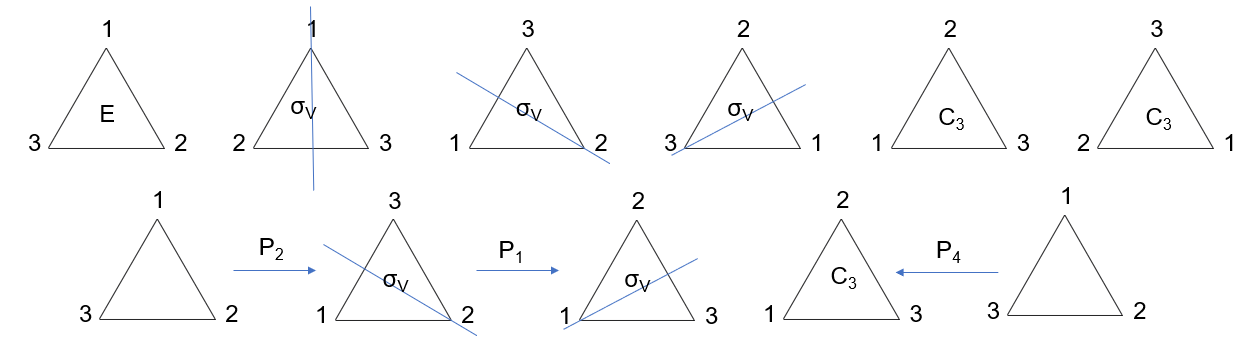
(1) 第二层变换的时候，注意三个不同的\(\sigma_{\text{v}}\)锚定的是数字\(123\)(因为对称本质是点的移动)，而不是绝对位置；
(2) \(E\)的一种，即旋转\(2\pi\)(正反都一样)，由于回到自身，所以是一种特殊的正三角形状态的本质是点的运动，那么所有状态就是三个点的全排列，\(3!=6\)种情况；
李老师的书上是这样写的： 是个几何图形的对称性，有三维欧式空间的一个正三角形，顶点是A、 B、C。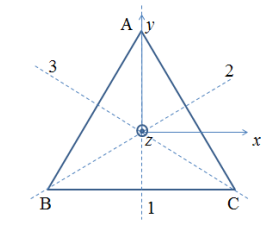 
不动、绕\(z\)轴转\(2 \pi / 3\)、绕\(z\)轴转\(4\pi/3\)、绕\(1\)轴转\(\pi\)、绕\(2\)轴转\(\pi\)、绕\(3\)轴转\(\pi\)，这六个几何操作又恰恰和三阶置换群的六个变换一一对应。因此它们形成一个群构成了\(D_3\)群。重复类似运算，可得完整\(D_3\)群乘法表：
它是图形中的三角形的纯转动群，当我们除了转动还包含反射、反演这些操作的时候，群元就会再多一些，群也不是这个\(D_3\)群了。这里的\(D_3\)群只包含转动操作。
【Abel群(可交换群)】：是一种特殊的群，除了满足普通群的四个公理，阿贝尔群还需要满足一个额外的公理：交换性(Commutative property )。
群的乘法一般不可交换(这个在群的定义里面没有体现，因此在一般的群中也不需要遵守)，当群中元素乘法可以任意互换时，这个群称为Abel群。(由这个定义我们很容易想象Abel群的乘法表都应该是相对于对角线对称的)。There are two main notational conventions for abelian groups – additive and multiplicative.
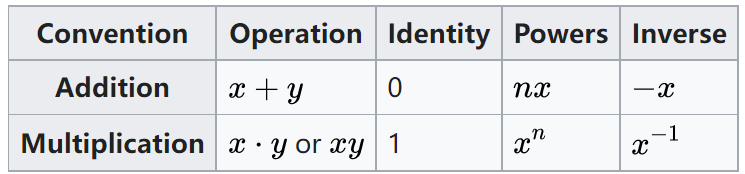
实数集是在加法下的阿贝尔群，非零实数集在乘法下是阿贝尔群。矩阵即使是可逆矩阵，一般不形成在乘法下的阿贝尔群，因为矩阵乘法一般是不可交换的。但是某些矩阵的群是在矩阵乘法下的阿贝尔群，一个例子是\(2x2\)旋转矩阵的群。
(1) 看到这里，那么从算符的角度去理解这些元素确实可以，两个算符之积本来就不一定是对易的，正是因为这样才有了量子力学中的测不准原理；
(2) 前面讨论的置换群\(G_p\)群不是阿贝尔群，但是\(C_3\)群是阿贝尔群；
(3) \( k\)阶循环群\(\{a, a^{2}, \cdots, a^{k-1}, a^{k}=e\}\)是Abel群；
(4) 质数阶群一定是循环群，循环群一定是Abel群，证明见这里；
(5) \(S_3\)是最小的非交换群。维基上说最小的非阿贝尔群是\( 4\)阶二面体群，为啥矛盾？
定理重排定理：设\(G=\left\{\cdots, g_{\alpha,} \cdots\right\}\)，对\(\forall u \in G\)，当\(g _\alpha\)取遍\(G\)中所有元素时， \(g_{\alpha}\)给出且仅仅一次给出\(G\)中所有元素。
【子群】(subgroup)：设\(H\)是群\(G\)的一个子集(部分元素的集合)，若对群\(G\)相同的乘法运算，对H也构成一个群，则称\(H\)为\(G\)的子群。换一种说法，给定群\(G\)，如果集合\(H \subseteq G\)，且\(H\)中包含了单位元，\(H\)中每个元素的逆元也在\(H\)中，则称\(H\)为\(G\)的子群(subgroup)。 因为\(H\) 存在单元和逆元，其封闭性和结合性直接继承了\(G\) ，它满足了群的四个公理，因此它就是一个 群。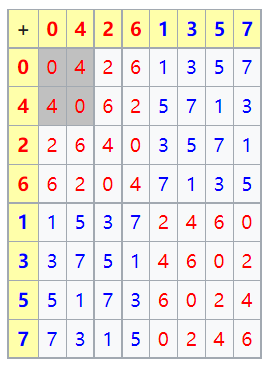
群\(G=\{0,1,2,3,4,5,6,7\}\)是和以8为模的加法为二元运算的群(此群亦同时是阿贝尔群)。其凯莱表如上图。此凯莱表是故意不用常规的排列法来表明此群有着一对非当然子群：\(J=\{0,4\}\)和\(H=\{0,2,4,6\}\)，其中\(J\)亦是\(H\)的子群。\(H\)的凯莱表是\(G\)的凯莱表之左上半部。\(G\)群是循环的，而其子群亦为。一般而言，循环群的子群亦为循环的。
对于群\(G\)来说，\({e}\)与\(G\)本身都是\(G\)的子群，由于太明显，所以称为【平庸子群】(Trivial subgroup)，而群\(G\)的非平庸子群称为【真子群】(proper subgroup)。一般我们找群\(G\)的子群的时候找的是它的固有子群(非平庸子群)。
(1) 其实只要满足封闭性和唯一逆，那么群\(G\)的该子集合就是一个子群；
(2) 在定义群的乘法为数的加法的时候，整数全体形成的群是实数全体形成的群的子群；
(3) 绕固定轴\(\vec{k}\)转动的元素形成的群\({C}_{\vec{k}}(\Psi)\)，是绕轴上某一点转动(过这点可 以有无数个轴)的群SO(3)群的子群。
求幂：给定群\((G, \cdot)\)，对任意一个元素\(a\)应用\(n\)次运算符"\(\cdot\)"，表示为$$ a^n=\underbrace{a \cdot a \cdot a \cdots a}_{n \text { 次 }} $$\(a^n\)叫做\(a\)的\(n\)次幂。注意定义在群\((G, \cdot)\)上的\(a^n\)不能单纯的理解为平时所见的乘方。它表示在一个元素上对抽象的二元运算的重复多次使用。 例如当\(G\)表示定义在加法上的群时，\(a^n=a+a+\cdots+a\)。
【阶】可以分为两种：
- 一个群的阶是指其势，即其元素的个数；
- 对任意一个有限群\(G\)，从中取一个元素\(a\)，从\(a\)出发作幂操作，总是可以构成\(G\)的一个循环子群\(Z_k\)的，这个\(Z_k\)等于\(\{a, a^{2}, \cdots, a^{k-1}, a^{k}=e\}\)，这时称\(k\)(满足这个性质的最小的\( k\))为群元素\(a\)的阶。
【循环群】(cyclic group)：是指能由群中的某个元素做幂运算而生成的群。定义为：设\((G, \cdot)\)为一个群，若存在一个\(G\)内的元素\(g\)，使得\(G=\left\{g^k ; k \in \mathbb{Z}\right\}\) ，则称\(G\)关于运算"\(\cdot\)"形成一个循环群。\(g\)叫作群的【生成元】(generator)。
- 循环群也分为有限循环群和无限循环群。若\(G\)为\(g\)生成的\(n\)阶有限循环群，那么集合\(G\) 可以写成 \(\left\{e, g, g^2, g^3, \ldots, g^{n-1}\right\}\)。其中\(e=g^0=g^n ， e\)为群的单位元。
- 对该循环群群\(G\)里面的任一元素\(a\)不断求幂都可以生成一个群，用符号\(\langle a\rangle\)表示。\(\langle a\rangle\)既可能是有限群，也有可能是无限群。
- \(\langle a\rangle\) 一定是 \(G\) 的子群。因为根据群运算的封闭性， \(\langle a\rangle\) 中的每个元素都属于 \(G\) ；
- \(\langle a\rangle\) 一定是循环群， \(a\) 就是它的一个生成元，元素\(a\) 的阶等于\(\langle a\rangle\) 的阶，进一步的如果还等于\(G\)的阶，那么\(a\)就是循环群\(G\)的生成元；
- 循环群的每个子群一定也是循环群；
- 所有循环群都是阿贝尔群。
- \(6\)次单位根在乘法下形成循环群。\( z\)是生成元而\( z^2\)不是，因为\( z\)的奇数次幂不是\( z^2\)的幂，见上面的图。
【陪集】(Coset)：若\(G\)为群，\(H\)为其子群，而\(g\)为\(G\)中的元素。
- \(H\)在\(G\)中的左陪集(\(H\)关于\(g\)的左陪集)\(g H=\{g h: h\) an element of \(H\}\) for \(g\) in \(G\)；
- \(H\)在\(G\)中的右陪集(\(H\)关于\(g\)的右陪集)\(H g=\{h g: h\) an element of \(H\}\) for \(g\) in \(G\)；
- 当\(H\)是有限子群时，陪集元素个数等于\(H\)的阶；
- 陪集可以为子群本身。如果上面取的\(g \in H\)，就是。如果不属于，就不是；
- 设群\(H\)是群\(G\)的子群，则\(H\)的两个左(或右)陪集或者完全相同，或者没有任何公共元素。
拉格朗日(Lagrange)定理：设\(H\)是有限群\(G\)的子群，则\(H\)的阶整除\(G\)的阶。
例子：\(D_3\)群的子群，我们说过它的子群有\(\{e\}, G,\{e, d, f\},\{e, a\},\{e, b\},\{e, c\}\)，这些子群的阶分别\(1,6,3,2,2,2\)，都是\(6\)的因子。
类与不变子群
【共轭】：群\(G\)中两个元素\(f\)、\(h\)，如果在\(G\)中存在一个\(g\)，使得\(f\)、\(h\)可以通过\(gfg^{-1} = h\)联系起来，则称\(f\)和\(h\)共轭，记为\(f\sim h\)。
- 显然，共轭具有可传递性；
- 类比线性代数：
- 矩阵对角化：矩阵对角化\( A=S \Lambda S^{-1}\)，其中\( S \)是特征列向量，\(\Lambda\)是矩阵\( A\)的特征值矩阵(对角线上)；
- 相似矩阵：矩阵\( A \)和\(B\)均是阶方阵，若存在可逆矩阵\( M\)使得\(B=M^{-1}AM\)成立，则\( A\)和\(B\)为相似矩阵。
- 两者拥有同样的特征值，尽管相应的特征向量一般不同；
- 两者拥有同样的特征多项式；
- 两者的秩相等；
【类】(class)：群\(G\)中所有相互共轭的元素形成的集合，称为群\(G\)的一个类。
而就由类中任何一个元素确定这个类的操作步骤而言，很简单，对一个类中元素\(f\)，取任意\(g\)属于\(G\)，做操作\((gfg^{-1} \)，当\(g\)走遍 \(G\)中所有元素的时候，那么\(f\)的所有同类元素，没跑，就一个个全出现了。(地毯式搜捕)
- 一个群的单位元素自成一类，因为对任意\(f \in G\)，有\(fef^{-1}=e\)；
- Abel群中每个元素自成一类，因为对任意\(f \in G\)，\(h \in G\)，有\(hfh^{-1}=hh^{-1}f=f \)；
- 有限群的每个(共轭)类中元素的个数都是群阶的因子。
【共轭子群】（conjugate subgroup）：设\(H\)和\(K\)是群\(G\)的两个子群，若存在\(g\)属于\(G\)，使得\(K = gHg^{-1} = \{gHg^{-1} |h \in H\} \)。这时称\(H\)和\(K\)是共轭子群。
【不变子群(正规子群)】(Normal subgroup)：设\(N\)是\(G\)的子群，如果\(N\)中所有元素的同类元素都属于\(N\)，则称\(N\)是\(G\)的不变子群。换用wiki上的说法，A subgroup that is invariant under conjugation by members of the group of which it is a part (其实就是\(gNg^{-1}=N\)). In other words, a subgroup \(N\) of the group \(G\) is normal in \(G\) if and only if \(g n g^{-1} \in N\) for all \(g \in G\) and \(n \in N\). The usual notation for this relation is \(N \triangleleft G\).
下列条件等价与子群\(N \)在\(G\)中是正规子群：
- \(\forall n \in \mathrm{N}, g n g^{-1} \in \mathrm{N}\)
- For all \(g \in G\), the left and right cosets are equal: \(gN = Ng\)
- \(N\)是\(G\)的一个共轭类的并集；
- 存在这样一个群同态\(f: G \rightarrow H\)，其中Ker \(f=N \triangleleft G\)；
- 所有 Abel 群的子群都是其不变子群，因为每个元素自成一类， 其同类元素自然在这个子群中。实际上根据阿贝尔群的乘法可交换性，显然有\(gNg^{-1}=N\)。
【商群】(Quotient group)：设群G有不变子群H，由H将G分为{g0H、g1H、g2H、…、giH、…}，把其中每个陪集看成一个新的元素，并由两个陪集中元素相乘得到另一陪集中的元素，定义新的元素乘法，即：
陪集串 → 新元素
g0H f0
g1H f1
g2H f2
⋮ ⋮
giH fi
⋮ ⋮
乘法规则对应关系：gihαgjhβ = gkhγ fifj = fk
这样得到的群{f0、f1、…、fi、…}称为G对其不变子群H的商群，记为G/H。
同构与同态
【同构】(Isomorphism)：若从群G到群F上，存在一一对应的满映射Φ，且这个映射本身保持群的乘法运算规律不变，也就是说G中两个元素乘积的映射，等于群G中两个元素映射的乘积，则称群G与群F同构，记作G≅F。映射Φ称为同构映射，它的作用是：(同构示意图)
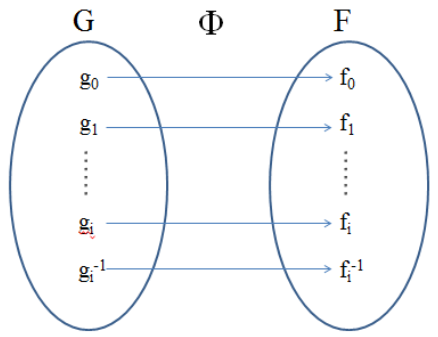
同构的群有完全相同的数学结构，但是具体可指代不同内容。比如2+3=5，在小孩眼里是糖，大人眼里是钱，科研工作者眼中是文章、引用、或者是真正看得懂你的文章的同行的赞。两个群同构的意思可以粗糙地理解为通常意义下所说的“相同结构”。也就是说，忽略组成每一个群的元素的具体属性、乘法操作的具体规定等等，仅仅将“群”的结构性质“抽”出来比较，两个群是相同的。插进一段通俗的比喻，也许可以使你更好地理解“同构”（比喻的例子不是群同构！）：两个3口之家，陈家和李家，都由父、母、子组成。如果我们只感兴趣研究每个家庭成员的性别及相互关系这种结构的话，可以说这两个家庭是“同构”的。尽管陈妈妈已经60岁，李家儿子刚出生，这些细节都无所谓，我们运用数学“抽象”，只看我们需要看的结构，从而认定两个家庭是“同构”的。而具体的陈家和李家，只不过是这种结构的两个不同的具体表示而已。再进一步，如果另有张姓两兄弟，都有老婆儿子，但大家住一起组成6口人的“张家”。那么显然的，陈家和张家不同构。
(1) 从数学角度，两个同构的群有完全相同的结构，没有本质的区别；
(2) 空间反演群{E、I}与二阶循环群{e、a}完全同构；
(3) 三阶置换群与D3群完全同构；
(4) 实数二维空间的旋转群SO(2)和一维复数空间的旋转群U(1)同构的。
将同构的限制弱化，就会得到同态
【同态】(Homomorphism)：设存在从群G到群F的满映射(注意，没有一对一，而是多对一，不可逆)Φ，且这个映射本身保持群的乘法运算规律不变，也就是说群G众两个元素乘积的映射，等于群G中两个元素映射的乘积，则称群G与群F同态，记作G~F。映射称为同态映射Φ，其作用是：(同态示意图)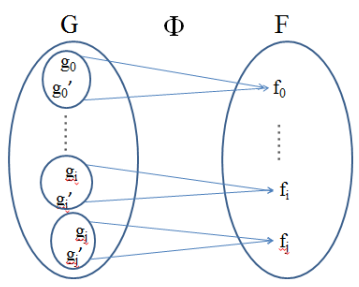
数学上，关于同态的严格定义是没有满映射这个要求的，他们唯一的要求是保持乘法规则。在我们的应用中，我们关注的是群的表示。在群表示的讨论中，满映射这个要求存在。
在数学中，给定两个群\((G, *)\)和\((H, \cdot)\)，从\((G, *)\)到\((H, \cdot)\)的群同态是函数\(h:(G, *) \rightarrow(H, \cdot)\)使得对于所有\(G\)中的\(u\)和\(v\)下述等式成立$$ h(u * v)=h(u) \cdot h(v) $$根据这一性质可以推断出\(h\)将\( G\)中的单位元映射到\(H\)中的单位元，逆元映射到逆元，即$$ \begin{aligned} &h\left(e_G\right)=e_H \\ &h\left(u^{-1}\right)=h(u)^{-1} \end{aligned} $$Hence one can say that \(h\) "is compatible with the group structure"(兼容于群结构).
补充
【同态核】(kernel of a homomorphism)：设G1与G2同态，那么G1中与G2的单位元素对应的所有元素的集合称为同态核。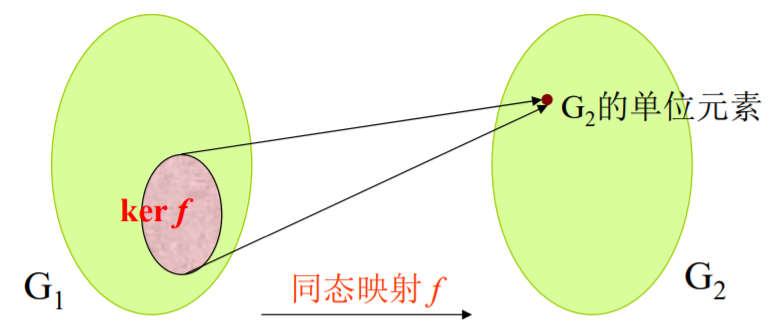
这里讨论一下核：
(1) 从线性代数的角度：核,一般将矩阵看成线性映射时,映射到0的所有向量。单纯理解矩阵时,可看成Ax=0的所有解,称为A的核,即ker(A)。
(2) 从假设G1，G2是群，f: G1 → G2是同态映射，定义集合\(\operatorname{ker} f=\left\{\mathbf{x} \mid \mathbf{x} \in \mathbf{G}_{1} \text {, 且 } f(\mathbf{x})=\mathbf{e}_{2}\right\}\)其中 e2是G2的单位元素，ker f称为同态核，如上图。
(3) 显然，ker f是正规子群。
同态核定理：设G与F同态，则有：补充
1) 同态核H是G的不变子群；
2) 商群G/H与F同构。
自同构映射：
内自同构映射：
例子-1：D3群与二阶循环群Z2同态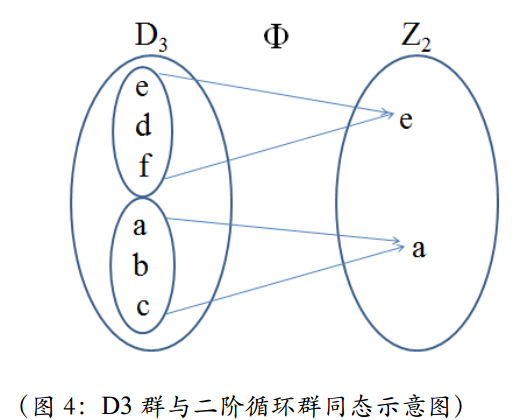
在这里，很显然{e、d、f}是同态核。如果大家翻到D3群乘法表的那一页的话，很容易看到一种超结构，就是6 × 6的部分可以化成以3 × 3为基本单元的2 × 2的结构。这个就是二阶循环群的超结构了。
例子-2：三阶循环群Z3={e、a、a2}的自同构群是什么样的?
变换群
变换群是以变换为群元形成的群，对它的讨论分变换对象以及变换操作。之所以把变换群单独拎出来讲，是因为它是我们物理问题研究中最常用到的一种群，包括我们后面要讲的点群、空间群，SO(3)群，它们都是些变换操作的集合，变换的对象是我们感兴趣的物理系统。在这些章节的讨论中，我们会用到变换群的一些概念。先看几个定义。
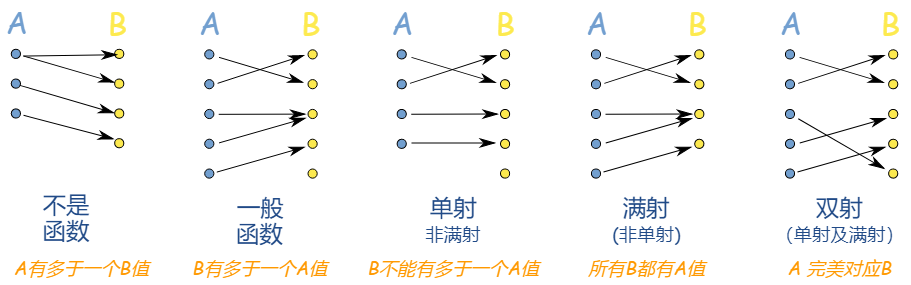
【变换】(Transformation)：A是非空集合，f: A → A称为A上的一个变换，集合A上的一一变换。
- 经常讨论的是一一变换，即f是双射；
- 变换就是函数，变换的"乘法"就是函数复合运算；
- 集合A上的一一变换关于变换乘法构成的群称为变换群。
【变换群】(Transformation groups)：设A是任意的非空集合，A上所有的一一变换一定构成群。
- 封闭性：双射的复合仍是双射；
- 结合律：变换乘法是关系复合运算的特例；
- 单位元：\(f: \mathrm{A} \rightarrow \mathrm{A}, \forall \mathrm{x} \in \mathrm{A}, f(\mathrm{x})=\mathrm{x}\) 满足对于任意\(g: \mathrm{A} \rightarrow \mathrm{A}, f \circ g=g \circ f=g\)(恒等变换)；
- 逆元素：任㚆双射 \(g: \mathrm{A} \rightarrow \mathrm{A}\) 均有反函数 \(g^{-1}: \mathrm{A} \rightarrow \mathrm{A}\), 即其逆元素。
变换群的例子：G是R上所有如下形式的变换构成的集合
\(\left\{f_{\mathrm{a}, \mathrm{b}} \mid f_{\mathrm{a}, \mathrm{b}}(\mathrm{x})=\mathrm{ax}+\mathrm{b} \text {,其中} \mathrm{a}, \mathrm{b} \text { 是有理数, } \mathrm{a} \neq 0\right\}\)，则 G是变换群。可以用封闭性、结合律、单位元、逆元素去检验。
直积与半直积/直和
直积和半直积可以用来剖析群的结构。直积的结构强，适用范围较小；半直积结构弱，适用性更强，本节的学习重点是半直积。
直积
由两个已知的群G1与G2，来构造一个新群G，而这个新群的元素，是由G1群和G2群中的元素结合而成: gα,βgα′,β′ = (g1αg2β)(g1α′g2β′)＝ (g1αg1α′g2βg2β′)。两个有序对中，属于G1的两个元素相乘，得到一个G1元素，属于G2的两个元素相乘，得到一个G2元素，再由这个G1与这个G2元素形成的有序对。这样得到的群就是G1与G2的直积群。
In group theory one can define the direct product of two groups \((G, \circ)\) and \((H, \cdot)\), denoted by \(G \times H\). It is defined as follows: (来自Wiki)
(1) the set of the elements of the new group is the Cartesian product of the sets of elements of \(G\) and \(H\), that is \(\{(g, h): g \in G, h \in H\}\)
(2) on these elements put an operation, defined element-wise:
\((g, h) \times\left(g^{\prime}, h^{\prime}\right)=\left(g \circ g^{\prime}, h \cdot h^{\prime}\right)\)
【直积因子】：一个群G，有两个子群G1与G2，如果G中的任何一个元素都可以唯一地表示为gαβ = g1αg2β，其中g1α属于G1、g2β属于G2，且g1αg2β = g2βg1α，则G是G1与G2的直积，G1与G2称为G的直积因子。
直积群这个概念有实际意义的情况是G1与G2中的元素有乘法，且互易，也就是从G可以找到其直积因子G1与G2的情况。 同时需要说明的是这个G1与G2本身不要求是Abel群，定义只要求它们之间乘法互易。同时，G1、G2与G之间存在两个结构关系，
1) 它们只有一个公共元素e；
2) 它们都是G的不变子群。
例子-1：参考知乎，所谓直积是针对线性空间的一个概念，可参考《线性代数》或《高等代数》的教材。最简单的一个例子：\(\mathbf{R}^{2}\)可表示为\(x\)轴与\(y\)轴的直积：\((x, y)=x(1,0)+y(0,1), \quad \forall(x, y) \in \mathbf{R}^{2}\)，当一个线性空间可分成\(k\)个除了零元素外没有其它公共元素的线性子空间的话，那么这个线性空间可表示为这\(k\)个线性子空间的直积。
半直积
直和
For abelian groups which are written additively, it may also be called the direct sum of two groups, denoted by \(G \oplus H\).
The direct sum of abelian groups is a prototypical example of a direct sum. Given two such groups \((A, \circ)\) and \((B, \bullet)\), their direct sum \(A \oplus B\) is the same as their direct product. That is, the underlying set is the Cartesian product \(A \times B\) and the group operation \(\cdot\) is defined component-wise:$$ \left(a_{1}, b_{1}\right) \cdot\left(a_{2}, b_{2}\right)=\left(a_{1} \circ a_{2}, b_{1} \bullet b_{2}\right) $$This definition generalizes to direct sums of finitely many abelian groups.
从矩阵的角度来理解直和更直观，直和可以由任何一对矩阵形成，其定义为：$$ A \oplus B=\left[\begin{array}{cc} A & 0 \\ 0 & B \end{array}\right]=\left[\begin{array}{cccccc} a_{11} & \cdots & a_{1 n} & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_{m 1} & \cdots & a_{m n} & 0 & \cdots & 0 \\ 0 & \cdots & 0 & b_{11} & \cdots & b_{1 q} \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & b_{p 1} & \cdots & b_{p q} \end{array}\right] $$一般地, \(n\) 个矩阵的直和可以写成:$$ \bigoplus_{i=1}^{n} A_{i}=\operatorname{diag}\left(A_{1}, A_{2}, A_{3}, \ldots, A_{n}\right)=\left[\begin{array}{llll} A_{1} & & & \\ & A_{2} & & \\ & & \ddots & \\ & & & A_{n} \end{array}\right] $$实例$$ \left[\begin{array}{lll} 1 & 3 & 2 \\ 2 & 3 & 1 \end{array}\right] \oplus\left[\begin{array}{ll} 1 & 6 \\ 0 & 1 \end{array}\right]=\left[\begin{array}{lllll} 1 & 3 & 2 & 0 & 0 \\ 2 & 3 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 6 \\ 0 & 0 & 0 & 0 & 1 \end{array}\right] $$
其他积
【笛卡尔积】(Cartesian product)在数学中，两个集合\(X\)和\(Y\)的笛卡尔积，又称为直积，在集合论中表示为\(X \times Y\)，是所有可能的有序对组成的集合，其中有序对的第一个对象是\(X\)中的成员，第而个对象是\(Y\)中的成员：$$X \times Y=\{(x, y) \mid x \in X \wedge y \in Y\}$$举个实例，如果集合\(X\)是13个元素的点数集合\(\{A, K, Q, J, 10,9,8,7,6,5,4,3,2\}\)，而集合\(Y\)是4个元素的花色集合{♠, ♥, ♦, ♣}，则这两个集合的笛卡儿积是有52个元素的标准扑克牌的集合，里面的元素比如(A, ♠)。
笛卡尔积的特点和性质：
- 对于任意集合\( A\)，根据定义有\(A \times \varnothing=\varnothing \times A=\varnothing\)；
- 一般来说笛卡儿积不满足交换律和结合律；
- 函数的笛卡儿积：如果\(f\)是从\( A\)到\( B\)的函数，而\( g\)是从\( X\)到\(Y\)的函数，则它们的笛卡儿积\(f \times g\)是从\( A \times X\)到\(B \times Y\)的函数，带有\((f \times g)(a, x)=(f(a), g(x))\)
张量积：
参考资料：
1. 知乎-「张量积」是否可以作为「直积」的同义词使用？
2. 笛卡儿积，直和和张量积，以及对直积的争议
克罗内克积(Kronecker product，张量积的特殊形式)：克罗内克积是两个任意大小的矩阵间的运算，表示为\(\otimes \)。克罗内克积是外积从向量到矩阵的推广，也是张量积在标准基下的矩阵表示。如果A是一个\( m \times n \)矩阵，B是一个\( p \times q\)矩阵，则克罗克内积\( A \otimes B\)是一个\( m p \times n q\)的分块矩阵。$$A \otimes B=\left[\begin{array}{ccc} a_{11} B & \cdots & a_{1 n} B \\ \vdots & \ddots & \vdots \\ a_{m 1} B & \cdots & a_{m n} B \end{array}\right]$$例子$$\left[\begin{array}{ll} 1 & 2 \\ 3 & 1 \end{array}\right] \otimes\left[\begin{array}{ll} 0 & 3 \\ 2 & 1 \end{array}\right]=\left[\begin{array}{llll} 1 \cdot 0 & 1 \cdot 3 & 2 \cdot 0 & 2 \cdot 3 \\ 1 \cdot 2 & 1 \cdot 1 & 2 \cdot 2 & 2 \cdot 1 \\ 3 \cdot 0 & 3 \cdot 3 & 1 \cdot 0 & 1 \cdot 3 \\ 3 \cdot 2 & 3 \cdot 1 & 1 \cdot 2 & 1 \cdot 1 \end{array}\right]=\left[\begin{array}{llll} 0 & 3 & 0 & 6 \\ 2 & 1 & 4 & 2 \\ 0 & 9 & 0 & 3 \\ 6 & 3 & 2 & 1 \end{array}\right]$$
外积(Outer product)：克罗内克积是外积从向量到矩阵的推广，向量的外积是克罗内克积的特殊情况，与外积相对，两向量的内积结果为标量。给定\(m \times 1\)列向量\(\mathbf{u}\)和\(1 \times n\)行向量\(\mathbf{v}\) ，它们的外积\(\mathbf{u} \otimes \mathbf{v}\)被定义为\(m \times n\)矩阵\(\mathbf{A}\)，结果出自：
\(\mathbf{u} \otimes \mathbf{v}=\mathbf{A}=\mathbf{u v}\)
这里的张量积就是向量的乘法。$$\left[\begin{array}{l} b_{1} \\ b_{2} \\ b_{3} \\ b_{4} \end{array}\right] \otimes\left[\begin{array}{lll} a_{1} & a_{2} & a_{3} \end{array}\right]=\left[\begin{array}{lll} a_{1} b_{1} & a_{2} b_{1} & a_{3} b_{1} \\ a_{1} b_{2} & a_{2} b_{2} & a_{3} b_{2} \\ a_{1} b_{3} & a_{2} b_{3} & a_{3} b_{3} \\ a_{1} b_{4} & a_{2} b_{4} & a_{3} b_{4} \end{array}\right]$$
注意：
(1) 上面关于外积的介绍是维基中文页面上的，在英文页面内容有些差异，但是不影响我们理解，英文页面关于外积的公式为(两个初始的向量都是列向量)：\(\mathbf{u} \otimes \mathbf{v}=\mathbf{u v}^{\top}=\left[\begin{array}{l} u_{1} \\ u_{2} \\ u_{3} \\ u_{4} \end{array}\right]\left[\begin{array}{lll} v_{1} & v_{2} & v_{3} \end{array}\right]=\left[\begin{array}{lll} u_{1} v_{1} & u_{1} v_{2} & u_{1} v_{3} \\ u_{2} v_{1} & u_{2} v_{2} & u_{2} v_{3} \\ u_{3} v_{1} & u_{3} v_{2} & u_{3} v_{3} \\ u_{4} v_{1} & u_{4} v_{2} & u_{4} v_{3} \end{array}\right]\)
(2) For complex vectors, it is often useful to take the conjugate transpose of \(\mathbf{v}\) \(\mathbf{u} \otimes \mathbf{v}=\mathbf{uv}^{\dagger}=\mathbf{u}\left(\mathbf{v}^{\top}\right)^{*}\)
外积辨析
注意：中文翻译的“外积”对应的英文可能是不同的概念
(1) In linear algebra, the outer product of two coordinate vectors is a matrix. If the two vectors have dimensions n and m, then their outer product is an n × m matrix. More generally, given two tensors (multidimensional arrays of numbers), their outer product is a tensor. The outer product of tensors is also referred to as their tensor product, and can be used to define the tensor algebra.
(2) 解析几何领域的cross product也翻译成外积，对应着向量叉乘的概念，用右手法则，\(\vec{a} \times \vec{b}=\left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{array}\right|\)
内积辨析：
(1) 在数学中，点积(Dot product) = 数量积 = 标量积 (Scalar Product)。点积是一种接受两个等长的数字序列（通常是坐标向量）、返回单个数字的代数运算。在欧几里得几何中，两个笛卡尔坐标向量的点积常称为内积。
(2) 内积是相对于内积空间来说的，它的含义要远远高于一般的「点积」或者「数量积」。内积空间由欧几里得空间抽象而来，内积是点积的抽象。????????
注： 数学上，欧几里得几何是平面和三维空间中常见的几何，基于点线面假设。欧几里得几何有时就指二维平面上的几何，即平面几何，三维空间的欧几里得几何通常叫做立体几何，更高维度的几何请参看欧几里得空间。
参考：
1. 知乎-内积、点积、数量积有何区别？
2. 向量空间、内积空间、欧式空间以及希尔伯特空间的关系
习题与思考
群表示理论
群表示
群表示的核心概念：是群G到线性空间V上的线性变换群L(V, C)的同态映射关系。也就是说表示是同态映射关系，它存在于一个我们要研究的抽象群和一个线性空间的线性变换群之间，其中的线性变换群可以简单地理解为矩阵群。
【线性空间】：它是定义在数域K(可以是实数域R，也可以是复数域C)上的向量集合 V={x、y、z、…..}，在V中可以定义加法和数乘两种运算，设x、y、z属于V，a、b、c属于K，向量加法和数乘具有封闭性，且满足八条规则。
- 向量线性无关：线性空间V中，如果一组向量的线性组合只有当所有的系数都为零的时候，该组合才为零，那么说这组向量线性无关；
- 线性空间的维数：线性空间中线性无关的向量的最大个数m，称为线性空间的维数，记为dim V=m；
- 基矢和线性表示：设V是n维线性空间，则V中任意一组n个线性无关的向量，都可以构成V的基矢，空间中任意矢量都可以表示成为这n个基矢的线性组合$$ \vec{X}=\sum_{i=1}^{\mathrm{n}} x_i \vec{e}_i=\left(\vec{e}_1, \vec{e}_2, \cdots \cdots, \vec{e}_{\mathrm{n}}\right)\left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ \vdots \\ x_{\mathrm{n}} \end{array}\right) $$其中我们用\([\vec{X}]\)表示向量在这组基上的坐标，就是上面等式右边的那个列向量。由此定义，显然有$$ \left[\vec{e}_1\right]=\left(\begin{array}{c} 1 \\ 0 \\ \vdots \\ \vdots \\ 0 \end{array}\right),\left[\vec{e}_2\right]=\left(\begin{array}{c} 0 \\ 1 \\ \vdots \\ \vdots \\ 0 \end{array}\right), \cdots \cdots,\left[\vec{e}_{\mathrm{n}}\right]=\left(\begin{array}{c} 0 \\ 0 \\ \vdots \\ \vdots \\ 1 \end{array}\right) $$
线性变换：\(\forall \vec{x}, \vec{y} \in V, a \in K, A: V \rightarrow V, A(\vec{x}) \in V, A(a \vec{x}+\vec{y})=a A(\vec{x})+A(\vec{y})\)。基变换和坐标变换，可以直接参考我的线性代数笔记—3。
【线性变换群】：定义两个线性变换的乘法为两个线性变换相继作用，则 n 维复线性空间 V 上的全部非奇异线性变换在此乘法下构成一个群，称为 n 维复 一般线性群 GL(V, C)，其子群 L(V, C)称为 V 上的线性变换群。
在这里需要对“非奇异”这个要求做个说明。为什么要非奇异，因为我们这个线性变换群或矩阵群是一个群，如果奇异了（矩阵的行列式为零），这个集合不能形成群。这个就像在实数乘法作为群元乘法的时候，所有实数不能形成一个群，因为零没有逆元，但所有非零实数就可以形成一个群，是一个道理。
【群表示】：设有群 G，如存在一个从 G 到 n 维线性空间 V 上的线性变换 群 L(V,C)的同态映射 A，则称 A 是群 G 的一个线性表示，V 为表示空间，n 是 表示的维数。记为：
等价表示、不可约表示、酉表示
群代数与正则表示
有限群表示理论
特征标理论
新表示的构成
习题与思考
点群与空间群
点群基础
第一类点群
第二类点群
晶体点群与空间群
晶体点群的不可约表示
习题与思考
群论与量子力学
哈密顿算符群与相关定理
围绕引起的能级分裂
投影算符与久期行列式的对角化
矩阵元定理与选择定则、电偶极跃迁
红外、拉曼谱、和频光谱
的
平移不变形与Bloch定理
布里渊区与晶格对称性
时间反演对称性
习题与思考
转动群
SO(3)群与二维特殊酉群SU(2)
- SO(3) 群
在经典力学与几何学里，所有环绕着三维欧几里得空间的原点旋转，组成的群定义为旋转群。根据定义，围绕着原点的旋转是一个保持空间取向的线性变换。
-
- 两个旋转的复合等于一个旋转；
- 每个旋转都有一个独特的逆旋转；
- 零角度的旋转是单位圆；
- 旋转满足结合律。
由于符合上述四个要求，所有旋转的集合是一个群。进一步地，旋转群拥有一个天然流形结构。对于这流形结构，旋转群的运算是光滑的；所以，它是一个李群。旋转群时常会用 SO(3) 来表示。
- 李群
-
- 是指具有群结构的光滑微分流形，其群作用与微分结构相容。
- 粗略地说，李群是连续的群，也即其元素可由几个实参数描述。因此，李群为连续对称性的概念提供了一个自然的模型，例如三维旋转对称性。整数的加法的例子显然不是连续的，因而它不是李群。
-
二维平面旋转群SO(2)：在线性代数中，我们知道对于线性变换 \(T: \mathbf{R}^{2} \rightarrow \mathbf{R}^{2}\)的旋转操作(假设逆时针)，将\( \mathbf{v} \)旋转\( \theta\)后得到的新向量为\(T(\mathbf{v})=R( \theta) \mathbf{v}\)，其中旋转矩阵\(R( \theta)\)为$$ R(\theta)=\left[\begin{array}{rr} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] $$
SO(2)是实数二维空间的旋转群，它其实是和一维复数空间的旋转群U(1)同构的，具体可以参考：
(1) 统一路-6-奇妙的旋转1-张天蓉
(2) 私房笔记 | SO(2)群与欧拉公式的证明-PeiLingX
(3) MP2：平面旋转群SO(2)-jRONI
三维空间的旋转旋转群SO(3)的特点
(1) 保长和保角
旋转前后，任意向量的长度不变，任意两个向量之间的角度不变。任意两个向量之间的内积为$$ \mathbf{u} \cdot \mathbf{v}=\frac{1}{2}\left(\|\mathbf{u}+\mathbf{v}\|^{2}-\|\mathbf{u}\|^{2}-\|\mathbf{v}\|^{2}\right) $$显然如果对这两个向量做保长的旋转(行列式为1的旋转矩阵分别作用在两个向量上)，显然旋转后向量的乘积不变，因而保角。
(2) 旋转矩阵
SO(2)中的旋转是围绕中心原点，而SO(3)中的旋转则是围绕特定旋转轴旋转。举例来说counterclockwise rotation about the positive \( z\)-axis by angle \( \varphi \) is given by$$ R_{z}(\varphi)=\left[\begin{array}{ccc} \cos \varphi & -\sin \varphi & 0 \\ \sin \varphi & \cos \varphi & 0 \\ 0 & 0 & 1 \end{array}\right] $$
拓展：
(1) 欧拉角-wiki、欧拉旋转定理-wiki
(2) 三維空間的旋轉矩陣-线性代数启示录
SO(3)群与SU(2)群的不可约表示
双群与自旋半奇数粒子的旋量波函数
Clebsch-Gordan系数
置换群
n阶置换群
(n元)置换：有限集合S上的双射σ: S → S称为S上的n元置换，记为$$\sigma=\left(\begin{array}{cccc} 1 & 2 & \ldots & n \\ \sigma(1) & \sigma(2) & \ldots & \sigma(n) \end{array}\right)$$
置换的例子：集合S={1,2,3}上共有6个不同的置换，它们的集合记为S3 ：$$\begin{aligned} &e=\left(\begin{array}{lll} 1 & 2 & 3 \\ 1 & 2 & 3 \end{array}\right) \quad \alpha=\left(\begin{array}{lll} 1 & 2 & 3 \\ 2 & 3 & 1 \end{array}\right) \quad \beta=\left(\begin{array}{lll} 1 & 2 & 3 \\ 3 & 1 & 2 \end{array}\right) \\ &\gamma=\left(\begin{array}{lll} 1 & 2 & 3 \\ 1 & 3 & 2 \end{array}\right) \quad \delta=\left(\begin{array}{lll} 1 & 2 & 3 \\ 3 & 2 & 1 \end{array}\right) \quad \varepsilon=\left(\begin{array}{lll} 1 & 2 & 3 \\ 2 & 1 & 3 \end{array}\right) \end{aligned}$$S3是最小的非交换群，注意质数阶群一定是可交换群。
参考陶先平—PPT